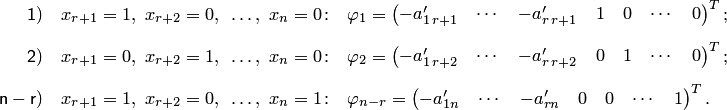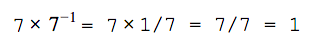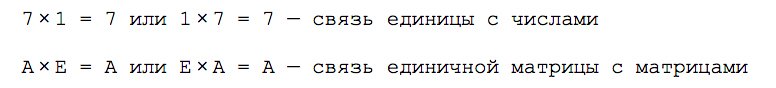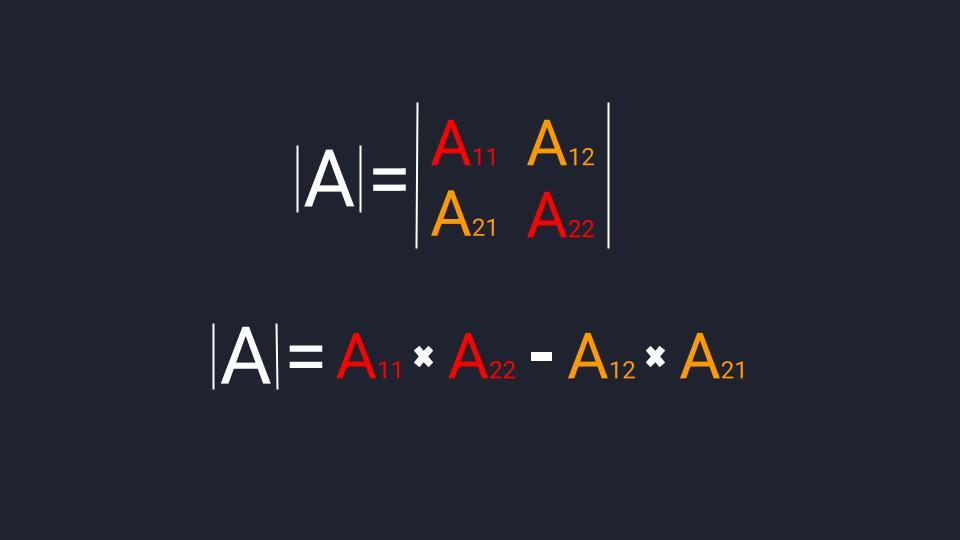Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
Способы нахождения обратной матрицы
Пусть
дана квадратная матрица .
Требуется найти обратную матрицу.
Первый
способ. В
теореме 4.1 существования и единственности
обратной матрицы указан один из способов
ее нахождения.
1. Вычислить
определитель данной
матрицы. Если,
то обратной матрицы не существует
(матрицавырожденная).
2. Составить
матрицу из
алгебраических дополненийэлементов
матрицы.
3. Транспонируя
матрицу ,
получить присоединенную матрицу.
4. Найти
обратную матрицу (4.1), разделив все
элементы присоединенной матрицы на
определитель
Второй
способ. Для
нахождения обратной матрицы можно
использовать элементарные преобразования.
1. Составить
блочную матрицу ,
приписав к данной матрицеединичную
матрицу того же порядка.
2. При
помощи элементарных преобразований,
выполняемых над строками матрицы ,
привести ее левый блокк
простейшему виду.
При этом блочная матрица приводится к
виду,
где—
квадратная матрица, полученная в
результате преобразований из единичной
матрицы.
3. Если ,
то блокравен
обратной матрице, т.е..
Если,
то матрицане
имеет обратной.
В
самом деле, при помощи элементарных
преобразований строк матрицы можно
привести ее левый блокк
упрощенному виду(см.
рис. 1.5). При этом блочная матрицапреобразуется
к виду,
где—
элементарная матрица, удовлетворяющая
равенству.
Если матрицаневырожденная,
то согласно п.2 замечаний 3.3 ее упрощенный
вид совпадает с единичной матрицей.
Тогда из равенстваследует,
что.
Если же матрицавырожденная,
то ее упрощенный видотличается
от единичной матрицы, а матрицане
имеет обратной.
11.Матричные
уравнения и их решение. Матричная форма
записи СЛАУ. Матричный способ (метод
обратной матрицы) решения СЛАУ и условия
его применимости.
Матричными
уравнениями называются уравнения вида
:
A*X=C;
X*A=C;
A*X*B=C
где матрица А,В,С известны ,матрица Х
не известна, если матрицы А и В не
вырождены, то решения исходных матриц
запишется в соответственном виде :
Х=А-1
*С; Х=С*А-1;
Х=А-1*С*В-1Матричная
форма записи систем линейных алгебраических
уравнений.С
каждой СЛАУ можно связать несколько
матриц; более того – саму СЛАУ можно
записать в виде матричного уравнения.
Для СЛАУ (1) рассмотрим такие матрицы:
Матрица A называется матрицей
системы.
Элементы данной матрицы представляют
собой коэффициенты заданной СЛАУ.
Матрица A˜ называется расширенной
матрицей системы.
Её получают добавлением к матрице
системы столбца, содержащего свободные
члены b1,b2,…,bm.
Обычно этот столбец отделяют вертикальной
чертой, – для наглядности.
Матрица-столбец B называется матрицей
свободных членов,
а матрица-столбец X – матрицей
неизвестных.
Используя
введённые выше обозначения, СЛАУ (1)
можно записать в форме матричного
уравнения: A⋅X=B.
Примечание
Матрицы,
связанные с системой, можно записать
различными способами: всё зависит от
порядка следования переменных и уравнений
рассматриваемой СЛАУ. Но в любом случае
порядок следования неизвестных в каждом
уравнении заданной СЛАУ должен быть
одинаков .
Матричный
метод подходит для решения СЛАУ, в
которых количество уравнений совпадает
с числом неизвестных переменных и
определитель основной матрицы системы
отличен от нуля. Если система содержит
больше трех уравнений, то нахождение
обратной матрицы требует значительных
вычислительных усилий, поэтому, в этом
случае целесообразно использовать для
решения метод
Гаусса.
12.Однородные
СЛАУ, условия существования их ненулевых
решений. Свойства частных решений
однородных СЛАУ.
Линейное
уравнение называется однородным, если
его свободный член равен нулю, и
неоднородным в противном случае. Система,
состоящая из однородных уравнений,
называется однородной и имеет общий
вид:
13.Понятие
линейной независимости и зависимости
частных решений однородной СЛАУ.
Фундаментальная система решений (ФСР)
и её нахождение. Представление общего
решения однородной СЛАУ через ФСР.
Система
функций y1(x), y2(x),
…, yn(x) называется линейно
зависимой на
интервале (a, b), если
существует набор постоянных коэффициентов ,
не равных нулю одновременно, таких, что
линейная комбинация этих функций
тождественно равна нулю
на (a, b): для
.
Если
равенство для
возможно
только при ,
система функций y1(x), y2(x),
…, yn(x) называется линейно
независимой на
интервале (a, b).
Другими
словами, функции y1(x), y2(x),
…, yn(x) линейно
зависимы на
интервале (a, b),
если существует равная нулю на (a, b) их
нетривиальная линейная комбинация.
Функции y1(x),y2(x),
…, yn(x) линейно
независимы на
интервале (a, b),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a, b).
Фундаментальной
системой решений (ФСР) однородной
СЛАУ называется базис этой системы
столбцов.
Количество
элементов в ФСР равно количеству
неизвестных системы минус ранг
матрицы системы.
Любое решение исходной системы есть
линейная комбинация решений ФСР.
Теорема
Общее
решение неоднородной СЛАУ равно сумме
частного решения неоднородной СЛАУ и
общего решения соответствующей однородной
СЛАУ.
1. Если
столбцы —
решения однородной системы уравнений,
то любая их линейная комбинациятакже
является решением однородной системы.
В
самом деле, из равенств следует,
что
т.е.
линейная комбинация решений является
решением однородной системы.
2. Если
ранг матрицы однородной системы равен ,
то система имеетлинейно
независимых решений.
Действительно,
по формулам (5.13) общего решения однородной
системы найдем частных
решений,
придавая свободным переменным
следующиестандартные
наборы значений (всякий
раз полагая, что одна из свободных
переменных равна единице, а остальные
— равны нулю):
которые
линейно независимы. В самом деле, если
из этих столбцов составить матрицу, то
последние ее
строк образуют единичную матрицу.
Следовательно, минор, расположенный в
последнихстроках
не равен нулю (он равен единице), т.е.
является базисным. Поэтому ранг матрицы
будет равен.
Значит, все столбцы этой матрицы линейно
независимы (см. теорему 3.4).
Любая
совокупность линейно
независимых решенийоднородной
системы называетсяфундаментальной
системой (совокупностью) решений.
14
Минор

порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы.
Минором
порядка k матрицы А называется детерминант
некоторой ее квадратной подматрицы
порядка k.
В
матрице А размеров m x n минор порядка r
называется базисным, если он отличен
от нуля, а все миноры большего порядка,
если они существуют, равны нулю.
Столбцы
и строки матрицы А, на пересечении
которых стоит базисный минор, называются
базисными столбцами и строками А.
Теорема
1. (О ранге матрицы). У любой матрицы
минорный ранг равен строчному рангу и
равен столбцовому рангу.
Теорема
2.(О базисном миноре). Каждый столбец
матрицы раскладывается в линейную
комбинацию ее базисных столбцов.
Рангом
матрицы (или минорным рангом) называется
порядок базисного минора или, иначе,
самый большой порядок, для которого
существуют отличные от нуля миноры.
Ранг нулевой матрицы по определению
считают 0.
Отметим
два очевидных свойства минорного ранга.
1)
Ранг матрицы не меняется при
транспонировании, так как при
транспонировании матрицы все ее
подматрицы транспонируются и миноры
не меняются.
2)
Если А’-подматрица матрицы А, то ранг
А’ не превосходит ранга А, так как
ненулевой минор, входящий в А’, входит
и в А.
15.Понятие

арифметического вектора. Равенство
векторов. Действия над векторами
(сложение, вычитание, умножение на число,
умножение на матрицу). Линейная комбинация
векторов.
Упорядоченная
совокупность n действительных
или комплексных чисел называется n-мерным
вектором.
Числа называются координатами
вектора.
Два
(ненулевых) вектора a и b равны,
если они равнонаправлены и имеют один
и тот же модуль. Все нулевые векторы
считаются равными. Во всех остальных
случаях векторы не равны.
Сложение
векторов. Для
сложения векторов есть два способа.1.
Правило параллелограмма. Чтобы сложить
векторы и
,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторови
.
2.
Второй способ сложения векторов —
правило треугольника. Возьмем те же
векторы и
.
К концу первого вектора пристроим
начало второго. Теперь соединим начало
первого и конец второго. Это и есть
сумма векторов и
.
По тому же
правилу можно сложить и несколько
векторов. Пристраиваем их один
за другим, а затем соединяем начало
первого с концом последнего.
Вычитание
векторов. Вектор направлен
противоположно вектору.
Длины векторови
равны.
Теперь
понятно, что такое вычитание векторов.
Разность векторов и
—
это сумма вектора и вектора
.
Умножение
вектора на число
При
умножении вектора на число k получается
вектор, длина которого в k раз
отличается от длины.
Он сонаправлен с вектором,
если k больше нуля, и направлен
противоположно,
если k меньше нуля.
Скалярным
произведением векторов называется
произведение длин векторов на косинус
угла между ними.
Если
векторы перпендикулярны, их скалярное
произведение равно нулю.
А вот
так скалярное произведение выражается
через координаты векторов и
.
Линейная
комбинация векторов
Линейной
комбинацией векторов называют
вектор
где –
коэффициенты линейной комбинации.
Если комбинация
называется тривиальной, если –
нетривиальной.
16.Скалярное
произведение арифметических векторов.
Длина вектора и угол между векторами.
Понятие ортогональности векторов.
Скалярным
произведением векторов а и в называется
число,
Скалярное
произведение используется для
вычисления:1)нахождения угла между
ними;2)нахождение проекции
векторов;3)вычисление длины вектора;4)условия
перпендикулярности векторов.
Длиной
отрезка АВ называют расстоянием между
точками А иВ. Угол между векторами А и
В называют угол α=(а,в)
,0≤
α
≤П. На который необходимо повернуть 1
вектор,чтоб его направления совпало с
другим вектором. При условии,что их
начала совпадут.
Ортом
а называется вектор а имеющий единичную
длину и направления а.
17.Система
векторов и её линейная комбинация.
Понятие линейной зависимости и
независимости системы векторов. Теорема
о необходимом и достаточном условиях
линейной зависимости системы векторов.
Система
векторов a1,a2,…,an называется
линейно зависимой, если существуют
числа λ1,λ2,…,λnтакие,
что хотя бы одно из них отлично от нуля
и λ1a1+λ2a2+…+λnan=0. В
противном случае система называется
линейно независимой.
Два
вектора a1 и a2 называются
коллинеарными если их направления
совпадают или противоположны.
Три
вектора a1,a2 и a3 называются
компланарными если они параллельны
некоторой плоскости.
Геометрические
критерии линейной зависимости:
а)
система {a1,a2} линейно
зависима в том и только том случае, когда
векторы a1 и a2 коллинеарны.
б)
система {a1,a2,a3} линейно
зависима в том и только том случае, когда
векторы a1,a2 и a3компланарны.
теорема.
(Необходимое и достаточное условие
линейной зависимости системы векторов.)
Система
векторов векторного пространства является линейно зависимой
тогда и только тогда, когда один из
векторов системы линейно выражается
через другие вектора этой
системы.
Следствие.1.
Система векторов векторного пространства
является линейно независимой тогда и
только тогда, когда ни один из векторов
системы линейно не выражается через
другие вектора этой системы.2. Система
векторов, содержащая нулевой вектор
или два равных вектора, является линейно
зависимой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:
- Познакомились с вектором
- Поделали с ними операции
- Научились определять их параллельность
- Познакомились с матрицами
Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.
С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Читать ли эту статью?
❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.
✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.
Обратное — это как?
В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:
Обратные числа при умножении друг на друга всегда дают единицу:
Обратная матрица
В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.
Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:
Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.
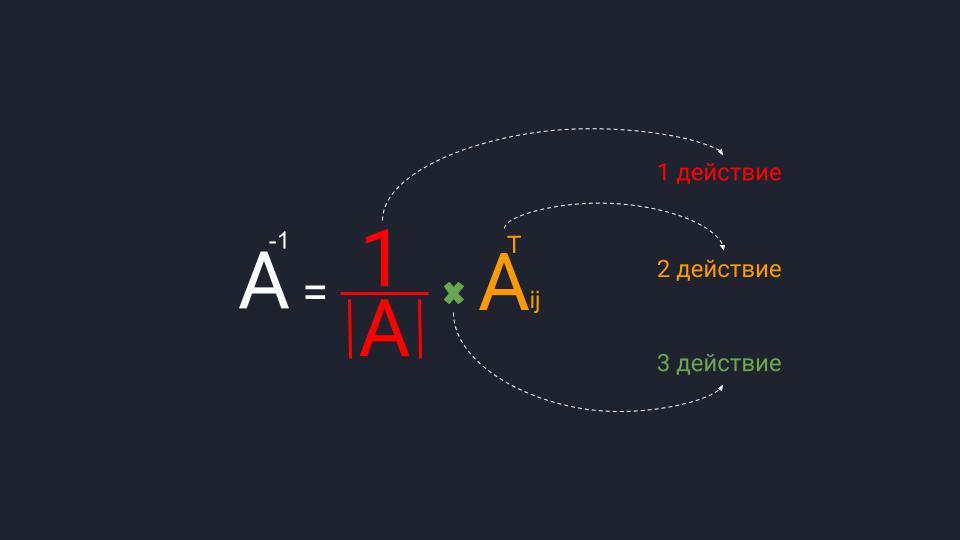
Как рассчитать обратную матрицу
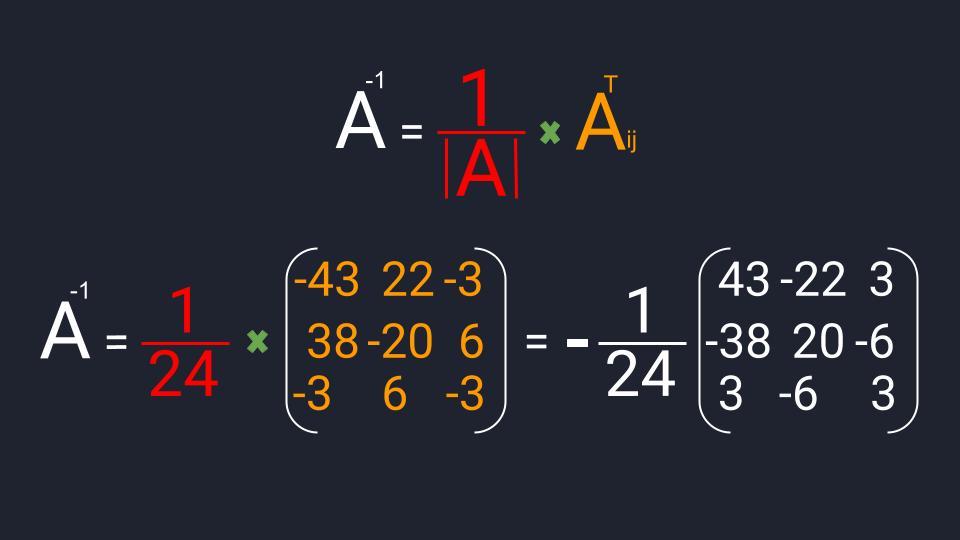
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:
- Разделить единицу на матричный определитель.
- Найти транспонированную матрицу алгебраических дополнений.
- Перемножить полученные значения.
Далее мы по порядку во всём разберёмся.
Определитель — это особое число, которое «определяет» свойства матрицы.
Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.
Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.
Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.
Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.
Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.
Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.
Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.
Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.
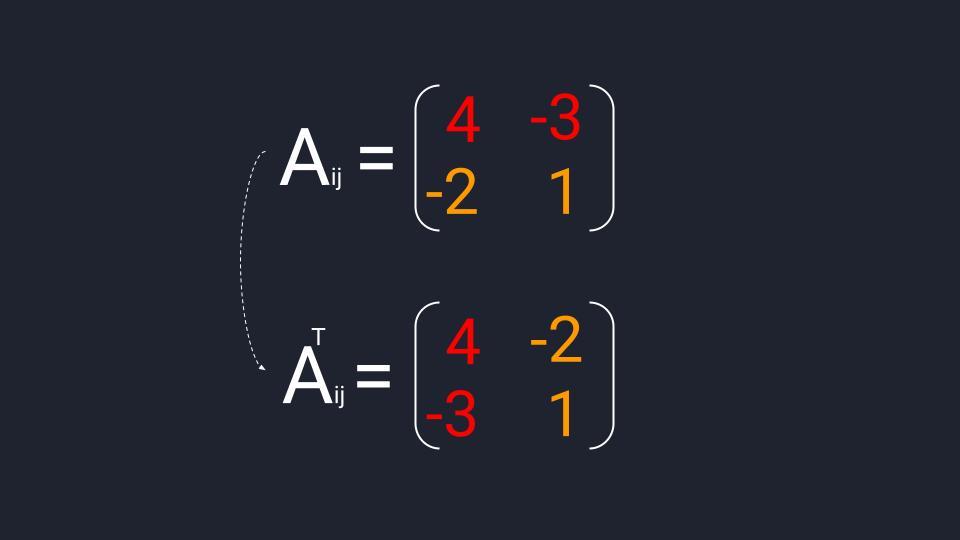
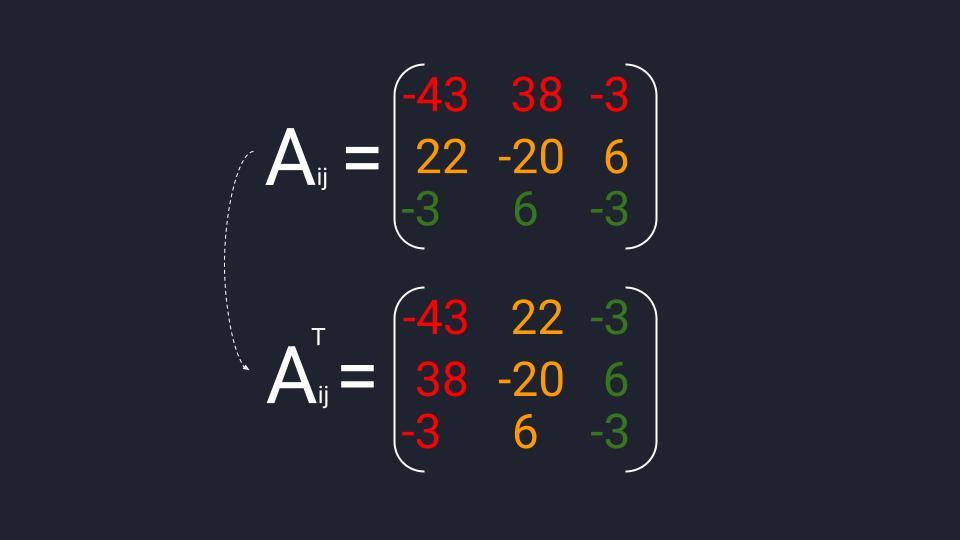
Транспонированная матрица алгебраических дополнений вычисляется в три шага:
- Мы из исходной матрицы находим матрицу миноров.
- Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
- Находим транспонированную матрицу из матрицы алгебраических дополнений.
Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.
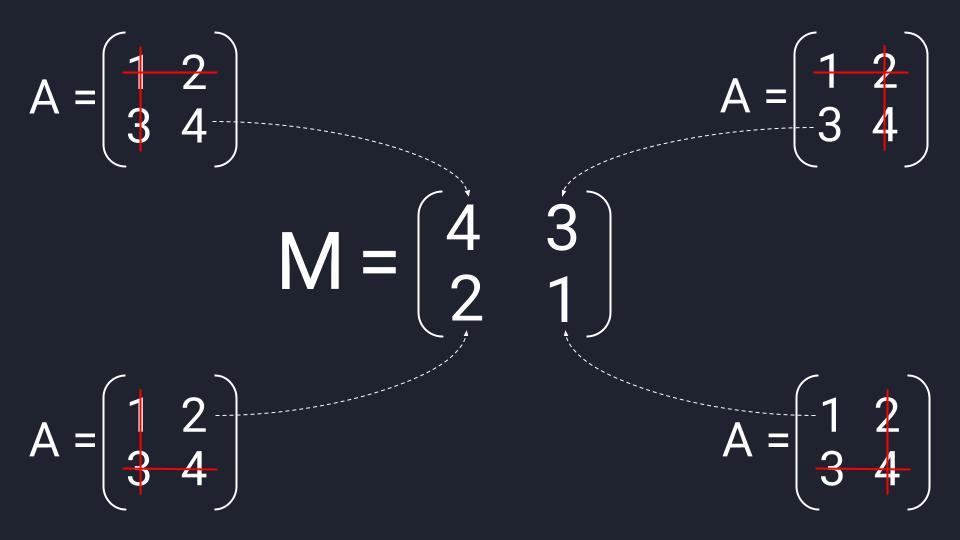
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:
- Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
- Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
- Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
- Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.
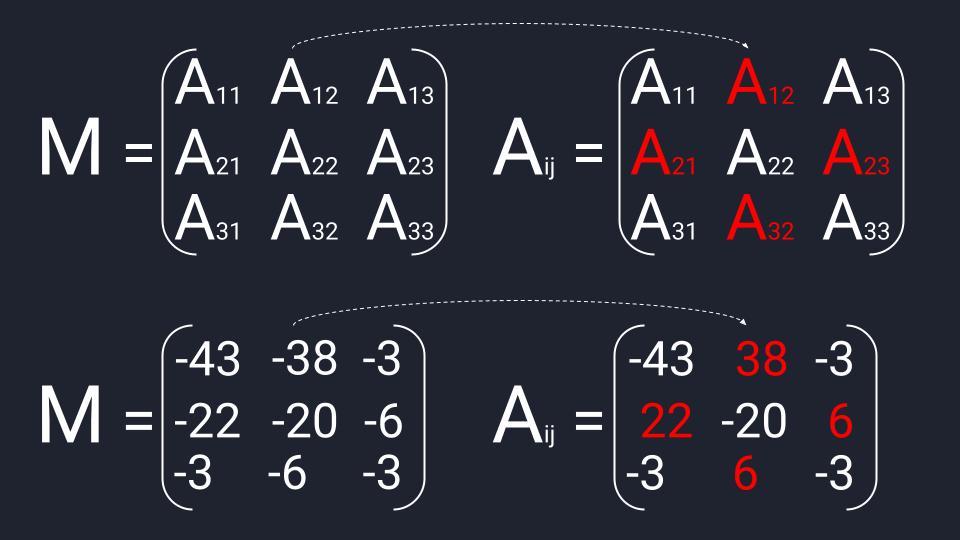
Матрица миноров третьего порядка рассчитывается по следующему принципу:
- Последовательно вычёркиваем строки и столбцы.
- Получаем четыре элемента и считаем определитель.
- Записываем результат в матрицу миноров третьего порядка.
Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:
- Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
- Найдите этот же элемент в исходной матрице и отметьте его точкой.
- Проведите от этой точки две линии: вдоль строки и вдоль столбца.
После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.
Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.
1-я строка 1-й элемент:
Δ = 5×1 – 8×6 = -43
1-я строка 2-й элемент:
Δ = 4×1 – 7×6 = -38
1-я строка 3-й элемент:
Δ = 4×8 – 7×5 = -3
2-я строка 1-й элемент:
Δ = 2×1 – 8×3 = -22
2-я строка 2-й элемент:
Δ = 1×1 – 7×3 = -20
2-я строка 3-й элемент:
Δ = 1×8 – 7×2 = -6
3-я строка 1-й элемент:
Δ = 2×6 – 5×3 = -3
3-я строка 2-й элемент:
Δ = 1×6 – 4×3 = -6
3-я строка 3-й элемент:
Δ = 1×5 – 4×2 = -3
Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:
Господи, зачем всё это?
Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?
Смотрите:
- Вам не нужно уметь решать все эти уравнения самостоятельно. Для этого давно есть мощные алгоритмы.
- Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
- В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
- И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.
Спокойствие, всё будет хорошо.