Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Содержание:
- Нахождение обратной матрицы с помощью присоединённой матрицы
- Нахождение обратной матрицы с помощью союзной матрицы
- Облегченный способ для матрицы второго порядка
Обратную матрицу
можно найти с помощью двух ниже описанных методов.
Нахождение обратной матрицы с помощью присоединённой матрицы
Пример
Задание. Для матрицы $ A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right) $
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
 справа
справа
единичную матрицу второго порядка:
$$ Aleft|E=left( begin{array}{cc|cc}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$$ Aleft|E = left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right. $$
Первую и вторую строки меняем местами:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right. $$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right. $$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Замечание
Если на некотором этапе в “левой” матрице получается
нулевая строка, то это
означает, что исходная матрица обратной не имеет.
Облегченный способ для матрицы второго порядка
Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:
Шаг 1. Находим определитель $ Delta $ заданной матрицы,
если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.
Шаг 2. Элементы, стоящие на
главной диагонали меняем местами, а у элементов
побочной диагонали меняем знак на противоположный.
Шаг 3. Делим все элементы на $ Delta $ и получаем обратную матрицу.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти обратную матрицу для
$ A=left( begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right) $
Решение. Шаг 1. $ Delta=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=4-4=0 $ ,
тогда обратной матрицы не существует.
Ответ. Так как
определитель матрицы $A$ равен нулю,
то она не имеет обратной.
Пример
Задание. Найти обратную матрицу для $ A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right) $
Решение. Шаг 1. Находим определитель: $ Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0 $
Шаг 2. $ A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Шаг 3. $ A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Нахождение обратной матрицы с помощью союзной матрицы
Определение
Матрица $ tilde{A} $ называется lt strong>союзной lt /strong> к квадратной матрице $A$ ,
если элементы матрицы $ tilde{A} $ равны
алгебраическим дополнениям соответствующих
элементов матрицы $A$ .
$$ A=left( begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right) Rightarrow tilde{A}=left( begin{array}{ccc}{A_{11}} & {A_{12}} & {A_{13}} \ {A_{21}} & {A_{22}} & {A_{23}} \ {A_{31}} & {A_{32}} & {A_{33}}end{array}right) $$
Имеет место следующее свойство: $ A cdot widetilde{A}^{T}=|A| cdot E $
Тогда, если $ |A| neq 0 $ , то
$ A cdot tilde{A}^{T} cdot frac{1}{|A|}=E $ , а тогда
$ A^{-1}=frac{1}{|A|} cdot tilde{A}^{T} $
Таким образом, матрица имеет союзную тогда и только тогда, когда она
невырожденная.
Пример
Задание. Найти обратную матрицу к матрице $ A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right) $
Решение. Вычисляем определитель матрицы:
$$ Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1- $$
$$ -1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0 $$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$$ A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T} $$
Найдем союзную матрицу $ tilde{A} $ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$$ A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2 $$
$$ A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3 $$
$$ A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7 $$
$$ A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6 $$
$$ A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3 $$
$$ A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3 $$
$$ A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2 $$
$$ A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3 $$
$$ A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1 $$
Таким образом, $ tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right) $
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$$ widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $$
Итак, $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Ответ. $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Читать дальше: линейно зависимые и линейно независимые строки.
Алгоритм вычисления обратной матрицы. (Метод присоединенной матрицы).
-
Находим
 .
.
Если =0,
=0,
то матрица вырожденная и А-1
не существует. Если
 ,
,
то А невырожденная и А-1
существует. -
Находим
АТ. -
Находим
алгебраические дополнения элементов
транспонированной матрицы
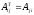 ,
,
(i=1,2,…,n; j=1,2,…,n) и составляем из них
присоединенную матрицу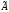 :
: (i=1,2,…,n; j=1,2,…,n).
(i=1,2,…,n; j=1,2,…,n). -
Вычисляем
обратную матрицу по формуле (10). -
Проверяем
правильность вычисления А-1
по определению:А-1А=Е.
Пример.
А= ,
, -5,
-5,
АТ=
А11=-4 А12=3 А13=-5
А21=-8 А22=6 А23=-5
А31=-5 А32=5 А33=-5
А-1=
Для
невырожденных матриц выполняются
следующие свойства:
1.
 ; 3.
; 3. ; 5.
; 5.
(А-1)Т=(АТ)-1.
2.
(А-1)-1=А; 4.
(АВ)-1=В-1А-1;
Элементарные преобразования над матрицами.
-
Отбрасывание
нулевой строки (столбца). -
Умножение
всех элементов строки (столбца) на
число, отличное от нуля. -
Перемена
местами двух строк (столбцов) местами. -
Прибавление
к элементам одной строки (столбца)
соответствующих элементов другой
строки (столбца), умноженных на любое
число. -
Транспонирование
матрицы.
Матрица
В, полученная из матрицы А с помощью
элементарных преобразований, называется
эквивалентной матрице А (В~А).
При
помощи элементарных преобразований
можно найти обратную матрицу к
невырожденной матрице А.
Метод
элементарных преобразований (метод
Гаусса).
Приписывая
справа к квадратной матрице А порядка
n единичную матрицу такого же порядка.
Получим прямоугольную матрицу В=(А|Е)
размера nx2n. С помощью элементарных
преобразований над строками матрицы В
приведем ее к виду (Е|А-1).
Пример.
А= .
.
Составим матрицу В.


 А-1=
А-1=
Матричные
ур-я. АХ=В, Х=А-1В
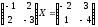 ,
,
Х=
Ранг матрицы. Рассмотрим произвольную, необязательно квадратную, матрицу а размера mxn. Линейная зависимость строк.
Понятие
ранга матрицы связано с понятием линейной
зависимости (независимости) строк
(столбцов) матрицы. Рассмотрим это
понятие для строк. Для столбцов –
аналогично.
Обозначим
стоки матрицы А:
е1=(а11,а12,…,а1n); е2=(а21,а22,…,а2n);…,
еm=(аm1,аm2,…,аmn)
ek=es
если akj=asj,
j=1,2,…,n
Арифметические
операции над строками матрицы (сложение,
умножение на число) вводятся как операции,
проводимые поэлементно: λеk=(λаk1,λаk2,…,λаkn);
ek+еs=[(аk1+as1),(ak2+as2),…,(аkn+asn)].
Строка
е называется линейной
комбинацией
строк е1,
е2,…,еk,
если она равна сумме произведений этих
строк на произвольные действительные
числа:
е=λ1е1+λ2е2+…+λkеk
Строки
е1,
е2,…,еm
называются линейно
зависимыми,
если существуют действительные числа
λ1,λ2,…,λm,
не все равные нулю, что линейная комбинация
этих строк равна нулевой строке:
λ1е1+λ2е2+…+λmеm=0,
где
0=(0,0,…,0) (1)
Если
линейная комбинация равна нулю тогда
и только тогда, когда все коэффициенты
λi
равны нулю (λ1=λ2=…=λm=0),
то строки е1,
е2,…,еm
называются линейно
независимыми.
Теорема
1.
Для
того, чтобы строки е1,е2,…,еm
были линейно зависимы, необходимо
и достаточно,
чтобы одна из этих строк была линейной
комбинацией
остальных строк.
Доказательство.
Необходимость.
Пусть строки е1,
е2,…,еm
линейно зависимы. Пусть, для определенности
в (1) λm≠0,
тогда

или


Т.о.
строка еm
является линейной комбинацией остальных
строк. Ч.т.д.
Достаточность.
Пусть одна из строк, например еm,
является линейной комбинацией остальных
строк. Тогда найдутся числа
 такие, что выполняется равенство
такие, что выполняется равенство ,
,
которое можно переписать в виде ,
,
где
хотя бы 1 из коэффициентов, (-1), не равен
нулю. Т.е. строки линейно зависимы.
Ч.т.д.
Определение.
Минором k-го порядка
матрицы А размера mxn называется
определитель k-го порядка с элементами,
лежащими на пересечении любых k строк
и любых k столбцов матрицы А. (k≤min(m,n)).
 .
.
Пример.
 ,
,
миноры 1-го порядка:
 =
=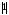 ,
, =
=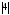 ;
;
миноры
2-го порядка:
 ,
,
3-го порядка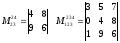
У
матрицы 3-го порядка 9 миноров 1-го порядка,
9 миноров 2-го порядка и 1 минор 3-го порядка
(определитель этой матрицы).
Определение.
Рангом матрицы А
называется наивысший порядок отличных
от нуля миноров этой матрицы. Обозначение
– rg A или r(A).
Свойства
ранга матрицы.
-
ранг
матрицы Anxm
не превосходит меньшего из ее размеров,
т.е.
r(A)≤min(m,n).
-
r(A)=0
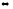 когда
когда
все элементы матрицы равны 0, т.е. А=0. -
Для
квадратной матрицы А n –го порядка
r(A)=n
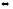 ,
,
когда А невырожденная.
(Ранг
диагональной
матрицы равен количеству
ее
ненулевых
диагональных
элементов).
4)
Если ранг матрицы равен r,
то матрица имеет хотя бы один минор
порядка r,
не равный нулю, а все миноры больших
порядков равны нулю.
Для
рангов матрицы справедливы следующие
соотношения:
-
r(AT)=r(A)
-
r(A+B)≤r(A)+r(B); 3)
r(AB)≤min{r(A),r(B)}; -
r(A+B)≥│r(A)-r(B)│; 4)
r(ATA)=r(A);
-
r(AB)=r(A),
если В – квадратная невырожденная
матрица. -
r(AB)≥r(A)+r(B)-n,
где n-число столбцов матрицы А или строк
матрицы В.
Определение.
Ненулевой минор порядка r(A) называется
базисным
минором. (У
матрицы А может быть несколько базисных
миноров). Строки и столбцы, на пересечении
которых стоит базисный минор, называются
соответственно базисными
строками и
базисными
столбцами.
Теорема
2 (о базисном миноре). Базисные
строки (столбцы) линейно независимы.
Любая строка (любой столбец) матрица А
является линейной комбинацией базисных
строк (столбцов).
Доказательство.
(Для строк). Если бы базисные строки были
линейно зависимы, то по теореме (1) одна
из этих строк была бы линейной комбинацией
других базисных строк, тогда, не изменяя
величины базисного минора, можно вычесть
из этой строки указанную линейную
комбинацию и получить нулевую строку,
а это противоречит тому, что базисный
минор отличен от нуля. Т.о. базисные
строки линейно независимы.
Докажем,
что любая строка матрицы А является
линейной комбинацией базисных строк.
Т.к. при произвольных переменах строк
(столбцов) определитель сохраняет
свойство равенства нулю, то, не ограничивая
общности, можно считать, что базисный
минор находится в верхнем левом углу
матрицы
А= ,т.е. расположен
,т.е. расположен
на первых r
строках и первых r
столбцах. Пусть 1jn,
1im.
Покажем, что определитель (r+1)-го
порядка
 равен
равен
0.
Если
jr
или ir,
то этот определитель равен нулю, т.к. у
него будет два одинаковых столбца или
две одинаковых строки.
Если
же j>r
и i>r,
то этот определитель является минором
(r+1)-го
порядка матрицы А. Т.к. ранг матрицы
равен r, значит любой минор большего
порядка равен 0.
Раскладывая
его по элементам последнего (добавленного)
столбца, получаем
a1jA1j+a2jA2j+…+arjArj+aijAij=0,
где последнее алгебраическое дополнение
Aij
совпадает с базисным минором Мr
и поэтому Aij=
Мr≠0.
Разделив
последнее равенство на Aij,
можем выразить элемент aij,
как линейную комбинацию:
 ,
,
где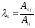 .
.
Зафиксируем
значение i (i>r) и получаем, что для любого
j (j=1,2,…,n) элементы i-й строки ei
линейно выражаются через элементы строк
е1,
е2,…,еr,
т.е. i-я строка является линейной
комбинацией базисных строк:
 .
.
Ч.т.д.
Теорема
3. (необходимое и достаточное условие
равенства нулю определителя). Для
того, чтобы определитель n-го
порядка
был равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
Доказательство
(с.40).
Необходимость.
Если определитель n-го
порядка
равен нулю, то базисный минор его матрицы
имеет порядок r<n.
Тогда хотя бы одна из его строк является
не базисной. По теореме 2 эта строка
является линейной комбинацией базисных
строк. В эту линейную комбинацию можно
включить и все оставшиеся строки с
коэффициентами 0.
Т.о.,
одна строка является линейной комбинацией
других остальных. Тогда по теореме 1
строки определителя линейно зависимы.
Достаточность.
Если строки
линейно зависимы, то по теореме 1 одна
строка Аi
является линейной комбинацией остальных
строк. Вычитая из строки Аi
указанную линейную комбинацию, не
изменив величины ,
получим нулевую строку. Следовательно,
по свойствам определителей, =0. ч.т.д.
Т.о.
можно считать, что ранг
матрицы равен максимальному числу ее
линейно независимых строк или столбцов.
Теорема
4. При
элементарных преобразованиях ранг
матрицы не меняется.
Доказательство.
Как было показано при рассмотрении
свойств определителей,
при преобразованиях
квадратных
матриц их определители
либо не изменяются, либо умножаются на
ненулевое число, либо меняют знак. При
этом наивысший порядок отличных от нуля
миноров исходной матрицы сохраняется,
т.е. ранг матрицы не изменяется. Ч.т.д.
Если
r(A)=r(B),
то А и В –эквивалентные:
А~В.
Теорема
5. При помощи
элементарных преобразований можно
привести матрицу к ступенчатому
виду. Матрица
называется
ступенчатой, если она имеет вид:
А= ,
,
где aii≠0,
i=1,2,…,r; r≤k.
Условия
r≤k всегда можно достигнуть транспонированием.
Теорема
6. Ранг
ступенчатой матрицы равен количеству
ее ненулевых строк.
Т.е.
Ранг ступенчатой матрицы равен r, т.к.
есть отличный от нуля минор порядка r:

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса).
Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.
Обратной матрицей называется матрицы A-1 при умножении на исходную матрицу A получается единичная матрица E.
A·A-1 = A-1 · A = E
Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:
- Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
- Найти матрицу миноров M.
- Из матрицы M найти матрицу алгебраических дополнений C*.
- Транспонировать матрицу (поменяем местами строки со столбцами) C*, получить матрицу C*T.
- По формуле найти обратную матрицу.
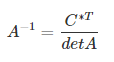
Пример
Рассмотрим данный метод на примере. Дана матрицы 3х3:
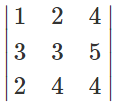
Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.
Найдем минор M11 и алгебраическое дополнение A11. В матрице А вычеркиваем строку 1 и столбец 1.
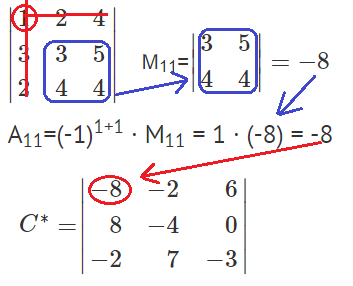
Найдем минор M12 и алгебраическое дополнение A12. В матрице А вычеркиваем строку 1 и столбец 2.
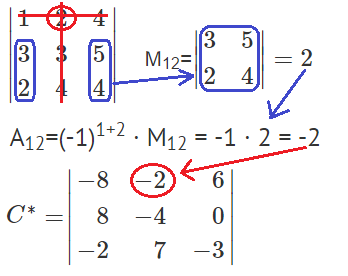
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу C*.
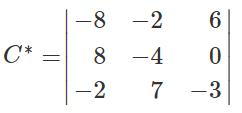
Найдем транспонированную союзную матрицу алгебраических дополнений C*T.
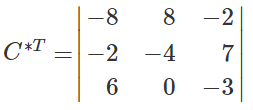
Найдем обратную матрицу. Ответ:
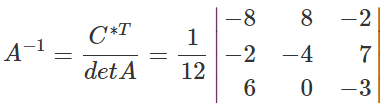
Обратная матрица.
Навигация по странице:
- Определение обратной матрицы
- Свойства обратной матрицы
- Методы вычисления обратной матрицы
- Вычисления обратной матрицы с помощью присоединённой матрицы
- Вычисления обратной матрицы с помощью союзной матрицы
Определение.
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A-1 = A-1·A = E
Замечание.
Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Свойства обратной матрицы
| ● | |
| ● | (A·B)-1 = A-1·B-1 |
| ● | (A-1)T = (AT)-1 |
| ● | |
| ● | (A-1)-1 = A |
Методы вычисления обратной матрицы
Вычисление обратной матрицы с помощью присоединённой матрицы
Теорема.
Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.
Замечание.
Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.
Вычисление обратной матрицы с помощью союзной матрицы
Определение.
Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.
Пример 1.
Найти обратную матрицу матрицы A
| A = | 2 | 4 | 1 | ||
| 0 | 2 | 1 | |||
| 2 | 1 | 1 |
Решение: Найдем определитель матрицы A:
| det(A) = | 2 | 4 | 1 | = |
| 0 | 2 | 1 | ||
| 2 | 1 | 1 |
= 2·2·1 + 4·1·2 + 1·0·1 – 1·2·2 – 2·1·1 – 4·0·1 = 4 + 8 + 0 – 4 – 2 – 0 = 6
Найдем алгебраические дополнения матрицы A:
| A11 = (-1)1 + 1· | 2 | 1 | = 2·1 – 1·1 = 1 |
| 1 | 1 |
| A12 = (-1)1 + 2· | 0 | 1 | = -(0·1 – 1·2) = 2 |
| 2 | 1 |
| A13 = (-1)1 + 3· | 0 | 2 | = 0·1 – 2·2 = -4 |
| 2 | 1 |
| A21 = (-1)2 + 1· | 4 | 1 | = -(4·1 – 1·1) = -3 |
| 1 | 1 |
| A22 = (-1)2 + 2· | 2 | 1 | = 2·1 – 1·2 = 0 |
| 2 | 1 |
| A23 = (-1)2 + 3· | 2 | 4 | = -(2·1 – 4·2) = 6 |
| 2 | 1 |
| A31 = (-1)3 + 1· | 4 | 1 | = 4·1 – 1·2 = 2 |
| 2 | 1 |
| A32 = (-1)3 + 2· | 2 | 1 | = -(2·1 – 1·0) = -2 |
| 0 | 1 |
| A33 = (-1)3 + 3· | 2 | 4 | = 2·2 – 4·0 = 4 |
| 0 | 2 |
Запишем союзную матрицу:
| Ã = | 1 | 2 | -4 | ||
| -3 | 0 | 6 | |||
| 2 | -2 | 4 |
Найдем обратную матрицу:
| Ответ: A-1 = | 1/6 | -1/2 | 1/3 | ||
| 1/3 | 0 | -1/3 | |||
| -2/3 | 1 | 2/3 |
