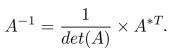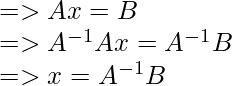Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
The inverse of a matrix is just a reciprocal of the matrix as we do in normal arithmetic for a single number which is used to solve the equations to find the value of unknown variables. The inverse of a matrix is that matrix which when multiplied with the original matrix will give as an identity matrix. The inverse of a matrix exists only if the matrix is non-singular i.e., determinant should not be 0. Using determinant and adjoint, we can easily find the inverse of a square matrix using below formula,
if det(A) != 0
A-1 = adj(A)/det(A)
else
"Inverse doesn't exist"
Matrix Equation
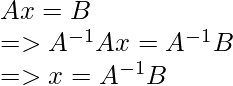
where,
A-1: The inverse of matrix A
x: The unknown variable column
B: The solution matrix
We can find out the inverse of any square matrix with the function numpy.linalg.inv(array).
Syntax: numpy.linalg.inv(a)
Parameters:
a: Matrix to be inverted
Returns: Inverse of the matrix a.
Example 1:
Python3
import numpy as np
arr = np.array([[1, 2], [5, 6]])
inverse_array = np.linalg.inv(arr)
print("Inverse array is ")
print(inverse_array)
print()
arr = np.array([[1, 2, 3],
[4, 9, 6],
[7, 8, 9]])
inverse_array = np.linalg.inv(arr)
print("Inverse array is ")
print(inverse_array)
print()
arr = np.array([[1, 2, 3, 4],
[10, 11, 14, 25],
[20, 8, 7, 55],
[40, 41, 42, 43]])
inverse_array = np.linalg.inv(arr)
print("Inverse array is ")
print(inverse_array)
print()
arr = np.array([[1]])
inverse_array = np.linalg.inv(arr)
print("Inverse array is ")
print(inverse_array)
Output:
Inverse array is [[-1.5 0.5 ] [ 1.25 -0.25]] Inverse array is [[-0.6875 -0.125 0.3125 ] [-0.125 0.25 -0.125 ] [ 0.64583333 -0.125 -0.02083333]] Inverse array is [[-15.07692308 4.9 -0.8 -0.42307692] [ 32.48717949 -10.9 1.8 1.01282051] [-20.84615385 7.1 -1.2 -0.65384615] [ 3.41025641 -1.1 0.2 0.08974359]] Inverse array is [[1.]]
Example 2:
Python3
import numpy as np
A = np.array([[[1., 2.], [3., 4.]],
[[1, 3], [3, 5]]])
print(np.linalg.inv(A))
Output:
[[[-2. 1. ] [ 1.5 -0.5 ]] [[-1.25 0.75] [ 0.75 -0.25]]]
Last Updated :
26 Feb, 2021
Like Article
Save Article
Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы
- Обратная матрица
- Ранг матрицы
Обратная матрица
Обратной матрицей A-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Исходная матрица:
Союзная ей матрица A*:
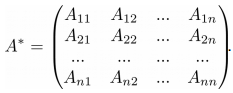
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*T:
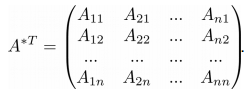
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A-1, обратную матрице A:
➣ Численный пример
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
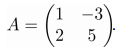
Для начала найдем определитель матрицы A:
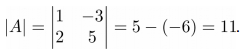
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
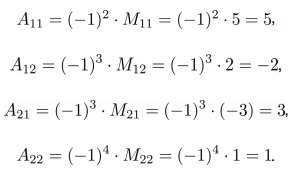
Союзная матрица будет иметь следующий вид:
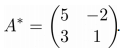
Присоединенная матрица получается из союзной путем транспонирования:
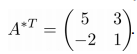
Находим обратную матрицу:
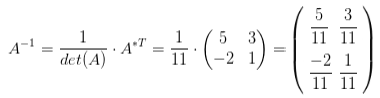
➤ Пример на Python
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():
>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
[-0.18181818 0.09090909]]
Рассмотрим свойства обратной матрицы.
Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:
![]()
➤Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np.linalg.inv(A_inv)
>>> print(A)
[[1. -3.]
[2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
[2. 5.]]
Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
![]()
➤ Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:
![]()
➤ Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
Ранг матрицы
Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
>>> m_eye = np.eye(4) >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():
>>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 4
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
>>> m_eye[3][3] = 0 >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 0.]] >>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 3
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

- linalg.inv(a)[source]#
-
Compute the (multiplicative) inverse of a matrix.
Given a square matrix a, return the matrix ainv satisfying
dot(a, ainv) = dot(ainv, a) = eye(a.shape[0]).- Parameters:
-
- a(…, M, M) array_like
-
Matrix to be inverted.
- Returns:
-
- ainv(…, M, M) ndarray or matrix
-
(Multiplicative) inverse of the matrix a.
- Raises:
-
- LinAlgError
-
If a is not square or inversion fails.
Notes
New in version 1.8.0.
Broadcasting rules apply, see the
numpy.linalgdocumentation for
details.Examples
>>> from numpy.linalg import inv >>> a = np.array([[1., 2.], [3., 4.]]) >>> ainv = inv(a) >>> np.allclose(np.dot(a, ainv), np.eye(2)) True >>> np.allclose(np.dot(ainv, a), np.eye(2)) True
If a is a matrix object, then the return value is a matrix as well:
>>> ainv = inv(np.matrix(a)) >>> ainv matrix([[-2. , 1. ], [ 1.5, -0.5]])
Inverses of several matrices can be computed at once:
>>> a = np.array([[[1., 2.], [3., 4.]], [[1, 3], [3, 5]]]) >>> inv(a) array([[[-2. , 1. ], [ 1.5 , -0.5 ]], [[-1.25, 0.75], [ 0.75, -0.25]]])
In this article, we will see NumPy Inverse Matrix in Python before that we will try to understand the concept of it. The inverse of a matrix is just a reciprocal of the matrix as we do in normal arithmetic for a single number which is used to solve the equations to find the value of unknown variables. The inverse of a matrix is that matrix which when multiplied with the original matrix will give an identity matrix.
The inverse of a matrix exists only if the matrix is non-singular i.e., the determinant should not be 0. Using determinant and adjoint, we can easily find the inverse of a square matrix using the below formula,
if det(A) != 0
A-1 = adj(A)/det(A)
else
"Inverse doesn't exist"
Matrix Equation:
where,
A-1: The inverse of matrix A
x: The unknown variable column
B: The solution matrix
Inverse Matrix using NumPy
Python provides a very easy method to calculate the inverse of a matrix. The function numpy.linalg.inv() is available in the NumPy module and is used to compute the inverse matrix in Python.
Syntax: numpy.linalg.inv(a)
Parameters:
- a: Matrix to be inverted
Returns: Inverse of the matrix a.
Example 1: In this example, we will create a 3 by 3 NumPy array matrix and then convert it into an inverse matrix using the np.linalg.inv() function.
Python3
import numpy as np
A = np.array([[6, 1, 1],
[4, -2, 5],
[2, 8, 7]])
print(np.linalg.inv(A))
Output:
[[ 0.17647059 -0.00326797 -0.02287582] [ 0.05882353 -0.13071895 0.08496732] [-0.11764706 0.1503268 0.05228758]]
Example 2: In this example, we will create a 4 by 4 NumPy array matrix and then convert it using np.linalg.inv() function into an inverse Matrix in Python.
Python3
import numpy as np
A = np.array([[6, 1, 1, 3],
[4, -2, 5, 1],
[2, 8, 7, 6],
[3, 1, 9, 7]])
print(np.linalg.inv(A))
Output:
[[ 0.13368984 0.10695187 0.02139037 -0.09090909] [-0.00229183 0.02673797 0.14820474 -0.12987013] [-0.12987013 0.18181818 0.06493506 -0.02597403] [ 0.11000764 -0.28342246 -0.11382735 0.23376623]]
Example 3: In this example, we will create multiple NumPy array matrices and then convert them into their inverse matrices using np.linalg.inv() function.
Python3
import numpy as np
A = np.array([[[1., 2.], [3., 4.]],
[[1, 3], [3, 5]]])
print(np.linalg.inv(A))
Output:
[[[-2. 1. ] [ 1.5 -0.5 ]] [[-1.25 0.75] [ 0.75 -0.25]]]
Last Updated :
05 May, 2023
Like Article
Save Article
It is a pity that the chosen matrix, repeated here again, is either singular or badly conditioned:
A = matrix( [[1,2,3],[11,12,13],[21,22,23]])
By definition, the inverse of A when multiplied by the matrix A itself must give a unit matrix. The A chosen in the much praised explanation does not do that. In fact just looking at the inverse gives a clue that the inversion did not work correctly. Look at the magnitude of the individual terms – they are very, very big compared with the terms of the original A matrix…
It is remarkable that the humans when picking an example of a matrix so often manage to pick a singular matrix!
I did have a problem with the solution, so looked into it further. On the ubuntu-kubuntu platform, the debian package numpy does not have the matrix and the linalg sub-packages, so in addition to import of numpy, scipy needs to be imported also.
If the diagonal terms of A are multiplied by a large enough factor, say 2, the matrix will most likely cease to be singular or near singular. So
A = matrix( [[2,2,3],[11,24,13],[21,22,46]])
becomes neither singular nor nearly singular and the example gives meaningful results… When dealing with floating numbers one must be watchful for the effects of inavoidable round off errors.