Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Содержание:
- Нахождение обратной матрицы с помощью присоединённой матрицы
- Нахождение обратной матрицы с помощью союзной матрицы
- Облегченный способ для матрицы второго порядка
Обратную матрицу
можно найти с помощью двух ниже описанных методов.
Нахождение обратной матрицы с помощью присоединённой матрицы
Пример
Задание. Для матрицы $ A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right) $
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
 справа
справа
единичную матрицу второго порядка:
$$ Aleft|E=left( begin{array}{cc|cc}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$$ Aleft|E = left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right. $$
Первую и вторую строки меняем местами:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right. $$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right. $$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Замечание
Если на некотором этапе в “левой” матрице получается
нулевая строка, то это
означает, что исходная матрица обратной не имеет.
Облегченный способ для матрицы второго порядка
Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:
Шаг 1. Находим определитель $ Delta $ заданной матрицы,
если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.
Шаг 2. Элементы, стоящие на
главной диагонали меняем местами, а у элементов
побочной диагонали меняем знак на противоположный.
Шаг 3. Делим все элементы на $ Delta $ и получаем обратную матрицу.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти обратную матрицу для
$ A=left( begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right) $
Решение. Шаг 1. $ Delta=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=4-4=0 $ ,
тогда обратной матрицы не существует.
Ответ. Так как
определитель матрицы $A$ равен нулю,
то она не имеет обратной.
Пример
Задание. Найти обратную матрицу для $ A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right) $
Решение. Шаг 1. Находим определитель: $ Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0 $
Шаг 2. $ A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Шаг 3. $ A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Нахождение обратной матрицы с помощью союзной матрицы
Определение
Матрица $ tilde{A} $ называется lt strong>союзной lt /strong> к квадратной матрице $A$ ,
если элементы матрицы $ tilde{A} $ равны
алгебраическим дополнениям соответствующих
элементов матрицы $A$ .
$$ A=left( begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right) Rightarrow tilde{A}=left( begin{array}{ccc}{A_{11}} & {A_{12}} & {A_{13}} \ {A_{21}} & {A_{22}} & {A_{23}} \ {A_{31}} & {A_{32}} & {A_{33}}end{array}right) $$
Имеет место следующее свойство: $ A cdot widetilde{A}^{T}=|A| cdot E $
Тогда, если $ |A| neq 0 $ , то
$ A cdot tilde{A}^{T} cdot frac{1}{|A|}=E $ , а тогда
$ A^{-1}=frac{1}{|A|} cdot tilde{A}^{T} $
Таким образом, матрица имеет союзную тогда и только тогда, когда она
невырожденная.
Пример
Задание. Найти обратную матрицу к матрице $ A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right) $
Решение. Вычисляем определитель матрицы:
$$ Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1- $$
$$ -1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0 $$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$$ A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T} $$
Найдем союзную матрицу $ tilde{A} $ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$$ A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2 $$
$$ A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3 $$
$$ A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7 $$
$$ A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6 $$
$$ A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3 $$
$$ A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3 $$
$$ A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2 $$
$$ A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3 $$
$$ A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1 $$
Таким образом, $ tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right) $
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$$ widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $$
Итак, $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Ответ. $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Читать дальше: линейно зависимые и линейно независимые строки.
Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса).
Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.
Обратной матрицей называется матрицы A-1 при умножении на исходную матрицу A получается единичная матрица E.
A·A-1 = A-1 · A = E
Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:
- Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
- Найти матрицу миноров M.
- Из матрицы M найти матрицу алгебраических дополнений C*.
- Транспонировать матрицу (поменяем местами строки со столбцами) C*, получить матрицу C*T.
- По формуле найти обратную матрицу.
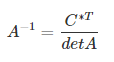
Пример
Рассмотрим данный метод на примере. Дана матрицы 3х3:
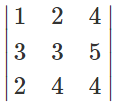
Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.
Найдем минор M11 и алгебраическое дополнение A11. В матрице А вычеркиваем строку 1 и столбец 1.
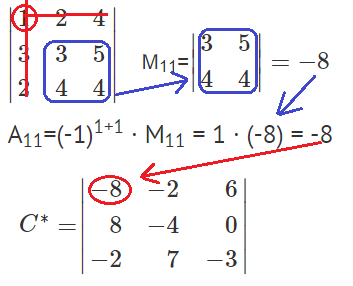
Найдем минор M12 и алгебраическое дополнение A12. В матрице А вычеркиваем строку 1 и столбец 2.
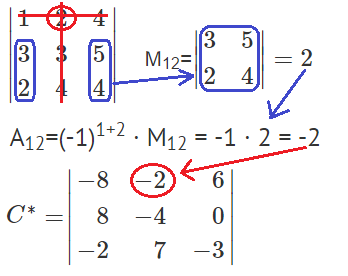
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу C*.
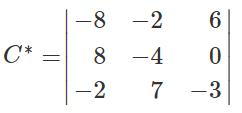
Найдем транспонированную союзную матрицу алгебраических дополнений C*T.
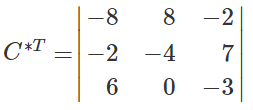
Найдем обратную матрицу. Ответ:
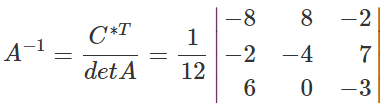
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если
выполняется условие: АА-1= А-1А=Е,
где Е – единичная матрица того же порядка,
что и матрица А. Обратная А-1матрица имеет ту же размерность, что и
матрица А.
Определение. Квадратная матрица
А= называется невырожденной, если её
называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
Теорема.Всякая невырожденная
матрица имеет обратную.
Определение. Присоединенной матрицей![]() к матрице А называется матрица вида:
к матрице А называется матрица вида:
![]() =
= ,
,
где Аij-алгебраическое
дополнение элемента аij.
Находят обратную матрицу по формуле:
А-1=![]() .
.
Пример 3.1
Найти обратную матрицу методом
присоединенной матрицы.
А=
Решение.
-
Выясним, является ли данная матрица
невырожденной. Для этого найдем
определитель матрицы:
![]() =3(-1)1+1
=3(-1)1+1![]() +0(-1)2+1
+0(-1)2+1![]() +1(-1)3+1
+1(-1)3+1![]() =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.
![]() 0,
0,
следовательно, данная матрица имеет
обратную.
-
Найдем транспонированную матрицу.
АТ=
-
Вычислим присоединенную матрицу. Для
этого найдем алгебраическое дополнение
каждого элемента матрицы.
![]() =
=
(-1)1+1![]() =12-4=8
=12-4=8
![]() =
=
(-1)1+2![]() =
=
-(4-4)= 0
![]() =
=
(-1)1+3![]() =
=
2-6= -4
![]() =
=
(-1)2+1![]() =
=
-(0-2)=2
![]() =
=
(-1)2+2![]() =
=
12-2=10
![]() =
=
(-1)2+3![]() =
=
-(6-0)= -6
![]() =
=
(-1)3+1![]() =
=
0-3= -3
![]() =
=
(-1)3+2![]() =
=
-(6-1)= -5
![]() =
=
(-1)3+3![]() =
=
9-0=9.
![]() =
=
4. Воспользуемся формулой: А-1=![]() .
.
А-1=![]()
 =
= .
.
Решение систем линейных уравнений
методом обратной матрицы
Пусть дана система линейных уравнений .
.
Обозначим её через (1). Выпишим основную
матрицу данной системы: А= ,
,
вектор-столбец неизвестных:X=![]() и
и
вектор-столбец свободных членов:B=![]() .
.
Теперь перепишем систему (1) в матричной
форме:AX=B![]() X=A-1B-
X=A-1B-
решение системы (1).
Пример 3.2
Решить систему линейных уравнений:
 методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить
решение системы: X=A-1B.
Основная матрица системы А= ,
,
вектор-столбец неизвестных:X=![]()
![]() и
и
вектор-столбец свободных членов:B=![]() .
.
Найдем определитель
![]() =3(-1)1+1
=3(-1)1+1![]() +0(-1)2+1
+0(-1)2+1![]() +1(-1)3+1
+1(-1)3+1![]() =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.
![]() 0,
0,
следовательно, данная матрица имеет
обратную.
Найдем обратную матрицу с помощью
присоединенной матрицы (см. пример 3.1):
А-1=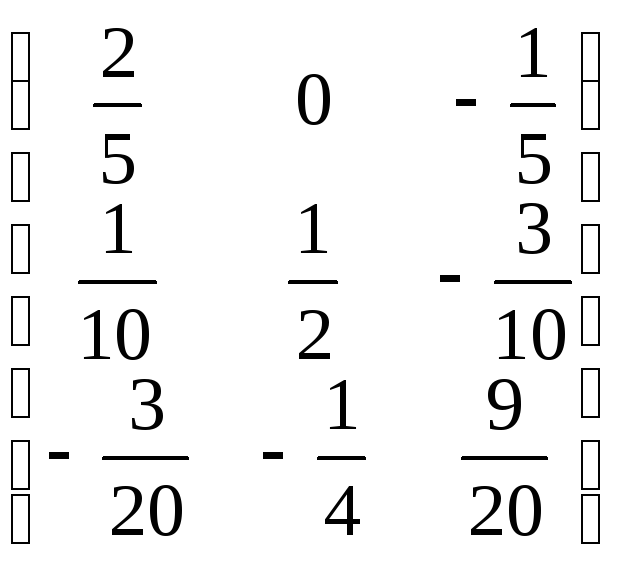 .
.
Подставим в формулу X=A-1B,
получим:X=
![]() =
= =
=![]()
Ответ:
![]() =
=![]() ,
,
![]() ,
,![]() .
.
Правильность решения легко проверить,
подставив полученные результаты![]() ,
,
![]() ,
,
![]() в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений .
.
Обозначим её через (1). Основная матрица
данной системы: А= ,
,
вектор-столбец неизвестных:X=![]() и
и
вектор-столбец свободных членов:B=![]() .
.
Теперь запишем систему (1) в матричной
форме:AX=B.
Теорема Крамера. Пусть
![]() –определитель
–определитель
матрицы А,
![]() j–определитель матрицы, получаемой из А
j–определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если![]()
![]() 0,
0,
то система имеет единственное решение:![]() ,
,
(1jn).
Пример 4.1
Решить систему линейных уравнений:
 методом Крамера.
методом Крамера.
Решение.
Основная матрица системы А= и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=![]() .
.
Найдем определитель
![]() =
=![]() =3(-1)1+1
=3(-1)1+1![]() +0(-1)2+1
+0(-1)2+1![]() +1(-1)3+1
+1(-1)3+1![]() =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к.![]() 0,
0,
следовательно, можно применить формулы
Крамера.
Найдем определители
![]() ,
,![]() ,
,![]() ,
,
полученные заменой соответствующих
столбцов столбцом свободных членов:
![]() =
= =1(12-4)-1(8-6)+2(4-9)=8-2-10=
=1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
![]() =
= =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4;
![]() =
= =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
![]() =
=![]() =
=
–![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() .
.
Ответ:
![]() =
=![]() ,
,
![]() ,
,![]() .
.
Решение систем линейных уравнений
методом Гаусса
Пусть дана система линейных уравнений .
.
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
Если ранг основной матрицы системы
меньше ранга расширенной матрицы
r(A)<r(АВ),
то система несовместна. Еслиr(A)=r(АВ)=n,
гдеn-число неизвестных,
то система совместна и определена. Еслиr(A)=r(АВ)<n,
гдеn-число неизвестных,
то система совместна и неопределенна.
Записываем систему линейных уравнений
из полученной ступенчатой матрицы.
Определяем базисные и свободные
переменные, и выражая базисные переменные
через свободные получаем решение
системы.
Пример 4.2
Решить систему линейных уравнений:
 методом Гаусса.
методом Гаусса.
Решение.

![]()

![]()

![]()

r(A)=r(АВ)=n![]() система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему
уравнений, имеем: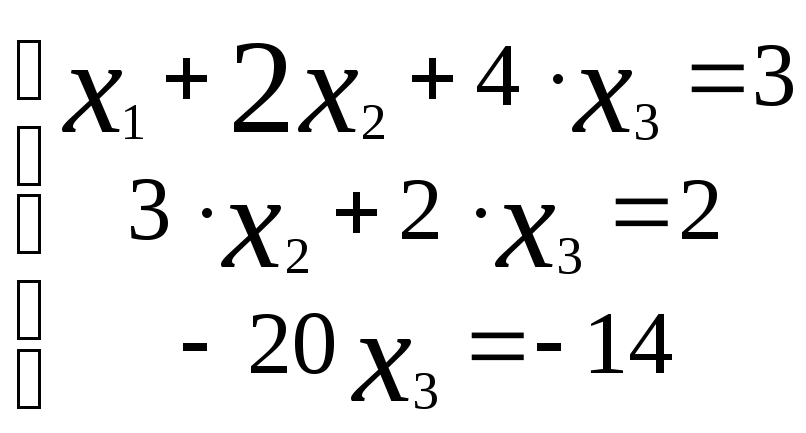
Решая её, получаем:

Ответ:
![]() =
=![]() ,
,
![]() ,
,![]() .
.
Пример 4.3
Найти общее решение системы:
 .
.
Решение.
Составим матрицу системы: А=
Приведем её к треугольному виду:

![]()

![]()

![]()

r(A)=2. Запишем
эквивалентную систему уравнений:
Примем за базисные переменные
![]() и
и![]() ,
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это![]() .
.
Выразим базисные переменные через
свободные:

![]()
 .
.
Обозначая свободную переменную:![]() =
=![]() ,
,
получаем общее решение в виде:
Пример
4.4
Найти общее решение системы:

Решение.
Приведем расширенную матрицу системы
к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n,
гдеn-число неизвестных,
то система совместная и неопределенная.
Запишем эквивалентную систему уравнений: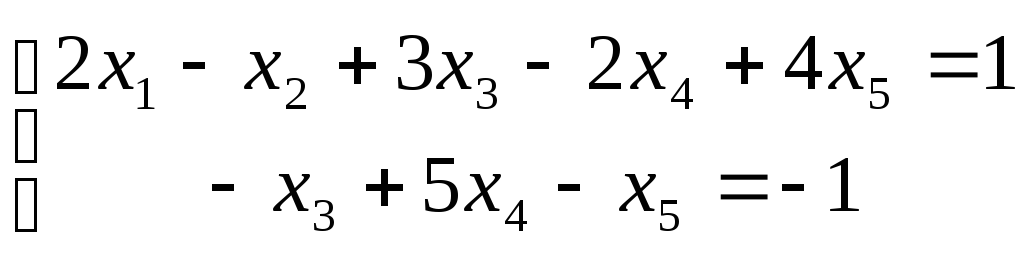
Примем за базисные переменные
![]() и
и![]() ,
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит![]() ,
,![]() -свободные
-свободные
переменные.
Выразим базисные переменные через
свободные:
 Обозначая свободную переменную:
Обозначая свободную переменную:![]() =
=![]() ,
,![]() ,
,![]() получаем
получаем
общее решение в виде: .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обратная матрица.
Навигация по странице:
- Определение обратной матрицы
- Свойства обратной матрицы
- Методы вычисления обратной матрицы
- Вычисления обратной матрицы с помощью присоединённой матрицы
- Вычисления обратной матрицы с помощью союзной матрицы
Определение.
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A-1 = A-1·A = E
Замечание.
Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Свойства обратной матрицы
| ● | |
| ● | (A·B)-1 = A-1·B-1 |
| ● | (A-1)T = (AT)-1 |
| ● | |
| ● | (A-1)-1 = A |
Методы вычисления обратной матрицы
Вычисление обратной матрицы с помощью присоединённой матрицы
Теорема.
Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.
Замечание.
Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.
Вычисление обратной матрицы с помощью союзной матрицы
Определение.
Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.
Пример 1.
Найти обратную матрицу матрицы A
| A = | 2 | 4 | 1 | ||
| 0 | 2 | 1 | |||
| 2 | 1 | 1 |
Решение: Найдем определитель матрицы A:
| det(A) = | 2 | 4 | 1 | = |
| 0 | 2 | 1 | ||
| 2 | 1 | 1 |
= 2·2·1 + 4·1·2 + 1·0·1 – 1·2·2 – 2·1·1 – 4·0·1 = 4 + 8 + 0 – 4 – 2 – 0 = 6
Найдем алгебраические дополнения матрицы A:
| A11 = (-1)1 + 1· | 2 | 1 | = 2·1 – 1·1 = 1 |
| 1 | 1 |
| A12 = (-1)1 + 2· | 0 | 1 | = -(0·1 – 1·2) = 2 |
| 2 | 1 |
| A13 = (-1)1 + 3· | 0 | 2 | = 0·1 – 2·2 = -4 |
| 2 | 1 |
| A21 = (-1)2 + 1· | 4 | 1 | = -(4·1 – 1·1) = -3 |
| 1 | 1 |
| A22 = (-1)2 + 2· | 2 | 1 | = 2·1 – 1·2 = 0 |
| 2 | 1 |
| A23 = (-1)2 + 3· | 2 | 4 | = -(2·1 – 4·2) = 6 |
| 2 | 1 |
| A31 = (-1)3 + 1· | 4 | 1 | = 4·1 – 1·2 = 2 |
| 2 | 1 |
| A32 = (-1)3 + 2· | 2 | 1 | = -(2·1 – 1·0) = -2 |
| 0 | 1 |
| A33 = (-1)3 + 3· | 2 | 4 | = 2·2 – 4·0 = 4 |
| 0 | 2 |
Запишем союзную матрицу:
| Ã = | 1 | 2 | -4 | ||
| -3 | 0 | 6 | |||
| 2 | -2 | 4 |
Найдем обратную матрицу:
| Ответ: A-1 = | 1/6 | -1/2 | 1/3 | ||
| 1/3 | 0 | -1/3 | |||
| -2/3 | 1 | 2/3 |
