Как найти обратную матрицу все способы

Как найти обратную матрицу все способы

Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.

Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.

Онлайн-калькулятор

Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.

Важно

В том случае, если обратная матрица может существовать, то она будет единственной.

Формула для вычисления обратной матрицы

Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:

A−1=1det⁡A⋅A∗A^{-1}=frac{1}{det A}cdot A^*

det⁡Adet A — определитель матрицы A,A,

A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.

Задача 1

Нужно найти обратную матрицу для следующей матрицы:

A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}

Решение

Вычислим детерминант:

det⁡A=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8

Так как det⁡A≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.

Посчитаем алгебраические дополнение:

A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,

A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,

A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,

A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,

A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,

A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,

A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,

A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,

A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.

Обратная матрица:

A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}

Важно

Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.

Задача 2

Найдите обратную матрицу для матрицы:

A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}

Решение

det⁡A=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.

A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,

A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,

A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,

A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.

Ответ:

A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}

Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.

Метод элементарных преобразований

Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:

  1. перестановка местами любых двух рядов (строк или столбцов) матрицы;
  2. умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
  3. прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.

Рассмотрим алгоритм нахождения обратной матрицы данным методом.

Алгоритм нахождения обратной матрицы методом элементарных преобразований

  1. Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
  2. С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
  3. Выписать обратную матрицу, которая находится справа от черты.
Задача 1

Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.

Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:

(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №3, умноженную на -3:

(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Задача 2

Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.

Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:

(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №2, умноженную на -1:

(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Прибавим к строке №3 строку №2, умноженную на -3:

(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.

Умножим строку №3 на 13frac{1}{3}:

(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!

Источник

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Как найти обратную матрицу

  1. Быстрый способ для матриц $2 times 2$
    1. Пример 1
    2. Пример 2
  2. Нахождение с помощью метода Гаусса
    1. Пример 3
    2. Пример 4
  3. Метод союзной матрицы(алгебраические дополнения)
    1. Пример 5

Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.

Быстрый способ для матриц $2 times 2$

Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$ 

Пример 1
Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$.
Решение

Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$

Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$
Ответ
$$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$
Пример 2
Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$.
Решение

Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$

Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$
Ответ
$$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$

Нахождение с помощью метода Гаусса

На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.

$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$

Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:

$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$

$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$

Пример 3
Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$
Решение

Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$

Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$

Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу.

Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$

Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$
Пример 4
Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$
Решение

Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$

Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$

Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу.

Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$

Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$

Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$
Ответ
$$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$

Метод союзной матрицы(алгебраические дополнения)

Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом

$$A^{-1} = frac{1}{|A|} (A^*)^T. $$

Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:

$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$

$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.

Пример 5
Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$
Решение

Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $

Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю:

$$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$

Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление.

Вычеркиваем первую строку и первый столбец:

$$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$

Убираем первую строку и второй столбец:

$$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$

Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя.

$$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$

$$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$

$$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$

$$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$

$$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$

$$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$

$$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$

Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений:

$$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$

Транспонируем её и обозначаем $ (A^*)^T $:

$$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

В итоге находим обратную матрицу $ A^{-1} $:

$$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$
Ответ
$$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$
Источник

Обра́тная ма́трица — такая матрица A^{{-1}}, при умножении которой на исходную матрицу A получается единичная матрица E:

{displaystyle AA^{-1}=A^{-1}A=E.}

Обратную матрицу можно определить как:

{displaystyle A^{-1}={frac {{mbox{adj}}A}{|A|}},}
где {displaystyle {mbox{adj}}A} — соответствующая присоединённая матрица,
|A| — определитель матрицы A.

Из этого определения следует критерий обратимости: матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы[править | править код]

Пусть квадратные матрицы {displaystyle A,~B} — невырожденные. Тогда:

Способы нахождения обратной матрицы[править | править код]

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы[править | править код]

Метод Жордана—Гаусса[править | править код]

Возьмём две матрицы: саму A и единичную матрицу E. Приведём матрицу A к единичной методом Гаусса—Жордана, применяя преобразования по строкам (можно также применять преобразования и по столбцам). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A^{{-1}}.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Lambda _{i} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

{displaystyle Lambda _{1}cdot dots cdot Lambda _{n}cdot A=Lambda A=ERightarrow Lambda =A^{-1}.}
{displaystyle Lambda _{m}={begin{bmatrix}1&dots &0&-a_{1m}/a_{mm}&0&dots &0\&&&dots &&&\0&dots &1&-a_{m-1m}/a_{mm}&0&dots &0\0&dots &0&1/a_{mm}&0&dots &0\0&dots &0&-a_{m+1m}/a_{mm}&1&dots &0\&&&dots &&&\0&dots &0&-a_{nm}/a_{mm}&0&dots &1end{bmatrix}}.}

Вторая матрица после применения всех операций станет равна Lambda , то есть будет искомой. Сложность алгоритма — O(n^{3}).

С помощью матрицы алгебраических дополнений[править | править код]

Матрица, обратная матрице A, представима в виде:

{displaystyle {A}^{-1}={{{mbox{adj}}(A)} over {det(A)}},}
где {mbox{adj}}(A) — присоединенная матрица (матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы).

Сложность алгоритма зависит от сложности {displaystyle O_{det }} алгоритма расчета определителя и равна {displaystyle O(n^{2})cdot O_{det }}.

Использование LU- или LUP-разложения[править | править код]

Матричное уравнение AX=I_{n} для обратной матрицы X можно рассматривать как совокупность n систем вида Ax=b. Обозначим i-й столбец матрицы X через X_{i}; тогда AX_{i}=e_{i}, i=1,ldots ,n, поскольку i-м столбцом матрицы I_{n} является единичный вектор e_{i}. Иными словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. Решение этих уравнений может быть упрощено с помощью LU- или LUP-разложения матрицы A. После выполнения LUP-разложения за время O(n^{3}) на решение каждого из n уравнений нужно время O(n^{2}), так что и этот алгоритм требует времени O(n^{3})[1].

Матрицу, обратную к заданной невырожденной матрице A, можно также вычислить непосредственно с помощью матриц, полученных в результате разложения.

Результатом LUP-разложения матрицы A является равенство PA=LU. Пусть PA=B, B^{{-1}}=D. Тогда из свойств обратной матрицы можно записать: D=U^{{-1}}L^{{-1}}. Если умножить это равенство на U и L то можно получить два равенства вида UD=L^{{-1}} и DL=U^{{-1}}. Первое из этих равенств представляет собой систему из n^{2} линейных уравнений, для n(n+1)/2 из которых известны правые части (из свойств треугольных матриц). Второе также представляет систему из n^{2} линейных уравнений, для n(n-1)/2 из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n^{2} равенств. С их помощью можно рекуррентно определить все n^{2} элементов матрицы D. Тогда из равенства {displaystyle (PA)^{-1}=A^{-1}P^{-1}=B^{-1}=D} получаем равенство A^{{-1}}=DP.

В случае использования LU-разложения (A=LU) не требуется перестановки столбцов матрицы D, но решение может разойтись даже если матрица A невырождена.

Сложность обоих алгоритмов — O(n^{3}).

Итерационные методы[править | править код]

Матрицу A^{{-1}} можно вычислить с произвольной точностью в результате выполнения следующего итерационного процесса, называющегося методом Шульца и являющегося обобщением классического метода Ньютона:

{displaystyle X_{k+1}=2X_{k}-X_{k}AX_{k}.}

Последовательность матриц X_{k} сходится к A^{{-1}} при kto infty . Существует также так называемый обобщённый метод Шульца, который описывается следующими рекуррентными соотношениями[2]:

{displaystyle {begin{cases}Psi _{k}=E-AX_{k},\X_{k+1}=X_{k}sum limits _{i=0}^{n}Psi _{k}^{i}.end{cases}}}

Выбор начального приближения[править | править код]

Проблема выбора начального приближения X_{0} в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору X_{0}, обеспечивающие выполнение условия {displaystyle rho (Psi _{0})<1} (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости итерационного процесса. Однако при этом, во-первых, требуется знать оценку сверху спектра обращаемой матрицы A либо матрицы {displaystyle AA^{T}} (а именно, если A — симметричная положительно определённая матрица и {displaystyle rho (A)leqslant beta }, то можно взять {displaystyle X_{0}={alpha }E}, где {displaystyle alpha in left(0,2/beta right)}; если же A — произвольная невырожденная матрица и {displaystyle rho (AA^{T})leqslant beta }, то полагают {displaystyle X_{0}={alpha }A^{T}}, где также {displaystyle alpha in left(0,2/beta right)}; можно, конечно, упростить ситуацию и, воспользовавшись тем, что {displaystyle rho (AA^{T})leqslant {mathcal {k}}AA^{T}{mathcal {k}}}, положить {displaystyle X_{0}=A^{T}/|AA^{T}|}). Во-вторых, при таком задании начальной матрицы нет гарантии, что {displaystyle |Psi _{0}|} будет малой (возможно, даже окажется {displaystyle |Psi _{0}|>1}), и высокий порядок скорости сходимости обнаружится далеко не сразу.

Для метода Ньютона в качестве начального приближения можно выбрать {displaystyle X_{0}=A^{H}/left(||A||_{1}||A||_{infty }right)}, где верхний индекс H обозначает эрмитово сопряжение, {displaystyle ||cdot ||_{1}} и {displaystyle ||cdot ||_{infty }} — соответствующие матричные нормы. Такое X_{0} вычисляется всего за O(n^{2}) операций, где n — порядок матрицы, и обеспечивает сходимость алгоритма[3].

Примеры[править | править код]

Матрица 2 × 2[править | править код]

{displaystyle mathbf {A} ^{-1}={begin{bmatrix}a&b\c&d\end{bmatrix}}^{-1}={frac {1}{det mathbf {A} }}{begin{bmatrix}d&-b\-c&a\end{bmatrix}}={frac {1}{ad-bc}}{begin{bmatrix}d&-b\-c&a\end{bmatrix}}.}[4]

Обращение матрицы 2 × 2 возможно только при условии, что ad-bc=det Aneq 0.

Примечания[править | править код]

  1. ↑ Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, — М.: Вильямс, 2006 (с. 700).
  2. ↑ Petković, M. D. Generalized Schultz iterative methods for the computation of outer inverses (англ.) // Computers & Mathematics with Applications. — 2014. — June (vol. 67, iss. 10). — P. 1837—1847. — doi:10.1016/j.camwa.2014.03.019.
  3. ↑ Pan, V., Reif, J. Fast and efficient parallel solution of dense linear systems (англ.) // Computers & Mathematics with Applications. — 1989. — Vol. 17, iss. 11. — P. 1481—1491. — doi:10.1016/0898-1221(89)90081-3.
  4. ↑ Как найти обратную матрицу? mathprofi.ru. Дата обращения: 18 октября 2017. Архивировано 17 октября 2017 года.

Ссылки[править | править код]

  • Реализация с полным выбором ведущего элемента на C++
Источник

Обра́тная
ма́трица —
такая матрица
(А-1),
что их умножение (с любой стороны) даст
в результате единичную матрицу

Свойства
обратной матрицы

Способы
нахождения обратной матрицы

  1. Нахождение обратной
    матрицы с помощью присоединенной

(АǀЕ) ̴ (ЕǀА-1)

Пример.
С помощью элементарных преобразований
строк найти обратную матрицу к матрице
A.

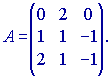
Определитель
равен –2, следовательно существует
обратная матрица. Припишем к исходной
матрице единичную, и будем преобразовывать
матрицу A, к виду единичной матрицы.
Тогда единичная матрица преобразуется
в обратную к матрице A.

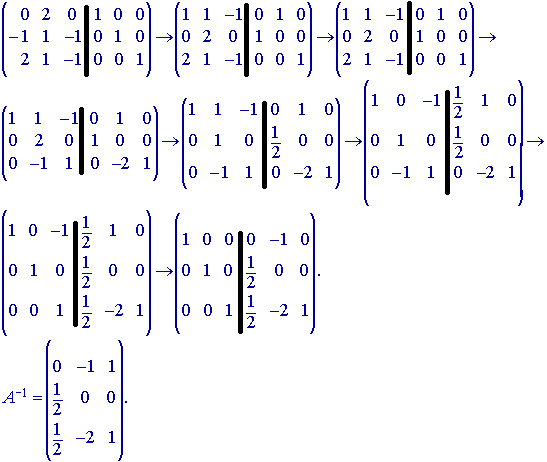
  1. Нахождение обратной
    матрицы по формуле:

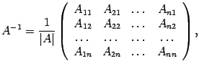
Пример.
Найдите обратную матрицу для
матрицы

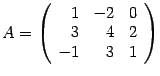
Решение.
Находим определитель

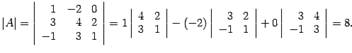
Так
как 

 то
матрица А – невырожденная, и обратная
для нее существует. Находим алгебраические
дополнения:

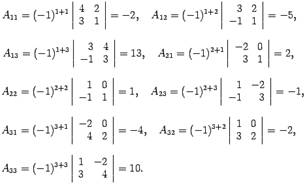
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй – строке:

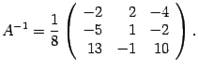
Полученная
матрица и служит ответом к задаче.

Билет 7. Решение систем линейных уравнений с помощью формул Крамера и с помощью обратной матрицы.

АХ=В

Умножим на А-1
обе части уравнения

А-1 * А * Х = А-1
*В

ЕХ = А-1В

Х

= А-1В

5х1 + 10х2 =
4

3х1 – х2 =
1

А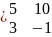
;

В =

;

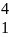
Х =

Метод Крамера
(правило Крамера) — способ решения
квадратных систем линейных алгебраических
уравнений (СЛАУ) с ненулевым определителем
основной матрицы (причём для таких
уравнений решение существует и оно
единственно)

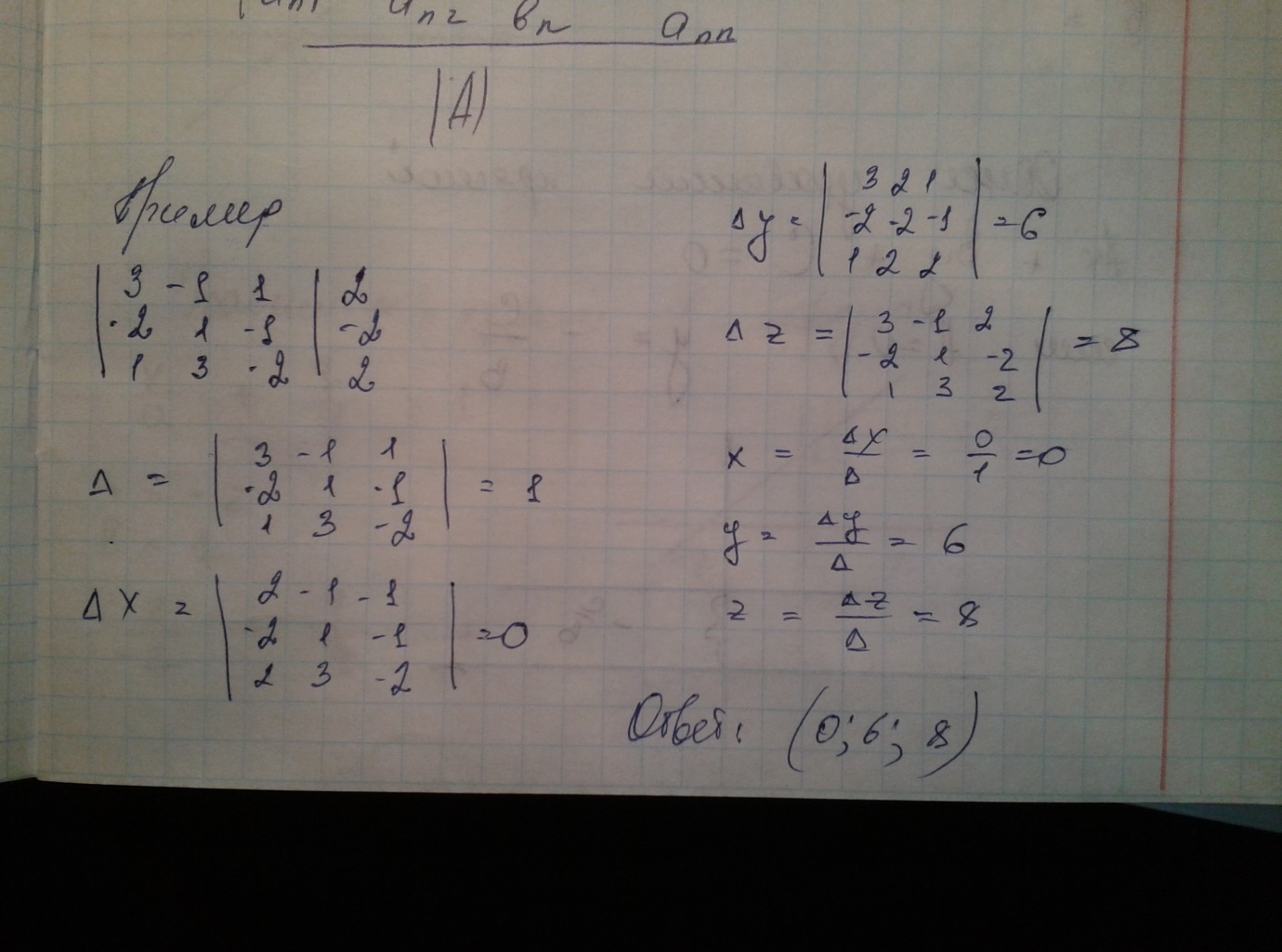
Билет 8. Векторы и линейные операции над ними. Арифметическое n-мерное векторное пространство Rn. Геометрический смысл пространств r2 и r1

Вектором называется
направленный отрезок.

Линейными
операциями
называются  операции сложения и
вычитания векторов и  умножения
вектора на число.

1. Сумма

векторов


и


находится
по правилу
треугольника

или
по  правилу
параллелограмма 


 

— эти
 правила равносильны.

Сложение
векторов
коммутативно и  ассоциативно:

2.
Разность векторов


можно
определить как сумму

,
т. е. вычитание заменяется прибавлением
противоположного вектора.  

Удобно
также правило
треугольника:
векторы

и

откладывают
от общего начала, тогда разность

есть
вектор, начало которого совпадает с
концом

,
а конец — с концом

3.
Произведением
 

(или  
)
вектора

на
действительное число λ называется
вектор

,
коллинеарный вектору

,
имеющий длину,  равную

,
и то же направление, что и вектор

,
если λ >
0, и направление, противоположное
направлению вектора

,
если λ <
0.

Так,  например,

есть
вектор, имеющий то же направление, что
и вектор

,
а длину, вдвое большую, чем вектор

(рис.
108).

В
случае, когда λ = 0 или

,
произведение

представляет
собой нулевой вектор.  

Противоположный
вектор

можно
рассматривать как результат умножения
вектора

на
λ = -1:

.

Очевидно, что

.

Множество
всех векторов размерности n называется
арифметическим n-мерным векторным
пространством и обозначается Rn.

Геометрический смысл
имеют лишь пространства R1, R2, R3 . Для R1 –
это прямая, для R2 – плоскость, для R3 –
трехмерное пространство.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Способы нахождения обратной матрицы

Пусть дана квадратная матрица A. Требуется найти обратную матрицу A^{-1}.

Первый способ. В теореме 4.1 существования и единственности обратной матрицы указан один из способов ее нахождения.

1. Вычислить определитель det{A} данной матрицы. Если det{A}=0, то обратной матрицы не существует (матрица A вырожденная).

2. Составить матрицу begin{pmatrix}A_{ij}end{pmatrix} из алгебраических дополнений A_{ij}=(-1)^{i+j}M_{ij} элементов матрицы A.

3. Транспонируя матрицу begin{pmatrix}A_{ij}end{pmatrix}, получить присоединенную матрицу A^{+}=(A_{ij})^{T}.

4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель det{A}:

A^{-1}=frac{1}{det{A}}cdot A^{+}.

Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.

1. Составить блочную матрицу (Amid E), приписав к данной матрице A единичную матрицу того же порядка.

2. При помощи элементарных преобразований, выполняемых над строками матрицы (Amid E), привести ее левый блок A к простейшему виду Lambda. При этом блочная матрица приводится к виду (Lambdamid S), где S — квадратная матрица, полученная в результате преобразований из единичной матрицы E.

3. Если Lambda=E, то блок S равен обратной матрице, т.е. S=A^{-1}. Если Lambdane E, то матрица A не имеет обратной.

В самом деле, при помощи элементарных преобразований строк матрицы (Amid E) можно привести ее левый блок A к упрощенному виду Lambda (см. рис. 1.5). При этом блочная матрица (Amid E) преобразуется к виду (Lambdamid S), где S — элементарная матрица, удовлетворяющая равенству Lambda=SA. Если матрица A невырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей Lambda=E. Тогда из равенства E=Lambda=SA следует, что S=A^{-1}. Если же матрица A вырожденная, то ее упрощенный вид Lambda отличается от единичной матрицы, а матрица A не имеет обратной.

Замечания 4.3

1. Для невырожденных квадратных матриц A=begin{pmatrix}a&b\c&dend{pmatrix} второго порядка можно указать простое правило нахождения обратной матрицы, следующее из первого способа:

а) поменять местами элементы на главной диагонали;

б) изменить знаки у элементов побочной диагонали;

в) поделить полученную матрицу на определитель det{A}=ad-bc.

В результате получим обратную матрицу

A^{-1}=frac{1}{ad-bc}!begin{pmatrix}d&-b\ -c&aend{pmatrix}!.

(4.2)

Действительно, следуя первому способу, имеем:

begin{aligned}&bold{1.}~det{A}=ad-bc;qquad bold{2.}~begin{pmatrix}A_{ij}end{pmatrix}= begin{pmatrix}d&-c\ -b&a end{pmatrix}!;\[5pt] &bold{3.}~A^{+}= begin{pmatrix}A_{ij} end{pmatrix}^T= begin{pmatrix}d&-b\-c&aend{pmatrix}!;quad bold{4.}~A^{-1}=frac{1}{ad-bc}= begin{pmatrix}d&-b\-c&aend{pmatrix}!,end{aligned}

2. Второй способ нахождения обратной матрицы при помощи элементарных преобразований данной матрицы может быть реализован следующим образом.

1. Составить блочную матрицу left(frac{A}{E}right), приписав к данной матрице A, единичную матрицу того же порядка.

2. При помощи элементарных преобразований над столбцами привести блочную матрицу к виду left(frac{E}{T}right). В полученной матрице блок T равен обратной матрице, т.е. T=A^{-1}.

Пример 4.2. Дана матрица A=begin{pmatrix}1&2\1&4end{pmatrix}. Найти обратную.

Решение. Первый способ. 1. Находим определитель det{A}= begin{vmatrix}1&2\1&4end{vmatrix}=2ne0 Поэтому матрица A невырожденная и, следовательно, имеет обратную.

2. Составляем матрицу из алгебраических дополнений:

begin{pmatrix}A_{ij}end{pmatrix}= begin{pmatrix}4&-1\ -2&1 end{pmatrix}!.

3. Транспонируя матрицу (A_{ij}), получаем присоединенную матрицу

A^{+}=begin{pmatrix}A_{ij}end{pmatrix}^T= begin{pmatrix}4&-2\-1&1 end{pmatrix}!.

4. Разделив все элементы присоединенной матрицы на определитель det{A}=2 находим обратную матрицу:

A^{-1}=frac{1}{2}cdot! begin{pmatrix}4&-2\-1&1end{pmatrix}= begin{pmatrix}2&-1\-1/2&1/2end{pmatrix}!.

Сделаем проверку begin{pmatrix}2&-1\-1/2&1/2end{pmatrix}!cdot! begin{pmatrix}1&2\1&4end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}!..

Используя правило, указанное в п.1 замечаний 4.3, для матрицы A=begin{pmatrix}1&2\ 1&4end{pmatrix}= begin{pmatrix}a&b\c&dend{pmatrix} получаем

A^{-1}=frac{1}{det{A}}! begin{pmatrix}d&-b\-c&aend{pmatrix}= frac{1}{2}! begin{pmatrix}4&-2\-1&1end{pmatrix}= begin{pmatrix}2&-1\-1/2&1/2 end{pmatrix}!.

Заметим, что det{A^{-1}}=frac{1}{2}=frac{1}{det{A}}.

Второй способ. 1. Составляем блочную матрицу

begin{pmatrix}Amid Eend{pmatrix}= begin{pmatrix}1&2!!&vline!!&1&0\ 1&4!!&vline!!&0&1end{pmatrix}!.

2. Элементарными преобразованиями над строками приводим ее к простейшему виду (Emid A^{-1}). Ко второй строке прибавляем первую строку, умноженную на (-1):

begin{pmatrix}Amid Eend{pmatrix}= begin{pmatrix} 1&2!!&vline!!&1&0\ 1&4!!&vline!!&0&1 end{pmatrix}sim begin{pmatrix} 1&2!!&vline!!&1&0\ 0&2!!&vline!!&-1&1 end{pmatrix}!.

Теперь к первой строке прибавим вторую, умноженную на (-1):

begin{pmatrix}1&2!!&vline!!&1&0\ 0&2!!&vline!!&-1&1end{pmatrix}sim begin{pmatrix}1&0!!&vline!!&2&-1\ 0&2!!&vline!!&-1&1end{pmatrix}!.

Для получения в левом блоке единичной матрицы надо разделить вторую строку на 2:

begin{pmatrix}1&0!!&vline!!&2&-1\ 0&2!!&vline!!&-1&1end{pmatrix}sim begin{pmatrix}1&0!!&vline!!&2&-1\ 0&1!!&vline!!&-1/2&1/2end{pmatrix}!.

В правом блоке получили обратную матрицу A^{-1}=begin{pmatrix}2&-1\ -1/2&1/2 end{pmatrix}.

Пример 4.3. Дана матрица A=begin{pmatrix}1&2&1\ 0&1&0\0&2&2 end{pmatrix}. Найти обратную.

Решение. Первый способ. 1. Находим определитель матрицы det{A}=2.

2. Находим алгебраические дополнения данной матрицы:

begin{array}{lll} A_{11}=(-1)^{1+1}!begin{vmatrix}1&0\2&2end{vmatrix}=2;&quad A_{12}=(-1)^{1+2}!begin{vmatrix}0&0\0&2end{vmatrix}=0;&quad A_{13}=(-1)^{1+3}!begin{vmatrix}0&1\0&2end{vmatrix}=0;\\[-5pt] A_{21}=(-1)^{2+1}!begin{vmatrix}2&1\2&2end{vmatrix}=-2;&quad A_{22}=(-1)^{2+2}!begin{vmatrix}1&1\0&2end{vmatrix}=2;&quad A_{23}=(-1)^{2+3}!begin{vmatrix}1&2\0&2end{vmatrix}=-2;\\[-5pt] A_{31}=(-1)^{3+1}!begin{vmatrix}2&1\1&0end{vmatrix}=-1;&quad A_{32}=(-1)^{3+2}!begin{vmatrix}1&1\0&0end{vmatrix}=0;&quad A_{33}=(-1)^{3+3}!begin{vmatrix}1&2\0&1end{vmatrix}=1. end{array}

и составляем из них матрицу (A_{ij})= begin{pmatrix}2&0&0\ -2&2&-2\ -1&0&1end{pmatrix}.

Транспонируя матрицу (A_{ij}), получаем присоединенную матрицу

A^{+}=begin{pmatrix}A_{ij}end{pmatrix}^T= begin{pmatrix}2&-2&-1\ 0&2&0\ 0&-2&1 end{pmatrix}!.

4. Разделив все элементы присоединенной матрицы на
определитель det{A}=2, получим обратную матрицу:

A^{-1}=frac{1}{det{A}}cdot A^{+}= begin{pmatrix}1&-1&-1/2\ 0&1&0\ 0&-1&1/2 end{pmatrix}!.

Проверим равенство A^{-1}A=E:

begin{pmatrix}1&-1&-1/2\ 0&1&0\ 0&-1&1/2end{pmatrix}!cdot! begin{pmatrix} 1&2&1\0&1&0\0&2&2end{pmatrix}= begin{pmatrix}1&0&0\0&1&0\ 0&0&1 end{pmatrix}!.

Второй способ. 1. Составим блочную матрицу (Amid E), приписав к матрице A единичную матрицу того же порядка:

(Amid E)= begin{pmatrix}1&2&1!!&vline!!&1&0&0\ 0&1&0!!&vline!!&0&1&0\ 0&2&2!!&vline!!&0&0&1 end{pmatrix}!.

2. Элементарными преобразованиями над строками приводим ее к виду (Emid A^{-1})colon

(Amid E)sim begin{pmatrix}1&0&1!!&vline!!&1&-2&0\ 0&1&0!!& vline!!&0&1&0\ 0&0&2!!&vline!!&0&-2&1end{pmatrix}sim begin{pmatrix} 1&0&1!!& vline!!&1&-2&0\ 0&1&0!!&vline!!&0&1&0\ 0&0&1!!& vline!!&0&-1&1/2end{pmatrix}sim begin{pmatrix} 1&0&0!!& vline!!&1&-1&-1/2\ 0&1&0!!& vline!!&0&1&0\ 0&0&1!!& vline!!&0&-1&1/2end{pmatrix}!.

В правом блоке получаем обратную матрицу A^{-1}=begin{pmatrix}1&-1&-1/2\ 0&1&0\ 0&-1&1/2 end{pmatrix}.

Обращение блочных матриц

Пусть квадратная невырожденная матрица Q (m+n)-го порядка разбита на блоки

Q=begin{pmatrix}A!!&vline!!&B\hline C!!&vline!!&D end{pmatrix}!,

где A– невырожденная квадратная матрица m-го порядка, а B,,C,,D -произвольные матрицы размеров mtimes n, ntimes m ntimes n соответственно.

Обратная матрица Q существует и находится по формуле Фробениуса

Q^{-1}=begin{pmatrix}A^{-1}+A^{-1}BNCA^{-1}!!&vline!!&-A^{-1}BN\hline -NCA^{-1}!!&vline!!&N end{pmatrix}!,

(4.3)

где N=(D-CA^{-1}B)^{-1}. Эта формула сводит обращение матрицы (m+n)-го порядка к обращению двух матриц A и N меньшего порядка (m и n соответственно).

Если предположить, что матрица D — невырожденная (вместо матрицы A), то формула имеет вид:

Q^{-1}=begin{pmatrix}M!!&vline!!&-MBD^{-1}\hline -D^{-1}CM!!&vline!!& D^{-1}+D^{-1}CMBD^{-1} end{pmatrix}!.

где M=(A-BD^{-1}C)^{-1} — квадратная матрица m-го порядка.

Наконец, если обе матрицы A и D невырожденные, то

Q^{-1}=begin{pmatrix}M!!&vline!!&-MBD^{-1}\hline -D^{-1}CM!!&vline!!&N end{pmatrix}= begin{pmatrix}M!!&vline!!&-A^{-1}BN\hline -NCA^{-1}!!&vline!!&N end{pmatrix}!,

(4.4)

где, как и ранее, M=(A-BD^{-1}C)^{-1},~N=(D-CA^{-1}B)^{-1} — квадратные матрицы порядков m и n соответственно.

Доказательство формул (4.3), (4.4) сводится к умножению блочных матриц.

Пример 4.4. Найти обратную для блочной матрицы

Q= Q=begin{pmatrix}1&-1!!&vline!!&0&1\ -1&2!!&vline!!&-1&0\hline 0&2!!&vline!!& 0&1\ 2&0!!&vline!!& 1&2end{pmatrix}= begin{pmatrix} A!!&vline!!&B\hline C!!&vline!!&Dend{pmatrix}!.

Решение. Матрица A — невырожденная второго порядка. Применяя правило (4.2), последовательно находим:

begin{gathered}A^{-1}=begin{pmatrix}1&-1\-1&2end{pmatrix}^{-1}=begin{pmatrix}2&1\1&1end{pmatrix}!;qquad CA^{-1}=begin{pmatrix}0&2\2&0end{pmatrix}!cdot! begin{pmatrix}2&1\1&1end{pmatrix}= begin{pmatrix}2&2\4&2end{pmatrix}!;hfill\[5pt] D-CA^{-1}B= begin{pmatrix}0&1\1&2end{pmatrix}- begin{pmatrix}2&2\4&2end{pmatrix}!cdot! begin{pmatrix}0&1\-1&0end{pmatrix}= begin{pmatrix}0&1\1&2end{pmatrix}- begin{pmatrix} -2&2\-2&4end{pmatrix}= begin{pmatrix}2&-1\3&-2end{pmatrix}!;hfill\[5pt]<br />N=(D-CA^{-1}B)^{-1}= frac{1}{-1}! begin{pmatrix}-2&1\-3&2end{pmatrix}= begin{pmatrix} 2&-1\3&-2end{pmatrix}hfill\[5pt] A^{-1}B=begin{pmatrix}2&1\1&1end{pmatrix}!cdot! begin{pmatrix}0&1\-1&0end{pmatrix}= begin{pmatrix}-1&2\-1&1end{pmatrix}!;quad A^{-1}BN=begin{pmatrix}-1&2\-1&1end{pmatrix}!cdot! begin{pmatrix}2&-1\3&-2end{pmatrix}= begin{pmatrix}4&-3\1&-1end{pmatrix}!;hfill\[5pt] A^{-1}BNCA^{-1}= begin{pmatrix} 4&-3\1&-1 end{pmatrix}!cdot! begin{pmatrix}2&2\4&2 end{pmatrix}= begin{pmatrix} -4&2\-2&0 end{pmatrix}!;quad A^{-1}+A^{-1}BNCA^{-1}= begin{pmatrix} -2&3\-1&1 end{pmatrix}!; hfill\[5pt] NCA^{-1}= begin{pmatrix}2&-1\3&-2end{pmatrix}!cdot! begin{pmatrix} 2&2\4&2 end{pmatrix}= begin{pmatrix}0&2\-2&2end{pmatrix}!. end{gathered}

По формуле (4.3) имеем

Q^{-1}= begin{pmatrix} -2&3!!&vline!!&-4&3\ -1&1!!&vline!!&-1&1\hline 0&-2!!&vline!!&2&-1\ 2&-2!!&vline!!&3&-2 end{pmatrix}!.

Учитывая, что матрица D в данной блочной матрице Q является невырожденной, обратную матрицу Q^{-1} можно aнайти по формуле (4.4). Вычисляем левый верхний блок матрицы Q^{-1} (остальные блоки такие же как формуле (4.3):

begin{gathered}A-BD^{-1}C= begin{pmatrix}1&-1\-1&2end{pmatrix}- begin{pmatrix}0&1\-1&0end{pmatrix}!cdot! begin{pmatrix}-2&1\1&0end{pmatrix}!cdot! begin{pmatrix}0&2\2&0end{pmatrix}= begin{pmatrix}1&-1\-1&2 end{pmatrix}- begin{pmatrix} 0&2\-2&4end{pmatrix}=begin{pmatrix}1&-3\ 1&-2end{pmatrix}!;hfill\[5pt] M=begin{pmatrix} A-BD^{-1}Cend{pmatrix}^{-1}= begin{pmatrix}1&-3\1&-2end{pmatrix}^{-1}= begin{pmatrix} -2&3\-1&1end{pmatrix}!. end{gathered}

Результаты вычислений по формулам (4.3) и (4.4) совпадают.

Замечание 4.4. Если определитель Delta=begin{vmatrix}A!!&vline!!&B\hline C!!&vline!!&Dend{vmatrix} разбит на четыре блока, где матрицы A и D — квадратные,то справедливы формулы:

Delta=|A|cdot|D-CA^{-1}B| при |A|ne0,;

Delta=|A-BD^{-1}C|cdot|D| при |D|ne0,.

В частном случае, когда все четыре матрицы A,,B,,C,,D квадратные одного и того же порядка, справедливы формулы Шура:

Delta=|AD-ACA^{-1}B| при |A|ne0,;

Delta=|AD-BD^{-1}CD| при |D|ne0,.

Если матрицы A и C перестановочны (AC=CA), то Delta=|AD-CB|, а если матрицы C и D перестановочны, то Delta=|AD-BC|.

Докажем, например, формулу Delta=|A|cdot|D-CA^{-1}B|. Пусть A и D -квадратные матрицы m-го и n-го порядков соответственно, причем |A|ne0. Составим блочную матрицу S=begin{pmatrix}E_m!!&vline!!&O\hline -CA^{-1}!!&vline!!&E_nend{pmatrix}, где O — нулевая матрица размеров mtimes n. Матрицу S можно рассматривать как элементарную блочную матрицу, так как она получена из единичной блочной матрицы E_{m+n}= begin{pmatrix} E_m!!&vline!!&O\hline O^{T}!!& vline!!& E_nend{pmatrix} в результате прибавления ко второй ее строке блоков первой строки блоков, умноженных на матрицу (-CA^{-1}). Умножим блочную матрицу begin{pmatrix}A!!&vline!!&B\hline C!!& vline!!&Dend{pmatrix} слева на матрицу S:

begin{pmatrix}E_m!!&vline!!&O\hline -CA^{-1}!!& vline!!& E_nend{pmatrix} !cdot! begin{pmatrix}A!!&vline!!&B\hline C!!& vline!!&Dend{pmatrix}= begin{pmatrix} A!!&vline!!&B\hline O^T!!& vline!!&D-CA^{-1}Bend{pmatrix}

Найдем определители матриц в левой и правой частях этого равенства. Определитель матрицы S равен единице, так как это нижняя треугольная числовая матрица с единицами на главной диагонали (см. п.1 замечаний 2.2). Определитель матрицы в правой части равен |A|cdot|D-CA^{-1}B|, так как это блочно-треугольная матрица (см. п.2 замечаний 2.4). По теореме 2.2 об определителе произведения матриц получаем доказываемую формулу

begin{array}{|c|c|}E_m&O\hline -CA^{-1}& E_nend{array} cdot begin{array}{|c|c|}A&B\hline C&Dend{array}= begin{array}{|c|c|}A&B\hline O^{T}& D-CA^{-1}Bend{array}quad Leftrightarrowquad 1cdotDelta= |A|cdot|D-CA^{-1}B|.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Добавить комментарий