Если — квадратная и
неособенная матрица, то для нее существует обратная матрица
. Если же
— не квадратная,
а прямоугольная -матрица
() или
квадратная, но особенная, то матрица не имеет
обратной и символ не имеет смысла. Однако, как
будет показано далее, для произвольной прямоугольной матрицы
существует
«псевдообратная» матрица , которая
обладает некоторыми свойствами обратной матрицы и имеет важные применения при
решении системы линейных уравнений. В случае, когда — квадратная неособенная матрица,
псевдообратная матрица совпадает с обратной
.
1. Скелетное разложение матрицы. В дальнейшем мы
будем пользоваться представлением произвольной прямоугольной -матрицы
ранга
в виде произведения
двух матриц и
, имеющих соответственно размеры
и
:

. (36)
Здесь ранги сомножителей и
обязательно равны
рангу произведения ,
. Действительно (см. стр. 22),
Но ранги
и
не могут
превосходить ,
так как —
один из размеров матриц и
. Поэтому
.
Для того чтобы получить
разложение (36), достаточно в качестве столбцов матрицы взять любые
линейно независимых
столбцов матрицы ,
либо любые линейно
независимых столбцов, через которые линейно выражаются столбцы матрицы . Тогда произвольный
-й столбец
матрицы будет
линейной комбинацией столбцов матрицы с коэффициентами
; эти коэффициенты и образуют
-й столбец
матрицы (
, см. стр. 19).
Поскольку
матрицы и
имеют
максимально возможный ранг , то квадратные матрицы
и
являются
неособенными:
,
.
(37)
Действительно, пусть столбец — произвольное
решение уравнения
.
(38)
Помножим это уравнение слева на строку . Тогда
. Отсюда следует
и (поскольку
— линейная
комбинация линейно независимых столбцов матрицы ; ср. с формулой (13″))
. Из того, что
уравнение (38) имеет только нулевое решение , вытекает, что
. Аналогично устанавливается
второе неравенство (37).
Разложение (36) будем называть скелетным разложением
матрицы .
2. Существование и единственность псевдообратной
матрицы. Рассмотрим матричное уравнение
.
(39)
Если — квадратная неособенная матрица, то
это уравнение имеет единственное решение . Если же
— произвольная прямоугольная
-матрица, то искомое
решение имеет
размеры но
не определяется однозначно. В общем случае уравнение (39) имеет бесчисленное
множество решений. Ниже будет показано, что среди этих решений имеется только
одно, обладающее тем свойством, что его строки и столбцы являются линейными
комбинациями соответственно строк и столбцов сопряженной матрицы . Именно это решение
мы будем называть псевдообратной матрицей для и обозначать через
.
Определение 5. Матрица размеров
называется псевдообратной для
-матрицы
, если выполняются
равенства
, (40)
, (41)
где и
— некоторые матрицы
Докажем сначала, что для данной матрицы не может существовать
двух различных псевдообратных матриц и
. Действительно, из равенств
,
,
,
Полагая ,
,
, найдем:
,
.
Отсюда
и, следовательно (см. конец § 3),
.
Но тогда , т.е.
.
Для того чтобы установить существование матрицы , мы воспользуемся
скелетным разложением (36) и будем искать сначала псевдообратные матрицы и
. Так как по
определению должны иметь место равенства
,
(42)
где — некоторая матрица, то
.
Умножая слева на и замечая, что
— неособенная квадратная
матрица, найдем:
.
Но тогда второе из равенств (42) дает искомое
выражение для :
. (43)
Совершенно аналогично найдем:
. (44)
Покажем теперь, что матрица
(45)
удовлетворяет условиям (40), (41)
и, следовательно, является псевдообратной матрицей для .
В самом деле,
.
С другой стороны, из равенств (43),
(44) и (45) с учетом равенства , полагая
, находим
,
,
где
,
.
Таким образом доказано, что для
произвольной прямоугольной матрицы существует одна и только одна псевдообратная матрица
, которая определяется формулой (45), где
и
— сомножители в скелетном разложении
матрицы
.
Из самого определения псевдообратной матрицы непосредственно следует, что в
случае квадратной неособенной матрицы псевдообратная матрица
совпадает с обратной
.
Пример. Пусть

Здесь . в качестве
столбцов матрицы первые два
столбца матрицы . Тогда
и
,

,

Поэтому,
согласно формуле (45)
3. Свойства
псевдообратной матрицы. Отметим
следующие свойства псевдообратной матрицы:
1 ;
2 ;
3 ,
;
4 ,
.
Первое свойство означает, что
операции перехода к сопряженной и к псевдообратной матрице перестановочны между
собой. Равенство 2° выражает собой взаимность понятия псевдообратной матрицы,
тан как согласно 2° псевдообратной матрицей для является
исходная матрица . Согласно равенствам 3° и 4°
матрицы и
являются
эрмитовыми и инволютивными (квадрат каждой из этих
матриц равен самой матрице).
Для вывода равенства 1°
воспользуемся скелетным разложением (36): . Тогда
равенство дает скелетное
разложение матрицы . Поэтому, заменяя в формуле
(45) матрицу на
, а матрицу
на
,
получим:
.
Равенства ,
,
являются скелетными
разложениями. Следовательно,
.
Используя свойство 1°, а также
выражения для и
, найдем:
.
Справедливость равенств 3° и 4°
проверяется непосредственно путем подстановки в эти равенства вместо соответствующего
выражения из формулы (45).
Заметим, что в общем случае, когда
разложение не
является скелетным, не всегда имеет место равенство . Так,
например
.
Здесь
,
,

Поэтому
.
4. Наилучшее
приближенное решение (по методу
наименьших квадратов). Рассмотрим произвольную систему линейных уравнений

или в
матричной записи
. (46′)
Здесь
–
заданные
числа, а –
искомые.
В
общем случае система (46) может быть и несовместной.
Столбец
(47)
называется наилучшим приближенным решением системы (46), если при значениях «квадратичное
отклонение»

(48)
достигает своего наименьшего
значения и среди всех столбцов , для которых это отклонение имеет минимальное
значение, столбец имеет наименьшую «длину», т. е. для этого столбца
величина

имеет наименьшее значение.
Покажем, что система (46) всегда
имеет одно и только одно наилучшее приближенное решение и это приближенное
решение определяется по формуле
, (50)
где — псевдообратная матрица для матрицы
.
Для этого рассмотрим произвольный
столбец и
положим
,
где
,
. (51)
Тогда
. (52)
Но
. (53)
Исходя из разложения (36) и формулы
(45), найдем:
.
Поэтому из равенства
(53) следует
,
(54)
но тогда и
.
(54′)
Поэтому
из равенства (52) находим
,
(55)
и,
следовательно, для любого столбца
.
(56)
Пусть
теперь
;
тогда,
согласно равенству (55)
,
(57)
где
.
С другой
стороны,
.
(58)
Вспоминая,
что (см.определение
5), получим в силу (57):
. (59)
Но
тогда и
.
Поэтому
из равенства (58) находим
,
и,
следовательно
,
(60)
причем
знак = имеет место только при , т.е. при
, где
.
Пример.
Найти наилучшее приближенное решение (по методу наименьших квадратов) системы
линейных уравнений:
,
,
.
Здесь

Но
тогда (см. пример на стр. 35)

и
поэтому

Следовательно,
,
,
,
.
Определим
норму
– матрицы
как
неотрицательное число, задаваемое формулой
.
(61)
При
этом очевидно, что
.
(61′)
Рассмотрим
матричное уравнение
,
(62)
где
и
– заданные
и
-матрицы, а
– искомая
-матрица.
Определим
наилучшее приближенное решение уравнения (62) из условия
,
причем
в случае, когда
,
требуется,
чтобы
.
Из
соотношений
,
(63)
(64)
следует,
что -й
столбец искомой матрицы должен быть наилучшим приближенным
решением системы линейных уравнений
Поэтому
Поскольку
это равенство справедливо при любом то
.
(65)
Таким
образом, уравнение (62) всегда имеет одно и только одно наилучшее приближенное
решение, определяемое формулой (65).
В
частном случае, когда — единичная матрица
-го порядка, имеем
. Следовательно,
псевдообратная матрица является наилучшим приближенным
решением (по методу наименьших квадратов) матричного уравнения
.
Это
свойство псевдообратной матрицы может быть принято в
качестве ее определения.
5.
Метод Гревилля последовательного нахождения псевдообратной матрицы состоит в
следующем. Пусть –
-й столбец в
-матрице
,
— матрица, образованная
первыми столбцами
матрицы .
—
последняя строка в матрице (
,
,
). Тогда

и
для имеют
место рекуррентные формулы

,
;
(67)
при
этом, если ,
то
;
(68)
если
же , т.е.
, то
.
(69)
Предлагаем читателю проверить, что
матрица является
псевдообратной для матрицы , если матрица
и строка
определяются формулами (61)-(64). Этот метод не
требует вычисления детерминантов и может быть использован для вычисления
обратной матрицы. Пример. Пусть

Заметим.
Что для каждой матрицы мы можем писать
вместо
. Тогда
,
,

,
.
Таким
образом

Далее
и
.
Поэтому
и

Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} – (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
1.
Как известно, для каждого числа
существует такое число
,
что.
Числоназывается обратным для
.
Если мы зафиксируем натуральное числои будем рассматривать квадратные матрицы
-го
порядка, то в этом множестве матриц
единичная матрицабудет играть роль единицы. Естественно
поставить вопрос о существовании
обратной матрицы, т.е. такой матрицы,
которая в произведении с данной матрицей
дает единичную.
Пусть
– квадратная матрица
-го
порядка. Квадратная матрица(того же порядка
)
называется обратной для,
если
.
Матрицу,
обратную к матрице
,
принято обозначать символом.
2. Способы вычисления обратной матрицы
Если
для квадратной матрицы
существует обратная матрица
,
то справедливо равенство,
где– единичная матрица. Переходя в этом
равенстве к определителям (и учитывая
свойство 9 определителей), имеем,
или.
Отсюда заключаем, что(в противном случае левая часть последнего
равенства равнялась бы нулю). Этим
доказано, что если,
то для матрицыне существует обратной. Другими словами,
условиеявляется необходимым условием
существования обратной матрицы.
Оказывается, это условие является и
достаточным.
Лемма
Если
обратная матрица существует, то она
единственна.
Квадратная
матрица
называетсяневырожденной,
если ее определитель не равен нулю (
). В противном случае матрица
называетсявырожденной
(
).
Пусть
матрица
имеет вид

ТЕОРЕМА.
Если
– невырожденная матрица, то для нее
существует обратная матрица,
которая вычисляется по формуле
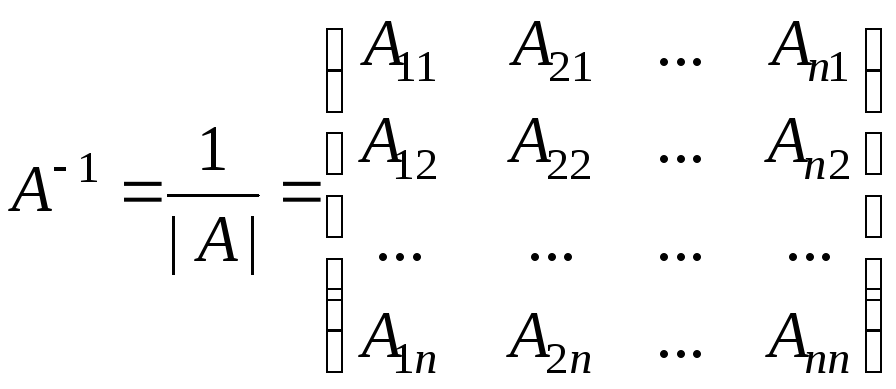
(5)
где
– алгебраическое дополнение для элемента
матрицы
.
Замечание
Обратим
внимание на расположение чисел
в правой
части формулы (5): число
расположено не в
-й
строке и-м
столбце, а наоборот, в-й
строке и-м
столбце. Таким образом, матрица, стоящая
в правой части (5), является транспонированной
матрицей алгебраических дополнений
элементов матрицы.
Типовой
пример.
Найдите
,
если
►
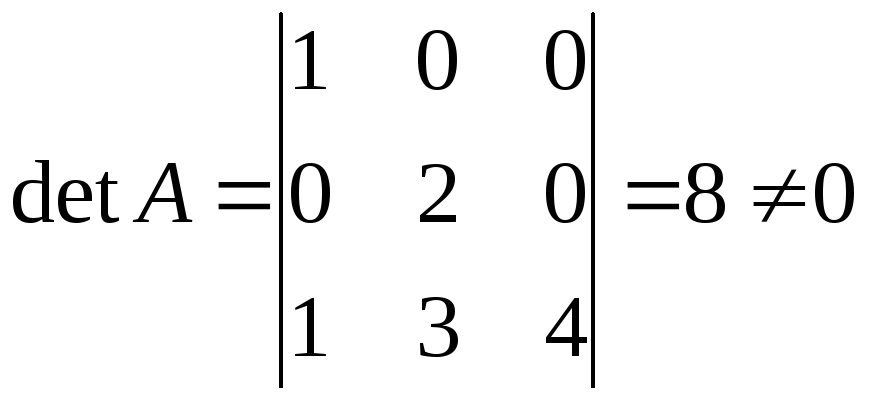
– невырожденная матрица, следовательно,
обратная для нее существует. Найдем ее
по формуле:

Обратите
внимание на
индексацию
алгебраических дополнений. Вычисляем
алгебраические дополнения
;
;
;
;
;
;
;
;
.
Тогда

Можно сделать
проверку:

Значит,
обратная матрица найдена верно.◄
3. Вычисление обратной матрицы методом элементарных преобразований. Элементарные преобразования матрицы
-
Перестановка
строк (столбцов). -
Умножение
строки (столбца) на число
.
3.
Прибавление к элементам строки (столбца)
соответствующих элементов другой строки
(столбца), предварительно умноженных
на любое число.
Чтобы
найти матрицу, обратную данной, делаем
следующее:
для
матрицы
записываем прямоугольную матрицу
,
приписывая справа единичную матрицу;
с
помощью элементарных преобразований
приводим матрицу
к виду
.
Тогда.
Эквивалентные матрицы обозначаются.
Типовой
пример
Найти
матрицу, обратную данной:
.
►~(первую
строку матрицы умножили на
)
~~
~
~
.
Следовательно,
.
Проверка:
.
◄
С
помощью обратной матрицы можно решать
простейшие матричные
уравнения,
где неизвестной является матрица X.
Это уравнения следующего вида
.
В
этих уравнениях
– матрицы таких размеров, что все
операции умножения возможны и с обеих
сторон от знаков равенств находятся
матрицы одинаковых размеров. Если в
первых двух уравнениях матрицаневырожденная, то их единственное
решение записывается следующим образом
соответственнои
.
Если в третьем матричном уравнении
матрицы
и
невырождены,
то его решение записывается в виде
.
Пример
В
табл. 6 приведены данные о дневной
производительности пяти предприятий,
выпускающих четыре вида продукции с
потреблением трех видов ресурсов, а
также количество рабочих дней в году
каждого предприятия и цены каждого вида
сырья.
Таблица 6
|
Вид |
Производительность |
Затраты |
||||||
|
1 |
2 |
3 |
4 |
5 |
1 |
2 |
3 |
|
|
1 |
4 |
5 |
3 |
6 |
7 |
2 |
3 |
4 |
|
2 |
0 |
2 |
4 |
3 |
0 |
3 |
5 |
6 |
|
3 |
8 |
15 |
0 |
4 |
6 |
4 |
4 |
5 |
|
4 |
3 |
10 |
7 |
5 |
4 |
5 |
8 |
6 |
|
Кол-во |
Цены |
|||||||
|
200 |
150 |
170 |
120 |
140 |
40 |
50 |
60 |
Требуется найти:
1)
годовую производительность каждого
предприятия по каждому виду продукции;
2)
годовую потребность каждого предприятия
по каждому виду ресурса;
3)
годовую сумму кредитования каждого
предприятия для закупки ресурсов,
необходимых для выпуска продукции
указанных видов и при определенном
количестве рабочих дней.
►Введем следующие
обозначения:
а)
Данная матрица является матрицей
производительности пяти предприятий
по всем четырем видам продукции. Каждый
столбец этой матрицы соответствует
дневной производительности отдельного
предприятия по каждому виду изделий.
Следовательно, годовая производительность
-го
предприятия по каждому виду изделий
получается умножением-го
столбца матрицы А на количество рабочих
дней в году для этого предприятия (к =
1,2,3,4,5)
А11=0,79
А21=0,16
А31=0,02
А12=0,16
А22=0,8
А32=0,1
А13=0,02
А23=0,1
А33=0,96,
тогда

Это
матрица коэффициентов полных материальных
затрат.
б)

т.е. валовой выпуск продукции 1-го, 2-го
и 3-го цехов будут соответственно.
в)
Найдем производственную программу
каждого цеха (промежуточный продукт)
по формуле
(
;
)
;
;
;
;
;
;
;
;
.
Результаты
представим в таблице 7:
Таблица
7
|
Цех |
Внутрипроизводственные |
Итого |
Конечный |
Валовый |
||
|
1 |
2 |
3 |
||||
|
1 2 3 |
0 48 0 |
37 0 19 |
0 40 80 |
37 88 99 |
200 100 300 |
237 186 400 |
г)
Коэффициенты косвенных затрат
определяются
как разности полных внутрипроизводственных
затрат
и прямых затрат
.
В матричной форме:


4.
Невырожденная
квадратная матрица
,
для которой,
называетсяортогональной.
Свойства
ортогональных матриц, играющих важную
роль во многих приложениях, можно
сформулировать в виде следующих теорем.
ТЕОРЕМА.
Для
ортогональной матрицы
справедливо равенство
.
ТЕОРЕМА.
Каждая
ортогональная матрица второго порядка
,
для которойможет быть представлена в виде
,
где
– некоторое число, а каждая ортогональная
матрица с
– в виде
.
может ли быть обратная матрица для не квадратной матрицы
Ученик
(69),
закрыт
2 года назад
chi-QN-off
Просветленный
(38475)
13 лет назад
Может, если исходить только из определения, что обратной называется такая матрица, при умножении на которую для заданной матрицы получаем единичную квадратную матрицу.
При этом нужно учесть, что при перестановке матриц сомножителей (при коммутации) могут получаться единичные квадратные матрицы разного порядка.
Например, матрицу с двумя строками и тремя столбцами умножаем справа на матрицу с тремя строками и двумя столбцами. Результатом может быть единичная матрица 2х2. А если переставить матрицы местами в произведении, то получим (если существует) единичную матрицу 3х3.
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |





