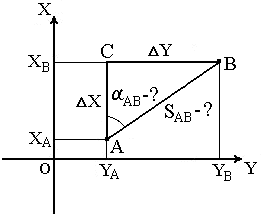Как найти обратные координаты

 Актуальные цены на услуги геодезистов в Москве и Московской области  в 2022 году.

Решение обратной геодезической задачи онлайн

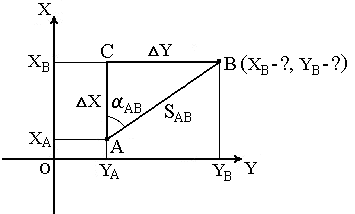
Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB

Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.

Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

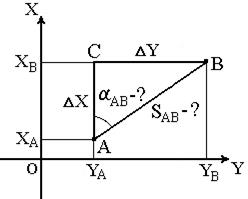
Величину угла r_AB определяем из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

Решение обратной геодезической задачи

Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точек А(X_A, Y_A) и В(X_B, Y_B) необходимо найти длину S_AB и направление линии АВ: осевой румб r_AB и дирекционный угол a_AB (рис. 10).

Координаты точекА(X_A, Y_A) и В(X_B, Y_B) определяют при решении предыдущей задачи (см. п.1.4.2).

Данная задача решается следующим образом.

Сначала находим приращения координат

Рис. 10. Обратная геодезическая задача

Величину осевого румба r_AB определяем из отношения

.

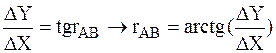
По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности, в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

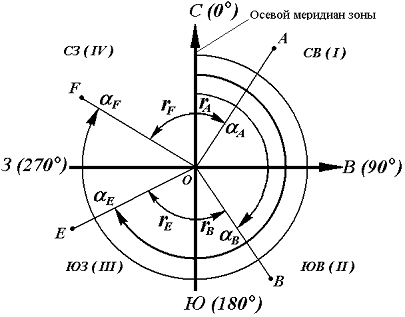
Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим a_AB.

Рис. 11. Осевые румбы и дирекционные углы

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = a ,

II четверть (ЮВ) r = 180° – a ,

III четверть (ЮЗ) r = a – 180° ,

IV четверть (СЗ) r = 360° – a .

Расстояние S_AB определяем по формуле

.

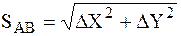
Для контроля расстояние S_AB вычисляют дважды по формулам:

,

.

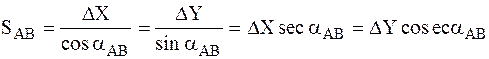
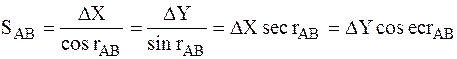
Пример.Координаты точек:А(5998.650 км, 2396.750 км);

В(6000.150 км, 2395.250 км).

Вычисляем осевой румб r_AB из отношения

,

.

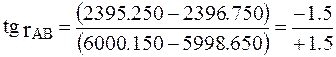
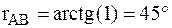
По знакам приращений координат ΔX>0 и ΔY

Лучшие изречения:

Начинайте делать все, что вы можете сделать – и даже то, о чем можете хотя бы мечтать. В смелости гений, сила и магия. © Иоганн Вольфганг Гете
==> читать все изречения. 175 — | 164 —

Источник

Решение обратной геодезической задачи

Основой решения является расчетная схема рис.1.5.

1. Выписать исходную информацию (расчетная схема соответствует рис.1.10).

2. Вычислить приращения координат по формулам (1.6).

3. На микрокалькуляторе вычислить румб и длину линии по формулам (1.7)-(1.8).

4. По знакам приращений определить название румба в соответствии с рис.1.6.

5. От румба перейти к дирекционному углу по формулам связи (рис.1.4).

6. Сравнить вычисленные значения с измеренными. Расхождения не должны превышать 2 мм в длине линии и 1 0 в дирекционном угле.

Задача решается на микрокалькуляторе. Но при этом непосредственно определить угол  по формуле:=arc tg(у/х), вытекающей из уравнений (1.4), невозможно из-за неоднозначного решения задачи. Так прих отрицательном,у положительном их положительном,у отрицательном получим одинаковые значения. Для контроля вычисления можно выполнить через радианы. Связь между градусами и радианами:

r рад =r 0 / 57.29578 ;r 0 =r рад 57.29578. (1.10)

2. Приращения координат: x=X_B -X_A=6064410 — 6065675 = -1265 м,y=У_В— У_А= -188318–(- 188030) = — 288 м.

3. Румб линии через градусы, установив программу DEG:

/r/ = arc tg ( Δу / Δх )=”288” : ” 1265” = ”2ndF» tg -1 ” = 12.826 0 = 12 0 50′ .

Длина линии (программа DEG):

d=x/Cosr=“12.826“Cos”2ndF“1/x”×”1265”=1297 м. Второе вычисление:d=y/Sinr=“12.826“Sin”2ndF“1/x”×”288” = 1297 м. Расхождений в вычислениях не должно быть.

4. В соответствии со знаками приращений румб r = ЮЗ:12 0 50′.

5. Дирекционный угол = 192 0 50′.

6. Расхождение в длине линии 3 м, в румбе 10′. Расхождения допустимы.

Пример вычисления румба через радианы. Программа RAD:

arctg(Δу/Δх )=”288”:”1265“=“2ndF»tg -1 ”=»×»57.2958″=12.826 0 =12 0 50′.

Вычисления следует выполнять по разным формулам. Так, решение прямой задачи выполняется через дирекционные углы по формулам (1.4) и через румбы по формулам (1.5), кроме первой четверти. В северо-восточной части r= , контроля не будет. В этом случае, как и при решении обратной задачи, вычисления следует вести через градусы и через радианы.

Определение отметок точек

Отметки точек определяют по правилам, см. фрагмент листа карты (рис.1.1).

1. Точка лежит на горизонтали. Отметка точки равна отметке горизонтали: Н₁=152.5 м.

2. Точка лежит между разноименными горизонталями. Отметка точки определяется графической интерполяцией на глаз: Н₂=150+2.5/3=150.8 м.

3. Седловина. Отметка точки равна отметке ближней горизонтали ± полсечения рельефа: Н₃=152.5+h/2=153.8 м или 155 – h/2 = 153.8 м.

4. Определяемая точка лежит между горизонталью и точкой с подписанной на карте отметкой. Отметка определяется графической интерполяцией: Н₄=155+(156.9–155)/2=155.7 м.

5. Точка лежит на полугоризонтали: Н₅ = 155 +h/ 2 = 156.2 м.

6 и 7. Отметки вершин: H₆ =155 +h/ 2 = 156.2 м;H₇ = 156.25 (полугоризонталь)+h/4=156.8 м.

Источник

Обратная геодезическая задача.

Обратная геодезическая задача (ОГЗ) на плоскости заключается в нахождении дирекционного угла α направления с одной точки на другую и расстояния Дмежду ними по прямоугольным координатам данных точек.

Из рисунка 24 и формулировки обратной геодезической задачи известны:

α – дирекционный угол направления с точки А на точку В;

Д – расстояние (дальность) между точками А и В.

В прямоугольном треугольнике АСВ катеты АС и СВ соответствуют приращениям координат:

Таким образом, в прямоугольном треугольнике АСВизвестны два катета, по которым можно определить все его остальные элементы: острый уголСАВ, равный дирекционному углуα, и гипотенузуД(дальность).

Обратная геодезическая задача решается теми же способами и средствами, что и прямая геодезическая задача.

Огз решают в следующей последовательности:

Пусть в точке А находится огневая позиция (ОП), а в точке В – цель (Ц).

1. По известным координатам ОП и цели вычисляют приращения координат ΔХ и ΔY:

(58)

2. Определить острый угол α´(рис. 22) по формуле:

(59)

От угла α´перейти к дирекционному углуα в соответствии со знаками приращений ΔX и ΔY, согласно схеме (рис. 23), или по таблице:

Источник

Тема 3. Прямая и обратная геодезическая задача.

При производстве строительных работ создается разбивочная основа в виде строительной сетки. Пункт Государственной геодезической сети выносится на территорию строительства для обеспечения исходными данными всех геодезических работ. Решение прямой геодезической задачи позволяет определить координаты всех точек, расположенных в зоне строительства.

В геодезии принята система плос­ких прямоугольных координат, в которой относительно оси XX , совпадающей с направлением меридиана, и оси YY , перпендику­лярной к оси XX , определяют положение каждой точки, т. е. её координаты х и у; при этом счет четвертей идет по ходу часовой стрелки, согласно возрастанию азимутов и дирекционных углов .

При составлении планов ситуацию накладывают от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала на­носят опорные точки по их координатам. Так как число этих точек весьма велико, то при геодезических работах часто решают прямую задачу на координаты. Она состоит в том, что по извест­ным координатам данной точки, а также дирекционному углу и горизонтальному проложению линии от этой точки до определяе­мой вычисляют координаты определяемой точки.

Решить прямую геодезическую задачу, т.е Пример

определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным:

Кординаты точки 1 — X, = 4250 м. У,=6730 м;

Расстояние между точками d =120,10 м; направление линии, т.е дирекционный угол 48°30′ =r.

Для определения координат точки 2 сначала нужно найти приращение координат –ΔХ и ΔУ,затем сами координаты Х₂;У_{2 .}

1.Определяем приращение координат ΔХ =d . cosr = 120,10 . 0,6626 =79,51 м

ΔУ= d . sinr =12,10 . 0,7490 =89,95 м

ΔУ

х₂ 2

r d

х₁ 1

2. Определяем координаты точки 2

В практике прикладной геодезии для нужд проектирования и выноса проекта на местность приходиться определять значения дирекционного угла и длинны стороны по известным координатам её конечных точек. Это и составляет сущность решения обратной геодезической задачи.

Решение обратной геодезической задачи состоит в том, что, зная координаты опорных точек, можно вычислить дирекционный угол и расстояние между данными точками.

Пример.

Решить обратную геодезическую задачу, т.е. найти расстояниеd между точками и направление этой линии ( румб, азимут), если координаты точки1 Х₁= 320,5 м, У₁ = 780,2 м; координаты т очки 2 Х₂= 230,7 м, У₂ =900,1 м.

1. Определяем приращение координатΔХ = Х₂-Х₁ = 230,7 -320,5 = -89,8 м

ΔХ = У₂ –У₁ =900,1 – 780,2 = 119,9 м

Знаки приращений говорят, что линия расположена во второй четверти (ЮВ)

Знаки приращения координат можно определить по следующей схеме:

СЗ С х

З +ΔХ — ΔУ +ΔХ + ΔУ В

у -ΔХ — ΔУ -ΔХ + ΔУ у

Они зависят от четверти, в которой расположена линия.

2. Величина румба определяется по формуле

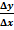
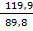
tg r= = = 1, 3352

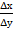
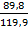
ctgr = = = 0,74,89

По таблицам Брадиса находим величину румба — 53⁰ 10ʹ

3. Расстояние между точками найдем по теореме Пифагора:

d= 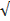ΔХ 2 + ΔУ 2 = 89,8 2 + 119,9 2 = 22440,05 = 149,8 м

Контрольные вопросы:

1. Какие знаки у приращения координат ΔХ и ΔУ, если наименование румба ЮЗ?

а) –ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+ ΔХ,–ΔУ;

2. Найдите координаты точки 2, если координаты точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ =15.

а) 30, 20; б) 20, 30; в) 20, 40; г) 30, 40;

3. Решить обратную геодезическую задачу: найти расстояние между двумя точками и румб линии, если координаты начала и конца линии Х₁= 320,5 м, У₁ = 780,2 м; Х₂ 230,7 м,

а); 160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰ 45ʹ; г) 456,7м, 45⁰ 15ʹ;

4. Решить прямую геодезическую задачу: определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным: Х₁ = 4250м, У₁= 6730м, расстояние d – 120, 1 м, дирекционный угол — 48⁰30ʹ.

Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»

Азимут лини находится в пределах 90°-180 каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-З60-r°

№	Вопросы (задания)	Ответы	Код
I	Осевого меридиана зоны	1
Ближайшего направления меридиана	2
Южного направления магнитного меридиана	3
Северного направления географического меридиана	4
II	Азимут лини находиться в пределах от 180°-270°	Сз	1
каково наименование румба?	Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для ЮВ:r	А°=180°+r°	1
А о =360°-r°	2
А°=180°-r°	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 270°-360° каково градусное значение румба?

Каково название румба линии и его величина, если азимут её определён по формуле А°- 180°+r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Осевого меридиана зоны	2
Южного	3
направления магнитного
меридиана
Ближайшего	4
направления меридиана
И	Азимут лини находиться в пределах от 0°-90° каково наименование румба?	Сз	1
Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для Юз:ч°	А°=180°-r°	1
А°-360°-r°	2
A°=180W	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 180°-270° каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-360°-r°

Источник

Adblock
detector

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Южного
направления магнитного	2
меридиана
Ближайшего
направления меридиана	3
Осевого	4
меридиана зоны
И	Азимут лини находиться в пределах 90°-180 каково	Сз	8
наименование румба?	Юв	9
Юз	1
Св	2
III	r°=А°	3
r°=180°-А°	4
r°=А°-180°	5
r°=360°-А°	6
IV	каково градусное значение азимута (А°) линии для румба св: r°	А°=180°-r°	7
А°=360°-r°	8
А°=180°+r°	9
А°=r°	1
V

Прямая
геодезическая задача

В
геодезии часто приходится передавать
координаты с одной точки на другую.
Например, зная исходные координаты
точки А (рис.23),
горизонтальное расстояние S_ABот
неё до точки В и
направление линии, соединяющей обе
точки (дирекционный угол α_AB или
румб r_AB),
можно определить координаты точки В.
В такой постановке передача координат
называется прямой
геодезической задачей.

Рис.
23. Прямая геодезическая задача

Для
точек, расположенных на сфероиде, решение
данной задачи представляет значительные
трудности. Для точек на плоскости она
решается следующим образом.

Дано:
Точка А(
X_A,
Y_A ), S_AB и α_AB.

Найти:
точку В(
X_B,
Y_B ).

Непосредственно
из рисунка имеем:

 ΔX
= X_B –
X_A ;

 ΔY
= Y_B –
Y_A .

Разности ΔX и ΔY координат
точек последующей и предыдущей называются
приращениями координат. Они представляют
собой проекции отрезка АВ на
соответствующие оси координат. Их
значения находим из прямоугольного
прямоугольника АВС:

ΔX
= S_AB · cos
α_AB ;

ΔY
= S_AB · sin
α_AB .

Так
как в этих формулах S_AB всегда
число положительное, то знаки приращений
координат ΔX  и  ΔY зависят
от знаков cos
α_AB  и  sin
α_AB.
Для различных значений углов
знаки ΔX и ΔY представлены
в табл.1.

Таблица
1.

Знаки
приращений координат ΔX и ΔY

Приращения координат	Четверть окружности в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

При
помощи румба приращения координат
вычисляют по формулам:

ΔX
= S_AB · cos
r_AB ;

ΔY
= S_AB · sin
r_AB .

Знаки
приращениям дают в зависимости от
названия румба.

Вычислив
приращения координат, находим искомые
координаты другой точки:

 X_B =
X_A + ΔX  ;

 Y_B =
Y_A + ΔY  .

Таким
образом можно найти координаты любого
числа точек по правилу: координаты
последующей точки равны координатам
предыдущей точки плюс соответствующие
приращения.

Обратная
геодезическая задача

Обратная
геодезическая задача заключается
в том, что при известных координатах
точек А(
X_A,
Y_A ) и В(
X_B,
Y_B ) необходимо
найти длину S_AB и
направление линииАВ: румб r_AB 
и  дирекционный угол α_AB (рис.24).

Рис.
24. Обратная геодезическая задача

Даннная
задача решается следующим образом.

Сначала
находим приращения координат:

 ΔX
= X_B –
X_A ;

 ΔY
= Y_B –
Y_A .

Величину
угла r_AB определем
из отношения

ΔY	= tg rAB
ΔX

 .

По
знакам приращений координат вычисляют
четверть, в которой располагается румб,
и его название. Используя зависимость
между дирекционными углами и румбами,
находим α_AB.

Для
контроля расстояние S_AB дважды
вычисляют по формулам:

SAB=	ΔX	=	ΔY	= ΔX · sec αAB = ΔY · cosec αAB
cos αAB	sin αAB

SAB=	ΔX	=	ΔY	= ΔX · sec rAB = ΔY · cosec rAB
cos rAB	sin rAB

Расстояние S_AB можно
определить также по формуле

.

Топографические
съемки.

Топографи́ческая
съёмка — совокупность работ по созданию
топографических карт или планов местности
посредством измерений расстояний,
высот, углов и т. п. с помощью различных
инструментов (наземная съёмка), а также
получение изображений земной поверхности
с летательных аппаратов (аэрофотосъёмка,
космическая съёмка).

Наземные съемки
бывают плановые, высотные и комбинированные.
При Плановой (теодолитной) получается
топографическая карта, но без учёта
рельефа, т.е. только ситуация (совокупность
объектов местности). Топографическая
(тахеометрическая) съёмка , особенно
крупных масштабов, является наиболее
востребованным видом геодезических
работ. Потребности в ней могут возникнуть
при изысканиях, обновлении топокарт,
составлении генпланов, составления
рабочих чертежей, для решения вертикальной
планировки и проектировании ландшафтного
дизайна. На основе топографической
съёмки возможно построить цифровую
модель местности. При Высотной (нивелирной)
съемке выполняется определение высотного
(вертикального) положения характерных
точек рельефа и конструктивных элементов
зданий.

Топографические
работы сильно облегчились после появления
специальных геодезических GPS и ГЛОНАСС
приёмников, совмещённых с компьютером
и синхронизированных между собой по
радиоканалу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как узнать противоположную точку земли

Каждый раз, когда мы говорим о направлении на Земле, мы говорим о местоположении и о движении. Но как нам найти противоположную точку Земли? Многие люди не задумываются об этом, но это может быть полезной информацией для многих, особенно для любителей путешествий.

Что такое противоположная точка Земли?

Противоположная точка Земли — это точка на Земле, которая находится прямо под вашими ногами, если вы стоите на противоположной стороне планеты. Это означает, что если вы начнете копать, то вы будете продолжать копать, пока не достигнете точки, которая находится прямо под вашей отправной точкой.

Как найти противоположную точку Земли?

Узнать противоположную точку Земли легко. Но нужно иметь в виду несколько факторов:

• Земля имеет форму геоида, то есть не идеальную сферу.
• Земля вращается вокруг своей оси.
• В процессе нахождения противоположной точки потребуется знание географических координат начальной точки.
• При нахождении противоположной точки необходимо учитывать дату и время.

Для того, чтобы найти противоположную точку Земли, вы должны знать две вещи: ваше текущее местоположение и координаты этой точки. Существует несколько способов вычисления противоположной точки, но мы рассмотрим метод, основанный на приложении Google Maps.

Шаг 1: Найдите свои координаты

Перед тем, как узнать противоположную точку Земли, вам нужно знать свои текущие географические координаты. Это можно сделать довольно просто с помощью приложения Google Maps.:

1. Откройте приложение Google Maps на своем устройстве.
2. Нажмите на значок местоположения внизу экрана.
3. После этого появится карты, на которых будет указан ваше местоположение, а также координаты адреса.

Шаг 2: Введите свои координаты в приложение

Когда вы найдете свои координаты, перейдите на сайт antipodemap.com. В верхней части введите ваши текущие координаты. Это сделать очень легко: введите градусы, долготу, северную или южную широту, и нажмите кнопку «Показать противоположный пункт». Карты покажут вам точку противоположную вашему местоположению.

Итог

Таким образом, чтобы узнать противоположную точку Земли, вам понадобится знать свои текущие географические координаты и использовать приложение, которое может вычислить эти координаты на основе местоположения. Теперь вы знаете, как найти точку на Земле, которая находится прямо под вашими ногами, если вы находитесь на противоположной стороне планеты.

Как узнать противоположную точку земли

Путешествия за пределы родных мест являются одной из самых волнующих и увлекательных вещей в жизни. Иногда путешественники задаются вопросом о том, как узнать, где находится противоположная точка земли от места, где они находятся.

Как вы знаете, земля является сферой, а это означает, что противоположные точки расположены на противоположных концах земли. Таким образом, для того чтобы узнать местонахождение противоположной точки, необходимо знать свою текущую широту и долготу. После чего, используя несколько математических формул, вы сможете рассчитать позицию противоположной точки.

Как узнать свою широту и долготу?

Прежде чем понять, как узнать местонахождение противоположной точки, необходимо знать свою текущую широту и долготу. Существуют различные способы определения вашей позиции с точностью до градусов:

• Используйте GPS-навигатор или приложение на вашем мобильном телефоне.
• Смотрите на карту и ищите себя на ней. После чего, используя линейку и чернила, отметьте свою позицию, а затем измерьте широту и долготу.
• Используйте сайты, которые предоставляют информацию о местоположении. Например, LatitudeLongitude.org.

Как только вы узнали свои координаты, вы готовы начать рассчитывать противоположную точку.

Как рассчитать противоположную точку земли?

Рассчитывая противоположную точку земли, мы должны учитывать несколько факторов.

1. Экваториальная ориентация

Экватор является нулевым параллелем на земном шаре и разделяет его на две части: северную и южную. Все параллели, проходящие через экватор, имеют широту 0 градусов. Это означает, что каждая точка на экваторе находится на расстоянии 90° от противоположной точки на экваторе.

2. Число градусов

Чтобы найти противоположную точку на земле, необходимо сделать 180° в направлении на запад или на восток из вашей текущей долготы. Например, если ваша текущая долгота равна 45° восточной долготы, то вам нужно сделать 135° на запад от вашей текущей долготы, чтобы найти противоположную точку.

3. Переход через Северный или Южный полюс

Если ваша позиция находится вблизи Северного или Южного полюса, для рассчета противоположной точки необходимо учитывать переход через полюс.

Таким образом, как только вы узнали свою текущую широту и долготу, вы можете рассчитать противоположную точку, используя вышеперечисленные формулы и способы рассчета.

Итог

Как видите, рассчет противоположной точки земли может показаться сложным, но на самом деле это простой математический расчет, который можно сделать при помощи нескольких формул и знания своей текущей широты и долготы. Эта информация может оказаться очень полезной для путешественников и любителей географии.

Как узнать противоположную точку земли

Если вы когда-либо задумывались об узнавании, где находится противоположная точка земли от вас, то у вас возникло еще одно любопытное занятие для дальнейшего исследования. И знаете ли вы, что это может быть не только увлекательной игрой, но и полезным занятием? Например, если вы планируете путешествие на другой конец земного шара, то знание противоположной точки может быть действительно полезным.

Географические координаты

Первое, что нам нужно знать, чтобы узнать противоположную точку земли, – это географические координаты местоположения, которое мы хотим проверить. Географические координаты обычно измеряются в градусах, минутах и секундах, их могут выразить два значения: широту (северную или южную) и долготу (восточную или западную).

Чтобы найти географические координаты вашего местоположения, вы можете использовать онлайн-сервисы, вроде Google Maps, Bing Maps и OpenStreetMap, с помощью GPS или карт можно найти ваше местоположение и узнать его координаты. Если вы используете GPS-устройство, то можете просто проверить настройки устройства, чтобы узнать свои координаты.

Противоположные координаты

Как только вы узнали свои географические координаты, вы можете использовать формулу, чтобы найти противоположные координаты. Координаты противоположной точки будут находиться на противоположной стороне земного шара, поэтому если у вас есть северная широта, то противоположная точка будет южной широтой, и наоборот. То же самое с западной и восточной долготой.

Формулы для определения противоположной точки

Для расчета противоположной точки можно использовать следующие формулы:

Широта противоположной точки: – (исходная широта) * 1

Долгота противоположной точки: – (исходная долгота) + 180

Например, если ваше местоположение имеет координаты 30° N (северной широты) и 70° W (западной долготы), то противоположная точка будет иметь координаты –30° S (южной широты) и 110° E (восточной долготы).

Проверка на карте

После того, как вы нашли координаты противоположной точки, их можно проверить на карте, используя онлайн-сервисы, такие как Google Maps, Bing Maps или OpenStreetMap. Это поможет убедиться, что вы правильно расчитали координаты и имеете более лучшее понимание географических данных и расположения на карте.

Выводы

Несмотря на то, что узнавание противоположной точки земли может показаться техническим или ненужным занятием, это действительно полезный навык, который вы можете использовать в различных ситуациях. Если вы путешествуете на другой конец земного шара, знание противоположной точки может помочь вам определить время циклического дня и ночи, или же узнать когда выходит солнце и заходит. Вы можете попрактиковаться в расчете противоположных координат, и это может быть интересным опытом, который улучшит ваши знания о географии и земном шаре в целом.