При расчёте освещения OpenArena (свободный порт Quake III: Arena) вычисляет углы падения и отражения через быстрый обратный квадратный корень. Обратите внимание на кожух оружия — при очень низкой детализации (8 четырёхугольников) игра делает вид, что он криволинейный.
Бы́стрый обра́тный квадра́тный ко́рень (также быстрый InvSqrt() или 0x5F3759DF по используемой «магической» константе, в десятичной системе 1 597 463 007) — это быстрый приближённый алгоритм вычисления обратного квадратного корня 
Алгоритм[править | править код]
Алгоритм принимает 32-битное число с плавающей запятой (одинарной точности в формате IEEE 754) в качестве исходных данных и производит над ним следующие операции:
- Трактуя 32-битное дробное число как целое, провести операцию y0 = 5F3759DF16 − (x >> 1), где >> — битовый сдвиг вправо. Результат снова трактуется как 32-битное дробное число.
- Для уточнения можно провести одну итерацию метода Ньютона: y1 = y0(1,5 − 0,5xy0²).
Реализация из Quake III[3]:
float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; }
Эта реализация считает, что float по длине равен long, и использует для преобразования указатели (может ошибочно сработать оптимизация «если изменился float, ни один long не менялся»; на GCC при компиляции в «выпуск» срабатывает предупреждение). По комментариям видно, что Джон Кармак, выкладывая игру в открытый доступ, не понял, что там делается.
Корректная по меркам современного Си реализация, с учётом возможных оптимизаций и кроссплатформенности:
#include <stdint.h> float Q_rsqrt( float number ) { const float x2 = number * 0.5F; const float threehalfs = 1.5F; union { float f; uint32_t i; } conv = {number}; // member 'f' set to value of 'number'. conv.i = 0x5f3759df - ( conv.i >> 1 ); conv.f *= threehalfs - x2 * conv.f * conv.f; return conv.f; }
На Си++20 можно использовать новую функцию bit_cast.
#include <bit> #include <limits> #include <cstdint> constexpr float Q_rsqrt(float number) noexcept { static_assert(std::numeric_limits<float>::is_iec559); // Проверка совместимости целевой машины float const y = std::bit_cast<float>( 0x5f3759df - (std::bit_cast<std::uint32_t>(number) >> 1)); return y * (1.5f - (number * 0.5f * y * y)); }
GCC и Clang (-std=c++20 -mx32 -O3) дают одинаковый машинный код для всех трёх вариантов и близкий — друг относительно друга. У MSVC (/std:c++20 /O2) третья функция незначительно отличается от первых двух.
История[править | править код]
Саму идею приближения дробного числа целым для вычисления 
Таролли, перешедший в 3dfx, принёс алгоритм туда, где он и применялся для расчёта углов падения и отражения света в трёхмерной графике. Джим Блинн, специалист по 3D-графике, переизобрёл метод в 1997 году с более простой константой[7]. Более сложный табличный метод, который считает до 4 знаков (0,01 %), найден при дизассемблировании игры Interstate ’76 (1997)[8].
Однако данный метод не появлялся на общедоступных форумах, таких как Usenet, до 2002—2003-х годов. Метод обнаружили в Quake III: Arena и приписали авторство Джону Кармаку. Тот предположил, что его в id Software принёс Майкл Абраш, специалист по графике, или Терье Матисен, специалист по ассемблеру; другие ссылались на Брайана Хука, выходца из 3dfx[9]. Изучение вопроса показало, что код имел более глубокие корни как в аппаратной, так и в программной сферах компьютерной графики. Исправления и изменения производились как Silicon Graphics, так и 3dfx Interactive, при этом самая ранняя известная версия написана Гэри Таролли для SGI Indigo.
С выходом в свет в 1998 году набора инструкций 3DNow! в процессорах фирмы AMD появилась ассемблерная инструкция PFRSQRT[10] для быстрого приближенного вычисления обратного квадратного корня. Версия для double бессмысленна — точность вычислений не увеличится[2] — потому её не добавили. В 2000 году в SSE2 добавили функцию RSQRTSS[11] более точную, чем данный алгоритм (0,04 % против 0,2 %). Потому данный метод больше не имеет смысла в современных компьютерах[12] (все x64-процессоры поддерживают SSE2), зато важен как дань истории и в более ограниченных машинах[13].
Анализ и погрешность[править | править код]
Битовое представление 4-байтового дробного числа в формате IEEE 754 выглядит так:
| Знак | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | |||||||||||||||||||||||||||||||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 
|
| 31 | 24 | 23 | 16 | 15 | 8 | 7 | 0 |

Имеем дело только с положительными числами (знаковый бит равен нулю), не денормализованными, не ∞ и не NaN. Такие числа в стандартном виде записываются как 1,mmmm2·2e. Часть 1,mmmm называется мантиссой, e — порядком. Головную единицу не хранят (неявная единица), так что величину 0,mmmm назовём явной частью мантиссы. Кроме того, у машинных дробных чисел смещённый порядок: 20 записывается как 011.1111.12.
На положительных числах биекция «дробное ↔ целое» (ниже обозначенная как 
Например, двоичное представление 16-ричного целого числа 0x5F3759DF есть 0|101.1111.0|011.0111.0101.1001.1101.11112 (точки — границы полубайтов, вертикальные линии — границы полей компьютерного дробного). Порядок 101 1111 02 равен 19010, после вычитания смещения 12710 получаем показатель степени 6310. Явная часть мантиссы 01 101 110 101 100 111 011 1112 после добавления неявной ведущей единицы превращается в 1,011 011 101 011 001 110 111 112 = 1,432 430 148…10. С учётом реальной точности компьютерных дробных 0x5F3759DF ↔ 1,432430110·263.
Обозначим 










Воспользовавшись этим приближением, целочисленное представление числа 
Соответственно, 
Проделаем это же[3] для 

2️⃣
Соединив 1️⃣ и 2️⃣, получаем[3]
Магическая константа 



Первое (кусочно-линейное) приближение быстрого обратного квадратного корня (c = 1,43)
Можно вычислить, чему равняется первое кусочно-линейное приближение[15] (в источнике используется не сама мантисса, а её явная часть 
На бо́льших или меньших 

Метод Ньютона даёт[15] 



После одного шага метода Ньютона результат получается довольно точный (+0 % −0,18 %)[1][2], что для целей компьютерной графики более чем подходит (1⁄256 ≈ 0,39 %). Такая погрешность сохраняется на всём диапазоне нормированных дробных чисел. Два шага дают точность в 5 цифр[1], после четырёх достигается погрешность double.
Метод Ньютона не гарантирует монотонности, но компьютерный перебор показывает, что монотонность всё-таки есть.
Исходный текст (C++)
#include <iostream> union FloatInt { float asFloat; int32_t asInt; }; int floatToInt(float x) { FloatInt r; r.asFloat = x; return r.asInt; } float intToFloat(int x) { FloatInt r; r.asInt = x; return r.asFloat; } float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; // i don't know, what the fuck! y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration return y; } int main() { int iStart = floatToInt(1.0); int iEnd = floatToInt(4.0); std::cout << "Numbers to go: " << iEnd - iStart << std::endl; int nProblems = 0; float oldResult = std::numeric_limits<float>::infinity(); for (int i = iStart; i <= iEnd; ++i) { float x = intToFloat(i); float result = Q_rsqrt(x); if (result > oldResult) { std::cout << "Found a problem on " << x << std::endl; ++nProblems; } } std::cout << "Total problems: " << nProblems << std::endl; return 0; }
Существуют аналогичные алгоритмы для других степеней, например, квадратного или кубического корня[3].
Мотивация[править | править код]
Поле нормалей: а) для призмы (угловатый объект); б) для низкополигонального цилиндра (криволинейный объект)[16]
«Прямое» наложение освещения на трёхмерную модель, даже высокополигональную, даже с учётом закона Ламберта и других формул отражения и рассеивания, сразу же выдаст полигональный вид — зритель увидит разницу в освещении по рёбрам многогранника[16]. Иногда так и нужно — если предмет действительно угловатый. А для криволинейных предметов поступают так: в трёхмерной программе указывают, острое ребро или сглаженное[16]. В зависимости от этого ещё при экспорте модели в игру по углам треугольников вычисляют нормаль единичной длины к криволинейной поверхности. При анимации и поворотах игра преобразует эти нормали вместе с остальными трёхмерными данными; при наложении освещения — интерполирует по всему треугольнику и нормализует (доводит до единичной длины).
Чтобы нормализовать вектор, надо разделить все три его компонента на длину. Или, что лучше, умножить их на величину, обратную длине: 
Quake III Arena использует алгоритм быстрого обратного квадратного корня для ускорения обработки графики центральным процессором, но с тех пор алгоритм уже был реализован в некоторых специализированных аппаратных вершинных шейдерах, используя специальные программируемые матрицы (FPGA).
Даже на компьютерах 2010-х годов, в зависимости от загрузки дробного сопроцессора, скорость может быть втрое-вчетверо выше, чем с использованием стандартных функций[15].
Дальнейшие улучшения[править | править код]
При желании можно перебалансировать погрешность, умножив коэффициенты 1,5 и 0,5 на 1,0009, чтобы метод давал симметрично ±0,09 % — так поступили[8] в игре Interstate ’76, которая также делает итерацию метода Ньютона.
Неизвестно, откуда взялась константа 0x5F3759DF ↔[a] 1,4324301·263. Перебором Крис Ломонт и Мэттью Робертсон выяснили[1][2], что наилучшая по предельной относительной погрешности константа[b] для float — 0x5F375A86 ↔ 1,4324500·263, для double — 0x5FE6EB50C7B537A9. Правда, для double алгоритм бессмысленный (не даёт выигрыша в точности по сравнению с float)[2]. Константу Ломонта удалось получить и аналитически (c = 1,432450084790142642179)[b], но расчёты довольно сложны[15][2].
Чех Ян Ка́длец двоичным поиском, а затем перебором в окрестности того, что поиск дал, нашёл алгоритм в 1,3 раза[c] более точный при той же вычислительной сложности — ±0,065 %[17]:
float inv_sqrt(float x) { union { float f; uint32 u; } y = {x}; y.u = 0x5F1FFFF9ul - (y.u >> 1); return 0.703952253f * y.f * (2.38924456f - x * y.f * y.f); }
Вместо метода Ньютона можно использовать метод Галлея, в данной задаче эквивалентный методу Ньютона для уравнения 
где 
Комментарии[править | править код]
- ↑ Здесь стрелка ↔ означает объяснённую выше биекцию двоичного представления целого числа и двоичного представления числа с плавающей запятой в формате IEEE 754.
- ↑ 1 2 Если в поле порядка поставить 127, получится 0x3FB75A86. Библиотека GRISU2, полностью целочисленная и не зависящая от тонкостей сопроцессора, говорит, что 0x3FB75A86 ↔ 1,43245 — это кратчайшее десятичное число, преобразующееся в данный float. Однако всё-таки единица младшего разряда равняется 1,19·10−7, и 0x3FB75A86 = 1,432450056 ≈ 1,4324501. Следующее дробное 0x3FB75A87 ↔ 1,4324502 без всяких тонкостей. Отсюда неинтуитивное округление 1,43245008 до 1,4324500.
- ↑ Метод Кадлеца даёт симметричную погрешность — и потому его нужно сравнивать с той версией исходного алгоритма, что даёт симметричную погрешность ±0,09 %.
Примечания[править | править код]
- ↑ 1 2 3 4 Архивированная копия. Дата обращения: 25 августа 2019. Архивировано 6 февраля 2009 года.
- ↑ 1 2 3 4 5 6 https://web.archive.org/web/20140202234227/http://shelfflag.com/rsqrt.pdf
- ↑ 1 2 3 4 5 Hummus and Magnets. Дата обращения: 1 февраля 2017. Архивировано 13 января 2017 года.
- ↑ http://www.netlib.org/fdlibm/e_sqrt.c
- ↑ Beyond3D — Origin of Quake3’s Fast InvSqrt() — Part Two. Дата обращения: 25 августа 2019. Архивировано 25 августа 2019 года.
- ↑ Symplectic Spacewar » Cleve’s Corner: Cleve Moler on Mathematics and Computing – MATLAB & Simulink
- ↑ Floating-point tricks | IEEE Journals & Magazine | IEEE Xplore. Дата обращения: 17 августа 2022. Архивировано 17 августа 2022 года.. Копия на Yumpu
- ↑ 1 2 Fast reciprocal square root… in 1997?! — Shane Peelar’s Blog. Дата обращения: 17 августа 2022. Архивировано 11 октября 2022 года.
- ↑ Beyond3D — Origin of Quake3’s Fast InvSqrt(). Дата обращения: 4 октября 2019. Архивировано 10 апреля 2017 года.
- ↑ PFRSQRT — Вычислить приблизительное значение обратной величины квадратного корня от короткого вещественного значения — Club155.ru. Дата обращения: 4 октября 2019. Архивировано 16 октября 2019 года.
- ↑ RSQRTSS — Compute Reciprocal of Square Root of Scalar Single-Precision Floating-Point Value. Дата обращения: 6 октября 2019. Архивировано 12 августа 2019 года.
- ↑ Some Assembly Required » Blog Archive » Timing square root
- ↑ z88dk/libsrc/_DEVELOPMENT/math/float/math32 at master · z88dk/z88dk · GitHub
- ↑ https://web.archive.org/web/20150511044204/http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf
- ↑ 1 2 3 4 Швидке обчислення оберненого квадратного кореня з використанням магічної константи — аналітичний підхід. Дата обращения: 12 июня 2022. Архивировано 17 апреля 2022 года.
- ↑ 1 2 3 Это норма: что такое карты нормалей и как они работают / Хабр. Дата обращения: 4 июля 2022. Архивировано 10 июля 2020 года.
- ↑ 1 2 Řrřlog :: Improving the fast inverse square root
Ссылки[править | править код]
- C. Lomont, Fast inverse square root, Technical Report, 2003.
- A Brief History of InvSqrt by Matthew Robertson
- 0x5f3759df, further investigations into accuracy and generalizability of the algorithm by Christian Plesner Hansen
У нас есть процессор, который умеет складывать-вычитать, а также умножать. Также в арсенале – сдвиги влево и вправо, которыми можно заменить умножение и деление на степени двойки, а ещё есть взятие модуля числа и нахождение максимума двух чисел. Ничего другого – деления, квадратного корня, тригонометрии – в самом АЛУ процессора НЕТ.
Как оказалось, один из двух наших алгоритмов, “алгоритм захвата”, он же “аффинный алгоритм”, замечательно реализуется на таком процессоре.
Для решения системы линейных уравнений (самый напряжённый момент второго алгоритма, “алгоритма сопровождения”) мне очень хотелось применить метод LDLT или UDUT-разложения, поскольку тогда мы обходимся чистой арифметикой. Деление я собирался либо реализовать аппаратно, либо опять свести к умножению на обратную величину, а её находить по методу Ньютона. Увы, оказалось, что эти методы приводят к чрезмерно большим разбросам диагональных элементов, независимо от того, как я попытаюсь отмасштабировать входные данные. В итоге 16 бит оказывается недостаточно.
Метод UUT оказался куда более многообещающим – благодаря применению квадратного корня удалось сократить разброс диагональных элементов, и теперь система линейных уравнений решалась нормально, не приводя ни к переполнению, ни к катастрофическому падению точности.
Кроме того, оказалось, что можно все деления и взятия квадратных корней заменить одной-единственной операцией (в дополнение к сложениям и умножениям) – это взятие “обратного квадратного корня”, т.е
Тогда на этапе разложения мы можем сразу заменить диагональные элементы на обратные, и при нахождении остальных элементов надо будет не делить на элементы главной диагонали, а умножать на них. И точно также все деления заменятся умножениями на этапах прямой и обратной подстановки.
У многих на слуху “магическая” функция нахождения обратного квадратного корня из недр Quake, которую иногда приписывают самому Кармаку, но скорее всего это было “совместное творчество”, и найти концы уже не так-то просто. Я раньше думал, что это просто какая-то аппроксимация по нескольким точкам, которая если даст плюс-минус 10% – то и ладно. Оказалось, точность этого метода – лучше 0,17% во всём диапазоне входных данных, при том, что метод сводится к сдвигу вправо, вычитанию из “магической константы” и одной итерации метода Ньютона. Очень рекомендую ознакомиться с подробностями (раз, два) – они того стоят.
Но к сожалению, эта магическая функция целиком опирается на представление числа с плавающей точкой, на тот факт, что после экспоненты идёт мантисса. Именно рассмотрение их как единого целого, 32-битного числа, позволило добиться столь впечатляющих результатов. Для нас это бесполезно.
Поэтому нужно было найти свой способ извлечения обратного квадратного корня из целого числа, причём требования весьма специфичны:
1. точность – максимально возможная для 16-битного результата,
2. размер функции – настолько малый, насколько это возможно, т.к памяти очень мало
3. быстродействие – практически пофиг. Нам этих корней понадобится 5-6 на одно измерение, т.е не больше 30 корней в секунду. Прямой перебор (проверить все 65535 разных значений) – это, пожалуй, перебор, а вот сделать десяток-другой итераций кажется вполне осмысленным.
В итоге получилась функция, которая вычисляет результат за 16 итераций метода Ньютона, на каждой итерации осуществляется 3 умножения и 1 вычитание. Ошибка составляет одну единицу младшего разряда, например, реальный ответ должен составлять 1023,5003659, что должно бы округлиться до 1024, а наша функция вместо этого получает 1023. Так происходит при 106 входных значениях из возможных 65535. Но начало работы функции навевает вселенскую тоску…
У нас есть число a, от которого надо взять обратный квадратный корень. Для этого мы берём нулевое приближение:
после чего выполняем итерации
Вот и весь метод. “Дьявол кроется в деталях”. Входное число мы воспринимаем как беззнаковое в формате 1.15, т.е значения от 0 до 65535 мы воспринимаем как 0 .. 1,999969.
При этом нулевое значение недопустимо – это будет “деление на ноль”. Все остальные мы хотим обработать без переполнения, потому как в реальной работе мы действительно встречаемся с широким диапазоном значений.
Самое большое выходное значение получится, когда на вход подано самое маленькое, “1”, т.е 1/32768. Имеем 1/sqrt(1/32768)≈181,01934 Чтобы оно поместилось в результат, мы обязаны представить данные в формате 8.8, т.е 8 бит целой части и 8 бит дробной, что позволяет представить числа от 0 до примерно 256. В таком случае наше значение 181,01934 будет представлено как 256 * 181,01934 = 46341.
Самое маленькое выходное значение получится, когда на вход подано самое большое значение “65535” т.е 65535/32768≈2. Имеем 1/sqrt(65535/32768)≈0,70711. В формате 8.8 оно будет представлено как 256*0,70711=181. По счастью, разрядности ещё хватает, чтобы получить сколько-нибудь точный результат. Наихудшая относительная погрешность получается для входного значения 65189, что должно было дать результат 181,5005, но округляется до 182, приводя к погрешности 0,27%. Нормально…
Теперь о выборе нулевого приближения. При записи “в действительных числах”, результат может получаться в диапазоне от 0,707 до 181, и нам может захотеться взять значение где-то посерединке, будь то среднее арифметическое (90,86) или среднее геометрическое (11,3). Увы, ни то, ни другое взять мы не имеем права – для многих значений результат попросту разойдётся.
Если нулевое приближение превысит , то значение в скобках (в итерации метода Ньютона) станет ниже минус единицы, т.е результат по модулю возрастёт и при этом поменяет знак. В итоге мы получим расходящуюся последовательность.
Если нулевое приближение будет в интервале от до
, то значение в скобках станет от минус единицы до нуля, т.е x1 поменяет знак, но снизится по модулю. Последовательность может с большой вероятности сойтись к
, тогда как мы хотели просто
. Либо оно может уйти в ноль, после чего так и останется в нуле.
Поэтому, для диапазона входных чисел от 1/32768 до 2, мы должны выбрать нулевое приближение не более
Довольно разумное значение для нулевого приближения – единица, или в нашем формате 8.8: 256. В таком случае, мы можем обещать, что при умножении a на x результат уместится в 24 бита, что может выцарапать нам немножко точности.
Как ни странно, при таком выборе начального значения, наш метод всегда будет сходиться к правильному ответу, другое дело, что иногда ОЧЕНЬ МЕДЛЕННО. К примеру, попробуем посчитать обратный квадратный корень из 1/32768 (это и есть наихудший случай)
Имеем x0=1.
Далее, x1=1 * (3/2 – 1/2/32768)≈1,49998;
x2=1,49998 * (3/2 – 1/2/32768*1,499982)≈2,24992;
x3≈3,37471;
x4≈5,06148;
x5≈7,59025;
x6≈11,37870;
x7≈17,04557;
x8≈25,49279;
x9≈37,98639;
x10≈56,14320;
x11≈81,51450;
x12≈114,00710;
x13≈148,39985;
x14≈172,73195;
x15≈180,45890;
x16≈181,01673;
Метод на первых порах получается даже хуже старого доброго “деления пополам” (поиска льва в пустыне). Там мы, по сути, получаем по одному значащему биту за раз, снижая неопределённость вдвое. Здесь мы долго и упорно выползаем из угла, каждый раз увеличивая начальное приближение не более чем в 1,5 раза. И только когда мы начинаем приближаться к правильному ответу, спустя 14-15 итераций, внезапно начинает проявляться квадратичная сходимость метода Ньютона, где количество правильных бит ответа удваивается на каждой итерации…
Мы могли бы существенно ускорить этот метод, если начать с битовых операций: сдвигать исходное значение влево на 2 бита, пока не наступает переполнения, и вместе с этим сдвигать конечный результат вправо на 1 бит. Тогда наше нулевое приближение будет содержать хотя бы одно верное значение, и сойдётся моментально. Ещё круче было бы ввести какую-то специальную аппаратную инструкцию типа “целочисленного логарифма”, которая подсчитывает, сколько нулей в старших разрядах числа перед первой единицей. Но это будет “преждевременная оптимизация” – пока мне кажется, что сильно переживать за быстродействие данной функции нам не стоит!
А вот с точностью вычислений нужно постараться! Если каждое промежуточное значение будет округляться до 16 бит, то время от времени функция начнёт “ходить кругами”. Например, если взять число 6 на входе (т.е 6/32768), то в какой-то момент начнётся последовательность:
18922,
18929,
18911,
18924,
18908,
18922, …
тогда как правильный ответ: 18919.
Максимальная ошибка (для входных значений от 1 до 65535) будет составлять 12 единиц (если сделать 20 итераций), что не есть хорошо.
Поэтому придётся несколько дополнить наш АЛУ командой, которая переносит 32-битный аккумулятор в 31-битный регистр B. До этого мы могли занести в него только старшие 16 бит, а остальное было нужно, чтобы в процессе умножения двух чисел его содержимое сдвигалось вправо и при единичном бите второго операнда прибавлялось к аккумулятору. Но если мы позволим производить такую замену, точность в кои-то веки дойдёт до одной единицы младшего разряда, а на самом деле и того лучше.
Конечно, ради одной этой функции такое дополнение АЛУ может показаться расточительным, уж лучше придумать другой алгоритм, да хоть того же льва, он точно не зациклится. Но как показала практика, и последующее решение системы линейных уравнений только в том случае даёт неплохие результаты, если и там мы не сбрасываем 32-битное промежуточное значение до 16 бит, прежде чем помножить на элемент главной диагонали. В противном случае – огромные ошибки и срыв сопровождения…
Сегодня мы поговорим про приближенные вычисления, Quake3 Arena, незаурядном инженере и программисте Джоне Кармаке. И даже вспомним одного из разработчиков MATLAB.
Итак, тема нашего нашего разговора – быстрый способ приближенного вычисления X-0.5. Во многих прикладных областях нормировка на квадратный корень из какой-либо величины используется довольно часто. Например, про обработки сигналов и говорить нечего, возьмем корреляцию, которая встречается практически повсеместно. На что ее нормировать? На квадратный корень из произведения квадратичного произведения сигналов (Айфечер, 5я глава, формула 5.8). В компьютерной графике дела обстоят схожим образом, упомянем на всякий случай поверхность нормалей.
Теперь переместимся в уже далекий 1999 год, а точнее самое начало 2000х. Времена компьютерных клубов, “кваки” и “каунтер стрике 1.1”. Когда можно было без проблем купить “отвертку” для папы, а главной целью в жизни было отпроситься у мамки на ночь в компьютерный клуб. Скажу честно, мне это так и не удалось, сходил на ночь я уже на свои и та магическая аура, исходившая от компьютеров Pentium III, уже улетучилась.
В 1999 году Id Software выпускают прорывной шутер, давший невероятный толчок развитию не только игр, но и компьютерной графики в целом. В реализации движка использовался тот самый быстрый обратный корень. Когда реализация игры была выложена в открытый доступ, то около данной функции был обнаружен комментарий, содержащий обсценное слово на английском языке, обозначающее половое сношение. Очевидно, Джон Кармак не разобрался в реализации, но она работала и работала хорошо. Про Кармака советую почитать отдельно, уж очень он незаурядная личность.
А теперь сам алгоритм. Это тот самый код из Quake III Арена и те самые комментарии, во многих русскоязычных источниках их удаляют, будем надеяться, у администрации платформы тестикулы на месте.
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}В принципе на этом статью можно заканчивать, алгоритм перед вами и он работает, сам проверял. Но все-таки давайте разберемся, что же тут происходит.
Во-первых, это отображение числа с плавающей точкой, как 32х битное целое число. В оригинальном алгоритме это сделано довольно витьевато, я предпочел бы применить union.
union {
float f;
int i;
} conv = {number};Признаюсь честно, для меня стало открытием, что такое преобразование дает довольно неплохую аппроксимацию логарифма числа по основанию 2. Разберем это преобразование по подробнее. Для начала запишем число в экспоненциальной форме:
Здесь mx мантисса а ex соответственно экспонента. Отметим также, что знаковый бит всегда должен быть равен нулю. Тогда логарифм от такого числа можно представить, как
Тогда биекцию между целочисленным представлением и представлением с плавающей точкой можно представить в следующем виде:
Здесь L это разрядность мантиссы, а B смещение порядка, для F32 эти параметры будут 27-1 соответственно. Также мы уже два раза встречается сигма, это не что иное, как параметр приближения. Теперь выразим логарифм по основанию 2 от x.
Все выражения, записанные выше приведены для y=x, давайте теперь подставим в них
y=x-0.5.
Этой формулой, как раз и описывается та самая строчка:
i = 0x5f3759df - ( i >> 1 ); // what the fuck? Точное происхождение именно это константы, установить так и не удалось. Далее проведем обратное преобразование:
В коде Кармака это выглядит следующим образом:
y = * ( float * ) &i;Затем проводится одна итерация приближения по методу Ньютона:
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iterationМетод широко распространен и описан во множестве источников, возможно, мы разберем его в будущем.
На рисунке выше приводится ошибка в расчетах с использованием приведенного метода.
Стоит только отметить, что многие ошибочно приписывают разработку этого алгоритма самому Кармаку, однако это неверно. Сам Джон предполагал, что алгоритм принес в компанию Майкл Абраш. Самая ранняя обнаруженная версия реализации алгоритма написана Гэрри Таролли, но также есть предположение, что алгоритм разработали его коллеги по Ardent Computer Грег Уолш и Клив Моулер. Кстати, Клив Моулер в последствии разработает тот самый MATLAB. Вот в принципе и все – такая история.
В 2005 году id Software опубликовала под лицензией GPL-2 исходный код своей игры 1999 года Quake III Arena. В файле code/game/q_math.c есть функция для вычисления обратного квадратного корня числа, которая на первый взгляд выглядит очень любопытным алгоритмом:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // зловещий хакинг чисел с плавающей запятой на уровне битов
i = 0x5f3759df - ( i >> 1 ); // какого чёрта?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // первая итерация
// y = y * ( threehalfs - ( x2 * y * y ) ); // вторая итерация, можно удалить
return y;
}Об этом алгоритме написано множество статей, и ему посвящена хорошая страница Википедии, где он назван fast inverse square root (быстрым обратным квадратным корнем). На самом деле, этот алгоритм упоминался на различных форумах ещё до публикации исходного кода Q3. Ryszard из Beyond3D провёл в 2004-2005 годах исследование и в конечном итоге выяснил, что первоначальным автором алгоритма был Грег Уолш из Ardent Computer, который создал его десятью годами ранее.
Как он работает?
Как же работает этот способ? Он выполняется в два этапа:
- получение грубой аппроксимации
yобратного квадратного корня нужного числаnumber:y = number; i = * ( long * ) &y; i = 0x5f3759df - ( i >> 1 ); y = * ( float * ) &i; - Уточнение аппроксимации при помощи одного шага метода Ньютона-Рафсона (NR):
const float threehalfs = 1.5F; x2 = number * 0.5F; y = y * ( threehalfs - ( x2 * y * y ) );
Первая аппроксимация
Самая интересная часть — это первый этап. На нём используется кажущееся «магическим» число 0x5f3759df и битовые сдвиги, что в результате каким-то образом даёт обратный квадратный корень. В первой строке 32-битное число с плавающей запятой y сохраняется как 32-битное целое число i получением указателя на y, преобразованием его в указатель long и разыменованием. То есть y и i содержат два идентичных 32-битных вектора, но один интерпретируется как число с плавающей запятой, а другой — как целое число. Затем целое число смещается на один шаг вправо, меняет знак, и к нему прибавляется константа 0x5f3759df. Наконец, получившееся значение интерпретируется как число с плавающей запятой при помощи разыменования указателя float, указывающего на целочисленное значение i.
Здесь сдвиг, смена знака и сложение выполняются во множестве целых чисел, так как же эти операции влияют на число во множестве чисел с плавающей запятой? Чтобы понять, как это может дать нам аппроксимацию обратного квадратного корня, нужно знать, как представлены в памяти числа с плавающей запятой. Число с плавающей запятой состоит из знака
, экспоненты
и дробной части
. Значение числа с плавающей запятой определяется как1:
1 Это относится только ко всем обычным числам с плавающей запятой, а ещё существуют два нуля, поднормальные числа и особые значения наподобие NaN и inf. В алгоритме они не учитываются.
В нашем случае можно допустить, что float имеет формат IEEE 754 binary322, где биты упорядочены следующим образом:
2 Согласно стандарту C, float необязательно binary32, но в большинстве архитектур, например, в современных x86, это так. Автор функции Q_rsqrt сделал допущение, что используется binary32.
Самый старший бит — это бит знака
, за которым идут 8 битов
, обозначающих экспоненту
, и 23 оставшихся бита (
), обозначающих дробную часть
. Число отрицательное, когда
. 8-битное число
не используется напрямую как экспонента, оно имеет смещение или перекос в
. То есть
означает, что экспонента равна
.
— это просто дробное двоичное число с десятичной точкой перед первой цифрой, такое, что
.
Мы можем написать на C программу interp.c, которая будет выводить интерпретации заданного числа и в целых числах, и в числах с плавающей запятой, а также выделять разные части:
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <stdint.h>
int main(int argc, char *args[]) {
/* парсим число из args */
uint32_t i;
int ret;
if (argc == 2) {
ret = sscanf(args[1], "%u", &i);
} else if (argc == 3 && strcmp(args[1], "-h") == 0) {
ret = sscanf(args[2], "%x", &i);
} else if (argc == 3 && strcmp(args[1], "-f") == 0) {
float y;
ret = sscanf(args[2], "%f", &y);
i = *(uint32_t*)&y;
} else {
return EXIT_FAILURE;
}
if (ret != 1) return EXIT_FAILURE;
/* выводим представления */
printf("hexadecimal: %xn", i);
printf("unsigned int: %un", i);
printf("signed int: %dn", i);
printf("floating-point: %fn", *(float*)&i);
/* выводим компоненты */
int S = i >> 31;
int E = (i >> 23) & ((1 << 8)-1);
int e = E - 127;
int F = i & ((1 << 23)-1);
float f = (float)F / (1 << 23);
printf("S: %dn", S);
printf("E: %d (0x%x) <=> e: %dn", E, E, e);
printf("F: %d (0x%x) <=> f: %fn", F, F, f);
return EXIT_SUCCESS;
}
Для примера можно рассмотреть число 0x40b00000:
$ ./interp -h 40b00000
hexadecimal: 40b00000
unsigned int: 1085276160
signed int: 1085276160
floating-point: 5.500000
S: 0
E: 129 (0x81) <=> e: 2
F: 3145728 (0x300000) <=> f: 0.375000Также можно извлечь части числа с плавающей запятой:
$ ./interp -f -32.1
hexadecimal: c2006666
unsigned int: 3254806118
signed int: -1040161178
floating-point: -32.099998
S: 1
E: 132 (0x84) <=> e: 5
F: 26214 (0x6666) <=> f: 0.003125Но даже теперь, когда мы знаем, как числа с плавающей запятой представлены в памяти, не совсем очевидно, как выполнение операций во множестве целых чисел может повлиять на множество чисел с плавающей запятой. Сначала мы можем попробовать итеративно обойти диапазон чисел с плавающей запятой и посмотреть, какие целые значения получим:
#include <stdio.h>
int main() {
float x;
for (x = 0.1; x <= 8.0; x += 0.1) {
printf("%ft%dn", x, *(int*)&x);
}
}Затем можно отметить значения с плавающей запятой на оси X и целые значения на оси Y (например, с помощью gnuplot), чтобы получить следующий график:
Хм, эта кривая выглядит довольно знакомой. Мы можем при помощи нашей программы рассмотреть другие точки данных:
$ ./interp -f 1.0
hexadecimal: 3f800000
unsigned int: 1065353216
signed int: 1065353216
floating-point: 1.000000
S: 0
E: 127 (0x7f) <=> e: 0
F: 0 (0x0) <=> f: 0.000000
$ ./interp -f 2.0
hexadecimal: 40000000
unsigned int: 1073741824
signed int: 1073741824
floating-point: 2.000000
S: 0
E: 128 (0x80) <=> e: 1
F: 0 (0x0) <=> f: 0.000000
$ ./interp -f 3.0
hexadecimal: 40400000
unsigned int: 1077936128
signed int: 1077936128
floating-point: 3.000000
S: 0
E: 128 (0x80) <=> e: 1
F: 4194304 (0x400000) <=> f: 0.500000Для 1.0 и 2.0 мы получаем
,
и ненулевую смещённую экспоненту
. Если мы устраним смещение в этом числе (вычтем
127 << 23), а затем сдвинем его до правого края, то получим экспоненту
; иными словами, логарифм числа с плавающей запятой по основанию 2. Однако это сработает только когда
и
, то есть при положительных целых числах. Если
, то мы имеем отрицательное число, для которого логарифм не определён. Но если
и мы сдвинем экспоненту до правого края, то просто потеряем все данные. Вместо этого мы можем преобразовать число в значение с плавающей запятой и разделить его на
, чтобы дробная часть масштабировала получившееся значение линейно:
(float) (*(int*)&x - (127 << 23)) / (1 << 23)Тогда мы получим не совсем логарифм, а линейную аппроксимацию всех значений, не являющихся степенью двойки. Мы можем наложить аппроксимацию на реальную логарифмическую функцию:
Это значит, что когда мы возьмём число с плавающей запятой и интерпретируем его как целое, то получим аппроксимацию логарифма этого числа с каким-то смещением и масштабом. А когда мы интерпретируем целое число как число с плавающей запятой, то получаем обратное, то есть показательную функцию или антилогарифм нашего целого значения. По сути, это означает, что когда мы выполняем операции во множестве целых чисел, то это как будто мы выполняем операции в логарифмической области определения. Например, если вспомнить логарифмические тождества, то можно понять, что если взять логарифм двух чисел и сложить их, то мы получим логарифм их произведения:
Иными словами, если мы выполняем сложение во множестве целых чисел, то получаем умножение во множестве чисел с плавающей запятой, только приближенное. Это можно проверить ещё одной простой программой на C. Нам нужно учесть влияние нашей операции на смещение экспоненты. Мы можем сложить два числа со смещёнными экспонентами и получить двойное смещение:
Мы хотим, чтобы смещение оставалось равным
, а не
, поэтому чтобы препятствовать этому, можно просто вычесть из результата
. Наша программа на C, выполняющая умножение чисел с плавающей запятой при помощи целочисленного сложения, может выглядеть так:
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
const uint32_t B = (127 << 23);
int main(int argc, char *args[]) {
/* парсим члены из аргументов args */
float a, b;
if (argc == 3) {
int ret = sscanf(args[1], "%f", &a);
ret += sscanf(args[2], "%f", &b);
if (ret != 2) return EXIT_FAILURE;
} else {
return EXIT_FAILURE;
}
/* выполняем умножение (целочисленное сложение) */
uint32_t sum = *(uint32_t*)&a + *(uint32_t*)&b - B;
float y = *(float*)& sum;
/* сравниваем с действительным */
float y_actual = a*b;
float rel_err = (y - y_actual) / y_actual;
printf("%f =? %f (%.2f%%)n", y, y_actual, 100*rel_err);
}Давайте проверим:
$ ./mul 3.14159 8.0
25.132721 =? 25.132721 (0.00%)
$ ./mul 3.14159 0.2389047
0.741016 =? 0.750541 (-1.27%)
$ ./mul -15.0 3.0
-44.000000 =? -45.000000 (-2.22%)
$ ./mul 6.0 3.0
16.000000 =? 18.000000 (-11.11%)
$ ./mul 0.0 10.0
0.000000 =? 0.000000 (inf%)Чаще всего результаты не полностью точны, они точны, только если один из членов — степень двойки, и наименее точны, когда оба члена находятся ровно между двумя степенями двойки.
А как насчёт обратного квадратного корня? Обратный квадратный корень
эквивалентен
, поэтому нам нужно ещё одно логарифмическое тождество:
Это значит, что если мы выполним умножение во множестве целых чисел, то получим возведение в степень во множестве чисел с плавающей запятой. В зависимости от экспоненты
мы можем получить множество разных функций, например:
Чтобы получить первую аппроксимацию обратного квадратного корня, нам просто нужно выполнить умножение на -1/2 во множестве целых чисел и учесть смещение. Тогда смещение будет
, а нам нужно, чтобы смещение было
, поэтому необходимо просто прибавить
. Итак, мы выполним умножение на -1/2, выполнив сдвиг вправо на один шаг и сменив знак, а затем прибавим смещение:
- (i << 1) + 0x5f400000;
Теперь этот код идентичен исходному коду Q3, только незначительно отличается значение константы. Разработчики Q3 использовали 0x5f3759df, мы пока используем 0x5f400000. Посмотрим, можно ли внести изменения, изучив нашу погрешность. Просто вычтем аппроксимированное значение из точного значения обратного квадратного корня и наложим результат для диапазона чисел на график:
График повторяется по горизонтали в обоих направлениях (только в разном масштабе), поэтому нам нужно только изучить эту часть, чтобы понять погрешность для всех (нормальных) чисел с плавающей запятой. Мы видим, что приблизительное значение всегда даёт слишком высокую оценку; просто вычтя константу, которая примерно вдвое меньше максимальной погрешности, мы можем сделать его симметричным, таким образом уменьшив среднюю абсолютную погрешность. Посмотрев на график, можно понять, что подойдёт вычитание примерно 0x7a120. Тогда наша константа будет равна 0x5f385ee0, что ближе к константе, использованной в Q3. Во множестве целых чисел наша константа просто центрирует погрешность по оси X на показанной выше схеме. Во множестве чисел с плавающей запятой влияние на погрешность будет схожим, за исключением того, что вычитание заимствует из экспоненты:
Потенциально мы могли бы найти реальный оптимум для какой-то разумной функции потерь, но мы остановимся на этом. Не совсем понятно, как была выбрана оригинальная константа Q3, возможно, путём проб и ошибок.
Улучшаем аппроксимацию
Вторая часть более привычна. После получения первой аппроксимации её можно улучшить методом Ньютона-Рафсона (NR). В Википедии есть хорошая статья о нём. Метод NR используется для уточнения аппроксимации корня уравнения.
Так как нам нужен обратный квадратный корень, необходимо воспользоваться уравнением
, которое равно нулю, когда
точно равен обратному квадратному корню
:
Если у нас есть приблизительное значение
, то можно получить более точную аппроксимацию
, вычислив место, где касательная к графику функции в
(то есть производная) пересекается с
. Это значение можно выразить как
и именно такое выражение используется во второй части функции в коде Q3.
Насколько он быстр?
В 2003 году Крис Ломонт написал статью о своём исследовании алгоритма. Его тесты показали, что алгоритм был в четыре раза быстрее, чем простое использование sqrt(x)3 из стандартной библиотеки и получение его обратного значения.
3 Ломонт написал (float)(1.0/sqrt(x)), однако sqrt (в отличие от sqrtf) работает с double, а не с float. Вероятно, это могло привести к замедлению наивного метода, потому что могло вызвать преобразование типов из double и обратно.
В 2009 году Илан Раскин написал пост Timing Square Root, где он в основном изучал функцию квадратного корня, но также и сравнил алгоритм быстрого обратного квадратного корня с другими методами. На его Intel Core 2 быстрый обратный квадратный корень был в четыре раза медленнее, чем rsqrtss, или на 30% медленнее, чем rsqrtss с одним шагом NR.
С тех пор в наборе команд x86 появилось множество новых расширений. Я попытался найти все имеющиеся сегодня команды, связанные с квадратным корнем:
Сегодня fsqrt устарел. Расширение 3DNow! тоже устарело и больше не используется. Все процессоры x86-64 поддерживают как минимум SSE и SSE2. Большинство процессоров поддерживает AVX, а некоторые поддерживают AVX-512, но, например, GCC в настоящее время по умолчанию не генерирует команд AVX.
p и s — это сокращения от «packed» и «scalar». Упакованные команды — это векторные команды SIMD, а скалярные работают за раз только с одним значением. Если ширина регистра, например, составляет 256 битов, то упакованная команда может выполнить параллельно
вычислений.
s или d — это сокращение от степени точности «single» или «double» чисел с плавающей запятой. Так как мы имеем дело с аппроксимациями, то будем использовать числа с плавающей запятой с одинарной точностью. Можно использовать варианты ps или ss.
Уже в 2009 году метод быстрого обратного квадратного корня с трудом можно было сравнить с командой rsqrtss. А с тех пор в современных процессорах x86 было реализовано множество расширений со специализированными командами SIMD. То есть сегодня быстрый обратный квадратный корень не имеет никаких шансов и его время прошло?
Почему бы не проверить это прямо сейчас: мы можем начать с выполнения тестов на моей машине с довольно современным процессором: AMD Zen 3 5950X, выпущенным в конце 2020 года.
Первоначальное тестирование
Мы напишем программу на C, которая будет пытаться вычислить обратный квадратный корень тремя разными способами:
exact: простым1.0 / sqrtf(x)с использованием функцииsqrtfиз стандартной библиотеки C,appr: первой аппроксимацией из исходного кода Q3, объяснённой выше,appr_nr: полной методикой Q3 с одной итерацией метода Ньютона-Рафсона.
При каждом методе мы выполним вычисление для каждого значения в рандомизированном входном массиве и измерим потраченное суммарно время. Чтобы получить время до и после вычислений, можно использовать функцию clock_gettime из libc (для систем POSIX), а затем получить разность. Потом мы повторим это множество раз, чтобы снизить влияние случайных колебаний. Программа на C выглядит следующим образом:
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
#include <time.h>
#include <math.h>
#define N 4096
#define T 1000
#define E9 1000000000
#ifndef CLOCK_REALTIME
#define CLOCK_REALTIME 0
#endif
enum methods { EXACT, APPR, APPR_NR, M };
const char *METHODS[] = { "exact", "appr", "appr_nr" };
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
static inline float rsqrt_appr(float x) {
uint32_t i = *(uint32_t*)&x;
i = -(i >> 1) + 0x5f3759df;
return *(float*)&i;
}
static inline float rsqrt_nr(float x, float y) { return y * (1.5f - x*0.5f*y*y); }
static inline float rsqrt_appr_nr(float x) {
float y = rsqrt_appr(x);
return rsqrt_nr(x, y);
}
int main() {
srand(time(NULL));
float y_sum[M] = {0};
double t[M] = {0};
for (int trial = 0; trial < T; trial++) {
struct timespec start, stop;
float x[N], y[N];
for (int i = 0; i < N; i++) { x[i] = rand(); }
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_exact(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[EXACT] += y[i]; }
t[EXACT] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_appr(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[APPR] += y[i]; }
t[APPR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_appr_nr(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[APPR_NR] += y[i]; }
t[APPR_NR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
}
printf("rsqrttps/optratioterrn");
for (int m = 0; m < M; m++) {
printf("%st%.0ft%.2ft%.4fn",
METHODS[m],
t[m] * 1000.0f / N / T,
(double) t[EXACT] / t[m],
(y_sum[m] - y_sum[EXACT]) / y_sum[EXACT]);
}
return 0;
}В конце программы мы выводим три показателя для каждого метода:
- среднее время вычисления одной операции в пикосекундах, чем меньше, тем лучше,
- коэффициент времени вычислений по сравнению с точным методом, чем больше, тем быстрее,
- среднюю погрешность между методом и точным методом, просто чтобы убедиться, что вычисления выполнены правильно.
Чего же мы ожидаем? В наборе команд x86 есть специализированные функции для вычисления обратного квадратного корня, которые компилятор должен иметь возможность генерировать. Их скорость, вероятно, выше, чем метод аппроксимации, при котором мы выполняем несколько операций.
Давайте проверим это: сначала скомпилируем код при помощи GCC без любых оптимизаций, в явном виде задав -O0. Так как мы используем math.h для точного метода, нам также понадобится скомпоновать математическую библиотеку при помощи -lm:
$ gcc -lm -O0 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 3330 1.00 0.0000
appr 2020 1.65 0.0193
appr_nr 6115 0.54 -0.0010Это кажется логичным. Погрешность заметна после первой аппроксимации, но уменьшается после одной итерации NR. Первая аппроксимация на самом деле быстрее точного метода, но совместно с одним шагом NR она вдвое медленнее. Метод NR требует количества операций больше разумного.
Но это лишь отладочная сборка, давайте попробуем добавлять оптимизации при помощи флага -O3. Это включит все оптимизации, не противоречащие стандартам.
$ gcc -lm -O3 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 1879 1.00 0.0000
appr 72 26.01 0.0193
appr_nr 178 10.54 -0.0010
Хм, теперь аппроксимации намного быстрее, чем раньше, однако время точного метода уменьшилось всего вдвое, поэтому аппроксимация с NR в десять с лишним раз быстрее точного метода. Возможно, компилятор не сгенерировал функции обратного квадратного корня? Может быть, ситуация улучшится, если мы используем флаг -Ofast, описанный на man-странице gcc(1):
Отключение строгого следования стандартам. -Ofast включает все оптимизации -O3. Также он включает оптимизации, валидные не для всех программ, соответствующих стандартам. Он включает -ffast-math, -fallow-store-data-races и специфичные для Fortran -fstack-arrays, если не задан fmax-stack-var-size, и -fno-protect-parens. Он отключает -fsemantic-interposition.
Наш точный метод может быть не таким точным, как раньше, но может оказаться быстрее.
$ gcc -lm -Ofast rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 153 1.00 0.0000
appr 118 1.30 0.0137
appr_nr 179 0.85 -0.0009И он действительно быстрее. Первая аппроксимация по-прежнему быстрее него, но с шагом NR она медленнее точного метода. Погрешность для аппроксимаций немного уменьшилась, потому что мы по-прежнему сравниваем с «точным» методом, который теперь даёт другие результаты. Довольно странно, что первая аппроксимация стала вдвое быстрее. Похоже, это особенность GCC, потому что Clang не имеет этой проблемы, а во всём остальном он создаёт схожие результаты:
$ clang -lm -O0 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 3715 1.00 0.0000
appr 1933 1.92 0.0193
appr_nr 6001 0.62 -0.0010$ clang -lm -O3 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 1900 1.00 0.0000
appr 61 31.26 0.0193
appr_nr 143 13.24 -0.0010
$ clang -lm -Ofast rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 148 1.00 0.0000
appr 62 2.40 0.0144
appr_nr 145 1.02 -0.0009Дизассемблирование
У обоих компиляторов есть достаточно большая разница между -O3 и -Ofast. Чтобы разобраться в происходящем, мы можем посмотреть на дизассемблированный код. Чтобы получить в двоичном файле отладочные символы, сообщающие нам, какой объектный код соответствует исходному коду, нужно передать компилятору флаг -g. Затем мы можем выполнить objdump -d с флагом -S, чтобы увидеть дизассемблированные команды рядом с исходным кодом:
$ gcc -lm -O3 -g rsqrt.c
$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
118e: 66 0f ef db pxor %xmm3,%xmm3
1192: 0f 2e d8 ucomiss %xmm0,%xmm3
1195: 0f 87 e1 02 00 00 ja 147c <main+0x3bc>
119b: f3 0f 51 c0 sqrtss %xmm0,%xmm0
119f: f3 0f 10 0d 99 0e 00 movss 0xe99(%rip),%xmm1 # 2040
11a6: 00
...
11ab: f3 0f 5e c8 divss %xmm0,%xmm1
...
2040: 00 00 80 3f 1.0f
Это синтаксис AT&T для ассемблерного кода x86-64. Обратите внимание, что операнд источника всегда находится перед операндом назначения. Скобки обозначают адрес, например, movss 0xecd(%rip),%xmm1 копирует значение, расположенное на 0xecd байтов перед адресом в регистре rip (указателе команд, или PC), в регистр xmm1. Регистры xmmN имеют ширину 128 битов или 4 слова. Однако команды ss предназначены для скалярных значений одинарной точности, поэтому команда применит операцию только к одному значению с плавающей запятой в самых младших 32 битах.
В случае -O3 мы используем скалярную sqrtss, за которой следует divss. Также присутствует сравнение ucomiss и переход ja, переводящий errno в режим EDOM в случае, если входящие данные меньше -0. Мы совершенно не используем errno, поэтому можно удалить присвоение значения errno, задав флаг -fno-math-errno:
$ gcc -lm -O3 -g -fno-math-errno rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 479 1.00 0.0000
appr 116 4.13 0.0193
appr_nr 175 2.74 -0.0010$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
1170: 0f 51 0c 28 sqrtps (%rax,%rbp,1),%xmm1
1174: f3 0f 10 1d c4 0e 00 movss 0xec4(%rip),%xmm3 # 2040
117b: 00
117c: 48 83 c0 10 add $0x10,%rax
1180: 0f c6 db 00 shufps $0x0,%xmm3,%xmm3
1184: 0f 28 c3 movaps %xmm3,%xmm0
1187: 0f 5e c1 divps %xmm1,%xmm0
...
2040: 00 00 80 3f 1.0f
Это позволяет нам не проверять каждое входное значение по отдельности, обеспечивая таким образом возможность использовать упакованные вариации команд, выполняя по четыре операции за раз. Это сильно повышает производительность. Однако мы по-прежнему используем sqrtps, за которым следует divps. Также нам придётся включить -funsafe-math-optimizations4 и -ffinite-math-only, чтобы заставить GCC генерировать rsqrtps. Тогда мы получим код, аналогичный тому, когда использовали -Ofast:
4 Это включает в себя -fno-signed-zeros, -fno-trapping-math, -fassociative-math и -freciprocal-math. Я попытался включить их все по отдельности, но не смог получить команды rsqrtps, пока не включил -funsafe-math-optimizations. Похоже, эта опция делает нечто большее, чем включение этих флагов.
$ gcc -lm -O3 -g -fno-math-errno -funsafe-math-optimizations -ffinite-math-only rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 155 1.00 0.0000
appr 120 1.29 0.0137
appr_nr 182 0.85 -0.0009$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
1170: 0f 52 0c 28 rsqrtps (%rax,%rbp,1),%xmm1
1174: 0f 28 04 28 movaps (%rax,%rbp,1),%xmm0
1178: 48 83 c0 10 add $0x10,%rax
117c: 0f 59 c1 mulps %xmm1,%xmm0
117f: 0f 59 c1 mulps %xmm1,%xmm0
1182: 0f 59 0d c7 0e 00 00 mulps 0xec7(%rip),%xmm1 # 2050
1189: 0f 58 05 b0 0e 00 00 addps 0xeb0(%rip),%xmm0 # 2040
1190: 0f 59 c1 mulps %xmm1,%xmm0
...
2040: 00 00 40 c0 -3.0f
...
2050: 00 00 00 bf -0.5f
Теперь в коде используется rsqrtps, но в нём есть множество команд умножения, а также сложения. Зачем они нужны, разве нам не требуется только обратный квадратный корень? Мы можем получить подсказку, взглянув на дизассемблированный код функции appr_nr:
static inline float rsqrt_nr(float x, float y) { return y * (1.5f - x*0.5f*y*y); }
12f8: f3 0f 10 1d 80 0d 00 movss 0xd80(%rip),%xmm3 # 2080
12ff: 00
...
1304: 0f 59 05 65 0d 00 00 mulps 0xd65(%rip),%xmm0 # 2070
...
1310: 0f c6 db 00 shufps $0x0,%xmm3,%xmm3
...
1318: 0f 28 d1 movaps %xmm1,%xmm2
131b: 0f 59 d1 mulps %xmm1,%xmm2
131e: 0f 59 d0 mulps %xmm0,%xmm2
1321: 0f 28 c3 movaps %xmm3,%xmm0
1324: 0f 5c c2 subps %xmm2,%xmm0
1327: 0f 59 c1 mulps %xmm1,%xmm0
...
2070: 00 00 00 3f 0.5f
...
2080: 00 00 c0 3f 1.5fПоследняя часть выглядит очень похожей, потому что на самом деле выполняет то же самое: итерацию метода Ньютона-Рафсона5. Это можно понять из man-страницы gcc(1):
5 Компилятор выполнил операции немного в другом порядке. Похоже, он вычисляет это как -0.5f*y*(x*y*y+-3.0f).
Эта опция включает использование команд приблизительного обратного значения и приблизительного обратного квадратного корня с дополнительными шагами метода Ньютона-Рафсона для повышения точности вместо выполнения деления или квадратного корня и деления для получения аргументов с плавающей запятой.
Команда rsqrtps гарантирует только относительную погрешность меньше
, а итерация NR уменьшает её точно так же, как в коде Q3.
Если нам не нужна дополнительная точность, можно ли обеспечить ускорение, пропустив этап NR? Можно использовать встроенные функции компилятора, чтобы заставить компилятор сгенерировать только команду rsqrtps. В руководстве по GCC есть список встроенных функции для набора команд x86. Существует функция __builtin_ia32_rsqrtps, генерирующая команду rsqrtps:
v4sf __builtin_ia32_rsqrtps (v4sf);
В руководстве также есть глава о том, как использовать эти векторные команды со встроенными функциями. Нам нужно добавить typedef для типа v4sf, содержащего четыре числа с плавающей запятой. Затем можно использовать массив
этих векторов и просто за раз передавать этой встроенной функции по одному вектору. N кратно четырём, поэтому векторов половинной длины не будет. Можно просто преобразовать предыдущий входной массив
float в указатель vfs4. Мы добавим эти части в свою предыдущую программу:
typedef float v4sf __attribute__ ((vector_size(16)));
v4sf rsqrt_intr(v4sf x) { return __builtin_ia32_rsqrtps(x); };
v4sf *xv = (v4sf*)x, *yv = (v4sf*)y;
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N/4; i++) { yv[i] = rsqrt_intr(xv[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[INTR] += y[i]; }
t[INTR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);Можно скомпилировать этот код, чтобы запустить и дизассемблировать его:
$ gcc -lm -O3 -g rsqrt_vec.c
$ ./a.out
rsqrt ps/op ratio err
exact 1895 1.00 0.0000
appr 72 26.39 0.0193
appr_nr 175 10.81 -0.0010
rsqrtps 61 31.00 0.0000$ objdump -d -S a.out
...
v4sf rsqrt_intr(v4sf x) { return __builtin_ia32_rsqrtps(x); };
1238: 41 0f 52 04 04 rsqrtps (%r12,%rax,1),%xmm0
...Мы уменьшили код до одной команды, и он стал чуть быстрее, чем раньше.
Существуют также расширения, поддерживаемые не всеми процессорами, которые мы можем попробовать применить. При помощи -march=native мы можем приказать компилятору использовать любые команды, которые есть в нашем процессоре. Однако это сделает двоичный файл несовместимым с другими процессорами.
$ gcc -lm -Ofast -g -march=native rsqrt_vec.c
$ ./a.out
rsqrt ps/op ratio err
exact 78 1.00 0.0000
appr 40 1.96 0.0137
appr_nr 85 0.91 -0.0009
rsqrtps 62 1.25 0.0000
Теперь мы оптимизировались почти до уровня первой аппроксимации. Встроенная функция по скорости примерно такая же. «Точный» метод мы заменили 256-битной vrsqrtps и одним шагом NR:
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
11d0: c5 fc 52 0c 18 vrsqrtps (%rax,%rbx,1),%ymm1
11d5: c5 f4 59 04 18 vmulps (%rax,%rbx,1),%ymm1,%ymm0
11da: 48 83 c0 20 add $0x20,%rax
11de: c4 e2 75 a8 05 79 0e vfmadd213ps 0xe79(%rip),%ymm1,%ymm0
11e5: 00 00
11e7: c5 f4 59 0d 91 0e 00 vmulps 0xe91(%rip),%ymm1,%ymm1
11ee: 00
11ef: c5 fc 59 c1 vmulps %ymm1,%ymm0,%ymm0
Теперь __builtin_ia32_rsqrtps использует одну vrsqrtps без шага NR, однако она по-прежнему использует только 128-битные регистры.
Быстрая обработка
Итак, мы провели тестирование на моей машине и получили представление о том, какие виды команд можно использовать для вычисления обратного квадратного корня и какая производительность у них может быть. Теперь мы попробуем выполнить эти бенчмарки на множестве разных машин, чтобы понять, как наши открытия применимы в общем случае. Это те машины, к которым у меня есть удобный SSH-доступ. Все полученные данные можно скачать отсюда, в них также включены результаты по отдельности для функций обратного значения и квадратного корня.
Ниже показан список протестированных x86-машин, с указанием их CPU и даты выпуска. Все предыдущие тесты выполнялись на компьютере «igelkott».
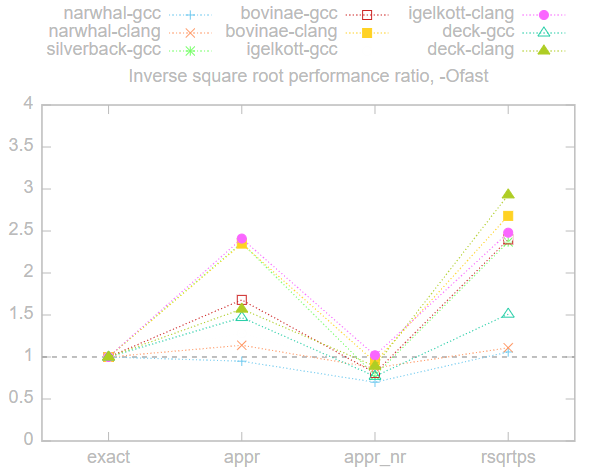
Ниже представлен график соотношений производительности по сравнению с точным методом exact, то есть время каждого метода, разделённое на время метода exact. Чем выше коэффициент, тем выше производительность, всё, что ниже 1, медленнее exact, а всё, что выше, — быстрее. Здесь мы использовали флаг -Ofast, потому что это самая быстрая опция, которую можно использовать без ущерба для портируемости.
Результаты довольно схожи на всех машинах, время методов приблизительно ранжировано в порядке rsqrtps <= appr < exact <= appr_nr. Применение метода appr_nr или медленнее, или схоже с методом exact, то есть в данном случае не даёт реальной выгоды.
Машина «jackalope» не включена в показанный выше график, потому что метод exact был на ней чрезвычайно медленным. Особенно когда не использовался -march=native, потому что компилятор в таком случае откатывался к применению древней команды fsqrt.
Ниже представлена таблица таймингов при использовании -Ofast, числа в скобках получения при использовании -march=native. Каждое число определяет, сколько отдельная операция занимает времени в пикосекундах.
Функция квадратного корня даёт немного иные результаты:
Довольно странно, что встроенная функция sqrtps медленнее, чем метод exact, а appr без NR теперь быстрее. Метод appr_nr по-прежнему не даёт никаких преимуществ, он стабильно хуже exact.
Вот исходные тайминги для функции квадратного корня с -Ofast. Числа в скобках снова указаны для -march=native:
Как указал пользователь thegeomaster, в некоторых случаях может требоваться детерминированность, то есть гарантия, что на разных машинах будет получаться одинаковый результат. Команда rsqrtps требуется только для того, чтобы относительная погрешность была меньше
, поэтому на разных машинах может реализована по-разному6.
6 Согласно исследованию Роберта О’Каллахана, реализации команд rsqrt в AMD и Intel отличаются для ровно 22 из возможных входных значений.
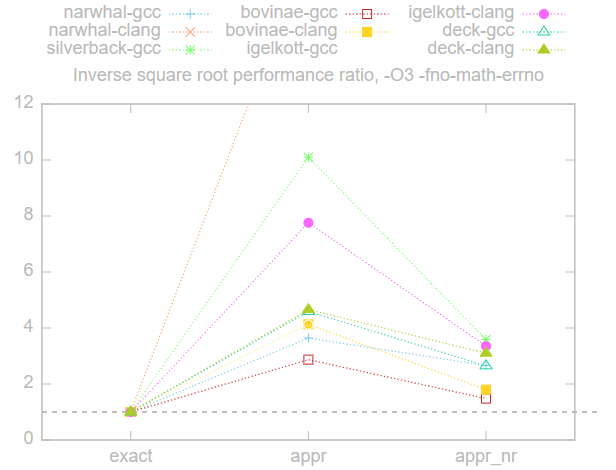
Однако в спецификации IEEE 754 есть спецификация для функции квадратного корня, которой гарантированно соответствует функция sqrtps. Поэтому в лучшем случае мы можем использовать sqrtps, за которой следует divps — именно это мы получили при использовании -O3 и -fno-math-errno. Воспроизводимость мы потеряли, только когда добавили -funsafe-math-optimzations. Если воспроизводимость обязательна, то при честном сравнении следует использовать только операции с плавающей запятой, соответствующие требованиям IEEE-754:
Это сдвигает чашу весов в пользу аппроксимаций. Применение метода appr_nr приводит к реализации, которая в 2-4 раза быстрее метода exact. Здесь narwhal-clang стал выбросом из-за удивительно медленного метода exact.
Попробуйте самостоятельно
Можете попробовать запустить бенчмарки на своей машине и проверить, получите ли вы схожие результаты. Есть шелл-скрипт bench/run.sh, который генерирует и запускает бенчмарки при помощи файла bench/bench.c.m4. Эти файлы можно найти в репозитории этой статьи. Просто запустите скрипт без аргументов, и он сгенерирует файл .tsv со всеми результатами:
$ cd bench
$ sh run.sh
$ grep rsqrt bench.tsv | sort -nk3 | head
rsqrt appr 40 1.91 0.0139 clang-Ofast-march=native
rsqrt rsqrtps 56 32.08 0.0000 clang-O3
rsqrt appr 58 31.08 0.0193 clang-O3
rsqrt rsqrtps 58 2.48 0.0000 clang-O3-fno-math-errno-funsafe-math-optimizations-ffinite-math-only
rsqrt rsqrtps 59 2.45 0.0000 gcc-Ofast
rsqrt rsqrtps 59 2.48 0.0000 clang-Ofast
rsqrt rsqrtps 59 31.07 0.0000 gcc-O3
rsqrt rsqrtps 59 7.83 0.0000 gcc-O3-fno-math-errno
rsqrt appr 60 2.41 0.0144 clang-O3-fno-math-errno-funsafe-math-optimizations-ffinite-math-only
rsqrt rsqrtps 60 8.09 0.0000 clang-O3-fno-math-errnoВ заключение
Подведём итог: использование простого 1/sqrtf(x) на современных процессорах x86 может быть и быстрее, и точнее, чем метод быстрого обратного квадратного корня из функции Q_rsqrt игры Quake III.
Однако основной вывод заключается в том, что необходимо приказать компилятору сделать его быстрее. При простой компиляции с помощью -O3 метод быстрого обратного квадратного корня на самом деле существенно быстрее, чем наивная реализация. Нам придётся позволить компилятору нарушить строгие требования спецификации, чтобы он сгенерировал более быструю реализацию.
Как говорилось в обсуждениях на HN, в некоторых случаях обязательным требованием становится детерминированность, то есть воспроизводимость между разными машинами. В таком случае мы можем использовать только те операции с плавающей запятой, которые детерминированы по стандартам, а к команде rqsrtps это неприменимо. Для таких случаев метод быстрого обратного квадратного корня может быть в 2-4 раза быстрее наивной реализации.
Если допустима очень низкая точность, то можно получить чуть более быструю реализацию, пропустив этап метода Ньютона-Рафсона из метода быстрого обратного квадратного корня. Любопытно, что компилятор тоже выполняет шаг NR после использования реализаций аппроксимаций обратного квадратного корня. Их тоже можно чуть ускорить, пропустив шаг NR, просто сгенерировав команду аппроксимации с помощью встроенных функций компилятора.
В этом посте мы рассматривали x86, но что насчёт других наборов команд?7 Метод быстрого обратного квадратного корня может по-прежнему быть полезен для процессоров без специализированных команд квадратного корня.
7 Я провёл быстрые тесты на своём телефоне с armv7 phone; скорость appr_nr была схожа со скоростью exact. Также я попробовал запустить тесты на машине с MIPS32, но столкнулся с проблемами в тулчейне кросс-компиляции. Оставим это на следующий раз…
Как обычно реализуются аппаратные реализации приблизительных квадратных корней? Может ли приблизительная аппаратная реализация потенциально использовать нечто похожее на первую аппроксимацию быстрого обратного квадратного корня?
Fast inverse square root, sometimes referred to as Fast InvSqrt() or by the hexadecimal constant 0x5F3759DF, is an algorithm that estimates 

The algorithm accepts a 32-bit floating-point number as the input and stores a halved value for later use. Then, treating the bits representing the floating-point number as a 32-bit integer, a logical shift right by one bit is performed and the result subtracted from the number 0x5F3759DF, which is a floating-point representation of an approximation of 
The algorithm was often misattributed to John Carmack, but in fact the code is based on an unpublished paper by William Kahan and K.C. Ng circulated in May 1986. The original constant was produced from a collaboration between Cleve Moler and Gregory Walsh, while they worked for Ardent Computing in the late 1980s.
With subsequent hardware advancements, especially the x86 SSE instruction rsqrtss, this method is not generally applicable to general purpose computing,[3] though it remains an interesting example both historically[4] and for more limited machines, such as low-cost embedded systems. However, more manufacturers of embedded systems are including trigonometric and other math accelerators such as CORDIC, avoiding the need for such algorithms.
History[edit]
William Kahan and K.C. Ng at Berkeley wrote an unpublished paper in May 1986 describing how to calculate the square root using bit-fiddling techniques followed by Newton iterations.[5] In the late 1980s, Cleve Moler at Ardent Computer learned about this technique[6] and passed it along to his coworker Greg Walsh. Greg Walsh devised the now-famous constant and fast inverse square root algorithm. Gary Tarolli was consulting for Kubota, the company funding Ardent at the time, and likely brought the algorithm to 3dfx Interactive circa 1994.[7][8]
Jim Blinn demonstrated a simple approximation of the inverse square root in a 1997 column for IEEE Computer Graphics and Applications.[9] Reverse engineering of other contemporary 3D video games uncovered a variation of the algorithm in Activision’s 1997 Interstate ’76.[10]
Quake III Arena, a first-person shooter video game, was released in 1999 by id Software and used the algorithm. Brian Hook may have brought the algorithm from 3dfx to id Software.[7] Copies of the fast inverse square root code appeared on Usenet and other forums as early as 2002 or 2003. Speculation arose as to who wrote the algorithm and how the constant was derived; some guessed John Carmack.[8] Quake III’s full source code was released at QuakeCon 2005, but provided no answers. The authorship question was answered in 2006.[7]
In 2007 the algorithm was implemented in some dedicated hardware vertex shaders using field-programmable gate arrays (FPGA).[11]
Motivation[edit]
Surface normals are used extensively in lighting and shading calculations, requiring the calculation of norms for vectors. A field of vectors normal to a surface is shown here.
A two-dimensional example of using the normal 
The inverse square root of a floating point number is used in calculating a normalized vector.[12] Programs can use normalized vectors to determine angles of incidence and reflection. 3D graphics programs must perform millions of these calculations every second to simulate lighting. When the code was developed in the early 1990s, most floating point processing power lagged the speed of integer processing.[8] This was troublesome for 3D graphics programs before the advent of specialized hardware to handle transform and lighting.
The length of the vector is determined by calculating its Euclidean norm: the square root of the sum of squares of the vector components. When each component of the vector is divided by that length, the new vector will be a unit vector pointing in the same direction. In a 3D graphics program, all vectors are in three-dimensional space, so 

is the Euclidean norm of the vector.
is the normalized (unit) vector, using 

which relates the unit vector to the inverse square root of the distance components. The inverse square root can be used to compute 
where the fraction term is the inverse square root of 
At the time, floating-point division was generally expensive compared to multiplication; the fast inverse square root algorithm bypassed the division step, giving it its performance advantage.
Overview of the code[edit]
The following code is the fast inverse square root implementation from Quake III Arena, stripped of C preprocessor directives, but including the exact original comment text:[13]
float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; }
At the time, the general method to compute the inverse square root was to calculate an approximation for 
The advantages in speed offered by the fast inverse square root trick came from treating the 32-bit floating-point word[note 2] as an integer, then subtracting it from a “magic” constant, 0x5F3759DF.[8][17][18][19] This integer subtraction and bit shift results in a bit pattern which, when re-defined as a floating-point number, is a rough approximation for the inverse square root of the number. One iteration of Newton’s method is performed to gain some accuracy, and the code is finished. The algorithm generates reasonably accurate results using a unique first approximation for Newton’s method; however, it is much slower and less accurate than using the SSE instruction rsqrtss on x86 processors also released in 1999.[3][20]
Worked example[edit]
As an example, the number 

0011_1110_0010_0000_0000_0000_0000_0000 Bit pattern of both x and i 0001_1111_0001_0000_0000_0000_0000_0000 Shift right one position: (i >> 1) 0101_1111_0011_0111_0101_1001_1101_1111 The magic number 0x5F3759DF 0100_0000_0010_0111_0101_1001_1101_1111 The result of 0x5F3759DF - (i >> 1)
Interpreting as IEEE 32-bit representation:
0_01111100_01000000000000000000000 1.25 × 2−3 0_00111110_00100000000000000000000 1.125 × 2−65 0_10111110_01101110101100111011111 1.432430... × 263 0_10000000_01001110101100111011111 1.307430... × 21
Reinterpreting this last bit pattern as a floating point number gives the approximation 

Avoiding undefined behavior[edit]
According to the C standard, reinterpreting a floating point value as an integer by casting then dereferencing the pointer to it is not valid (undefined behavior). Another way would be to place the floating point value in an anonymous union containing an additional 32-bit unsigned integer member, and accesses to that integer provides a bit level view of the contents of the floating point value. However, type punning through a union is also undefined behavior in C++.
#include <stdint.h> // uint32_t float Q_rsqrt(float number) { union { float f; uint32_t i; } conv = { .f = number }; conv.i = 0x5f3759df - (conv.i >> 1); conv.f *= 1.5F - (number * 0.5F * conv.f * conv.f); return conv.f; }
In C++ the usual method for implementing this function’s casts is through C++20’s std::bit_cast. This also allows the function to work in constexpr context:
#include <bit> #include <limits> #include <cstdint> constexpr float Q_rsqrt(float number) noexcept { static_assert(std::numeric_limits<float>::is_iec559); // (enable only on IEEE 754) float const y = std::bit_cast<float>( 0x5f3759df - (std::bit_cast<std::uint32_t>(number) >> 1)); return y * (1.5f - (number * 0.5f * y * y)); }
Algorithm[edit]
The algorithm computes 
- Alias the argument
to an integer as a way to compute an approximation of the binary logarithm
- Use this approximation to compute an approximation of
- Alias back to a float, as a way to compute an approximation of the base-2 exponential
- Refine the approximation using a single iteration of Newton’s method.
Floating-point representation[edit]
Since this algorithm relies heavily on the bit-level representation of single-precision floating-point numbers, a short overview of this representation is provided here. To encode a non-zero real number 

where the exponent 



These fields are then packed, left to right, into a 32-bit container.[23]
As an example, consider again the number 

and thus, the three unsigned integer fields are:
these fields are packed as shown in the figure below:
Aliasing to an integer as an approximate logarithm[edit]
If 


If 
then
and since 
where 


The integer aliased to a floating point number (in blue), compared to a scaled and shifted logarithm (in gray).
Thus there is the approximation
Interpreting the floating-point bit-pattern of 

It then appears that 


First approximation of the result[edit]
The calculation of 
Using the approximation of the logarithm above, applied to both 

Thus, an approximation of 
which is written in the code as
-
i = 0x5f3759df - ( i >> 1 );
The first term above is the magic number
from which it can be inferred that 


Newton’s method[edit]
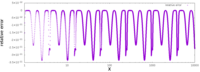
Relative error between direct calculation and fast inverse square root carrying out 0, 1, 2, 3, and 4 iterations of Newton’s root-finding method. Note that double precision is adopted and the smallest representable difference between two double precision numbers is reached after carrying out 4 iterations.
With 









where 

Treating 
y = y*(threehalfs - x/2*y*y); is equivalent to
By repeating this step, using the output of the function (

Accuracy[edit]
As noted above, the approximation is very accurate. The single graph on the right plots the error of the function (that is, the error of the approximation after it has been improved by running one iteration of Newton’s method), for inputs starting at 0.01, where the standard library gives 10.0 as a result, and InvSqrt() gives 9.982522, making the relative difference 0.0017478, or 0.175% of the true value, 10. The absolute error only drops from then on, and the relative error stays within the same bounds across all orders of magnitude.
Subsequent improvements[edit]
Magic number[edit]
It is not known precisely how the exact value for the magic number was determined. Chris Lomont developed a function to minimize approximation error by choosing the magic number 
Jan Kadlec reduced the relative error by a further factor of 2.7 by adjusting the constants in the single Newton’s method iteration as well,[31] arriving after an exhaustive search at
conv.i = 0x5F1FFFF9 - ( conv.i >> 1 ); conv.f *= 0.703952253f * ( 2.38924456f - x * conv.f * conv.f ); return conv.f;
A complete mathematical analysis for determining the magic number is now available for single-precision floating-point numbers.[32][33]
Zero finding[edit]
Intermediate to the use of one vs. two iterations of Newton’s method in terms of speed and accuracy is a single iteration of Halley’s method. In this case, Halley’s method is equivalent to applying Newton’s method with the starting formula 
where the implementation should calculate 
See also[edit]
- Methods of computing square roots § Approximations that depend on the floating point representation
- Magic number
Notes[edit]
References[edit]
- ^ “Discussion on CSDN”. Archived from the original on 2015-07-02.
- ^ Munafo, Robert. “Notable Properties of Specific Numbers”. mrob.com. Archived from the original on 16 November 2018.
- ^ a b Ruskin, Elan (2009-10-16). “Timing square root”. Some Assembly Required. Archived from the original on 2021-02-08. Retrieved 2015-05-07.
- ^ feilipu. “z88dk is a collection of software development tools that targets the 8080 and z80 computers”. GitHub.
- ^ “sqrt implementation in fdlibm – See W. Kahan and K.C. Ng’s discussion in comments in lower half of this code”.
- ^ Moler, Cleve. “Symplectic Spacewar”. MATLAB Central – Cleve’s Corner. MATLAB. Retrieved 2014-07-21.
- ^ a b c Sommefeldt, Rys (2006-12-19). “Origin of Quake3’s Fast InvSqrt() – Part Two”. Beyond3D. Retrieved 2008-04-19.
- ^ a b c d Sommefeldt, Rys (2006-11-29). “Origin of Quake3’s Fast InvSqrt()”. Beyond3D. Retrieved 2009-02-12.
- ^ Blinn 1997, pp. 80–84.
- ^ Peelar, Shane (1 June 2021). “Fast reciprocal square root… in 1997?!”.
- ^ Middendorf 2007, pp. 155–164.
- ^ Blinn 2003, p. 130.
- ^ “quake3-1.32b/code/game/q_math.c”. Quake III Arena. id Software. Archived from the original on 2020-08-02. Retrieved 2017-01-21.
- ^ Eberly 2001, p. 504.
- ^ Lomont 2003, p. 1.
- ^ Lomont 2003.
- ^ Lomont 2003, p. 3.
- ^ McEniry 2007, p. 2, 16.
- ^ a b Eberly 2001, p. 2.
- ^ Fog, Agner. “Lists of instruction latencies, throughputs and micro-operation breakdowns for Intel, AMD and VIA CPUs” (PDF). Retrieved 2017-09-08.
- ^ Goldberg 1991, p. 7.
- ^ Goldberg 1991, pp. 15–20.
- ^ Goldberg 1991, p. 16.
- ^ McEniry 2007, p. 3.
- ^ Hennessey & Patterson 1998, p. 305.
- ^ Hardy 1908, p. 323.
- ^ McEniry 2007, p. 6.
- ^ a b Lomont 2003, p. 10.
- ^ Lomont 2003, pp. 10–11.
- ^ Matthew Robertson (2012-04-24). “A Brief History of InvSqrt” (PDF). UNBSJ.
- ^ Kadlec, Jan (2010). “Řrřlog::Improving the fast inverse square root” (personal blog). Retrieved 2020-12-14.
- ^ Moroz et al. 2018.
- ^ Muller, Jean-Michel (December 2020). “Elementary Functions and Approximate Computing”. Proceedings of the IEEE. 108 (12): 2146. doi:10.1109/JPROC.2020.2991885. ISSN 0018-9219. S2CID 219047769.
Bibliography[edit]
- Blinn, Jim (July 1997). “Floating Point Tricks”. IEEE Computer Graphics & Applications. 17 (4): 80. doi:10.1109/38.595279.
- Blinn, Jim (2003). Jim Blinn’s Corner: Notation, notation notation. Morgan Kaufmann. ISBN 1-55860-860-5.
- Eberly, David (2001). 3D Game Engine Design. Morgan Kaufmann. ISBN 978-1-55860-593-0.
- Goldberg, David (1991). “What every computer scientist should know about floating-point arithmetic”. ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. S2CID 222008826.
- Hardy, Godfrey (1908). A Course of Pure Mathematics. Cambridge, UK: Cambridge University Press. ISBN 0-521-72055-9.
- Hennessey, John; Patterson, David A. (1998). Computer Organization and Design (2nd ed.). San Francisco, CA: Morgan Kaufmann Publishers. ISBN 978-1-55860-491-9.
- Lomont, Chris (February 2003). “Fast Inverse Square Root” (PDF). Retrieved 2009-02-13.
- McEniry, Charles (August 2007). “The Mathematics Behind the Fast Inverse Square Root Function Code” (PDF). Archived from the original (PDF) on 2015-05-11.
- Middendorf, Lars; Mühlbauer, Felix; Umlauf, George; Bodba, Christophe (June 1, 2007). “Embedded Vertex Shader in FPGA” (PDF). In Rettberg, Achin (ed.). Embedded System Design: Topics, Techniques and Trends. IFIP TC10 Working Conference:International Embedded Systems Symposium (IESS). et al. Irvine, California: Springer. doi:10.1007/978-0-387-72258-0_14. ISBN 978-0-387-72257-3. Archived (PDF) from the original on 2019-05-01.
- Striegel, Jason (2008-12-04). “Quake’s fast inverse square root”. Hackszine. O’Reilly Media. Archived from the original on 2009-02-15. Retrieved 2013-01-07.
- IEEE Computer Society (1985), 754-1985 – IEEE Standard for Binary Floating-Point Arithmetic, Institute of Electrical and Electronics Engineers
- Moroz, Leonid V.; Walczyk, Cezary J.; Hrynchyshyn, Andriy; Holimath, Vijay; Cieslinski, Jan L. (January 2018). “Fast calculation of inverse square root with the use of magic constant analytical approach”. Applied Mathematics and Computation. Elsevier Science Inc. 316 (C): 245–255. arXiv:1603.04483. doi:10.1016/j.amc.2017.08.025. S2CID 7494112.
Further reading[edit]
- Kushner, David (August 2002). “The wizardry of Id”. IEEE Spectrum. 39 (8): 42–47. doi:10.1109/MSPEC.2002.1021943.
External links[edit]
- 0x5f3759df, further investigations into accuracy and generalizability of the algorithm by Christian Plesner Hansen
- Origin of Quake3’s Fast InvSqrt()
- Quake III Arena source code (archived in Software Heritage)
- Implementation of InvSqrt in DESMOS
- “Fast Inverse Square Root — A Quake III Algorithm” (YouTube)




![{displaystyle yapprox I^{-1}left[{tfrac {3}{2}}L(B-sigma )-{tfrac {1}{2}}I_{x}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c352f2d00e5a1d74a13e3b99275d382a9f431c7)