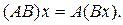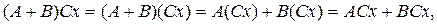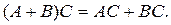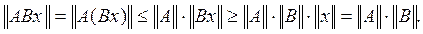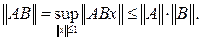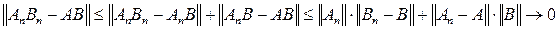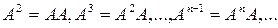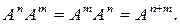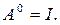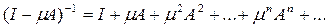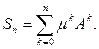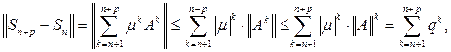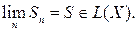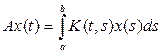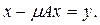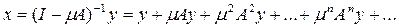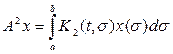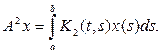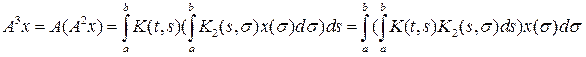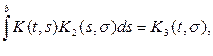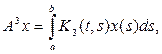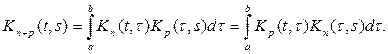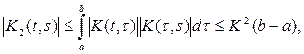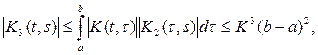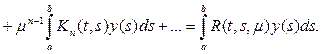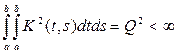Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 апреля 2019 года; проверки требует 1 правка.
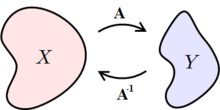
Если A отображает X на Y, то A−1 отображает Y на X
Обратный оператор к оператору 













Определение и условия существования[править | править код]
Другое определение: оператор 








Оператор 







Линейный оператор (даже ограниченный) может иметь обратный, определённый не на всём пространстве. Например, в пространстве 
имеет обратный, который определен для векторов с первой координатой равной нулю: 
Свойства[править | править код]
Теоремы об обратном операторе[править | править код]
Теорема Банаха[править | править код]
Теорема Банаха является одним из основных принципов линейного анализа[8]. Из неё следует теорема об открытом отображении: линейное непрерывное отображение 


Достаточные условия существования обратного оператора[править | править код]
где 

[11][12].
[13].
Примеры[править | править код]
Преобразование Фурье[править | править код]
можно рассматривать как линейный ограниченный оператор, действующим из пространства 
[14].
Операторы интегрирования и дифференцирования[править | править код]
Для оператора интегрирования
действующего в пространстве непрерывных функций ![{displaystyle C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)
определённый на линейном многообразии непрерывно дифференцируемых функций, таких что 
Оператор Штурма-Лиувилля[править | править код]
Для дифференциального оператора Штурма-Лиувилля
определённого на линейном многообразии дважды непрерывно дифференцируемых функций таких, что 
обратным оператором является интегральный оператор
где 

![{displaystyle C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)
Интегральный оператор[править | править код]
Пусть
— интегральный оператор в пространстве непрерывных функций ![{displaystyle C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)



,
где 

при любом свободном члене 
Обратный оператор в конечномерном пространстве[править | править код]
Оператор в конечномерном пространстве обратим тогда и только тогда, когда его ранг совпадает с размерностью пространства. Иначе говоря, определитель его матрицы отличен от нуля. Обратному оператору отвечает обратная матрица[17].
См. также[править | править код]
- Линейное отображение
- Обратная функция
- Изоморфизм
- Банахово пространство
- Линейный непрерывный оператор
Примечания[править | править код]
- ↑ 1 2 Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 225.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 128.
- ↑ 1 2 Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 168.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 351.
- ↑ 1 2 Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 319.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 154.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 207.
- ↑ Хелемский А. Я. Линейный оператор // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1982. — Т. 3: Коо — Од. — 1184 стб. : ил. — 150 000 экз.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава IV, §5, п. 4.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 155.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 157.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 229.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 230.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава VIII.
- ↑ 1 2 Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 161.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 163.
- ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра. Учеб. для вузов. — 5-e изд.. — М.: Физматлит, 2002. — 320 с. — ISBN 5-9221-0129-3.
Литература[править | править код]
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — Наука, Гл. ред. физ.-мат. лит.. — М., 1976.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа. — Изд. 2-е, перераб.. — М.: Наука, 1965. — 520 с.
- Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу. — М.: Мир, 1979. — 592 с.
- Соболев В. И. Обратное отображение // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1982. — Т. 3: Коо — Од. — 1184 стб. : ил. — 150 000 экз.
Рассмотрим теперь
множество линейных ограниченных
операторов, отображающих линейное
нормированное пространство
в себя.
B
пространстве операторов
,
действующих в банаховом пространстве
X
можно
рассматривать произведение операторов.
Именно, если
,
то АВ
есть оператор, определяемый равенством
Отличительной
особенностью этого произведения является
его некоммутативность, потому что,
вообще говоря, АВ
ВА. Чтобы
получить пример некоммутирующих
операторов, достаточно взять в Rn
два оператора, A
и В,
заданные некоммутирующими матрицами
и
.
Так как оператор АВ
задается произведением матриц
и
,
что легко проверить, то некоммутируемость
таких операторов очевидна. Свойством
дистрибутивности произведение операторов
обладает, так как из определения
суммы и произведения операторов
следует, что
т.е. что
Отметим, что если
I –
единичный оператор, то
для любого
.
Нетрудно проверить,
что
В самом деле, пусть
и
Тогда
Поэтому
Из доказанного
неравенства, в частности, следует, что
если
и
в смысле равномерной сходимости, то
Прежде всего из
сходимости последовательности
к А
следует, что
есть ограниченная числовая
последовательность, т. е.
для любого n.
Поэтому
при
так как в каждом слагаемом справа один
множитель ограничен, а другой стремиться
к нулю.
Частным случаем
произведения операторов являются
степени оператора
Ясно, что
Положим, кроме
того, по определению, что
Теорема 7. Пусть
где X
– банахово пространство и
Тогда оператор
имеет обратный линейный и ограниченный
оператор, причём
Доказательство.
Рассмотрим
ряд
(12)
и составим частичные
суммы этого ряда:
Имеем
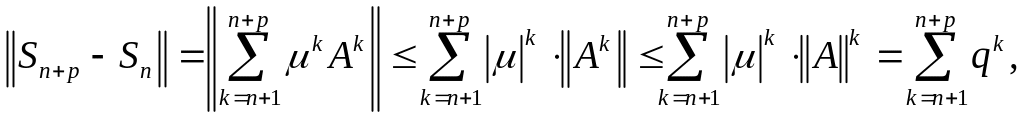
где
Отсюда следует, что
при
т.е. последовательность частичных сумм
ряда (12) является фундаментальной. В
силу полноты пространства операторов
существует
Покажем, что
Имеем
ибо
как общий член сходящегося ряда.
Аналогично убеждаемся, что
и теорема полностью доказана.
Применим доказанную
теорему к интегральным уравнениям.
Пример 19.
Пусть
непрерывное
на
ядро и
непрерывная на
функция. Тогда
есть линейный
оператор, действующий в пространстве
а интегральное уравнение
(13)
называется
уравнением
Фредгольма второго рода,
можно записать в операторной форме
На основании
предыдущей теоремы мы получаем, что
если
то уравнение (13) имеет единственное
решение, которое даётся равенством
Рассмотрим подробнее
это решение и условия, при которых оно
существует. Так как
то условие
очевидно, выполняется, если
Будем считать, что
удовлетворяет этому неравенству.
Выясним, что представляют в нашем случае
степени оператора. Имеем
Пусть
Функция
называется второй
итерацией ядра
Итак,
или, меняя обозначение
переменной интегрирования,
Далее,

и, снова пологая
можем написать
где
третья
итерация ядра
Вообще
где
– n-я
итерация ядра
определяемая формулой
Равенства
которое мы отмечали выше, дают
С помощью
итерированных ядер решение интегрального
уравнения может быть записано так:
(14)
Ряд, стоящий в
правой части этого равенства, сходится
в смысле сходимости в пространстве C[a,
b],
т.е. равномерно. Преобразуем выражение
для решения интегрального уравнения.
Рассмотрим формальный ряд
(15)
Этот ряд равномерно
сходится на
если
.
В самом деле, прежде всего имеем
и вообще
Отсюда
где
Таким образом, общий член исследуемого
функционального ряда не превосходит
по абсолютной величине члена сходящегося
числового ряда, и требуемая равномерная
сходимость доказана. Обозначим сумму
этого ряда R(t,
s,
).
Это – непрерывная функция. Умножая члены
ряда (15) на
и интегрируя ряд почленно, получим
Сравнивая это
выражение с выражением (14) для решения
интегрального уравнения, можем написать
(16)
Это и есть выражение
для обратного оператора
в компактной форме. Функция R(t,
s,
)
называется
разрешающим
ядром
рассматриваемого уравнения Фредгольма.
Сравните полученное
решение с решение в главе 2 п. 2.
Пример. 20.
Рассуждениями, аналогичными проведённым
выше, легко показать, что если
и
то интегральное уравнение (13) при
значениях параметра ,
удовлетворяющих неравенству
имеет решение, выражаемое формулой
(16), где разрешающее ядро R(t,
s,
),
по переменным
t
и s
имеет интегрируемый квадрат, и ряд (15),
его изображающий, сходится в среднем.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет, Вы узнаете про 5. Примеры обратных операторов. Обратимость операторов вида (I – A) и (A – C)., Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
5. Примеры обратных операторов. Обратимость операторов вида (I – A) и (A – C). , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Рассмотрим теперь множество линейных ограниченных операторов, отображающих линейное нормированное пространство 
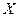
B пространстве операторов 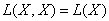
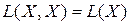
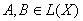
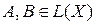
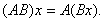
Отличительной особенностью этого произведения является его некоммутативность, потому что, вообще говоря, АВ 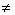
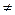
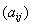
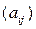
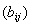
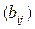
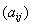
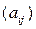
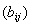
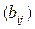
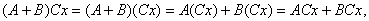
т.е. что 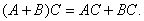
Отметим, что если I – единичный оператор, то 
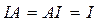


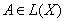
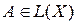
Нетрудно проверить, что 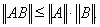


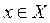
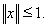
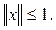
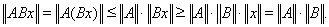
Поэтому

Из доказанного неравенства, в частности, следует, что если 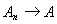
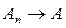
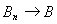

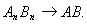
Прежде всего из сходимости последовательности 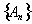
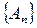
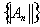


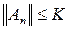
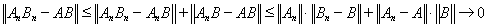
при 
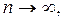
Частным случаем произведения операторов являются степени оператора

Ясно, что 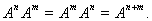
Положим, кроме того, по определению, что 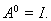
Теорема 7 . Об этом говорит сайт https://intellect.icu . Пусть 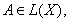
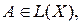
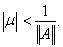

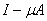

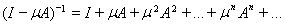
Доказательство. Рассмотрим ряд
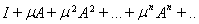
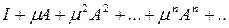
и составим частичные суммы этого ряда:
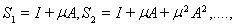
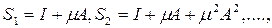

Имеем
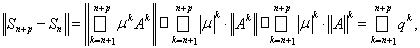
где 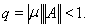
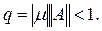
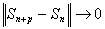
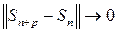
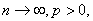

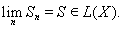
Покажем, что 
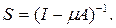
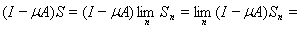
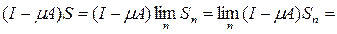
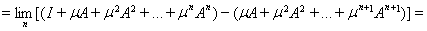
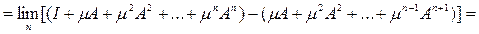
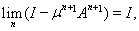
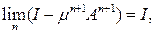
ибо 

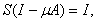
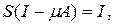
Применим доказанную теорему к интегральным уравнениям.
Пример 19. Пусть 
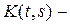
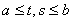
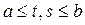
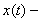
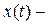
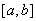
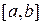
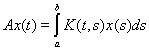
есть линейный оператор, действующий в пространстве 
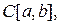

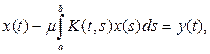
называется уравнением Фредгольма второго рода, можно записать в операторной форме 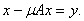
На основании предыдущей теоремы мы получаем, что если 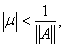
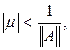

Рассмотрим подробнее это решение и условия, при которых оно существует. Так как 

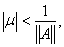
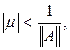
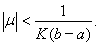
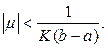


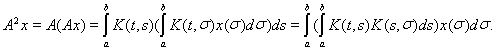
Пусть 
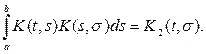
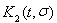
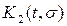

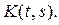
Итак,

или, меняя обозначение переменной интегрирования,
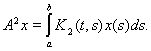
Далее,
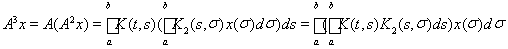
и, снова пологая
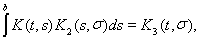
можем написать
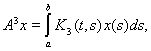
где 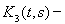
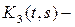

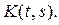
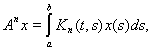
где 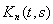

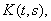

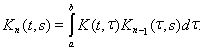
Равенства 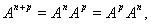
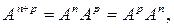
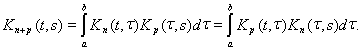
С помощью итерированных ядер решение интегрального уравнения может быть записано так:
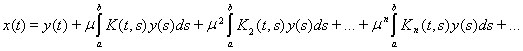
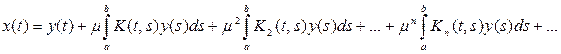
Ряд, стоящий в правой части этого равенства, сходится в смысле сходимости в пространстве C[a, b], т.е. равномерно. Преобразуем выражение для решения интегрального уравнения. Рассмотрим формальный ряд
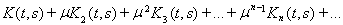

Этот ряд равномерно сходится на 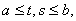
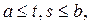
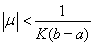



и вообще 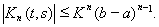
Отсюда 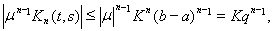


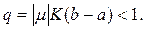
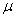


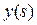

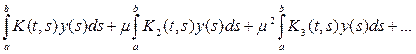

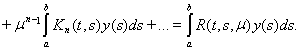
Сравнивая это выражение с выражением (14) для решения интегрального уравнения, можем написать
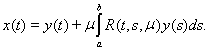
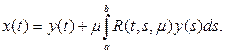
Это и есть выражение для обратного оператора 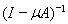



Сравните полученное решение с решение в главе 2 п. 2.
Пример. 20. Рассуждениями, аналогичными проведенным выше, легко показать, что если

и 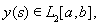
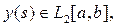
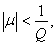
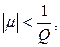
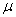

В общем, мой друг ты одолел чтение этой статьи об 5. Примеры обратных операторов. Обратимость операторов вида (I – A) и (A – C).. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое 5. Примеры обратных операторов. Обратимость операторов вида (I – A) и (A – C).
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Функциональный анализ
Из статьи мы узнали кратко, но емко про