Как найти образ фурье функции - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Преобразование Фурье — это интегральное преобразование, которое нашло широкое применение в физике и инженерных расчетах. Его часто используют для анализа сигналов и решения некоторых дифференциальных уравнений в частных производных.

Критерии сходимости преобразования Фурье (а именно, что функция должна быть абсолютно интегрируемой в вещественной области) довольно строги из-за отсутствия члена с экспоненциальным затуханием, который имеется в преобразовании Лапласа, и это означает, что такие функции, как полиномы, экспоненты и тригонометрические функции, не имеют преобразования Фурье в обычном смысле. Тем не менее с помощью дельта-функции Дирака можно осуществить преобразование Фурье этих функций корректным образом.

Такая процедура может потребоваться даже для самых простых функций, поэтому для лучшего понимания изложенного ниже материала желательно ознакомиться со свойствами преобразования Лапласа. Кроме того, лучше начать со свойств преобразования Фурье, и лишь затем переходить к рассмотрению конкретных примеров.

Предварительные сведения

1

Найдем преобразование Фурье производной. Простое интегрирование по частям и учет того, что должна стремиться к нулю на бесконечности, дают следующий результат:
2

Найдем преобразование Фурье функции, умноженной на $t^{{n}}$ . Симметрия преобразования Фурье дает аналогичное свойство в пространстве частот. Сначала рассмотрим случай , а затем обобщим полученный результат.
3
4
5
Найдем преобразование Фурье функции . В этом случае имеем свойство растяжения, которое наблюдается и для преобразования Лапласа:
- ${begin{aligned}{mathcal {F}}{f(ct)}&=int _{{-infty }}^{{infty }}f(ct)e^{{-iomega t}}{mathrm {d}}t,quad u=ct\&={frac {1}{|c|}}int _{{-infty }}^{{infty }}f(u)e^{{-iomega u/c}}{mathrm {d}}u\&={frac {1}{|c|}}{hat {f}}left({frac {omega }{c}}right)end{aligned}}$
6
Найдем преобразование Фурье свертки двух функций. Как и в случае преобразования Лапласа, свертка в реальном пространстве соответствует умножению в пространстве Фурье:
- ${begin{aligned}{mathcal {F}}{f(t)*g(t)}&=int _{{-infty }}^{{infty }}e^{{-iomega t}}{mathrm {d}}tint _{{-infty }}^{{infty }}f(t-y)g(y){mathrm {d}}y,quad u=t-y\&=int _{{-infty }}^{{infty }}e^{{-iomega (u+y)}}{mathrm {d}}uint _{{-infty }}^{{infty }}f(u)g(y){mathrm {d}}y\&=int _{{-infty }}^{{infty }}f(u)e^{{-iomega u}}{mathrm {d}}uint _{{-infty }}^{{infty }}g(y)e^{{-iomega y}}{mathrm {d}}y\&={hat {f}}(omega ){hat {g}}(omega )end{aligned}}$
7

Рассмотрим преобразование Фурье четных и нечетных функций. Четные и нечетные функции обладают особой симметрией. Для получения результата используем формулу Эйлера и свойства умножения четных и нечетных функций.

Реклама

1
Подставьте функцию в формулу для преобразования Фурье. Как и в случае преобразования Лапласа, преобразование Фурье функции можно выполнить непосредственно с помощью его определения. В качестве примера рассмотрим функцию $f(t)={frac {1}{t^{{2}}+1}}$ , которая однозначно удовлетворяет критериям сходимости.
- ${mathcal {F}}left{{frac {1}{t^{{2}}+1}}right}=int _{{-infty }}^{{infty }}{frac {e^{{-iomega t}}}{t^{{2}}+1}}{mathrm {d}}t$
2
Оценим интеграл с помощью доступных методов. Хотя данный интеграл не вычисляется элементарными методами, его можно найти с помощью теории вычетов.
- Чтобы использовать метод вычетов, проведем контур , состоящий из линии вдоль действительной оси и соединенной с ней полукруглой дуги в нижней полуплоскости, которая обходится по часовой стрелке. Действительный интеграл равен интегралу по контуру, а интеграл вдоль дуги обращается в нуль:
  - $oint _{{gamma }}{frac {e^{{-iomega t}}}{t^{{2}}+1}}{mathrm {d}}t=int _{{-infty }}^{{infty }}{frac {e^{{-iomega t}}}{t^{{2}}+1}}{mathrm {d}}t+int _{{{text{arc}}}}{frac {e^{{-iomega t}}}{t^{{2}}+1}}{mathrm {d}}t$
- Можно разложить знаменатель на множители и показать, что функция имеет простые полюсы в $t_{{pm }}=pm i$ . Поскольку контур охватывает лишь $t_{{-}}$ , можно использовать теорему вычетов, чтобы вычислить интеграл по контуру:
  - $operatorname {Res}(f(t);-i)={frac {e^{{-omega }}}{-2i}}$
- Обратите внимание на дополнительный знак «–», который появился из-за того, что мы двигаемся по контуру по часовой стрелке.
  - $oint _{{gamma }}{frac {e^{{-iomega t}}}{t^{{2}}+1}}{mathrm {d}}t=-2pi icdot {frac {e^{{-omega }}}{-2i}}=pi e^{{-omega }}$
- Не менее важно показать, что интеграл вдоль дуги равен нулю. Это можно сделать с помощью леммы Жордана. Хотя в лемме не говорится непосредственно, что интеграл равен нулю, она позволяет оценить разность между интегралом по контуру и вещественным интегралом. Применим лемму к нижней полуплоскости для функции $f(t)=e^{{-iomega t}}g(t)$ , где . С параметризацией $C=Re^{{-iphi }}$ , где , лемма Жордана дает следующее ограничение для интеграла:
  - ${Bigg |}int _{{C}}f(t){mathrm {d}}t{Bigg |}leq {frac {pi }{omega }}max _{{phi in [0,pi ]}}g(Re^{{-iphi }})$
- Теперь осталось показать, что стремится к нулю при больших , что в данном случае тривиально, поскольку функция уменьшается как $1/R^{{2}}$ :
  - $lim _{{Rto infty }}{frac {1}{(Re^{{-iphi }})^{{2}}+1}}=0$
- Какова в данном случае область определения ? Как отмечалось выше, лемма Жордана применима лишь для . Тем не менее, если повторить данный расчет для контура в верхней полуплоскости, найти вычет для второго полюса, еще раз применить лемму Жордана и убедиться, что интеграл вдоль дуги равен нулю, мы получим $pi e^{{omega }}$ , и в этом случае областью определения будут отрицательные действительные числа. Таким образом, получаем окончательный результат:
  - ${mathcal {F}}left{{frac {1}{t^{{2}}+1}}right}=pi e^{{-|omega |}}$
3
4
Рассмотрим преобразование Фурье функции Гаусса. Функция Гаусса относится к тем немногим функциям, которые при преобразовании Фурье сохраняют свой вид. Дополним показатель степени до полного квадрата и проинтегрируем:
- ${begin{aligned}{mathcal {F}}{e^{{-t^{{2}}}}}&=int _{{-infty }}^{{infty }}e^{{-t^{{2}}}}e^{{-iomega t}}{mathrm {d}}t\&=int _{{-infty }}^{{infty }}e^{{-(t^{{2}}+iomega t-omega ^{{2}}/4+omega ^{{2}}/4)}}{mathrm {d}}t\&=e^{{-omega ^{{2}}/4}}int _{{-infty }}^{{infty }}e^{{-(t+iomega /2)^{{2}}}}{mathrm {d}}t\&={sqrt {pi }}e^{{-omega ^{{2}}/4}}end{aligned}}$
Реклама

1

Рассмотрим преобразование Фурье функции $e^{{iat}}$ . Если вы знакомы с преобразованием Лапласа, то знаете, что экспоненциальная функция имеет очень «простое» преобразование Лапласа. В случае преобразования Фурье дело обстоит сложнее, поскольку модуль данной функции не стремится к 0 при . Тем не менее ее образ Фурье представляет собой дельта-функцию:
2
Рассмотрим преобразование Фурье функции $t^{{n}}e^{{iat}}$ . С помощью свойства сдвига можно найти преобразование Фурье степенной функции, а следовательно, и любых полиномов. Обратите внимание, что при этом вычисляются производные дельта-функции:
- ${mathcal {F}}{t^{{n}}e^{{iat}}}=2pi i^{{n}}{frac {{mathrm {d}}^{{n}}}{{mathrm {d}}omega ^{{n}}}}delta (omega -a)$
3

Реклама

Советы

Существуют также две другие распространенные формы записи преобразования Фурье.

Об этой статье

Эту страницу просматривали 18 367 раз.

Была ли эта статья полезной?

Источник

Преобразование Фурье

Краткое имя/название	FT
Названо в честь	Фурье, Жан-Батист Жозеф
Описывающая закон или теорему формула	${displaystyle left({mathcal {F}}fright)(omega )=int limits _{-infty }^{infty }mathrm {e} ^{-mathrm {i} omega t}f(t)mathrm {d} t}$ ^[1]
Обозначение в формуле	, , и
Обратно к	обратное преобразование Фурье^[d]
Медиафайлы на Викискладе

Преобразование Фурье (символ ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Определение[править | править код]

Преобразование Фурье функции вещественной переменной является интегральным и задаётся следующей формулой:

${hat {f}}(omega )={frac {1}{{sqrt {2pi }}}}int limits _{{-infty }}^{{infty }}f(x)e^{{-ixomega }},dx.$

Разные источники могут давать определения, отличающиеся от приведённого выше выбором множителя перед интегралом (так называемого нормировочного множителя, который относится к вопросу о нормировке преобразования Фурье), а также знака «−» в показателе экспоненты. Но вне зависимости от таких вариаций все свойства будут сохранять свою силу, хотя вид некоторых формул может измениться.

Общая формула всех вариантов определения преобразования Фурье с параметрами и выглядит как

${displaystyle {hat {f}}(omega )={sqrt {frac {left|bright|}{(2pi )^{1-a}}}}int limits _{-infty }^{infty }f(x)e^{-ibxomega },dx.}$

Обратное преобразование определяется так

${displaystyle f(x)={sqrt {frac {left|bright|}{(2pi )^{1+a}}}}int limits _{-infty }^{infty }{hat {f}}(omega )e^{ibomega x},domega .}$

При выборе a=0 и или формулы становятся особенно просты, в них исчезают нормировочные множители и формулы отличаются только знаком степени, вследствие чего большинство нижеприведенных формул упрощаются на постоянные константы.

Кроме того, существуют разнообразные обобщения данного понятия (см. ниже).

Свойства[править | править код]

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса $L_{1}(mathbb{R} )$ , преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

Преобразование Фурье является линейным оператором:

widehat {(alpha f+beta g)}=alpha {hat {f}}+beta {hat {g}}.

${displaystyle int limits _{-infty }^{infty }|f(x)|^{2},dx=int limits _{-infty }^{infty }|{{hat {f}}(w)}|^{2},domega .}$

Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство $L_{2}(mathbb{R} )$ . Равенство Парсеваля будет при этом справедливо для всех $fin L_{2}(mathbb{R} )$ .

Формула обращения:

${displaystyle f(x)={frac {1}{sqrt {2pi }}}int limits _{-infty }^{infty }{hat {f}}(omega )e^{ixomega },domega }$

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция является достаточно гладкой. Если $fin L_{2}(mathbb{R} )$ , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний $e^{{iomega x}}$ с частотами omega , амплитудами ${frac {1}{{sqrt {2pi }}}}|{hat {f}}(omega )|$ и фазовыми сдвигами соответственно.

Теорема о свёртке: если $f,;gin L_{1}(mathbb{R} )$ , тогда

widehat {(fast g)}={sqrt {2pi }}widehat {f}widehat {g}

, где

$(fast g)(t)=int limits _{{-infty }}^{{infty }}f(t-s)g(s),ds.$

Эта формула может быть распространена и на случай обобщённых функций.

Преобразование Фурье и дифференцирование. Если $f,;f'in L_{1}(mathbb{R} )$ , то

Из этой формулы легко выводится формула для -й производной:

$widehat {(f^{{(n)}})}=(iomega )^{n}widehat {f}.$

Формулы верны и в случае обобщённых функций.

Преобразование Фурье и сдвиг.

${displaystyle {widehat {f(x-x_{0})}}=e^{-iomega x_{0}}{hat {f}}(omega ).}$

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией $delta (x-x_{0})$ , а дифференцирование — свёртка с производной дельта-функции.

Преобразование Фурье и растяжение.

${displaystyle {widehat {f(ax)}}=|a|^{-1}{hat {f}}(omega /a).}$

Формула суммирования Пуассона:

${displaystyle sum _{k=-infty }^{+infty }f(k)=sum _{n=-infty }^{+infty }{hat {f}}(n)}$

Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

$S({mathbb R}):=left{varphi in C^{{infty }}({mathbb R}):forall n,;min mathbb{N} ;x^{n}varphi ^{{(m)}}(x){xrightarrow {xto infty }}0right}.$

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство $S^{*}(mathbb{R} )$ . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции $fin S^{*}(mathbb{R} )$ её преобразованием Фурье называется обобщённая функция ${hat {f}}in S^{*}(mathbb{R} )$ , действующая на основные функции по правилу

langle {hat {f}},;varphi rangle =langle f,;{hat {varphi }}rangle .

Например, вычислим преобразование Фурье дельта-функции:

$langle {hat {delta }},;varphi rangle =langle delta ,;{hat {varphi }}rangle =leftlangle delta ,;{frac {1}{{sqrt {2pi }}}}int limits _{{-infty }}^{{infty }}varphi (x)e^{{-iomega x}},dxrightrangle ={frac {1}{{sqrt {2pi }}}}int limits _{{-infty }}^{{infty }}varphi (x)cdot 1,dx=leftlangle {frac {1}{{sqrt {2pi }}}},;varphi rightrangle .$

Таким образом, преобразованием Фурье дельта-функции является константа ${frac {1}{{sqrt {2pi }}}}$ .

Принцип неопределенности[править | править код]

Вообще говоря, чем больше концентрация f(x), тем более размазанным должно быть её преобразование Фурье f̂(ω). В частности, свойство масштабирования преобразования Фурье можно представить так: если сжать функцию в x раз, то её преобразование Фурье растягивается в ω раз. Невозможно произвольно сконцентрировать как функцию, так и её преобразование Фурье.

Компромисс между уплотнением функции и её преобразованием Фурье можно формализовать в виде принципа неопределенности, рассматривая функцию и её преобразование Фурье как сопряжённые переменные относительно симплектической формы на время-частоту: c точки зрения линейного канонического преобразования, преобразование Фурье является поворотом на 90° во временно-частотной области и сохраняет симплектическую форму.

Предположим, что f(x) — интегрируемая и квадратично-интегрируемая функция. Тогда норма выражается как

${displaystyle ||f||_{2}=int limits _{-infty }^{infty }|f(x)|^{2},dx.}$

Из теорема Планшереля следует, что f̂(ω) также нормировано.

Разброс вокруг математического ожидания ${displaystyle x_{0}={frac {1}{||f||_{2}^{2}}}int limits _{-infty }^{infty }x|f(x)|^{2},dx}$ может быть измерен дисперсией, определяемой как

${displaystyle (Delta f)^{2}={frac {1}{||f||_{2}^{2}}}int limits _{-infty }^{infty }(x-x_{0})^{2}|f(x)|^{2},dx.}$

В терминах вероятности это центральный второй момент функции ${displaystyle |f(x)|^{2}}$ .

Принцип неопределённости гласит, что если f(x) абсолютно непрерывна, а функции x f(x) и f′(x) квадратично-интегрируемы, то

${displaystyle (Delta f)^{2}(Delta {hat {f}})^{2}geq {frac {1}{16pi ^{2}}}}$

где нормировочный множитель перед преобразованием Фурье равен , при нормировочном множителе равном ${frac {1}{2pi }}$ правое выражение переходит в ${frac {1}{4}}$ . Извлекая корни из обоих выражений правое выражение становится ${displaystyle {frac {1}{4pi }}}$ и ${frac {1}{2}}$ соответственно, Delta определяет половину ширины окна (стандартное отклонение).

Равенство достигается только в случае

${displaystyle {begin{aligned}f(x)&=C_{1},e^{-pi {frac {x^{2}}{sigma ^{2}}}}\therefore {hat {f}}(xi )&=sigma C_{1},e^{-pi sigma ^{2}omega ^{2}}end{aligned}}}$

где σ > 0 произвольно и ${displaystyle C_{1}={frac {sqrt[{4}]{2}}{sqrt {sigma }}}}$ так, что f является L²-нормированным. Другими словами, где f — (нормированная) функция Гаусса с дисперсией σ², центрированная на нуле, а её преобразование Фурье — гауссовская функция с дисперсией σ^-2.

Фактически, из этого неравенства следует, что:

для любого x₀, ω₀ ∈ R.

В квантовой механике импульс и положение волновой функции являются парами преобразований Фурье с точностью до постоянной Планка. При правильном учёте этой постоянной, неравенство выше становится утверждением принцип неопределенности Гейзенберга.

Более сильным принципом неопределенности является принцип неопределенности Хиршмана, который выражается как:

${displaystyle Hleft(left|fright|^{2}right)+Hleft(left|{hat {f}}right|^{2}right)geq ln left({frac {e}{2}}right)}$

где H(p) — дифференциальная энтропия функции плотности вероятности p(x):

${displaystyle H(p)=-int limits _{-infty }^{infty }p(x)ln {bigl (}p(x){bigr )},dx}$

где логарифмы могут быть в любой последовательной базе. Равенство достигается для функции Гаусса, как и в предыдущем случае.

Применения[править | править код]

Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть обратимый переход от временно́го пространства в частотное пространство. Богатые возможности применения основываются на нескольких полезных свойствах преобразования:

Преобразования являются линейными операторами и, с соответствующей нормализацией, унитарными (свойство, известное как теорема Парсеваля, или, в более общем случае, как теорема Планшереля, или, в наиболее общем, как дуализм Понтрягина).
Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
Синусоидальные базисные функции (вернее, комплексные экспоненты) являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо).
По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
Дискретная версия преобразования Фурье может быть быстро рассчитана на компьютерах с использованием алгоритма быстрого преобразования Фурье (БПФ).

Разновидности[править | править код]

Многомерное преобразование[править | править код]

Преобразование Фурье функций, заданных на пространстве $mathbb {R} ^{n}$ , определяется формулой

${hat {f}}(omega )={frac {1}{(2pi )^{{n/2}}}}int limits _{{mathbb{R} ^{n}}}f(x)e^{{-ixcdot omega }},dx.$

Здесь omega и — векторы пространства $mathbb {R} ^{n}$ , — их скалярное произведение. Обратное преобразование в этом случае задается формулой

$f(x)={frac {1}{(2pi )^{{n/2}}}}int limits _{{mathbb{R} ^{n}}}{hat {f}}(omega )e^{{ixcdot omega }},domega .$

Эта формула может быть интерпретирована как разложение функции в линейную комбинацию (суперпозицию) «плоских волн» вида $e^{{ixcdot omega }}$ с амплитудами ${frac {1}{(2pi )^{{n/2}}}}|{hat {f}}(omega )|$ , частотами omega и фазовыми сдвигами соответственно. Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.

Замечание относительно области задания преобразования Фурье и его основные свойства остаются справедливыми и в многомерном случае, со следующими уточнениями:

Взятие частных производных под действием преобразования Фурье превращается в умножение на одноимённую координату:

$widehat {{frac {partial f}{partial x_{k}}}}=iomega _{k}{hat {f}}(omega ).$

Изменяется константа в теореме о свёртке:

$widehat {(fast g)}=(2pi )^{{n/2}}{hat {f}}{hat {g}}.$

Преобразование Фурье и сжатие координат:

$widehat {left(fleft({frac {x}{|a|}}right)right)}=|a|^{n}{hat {f}}(omega |a|).$

Более общо, если ${displaystyle Acolon mathbb {R} ^{n}to mathbb {R} ^{n}}$ — обратимое линейное отображение, то

${displaystyle {widehat {left(f(Ax)right)}}=|det(A)|^{-1}{hat {f}}((A^{T})^{-1}omega ).}$

Ряды Фурье[править | править код]

Непрерывное преобразование само фактически является обобщением более ранней идеи рядов Фурье, которые определены для 2pi -периодических функций и представляют собой разложение таких функций в (бесконечную) линейную комбинацию гармонических колебаний с целыми частотами:

$f(x)=sum _{{n=-infty }}^{{infty }}{hat {f}}_{n},e^{{inx}}.$

Разложение в ряд Фурье применимо также к функциям, заданным на ограниченных промежутках, поскольку такие функции могут быть периодически продолжены на всю прямую.

Ряд Фурье является частным случаем преобразования Фурье, если последнее понимать в смысле обобщённых функций. Для любой 2pi -периодической функции имеем

${hat {f}}(omega )={sqrt {2pi }}sum _{{n=-infty }}^{{infty }}{hat {f}}_{n}delta (omega -n).$

Иными словами, преобразование Фурье периодической функции представляет собой сумму точечных нагрузок в целых точках и равно нулю вне их.

Дискретное преобразование[править | править код]

Дискретное преобразование Фурье — преобразование конечных последовательностей (комплексных) чисел, которое, как и в непрерывном случае, превращает свёртку в поточечное умножение. Используется в цифровой обработке сигналов и в других ситуациях, где необходимо быстро выполнять свёртку, например, при умножении больших чисел.

Пусть $x_{0},;x_{1},;ldots ,;x_{{n-1}}$ — последовательность комплексных чисел. Рассмотрим многочлен $f(t)=x_{0}+x_{1}t+x_{2}t^{2}+ldots +x_{{n-1}}t^{{n-1}}$ . Выберем какие-нибудь точек на комплексной плоскости $z_{0},;z_{1},;ldots ,;z_{{n-1}}$ . Теперь многочлену f(t) мы можем сопоставить новый набор из чисел: $f_{0}:=f(z_{0}),;f_{1}:=f(z_{1}),;ldots ,;f_{{n-1}}:=f(z_{{n-1}})$ . Заметим, что это преобразование обратимо: для любого набора чисел $f_{0},;f_{1},;ldots ,;f_{{n-1}}$ существует единственный многочлен f(t) степени не выше n-1 с такими значениями в $z_{0},;ldots ,;z_{{n-1}}$ соответственно (см. Интерполяция).

Набор ${f_{k}}$ и называется дискретным преобразованием Фурье исходного набора ${x_{k}}$ . В качестве точек $z_{k}$ обычно выбирают корни -й степени из единицы:

$z_{k}=e^{{frac {2pi ik}{n}}}$

Такой выбор продиктован тем, что в этом случае обратное преобразование принимает простую форму, а также тем, что вычисление преобразования Фурье может быть выполнено особенно быстро. Так, в то время как вычисление свёртки двух последовательностей длины напрямую требует порядка $n^{2}$ операций, переход к их преобразованию Фурье и обратно по быстрому алгоритму может быть выполнен за операций. Для преобразований Фурье свёртке соответствует покомпонентное умножение, которое требует лишь порядка операций.

Оконное преобразование[править | править код]

$F(t,;omega )=int limits _{{-infty }}^{infty }f(tau )W(tau -t)e^{{-iomega tau }},dtau ,$

где даёт распределение частот (вообще говоря, несколько искажённое) части оригинального сигнала f(t) в окрестности момента времени .

Классическое преобразование Фурье имеет дело со спектром сигнала, взятым во всём диапазоне существования переменной. Нередко интерес представляет только локальное распределение частот, в то время как требуется сохранить изначальную переменную (обычно время). В этом случае используется обобщение преобразования Фурье — так называемое оконное преобразование Фурье. Для начала необходимо выбрать некоторую оконную функцию , причём эта функция должна иметь хорошо локализованный спектр.

На практике дискретный спектральный анализ реализован в современных цифровых осциллографах и анализаторах спектра. Используется, как правило, выбор окна из 3—10 типов. Применение окон принципиально необходимо, поскольку в реальных приборах исследуется всегда некоторая вырезка из исследуемого сигнала. При этом разрывы сигнала вследствие вырезки резко искажают спектр из-за наложения спектров скачков на спектр сигнала.

Некоторые анализаторы спектра используют быстрое (или кратковременное) оконное преобразование. При нём сигнал заданной длительности разбивается на ряд интервалов с помощью скользящего окна того или иного типа. Это позволяет получать, исследовать и строить в виде спектрограмм динамические спектры и анализировать их поведение во времени. Спектрограмма строится в трёх координатах — частота, время и амплитуда. При этом амплитуда задаётся цветом или оттенком цвета каждого прямоугольника спектрограммы. Подобные анализаторы спектра называют анализаторами спектра реального времени. Основным их производителем является корпорация Keysight Technologies (США), Rohde & Schwarz (Германия), Tektronix (США). Такие анализаторы появились в конце прошлого века и ныне бурно развиваются. Частотный диапазон исследуемых ими сигналов достигает сотен гигагерц.

Указанные методы спектрального анализа реализуются и в системах компьютерной математики, например, Mathcad, Mathematica, Maple и MATLAB.

Другие варианты[править | править код]

Дискретное преобразование Фурье является частным случаем (и иногда применяется для аппроксимации) дискретного во времени преобразования Фурье (DTFT), в котором x_k определены на дискретных, но бесконечных областях, и таким образом спектр является непрерывным и периодическим. Дискретное во времени преобразование Фурье является по существу обратным для рядов Фурье.

Эти разновидности преобразования Фурье могут быть обобщены на преобразования Фурье произвольных локально компактных абелевых топологических групп, которые изучаются в гармоническом анализе; они преобразуют группу в её дуальную группу. Эта трактовка также позволяет сформулировать теорему свёртки, которая устанавливает связь между преобразованиями Фурье и свёртками. См. также дуализм Понтрягина.

Интерпретация в терминах времени и частоты[править | править код]

В терминах обработки сигналов преобразование берёт представление функции сигнала в виде временны́х рядов и отображает его в частотный спектр, где omega — угловая частота. То есть оно превращает функцию времени в функцию частоты; это разложение функции на гармонические составляющие на различных частотах.

Когда функция является функцией времени и представляет физический сигнал, преобразование имеет стандартную интерпретацию как спектр сигнала. Абсолютная величина получающейся в результате комплексной функции представляет амплитуды соответствующих частот ( omega ), в то время как фазовые сдвиги получаются как аргумент этой комплексной функции.

Однако преобразования Фурье не ограничиваются функциями времени и временными частотами. Они могут в равной степени применяться для анализа пространственных частот, также как для практически любых других функций.

Важные формулы[править | править код]

Следующая таблица содержит список важных формул для преобразования Фурье. и обозначают Фурье компоненты функций f(t) и g(t) , соответственно. и должны быть интегрируемыми функциями или обобщёнными функциями.

Соотношения в этой таблице и в особенности множители, такие как , зависят от соглашения, какая форма определения для преобразования Фурье использовалась прежде (хотя в общем виде соотношения, конечно, правильны).

	Функция	Образ	Примечания
1			Линейность
2		${displaystyle e^{-iomega a}F(omega )}$	Запаздывание
3	${displaystyle e^{iat}f(t)}$		Частотный сдвиг
4		$\|a\|^{{-1}}Fleft({frac {omega }{a}}right)$	Если большое, то сосредоточена около нуля, и $\|a\|^{{-1}}Fleft({frac {omega }{a}}right)$ становится плоским
5	${displaystyle {frac {d^{n}f(t)}{dt^{n}}}}$	${displaystyle (iomega )^{n}F(omega )}$	Свойство преобразования Фурье от -й производной
6	${displaystyle t^{n}f(t)}$	${displaystyle i^{n}{frac {d^{n}F(omega )}{domega ^{n}}}}$	Это обращение правила 5
7			Запись означает свёртку и . Это правило — теорема о свёртке
8		${displaystyle {frac {(F*G)(omega )}{sqrt {2pi }}}}$	Это обращение 7
9		${frac {1}{{sqrt {2pi }}}}$	означает дельта-функцию Дирака
10			Обращение 9.
11	$t^{n}$	${displaystyle i^{n}{sqrt {2pi }}delta ^{(n)}(omega )}$	Здесь — натуральное число, $delta ^{{(n)}}(omega )$ — -я обобщённая производная дельта-функции Дирака. Следствие правил 6 и 10. Использование его вместе с правилом 1 позволяет делать преобразования любых многочленов
12	${displaystyle e^{iat}}$		Следствие 3 и 10
13		${displaystyle {sqrt {2pi }}{frac {delta (omega -a)+delta (omega +a)}{2}}}$	Следствие 1 и 12 с использованием формулы Эйлера ${displaystyle cos(at)={frac {1}{2}}left(e^{iat}+e^{-iat}right)}$
14		${displaystyle {sqrt {2pi }}{frac {delta (omega -a)-delta (omega +a)}{2i}}}$	Также из 1 и 12
15	${displaystyle exp(-at^{2})}$	${displaystyle {frac {1}{sqrt {2a}}}exp left({frac {-omega ^{2}}{4a}}right)}$	Показывает, что функция Гаусса $exp(-t^{2}/2)$ совпадает со своим изображением
16	${displaystyle W{sqrt {frac {2}{pi }}}mathrm {sinc} (Wt)}$	${displaystyle mathrm {rect} left({frac {omega }{2W}}right)}$	Прямоугольная функция — идеальный фильтр нижних частот, а функция sinc(x) — её временной эквивалент
17	${displaystyle {frac {1}{t}}}$	${displaystyle -i{sqrt {frac {pi }{2}}}operatorname {sgn}(omega )}$	Здесь — функция sgn. Это правило согласуется с 6 и 10
18	${displaystyle {frac {1}{t^{n}}}}$	${displaystyle -i{sqrt {frac {pi }{2}}}{frac {(-iomega )^{n-1}}{(n-1)!}}operatorname {sgn}(omega )}$	Обобщение 17
19		${displaystyle {sqrt {frac {2}{pi }}}(iomega )^{-1}}$	Обращение 17
20		${displaystyle {frac {1}{iomega }}+pi delta (omega )}$	Здесь — функция Хевисайда. Следует из правил 1 и 19

См. также[править | править код]

Ортогональные функции
Дискретное преобразование Фурье над конечным полем
Вейвлет
Чирплет
Преобразование Гильберта — Хуанга
Гильбертово пространство

Примечания[править | править код]

↑ 2-19.1 // ISO 80000-2:2019Quantities and units — Part 2: Mathematics — 2 — Международная организация по стандартизации, 2019. — 36 с.

Литература[править | править код]

Зорич В. А. Математический анализ. — М.: Физматлит, 1984. — 544 с.
Афонский А. А., Дьяконов В. П. Цифровые анализаторы спектра, сигналов и логики / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2009. — С. 248. — ISBN 978-5-913-59049-7.
Дьяконов В. П. MATLAB 6.5 SP1/7.0 + Simulink 5/6. Обработка сигналов и проектирование фильтров. — М.: СОЛОН-Пресс, 2005. — С. 576. — ISBN 5-980-03206-1.
Сергиенко А. Б. Цифровая обработка сигналов. — 2-е изд. — СПб.: Питер, 2006. — С. 751. — ISBN 5-469-00816-9.
М. А. Павлейно, В. М. Ромаданов. Спектральные преобразования в MatLab. — СПб., 2007. — С. 160. — ISBN 978-5-983-40121-1.

Ссылки[править | править код]

Интегральные преобразования Архивная копия от 11 июля 2007 на Wayback Machine EqWorld: Мир математических уравнений
Online Computation of the transform or inverse transform
«Преобразование Фурье» Архивная копия от 4 июля 2015 на Wayback Machine — перевод статьи An Interactive Guide To The Fourier Transform | BetterExplained Архивная копия от 4 июля 2015 на Wayback Machine (англ.)
Рональд Н. Брейсуэлл. Преобразование Фурье. Scientific American. В мире науки. № 8, 1989, стр. 48-56 Архивная копия от 24 мая 2017 на Wayback Machine

Источник

Интеграл Фурье
Комплексная форма интеграла Фурье
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Косинус- и синус-преобразования Фурье
Амплитудный и фазовый спектры интеграла Фурье
Свойства преобразования Фурье
Приложения преобразования Фурье
Понятие о многомерном преобразовании Фурье
Дополнение к преобразованию Фурье

Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.

Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)

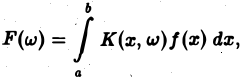
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).

Интеграл Фурье

Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)

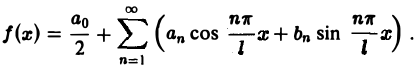
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)

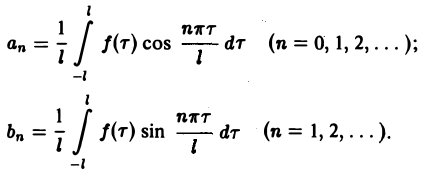
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos 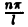х и sin 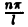х (что возможно, поскольку переменной интегрирования является τ) и используем формулу для косинуса разности. Будем иметь
(3)

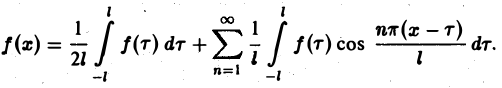
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).

Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:

1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;

2. функция f(x) абсолютно интегрируема на всей числовой оси,

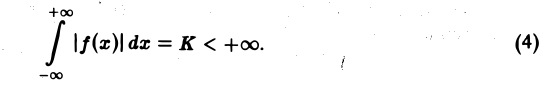
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,

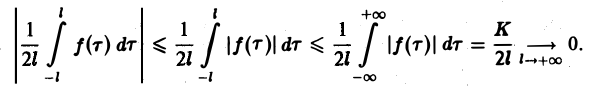
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим

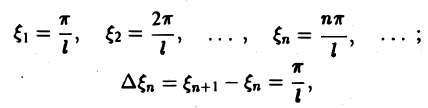
так, что 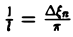. Тогда сумма в правой части (3) примет вид

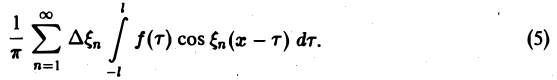
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения

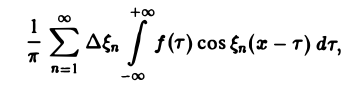
которое напоминает интегральную сумму для функции переменного ξ

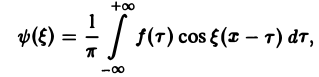
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ (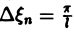 → 0) сумма (5) перейдет в интеграл

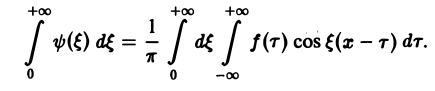
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что

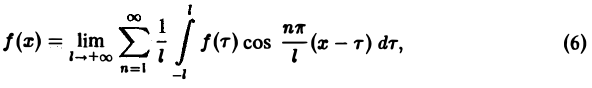
и мы получаем равенство
(7)

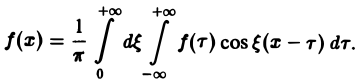
Достаточное условие справедливости формулы (7) выражается следующей теоремой.

Теорема:

Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞ < х < + ∞ и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, b], то справедливо равенство

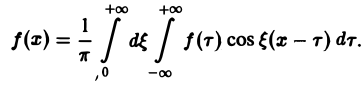
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно

j [/(^о — 0) + f(xo + 0)].

Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.

Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)

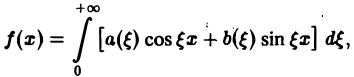
где

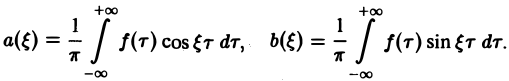
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).

Комплексная форма интеграла Фурье

Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл

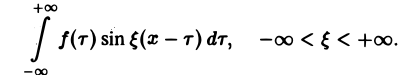
Этот интеграл равномерно сходится для — ∞ < ξ < + ∞, так как

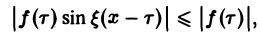
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда

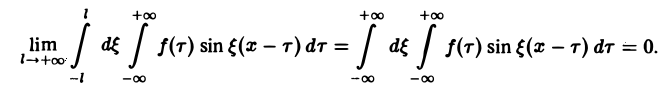
С другой стороны, интеграл

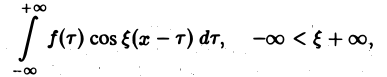
есть четная функция переменной так что

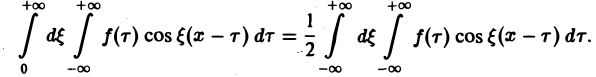
Поэтому интегральную формулу Фурье можно записать так:

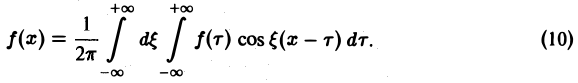
Умножим равенство

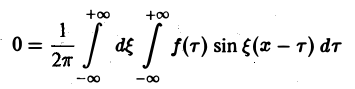
на мнимую единицу i и прибавим к равенству (10). Получим

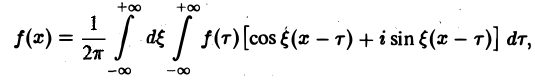
откуда, в силу формулы Эйлера (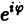= cos φ + i sin φ), будем иметь
(11)

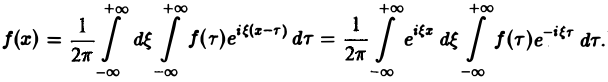
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:

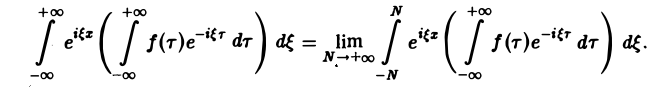
Преобразование Фурье. Косинус- и синус-преобразования Фурье

Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.

Определение:

Функция

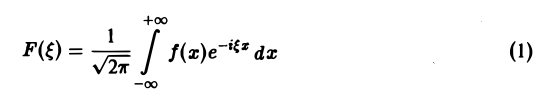
называется преобразованием Фурье функции f(x) (спектральной функцией).

Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром

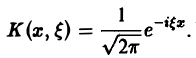
Используя интегральную формулу Фурье

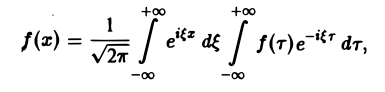
получаем
(2)

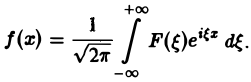
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:

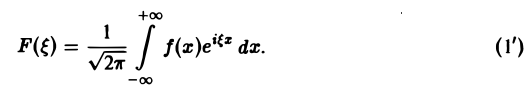
Тогда обратное преобразование Фурье определится формулой

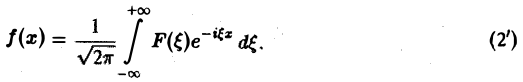
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:

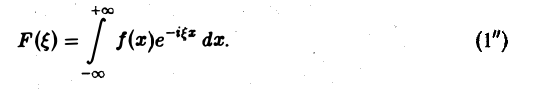
Тогда, в свою очередь,

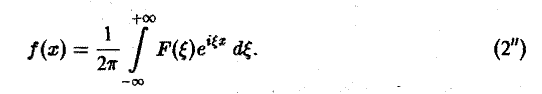
При этом положение множителя 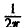достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).

Пример:

Найти преобразование Фурье функции

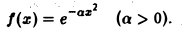
Имеем

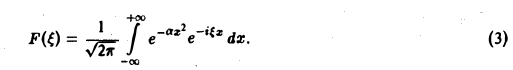
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):

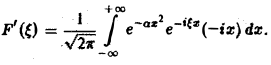
Интегрируя по частям, будем иметь

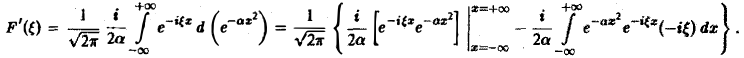
Внеинтегральное слагаемое обращается в нуль, и мы получаем

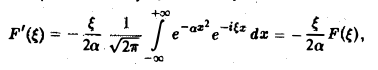
откуда

(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем

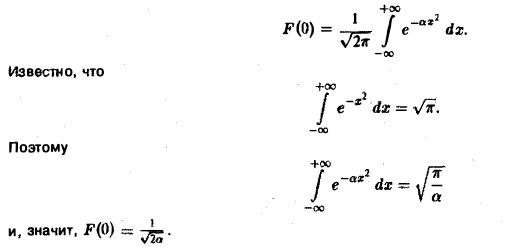
Таким образом,

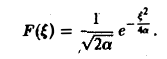
В частности, для

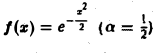
получаем, что

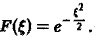
Пример:

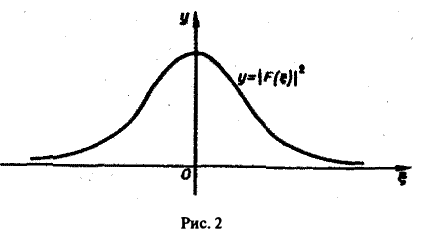
Разряд конденсатора через сопротивление. Рассмотрим функцию

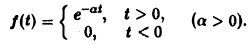
Для спектральной функции F( ξ ) получаем

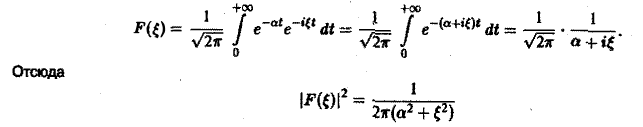
(рис. 2).

Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x³, f(х) = cosx, f(х) = е^х, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.

Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).

Косинус- и синус-преобразования Фурье

Используя формулу косинуса, разности, перепишем интегральную формулу Фурье

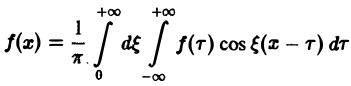
в следующем виде:

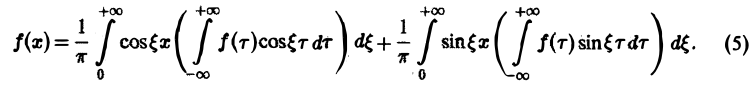
Пусть f(x) — четная функция. Тогда

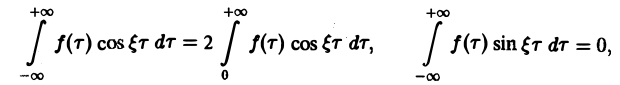
так что из равенства (5) имеем
(6)

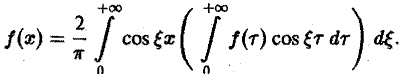
В случае нечетной f(x) аналогично получаем
(7)

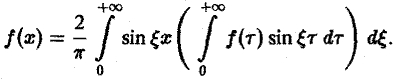
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.

Определение:

Функция

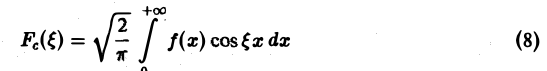
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)

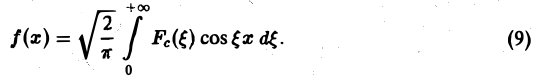
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.

Определение:

Функция

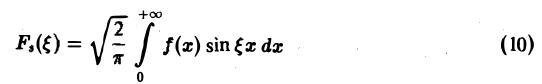
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)

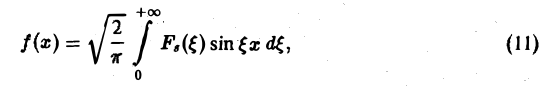
т.е. f и Fs являются взаимными синус-преобразованиями.

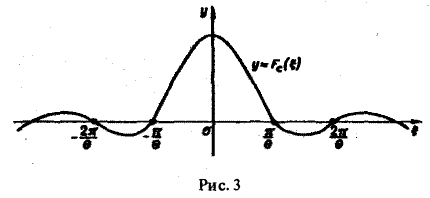
Пример:

Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:

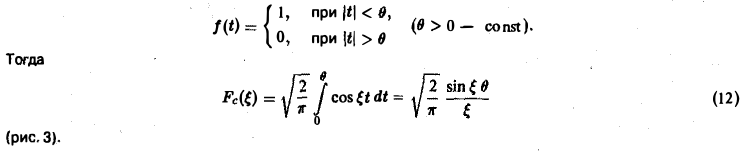
Воспользуемся полученным результатом для вычисления интеграла

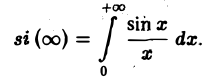
В силу формулы (9) имеем

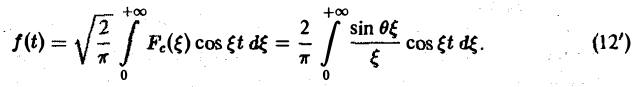
В точке t = 0 функция f(t) непрерывна и равна единице.

Поэтому из (12′) получим

Амплитудный и фазовый спектры интеграла Фурье

Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье

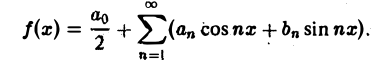
Это равенство можно записать в виде

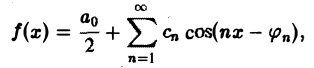
где Cn = 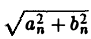— амплитуда колебания с частотой п, φn — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.

Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье

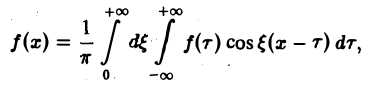
осуществляющим разложение этой функции по всем частотам 0 < ξ < + ∞ (разложение по непрерывному спектру частот).

Определение:

Спектральной функцией, или спектральной плотностью интеграла Фурье, называется выражение

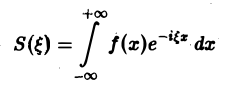
(прямое преобразование Фурье функции f(х)).

Функция

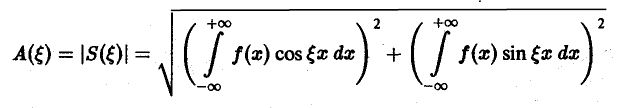
называется амплитудным спектром, а функция

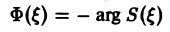
(0 — фазовым спектром функции f(x).

Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).

Пример:

Найти амплитудный и фазовый спектры функции

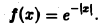
Находим спектральную функцию

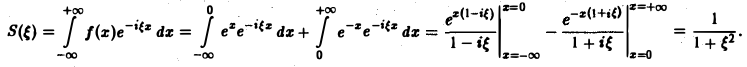
Отсюда

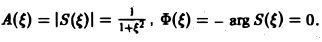
Графики этих функций изображены на рис. 4.

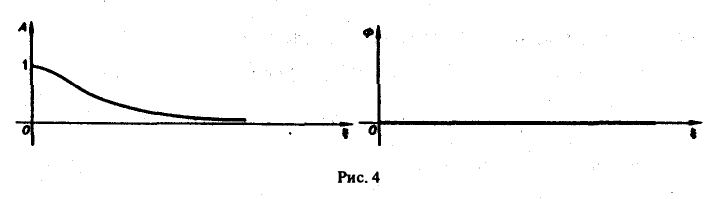
Свойства преобразования Фурье

1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).

Пользуясь свойством линейности интеграла, имеем

Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать

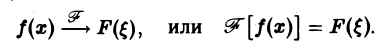
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).

Пусть функция f(х) абсолютно интегрируема на всей оси — ∞ < х < + ∞,

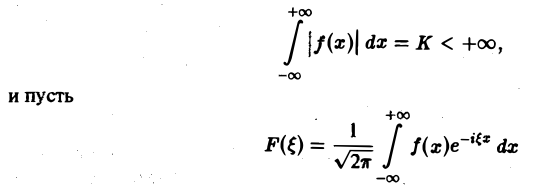
— преобразование Фурье функции f(х). Тогда

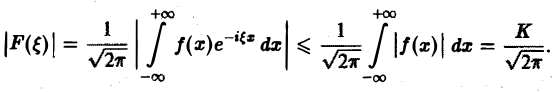
Задача:

Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что

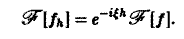
Задача:

Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что

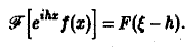
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем

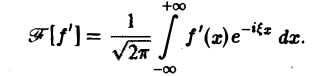
Интегрируя по частям, будем иметь

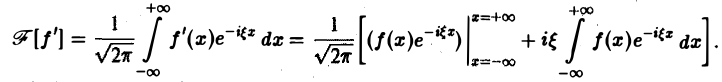
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)

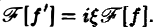
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье [f] на множитель iξ.

Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим

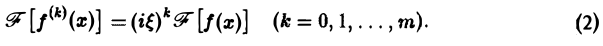
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.

Так как преобразование Фурье 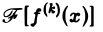абсолютно интегрируемой функции 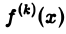есть ограниченная функция от ξ (свойство 2), то из соотношения (2) получаем для 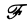[f] следующую оценку:

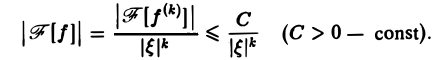
Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.

Замечание:

Условие 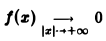является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.

4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье

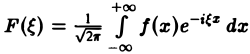
функции f(x) будет дифференцируемой функцией.

Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу

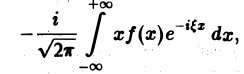
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и

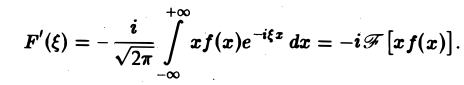
Таким образом,

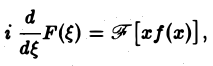
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию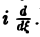

Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х^mf(х), то процесс дифференцирования можно продолжить.

Получим, что функция F( ξ ) = 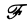[f(х)] имеет производные до порядка m включительно, причем

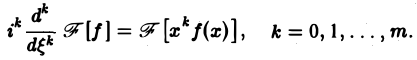
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = 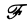[f(х)].

Теорема:

О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда

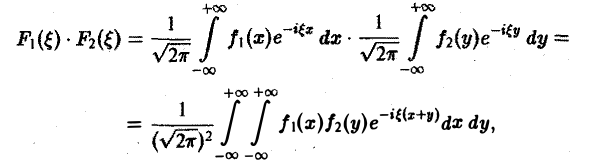
причем двойной интеграл в правой части сходится абсолютно.

Положим х + у = т, так что у = т — х. Тогда будем иметь

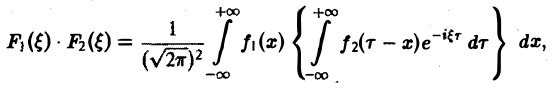
или, меняя порядок интегрирования,

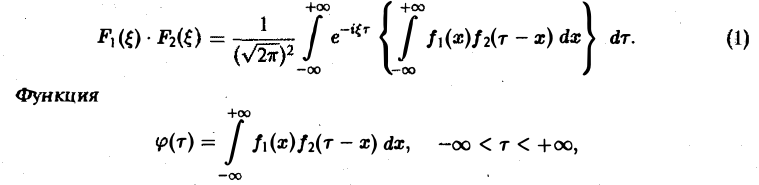
называется сверткой функций f(x) и f2(x) и обозначается символом 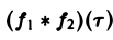. Формула (1) может быть теперь записана так:

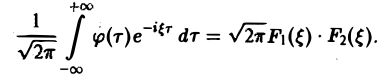
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 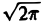произведению преобразований Фурье свертываемых функций,

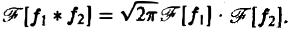
Замечание:

Нетрудно установить следующие свойства свертки:

1) линейность:

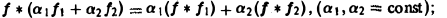
2) коммутативность:

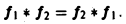
Приложения преобразования Фурье

1, Пусть 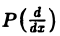— линейный дифференциальный оператор порядка m с постоянными коэффициентами,

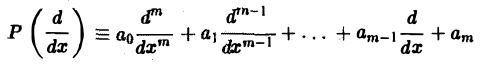
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим

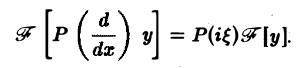
Рассмотрим дифференциальное уравнение

где 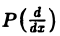— введенный выше дифференциальный оператор.

Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)

так что формально

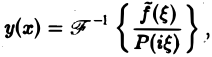
где символ 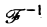обозначает обратное преобразование Фурье.

Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида

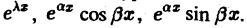
Они не являются абсолютно интегрируемыми на оси — ∞ < х < + ∞, и преобразование Фурье для них не определено, так что, строго говоря, применять данный метод нельзя. Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме.

Пример:

Найти решение u = u(x,t) уравнения

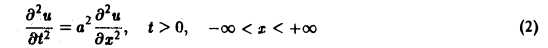
(а = const), при начальных условиях

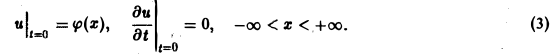
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.

Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что

1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при х → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье

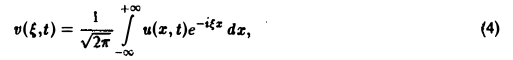
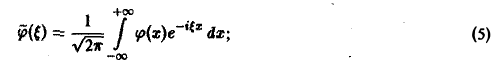
2) допустимы операции дифференцирования, так что

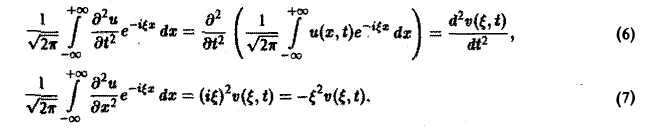
Умножая обе части (2) на 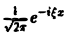и интегрируя по x от — ∞ до + ∞, получим

а из начальных условий (3) найдем

Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция

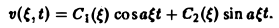
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим

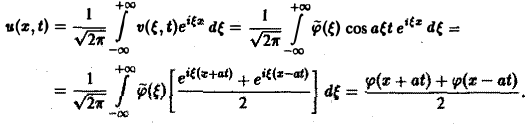
Это частный случай формулы Даламбера решения задачи (2)-(3).

2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.

Рассмотрим, например, уравнение

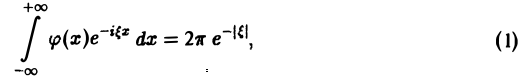
где φ(х) — искомая функция. Записав (1) в виде

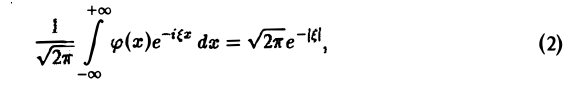
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:

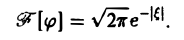
Тогда по формуле обращения

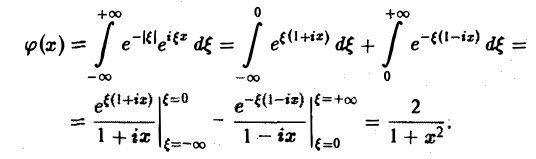
Функция 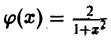есть решение уравнения (1).

Понятие о многомерном преобразовании Фурье

Преобразование Фурье:

Пусть

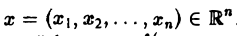
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция

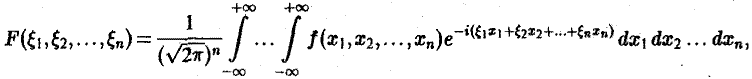
или, короче,

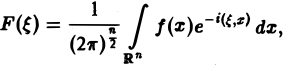
где

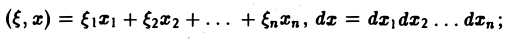
символ 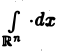обозначает интегрирование по всему пространству Rⁿ.

Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда

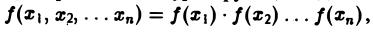
имеем

Дополнение к преобразованию Фурье

Смотрите также:

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

2.1 Интегральная формула Фурье как предельный случай ряда.

Как следует из
теории ряда Фурье, он применим при
обращении с периодическими функциями
и с функциями с ограниченным интервалом
изменения независимых переменных (
поскольку этот интервал может быть
расширен на всю ось путем периодического
продолжения функции). Однако периодические
функции сравнительно редки на практике.
Эта ситуация требует создания более
общего математического аппарата для
обращения с непериодическими функциями,
а именно интеграла Фурье и на его основе,
преобразования Фурье.

Рассмотрим
непериодическую функцию f(t) как предел
периодической с периодом T=2l при l®¥.

Периодическая
функция с периодом 2l может быть
представлена в виде разложения в ряд
Фурье ( воспользуемся комплексной его
формой)

(1)

где выражения для
коэффициентов имеют вид:

(2)

Введем следующее
обозначение для частот:

(3)

Запишем разложение
в ряд Фурье в виде одной формулы, подставив
в (1), выражение для коэффициентов

(2) и для частоты (3) :

(4)

Спектр периодической
функции с периодом 2l дискретный

Обозначим
минимальное расстояние между точками
спектра, равное основной частоте
колебаний

за
,
т.е.

и введем это
обозначение в (4):

(5).

В таких обозначениях
ряд Фурье напоминает интегральную
сумму для функции

.

Переходя к пределу
при T=2l®¥
к непериодической функции, получим,
что частотный интервал

становится
бесконечно малым ( обозначим его за dw),
а спектр становится непрерывным. С
математической точки зрения это
соответствует замене суммирования по
дискретному набору интегрированием по
соответствующей переменной в бесконечных
пределах.

(5)

Это выражение и
есть интегральная формула Фурье.

2.2 Формулы преобразования Фурье.

Интеграл Фурье
удобно представить в виде суперпозиции
двух

формул:

(6)

(7)

Функция F(w),
сопоставляемая по первой формуле функции
f(t), называется ее преобразованием
Фурье. В
свою очередь, вторая формула, позволяющая
найти исходную функцию по ее образу,
называется обратным
преобразованием Фурье.
Обратим внимание на симметрию формул
для прямого и обратного преобразования
Фурье с точность до постоянного множителя
1/2p
и знака в показателе экспоненты.

Символически
прямое и обратное преобразование Фурье
будем обозначать как f(t)~F(w).

Проводя аналогию
с тригонометрическим рядом Фурье, можно
прийти к выводу, что образ Фурье (6)
является аналогом коэффициента Фурье
(см.(2)), а обратное преобразование Фурье
(7) является аналогом разложения функции
в тригонометрический ряд Фурье (см.(1)).

Отметим, что
множитель

вместо обратного преобразования можно
отнести к прямому преобразованию Фурье
или сделать симметричные множители

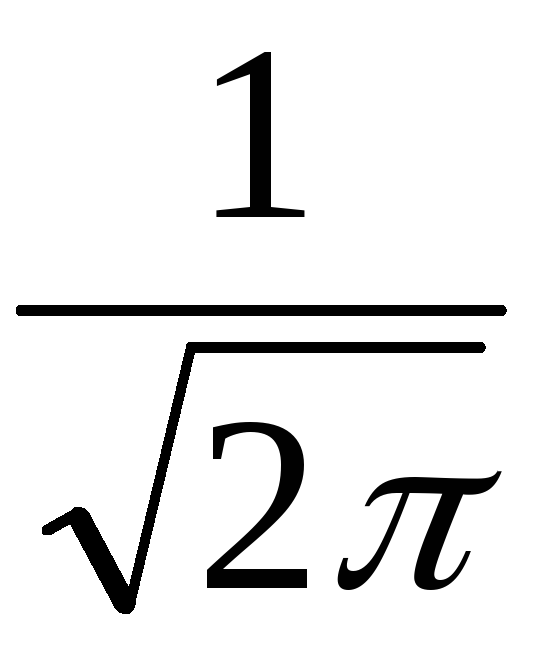
для прямого и
обратного преобразований . Главное,
чтобы оба преобразования вместе
составляли интегральную формулу Фурье
(5), т.е. произведение постоянных множителей
при прямом и обратном преобразовании
должно быть равно
..

Отметим, что для
прикладных целей более удобной оказывается
не угловая частота w,
а частота n,
связанная с первой соотношением w=2pn.
и измеряемая в герцах (Гц). В терминах
этой частоты формулы преобразования
Фурье будут иметь вид:

(6б),

(7б).

Сформулируем без
доказательства достаточные условия
существования преобразования Фурье.

1) f(t) – ограничена
при tÎ(-¥,¥);

2) f(t) – абсолютно
интегрируема на tÎ(-¥,¥);

3) Число точек
разрыва, максимума и минимума функции
f(t) конечно.

Другим достаточным
условием является требование квадратичной
интегрируемости функции на свей
действительной оси, что физически
соответствует требованию конечной
мощности сигнала.

Таким образом, с
помощью преобразования Фурье мы имеем
два способа представления сигнала:
временное f(t) и частотное F(w).

2.3 Свойства
преобразования Фурье.

1. Линейность.

Если
f(t)~F(w),g(t)~G(w),

то аf(t)+bg(t)
~aF(w)+bG(w).

Доказательство
основано на линейных свойствах интегралов.

2. Четность.

2.1 Если f(t)
действительная четная функция и
f(t)~F(w),
то F(w)
также действительная четная функция.

Доказательство:

Используя
определение (6), а также формулу Эйлера

получим

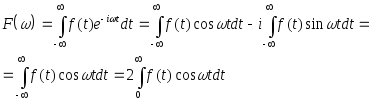
-четная
функция.

2.2 Если f(t) -нечетная
действительная функция,то F(w)-
нечетная мнимая функция.

2.3 Если f(t)
произвольная действительная функция,
F(w)
имеет четную действительную часть и
нечетную мнимую часть.

Доказательство:

Cвойства четности
2 можно суммировать в формуле :

3. Подобие

Если f(t)~F(w),
то f(at) ~
.

4. Смещение.

4.1 Если f(t)~F(w),
то f(t-a) ~.

Т.е. запаздыванию
во времени соответствует умножение на
комплексную экспоненту в области частот.

4.2 Если f(t)~F(w),
то~.

Т.е.
смещение по частоте соответствует
умножению на комплексную экспоненту
во временной области.

5. Если f(t)~F(w),то

5.1 f’(t)~iwF(w),~

если f(t) имеет n
непрерывных производных .

Доказательство:

5.2
~,~,

если F(w)
имеет n непрерывных производных.

Доказательство:

2.4 Важнейшие
примеры нахождения преобразования
Фурье.

1)
~

где
–
прямоугольный импульс

2)
~

3)
~

При этом мы учли,
что

– интеграл Пуассона.

Нахождение
последнего интеграла можно пояснить
следующим образом. Контур интегрирования
С есть прямая в комплексной плоскости
(t,w),
параллельная действительной оси
(w-постоянное
число). Интеграл от скалярной функции
по замкнутому контуру равен нулю.
Образуем замкнутый контур, состоящий
из прямой С и действительной оси t,
замыкающихся на бесконечности. Т.к. на
бесконечности подинтегральная функция

стремится к нулю, то интегралы по
замыкающим кривым равны нулю. Значит
интеграл по прямой С равен интегралу,
взятому по действительной действительной
оси, проходимой в положительном
направлении.

Соседние файлы в папке лекции

Источник

Предварительные сведения

Советы

Об этой статье

Была ли эта статья полезной?

Определение[править | править код]

Свойства[править | править код]

Принцип неопределенности[править | править код]

Применения[править | править код]

Разновидности[править | править код]

Многомерное преобразование[править | править код]

Ряды Фурье[править | править код]

Дискретное преобразование[править | править код]

Оконное преобразование[править | править код]

Другие варианты[править | править код]

Интерпретация в терминах времени и частоты[править | править код]

Важные формулы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Интеграл Фурье

Комплексная форма интеграла Фурье

Преобразование Фурье. Косинус- и синус-преобразования Фурье

Косинус- и синус-преобразования Фурье

Амплитудный и фазовый спектры интеграла Фурье

Свойства преобразования Фурье

Приложения преобразования Фурье

Понятие о многомерном преобразовании Фурье

Дополнение к преобразованию Фурье

2.1 Интегральная формула Фурье как предельный случай ряда.

2.2 Формулы преобразования Фурье.

Вам также может понравиться

Как составить запрос в пфр

Как найти пин код на рутокене

Как найти у кого мои фото вконтакте

Добавить комментарий Отменить ответ