Как найти образ линейного оператора пример

Линейный
оператор ,
действующий из пространства
в пространство ,
ставит в соответствие каждому вектору

определенный вектор
из .
При этом вектор
называется образом
вектора
,
а вектор
– прообразом
вектора

при отображении .

Пусть

и
– некоторые базисы линейных пространств

и
соответственно. Тогда ,

и координаты вектора – образа
связаны с координатами вектора – прообраза

соотношением

,

(7.2.1)

в
котором
– матрица линейного оператора
в паре базисов
и .

В
случае, когда пространства
и
совпадают, базисы
и
также совпадают, и формула (7.2.1) принимает
вид

.

(7.2.2)

Образом
(областью
значений)
линейного
оператора


называется
множество всех элементов
вида .
Образ линейного оператора является
подпространством пространства
и обозначается .
Размерность образа называется рангом
оператора
и обозначается .

Ядром
линейного оператора


называется
множество всех векторов пространства
,
которые переводятся оператором
в нулевой вектор пространства .
Ядро линейного оператора является
подпространством пространства
и обозначается .
Размерность ядра называется дефектом
оператора
и обозначается .

Сумма
ранга и дефекта оператора

равна размерности пространства
.

Ранг
линейного оператора равен рангу матрицы
этого оператора.

Базис
системы векторов – столбцов матрицы
линейного оператора
образует систему координатных столбцов
базиса образа .
Базис подпространства решений однородной
системы линейных алгебраических
уравнений с матрицей оператора
образует базис ядра .

Пример
1.
Из пространства
с базисом
в пространство
с базисом
действует линейный оператор ,
имеющий в данной паре базисов матрицу
.
Найдите столбец координат в базисе
образа вектора
и столбец координат в базисе
прообраза вектора .

Решение.
Столбец координат образа вектора
в базисе находим
непосредственно по формуле (7.2.1):

.

Для
определения прообраза вектора
по той же формуле (7.2.1) имеем

,

или,
что то же самое,

Отсюда
находим все прообразы
вектора ,
где
– свободная переменная, принимающая
произвольные значения.

Пример
2.
В пространстве с
базисом линейный
оператор
переводит векторы ,
в
векторы ,

соответственно. Найдите матрицу оператора
в
базисе .

Решение.
Пусть –
матрица оператора в
базисе .
Тогда из условий ,

по формуле (7.2.2) имеем ,

или,
в подробной записи,

Отсюда
получаем
Следовательно,
.

Пример
3.
Найдите базис ядра и базис образа
линейного оператора пространства ,
если этот оператор задан матрицей .

Решение.
При помощи элементарных преобразований
над строками матрицы
приведём её к ступенчатому виду:

.

Отсюда
следует, что .
Базис составляют,
например, векторы
и .

Дефект
оператора найдём по формуле

,

т.е.
фундаментальная система решений
однородной системы линейных алгебраических
уравнений с матрицей
будет состоять из одного вектора. Общее
решение однородной системы можно
записать в виде .
Полагая
получаем базисный вектор .

7.2.1.
Линейный оператор переводит
вектор
в вектор.
Найдите образ вектора
и прообраз вектора ,
если

,

,
;

,

,
;

,

,
.

7.2.2.
Линейный оператор в
паре базисов и

имеет матрицу .
Найдите прообраз вектора ,
если

,
;

б)
,
;

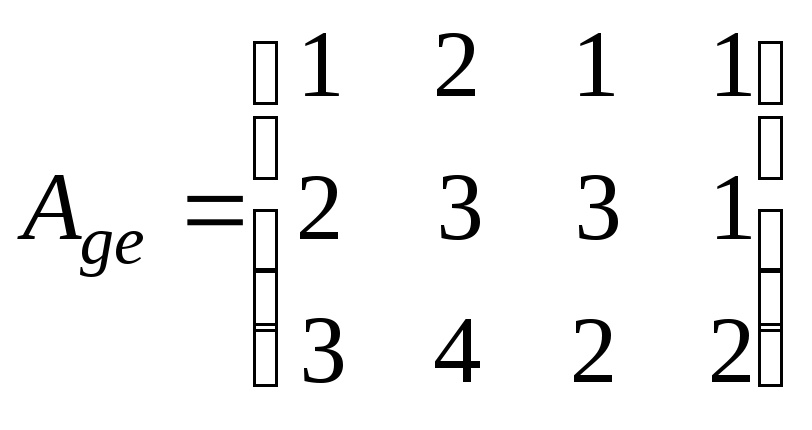в)
,
.

7.2.3.
Выясните, существует ли линейный оператор
двумерного пространства, переводящий
векторы ,

соответственно в векторы ,
,
и найдите матрицу этого оператора в
базисе ,
:

а)

б)

в)

7.2.4.
Выясните, существует ли линейный оператор
трехмерного пространства, переводящий
векторы ,
,

соответственно в векторы ,
,
,
и найдите матрицу этого оператора в том
же базисе, в котором даны координаты
всех векторов:

а)

б)

7.2.5.
Для указанных линейных операторов
пространства
найдите дефект и ранг, а также постройте
базисы ядра и образа. Каждый оператор
описывается своим действием на
произвольный вектор :

а)

б)

в)

7.2.6.
Найдите образ и ядро оператора
дифференцирования в пространстве .

7.2.7.
В пространстве
рассмотрите разностный
оператор

где

– фиксированное
число, отличное от нуля. Найдите его
образ и ядро.

7.2.8.
Найдите образ и ядро оператора
проектирования (см. задачу 7.1.2) на
параллельно
и оператора отражения (см. задачу 7.1.3) в

параллельно .

7.2.9.
Найдите базис ядра и базис образа
линейного
оператора из ,
заданного в некотором базисе матрицей
:

а)
;
б)
;
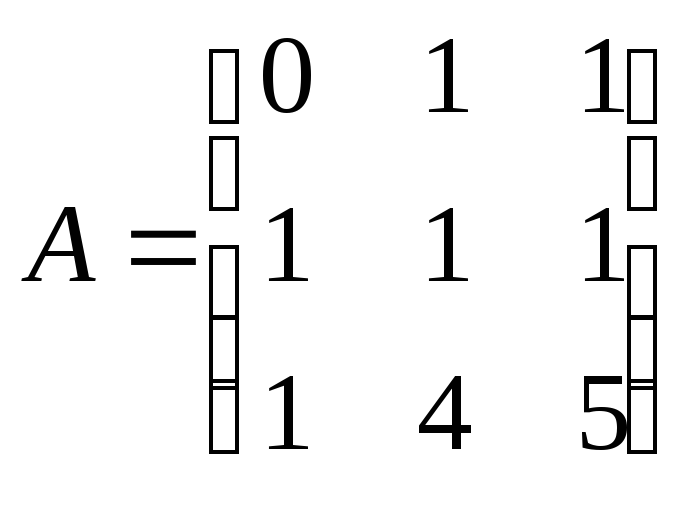в)
.

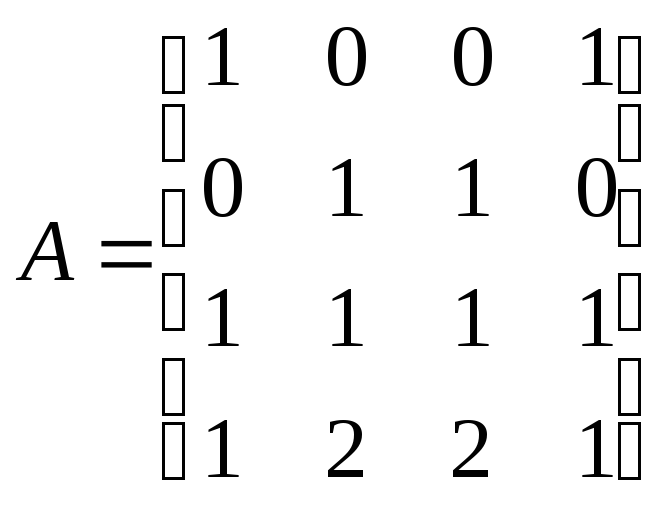7.2.10.
Найдите размерность линейного пространства

всех линейных операторов, действующих
в
– мерном линейном пространстве
и постройте базис пространства .

Соседние файлы в папке Задачник-2

• #
• #
• #
• #
• #
• #

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

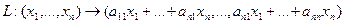
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 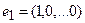, найдём его образ, это будет вектор 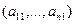. Для этого в формуле, задающей образ вектора, полагаем 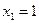, ,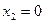…, 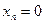. Аналогично находим образы для 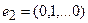,…, 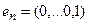. Из координат образа вектора 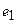составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

.

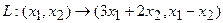Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

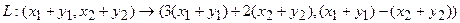Теперь каждую координату получившегося вектора можем преобразовать:

.

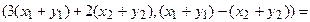
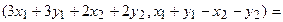
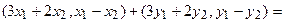
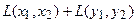Аналогично для умножения на константу:

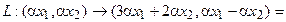
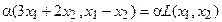
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

.

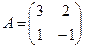Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .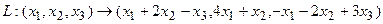

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

.

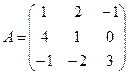2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

Если задана система 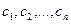из n векторов, образующих базис, и какая-нибудь произвольная система n векторов 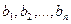(возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

Пусть 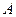– матрица оператора в базисе 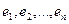. По условию, 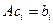для всех индексов 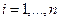. Данные n равенств можно записать в виде одного матричного равенства: 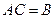, при этом столбцы матрицы 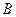– это векторы 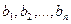, а столбцы матрицы 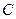– векторы 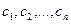. Тогда матрица 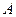может быть найдена в виде .

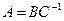Пример. Найти матрицу линейного оператора, отображающего базис

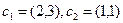в систему векторов .

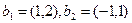Здесь 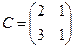, , 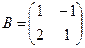, 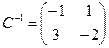и получаем:

.

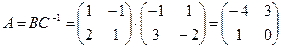Проверка осуществляется умножением получившейся матрицы на каждый вектор: .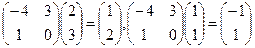

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

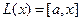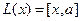Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, 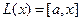. Для этого найдём образы всех трёх базисных векторов линейного пространства.

.

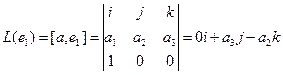Аналогично, ,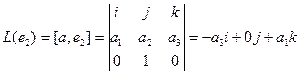

.

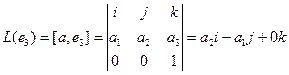Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .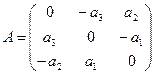

Аналогично можно построить матрицу линейного оператора :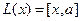

.

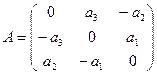Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .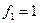

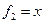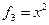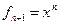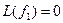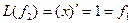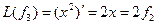, , , аналогично получим ,…, .

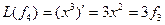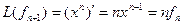Матрица этого линейного оператора:

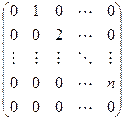
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

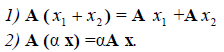
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 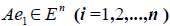, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

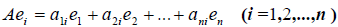
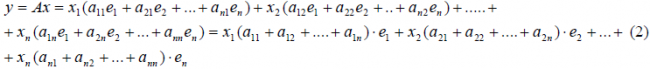
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

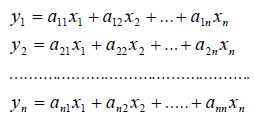
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

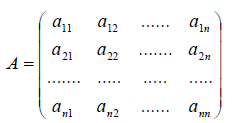
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

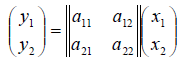
связывающее вектор-прообраз 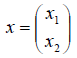с вектором-образом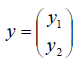

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

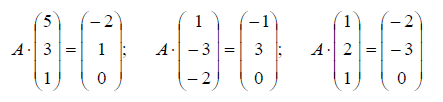
Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

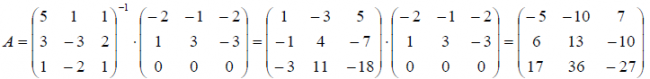
Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .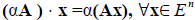

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

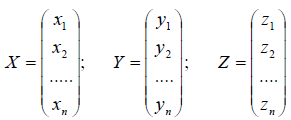
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 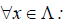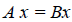. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 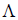он ставит в соответствие тот же самый элемент, то есть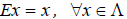

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

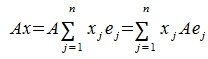
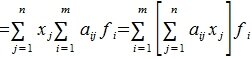
Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

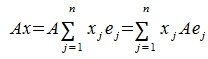
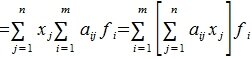
Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya

http://matworld.ru/linear-algebra/linear-operator.php

[/spoiler]

Решение:

Линейность оператора следует из линейности матричных операций умножения на скаляр, транспонирования и умножения на матрицу.

Если в каноническом базисе пространства М₂₂

то

т.е. матрица данного оператора в каноническом базисе имеет вид:

Находим ядро данного оператора:

Для получения базиса образа данного линейного оператора находим:

Полученные векторы линейно независимы:

и могут быть выбраны в качестве базиса образа данного оператора, т.е.

Данный оператор имеет ненулевое ядро, следовательно, он необратим.

3.17. Оператор А действует на матрицы второго порядка по правилу , где . Показать, что А – линейный оператор. Составить его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?

Решение:

Линейность оператора следует из линейности матричных операций умножения на скаляр, транспонирования и умножения на матрицу.

Если в каноническом базисе пространства М₂₂

то

т.е. матрица данного оператора в каноническом базисе имеет вид:

Поскольку detA=-34≠0, то KerA=0, ImA=M₂₂.

Данный оператор имеет нулевое ядро, следовательно, он обратим.

3.18. В пространстве Р₂ многочленов степени не выше 2 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе. Найти образ многочлена . Найти ядро и образ оператора. Существует ли обратный оператор?

Решение:

Проверяем линейность оператора:

Свойства линейности выполнены – оператор линеен.

Если в базисе пространства P₂

то

т.е. матрица данного оператора в базисе имеет вид:

Для данного многочлена получаем:

Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (1;0;0): .

Данный оператор имеет ненулевое ядро, следовательно, он необратим.

3.19. В пространстве Р₃ многочленов степени не выше 3 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе. Найти ядро и образ оператора. Существует ли обратный оператор?

Решение:

Проверяем линейность оператора:

Свойства линейности выполнены – оператор линеен.

Если в базисе пространства P₃

то

т.е. матрица данного оператора в базисе имеет вид:

Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (0;0;0;1): .

Данный оператор имеет ненулевое ядро, следовательно, он необратим.

3.20. В пространстве Р₂ многочленов степени не выше 2 оператор А действует по правилу . Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе .

Решение:

Проверяем линейность оператора:

Свойства линейности выполнены – оператор линеен.

Если в базисе пространства P₂

то

т.е. матрица данного оператора в каноническом базисе имеет вид:

Матрица перехода от базиса к базису имеет вид:

следовательно, матрица данного оператора в базисе S имеет вид:

3.21. Показать, что оператор А, действующий на функции f(t) по правилу , является линейным оператором в пространстве функций . Найти матрицу оператора в каком-нибудь базисе пространства. Обратим ли оператор? Найти ядро и образ оператора.

Решение:

Проверяем линейность оператора:

Свойства линейности выполнены – оператор линеен.

Если в базисе пространства L

то

т.е. матрица данного оператора в базисе имеет вид:

При этом detA=0, следовательно, данный оператор необратим.

Находим ядро оператора:

Образ оператора находим как дополнение ядра до всего пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (-1;1;0):

3.22. Показать, что оператор дифференцирования является линейным оператором в пространстве функций . Найти матрицу оператора в каком-нибудь базисе пространства. Существует ли обратный оператор? Найти ядро и образ оператора.

Решение:

Если то

т.е. и матрица оператора в базисе имеет вид:

Поскольку detA=0, то данный оператор не имеет обратного.

Находим ядро данного оператора:

т.е. KerA = L{(0;0;1)} =

Отсюда получаем образ данного оператора как дополнения ядра до полного пространства L, для этого выбираем базисные векторы с нулями в тех координатах, которые отличны от нуля в уже выбранном векторе (0;0;1):

ImA = L{(1;0;0).(0;1;0)} =

3.23. Показать, что оператор сдвига является линейным оператором в пространстве функций . Найти матрицу оператора в каком-нибудь базисе пространства. Существует ли обратный оператор? Найти ядро и образ оператора.

Решение:

Данный оператор линеен, поскольку выполнены свойства

Если , то

т.е. и матрица оператора в базисе имеет вид:

Поскольку detA≠0, то данный оператор имеет обратный.

Находим ядро данного оператора:

т.е. KerA = 0 и поэтому ImA = L.

3.24. Линейный оператор А в пространстве V₃ имеет в базисе матрицу . Найти собственные значения и собственные векторы оператора А, показать, что это оператор простого типа.

Решение:

Матрица линейного оператора из задачи 3.24 в базисе имеет вид:

Находим собственные значения и собственные векторы матрицы:

Для

Для

Т.е. собственному значению соответствуют два собственных вектора собственному значению – один собственный вектор .

По определению, линейный оператор называется оператором простого типа (или простым оператором), если из собственных векторов этого оператора можно составить базис линейного пространства. Собственные векторы данного оператора образуют базис пространства V₃, следовательно, это оператор простого типа.

3.25. В пространстве V₃ оператор линейный оператор А – зеркальное отражение относительно плоскости YOZ. Найти собственные значения и собственные векторы оператора А.

Решение:

Зеркальное отражение относительно плоскости YOZ в пространстве V₃ переводит точку с координатами (a;b;c) в точку с координатами (-a;b;c), т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Для

Получаем два собственных значения , первому соответствует один собственный вектор , второму – два собственных вектора: .

3.26. В пространстве V₃ оператор линейный оператор А – проекция на ось OY. Найти собственные значения и собственные векторы оператора А.

Решение:

Проекция на ось OY в пространстве V₃ переводит точку с координатами (a;b;c) в точку с координатами (0;b;0), т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Для

Получаем два собственных значения , первому соответствуют два собственных вектора: , второму – один собственный вектор .

3.27. Линейный оператор А – проекция на ось . Найти собственные значения и собственные векторы оператора А.

Решение:

Проекция на ось переводит точку с координатами (a;b) в точку с координатами (a–b;b–a):

т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Получаем единственное собственное значение , которому соответствует один собственный вектор: .

3.28. В пространстве V₃ оператор действует по правилу , где . Найти собственные значения и собственные векторы оператора А.

Решение:

Если , то

т.е. матрица данного оператора имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Для

Получаем два собственных значения , первому соответствуют два собственных вектора: , второму – один собственный вектор .

3.29. В каноническом базисе пространства R³ оператор А действует по правилу . Найти собственные значения и собственные векторы оператора А.

Решение:

Матрица данного оператора в каноническом базисе имеет вид:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Для

Получаем два собственных значения , которым соответствуют собственные вектора: .

3.30. Найти

Решение:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Для

Отсюда получаем представление данной матрицы в виде

Тогда

=

3.31. Линейный оператор А в каноническом базисе пространства Р₂ многочленов степени не выше 2 имеет матрицу . Найти собственные значения и собственные векторы оператора А. Является ли оператор оператором простого типа?

Решение:

Находим собственные значения и собственные векторы матрицы оператора:

Для

Получаем единственное собственное значение , которому соответствуют два собственных вектора: .

По определению, линейный оператор называется оператором простого типа (или простым оператором), если из собственных векторов этого оператора можно составить базис линейного пространства. Данный оператор имеет всего два собственных вектора, размерность пространства Р₂ равна 3, следовательно, данный оператор не является оператором простого типа.