Онлайн-сервисы
Алгоритмы JavaScript
Введение в анализ
Теория множеств
Математическая логика
Алгебра высказываний
Булевы функции
Теория формального
Логика предикатов
Неформальные и формаль-
ные аксиоматические теории
Теория алгоритмов
Математическая логика и компьютеры
Дискретная математика
Множества и отношения
Группы и кольца
Полукольца и булевы алгебры
Алгебраические системы
Теория графов
Булева алгебра и функции
Конечные автоматы и регулярные языки
Контекстно-свободные языки
Интегральное исчисление
Неопределённый и определённый
Приложения интегралов
Интегралы в физике
Основные интегралы
Вариационное исчисление
Финансовый анализ
Анализ эффективности
Анализ устойчивости
Рыночная активность
Инвестиционная деятельность
Анализ инвестиций
Стоимость компании
Форвардные контракты
Теория вероятностей
Математическая статистика
Теория очередей (СМО)
Аналитическая геометрия
Векторная алгебра
Системы координат
Геометрия на плоскости
Линии 2-го порядка
Инварианты линий
Геометрия в пространстве
Поверхности 2-го порядка
Инварианты поверхностей
Линейная алгебра
Матрицы и операции
Определители
Ранг матрицы
Обратная матрица
Системы уравнений
Функциональные матрицы
Многочленные матрицы
Функции от матриц
Линейные пространства
Подпространства
Линейные отображения
Линейные операторы
Евклидовы пространства
Комплексный анализ
Комплексные числа
Комплексные функции
Функциональные ряды в комплексной области
Особые точки, Вычеты
Операционное исчисление
Дифференциальные уравнения
ДУ первого порядка
ДУ высших порядков
Системы ДУ
Теория устойчивости
Численные методы
Методы алгебры
Методы теории приближений
Методы решения обыкновенных ДУ
Методы решения ДУ в частных производных
Конформные отображения и их свойства
Геометрические свойства конформных отображений
Рассмотрим подробнее геометрические свойства конформных отображений с помощью аналитических функций.
Исследование геометрического смысла модуля и аргумента производной аналитической функции показало, что отображение с помощью аналитической функции является конформным в любой точке аналитичности функции, где выполняется условие
. По определению конформного отображения оно обладает в такой точке свойствами сохранения углов и постоянства растяжения.
Взаимно однозначное в конечной области отображение, т.е. отображение, осуществляемое однолистной функцией, конформное в каждой точке области, называется конформным в области
.
Можно показать, что условие является следствием (необходимым условием) однолистности функции
в
. Действительно, отображение
можно записать в виде, где
(2.32)
Из свойств отображения (2.32), изучаемого в действительном анализе, известно, что условием его взаимной однозначности в является условие
, где
— якобиан отображения, определяемый равенством
Отображение (2.32), удовлетворяющее условию , обладает в
следующими свойствами: переводит внутреннюю точку во внутреннюю, граничную — в граничную.
Для функции , аналитической в
, условие
в силу условий Коши-Римана принимает вид
или, раскрывая определитель, . Это последнее условие означает, что
, так как производная аналитической функции
может быть записана в виде
.
Утверждение 2.15. Отображение с помощью аналитической, однолистной в конечной области функции является конформным в
.
Если функция , аналитическая в
, осуществляет взаимно однозначное отображение, то точки
называются образами точек
, а точки
— прообразами. В силу свойств взаимно однозначного отображения образом области
как открытого множества, состоящего из внутренних точек, является область
, а образом кривой
— границы области
— является кривая
— граница области
.
В теории и практике конформных отображений ставятся и решаются две задачи. Первая задача заключается в нахождении образа данной линии или области при заданном отображении — прямая задача. Вторая — заключается в нахождении функции, осуществляющей отображение данной линии или области на другую заданную линию или область — обратная задача.
При решении прямой задачи учитывается, что образом точки при отображении
является точка
, такая, что
, т.е. результат подстановки значения
в
. Поэтому для нахождения образа множества нужно решить систему, состоящую из двух соотношений. Одно из них задает отображающую функцию
, другое — уравнение линии, если решается задача нахождения образа линии, или неравенство, определяющее множество точек прообраза, если решается задача отображения областей. В обоих случаях процедура решения сводится к исключению переменной
из двух заданных соотношений.
Рассмотрим подробнее задачу отображения линии. Чтобы исключить из заданных соотношений, следует выразить
из первого уравнения и подставить во второе, либо наоборот.
Если уравнение линии задано в параметрической форме: , то, записав уравнение
и подставив его в отображающую функцию
, получим соотношение, содержащее параметр
и связывающее координаты точек, принадлежащих соответствующему образу, т.е. уравнение образа данной линии.
Если линия задана уравнением , что в комплексной форме соответствует равенству
, то в последнее соотношение подставляются
и
, полученные из
, то есть
и
. В результате получаем соотношение
, или после подстановки
. Это соотношение будет искомым уравнением образа.
Таким же методом можно решить задачу отображения области. Для этого в неравенство, определяющее заданную область, следует подставить , полученное из отображающей функции
.
Можно решать эту задачу иначе. Известно, что любая замкнутая кривая разбивает плоскость на две области. По свойству конформного отображения граница области переходит в границу, а любая внутренняя точка во внутреннюю. Поэтому для нахождения образа области достаточно найти образ ее границы, а затем по соответствию пары внутренних точек определить, какая из двух областей, имеющих полученную линию своей границей, является искомой.
Результаты приведенных рассуждений сформулируем в виде правил решения прямой задачи для линии и области соответственно.
Правило 2.4. Для нахождения образа данной линии при отображении необходимо:
1. Записать уравнение линии в параметрической форме или в комплексной форме
.
2. В зависимости от вида уравнения линии, заданного или выбранного в п.1, рассмотреть соответствующий случай:
– если линия задана в параметрической форме, подставить выражение в
. Полученное соотношение
— уравнение образа линии
при отображении
;
– если линия задана в комплексной форме, то выразить из
, то есть
, и найти
. Затем следует подставить
и
в уравнение линии. Полученное соотношение — уравнение образа данной линии.
Правило 2.5. Для нахождения образа данной области следует воспользоваться одним из двух способов.
Первый способ.
1. Записать уравнение границы заданной области.
2. Найти образ границы заданной области по правилу 2.4.
3. Выбрать произвольную внутреннюю точку заданной области и найти ее образ при заданном отображении. Область, которой принадлежит полученная точка, является искомым образом заданной области.
Второй способ.
1. Выразить z из соотношения .
2. Подставить полученное в п.1 выражение в неравенство, определяющее заданную область. Полученное соотношение — искомый образ.
Замечания 2.9
1. На практике при нахождении образов с помощью отображений
и других используются свойства этих отображений, например круговое свойство дробно-линейного отображения или свойство функции
увеличивать углы в
раз.
2. При решении обратной задачи используются свойства простейших отображений и некоторый набор известных отображений — “таблица” отображений.
Далее в лекции рассмотрим отображения с помощью простейших функций.
Линейное отображение на комплексной плоскости
Линейная функция , где
и
— любые комплексные числа,
, определена в
, а если положить
, то в
. Отображение является однолистным в
, что вытекает из равенства
, так как при
из условия
следует
(см. также пример 2.4).
Функция является аналитической в . Исходя из сказанного заключаем, что линейное отображение является конформным всюду в
.
Выясним геометрический смысл линейного отображения на комплексной плоскости. Для этого запишем параметр в показательной форме:
и рассмотрим следующие частные случаи отображения как составляющие:
Первому из этих отображений соответствует изменение длины радиуса-вектора любой точки в раз, а именно растяжение, если
, и сжатие при
. Это следует из соотношений
.
Для второго отображения из соотношений получаем, что оно определяет преобразование поворота — радиус-вектор любой точки
поворачивается относительно начала координат на угол а по часовой стрелке, если
, и против — если
.
Геометрический смысл отображения получается из геометрического смысла сложения комплексных чисел, как векторов, или, что то же, из соотношений
. Отображение
есть параллельный перенос радиуса-вектора любой точки
в направлении вектора
на его величину.
На рис. 2.18 проиллюстрированы операции, соответствующие всем рассмотренным отображениям; для наглядности все плоскости совмещены (совмещены их действительные и мнимые оси).
Представляя линейное отображение как суперпозицию рассмотренных отображений, можно сформулировать утверждение.
Утверждение 2.16
1. Отображение геометрически сводится к последовательному выполнению над радиусом-вектором любой точки плоскости z следующих операций: растяжению (сжатию) в
раз, повороту на угол
и смещению (параллельному переносу) в направлении вектора
на величину
.
2. Отображение изменяет линейные размеры любой фигуры плоскости в
раз (гомотетия — подобие с центром в начале координат и коэффициентом подобия
), поворачивает эту фигуру на угол
вокруг начала координат и смещает ее в направлении вектора
на его величину (рис. 2.19).
3. Линейное отображение обладает круговым свойством, т.е. переводит окружности плоскости в окружности плоскости
(и обратно); прямые переводит в прямые.
Справедливость последнего утверждения следует из геометрических свойств составляющих, так как они, очевидно, обладают круговым свойством. Оно также может быть доказано аналитически.
А именно запишем в комплексной форме уравнение прообраза — окружности в плоскости (см. пример 1.27):
и подставим в него выражение для , полученное из
, то есть
. Будем иметь
или после преобразований: , где
. А это и есть уравнение окружности в плоскости
.
При и прообраз, и образ определяют прямые.
Заметим, что доказательство можно рассматривать как пример решения прямой задачи — найти образ окружности (прямой) при линейном отображении и убедиться, что это — окружность (прямая) (см. правило 2.4).
Если использовать уравнение прообраза в виде (см. правило 2.4), после подстановки
получим
, т.е. образом центра данной окружности при линейном отображении является центр
её образа — центр отображается в центр.
▼ Примеры 2.54-2.62 задач на линейные отображения
Пример 2.54. Найти образ отрезка , где
, при отображении
(рис. 2.20).
Решение
Пример 2.55. Найти образ окружности при отображении
.
Решение
Пример 2.56. Найти образ окружности: a) ; б)
при отображении
.
Решение
Пример 2.57. Найти образ оси при отображении
.
Решение
Первый способ. Решаем по правилу 2.4. Уравнение оси выберем в параметрической форме.
1. Так как в действительной форме уравнение имеет вид , то в комплексной форме запишется как
. Это — параметрическое уравнение, в качестве параметра выбран
.
2. Выражаем из
и подставляем в уравнение оси
или, что о же, подставляем
в выражение
. Получаем уравнение образа в параметрической форме:
; параметром является
. Отделив действительную и мнимую части, получим уравнение в действительной норме:
или
. Это есть уравнение прямой в плоскости
, параллельной действительной оси.
Второй способ. Решаем по правилу 2.4, но уравнение оси выберем в комплексной форме.
1. Записываем комплексное уравнение оси .
2. Выражаем из
и подставляем
и
в уравнение
. Получаем в комплексной форме уравнение образа оси
, или
. В действительной форме результат записывается в виде
или
.
Третий способ. Используем для решения круговое свойство линейного отображения — образом прямой является прямая. Так как прямая определяется двумя точками, то достаточно на оси выбрать любые две точки и найти их образы. Прямая, проходящая через найденные точки, и будет искомой. Выберем точки
, их образы
при отображении лежат на прямой
. Следовательно, образом прямой
является прямая
.
Четвертый способ. Можно привести геометрическое решение, как и в примере 2.54. Так как из условия следует, что
, то нужно заданную линию (ось
) повернуть на
(относительно начала координат), а затем сместить вниз на 3 единицы. Растяжение в 2 раза не меняет геометрического вида исходной линии (оси
), так как она проходит через начало координат.
Пример 2.58. Найти какую-либо линейную функцию, отображающую линию на линию
.
Решение
Поставленная задача есть обратная задача теории отображений — по заданным образу и прообразу найти соответствующее отображение. Без дополнительных условий задача не имеет единственного решения. Действительно, существует множество функций, осуществляющих искомое отображение. Для нахождения любой из них достаточно выбрать две точки и
в плоскости
, принадлежащие прообразу (т.е. линии
), и две любые точки
и
в плоскости
, принадлежащие линии
(т.е. два действительных числа), и из двух соотношений
и
определить величины
и
.
Одно из отображений можно просто получить из рассмотрения рис. 2.22.
Для геометрического решения достаточно повернуть луч , принадлежащий прообразу, на угол
против часовой стрелки, т.е. выбрать отображение
. При этом образом точки
будет точка
, а образом точки
— точка
. Можно выбрать отображение
— поворот на угол
по часовой стрелке. Тогда точке
будет соответствовать точка
, а точка
будет образом точки
.
Заметим, что ответом может быть также , где
— любое положительное число, и
, где
и
— любые действительные числа.
Пример 2.59. Найти какую-либо линейную функцию, отображающую окружность на окружность
.
Решение
Как и предыдущая, это — обратная задача отображений. Решать её будем, используя свойства линейного отображения — геометрический смысл его составляющих. В связи с этим при решении удобно выделить следующие этапы (см. рис. 2.23).
Первый этап. Переместим центр окружности в начало координат. Для .того применим отображение .
Второй этап. В плоскости применим отображение, дающее растяжение в 2 раза,
. Окружность изображена в плоскости
(считаем плоскости
и
совмещенными) пунктиром.
Третий этап. Окончательный результат получаем, применяя преобразование смещения, , то есть
или
.
Здесь, как и в примере 2.58, ответ не единственный и можно рассмотреть другой порядок выполнения операций. Из геометрических соображений ясно, что можно сначала применить не смещение, а поворот или растяжение и получить в результате соответствующее отображение.
Можно получить общий вид линейной функции, осуществляющей заданное отображение, используя тот факт, что окружность определяется положением центра и величиной радиуса, и свойство линейного отображения, переводящего центр окружности в центр.
Поэтому, подбирая искомое отображение в виде , из соотношения
, то есть
, получаем
или
. Далее из
, учитывая условие задачи, находим
и
, где
— любое действительное число.
Окончательный результат , что также объяснимо из рис. 2.23, так как геометрический вид окружности с центром в начале координат (см.
или пунктир в плоскости
) не изменяется в результате поворота (умножения на
).
Пример 2.60. Найти образ полосы при отображена
.
Решение
Заданная область — неограниченная односвязная область, границей её на является линия, состоящая из двух параллельных прямых (образами эти: прямых на сфере Римана являются две окружности, пересекающиеся в точке
. Эта линия делит
на две области — внутреннюю (полоса) и внешнюю (внешность полосы).
Образом полосы является полоса, так как при линейном отображение прямые переходят в прямые, а в силу конформности отображения параллельность прямых сохраняется.
Решаем по правилу 2.5 первым способом.
1. Границу области образуют две прямые с уравнениями и
.
2. Находим образы прямых и
. Образ прямой
получен в примере 2.57. Его уравнение
. Образ прямой
можно получить так же или, учитывая параллельность линий, достаточно найти образ одной точки. Например, точке
соответствует
. Поэтому o6pазом прямой
будет прямая
, проходяшая через точку
.
3. Выбираем внутреннюю точку полосы , например
, её oбраз
. Эта точка должна принадлежать искомому образу. Ответом является множество
— полоса, границами которой являются
и
(рис. 2.24).
Очень простое решение задачи — геометрическое, которое сводится к повороту на против часовой стрелки, растяжению в два раза и смешению вниз мнимой оси на 3 единицы (рис. 2.24).
Пример 2.61. Найти линейную функцию, отображающую область на область
.
Решение
По свойствам искомого отображения как взаимно однозначного отображения граница области , прямая
, переходит в границу области
. Функция, устанавливающая соответствие границ, получена в примере 2.58. Это — либо
, либо
,
. Одна из них отображает область
на
(а
соответственно на
), другая — область
на
. Чтобы выбрать необходимую функцию, достаточно установить соответствие двух пар граничных точек или пары внутренних.
Выберем две граничные точки области — точки
и
(см. рис. 2.22, решение примера 2.58). Направление обхода границы области
от точки
к точке
(область при обходе расположена слева), области
— от точки
к точке
. Поэтому искомая функция — та, которая переводит точку
в точку
, то есть
,
или, в частности,
(см. пример 2.58). Можно выбрать внутреннюю точку, .например
. Ее образом при отображении
,
является
, то есть
.
При отображении же ,
образом точки
является
,
.
Пример 2.62. Найти какую-либо линейную функцию, отображающую область на область
.
Решение
Как и в предыдущем примере, нужно найти функцию, устанавливающую соответствие границ: прямой в плоскости
и прямой
в плоскости
(рис. 2.25,а и г).
Применим геометрический способ решения (см. пример 2.59), используя геометрические свойства составляющих.
Первый этап. Сдвинем границу области на единицу влево, т.е. рассмотрим отображение
. Образом области
будет область
(рис. 2.25,б).
Второй этап. Повернем границу области на угол
по часовой стрелке, т.е. рассмотрим отображение
. Образом области
будет область
(рис. 2.25,в).
Третий этап. Сдвинем границу области на единицу вниз, т.е. рассмотрим отображение
. Образом области
будет область
. Искомое отображение получим как суперпозицию составляющих, т.е.
Напомним, что задачи такого типа без дополнительных условий имеют неединственное решение, что в данном случае очевидно из рассмотрения рис. 2.25.
Например, решением будет также функция и др.
Дробно-линейное отображение на комплексной плоскости
Дробно-линейным называется отображение с помощью функции , где
— произвольные комплексные числа (параметры).
Полагаем , так как при
получается рассмотренная выше линейная функция, и
, иначе, в силу пропорциональности числителя и знаменателя,
.
Функция определена в . Если положить
и
, то получаем функцию, которая определена на всей расширенной комплексной плоскости
.
Функция является однолистной в и аналитической в
за исключением точки
. Аналитичность
следует из определения, так как аналитической в
является функция
.
Так как однолистное отображение с помощью аналитической функции является конформным, то заключаем, что дробно-линейное отображение конформно в , конформно в любой области
. Заметим, что
для любой точки
.
Геометрические свойства дробно-линейного отображения
Исследуем геометрические свойства дробно-линейного отображения. Как и в случае линейной функции, выделим составляющие. Выделяя целую часть дроби, получаем или, вводя обозначения
, имеем
, из чего следует, что дробно-линейное отображение есть суперпозиция линейного отображения и отображения
. Действительно, можно записать цепочку составляющих
Рассмотрим отдельно отображение как частный случай дробно-линейного отображения
. Его также можно записать в виде более простых для исследования составляющих
. Особенность первого отображения заключается в соотношениях
, которые, учитывая, что
и
, можно переписать в виде
(2.33)
Геометрически эти соотношения означают, что точки и
расположены на одном луче, а произведение длин их радиусов-векторов равно единице. Точки, обладающие таким свойством, называются точками, симметричными (или сопряженными) относительно окружности единичного радиуса с центром в начале координат.
Функция отображает любую точку, лежащую внутри единичного круга, в точку, лежащую вне единичного круга, так как из
следует
и обратно.
Следовательно, функция переводит внутренность единичного круга во внешность и наоборот. Преобразование такого вида называется инверсией относительно единичной окружности.
Заметим, что для построения точки по заданной точке
нужно сначала провести луч из центра окружности
, а затем к этому лучу в точке
восставить перпендикуляр и провести касательную к окружности в точке её пересечения с перпендикуляром. Точкой пересечения касательной и луча будет
. Обоснование построения следует из рассмотрения подобных треугольников (рис. 2.26). Очевидно, проводя построение в обратном порядке, можно построить по точке, лежащей вне круга (на рис. 2.26 точка
), симметричную относительно окружности точку
, которая будет расположена внутри круга.
Вторая составляющая отображения функция
геометрически есть симметрия относительно действительной оси (рис. 2.26).
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 2.17
1. Отображение геометрически сводится к построению инверсии относительно окружности
и симметрии относительно действительной оси.
2. Дробно-линейное отображение геометрически сводится к преобразованиям растяжения, поворота, сдвига (см. линейное отображение), симметрии относительно окружности и симметрии относительно действительной оси.
Круговое свойство дробно-линейного отображения
Дробно-линейное отображение на комплексной плоскости обладает круговым свойством. Достаточно доказать это свойство для функции , так как для линейных составляющих дробно-линейного отображения оно установлено.
Доказательство проведем в соответствии с правилом 2.4 решения прямой задачи.
1. Записываем уравнение произвольной окружности в комплексной форме: . Заметим, что при
уравнение определяет прямую. При
линия не проходит через начало координат (точку
), при
— проходит.
2. Выражая из
, получаем
и подставляем в уравнение прообраза. Преобразуем полученное равенство:
, или
.
Полученное уравнение есть уравнение окружности, в частности, при — прямая.
Для отображения роль точки
, очевидно, играет
.
Утверждение 2.18 (круговое свойство дробно-линейного отображения).
1. Окружности и прямые, не проходящие через особую точку , отображаются в окружности, а окружности и прямые, проходящие через эту точку, — в прямые.
2. Дробно-линейное отображение переводит окружности расширенной комплексной плоскости в окружности , так как прямые на расширенной комплексной плоскости рассматриваются как окружности.
▼ Примеры 2.63-2.68 задач на дробно-линейные отображения
Пример 2.63. При отображении найти образы:
а) окружностей и
;
б) прямых и
.
Решение
а) Первая окружность проходит через точку — особую точку функции, поэтому её образом будет прямая. Образом второй окружности, уравнение которой можно переписать как
, является окружность. Решаем согласно правилу 2.4.
1. Записываем уравнения окружностей в комплексной форме: и
.
2. Подставляем в эти уравнения выражения и
Для первой окружности получаем
, или
, что можно записать
, или
. Это — уравнение прямой, параллельной мнимой оси (рис. 2.21,а). Для второй окружности имеем
. Наличие слагаемого
говорит о том, что образом является окружность. Чтобы определить её центр и радиус, перейдем к действительной форме уравнения, используя равенства
. Получим уравнение
, или, выделив полный квадрат переменной
. Это — уравнение окружности радиуса
с центром в точке
(рис. 2.21,а).
б) Образом первой прямой является окружность, второй — прямая. Чтобы получить уравнения соответствующих образов, подставим и
в уравнения данных линий, записанных в комплексной форме:
и
. Получим
— образ первой прямой и
— второй. Первая линия — окружность
или
; её радиус
, центр в точке
(рис. 2.27,6). Уравнение
или
определяет мнимую ось (рис. 2.21,б).
Пример 2.64. Найти образ полосы при отображении
.
Решение
Пример 2.65. Найти образ области при отображении
.
Решение
Область есть пересечение полуплоскости и внешности круга — полуплоскость
с выброшенным кругом (рис. 2.28).
В соответствии с правилом 2.5 решения задач для областей, как и в предыдущем примере, найдем прежде образ границы области , которая состоит из двух линий, описываемых уравнениями
и
. Так как обе линии проходят через особую точку
, то их образами будут прямые. Для каждой линии решаем задачу по правилу 2.4.
Найдем образ прямой .
1. Запишем уравнение в комплексной форме:
.
2. Выражаем из
, то есть
. Подставляем эти значения в уравнение
. Получаем
, или
. Это уравнение определяет прямую
, параллельную действительной оси (рис. 2.28).
Найдем образ окружности .
1. Запишем уравнение окружности в виде .
2. Выразим из
и подставим
в уравнение
. Получаем
. Это равенство определяет уравнение прямой, проходящей перпендикулярно отрезку, соединяющему точки
и
, через его середину. Этой прямой является действительная ось
(рис. 2.28). В результате получили, что образ границы области
состоит из двух параллельных прямых:
и
.
Далее в соответствии с п.3 правила 2.5 выберем произвольную точку, например . Так как ее образом при заданном отображении является
, то образом области
будет полоса
.
Пример 2.66. Найти какую-либо дробно-линейную функцию, отображающую круг единичного радиуса с центром в начале координат:
а) на левую полуплоскость;
б) на нижнюю полуплоскость.
Решение
Решается обратная задача отображения областей. Требуется найти отображение области на область
a)
; б)
. Границей области
является окружность
. Так как в обоих случаях ее образ — прямая, то, согласно утверждению 2.18, искомая функция должна иметь особой точкой одну из точек окружности — окружность проходит через особую точку.
Используя это свойство, “распрямим” окружность, т.е. на первом этапе решения подберем функцию, переводящую одну из точек окружности в бесконечно удаленную точку.
Первый этап. Рассмотрим , где
при
.
Найдем уравнение прямой, в которую переходит при отображении
, т.е. решим прямую задачу:
. Получено уравнение прямой, проходящей перпендикулярно отрезку, соединяющему точки
и
, через его середину, т.е.
. Образом области
будет
, так как, например, точка
переходит в точку
.
Второй этап. Сравнивая полученный результат и вид области , заключаем, что нужно применить преобразование смещения (сдвиг) влево на
, т.е. линейное отображение
. Образом
будет
. Соответствие границ установлено функцией
или
. Но при этом отображении образом области
является правая полуплоскость
, так как точка
, принадлежащая
, переходит в точку
.
Третий этап. Чтобы получить искомое отображение и для случая “а” , и для случая “б”, достаточно сделать поворот.
Решим задачу для случая “а”. Применим преобразование поворота на угол против часовой стрелки, т.е. линейное отображение
(2.34)
Таким образом, найдено отображение, переводящее круг на полуплоскость
(рис. 2.29).
Заметим, что в силу взаимной однозначности обратная функция отображает левую полуплоскость
на крут
. Отсюда следует вид отображения, переводящего левую полуплоскость
на круг
(рис. 2.30):
(2.35)
Решим задачу для случая “б”. Чтобы получить отображение круга на нижнюю полуплоскость
(рис. 2.31), достаточно в плоскости
рассмотреть поворот на
, по часовой стрелке, т.е.
(2.36)
Пример 2.67. Отобразить область на область
.
Решение
Так как образами окружностей — границы области являются прямые, то нужно применить отображение, “распрямляющее” прямые. Для этого следует использовать отображение, переводящее общую точку окружностей
в
.
Первый этап. Применяем преобразование .
Найдем образ области при этом отображении. Для этого, как и при решении предыдущих примеров, в уравнения границы — окружностей
и
подставляем
, то есть
или
.
Эти уравнения определяют прямые, уравнения которых в действительной форме имеют вид и
, или
. Эти прямые, параллельные мнимой оси, определяют границу области
; область
— внутренность полосы, так как, например, образом точки
является точка
, принадлежащая полосе (рис. 2.32).
Второй этап. Сравнивая вид областей и
, убеждаемся, что следует увеличить ширину области
в 4 раза и повернуть ее на угол
против часовой стрелки, т.е. применить преобразование
. Образом
будет полоса
.
Третий этап. Окончательный результат получаем смещением на единиц влево, , то есть
.
Пример 2.68. При отображении, полученном в примере 2.67, найти образы прямых .
Решение
Примеры 2.67 и 2.68 иллюстрируют круговое свойство отображения у свойство конформности. Так, прямая касается окружностей в плоскости
и параллельна прямой
, т.е. образует с каждой из них угол
. Её образ в плоскости
с соответствующими линиями также образует угол
.
Прямая перпендикулярна любой из рассматриваемых здесь линий — и прямым
, и окружностям, так как проходит через их центры. Образ этой прямой (действительная ось
) также перпендикулярен соответствующим линиям — трем прямым и окружности.
Прямая образует угол
с окружностью
1 и прямой
, а с другой окружностью
и прямой
— угол
. Такие же углы образует окружность — образ этой прямой в плоскости
с соответствующими линиями.
Условия, определяющие дробно-линейное отображение
Дробно-линейное отображение рассматривается, как отмечено выше, при , поэтому можно записать
или
,
т.е. оно определяется тремя параметрами. Следовательно, для задания дробно-линейного отображения достаточно задать три условия, например соответствие трех пар точек. При этом, так как отображение рассматривается на , одна из точек может быть бесконечно удаленной. Имеет место утверждение.
Утверждение 2.19 (условия, определяющие дробно-линейное отображение). Каковы бы ни были три различные точки , плоскости
и три различные точки
плоскости
, существует единственное дробно-линейное отображение
такое, что
. При этом справедливо соотношение
(2.37)
Равенство (2.37) называется ангармоническим отношением. Если его переписать в виде произведения:
(2.38)
то, рассматривая предельный переход в (2.38) при или
, замечаем, что предел частного, содержащего соответствующие величины, равен единице. Например,
. Можно сделать заключение.
Если одна из точек или
есть бесконечно удаленная точка, то в (2.37) (или (2.38)) соответствующая разность заменяется единицей.
Справедливость утверждения о единственности отображения, определяемого указанными условиями, и справедливость отношения (2.37) могут быть установлены из рассмотрения линейной системы или
.
Отметим некоторые особенности отображения (2.37), запишем их в виде утверждения.
Утверждение 2.20
1. Дробно — линейное отображение переводит круг, граница которого проходит через три данные точки , в круг (или во внешность круга), граница которого проходит через три точки
. Это следует из того, что положение любой окружности (на плоскости) однозначно определяется тремя точками.
2. Любое дробно-линейное отображение, переводящее точку в ноль и
в бесконечно удаленную точку, имеет вид (что следует из формулы (2.38))
(2.39)
С учетом этого утверждения можно сократить процедуру решения примера 2.66. А именно, так как граница области — прямая
проходит через
, то, полагая
, отображение ищем в виде
(на первом этапе). Можно взять
, так как наличие множителя
в таких случаях будет определять только поворот на
, a растяжение в
для геометрического положения прямых, проходящих через начало координат, не имеет значения. Далее, для решения задачи в случае “а” убеждаемся, что искомое отображение уже получено:
, а для решения в случае “б” нужно ещё сделать поворот.
Пример 2.69. Найти дробно-линейную функцию , такую, что
.
Решение
В утверждении 2.20 сказано, что дробно-линейное отображение переводит любой круг (внутренность, внешность) на любой круг (внутренность, внешность) заданием соответствия трех пар граничных точек. Так как прямые на рассматриваются как окружности
, то речь здесь идет и о прямых, т.е. любой круг (внутренность, внешность) переводится на любую полуплоскость и обратно заданием соответствия трех граничных пар (для прямой одна из точек
).
По формуле (2.38) при условии будет получено определенное отображение области
(ее граница — окружность, прямая) на область
(граница — окружность, прямая). При этом любой внутренней точке
будет соответствовать определенная
.
Сохранение симметричных точек дробно-линейным отображением
Представляют практический интерес задачи, где образом данной точки должна быть заранее заданная
.
Задание соответствия внутренних точек накладывает ограничение на выбор других соответствующих пар. Это связано со следующим свойством дробно-линейного отображения.
Утверждение 2.21
1. Дробно-линейное отображение переводит любые две точки, симметричные относительно окружности расширенной комплексной плоскости, в точки, симметричные относительно образа этой окружности при данном отображении. Свойство называется свойством сохранения симметричных точек.
2. Точки, симметричные границе области (окружности или прямой) при дробно-линейном отображении, переходят в точки, симметричные относительно ее образа при этом отображении.
Свойство означает, что если точки и
симметричны относительно линии у (окружности или прямой) в плоскости
, а точки
и
и линия
— их образы при дробно-линейном отображении, то точки
и
симметричны относительно
. Линия
, согласно круговому свойству отображения, также является окружностью или прямой. Симметрия точек относительно прямой понимается в обычном смысле. Симметрия относительно окружности единичного радиуса с центром в начале координат рассматривалась при исследовании отображения
(формула (2.33)). В общем случае имеет место следующее определение.
Точки и
называются симметричными (или сопряженными) относительно окружности
, если они лежат на одном луче, выходящем из центра окружности, и произведение их расстояний от центра окружности равно квадрату ее радиуса, т.е. справедливо равенство
(2.40)
Точкой, симметричной точке — центру окружности, очевидно, является бесконечно удаленная точка.
Полученные при решении примера 2.71 (см. ниже в спойлере) результаты запишем в виде утверждения.
Утверждение 2.22
1. Любое дробно-линейное отображение полуплоскости на круг
имеет вид
(2.41)
2. Любое дробно-линейное отображение круга на круг
имеет вид
(2.42)
3. Значение а определяется из дополнительного условия. Это, как правило, задание аргумента производной искомой функции в некоторой точке, например .
Формулы (2.41) и (2.42) дают решение двух канонических задач. Для удобства использования изобразим их на рис. 2.34 и рис. 2.35 соответственно.
▼ Примеры 2.70-2.73 решения задач с отображениями
Пример 2.70. Отобразить область на область
так, чтобы точки 0 и 2i остались неподвижными.
Решение
Задание неподвижной точки для отображения
означает условие
, то есть
В данном случае имеет место соответствие двух пар точек:
, причем первая пара — пара граничных точек, вторая -внутренних. Третью пару, необходимую для применения формулы (2.37), находим, используя свойство сохранения симметричных точек.
Найдем точки, симметричные точкам и
относительно соответствующих окружностей.
Для точки точкой, симметричной относительно окружности
, будет
, так как
— центр круга. Для точки
точку, симметричную относительно окружности
, находим, используя формулу (2.40),
, или
. Из полученного равенства следует, что
расположена на расстоянии
от центра круга
и, по определению симметричных точек , на одном луче с центром и точкой
. Из этих рассуждений очевидно, что
. Таким образом, имеем соответствие трех пар точек:
.
Применяя формулу (2.37), получаем , или после преобразований
.
Пример 2.71. Отобразить область на круг
так, чтобы
, если: a)
; б)
.
Решение
Так как точка отображается в
, т.е. в центр круга
, то точка
, сопряженная точке
относительно границы области
, отображается в
. Имеем соответствие двух пар точек, причем
и
. Можем искать отображение в виде
(см. (2.39)). Нужно найти величины
и
.
1. Найдем — точку, симметричную точке го относительно границы области
в каждом случае:
а) так как граница области — действительная ось, то
;
б) здесь симметрична точке
относительно окружности
, поэтому
(см. (2.33)).
2. Значение определяем из соответствия граничных точек:
, где
. Так как
, то получаем условие для нахождения
.
Получим решение для каждого из рассматриваемых случаев.
а) Имеем . Так как
, то
— действительное число и поэтому
. Получаем
и
. Искомое отображение
, где
— любое число.
Заметим, что неоднозначность ответа, вызванная произволом выбора а, связана с неопределенностью соответствия . Указана принадлежность этих точек границам соответствующих областей, но не заданы определенные значения. Каждому фиксированному значению
можно поставить в соответствие произвольное значение
, удовлетворяющее условию
. Отображение найдено с точностью до поворота окружности
, что геометрически очевидно. При задании дополнительного условия для нахождения
решение поставленной задачи единственное.
б) Отображение ищем в виде , то есть
, или, если обозначить
, то
.
Из условия для
получаем
.
Так как для
, то, подставляя
, перепишем равенство
, или
.
В последнем равенстве как модули комплексных сопряженных чисел и
. Поэтому
и
.
Искомое отображение . Как и в предыдущем случае, оно не является единственным.
Пример 2.72. Отобразить область на
так, чтобы выполнялись условия
.
Решение
По условию точка отображается в
, следовательно, точка
, симметричная точке
относительно прямой
, отображается в центр окружности
, т.е. в точку
(рис. 2.36,а).
Задача, очевидно, эквивалентна задаче нахождения отображения полуплоскости на круг
, при условии, что данная точка
полуплоскости переходит в центр круга (незаштрихованная область на рис. 2.36,а).
Эта задача отображения полуплоскости на круг может быть приведена к канонической. Но чтобы воспользоваться формулой (2.41), нужно применить предварительно два линейных отображения, переводящих область в верхнюю полуплоскость, а круг
в единичный круг с центром в начале координат (рис. 2.36,б).
Первый этап. Первое из этих преобразований — поворот на угол по часовой стрелке осуществляется функцией
при этом точка
переходит в
.
Для второго преобразования используем функцию — смещение и сжатие; при этом центр круга перейдет в
.
Второй этап. Для переменных и
используем формулу (2.41), т.е. запишем
, или после сокращения на
.
Полученная функция при любом осуществляет отображение
на
, при этом
.
Третий этап. Для определения параметра используем условие
. Находим производную
и ее значение в точке
, то есть
.
По правилу нахождения аргумента произведения комплексных чисел из последнего равенства получаем , то есть
. Из этого равенства и условия
находим
. Подставляя
в полученное выше выражение, находим окончательный результат:
, или
. Искомое отображение
.
Пример 2.73. Найти образ прямой при отображении, полученном в примере 2.72.
Решение
Заметим, что данная прямая перпендикулярна границе области из примера 2.72, поэтому, по свойству отображения ее образ — линия, перпендикулярная окружности
. Кроме того, так как данная прямая не проходит через особую точку функции, то, по круговому свойству, ее образом будет окружность. Эта окружность ортогональна окружности
в точке их пересечения. Найдем ее уравнение. Решается прямая задача по правилу 2.4.
1. Запишем уравнение линии в форме
, или после преобразований:
.
2. Из выражаем
, получаем
. Подставляем
и
в уравнение и преобразуем равенство
Полученное уравнение — уравнение окружности, так как в нем присутствует слагаемое . Запишем это уравнение в действительной форме:
, или
, где
.
Центр окружности в точке (2,1), радиус равен 2 (рис. 2.37).
Заметим, что эта окружность пересекает окружность из примера 2.72 под прямым углом, так как касательная к одной совпадает с радиусом другой и наоборот. Под прямым углом пересекаются и их прообразы (рис. 2.37), что иллюстрирует конформность отображения в точке .
Отображение степенной функции на комплексной плоскости
Рассмотрим пример не всюду конформного отображения с помощью функции, которая не является однолистной в . Ранее исследовалась такая функция :
(степенная функция), в частности
. Напомним полученные результаты.
Утверждение 2.23
1. Отображение неоднолистно в
; областью однолистности является любая область, принадлежащая углу раствора
(сектору), т.е.
, где
— любое.
2. Функция , аналитическая в
и
, то есть
для любого
. Отображение является конформным в
, за исключением, быть может, точки
.
3. Функция конформно и взаимно однозначно отображает любой сектор
на плоскость с разрезом по лучу
, а плоскость
с выброшенной точкой
— на риманову поверхность этой функции.
4. Функция — обратная к неоднолистной (n-листной) функции
является неоднозначной (n-значной). В областях, не содержащих точек
и
(точек ветвления функции), возможно выделение однозначных ветвей. Каждая ветвь отображает плоскость с разрезом
на один из секторов
. Риманову поверхность функции
функция
отображает на
с выброшенной точкой.
Выясним геометрические свойства отображения в точке . Запишем переменные в показательной форме:
и из равенства
получим:
, или
и
. При отображении
увеличивается в
раз аргумент — угол наклона радиуса-вектора точки к действительной оси, а при отображении
— уменьшается в
раз. Можно сделать заключение.
Утверждение 2.24
1. При отображении увеличиваются в
раз углы между любыми прямыми, проходящими через начало координат. Поэтому отображением
пользуются, если нужно увеличить углы при переходе от прообраза к образу.
2. При отображении уменьшаются в
раз углы между любыми прямыми, проходящими через начало координат. Поэтому отображением
пользуются, если нужно уменьшить углы при переходе от прообраза к образу.
3. Используя комбинацию дробно-линейного отображения и отображений и
, можно конформно отобразить любую “луночку” — область, ограниченную двумя дугами пересекающихся окружностей, на верхнюю полуплоскость.
▼ Примеры 2.74-2.78 задач со степенными отображениями
Пример 2.74. При отображении найти образ области, ограниченной двумя лучами, выходящими из начала координат и образующими угол
.
Решение
Область есть угол раствора
, и при отображении
переходит в угол раствора
. Границами области
являются лучи
и
, их параметрические уравнения имеют вид
и
, где
— любое,
— параметр.
Образами этих прямых будут прямые-лучи и
или
и
, где
. Геометрически линии совпадают. Для однозначности отображения на границе проводим разрез по лучу
(рис. 2.38). Образом области
является плоскость с разрезом получу
; угол
отображается в угол
.
Заметим, что этот же результат получается и для каждого из трех других углов, образованных продолжением выбранных лучей за начало координат (рис. 2.38). Так, для области , имеем
и поэтому
или
, где
совпадает геометрически с
.
Для области из
получаем
, или
и
совпадает геометрически с
.
Наконец, для из
получаем
и
и
совпадает геометрически с
.
В частности, при область
определяется условием
— первый квадрант;
— другие квадранты. Все эти области функцией
отображаются на плоскость с разрезом по лучу
(рис. 2.39).
При соответствующие области отображаются на плоскость с разрезом по лучу
(рис. 2.40).
Пример 2.75. Отобразить “луночку” на верхнюю полуплоскости.
Решение
Границу “луночки” образуют дуги двух окружностей, пересекающихся t точках и
под углом
, а границу ее образа — два луча, образующие действительную ось, угол между ними равен
(рис. 2.41).
Так как нужно увеличить угол вдвое, применим отображение . Но прежде надо “распрямить” дугу, т.е. применить преобразование, переводящее все окружности в прямые. Для этого достаточно, чтобы одна из их общих точек отображалась в бесконечно удаленную точку (см. пример 2.67).
Первый этап. Применяем дробно-линейное преобразование , где, например,
, то есть переводим 0 в 0
в
.
Образами дуг при отображении будут два луча, пересекающиеся в начале координат под прямым углом. Положение лучей (наклон) определяется параметром
.
Для определенности отображения на этом этапе зададим значение или найдем его, задав третью пару — соответствие внутренних точек. Из соображений симметрии удобно взять, например,
. Образом точки
, принадлежащей луночке , будет точка
, принадлежащая первая квадранту.
Из равенства находим
и получаем отображение
.
Образом “луночки” будет первый квадрант, а образами дуг — действительная и мнимая полуоси, так как из соответствия и
следует, что образом прямой, соединяющей точки
и
, будет биссектриса первого координатного угла в плоскости
.
Второй этап. Применяем преобразование , удваивающее углы, и получаем окончательный ответ:
или
.
Пример 2.76. Отобразить полукруг на верхнюю полуплоскость.
Решение
Рассуждая, как и в предыдущем примере, замечаем, что нужно прежде “распрямить” окружность; при этом образом прямой должна быть также прямая. Поэтому нужно взять преобразование, переводящее одну из точек пересечения дуги и прямой в бесконечность.
Первый этап. Пусть (на рис. 2.42,а точки
и
) , т.е. выбираем отображение
. При
это
и
при
.
Второй этап. Определим образ полукруга при выбранном отображении. Для этого достаточно взять еще по одной точке на каждой из частей границы полукруга, например, (точка
на рис. 2.42,а) и
(точка
на рис. 2.42,а), найти их образы и по направлению обхода границы определить вид области.
Так, в случае точке
соответствует
, точке
соответствует
. Образом полукруга будет третий квадрант (рис. 2.42,б).
Если взять , т.е. отображение
, то из соответствия
находим, что образом полукруга будет первый квадрант (рис. 2.42,в)
Третий этап. В случае выбранного выше отображения при
ответом, очевидно, будет
, то есть
. В случае
отображение
приводит к тому же результату. Можно предварительно применить преобразование поворота
, в результате чего получим первый квадрант и окончательный ответ:
, то есть
.
Пример 2.77. Найти образ плоскости с разрезом по лучу при отображении
с условием
.
Решение
Пример 2.78. Отобразить плоскость с разрезом на верхнюю полуплоскость.
Решение
Из свойств отображения и анализа решений примеров 2.74 и 2.77 замечаем, что для отображения плоскости с разрезом по лучу
на верхнюю полуплоскость нужно применить функцию
. В данном случае границa области состоит из двух лучей, пробегаемых дважды и соединяющихся в бесконечности (рис. 2.43). Чтобы получить плоскость с одним разрезом, можно сначала применить преобразование, соединяющее разрезы — сдвиг. При этом одна из точек границы должна отображаться в бесконечно удаленную точку. Следовательно, требуется применить дробно-линейное отображение.
Первый этап. Применим преобразование , где, например,
, то есть
.
Запишем отображение . При этом получим
и
, так как
. Образом данной области будет плоскость c разрезом
(рис. 2.43).
Второй этап. Применяем при условии
. Получим отображение, переводящее заданную область в верхнюю полуплоскость.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Рассмотрим основные свойства данной
функции.
1. Однолистность.
Найдем условие, которому должна
удовлетворять область
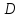 ,
,
чтобы отображение
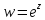 (3.1.1)
(3.1.1)
было однолистным в этой области.
Если
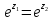 ,
,
т.е.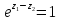 ,
,
то
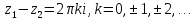 (3.1.2)
(3.1.2)
Следовательно, для однолистности
отображения (3.1.1) необходимо и достаточно,
чтобы область
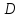 не содержала никакой пары различных
не содержала никакой пары различных
точек, удовлетворяющих условию (3.1.2).
2. Периодичность.
По формуле Эйлера
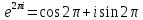 =1,
=1,
то для любого имеем
имеем .
.
С другой стороны, пусть
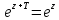 .
.
Умножая обе части на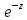 получаем
получаем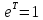 откуда, полагая
откуда, полагая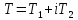 ,
,
имеем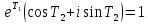 .
.
Но тогда ,
,
то есть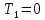 и
и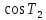 =1
=1
и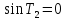 ,
,
то есть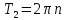 ,
,
где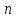 – целое число. Таким образом,
– целое число. Таким образом,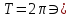 и
и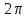 являются основными периодами.
являются основными периодами.
3. Конформность.
Так как производная функции (3.1.1) во всех
точках отлична от нуля, то отображение
конформно во всех точках конечной
плоскости
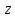 .
.
4. Образы точек конечной плоскости.
Рассмотрим отображения, осуществляемые
посредством этой функции. Заметим, что
функция никогда не принимает значение
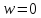 .
.
Это значит, что начало координат плоскости не принадлежит к образу конечной
не принадлежит к образу конечной
плоскости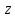 при отображении (3.1.1). Покажем, что всякая
при отображении (3.1.1). Покажем, что всякая
другая конечная точка плоскости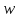 принадлежит к этому образу. В самом
принадлежит к этому образу. В самом
деле, из уравнения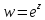 ,
,
где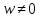 задано, а
задано, а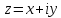 – неизвестное, получаем:
– неизвестное, получаем:
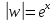 ,
,
откуда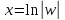 и
и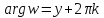 ,
,
то есть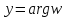 .
.
Итак, прообразами точек
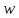 могут быть только точки вида
могут быть только точки вида
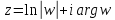 .
.
Очевидно, их бесконечно много, так как
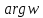 имеет бесконечное множество значений,
имеет бесконечное множество значений,
различающиеся попарно на целые кратные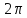 .
.
Кроме того, каждая из найденных точек
действительно есть прообраз точки ,
,
так как
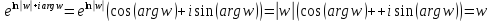 . (3.1.3)
. (3.1.3)
Итак, множество всех корней уравнения
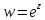 ,
,
где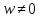 представляются формулой
представляются формулой
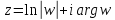 =
=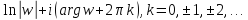
Все эти точки расположены на одной
прямой, параллельной мнимой оси на
расстоянии
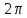 друг от друга.
друг от друга.
То есть функция (3.1.1) отображает конечную
плоскость
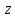 на область, получающуюся из конечной
на область, получающуюся из конечной
плоскости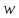 путем исключения одной точки
путем исключения одной точки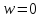 ,
,
при чем отображение не взаимно однозначно,
так как каждая точка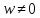 имеет бесконечное множество прообразов
имеет бесконечное множество прообразов
(3.1.3).
5. Образы прямых, параллельных осям
координат.
Заставим
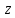 описывать какую-нибудь прямую, параллельную
описывать какую-нибудь прямую, параллельную
одной из координатных осей (Рис. 3.1.1).
Рисунок 3.1.1.
Если это будет прямая
 ,
,
параллельная мнимой оси, то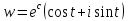 ,
,
то есть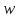 будет находиться на окружности с центром
будет находиться на окружности с центром
в начале координат и радиусом, равным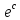 .
.
При этом, когда точка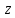 описывает прямую однократно так, что
описывает прямую однократно так, что
ордината этой точки, равная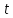 ,
,
непрерывно растет от -∞ до +∞, то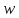 описывает соответствующую окружность
описывает соответствующую окружность
бесконечное множество раз в одном и том
же положительном направлении.
Если же точка
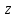 описывает прямую
описывает прямую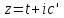 ,
,
параллельную действительной оси, то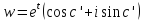 ,
,
очевидно, пробегает прямолинейный луч,
выходящий из начала координат и образующий
с положительной частью действительной
оси угол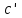 .
.
При этом, когда точка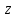 описывает однократно так, что абсцисса
описывает однократно так, что абсцисса
этой точки, равная ,
,
непрерывно растет от -∞ до +∞, то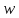 описывает соответствующий луч однократно
описывает соответствующий луч однократно
так, что расстояние этой точки от начала
координат непрерывно растет от 0до ∞
(и тот и другой пределы исключаются, так
как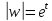 ).
).
Итак, при отображении плоскости
 посредством функции
посредством функции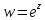 семейство прямых, параллельных мнимой
семейство прямых, параллельных мнимой
оси преобразуется в семейство окружностей
с центром в начале координат, а семейство
прямых, параллельных действительной
оси, – в семейство прямолинейных лучей,
выходящих из начала координат.
6. Образы полос, параллельных
действительной оси.
Рассмотрим область
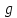 ,
,
представляющую внутренность прямоугольной
полосы шириной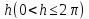 ,
,
параллельной действительной оси. Пусть
эта полоса ограничена линиями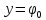 и
и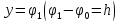 .
.
Из установленного выше следует, что
образ области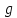 в плоскости
в плоскости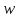 будет область
будет область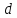 ,
,
представляющая угол раствора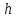 с вершиной в начале координат, ограниченный
с вершиной в начале координат, ограниченный
прямолинейными лучами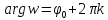 и
и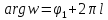 (Рис. 3.1.2).
(Рис. 3.1.2).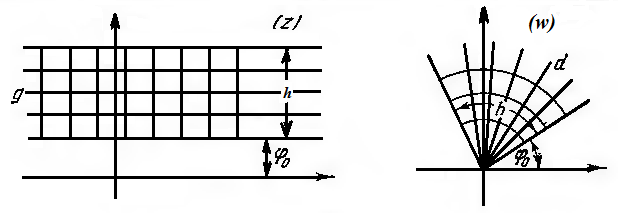
Рисунок 3.1.2.
При этом соответствие между точками
областей
 и
и ,
,
устанавливаемое посредством функции
(3.4.1.), будет взаимно однозначным, поскольку
прообразами некоторой точки из области
из области могут быть только точки
могут быть только точки ,
,
различающиеся друг от друга значениями
мнимой части. Две такие точки лежат на
одной прямой, параллельной мнимой оси,
на расстоянии, кратном .
.
Но полоса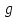 имеет ширину не более
имеет ширину не более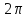 ,
,
поэтому она может содержать внутри лишь
один прообраз точки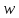 .
.
Итак, каждая точка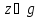 имеет лишь один образ и каждая точка
имеет лишь один образ и каждая точка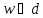 лишь один прообраз внутри
лишь один прообраз внутри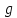 ,
,
что выражает взаимную однозначность
отображения.
При этом показательная функция взаимно
однозначно и конформно отображает
полосу ширины
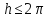 ,
,
параллельную действительной оси, на
угол раствора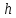 с вершиной в начале координат. Поэтому
с вершиной в начале координат. Поэтому
к показательной функции прибегают
каждый раз, когда надо отобразить
некоторую прямолинейную полосу на
внутренность угла.
7. Образ прямой, не параллельной ни
одной из оси координат.
Если прямая плоскости
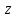 не является параллельной какой-либо
не является параллельной какой-либо
оси координат, то образ её в плоскости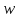 будет уже не прямой и не окружностью, а
будет уже не прямой и не окружностью, а
логарифмической спиралью. В самом деле,
если эта прямая есть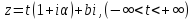
(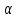 – угловой коэффициент прямой, а
– угловой коэффициент прямой, а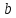 – ордината в начале), то образом будет
– ордината в начале), то образом будет
кривая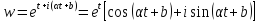 .
.
Здесь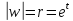 ,
,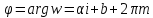 ,
,
или, исключая параметр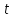 :
: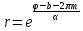 .
.
Но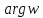 или полярный угол
или полярный угол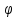 определен только с точностью до целого
определен только с точностью до целого
кратного от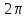 .
.
Поэтому, обозначая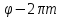 снова через
снова через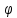 получаем:
получаем: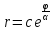 ,
,
где .
.
Это и есть уравнение логарифмической
спирали (Рис. 3.1.3). Из того, что она является
образом прямой есть
 пересекающей прямые, параллельные
пересекающей прямые, параллельные
действительной оси под постоянным углом ,
,
следует в силу конформности отображения,
что и логарифмическая спираль пересекается
под тем же углом образы указанных прямых,
то есть все лучи, выходящие из начала
координат. Мы получили характеристическое
свойство логарифмической спирали.
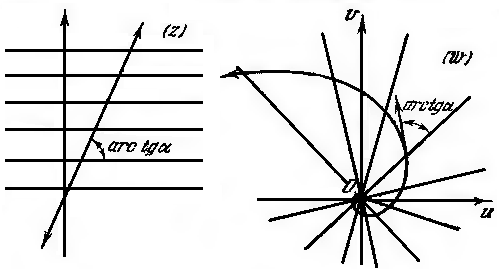
Рисунок 3.1.3.
Пример 3.1.1. Из приведенных свойств
(1) и (2) вытекает, что функция конформно
конформно
отображает прямоугольник ,
, ,
,
где ,
, на кольцевой сектор
на кольцевой сектор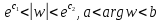 .
.
Частные случаи таких отображений
показаны на рис. 3.1.4.
Рисунок 3.1.4.
Пример 3.1.2. Найдем образ отрезка при отображении
при отображении .
.
Рисунок 3.1.5.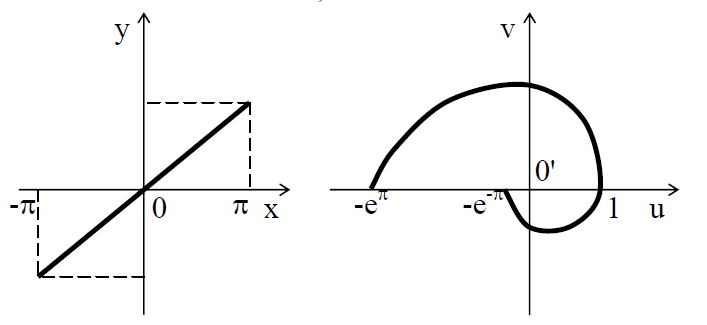
Любая точка отрезка имеет комплексную
координату
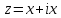 ,
,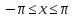 .
.
Поэтому её образом служит линия,
параметрически заданная уравнениями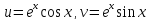 .
.
Это дуга логарифмической спирали
(рис. 3.4.5).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найдите правильный ответ на вопрос ✅ «Найдите образ отрезка [-1; 3] при отображении f (x) = 3x-5. В ответ запишите длину образа отрезка. …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Новые вопросы по математике
Главная » Математика » Найдите образ отрезка [-1; 3] при отображении f (x) = 3x-5. В ответ запишите длину образа отрезка.
ДРОБНО-ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ
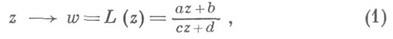
где ad—bс неравно 0;часто применяется унимодулярная нормировка ad—bс=1. Всякое Д.-л. о. доопределяется соответствиями 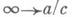 и
и 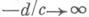 до взаимно однозначного отображения расширенной плоскости С на себя. Простейшими среди Д.-л. о. являются линейные:
до взаимно однозначного отображения расширенной плоскости С на себя. Простейшими среди Д.-л. о. являются линейные: 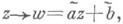 получающиеся при с=0. Всякое нелинейное Д.-л. о. представимо в виде суперпозиции двух линейных отображений и отображения L0:
получающиеся при с=0. Всякое нелинейное Д.-л. о. представимо в виде суперпозиции двух линейных отображений и отображения L0: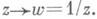 Свойства Д.-л. о. L0 становятся наглядными на Римана сфере, так как при стереографич. проекции ему соответствует поворот сферы на 180° вокруг диаметра, проходящего через образы точек
Свойства Д.-л. о. L0 становятся наглядными на Римана сфере, так как при стереографич. проекции ему соответствует поворот сферы на 180° вокруг диаметра, проходящего через образы точек 
Основные свойства. Д.-л. о. отображает взаимно однозначно и конформно С на себя. Круговое свойство: при Д.-л. о. любая окружность на С (т. е. окружность на С или прямая, пополненная точкой бесконечности) переходит в окружность на С. Инвариантность отношения симметрии двух точек: пара точек z, z*, симметричных относительно какой-либо окружности на 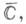 при Д.-л. о. переходит в пару точек w, w*, симметричных относительно образа этой окружности. Двойное отношение четырех точек на С инвариантно относительно Д.-л. о., т. е. если точки x1, x2, x3,x4 при Д.-л. о. переходят соответственно в z1,z2, z3, z4, то
при Д.-л. о. переходит в пару точек w, w*, симметричных относительно образа этой окружности. Двойное отношение четырех точек на С инвариантно относительно Д.-л. о., т. е. если точки x1, x2, x3,x4 при Д.-л. о. переходят соответственно в z1,z2, z3, z4, то
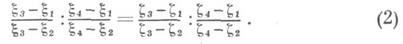
Для любых заданных троек x1, x2,x3 и z1, z2, z3, попарно различных точек на С, существует и притом только одно Д.-л. о., переводящее соответственно  k=1, 2, 3.
k=1, 2, 3.
Это Д.-л. о. можно найти из уравнения (2), подставляя в него zи wсоответственно вместо x4 и z4. Групповое свойство: совокупность всех Д.-л. о. образует некоммутативную группу относительно суперпозиции (L1L2)(z) = L1(L2(z)) с единицей E(z) = z. Свойство универсальности: всякий конформный автоморфизм С есть Д.-л. о., и, таким образом, группа всех Д.-л. о. совпадает с группой Aut С всех конформных автоморфизмов С.
Все конформные автоморфизмы единичного круга 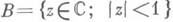 . образуют подгруппу Aut Вгруппы Aut С, состоящую из Д.-л. о. вида:
. образуют подгруппу Aut Вгруппы Aut С, состоящую из Д.-л. о. вида:
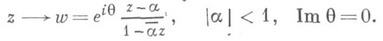
Так же обстоит дело с конформными автоморфизмами верхней полуплоскости , имеющими вид:
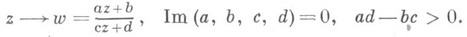
Все конформные гомеоморфизмы верхней полуплоскости на единичный круг имеют, вид:
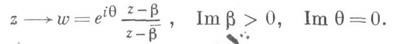
Исключив тождественное Д.-л. о. E(z), можно сказать, что Д.-л. о. имеет не более двух различных неподвижных точек x1, x2 на С. В случае двух различных неподвижных точек 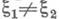 семейство окружностей 2, проходящих через x1 и x2, переводится Д.-л. о. (1) само в себя. При этом семейство е’ всех окружностей, ортогональных к окружностям е, также переходит само в себя. Здесь возможны в свою очередь три случая.
семейство окружностей 2, проходящих через x1 и x2, переводится Д.-л. о. (1) само в себя. При этом семейство е’ всех окружностей, ортогональных к окружностям е, также переходит само в себя. Здесь возможны в свою очередь три случая.
1) Каждая окружность е переходит сама в себя; такое Д.-л. о. наз. гиперболическим, и оно представимо в нормальной форме:

где множитель Д.-л. о. m>0, 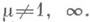 Унимодулярное Д.-л. о. (1) является гиперболическим тогда и только тогда, когда
Унимодулярное Д.-л. о. (1) является гиперболическим тогда и только тогда, когда 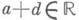 и |a+d|>2.
и |a+d|>2.
2) Каждая окружность 2′ переходит сама в себя; такое Д.-л. о. наз. эллиптическим ив нормальной форме (3) характеризуется множителем m таким, что |m| = 1, 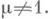 Унимодулярное Д.-л. о. (1) является эллиптическим тогда и только тогда, когда
Унимодулярное Д.-л. о. (1) является эллиптическим тогда и только тогда, когда
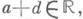 |a+d|<2.
|a+d|<2.
3) Ни одна из окружностей семейств 2 и 2′ не переходит сама в себя; такое Д.-л. о. называется локсодромическим и в нормальной форме (3) характеризуется множителем 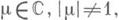 таким, что либо
таким, что либо
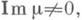 либо m<0. Унимодулярное Д.-л. о. (1) является
либо m<0. Унимодулярное Д.-л. о. (1) является 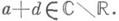 локсодромическим тогда и только тогда, когда
локсодромическим тогда и только тогда, когда
Если же две неподвижные точки сливаются в одну x1, то Д.-л. о. наз. параболическим. Семейство 2 состоит при этом из всех окружностей, имеющих в x1 общую касательную; каждая окружность 2 переходит сама в себя. Нормальная форма параболичД.-л. о. имеет вид либо
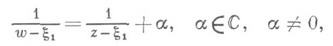
при 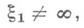 либо
либо
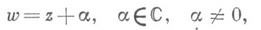
при 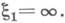 Унимодулярное Д.-л. о. (1) является параболическим тогда и только тогда, когда a+d=
Унимодулярное Д.-л. о. (1) является параболическим тогда и только тогда, когда a+d=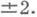
Благодаря перечисленным богатым элементарным свойствам, Д.-л. о. находят самое широкое применение во всех разделах теории функций комплексного переменного и в различных прикладных дисциплинах. В частности, Д.-л. о. позволяют построить модель Лобачевского геометрии.
Среди подгрупп общей группы всех Д.-л. о. наиболее важны, с точки зрения их применений для аналитич. теории дифференциальных уравнений, теории автоморфных функций и других вопросов анализа, дискретные группы Г Д.-л. о. Элементарные дискретные группы Д.-л. о.- это конечные группы; они изоморфны либо циклическим группам вращений сферы Римана, либо группам вращений правильных многогранников. Дискретные группы Д.-л. о. Г, имеющие инвариантную окружность уна С, общую для всех преобразований Г, причем внутренность упри всех преобразованиях Г переходит сама в себя, наз. фуксовими группами. Локсодромич. Д.-л. о. не может быть фуксовым. Исторически первым примером фуксовой группы была модулярная группа, возникшая в теории эллиптич. функций (см. также Модулярная функция). Модулярная группа состоит из всех унимодулярных Д.-л. о. (1), у к-рых коэффициенты а, b, с, d— целые действительные числа; действительная ось инвариантна относительно модулярных Д.-л. о. Более сложны и менее изучены неэлементарные группы Д.-л. о., не являющиеся фуксовыми,- клейновы группы.
Д.-л. о. комплексного пространства С n , n>1, наз. невырожденное отображение

осуществляемое дробно-линейными функциями
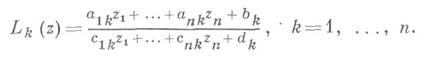
Наиболее важны те Д.-л. о. С n , к-рые продолжаются в какую-либо компактификацию С n . Так, в пространство теории функций 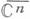 продолжаются все линейные преобразования, переставляющие координаты, а также Д.-л. о. вида
продолжаются все линейные преобразования, переставляющие координаты, а также Д.-л. о. вида
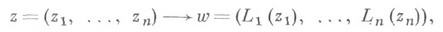
где Lk(zk) — Д.- л. о. вида (1) на плоскости zk. Порождаемая перечисленными отображениями группа Д.-л. о. совпадает с группой Aut 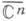 всех биголоморфных автоморфизмов компактификации
всех биголоморфных автоморфизмов компактификации 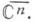 Соответствующая подгруппа Aut U n с
Соответствующая подгруппа Aut U n с
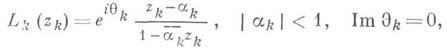
исчерпывает все автоморфизмы единичного поликруга U n =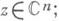 .|zj|<1, j=1, . п). В проективное замыкание СР n пространства С n продолжаются Д.-л. о., у к-рых
.|zj|<1, j=1, . п). В проективное замыкание СР n пространства С n продолжаются Д.-л. о., у к-рых
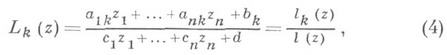
в однородных координатах это продолжение имеет вид
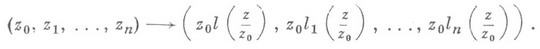
Этими отображениями исчерпывается группа AutCP n всех биголоморфных автоморфизмов СР». Автоморфизмы единичного шара В п = ; |z|<l> образуют подгруппу AutB n группы AutCP n , состоящую из всех Д.-л. о. вида (4), у к-рых коэффициенты подчинены известным дополнительным условиям (см. [2], ч. 2). Лит.:[1] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [3] Стоилов С, Теория функций комплексного переменного, пер. с рум., т. 1, М., 1962; [4] Форд Л. Р., Автоморфные функции, пер. с англ., М.- л., 1936.
Е. П. Долженко, Е. Д. Соломенцев, Е. М. Чирка.
Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Занятия 7, 8. Дробно-линейная функция и отображения, осуществляемые ею
Функция 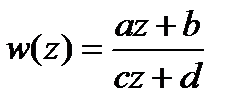 , где
, где  – комплексные числа, удовлетворяющие условию
– комплексные числа, удовлетворяющие условию 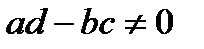 , называется дробно-линейной, а отображение, осуществляемое ею – дробно-линейным отображением. При
, называется дробно-линейной, а отображение, осуществляемое ею – дробно-линейным отображением. При 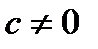 надо считать, что
надо считать, что 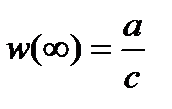 ,
, 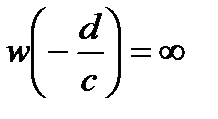 , а при
, а при 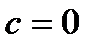 считать
считать 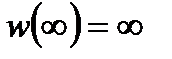 .
.
Существует единственная дробно-линейная функция, отображающая заданные три различные точки 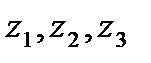 расширенной комплексной плоскости в заданные три различные точки
расширенной комплексной плоскости в заданные три различные точки 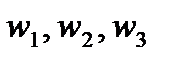 соответственно. Она находится из соотношения
соответственно. Она находится из соотношения
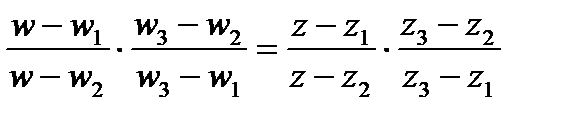 , (1)
, (1)
которое надо рассматривать как уравнение относительно  . При этом, если некоторые из чисел
. При этом, если некоторые из чисел 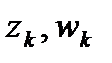 равны
равны  , то дробь, у которой в числителе и знаменателе присутствует
, то дробь, у которой в числителе и знаменателе присутствует  , надо считать равной 1. Например, если w1 =
, надо считать равной 1. Например, если w1 =  , то надо считать
, то надо считать
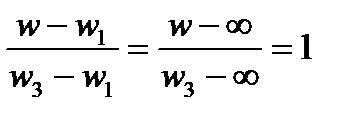 .
.
Точки 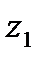 и
и 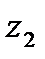 называются симметричными относительно окружности
называются симметричными относительно окружности 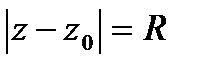 , если они расположены на одном луче, выходящем из центра
, если они расположены на одном луче, выходящем из центра 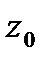 , и
, и
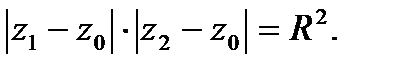
Дробно-линейная функция отображает окружность в окружность (круговое свойство), а точки, симметричные относительно окружности – в точки, симметричные относительно образа этой окружности (свойство симметрии). При этом прямую надо рассматривать как окружность, проходящую через ∞ и замкнутую в бесконечно удаленной точке.
Чтобы найти образ ориентированной окружности (или прямой) при дробно-линейном отображении  , надо взять на данной окружности три различные точки
, надо взять на данной окружности три различные точки 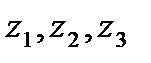 согласно направлению обхода, найти их образы
согласно направлению обхода, найти их образы 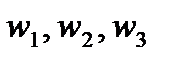 и провести через них окружность, которая и будет образом данной окружности. Направление обхода на ней надо брать от точки
и провести через них окружность, которая и будет образом данной окружности. Направление обхода на ней надо брать от точки 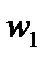 к точке
к точке 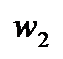 и от
и от 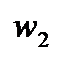 к
к 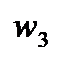 .
.
Чтобы найти образ части окружности или прямой (дуги, отрезка, луча) при дробно-линейном отображении 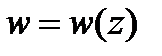 , надо взять на ней три точки: начальную
, надо взять на ней три точки: начальную 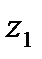 , какую-нибудь «среднюю»
, какую-нибудь «среднюю» 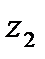 и конечную
и конечную 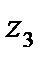 , найти их образы
, найти их образы 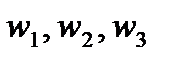 , провести через них окружность и взять ту часть, для которой
, провести через них окружность и взять ту часть, для которой 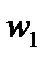 – начальная точка,
– начальная точка, 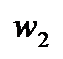 – «средняя точка» и
– «средняя точка» и 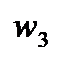 – конечная точка.
– конечная точка.
Чтобы найти образ области, ограниченной дугами окружностей и частями прямых, надо выбрать на границе области направление обхода так, чтобы область оставалась слева, и найти образы всех частей границы с учетом их направлений. Эти образы в совокупности образуют некоторую ориентированную замкнутую линию, может быть, неограниченную, т.е. замкнутую в 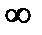 . Тогда область, остающаяся слева от этой линии, будет образом исходной области.
. Тогда область, остающаяся слева от этой линии, будет образом исходной области.
Чтобы найти какое-нибудь одно конформное отображение области 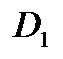 , ограниченной окружностью (или прямой), на подобную же область
, ограниченной окружностью (или прямой), на подобную же область 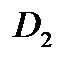 , надо выбрать направления обходов границ
, надо выбрать направления обходов границ 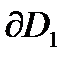 и
и 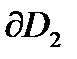 областей
областей 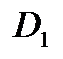 и
и  так, чтобы области оставались слева. Затем на границах
так, чтобы области оставались слева. Затем на границах 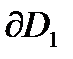 и
и 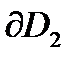 взять согласно направлениям обходов по три различных точки
взять согласно направлениям обходов по три различных точки 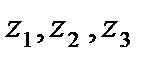 и
и 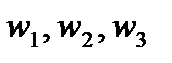 соответственно и из уравнения (1) найти дробно-линейную функцию
соответственно и из уравнения (1) найти дробно-линейную функцию 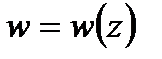 , которая и будет одним из конформных отображений области
, которая и будет одним из конформных отображений области 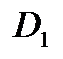 на область
на область 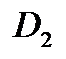 .
.
В общем случае конформное отображение единичного круга 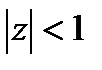 на единичный круг
на единичный круг 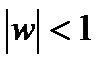 имеет вид:
имеет вид:
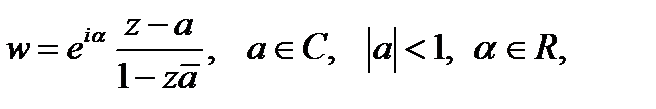
конформное отображение верхней полуплоскости Im z > 0 на единичный круг 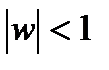 имеет вид:
имеет вид:
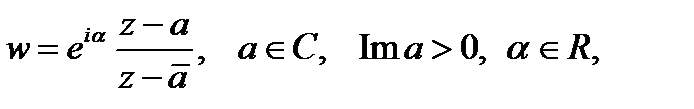
конформное отображение верхней полуплоскости Im z > 0 на верхнюю полуплоскость Im w > 0 имеет вид:
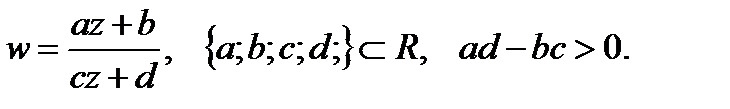
Задачи
1. Найти дробно-линейную функцию, отображающую точки 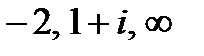 соответственно в точки
соответственно в точки 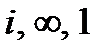 .
.
Решение:Подставив в соотношение (1) заданные значения
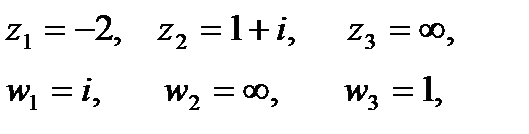
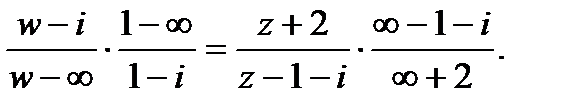
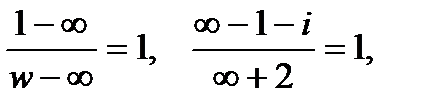
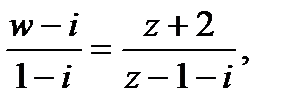
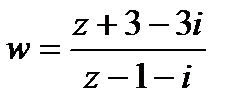 .
.
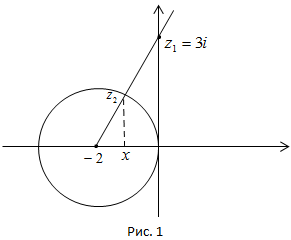
2. Найти точку, симметричную с точкой 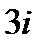 относительно окружности
относительно окружности 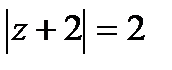 .
.
Решение. Из рис. 1, на котором изображены точка z1 = 3  и окружность
и окружность 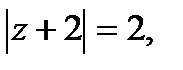 видно, что искомая симметричная точка расположена внутри окружности и имеет вид
видно, что искомая симметричная точка расположена внутри окружности и имеет вид 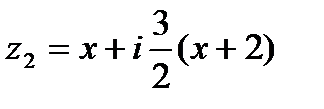 , где x > -2. Это следует из подобия соответствующих треугольников. Подставив z1, z2 в равенство
, где x > -2. Это следует из подобия соответствующих треугольников. Подставив z1, z2 в равенство
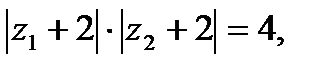
получим: 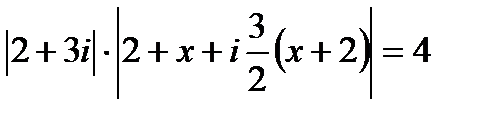 , откуда с учетом неравенства x > -2 находим
, откуда с учетом неравенства x > -2 находим 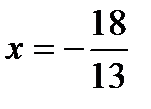 . Тогда
. Тогда 
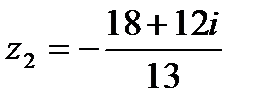 .
.
3. Найти образы окружностей 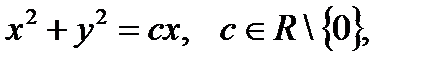 при отображении
при отображении 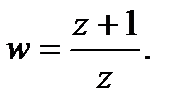
Решение. Так как
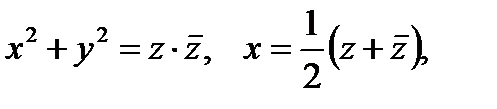
то уравнения окружностей имеют вид:
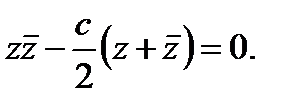
Подставив сюда 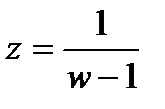 , найденное из уравнения
, найденное из уравнения 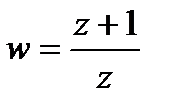 , получим:
, получим:
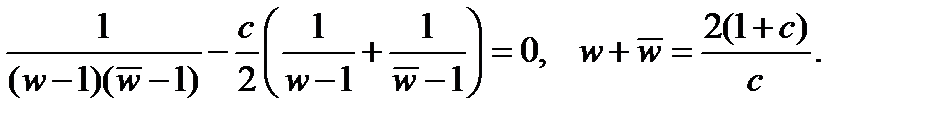
Считая 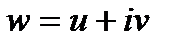 , получим семейство вертикальных прямых
, получим семейство вертикальных прямых
4. Найти образы области D при отображении  , если
, если
а) 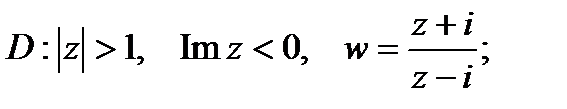
б) 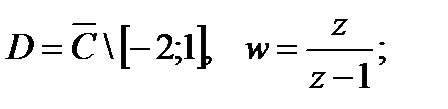
в) 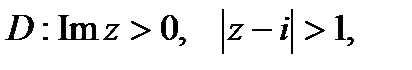
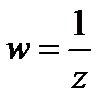 .
.
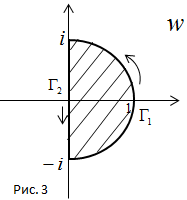
Решение. а) Область D и положительная ориентация ее границы указаны на рис. 2.
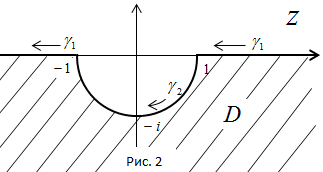
Граница  области в данном случае состоит из двух частей: полуокружности
области в данном случае состоит из двух частей: полуокружности  и двух лучей, которые надо рассматривать как одну непрерывную часть
и двух лучей, которые надо рассматривать как одну непрерывную часть 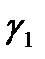 прямой Im z = 0, так как прямая считается окружностью, проходящей через
прямой Im z = 0, так как прямая считается окружностью, проходящей через  , т.е. непрерывной кривой, замкнутой в
, т.е. непрерывной кривой, замкнутой в  . На этих лучах, как на одной части границы
. На этих лучах, как на одной части границы 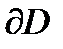 , выберем начальную точку z1 = -1, среднюю точку z2 =
, выберем начальную точку z1 = -1, среднюю точку z2 =  , конечную точку z3 = 1 и найдем их образы
, конечную точку z3 = 1 и найдем их образы
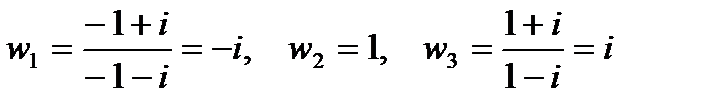 .
.
Проведем через точку –  , 1,
, 1,  окружность и возьмем ту часть, для которой —
окружность и возьмем ту часть, для которой —  – начало, 1 – средняя точка,
– начало, 1 – средняя точка,  – конец. Ею будет дуга Г1 (рис. 3). Направление обхода на дуге Г1 берется от –
– конец. Ею будет дуга Г1 (рис. 3). Направление обхода на дуге Г1 берется от –  к 1 и от 1 к
к 1 и от 1 к  . Эта дуга будет образом совокупности двух лучей
. Эта дуга будет образом совокупности двух лучей  .
.
Найдем образ полуокружности  . Образами начала 1, средней точки –
. Образами начала 1, средней точки –  и конца -1 полуокружности
и конца -1 полуокружности 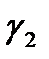 будут точки
будут точки  , 0 и –
, 0 и –  соответственно. Окружность, проходящая через эти точки, есть прямая Re w = 0, поэтому образом полуокружности
соответственно. Окружность, проходящая через эти точки, есть прямая Re w = 0, поэтому образом полуокружности  будет отрезок Г2 с концами
будет отрезок Г2 с концами  и –
и –  , направленный сверху вниз (рис. 3).
, направленный сверху вниз (рис. 3).
Следовательно, образом границы  при отображении
при отображении 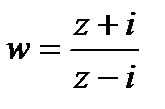 будет замкнутая кривая Г1
будет замкнутая кривая Г1 Г2, направленная против часовой стрелки, а образом области D – полукруг, изображенный на рис. 3.
Г2, направленная против часовой стрелки, а образом области D – полукруг, изображенный на рис. 3.
б) В данном случае область D представляет собой расширенную комплексную плоскость С с разрезом по отрезку [-2; 1] (рис. 4).
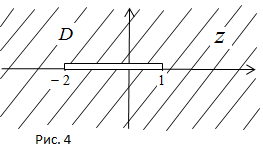
Так как дробно-линейная функция отображает  на
на  , то образом области D будет
, то образом области D будет 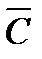 , из которой надо выкинуть образ отрезка [-2;1]. Так как образами начала -2, «средней точки» 0 и конца 1 при отображении
, из которой надо выкинуть образ отрезка [-2;1]. Так как образами начала -2, «средней точки» 0 и конца 1 при отображении 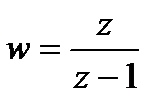 будут соответственно точки
будут соответственно точки  , то образом отрезка [-2;1] будет луч
, то образом отрезка [-2;1] будет луч  . Тогда образом области D будет плоскость с разрезом по лучу
. Тогда образом области D будет плоскость с разрезом по лучу  (рис.5).
(рис.5).
в) Граница области D состоит из прямой 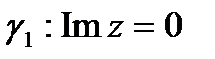 , ориентированной слева направо, и окружности
, ориентированной слева направо, и окружности 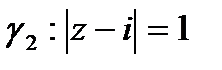 , ориентированной против часовой стрелки (рис. 6). При отображении
, ориентированной против часовой стрелки (рис. 6). При отображении 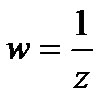 точки
точки  , расположенные на прямой
, расположенные на прямой  согласно направлению обхода, переходят соответственно в точки
согласно направлению обхода, переходят соответственно в точки  Значит, прямая
Значит, прямая 
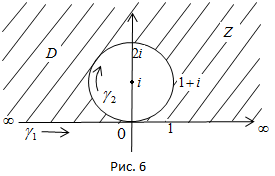
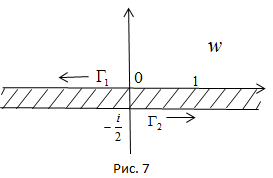
переходит в прямую  , ориентированную справа налево (рис.7). Аналогично, взяв на окружности
, ориентированную справа налево (рис.7). Аналогично, взяв на окружности  точки 2
точки 2  , 1+
, 1+  , 0 и вычислив их образы
, 0 и вычислив их образы  , найдем образ окружности
, найдем образ окружности 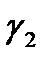 . Им будет прямая
. Им будет прямая  , ориентированная слева направо. Значит, образом границы
, ориентированная слева направо. Значит, образом границы  будет совокупность прямых Г1 и Г2, а образом области D будет полоса
будет совокупность прямых Г1 и Г2, а образом области D будет полоса  , изображенная на рис. 7.
, изображенная на рис. 7.
5. Найти какое-нибудь конформное отображение области 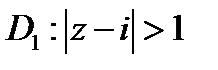 на полуплоскость
на полуплоскость 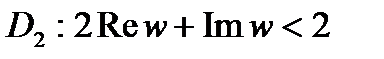 .
.
Решение. Выберем направления обходов границ областей D1 и D2 (рис.8) так, чтобы области оставались слева. Согласно этим направлениям на границах  и
и  возьмем по три точки
возьмем по три точки  и
и  и, подставив их в уравнение (1), найдем дробно-линейное отображение
и, подставив их в уравнение (1), найдем дробно-линейное отображение
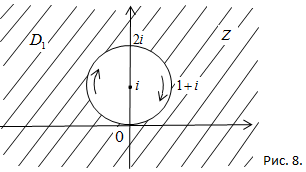
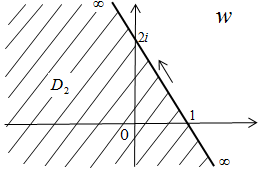

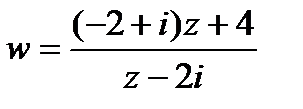 ,
,
которое и будет одним из искомых конформных отображений.
6. Найти конформное отображение  верхней полуплоскости
верхней полуплоскости  на единичный круг
на единичный круг  удовлетворяющее условиям
удовлетворяющее условиям 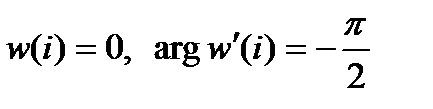 .
.
Решение. Так как общий вид конформного отображения верхней полуплоскости на единичный круг имеет вид
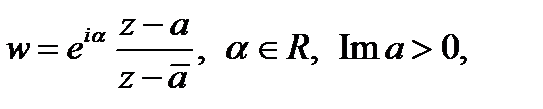
то числа  надо выбрать так, чтобы
надо выбрать так, чтобы
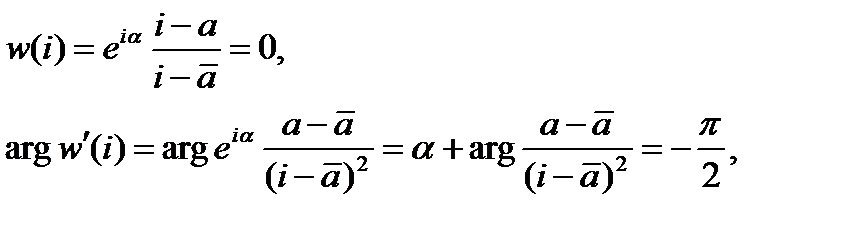
откуда 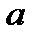 =
= 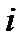 ,
,
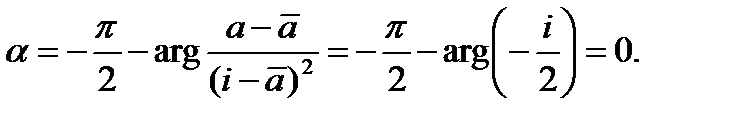
Значит, искомое конформное отображение имеет вид 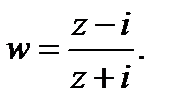
7. Найти конформное отображение 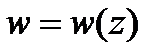 полуплоскости Re z + Im z < 0 на круг
полуплоскости Re z + Im z < 0 на круг 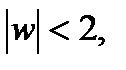 удовлетворяющее условиям
удовлетворяющее условиям 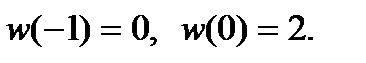
Решение. Так как любое конформное отображение области, ограниченной окружностью (или прямой), на подобную область является дробно-линейным, то согласно свойству симметрии дробно-линейной функции при искомом отображении точка 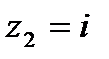 , симметричная точке
, симметричная точке 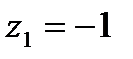 относительно прямой Re z + Im z = 0 (рис. 9), перейдет в точ-
относительно прямой Re z + Im z = 0 (рис. 9), перейдет в точ-

ку 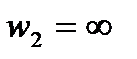 , симметричную точке
, симметричную точке 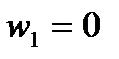 относительно окружности
относительно окружности 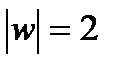 (рис. 10), которая является образом прямой Re z + Im z = 0, при искомом отображении. Следовательно, точки
(рис. 10), которая является образом прямой Re z + Im z = 0, при искомом отображении. Следовательно, точки 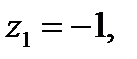
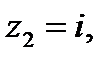
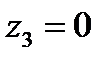 переходят соответственно в точки
переходят соответственно в точки 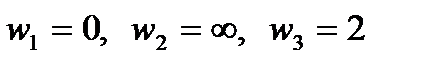 , подставив которые в уравнение (1), найдем искомое отображение:
, подставив которые в уравнение (1), найдем искомое отображение:
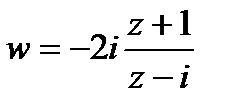 .
.
8. Найти конформное  отображение круга
отображение круга 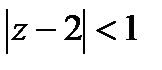 на круг
на круг 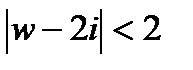 , удовлетворяющее условиям
, удовлетворяющее условиям 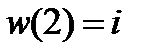 ,
, 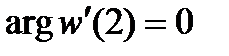 .
.
Решение. Точке 2 симметрична относительно окружности 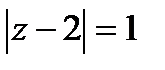 точка
точка  , а точке
, а точке 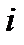 симметрична относительно окружности
симметрична относительно окружности 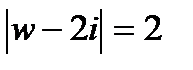 точка -2
точка -2  . Следовательно, при искомом дробно-линейном отображении точки 2 и
. Следовательно, при искомом дробно-линейном отображении точки 2 и 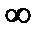 перейдут соответственно в точки
перейдут соответственно в точки 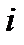 и 2
и 2 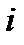 . Пусть в точку
. Пусть в точку 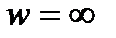 переходит некоторая неизвестная пока точка
переходит некоторая неизвестная пока точка 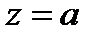 . Тогда дробно-линейное отображение, переводящее точки 2,
. Тогда дробно-линейное отображение, переводящее точки 2, 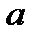 ,
,  соответственно в точки
соответственно в точки 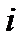 ,
,  , -2
, -2 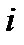 найдется из уравнения
найдется из уравнения
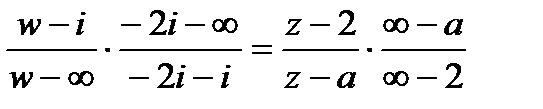 ,
,
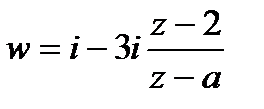 .
.
Для нахождения 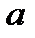 воспользуемся условием
воспользуемся условием 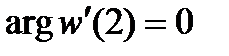 и условием
и условием 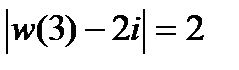 , означающим, что при искомом отображении граничная точка z = 3 круга
, означающим, что при искомом отображении граничная точка z = 3 круга 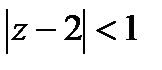 переходит в некоторую граничную точку круга
переходит в некоторую граничную точку круга 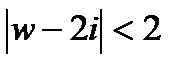 .
.
Из первого условия
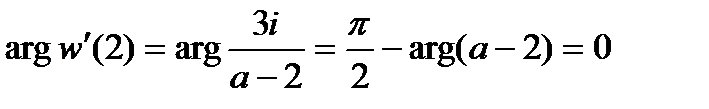
находим 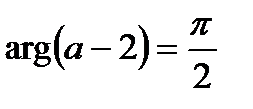 . Следовательно, комплексное число
. Следовательно, комплексное число  –2 имеет вид
–2 имеет вид
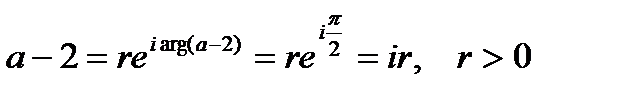 ,
,
откуда 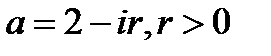 . Из второго условия
. Из второго условия
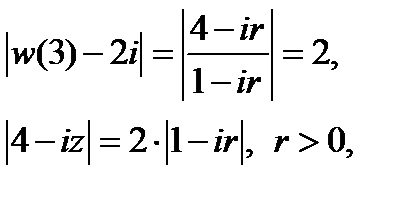
находим r = 2. Значит, 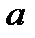 = 2 + 2
= 2 + 2 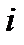 и
и
Дробно-линейные отображения
Дробно-линейной функцией называется функция вида: ![]() , где
, где ![]() — произвольные комплексные числа, такие, что
— произвольные комплексные числа, такие, что ![]() .
.
Перечислим без доказательства свойства дробно-линейной функции.
- Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка
 отображается в точку
отображается в точку  , а точка
, а точка  отображается в
отображается в  .
. - Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного
 , отображения
, отображения  и сдвига
и сдвига  .
. - Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
- Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
- Дробно-линейное отображение, переводящее три заданные точки в три заданные точки:
 дается формулой:
дается формулой: 
Пример 1 Найти образ мнимой оси при отображении
.
Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: ![]() . Так как образ одной из точек
. Так как образ одной из точек ![]() , то мнимая ось переходит в прямую проходящую через
, то мнимая ось переходит в прямую проходящую через ![]() и
и ![]() , то есть в действительную ось.
, то есть в действительную ось.
Пример 2 Найти дробно линейное отображение, переводящее точки
.
Пример 3 Найти образ области
при отображении
Найдем образ мнимой оси при данном отображении. Возьмем три точки : ![]() .
.
Отметим также, что ![]() . Куда же перешел луч
. Куда же перешел луч ![]() ? Подставим в формулу отображения:
? Подставим в формулу отображения: ![]() . При
. При ![]() , точки
, точки ![]() переходят в точки луча
переходят в точки луча ![]() действительной оси. Точки
действительной оси. Точки ![]() переходят в луч
переходят в луч ![]() . Образы двух точек действительной оси у нас есть:
. Образы двух точек действительной оси у нас есть: ![]() Действительная ось переходит в окружность, проходящую через точки
Действительная ось переходит в окружность, проходящую через точки ![]() .
.
Найдем образ точки ![]() из границы нашей области:
из границы нашей области:
![]()
Итак, образ луча ![]() будет полуокружность
будет полуокружность ![]() .
.
Теперь мы можем изобразить схему самого отображения:

Пример 4 Найти образы всех квадрантов при отображении .
Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:
Пусть функция ![]() отображает область
отображает область ![]() в
в ![]() и
и ![]() — дуга окружности или отрезок, принадлежащий границе области
— дуга окружности или отрезок, принадлежащий границе области ![]() , и
, и ![]() — область, симметричная
— область, симметричная ![]() относительно
относительно ![]() .
.
Пусть ![]() непрерывна на
непрерывна на ![]() и области
и области ![]() и
и ![]() не пересекаются. Тогда функция
не пересекаются. Тогда функция ![]() конформно отображает
конформно отображает ![]() на
на ![]() , где
, где ![]() и
и ![]() — образы
— образы ![]() и
и ![]() соответственно при отображении
соответственно при отображении ![]() .
.
На следующем рисунке видно, что области ![]() и
и ![]() симметричны относительно луча
симметричны относительно луча ![]() , который переходит в полуокружность
, который переходит в полуокружность ![]() . Так находится образ области
. Так находится образ области ![]() . Он для удобства обозначен штриховкой. Точно так же находятся образы остальных двух квадрантов.
. Он для удобства обозначен штриховкой. Точно так же находятся образы остальных двух квадрантов.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Решение.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Пример 1
Пусть G – множество всех пар действительных чисел (х, у), удовлетворяющих соотношению
(х-3)2 + (у – 2)2 £ 1. Графически такое соответствие G представляет собой круг радиуса 1 с центром в точке (3, 2). Таким образом, круг G задает соответствие между R и R (осью абсцисс и осью ординат, рис.2).
Определите, чему равны:
а) образы и прообразы чисел 2, 3, 4;
б) образы и прообразы отрезков [2,3], [2,4].
Каковы свойства соответствия G?
а) Образом числа 2 Î пр1G (на оси абсцисс) при соответствии G (см. рис.2) является единственное число 2 Î пр2 G (на оси ординат).
Образ числа 3 при соответствии G есть множество всех действительных чисел отрезка [1, 3], а образ числа 4-число 3.
Рис.2
Прообразом числа 2 Î пр2 G (на оси ординат) при соответствии G будет множество всех действительных чисел отрезка [2, 4] Î пр1 G (на оси абсцисс), прообразом числа 3 при соответствии G — число 3, а прообраза числа 4 при соответствии G не существует.
б) Образом множества чисел отрезка [2,3] Î пр1 G является объединение образов всех чисел отрезка, т.е. отрезок [1, 3] Í пр2 G. Аналогично образом отрезка [2,4] будет отрезок [1,3] при соответствии G.
Прообраз отрезка [2,3] при соответствии G-это отрезок [2,4], а прообраз отрезка [2,4] – также [2,4].
Если допустить, что соответствие G установлено на множестве действительных чисел, т.е. G Í R ´ R, то оно является:
• частично определенным, так как пр1 G ¹ R (пр1 G Ì R);
• не сюръективным, поскольку пр1 G ¹ R (пр2 G Ì R);
• не функциональным, ибо для любого числа отрезка [2,4] = пр1 G (кроме чисел 2, 4) отсутствует единственность образа;
• не взаимно однозначным, так как отсутствуют необходимые условия: G не является всюду определенным на R, не сюръективно, не функционально, а также для любого числа отрезка [1,3] = пр2 G (кроме чисел 1, 3) отсутствует единственность прообраза.
Если определить соответствие G Í [2, 4] ´ [1, 3], то, очевидно, оно будет всюду определенным и сюръективным, однако останется не функциональным и не взаимно однозначным.
Пример 2
Пусть G – множество точек прямой линии, удовлетворяющей соотношению х – 2 = у при х, у ³0 (рис.3). Каковы свойства соответствия G?
1. Если соответствие G задано на множестве действительных чисел, т.е. G Í R ´ R, то G:
• частично определено, так как пр1 G = [2, ¥) Ì R;
• не сюръективно, поскольку пр2 G = R+ Ì R, где R+ = [0, ¥] – множество всех положительных действительных чисел с нулем;
Рис.3
• функционально, ибо любому х из области определения соответствует единственный у из области значений, т.е. для соответствия G имеет место единственность образа для любого х Î пр1 G;
• не взаимно однозначно, так как не выполняются условия – всюду определенности и сюръективности.
2. В случае, если соответствие G задано на множестве R+ с нулем, т.е. G Í R+ ´ R+, тогда соответствие G:
• частично определено, так как пр1 G = [2, ¥) и пр1 G Í R+;
• сюръективно, поскольку пр2 G = R+;
• функционально;
• не взаимно однозначно, так как не выполняется условие – всюду определенности.
3. При G Í [2, ¥) ´ R+ соответствие G:
• всюду определено;
• сюръективно;
• функционально;
• взаимно однозначно, так как наряду с выполнением перечисленных выше условий имеет место также единственность прообраза для любого у Î пр2 G.
Пример 3
Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Каковы свойства этого соответствия?
Данное соответствие не является:
• всюду определенным (всегда можно найти английское слово, не содержащееся в словаре);
• сюръективным (по отношению русских слов, имеющихся в словаре);
• функциональным (одному английскому слову ставится в соответствие, как правило, несколько русских);
• взаимно однозначным (в силу предыдущего).
Пример 4
Пусть множества b(U), где U= {а, b, с}, и B3 определены следующим образом:
b(U) – множество всех подмножеств (булеан) множества U= {а, b, с};
В3 – множество всех двоичных векторов длины 3, т.е. В3=А´А´А, где A = {0, 1}.
Показать, что между множествами b(U) и В3где U= {a, b, с}, имеет место взаимно однозначное соответствие.
b(U) = {Æ, {а}, {b}, {с}, {а, b}, {а, с}, {b, с}, {а, b, с}};
| b(U) | = 8.
В3= {(000), (001), (010), (011), (100), (101), (110), (111)};
| В3 | = 8
(для упрощения обозначений запятые между компонентами векторов опущены).
Установим следующее соответствие G между множествами из b(U)и векторами из B3:
• если в множестве из b(U) присутствует элемент а, то в соответствующем ему векторе из B3 первая компонента равна 1, а если отсутствует – то 0;
• если в множестве из b(U) присутствует элемент b, то в соответствующем ему векторе из B3 вторая компонента равна 1, а если отсутствует – то 0;
• аналогичное соответствие установим между элементом с в множестве из b(U) и значением третьей компоненты вектора из В3.
Например, множеству {b} из b(U) соответствует вектор (010) из В3множеству {а, с} – вектор (101) и т.д.:
G :Æ ® (000), {а} ® (100), {b} ® (010), {с} ® (001), {а, b} ®(110), {а,с} ®(101), {a, с} ® (011), {а, b, с} ®(111).
Установленное, таким образом соответствие G является взаимно однозначным, так как выполняются все условия для взаимно однозначного соответствия.
Пример 5
Используя определение равномощности множеств, покажите, что множество М2n натуральных чисел, являющихся степенями двойки, счётно.
Для доказательства следует установить взаимно однозначное соответствие между множествами М2n и N. Если каждому натуральному п Î N поставить в соответствие число 2n-1 Î М2n , то установленное таким образом соответствие G Î N ´ M2n, очевидно, является взаимно однозначным (удовлетворяет всем требованиям для взаимно однозначного соответствия) и представляет множество всех векторов G = {(п, 2n-1): п Î N}. А так как мощность множества N cчетна, то из установленной взаимной однозначности между множествами N и М2n согласно определению равномощности бесконечных множеств, следует, что множество М2n также счетно.
Упражнения
1. Соответствия G1,- G4 определены графически:
а) б)
в) г)
Рис. 3.4
Найдите образы и прообразы: чисел 1, 2, 3, 4; отрезков [2, 3], [1, 2], [2, 4], [3, 4], [3, 5].
