Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17.1 изображены отрезок 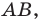
Мы указали правило, с помощью которого каждой точке  отрезка
отрезка  поставлена в соответствие единственная точка
поставлена в соответствие единственная точка 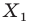 отрезка
отрезка 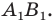 В этом случае говорят, что отрезок
В этом случае говорят, что отрезок 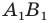 получен в результате преобразования отрезка
получен в результате преобразования отрезка 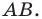
Пример:
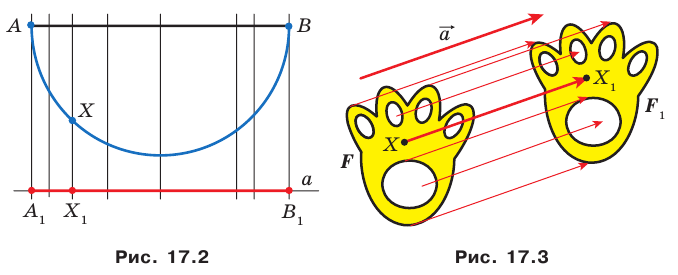
На рисунке 17.2 изображены полуокружность 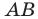 и прямая
и прямая 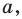 параллельная диаметру
параллельная диаметру 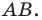 Каждой точке
Каждой точке 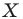 полуокружности поставим в соответствие точку
полуокружности поставим в соответствие точку 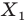 прямой а так, чтобы прямая
прямой а так, чтобы прямая 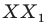 была перпендикулярна прямой
была перпендикулярна прямой 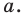 Понятно, что все такие точки
Понятно, что все такие точки 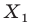 образуют отрезок
образуют отрезок  В этом случае говорят, что отрезок
В этом случае говорят, что отрезок  получен в результате преобразования полуокружности
получен в результате преобразования полуокружности 
Пример:
Пусть даны некоторая фигура 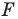 и вектор
и вектор 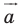 (рис. 17.3). Каждой точке
(рис. 17.3). Каждой точке 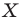 фигуры
фигуры 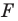 поставим в соответствие точку
поставим в соответствие точку 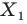 такую, что
такую, что 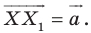 В результате такого преобразования фигуры
В результате такого преобразования фигуры  получим фигуру
получим фигуру  (рис. 17.3). Такое преобразование фигуры
(рис. 17.3). Такое преобразование фигуры 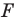 называют параллельным переносом на вектор
называют параллельным переносом на вектор 
Обобщим приведенные примеры.
Пусть задана некоторая фигура  Каждой точке фигуры
Каждой точке фигуры  поставим в соответствие (сопоставим) по определенному правилу некоторую точку. Все полученные сопоставленные точки образуют фигуру
поставим в соответствие (сопоставим) по определенному правилу некоторую точку. Все полученные сопоставленные точки образуют фигуру 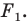 Говорят, что фигура
Говорят, что фигура 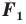 получена в результате преобразования фигуры
получена в результате преобразования фигуры 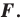 При этом фигуру
При этом фигуру 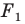 называют образом фигуры
называют образом фигуры 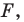 а фигуру
а фигуру 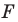 — прообразом фигуры
— прообразом фигуры 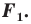
Так, в примере 1 отрезок 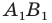 является образом отрезка
является образом отрезка 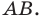 Точка
Точка 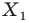 является образом точки
является образом точки 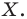 Отрезок
Отрезок 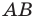 — это прообраз отрезка
— это прообраз отрезка 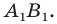
Обратим внимание на то, что в примере 3 фигура 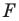 равна своему образу
равна своему образу 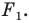 Преобразования, описанные в примерах 1 и 2, таким свойством не обладают.
Преобразования, описанные в примерах 1 и 2, таким свойством не обладают.
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 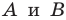 — произвольные точки фигуры
— произвольные точки фигуры 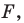 а точки
а точки 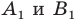 — их образы, то должно выполняться равенство
— их образы, то должно выполняться равенство 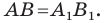
Что такое преобразование фигур
Определение. Преобразование фигуры 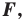 сохраняющее расстояние между точками, называют движением (перемещением) фигуры
сохраняющее расстояние между точками, называют движением (перемещением) фигуры 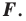
Если каждой точке 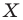 фигуры
фигуры 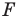 поставлена в соответствие эта же точка
поставлена в соответствие эта же точка 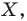 то такое преобразование фигуры
то такое преобразование фигуры 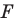 называют тождественным. При тождественном преобразовании образом фигуры
называют тождественным. При тождественном преобразовании образом фигуры 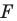 является сама фигура
является сама фигура 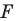 . Очевидно, что тождественное преобразование является движением.
. Очевидно, что тождественное преобразование является движением.
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 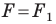 означает, что фигуры
означает, что фигуры  равны.
равны.
Если существует движение, при котором фигура  является образом фигуры
является образом фигуры  то обязательно существует движение, при котором фигура
то обязательно существует движение, при котором фигура  является образом фигуры
является образом фигуры  Такие движения называют взаимно обратными.
Такие движения называют взаимно обратными.
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры  на фигуру
на фигуру  можно рассматривать как движение фигуры
можно рассматривать как движение фигуры  при котором ее образом будет фигура
при котором ее образом будет фигура 
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры  равны, понятно из наглядных соображений. Строгое обоснование этого факта дает следующая теорема.
равны, понятно из наглядных соображений. Строгое обоснование этого факта дает следующая теорема.
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
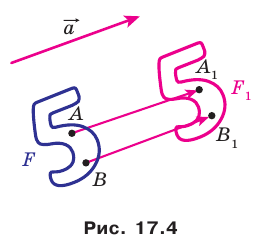
Доказательство: Пусть  — произвольные точки фигуры
— произвольные точки фигуры 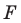 (рис. 17.4), точки
(рис. 17.4), точки 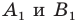 — их соответствующие образы при параллельном переносе на вектор
— их соответствующие образы при параллельном переносе на вектор 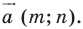 Докажем, что
Докажем, что 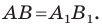
Имеем: 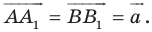 Векторы
Векторы 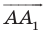 и
и 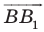 имеют координаты
имеют координаты 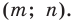 Следовательно, координатами точек
Следовательно, координатами точек 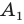 и
и 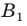 являются соответственно пары чисел
являются соответственно пары чисел 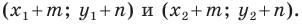
Найдем расстояние между точками 
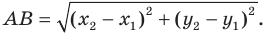
Найдем расстояние между точками 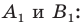
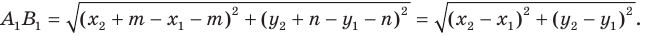
Следовательно, мы показали, что 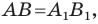 то есть параллельный перенос сохраняет расстояние между точками.
то есть параллельный перенос сохраняет расстояние между точками. 
Следствие. Если фигура 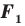 — образ фигуры
— образ фигуры 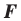 при параллельном переносе, то
при параллельном переносе, то 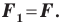
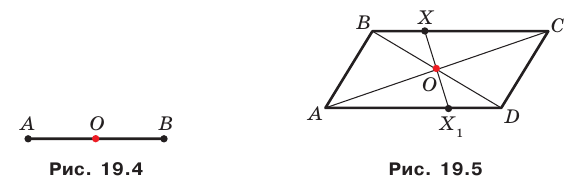
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5). 
Если фигура 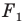 является образом фигуры
является образом фигуры 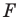 при параллельном переносе на вектор
при параллельном переносе на вектор 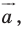 то фигура
то фигура 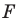 является образом фигуры
является образом фигуры 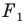 при параллельном переносе на вектор
при параллельном переносе на вектор 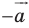 (рис. 17.6).
(рис. 17.6).
Параллельные переносы на векторы 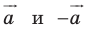 являются взаимно обратными движениями.
являются взаимно обратными движениями.
Пример №1
Каждой точке 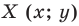 фигуры
фигуры 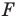 ставится в соответствие точка
ставится в соответствие точка 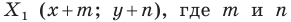 — заданные числа. Докажите, что такое преобразование фигуры
— заданные числа. Докажите, что такое преобразование фигуры 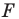 является параллельным переносом на вектор
является параллельным переносом на вектор 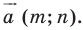
Решение:
Рассмотрим вектор 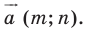 Заметим, что координаты вектора
Заметим, что координаты вектора 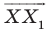 равны
равны 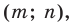 то есть
то есть 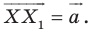 Следовательно, описанное преобразование фигуры
Следовательно, описанное преобразование фигуры 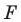 — параллельный перенос на вектор
— параллельный перенос на вектор 
Пример №2
Точка 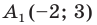 является образом точки
является образом точки 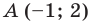 при параллельном переносе на вектор
при параллельном переносе на вектор 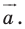 Найдите координаты вектора
Найдите координаты вектора 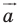 и координаты образа точки
и координаты образа точки 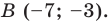
Решение:
Из условия следует, что 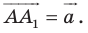 Отсюда
Отсюда 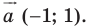
Пусть 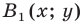 — образ точки
— образ точки 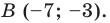 Тогда
Тогда 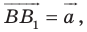 то есть
то есть 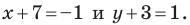 Отсюда
Отсюда 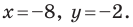
Ответ: 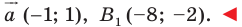
Пример №3
Даны угол 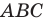 и прямая
и прямая 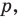 не параллельная ни одной из сторон этого угла (рис. 17.7). Постройте прямую
не параллельная ни одной из сторон этого угла (рис. 17.7). Постройте прямую  параллельную прямой
параллельную прямой  так, чтобы стороны угла отсекали на ней отрезок заданной длины
так, чтобы стороны угла отсекали на ней отрезок заданной длины 
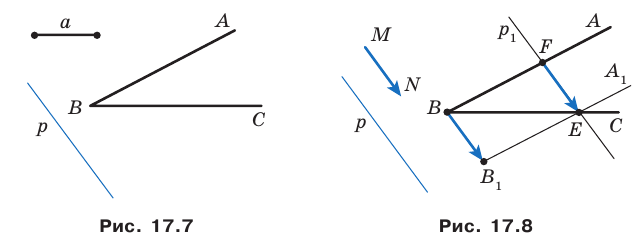
Решение:
Рассмотрим вектор 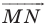 такой, что
такой, что  и
и 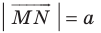 (рис. 17.8). Построим луч
(рис. 17.8). Построим луч 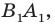 являющийся образом луча
являющийся образом луча 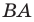 при параллельном переносе на вектор
при параллельном переносе на вектор  Обозначим точку пересечения лучей
Обозначим точку пересечения лучей  буквой
буквой  Пусть
Пусть  — прообраз точки
— прообраз точки 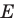 при рассматриваемом параллельном переносе. Тогда
при рассматриваемом параллельном переносе. Тогда 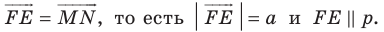
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
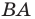 при параллельном переносе на вектор
при параллельном переносе на вектор 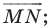
- отметить точку пересечения луча
 с построенным образом;
с построенным образом; - через найденную точку провести прямую
 параллельную прямой
параллельную прямой  Прямая
Прямая  будет искомой.
будет искомой.
Осевая симметрия
Определение. Точки 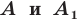 называют симметричными относительно прямой
называют симметричными относительно прямой 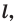 если прямая
если прямая 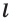 является серединным перпендикуляром отрезка
является серединным перпендикуляром отрезка 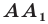 (рис. 18.1). Если точка
(рис. 18.1). Если точка 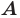 принадлежит прямой
принадлежит прямой 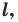 то ее считают симметричной самой себе относительно прямой
то ее считают симметричной самой себе относительно прямой 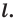
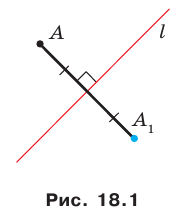
Например, точки 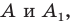 у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18.2).
у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18.2).
Рассмотрим фигуру 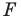 и прямую
и прямую 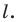 Каждой точке
Каждой точке 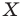 фигуры
фигуры 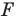 поставим в соответствие симметричную ей относительно прямой
поставим в соответствие симметричную ей относительно прямой 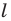 точку
точку 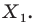
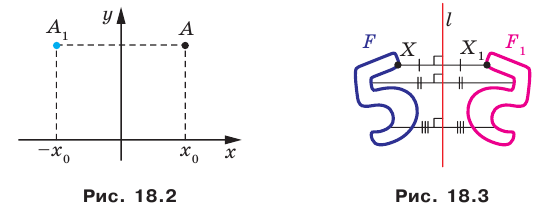
В результате такого преобразования фигуры 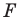 получим фигуру
получим фигуру 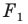 (рис. 18.3). Такое преобразование фигуры
(рис. 18.3). Такое преобразование фигуры 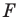 называют осевой симметрией относительно прямой
называют осевой симметрией относительно прямой 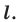 Прямую
Прямую 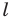 называют осью симметрии. Говорят, что фигуры
называют осью симметрии. Говорят, что фигуры 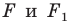 симметричны относительно прямой
симметричны относительно прямой 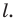
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 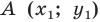 и
и 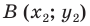 — произвольные точки фигуры
— произвольные точки фигуры 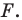 Тогда точки
Тогда точки  и
и  — их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
— их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
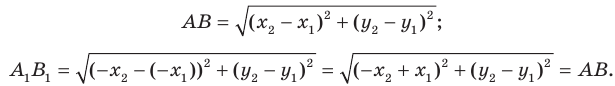
Мы получили, что 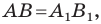 то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением.
то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением. 
Следствие. Если фигуры 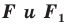 симметричны относительно прямой, то
симметричны относительно прямой, то 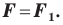
Определение. Фигуру называют симметричной относительно прямой  если для каждой точки данной фигуры точка, симметричная ей относительно прямой
если для каждой точки данной фигуры точка, симметричная ей относительно прямой  также принадлежит этой фигуре.
также принадлежит этой фигуре.
Прямую  называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
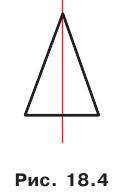
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5). 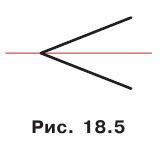
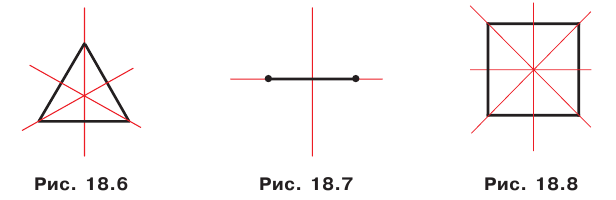
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник  Провели прямую
Провели прямую  содержащую биссектрису угла
содержащую биссектрису угла  Потом рисунок стерли, оставив только точки
Потом рисунок стерли, оставив только точки 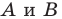 и прямую
и прямую  Восстановите треугольник
Восстановите треугольник 
Решение:
Поскольку прямая  является осью симметрии угла
является осью симметрии угла  то точка
то точка  — образ точки
— образ точки  при симметрии относительно прямой
при симметрии относительно прямой 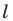 — принадлежит лучу
— принадлежит лучу 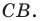 Тогда пересечением прямых
Тогда пересечением прямых 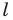 и
и 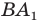 является вершина
является вершина  искомого треугольника
искомого треугольника  (рис. 18.10).
(рис. 18.10).
Эти соображения подсказывают, как построить искомый треугольник: строим точку  симметричную точке
симметричную точке  относительно прямой
относительно прямой  Находим вершину
Находим вершину  как точку пересечения прямых
как точку пересечения прямых  и
и 
Пример №5
Точка 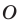 принадлежит острому углу
принадлежит острому углу  (рис. 18.11). На сторонах
(рис. 18.11). На сторонах  угла найдите такие точки
угла найдите такие точки 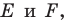 чтобы периметр треугольника
чтобы периметр треугольника 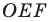 был наименьшим.
был наименьшим.
Решение:
Пусть точки 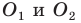 — образы точки
— образы точки 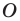 при симметриях относительно прямых
при симметриях относительно прямых 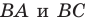 соответственно (рис. 18.12), а прямая
соответственно (рис. 18.12), а прямая  пересекает стороны
пересекает стороны 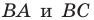 в точках
в точках  соответственно. Докажем, что точки
соответственно. Докажем, что точки  — искомые.
— искомые.
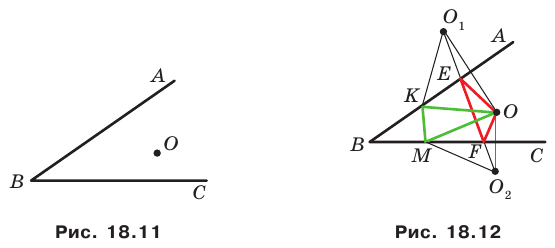
Заметим, что отрезки  симметричны относительно прямой
симметричны относительно прямой  Следовательно,
Следовательно, 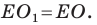 Аналогично
Аналогично 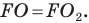 Тогда периметр треугольника
Тогда периметр треугольника 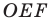 равен длине отрезка
равен длине отрезка 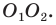
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 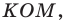 где
где 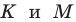 — произвольные точки соответственно лучей
— произвольные точки соответственно лучей 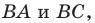 причем точка
причем точка 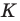 не совпадает с точкой
не совпадает с точкой 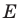 или точка
или точка 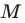 не совпадает с точкой
не совпадает с точкой 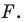
Понятно, что 
Тогда периметр треугольника  равен сумме
равен сумме 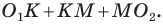 Однако
Однако 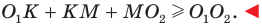
Центральная симметрия. Поворот
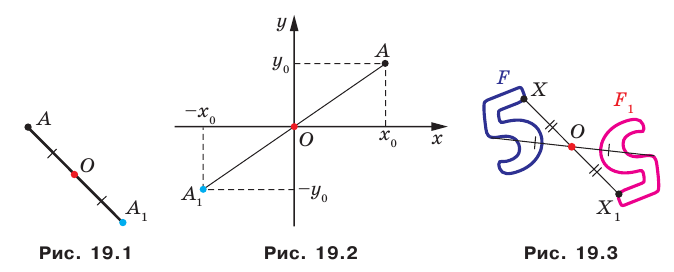
Определение. Точки 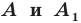 называют симметричными относительно точки
называют симметричными относительно точки  если точка
если точка  является серединой отрезка
является серединой отрезка 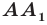 (рис. 19.1). Точку
(рис. 19.1). Точку  считают симметричной самой себе.
считают симметричной самой себе.
 Например, точки
Например, точки 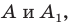 у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19.2).
у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19.2).
Рассмотрим фигуру 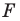 и точку
и точку  Каждой точке
Каждой точке 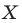 фигуры
фигуры 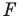 поставим в соответствие симметричную ей относительно точки
поставим в соответствие симметричную ей относительно точки 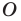 точку
точку 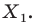 В результате такого преобразования фигуры
В результате такого преобразования фигуры  получим фигуру
получим фигуру  (рис. 19.3). Такое преобразование фигуры
(рис. 19.3). Такое преобразование фигуры  называют центральной симметрией относительно точки
называют центральной симметрией относительно точки  Точку
Точку 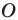 называют центром симметрии. Также говорят, что фигуры
называют центром симметрии. Также говорят, что фигуры 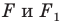 симметричны относительно точки
симметричны относительно точки 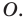
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 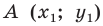 и
и 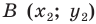 — произвольные точки фигуры
— произвольные точки фигуры 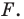 Точки
Точки 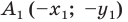 и
и  — соответственно их образы при центральной симметрии относительно начала координат. Имеем:
— соответственно их образы при центральной симметрии относительно начала координат. Имеем: 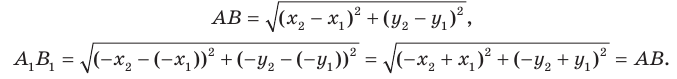
Мы получили, что 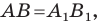 то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением.
то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением. 
Следствие. Если фигуры 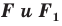 симметричны относительно точки, то
симметричны относительно точки, то 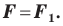
Определение. Фигуру называют симметричной относительно точки  если для каждой точки данной фигуры точка, симметричная ей относительно точки
если для каждой точки данной фигуры точка, симметричная ей относительно точки  также принадлежит этой фигуре.
также принадлежит этой фигуре.
Точку 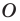 называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 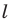 при симметрии относительно точки
при симметрии относительно точки  не принадлежащей прямой
не принадлежащей прямой  является прямая, параллельная данной.
является прямая, параллельная данной.
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 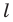 будет прямая. Для построения прямой достаточно найти две любые ее точки.
будет прямая. Для построения прямой достаточно найти две любые ее точки.
Выберем на прямой 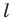 произвольные точки
произвольные точки 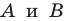 (рис. 19.7). Пусть точки
(рис. 19.7). Пусть точки 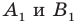 — их образы при центральной симметрии относительно точки
— их образы при центральной симметрии относительно точки 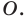 Тогда прямая
Тогда прямая 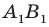 — образ прямой
— образ прямой 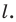
Поскольку 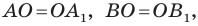 углы
углы 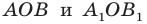 равны как вертикальные, то треугольники
равны как вертикальные, то треугольники 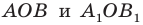 равны по первому признаку равенства треугольников. Отсюда
равны по первому признаку равенства треугольников. Отсюда 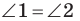 (рис. 19.7). Следовательно, по признаку параллельных прямых
(рис. 19.7). Следовательно, по признаку параллельных прямых 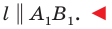
Пример №7
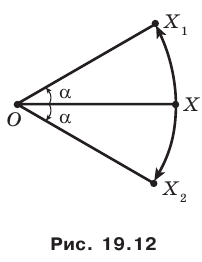
Точка 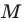 принадлежит углу
принадлежит углу 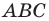 (рис. 19.8). На сторонах
(рис. 19.8). На сторонах 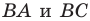 угла постройте такие точки
угла постройте такие точки 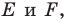 чтобы точка
чтобы точка 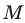 была серединой отрезка
была серединой отрезка 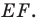
Решение:
Пусть прямая 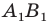 — образ прямой
— образ прямой 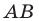 при центральной симметрии относительно точки
при центральной симметрии относительно точки 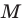 (рис. 19.9). Обозначим буквой
(рис. 19.9). Обозначим буквой 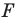 точку пересечения прямых
точку пересечения прямых 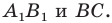
Найдем прообраз точки 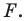 Очевидно, что он лежит на прямой
Очевидно, что он лежит на прямой 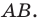 Поэтому достаточно найти точку пересечения прямых
Поэтому достаточно найти точку пересечения прямых 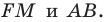
Обозначим эту точку буквой 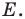 Тогда
Тогда 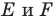 — искомые точки.
— искомые точки.
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». 
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).

На рисунке 19.12 изображены точки 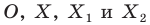 такие, что
такие, что 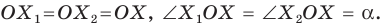
Говорят, что точка 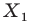 является образом точки
является образом точки 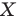 при повороте вокруг центра
при повороте вокруг центра 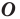 против часовой стрелки на угол
против часовой стрелки на угол 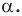
Так же говорят, что точка 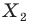 — это образ точки
— это образ точки 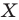 при повороте вокруг центра
при повороте вокруг центра 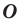 по часовой стрелке на угол
по часовой стрелке на угол 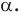
Точку 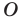 называют центром поворота, угол
называют центром поворота, угол 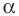 — углом поворота.
— углом поворота.
Рассмотрим фигуру 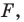 точку
точку 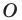 и угол
и угол 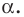 Каждой точке
Каждой точке 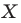 фигуры
фигуры 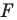 поставим в соответствие точку
поставим в соответствие точку 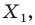 являющуюся образом точки
являющуюся образом точки 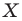 при повороте вокруг центра
при повороте вокруг центра 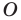 против часовой стрелки на угол
против часовой стрелки на угол 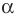 (если точка
(если точка 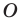 принадлежит фигуре
принадлежит фигуре 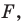 то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры 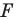 получим фигуру
получим фигуру 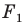 (рис. 19.13). Такое преобразование фигуры
(рис. 19.13). Такое преобразование фигуры 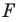 называют поворотом вокруг центра
называют поворотом вокруг центра  против часовой стрелки на угол
против часовой стрелки на угол  Точку
Точку 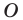 называют центром поворота.
называют центром поворота. 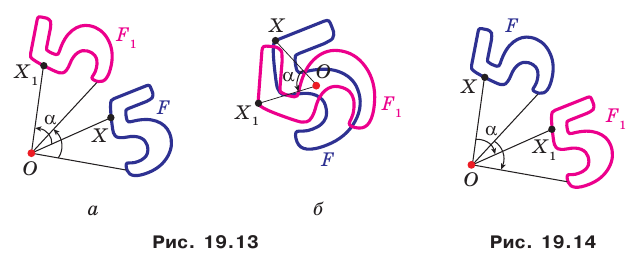
Аналогично определяют преобразование поворота фигуры 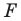 по часовой стрелке на угол
по часовой стрелке на угол 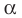 (рис. 19.14).
(рис. 19.14).
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол 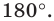
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 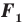 — образ фигуры
— образ фигуры  при повороте, то
при повороте, то 
Пример №8
Даны прямая  и точка
и точка  вне ее. Постройте образ прямой
вне ее. Постройте образ прямой  при повороте вокруг точки
при повороте вокруг точки  против часовой стрелки на угол
против часовой стрелки на угол 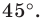
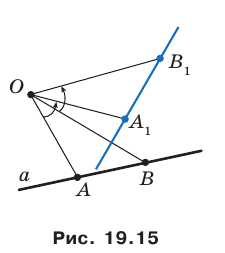
Решение:
Поскольку поворот — это движение, то образом прямой 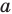 будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой 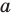 произвольные точки
произвольные точки 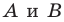 (рис. 19.15). Построим точки
(рис. 19.15). Построим точки 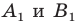 — их образы при повороте вокруг точки
— их образы при повороте вокруг точки 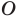 против часовой стрелки на угол
против часовой стрелки на угол 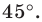 Тогда прямая
Тогда прямая 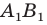 — образ прямой
— образ прямой 
Пример №9
Точка 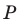 принадлежит углу
принадлежит углу  но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой
но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой  а две другие принадлежат сторонам
а две другие принадлежат сторонам 
Решение:
Пусть прямая  — образ прямой
— образ прямой 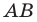 при повороте вокруг центра
при повороте вокруг центра  против часовой стрелки на угол
против часовой стрелки на угол 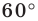 (рис. 19.16). Обозначим буквой
(рис. 19.16). Обозначим буквой  точку пересечения прямых
точку пересечения прямых 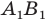 и
и 
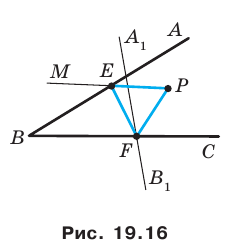
Пусть точка  — прообраз точки
— прообраз точки 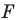 при рассматриваемом повороте. Точка
при рассматриваемом повороте. Точка 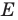 принадлежит стороне
принадлежит стороне 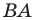 угла
угла 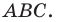
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 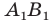 как образ прямой
как образ прямой 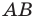 при повороте вокруг центра
при повороте вокруг центра 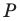 против часовой стрелки на угол
против часовой стрелки на угол 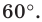 Пусть
Пусть 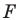 — точка пересечения прямых
— точка пересечения прямых 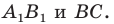
Строим угол 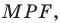 равный
равный 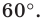 Пусть прямые
Пусть прямые 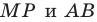 пересекаются в точке
пересекаются в точке 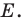 Эта точка и является прообразом точки
Эта точка и является прообразом точки 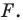
Имеем: 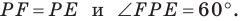 Следовательно, треугольник
Следовательно, треугольник  равносторонний.
равносторонний. 
Подобие фигур
На рисунке 20.1 изображены точки 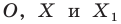 такие, что
такие, что 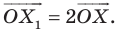 Говорят, что точка
Говорят, что точка 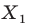 — это образ точки
— это образ точки 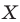 при гомотетии с центром
при гомотетии с центром 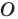 и коэффициентом 2.
и коэффициентом 2. 
На рисунке 20.2 изображены точки 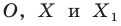 такие, что
такие, что 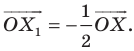 Говорят, что точка
Говорят, что точка 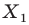 — это образ точки
— это образ точки 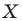 при гомотетии с центром
при гомотетии с центром 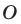 и коэффициентом
и коэффициентом 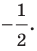
Вообще, если точки 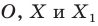 таковы, что
таковы, что 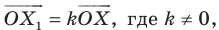 то говорят, что точка
то говорят, что точка 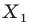 — это образ точки
— это образ точки 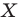 при гомотетии с центром
при гомотетии с центром 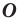 и коэффициентом
и коэффициентом 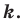
Точку 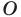 называют центром гомотетии, число
называют центром гомотетии, число 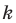 — коэффициентом гомотетии,
— коэффициентом гомотетии, 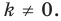
Рассмотрим фигуру 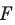 и точку
и точку 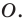 Каждой точке
Каждой точке 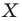 фигуры
фигуры 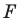 поставим в соответствие точку
поставим в соответствие точку 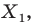 являющуюся образом точки
являющуюся образом точки 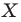 при гомотетии с центром
при гомотетии с центром 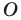 и коэффициентом
и коэффициентом 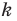 (если точка
(если точка 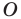 принадлежит фигуре
принадлежит фигуре 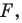 то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры 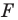 получим фигуру
получим фигуру  (рис. 20.3). Такое преобразование фигуры
(рис. 20.3). Такое преобразование фигуры  называют гомотетией с центром
называют гомотетией с центром  и коэффициентом
и коэффициентом  Также говорят, что фигура
Также говорят, что фигура 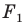 гомотетична фигуре
гомотетична фигуре 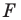 с центром
с центром 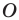 и коэффициентом
и коэффициентом 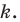
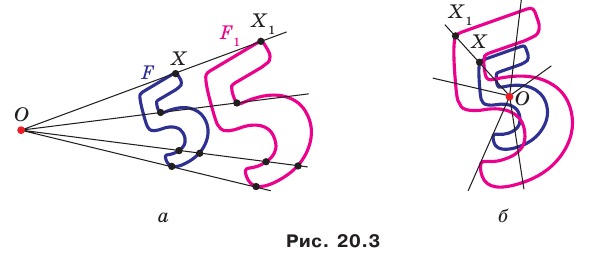
Например, на рисунке 20.4 треугольник  гомотетичен треугольнику
гомотетичен треугольнику  с центром
с центром  и коэффициентом, равным -3.
и коэффициентом, равным -3.
можно сказать, что треугольник 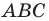 гомотетичен треугольнику
гомотетичен треугольнику 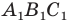 с тем же центром, но коэффициентом гомотетии, равным
с тем же центром, но коэффициентом гомотетии, равным 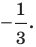
Отметим, что при 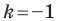 гомотетия с центром
гомотетия с центром 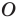 является центральной симметрией с центром
является центральной симметрией с центром 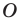 (рис. 20.5). Если
(рис. 20.5). Если 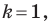 то гомотетия является тождественным преобразованием.
то гомотетия является тождественным преобразованием.
Очевидно, что при 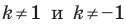 гомотетия не является движением.
гомотетия не является движением.
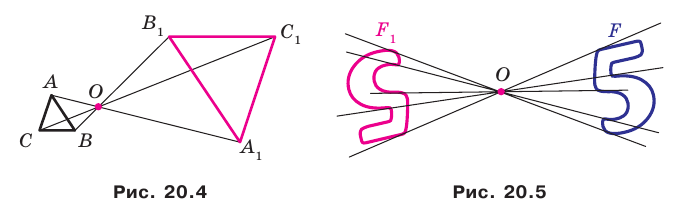
Теорема 20.1. При гомотетии фигуры 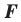 с коэффициентом
с коэффициентом  все расстояния между ее точками изменяются в
все расстояния между ее точками изменяются в  раз, то есть если
раз, то есть если 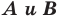 — произвольные точки фигуры
— произвольные точки фигуры 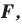 а точки
а точки 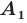 и
и 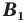 — их соответствующие образы при гомотетии с коэффициентом
— их соответствующие образы при гомотетии с коэффициентом 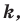 то
то 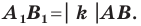
Доказательство: Пусть точка 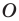 — центр гомотетии. Тогда
— центр гомотетии. Тогда 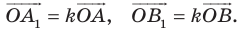 Имеем:
Имеем: 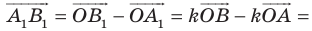
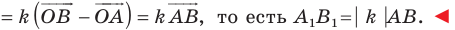
Следствие. Если треугольник  гомотетичен треугольнику
гомотетичен треугольнику  с коэффициентом гомотетии
с коэффициентом гомотетии 
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
На рисунке 20.6 фигура 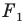 гомотетична фигуре
гомотетична фигуре 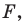 а фигура
а фигура 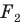 симметрична фигуре
симметрична фигуре 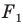 относительно прямой
относительно прямой 
Говорят, что фигура  получена из фигуры
получена из фигуры 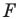 в результате композиции двух преобразований: гомотетии и осевой симметрии.
в результате композиции двух преобразований: гомотетии и осевой симметрии.
Поскольку 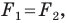 то фигуры
то фигуры 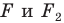 имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура
имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура 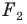 получена из фигуры
получена из фигуры  в результате преобразования подобия.
в результате преобразования подобия.
На рисунке 20.7 фигура  гомотетична фигуре
гомотетична фигуре  а фигура
а фигура  — образ фигуры
— образ фигуры 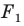 при некотором движении. Здесь также можно утверждать, что фигуры
при некотором движении. Здесь также можно утверждать, что фигуры  подобны.
подобны.
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8. 
Запись  означает, что фигуры
означает, что фигуры 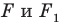 подобны. Также говорят, что фигура
подобны. Также говорят, что фигура 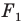 — образ фигуры
— образ фигуры  при преобразовании подобия.
при преобразовании подобия.
Из приведенного определения следует, что при преобразовании подобия фигуры  расстояния между ее точками изменяются в одно и то же количество раз.
расстояния между ее точками изменяются в одно и то же количество раз.
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 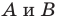 — произвольные точки фигуры
— произвольные точки фигуры  а точки
а точки 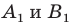 — их образы при преобразовании подобия. Точки
— их образы при преобразовании подобия. Точки 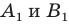 принадлежат фигуре
принадлежат фигуре 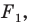 которая подобна фигуре
которая подобна фигуре 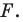 Число
Число 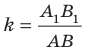 называют коэффициентом подобия. Говорят, что фигура
называют коэффициентом подобия. Говорят, что фигура 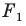 подобна фигуре
подобна фигуре 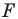 с коэффициентом подобия
с коэффициентом подобия 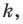 а фигура
а фигура 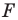 подобна фигуре
подобна фигуре 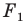 с коэффициентом подобия
с коэффициентом подобия 
Заметим, что преобразование подобия с коэффициентом 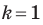 является движением. Отсюда следует, что движение — частный случай преобразования подобия.
является движением. Отсюда следует, что движение — частный случай преобразования подобия.
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 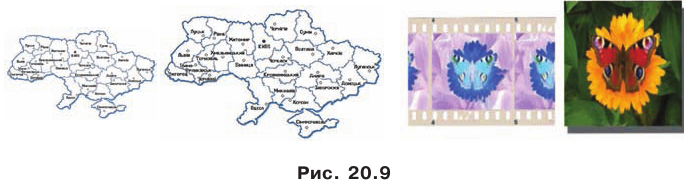 Теорема 20.2. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Теорема 20.2. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
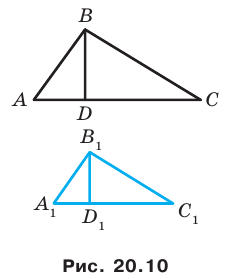
Доказательство: Пусть треугольник 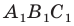 — образ треугольника
— образ треугольника  при преобразовании подобия с коэффициентом
при преобразовании подобия с коэффициентом  (рис. 20.10). Сторона
(рис. 20.10). Сторона 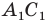 — образ стороны
— образ стороны 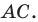 Тогда
Тогда 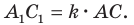 Проведем высоту
Проведем высоту 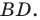 Пусть точка
Пусть точка 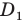 — образ точки
— образ точки 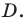
Поскольку при преобразовании подобия сохраняются углы, то отрезок 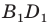 — высота треугольника
— высота треугольника 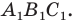
Тогда 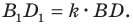 Имеем:
Имеем:
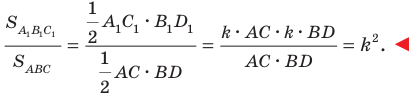
Пример №10
Докажите, что образом прямой  при гомотетии с центром
при гомотетии с центром 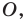 не принадлежащим прямой
не принадлежащим прямой 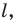 является прямая, параллельная данной.
является прямая, параллельная данной.
Решение:
Из свойств гомотетии следует, что образом прямой 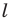 будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой 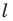 произвольные точки
произвольные точки 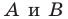 (рис. 20.11). Пусть точки
(рис. 20.11). Пусть точки 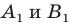 — их образы при гомотетии с центром
— их образы при гомотетии с центром 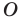 и коэффициентом
и коэффициентом 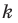 (рисунок 20.11 соответствует случаю, когда
(рисунок 20.11 соответствует случаю, когда 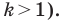 Тогда прямая
Тогда прямая 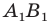 — образ прямой
— образ прямой 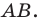
При доказательстве теоремы 20.1 мы показали, что 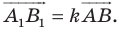 Следовательно,
Следовательно, 
Пример №11
В остроугольный треугольник 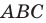 впишите квадрат так, чтобы две его вершины лежали соответственно на сторонах
впишите квадрат так, чтобы две его вершины лежали соответственно на сторонах 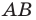 и
и 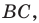 а две другие — на стороне
а две другие — на стороне 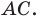
Решение:
Из произвольной точки 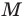 стороны
стороны 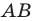 опустим перпендикуляр
опустим перпендикуляр 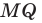 на сторону
на сторону 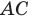 (рис. 20.12). Построим квадрат
(рис. 20.12). Построим квадрат 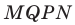 так, чтобы точка
так, чтобы точка 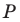 лежала на луче
лежала на луче 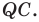 Пусть луч
Пусть луч 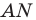 пересекает сторону
пересекает сторону 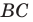 в точке
в точке 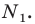
Рассмотрим гомотетию с центром 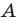 и коэффициентом
и коэффициентом 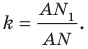 Тогда точка
Тогда точка 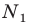 образ точки
образ точки 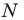 при этой гомотетии. Образом отрезка
при этой гомотетии. Образом отрезка 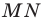 является отрезок
является отрезок 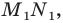 где точка
где точка 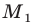 принадлежит лучу
принадлежит лучу 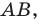 причем
причем 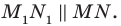 Аналогично отрезок
Аналогично отрезок 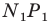 такой, что точка
такой, что точка 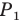 принадлежит лучу
принадлежит лучу 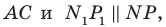 является образом отрезка
является образом отрезка 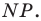 Следовательно, отрезки
Следовательно, отрезки 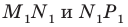 — соседние стороны искомого квадрата. Для завершения построения осталось опустить перпендикуляр
— соседние стороны искомого квадрата. Для завершения построения осталось опустить перпендикуляр  на сторону
на сторону 
Пример №12
Отрезок  — высота прямоугольного треугольника
— высота прямоугольного треугольника 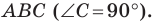 Найдите радиус
Найдите радиус 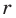 вписанной окружности треугольника
вписанной окружности треугольника 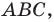 если радиусы окружностей, вписанных в треугольники
если радиусы окружностей, вписанных в треугольники 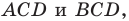 соответственно равны
соответственно равны 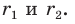
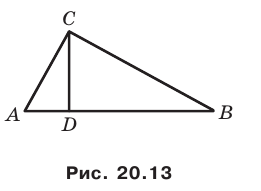
Решение:
Поскольку угол 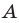 — общий для прямоугольных треугольников
— общий для прямоугольных треугольников 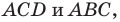 то эти треугольники подобны (рис. 20.13). Пусть коэффициент подобия равен
то эти треугольники подобны (рис. 20.13). Пусть коэффициент подобия равен 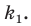 Очевидно, что
Очевидно, что 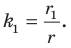 Аналогично
Аналогично 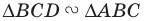 с коэффициентом подобия
с коэффициентом подобия 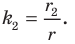
Обозначим площади треугольников 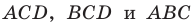 соответственно
соответственно 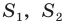 и
и 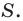 Имеем:
Имеем:
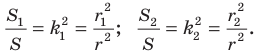
Отсюда 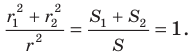 Получаем, что
Получаем, что 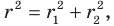
Ответ: 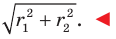
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
На сторонах  остроугольного треугольника
остроугольного треугольника  постройте такие точки
постройте такие точки 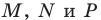 соответственно, чтобы периметр треугольника
соответственно, чтобы периметр треугольника 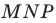 был наименьшим.
был наименьшим.
Решение:
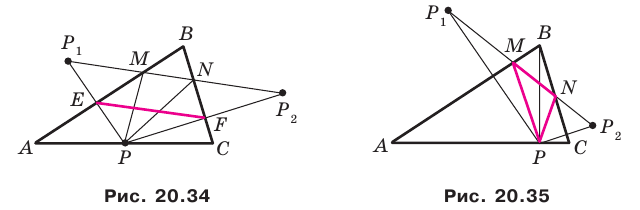
Пусть 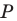 — произвольная точка стороны
— произвольная точка стороны 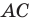 треугольника
треугольника  точки
точки  — ее образы при симметрии относительно прямых
— ее образы при симметрии относительно прямых  соответственно (рис. 20.34). Прямая
соответственно (рис. 20.34). Прямая  пересекает стороны
пересекает стороны 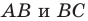 соответственно в точках
соответственно в точках 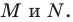 Из решения задачи 2 п. 18 следует, что из периметров всех треугольников, для которых точка
Из решения задачи 2 п. 18 следует, что из периметров всех треугольников, для которых точка 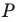 фиксирована, а точки
фиксирована, а точки 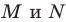 принадлежат сторонам
принадлежат сторонам 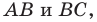 периметр треугольника
периметр треугольника 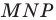 является наименьшим. Этот периметр равен длине отрезка
является наименьшим. Этот периметр равен длине отрезка 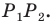
Заметим, что отрезок 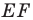 — средняя линия треугольника
— средняя линия треугольника 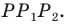
Тогда 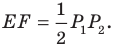
Поскольку 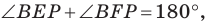 то точки
то точки 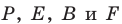 лежат на одной окружности с диаметром
лежат на одной окружности с диаметром  Отсюда
Отсюда  Следовательно, длина отрезка
Следовательно, длина отрезка  будет наименьшей при наименьшей длине отрезка
будет наименьшей при наименьшей длине отрезка  то есть тогда, когда
то есть тогда, когда  — высота треугольника
— высота треугольника 
На рисунке 20.35 отрезок  — высота треугольника
— высота треугольника  Алгоритм построения точек
Алгоритм построения точек  понятен из рисунка.
понятен из рисунка.
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника  больше периметра треугольника
больше периметра треугольника 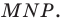 Поэтому искомый треугольник является единственным — это построенный треугольник
Поэтому искомый треугольник является единственным — это построенный треугольник 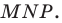
Можно показать (сделайте это самостоятельно), что точки 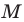 и
и 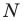 являются основаниями высот, проведенных соответственно из вершин
являются основаниями высот, проведенных соответственно из вершин 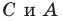 треугольника
треугольника 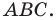
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 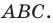 Такой треугольник называют ортоцентрическим.
Такой треугольник называют ортоцентрическим.
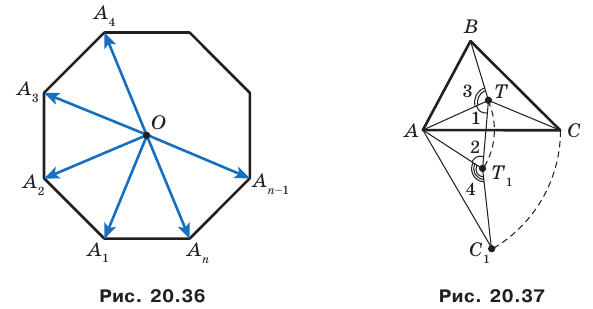
Пример №14
Точка  — центр правильного
— центр правильного  угольника
угольника 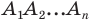 (рис. 20.36). Докажите, что
(рис. 20.36). Докажите, что 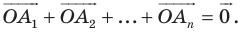
Решение:
Пусть 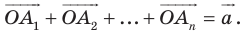 Рассмотрим поворот с центром
Рассмотрим поворот с центром  на угол
на угол 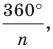 например, против часовой стрелки. При таком преобразовании образом данного
например, против часовой стрелки. При таком преобразовании образом данного 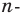 -угольника будет этот же
-угольника будет этот же 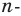 угольник. Следовательно, искомая сумма не изменится. А это возможно лишь тогда, когда
угольник. Следовательно, искомая сумма не изменится. А это возможно лишь тогда, когда 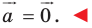
Пример №15
Внутри треугольника 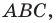 все углы которого меньше
все углы которого меньше  найдите такую точку
найдите такую точку  чтобы сумма
чтобы сумма 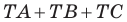 была наименьшей.
была наименьшей.
Решение:
Пусть 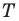 — произвольная точка данного треугольника
— произвольная точка данного треугольника 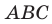 (рис. 20.37). Рассмотрим поворот с центром
(рис. 20.37). Рассмотрим поворот с центром 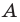 на угол
на угол 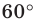 по часовой стрелке. Пусть точки
по часовой стрелке. Пусть точки 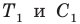 — образы точек
— образы точек 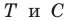 соответственно (рис. 20.37). Поскольку поворот является движением, то
соответственно (рис. 20.37). Поскольку поворот является движением, то 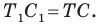 Очевидно, что треугольник
Очевидно, что треугольник 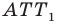 равносторонний. Тогда
равносторонний. Тогда 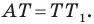
Имеем: 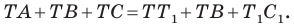
Понятно, что сумма 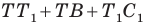 будет наименьшей, если точки
будет наименьшей, если точки 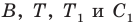 лежат на одной прямой. Поскольку
лежат на одной прямой. Поскольку 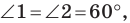 то это условие будет выполнено тогда, когда
то это условие будет выполнено тогда, когда 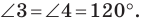
Так как угол 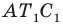 — образ угла
— образ угла 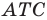 при указанном повороте, то должно выполняться равенство
при указанном повороте, то должно выполняться равенство 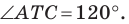
Итак, точки 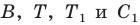 будут принадлежать одной прямой тогда и только тогда, когда
будут принадлежать одной прямой тогда и только тогда, когда 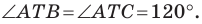 Отсюда
Отсюда 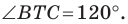
Таким образом, сумма 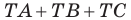 будет наименьшей, если
будет наименьшей, если 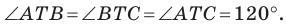
Найти точку 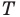 можно, например, построив ГМТ, из которых отрезки
можно, например, построив ГМТ, из которых отрезки 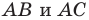 видны под углами
видны под углами 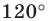 (рис. 20.38).
(рис. 20.38).
Понятно, что если один из углов треугольника 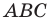 не меньше
не меньше 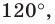 то точка пересечения построенных дуг не будет расположена внутри треугольника. Можно показать, что в треугольнике с углом, не меньшим
то точка пересечения построенных дуг не будет расположена внутри треугольника. Можно показать, что в треугольнике с углом, не меньшим 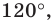 точка
точка 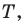 сумма расстояний от которой до вершин треугольника является наименьшей, совпадает с вершиной тупого угла.
сумма расстояний от которой до вершин треугольника является наименьшей, совпадает с вершиной тупого угла. 
Пример №16
Отрезки 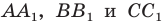 — высоты остроугольного треугольника
— высоты остроугольного треугольника 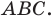 Докажите, что радиус описанной окружности треугольника
Докажите, что радиус описанной окружности треугольника  в два раза больше радиуса описанной окружности треугольника
в два раза больше радиуса описанной окружности треугольника 
Решение:
Пусть прямые 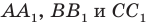 пересекают описанную окружность треугольника
пересекают описанную окружность треугольника  соответственно в точках
соответственно в точках 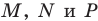 (рис. 20.39). Докажем, что
(рис. 20.39). Докажем, что  где точка
где точка 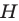 — ортоцентр треугольника
— ортоцентр треугольника 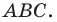
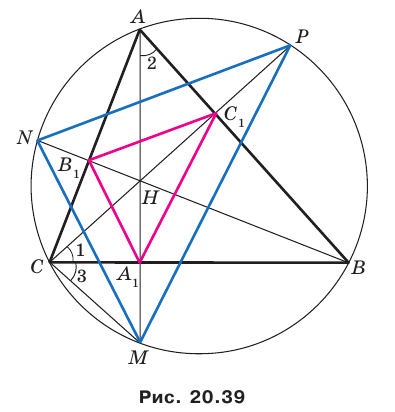
Имеем: 
Углы 2 и 3 равны как вписанные, опирающиеся на дугу  Следовательно,
Следовательно, 
Тогда в треугольнике  отрезок
отрезок 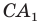 является биссектрисой и высотой, а следовательно, и медианой. Отсюда
является биссектрисой и высотой, а следовательно, и медианой. Отсюда 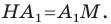
Аналогично можно доказать, что 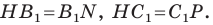
Теперь понятно, что треугольник 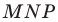 гомотетичен треугольнику
гомотетичен треугольнику 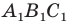 с центром
с центром 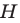 и коэффициентом 2. Тогда радиус описанной окружности треугольника
и коэффициентом 2. Тогда радиус описанной окружности треугольника 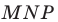 в два раза больше радиуса описанной окружности треугольника
в два раза больше радиуса описанной окружности треугольника 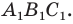 Осталось заметить, что треугольники
Осталось заметить, что треугольники 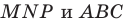 вписаны в одну и ту же окружность.
вписаны в одну и ту же окружность.
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
§ 3. Аналитическое
задание движения.
Задачи.
-
Записать формулы движения, имеющего
единственную инвариантную точку и
переводящего
 ,
,
а окружность

в окружность
 .
.
Решение. Во-первых, определим вид
движения. Смотрим в таблицу §1 и видим,
что единственную инвариантную точку
имеет поворот. Во-вторых, нарисуем
картинку и решим задачу “на картинке”,
как мы делали это в §1, 2. Мы знаем, что
при движении центр окружности переходит
в центр ее образа, то есть
![]()
при этом повороте перейдет в точку
![]() .
.
Итак, поворот задан двумя парами
соответствующих точек:
![]()
и
![]()
![]() .
.
Такую задачу мы уже решали в §1. Центр
поворота О есть пересечение серединных
перпендикуляров к отрезкам
![]()
и
![]() .
.
Напишем уравнения этих прямых. Пусть
![]() –
–
середина отрезка
![]() .
.
Тогда
 .
.
Серединный перпендикуляр
![]()
задается точкой

и перпендикулярным вектором
![]() .
.
Тогда

![]() .
.
Аналогично найдем второй серединный
перпендикуляр
![]() .
.
Имеем
![]()
– середина отрезка
![]()
и
![]() .
.
Тогда серединный перпендикуляр
![]()
задается точкой
![]()
и перпендикулярным вектором
![]() .
.
Тогда
![]() .
.
Найдем координаты точки
![]() :
:
 ,
,
то есть
![]() .
.
Найдем угол поворота
![]() .
.
Используем формулы для нахождения
синуса и косинуса ориентированного
угла. Тогда
 .
.
Нам достаточно данных, чтобы составить
формулы поворота. Посмотрим в таблицу
§1 и подставим в общие формулы поворота
наши данные:
 .
.
-
Найти
уравнение образа прямой

при движении, не имеющем инвариантных
точек, при котором прямая

и
 .
.
Решение. Разделим задачу на три части:
во-первых, определим вид движения,
во-вторых, запишем его формулы, в-третьих,
по формулам найдем образ заданной
прямой.
Для определения вида движения берем
только вторую часть задачи (временно
забудем про первую прямую). Нарисуем
картинку. Мы видим, что
![]() ,
,
![]()
и
![]() .
.
Движениями, не имеющими инвариантных
точек, являются параллельный перенос
и скользящая симметрия. Скользящая
симметрия переводит прямую
![]()
в параллельную ей прямую
![]()
только когда прямая параллельна оси
или перпендикулярна ей. Если бы скользящая
симметрия переводила
![]() ,
,
то
![]() .
.
Что противоречит условию задачи.
Следовательно, это параллельный перенос.
Найдем координаты вектора этого
параллельного переноса.
Рассмотрим точку
![]()
и найдем образ этой точки при параллельном
переносе. Удобно записывать следующим
образом:
![]() ,
,
то есть
![]() .
.
Ищем координаты точек
![]()
и![]() ,
,
затем вектора
![]() .
.
 ;
;
 .
.
Тогда
![]() .
.
Запишем уравнения параллельного
переноса:
 .
.
Приступим к третьей части задачи. Чтобы
найти образ прямой
![]() ,
,
выразим из формул параллельного переноса
![]()
и
![]()
и подставим в уравнение прямой
![]() .
.
Удобная запись:
![]() .
.
Итак,
![]() .
.
-
Найти
прообраз прямой
 при
при
движении, имеющем инвариантную прямую

и инвариантную точку
 .
.
Решение. Во-первых, определим вид
движения. Нарисуем картинку. Мы видим,
что точка
![]()
не принадлежит данной прямой. Инвариантные
точки имеют поворот (центральная
симметрия) и осевая симметрия. Инвариантные
прямые имеют центральная симметрия и
осевая симметрия. Но у центральной
симметрии все инвариантные прямые
проходят через инвариантную точку.
Следовательно, это – осевая симметрия
![]() .
.
Найдем уравнение оси
![]() .
.
Все инвариантные точки лежат на оси
![]() ,
,
следовательно,
![]() .
.
Инвариантные прямые осевой симметрии,
отличные от ее оси, перпендикулярны ей,
то есть
![]()
![]() .
.
Пишем уравнение прямой, проходящей
через данную точку перпендикулярно
данной прямой. Тогда
 .
.
Смотрим в таблицу §1 и записываем формулы
осевой симметрии с осью
![]() .
.
 .
.
Найдем прообраз прямой
![]()
при этой осевой симметрии. Данная прямая
является образом для своего прообраза,
значит, ее переменные должны быть
обозначены буквами со штрихами:
![]() .
.
Чтобы найти ее прообраз, нужно подставить
![]()
и
![]()
из формул осевой симметрии в уравнение
прямой
![]() .
.
Получим уравнение прямой
![]()
– прообраза прямой
![]() .
.
-
Написать
формулы движения, имеющего единственную
инвариантную прямую
 ,
,
при котором
 .
.
Решение. Единственную инвариантную
прямую имеет только скользящая симметрия.
Эта прямая является ее осью, то есть ось
скользящей симметрии
![]() .
.
Нам осталось найти только вектор
параллельного переноса. Нарисуем
картинку. Пусть
![]() .
.
Тогда искомый вектор
![]() .
.
Определив координаты точки
![]() ,
,
мы найдем координаты вектора
![]() .
.
Рассмотрим одно из возможных решений
этой вспомогательной задачи. Оно не
самое короткое, но самое универсальное.
Идея этого решения у нас уже записана:
![]() !
!
Здесь написано, что мы должны сначала
записать формулы осевой симметрии, а
затем найти образ точки
![]() ,
,
пользуясь этими формулами. Реализуем
эту идею. Подставим в общие формулы
осевой симметрии наши данные.
 .
.
Чтобы найти координаты образа точки
![]() ,
,
нужно подставить ее координаты в формулы
![]()
вместо
![]()
и
![]() .
.
Получим
![]() .
.
Тогда
![]() .
.
У нас достаточно данных, чтобы записать
ответ задачи. Смотрим в таблицу и
записываем формулы скользящей симметрии:
 .
.
-
На
прямых

и

найти точки, которые являются соседними
вершинами квадрата с центром в точке
О(0,1).
Идея решение. Забудем сначала про
уравнения и решим задачу “в картинках”
как мы делали это в §1,2. Нам даны две не
параллельные прямые и точка, не
принадлежащая этим прямым. Пусть задача
решена и построен квадрат
![]() ,
,
где
![]()
и
![]()
– центр квадрата. Рассмотрим поворот
вокруг точки О на угол
![]() .
.
Тогда
![]()
и по условию
![]() ,
,
следовательно,
![]() .
.
Из этой записи мы видим, как построить
вершину
![]()
квадрата: надо построить образ прямой
![]()
при повороте вокруг точки
![]()
на угол
![]()
и пересечь его с прямой
![]() .
.
Тогда вершину
![]()
легко найти как прообраз точки
![]()
при рассматриваемом повороте. Точки
![]()
найдем, зная, что
![]()
– середина отрезков
![]()
и
![]() .
.
Осталось только провести занудные
вычисления. Проведите их самостоятельно!
Задачи
к проверочной работе.
-
Найти уравнение образа прямой

при движении с единственной инвариантной
точкой, при котором точки
 ,
,
а
 .
. -
На
плоскости дан квадрат
 .
.
Составить формулы движений 1 рода, не
имеющих инвариантных прямых, при которых
квадрат переходит в себя, если
 ,
,
 .
. -
Записать
уравнения скользящей симметрии, при
которой синусоида

инвариантна. -
Написать
формулы движения, имеющего одну
единственную инвариантную точку,
инвариантные прямые, и переводящего
окружность

в окружность
 .
.
-
Написать
формулы движения, имеющего инвариантную
прямую и инвариантную окружность,
заданные уравнениями

и
 ,
,
соответственно. Найти уравнение
прообраза прямой

при этом движении. -
Написать
формулы движения, единственная
инвариантная прямая которого параллельна
прямой

и
 .
. -
Найти
уравнение прообраза прямой

при движении 1 рода, при котором прямая

инвариантна, а прямая

переходит в прямую
 .
.
-
Найти
образ точки

при движении, не имеющем инвариантных
точек и переводящем
 ,
,
а
 .
. -
Найти
координаты прообраза точки

при движении первого рода, для которого
точка
 инвариантна,
инвариантна,
прямая

переходит в прямую
 .
. -
Написать
формулы движения 1 рода, при котором
прямая
 ,
,
и точка

инвариантна. -
Найти
координаты вершин А и В равнобедренного
прямоугольного треугольника АВС с
прямым углом С, если С(1,0), точка А лежит
на прямой
 ,
,
а точка В принадлежит окружности
 .
. -
Найти
координаты вершин квадрата
 ,
,
если уравнение прямой, содержащей его
диагональ АС
 ,
,
а вершины В и

принадлежат соответственно оси ординат
и окружности
 .
.
13*. Составить формулы движений второго
рода, если известно, что образы точек
А(0,1), В(1,0), С(1,1) принадлежат соответственно
прямым
![]() .
.
14*. Дан треугольник АВС. Определить вид
движения
![]()
и элементы его задающие.
15*. Дан треугольник АВС. Во внешнюю
сторону построены правильные треугольники.
Доказать, что их центры образуют
правильный треугольник.
§4. Определение
вида движения.
Рассмотрим
три типа задач на определение вида
движения:
1.
Движение задано парой ортонормированных
реперов.
Пусть даны два
ортонормированных репера
![]()
и
![]()
(проще говоря, нарисованы два прямоугольных
равнобедренных треугольника
![]()
и
![]() ,
,
у которых углы
![]()
– прямые). Чтобы определить вид движения
нужно:
1) Определим, сохраняет или
меняет движение ориентацию плоскости.
Для этого нарисуем стрелки от вектора
![]()
к вектору
![]()
и от вектора
![]()
к вектору
![]() .
.
Если стрелки обе направлены по часовой
стрелке (или обе – против часовой
стрелки), то движение не меняет ориентации
плоскости, то есть является движением
первого рода. Если одна стрелка направлена
по часовой, а другая – против часовой
стрелки, то движение меняет ориентацию
плоскости, то есть является движением
второго рода.
2) Если движение первого
рода, то это либо параллельный перенос,
либо поворот. Параллельный перенос
характеризуется тем, что векторы
![]()
равны между собой – это вектор
параллельного переноса. Поворот
характеризуется тем, что серединные
перпендикуляры к отрезкам, соединяющим
соответствующие точки движения,
пересекаются в одной точке, то есть если
провести через середины отрезков
![]()
перпендикуляры, то они пересекутся в
одной точке – центре поворота. Рисуем
картинку и смотрим, что получается.
Найдите на картинке угол поворота.
3)
Если движение второго рода, то это либо
осевая симметрия, либо скользящая
симметрия. Рассмотрим середины отрезков
![]() .
.
В обоих случаях они будут лежать на
одной прямой
![]() .
.
Если прямая
![]()
перпендикулярна отрезкам
![]() ,
,
то это осевая симметрия, а если – нет,
то скользящая симметрия. Сообразите,
как найти вектор переноса для этой
скользящей симметрии.
2.
Движение задано формулами.
Напомним, что
формулы
 ,
,
где матрица

– ортогональна, задают движение.
Напомним,
что матрица С называется ортогональной,
если
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Чтобы определить вид движения, нужно
-
Определить род движения (вычислить
определитель
 ).
). -
Найти
количество инвариантных точек (в формулы
движения подставить

и решить систему уравнений
 .
.
Количество ее решений

равно количеству инвариантных точек
движения). -
Посмотреть
в таблицу §1.
3.
Определение вида движения с помощью
разложения в композицию осевых симметрий.
Напомним,
что
![]() ,
,
где
![]() ,
,
![]()
![]() ,
,
где
![]() ,
,
![]()
Например,
надо определить вид движения
![]() (рисуем
(рисуем
картинку). Постараемся разложим каждое
из этих движений в композицию двух
осевых симметрий так, чтобы первая
осевая симметрия от поворота была такая
же, как вторая осевая симметрия от
параллельного переноса, то есть
![]() .
.
Тогда эти прямые должны удовлетворять
требованиям
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из этих требований видим, что прямая
![]()
должна проходить через точку О
перпендикулярно вектору
![]() .
.
Две остальные прямые достраиваются по
прямой
![]()
однозначно (рисуем их на картинке). Итак,
![]() ,
,
где
![]() ,
,
![]()
(так как
![]() ),
),
то есть
![]() =
=![]()
является поворотом вокруг точки
![]()
на угол
![]()
(нарисуйте картинку).
Задачи.
-
Выяснить, определяют ли формулы
 ,
,
записанные в ПДСК, движение? Найти образ
и прообраз точки

при этом движении; образ и прообраз
прямой

при этом же движении.
Решение. Проверим, является ли матрица

ортогональной. Действительно,
 ,
,
 ,
,
![]() .
.
Матрица ортогональна, следовательно,
формулы задают движение. Найдем образ
точки
![]() .
.
Запишем
![]() .
.
Из этой записи хорошо видно, что координаты
точки
![]()
нужно подставить вместо
![]()
и
![]()
в формулы движения. Тогда вычислив
значения
![]() ,
,
получим координаты точки
![]() .
.
Считаем
![]() ,
,
![]()
![]() .
.
Найдем прообраз точки
![]() .
.
Запишем
![]() ,
,
где точка
![]()
– прообраз точки
![]() .
.
Теперь точка М сама является образом и
ее координаты нужно подставлять в
формулы движения вместо
![]() .
.
Получим систему, решив которую найдем
координаты точки
![]() .
.

![]()
![]() .
.
Найдем образ прямой
![]() .
.
Первый способ. Взять две точки на прямой
![]() ,
,
найти их образы и через них провести
прямую. Это будет
![]() .
.
Второй способ. Запишем
![]() .
.
Нужно из формул движения выразить
![]()
и подставить в уравнение прямой
![]() .
.
Получим уравнение с переменными
![]() .
.
Это и будет уравнение прямой
![]() .
.
Запишем его на место, которое мы оставили.
Проведите вычисление тем способом,
который вам понравился больше.
Найдем прообраз прямой
![]() .
.
Первый способ решения такой же как для
нахождения образа. Второй способ. Запишем
![]() .
.
Теперь прямая
![]()
сама является образом, следовательно,
ее переменные надо обозначать
![]() .
.
Переобозначим
![]() .
.
Теперь видно, чтобы найти ее прообраз,
нужно подставить выражения для
![]()
из формул в уравнение прямой
![]() .
.
Ответ запишем на свободное место.
![]() .
.
Раскрывая скобки и приводя подобные,
получим уравнение прообраза прямой
![]() .
.
-
Определить
вид движения и элементы его определяющие
а)
 ;
;
б)
 ;
;
в)
 ;
;
г)
 ;
;
д)
 ;
;
е)
 ;
;
ж)
 .
.
Записать уравнения инвариантных прямых.
Решение.
а) Определим род движения
 1
1
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
![]() ,
,
то есть
![]() .
.
Подставим в формулы движения:

 .
.
Движение 1 рода и имеет одну инвариантную
точку – это поворот вокруг точки
![]()
на угол
![]()
такой, что
![]() .
.
Инвариантных прямых нет.
б)
Определим род движения
 II
II
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
![]() ,
,
то есть
![]() .
.
Подставим в формулы движения:
 .
.
Система противоречива, следовательно,
инвариантных точек нет. Это скользящая
симметрия. Найдем элементы ее определяющие
(см. таблицу). Рассмотрим точку
![]() .
.
Найдем ее образ по формулам
![]() .
.
Найдем координаты середины отрезка
![]() :
:
![]() .
.
Эта точка принадлежит оси скользящей
симметрии, также как и точка
![]()
(мы подставили координаты точки
![]()
в формулы движения). Вектор
![]()
параллельного переноса, входящего в
скользящую симметрию, есть вектор
![]() .
.
Ось скользящей симметрии:

![]() .
.
Единственная инвариантная прямая –
ось скользящей симметрии
![]() .
.
в)
Определим род движения
 II
II
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
![]() ,
,
то есть
![]() .
.
Подставим в формулы движения:
 .
.
Система имеет бесконечно много решений,
то есть движение имеет прямую
![]()
инвариантных точек. Это осевая симметрия
с осью
![]() .
.
Инвариантными прямыми являются ось
осевой симметрии
![]()
и все прямые перпендикулярные оси:
![]() ,
,
С – произвольная константа.
г)
Определим род движения:

род. Найдем инвариантные точки:
![]()
. Система противоречива, следовательно,
инвариантных точек нет. Это параллельный
перенос на вектор
![]()
(свободные члены в формулах движения).
Инвариантные прямые: все прямые,
параллельные вектору
![]() .
.
Их уравнения:
![]() ,
,
где С – произвольная константа.
д)
Определим род движения:

род. Найдем инвариантные точки:
![]() .
.
Система противоречива, следовательно,
инвариантных точек нет. Это скользящая
симметрия. Найдем ее определяющие
элементы. Рассмотрим точку
![]() .
.
Найдем ее образ по формулам
![]() .
.
Найдем координаты середины отрезка
![]() :
:
![]() .
.
Эта точка принадлежит оси скользящей
симметрии, также как и точка
![]()
(мы подставили координаты точки
![]()
в формулы движения). Вектор
![]()
параллельного переноса, входящего в
скользящую симметрию, есть вектор
![]() .
.
Ось скользящей симметрии:

![]() .
.
Единственная инвариантная прямая –
ось скользящей симметрии
![]() .
.
е)
Определим род движения:

род. Найдем инвариантные точки:
![]() .
.
Система имеет бесконечно много решений,
то есть движение имеет бесконечно много
инвариантных точек, лежащих на прямой
![]() .
.
Это осевая симметрия с осью
![]() .
.
Инвариантными прямыми являются ось
осевой симметрии
![]()
и все прямые перпендикулярные оси:
![]() ,
,
С – произвольная константа.
ж)
Определим род движения:

род. Найдем инвариантные точки:
![]() .
.
Движение имеет единственную инвариантную
точку, следовательно, это поворот вокруг
этой точки
![]()
на угол
![]() ,
,
для которого
![]() ,
,
то есть
![]() .
.
Это центральная симметрия. Инвариантными
прямыми являются все прямые, проходящие
через точку
![]() ,
,
то есть прямые

для любых
![]() .
.
Задачи
к проверочной работе.
1.
Доказать, что формулы, записанные в
ПДСК, задают движение, определить его
вид и задающие элементы, записать
уравнения инвариантных прямых, найти
образ и прообраз прямой
![]()
при этом движении, образ и прообраз
окружности
![]() .
.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() .
.
2.
Нарисована пара ортонормированных
реперов. Определить вид движения и
элементы, его задающие.
3.
Определить вид движения
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
§ 5. Преобразование подобия.
Гомотетия.
Определение.
Пусть на плоскости фиксирована точка
![]()
и дано число
![]() .
.
Гомотетией называется такое преобразование
плоскости
![]() ,
,
что
![]() .
.
Точка
![]()
называется центром гомотетии, а число
![]()
называется коэффициентом гомотетии.
Свойства
гомотетии.
1.
![]()
– единственная инвариантная точка
гомотетии.
2.
Гомотетия
![]()
является подобием первого рода с
коэффициентом
![]() .
.
3.
![]() ;
;
![]() .
.
Формулы
гомотетии:

Задачи.
-
Построить
образ и прообраз точки, прямой, окружности
при гомотетии, заданной центром

и парой соответствующих точек
 .
.
Решение. Изобразим на картинке точку
![]()
и пару соответствующих точек
![]() .
.
Посмотрим на определение гомотетии и
убедимся, что все три точки лежат на
одной прямой.
Возьмем точку В на плоскости и построим
ее образ. Во-первых, точка
![]()
должна лежать на одной прямой с точками
![]()
и В. Проводим прямую
![]() .
.
Во-вторых, прямые
![]()
и
![]()
должны быть параллельны по свойству
гомотетии, следовательно,
![]()
принадлежит прямой, проходящей через
точку
![]()
параллельно прямой
![]() .
.
Обозначим эту прямую
![]() .
.
Тогда
![]() .
.
Возьмем точку
![]() на
на
плоскости и построим ее прообраз.
Рассуждения полностью аналогичны
проведенным выше. Во-первых, точка
![]()
(прообраз точки
![]() )
)
лежит на одной прямой с точками
![]()
и
![]() .
.
Во-вторых, прямые
![]()
и
![]()
должны быть параллельны по свойству
гомотетии, следовательно,
![]()
принадлежит прямой, проходящей через
точку
![]()
параллельно прямой
![]() .
.
Обозначим эту прямую
![]() .
.
Тогда
![]() .
.
Чтобы построить образ (прообраз) данной
прямой при гомотетии, достаточно
построить образ (прообраз) одной ее
точки и через эту точку провести прямую
параллельную денной. Подумайте, почему
это так?
Чтобы построить образ (прообраз) данной
окружности, достаточно построить образ
![]()
(прообраз) ее центра
![]()
и какой-нибудь точки
![]() этой
этой
окружности. Получим точку
![]() .
.
Проведем окружность с центром в точке
![]()
радиуса
![]() .
.
Это будет образ данной окружности.
-
На
плоскости даны две прямые

и точка О, им не принадлежащая. Построить
образ и прообраз произвольной прямой

при гомотетии с центром в точке О и
переводящей
 .
.
Решение. Проведем через точку О
какую-нибудь прямую
![]() .
.
Обозначим
![]()
и
![]() .
.
Убедимся, что такое обозначение не
случайно и точка
![]()
действительно является образом точки
![]() .
.
Как обычно запишем
![]()
(действительно, прямая
![]()
инвариантна, так как проходит через
центр гомотетии). Теперь гомотетия у
нас задана центром и парой соответствующих
точек. Такие задачи мы уже умеем решать
(см. задачу 1).
-
Составить
формулы гомотетии, зная две инвариантные
прямые

и

и коэффициент гомотетии
 .
.
Найти образ окружности
 при
при
этой гомотетии.
Решение. Общие формулы для гомотетии у
нас есть. Если мы подставим в них
координаты центра и коэффициент
гомотетии, то получим ответ. Коэффициент
у нас дан:
![]() .
.
Ищем координаты центра гомотетии. По
свойству гомотетии все ее инвариантные
прямые пересекаются в ее центре,
следовательно, определив координаты
точки пересечения прямых
![]()
и
![]()
мы найдем координаты центра
![]()
гомотетии.
 .
.
Получаем
 .
.
Найдем теперь образ
![]()
окружности
![]() .
.
Вычислим координаты образа точки
![]()
– центра окружности
![]() –
–
при данной гомотетии (подставим координаты
точки
![]()
в формулы гомотетии). Получим
![]() .
.
Так как гомотетия является подобием с
коэффициентом
![]() ,
,
то окружность
![]() будет
будет
иметь радиус в 2 раза больше, чем исходная
окружность. Итак, окружность
![]()
имеет центр в точке
![]()
и радиус 4. Запишем ее уравнение:
![]() .
.
-
Подобие
задано парой реперов. Представить его
в виде композиции гомотетии с тем же
коэффициентом и любым центром и движения.
Определить вид движения.
Решение. Пусть даны ортонормированный
репер
![]()
и репер
![]() .
.
Так как они задают подобие, должны
выполняться условия:
![]()
и
![]()
(почему?) Определим коэффициент подобия.
Он равен
![]()
![]() .
.
Возьмем произвольную точку плоскости
![]()
– это будет центр гомотетии. Построим
образ репера
![]()
при гомотетии с центром
![]()
и коэффициентом
![]()
(для построения воспользуемся теоремой
Фалеса). В результате получим репер
![]() .
.
Тогда пара реперов
![]()
и
![]()
задаст движение. Нам нужно определить
вид этого движения. Во-первых, определим
род движения по ориентации реперов
(одинаковая ориентация – первый род,
противоположная – второй род).
Движение 1 рода:
а)
![]() параллельный
параллельный
перенос на вектор
![]() ;
;
б) иначе, поворот. Определим центр и угол
поворота. Пусть прямая
![]()
– серединный перпендикуляр к отрезку
![]() ,
,
прямая
![]()
– серединный перпендикуляр к отрезку
![]() .
.
Тогда точка
![]()
– центр поворота. Угол поворота
![]() .
.
Движение
2 рода:
а) если
прямая
![]() ,
,
проходящая через середины отрезков
![]()
перпендикулярна им, то данное движение
– осевая симметрия с осью
![]() .
.
б) иначе
это скользящая симметрия с осью
![]() ,
,
проходящей через середины отрезков
![]() .
.
Чтобы найти вектор параллельного
переноса этой скользящей симметрии,
отразим точку
![]()
от оси
![]() .
.
Получим точку
![]() .
.
Тогда вектор
![]()
будет искомым вектором.
-
Представить
преобразование подобия

в виде композиции гомотетии с отрицательным
коэффициентом и движения. Определить
вид движения.
Решение. Вспомним общий вид формул
подобия:
 ,
,
где
![]() .
.
Тогда
![]()
– коэффициент подобия.
Мы видим, что формулы из задачи
удовлетворяют этим условиям, следовательно,
задают подобие с коэффициентом
![]() .
.
Пусть данное подобие
![]()
представлено в виде
![]() ,
,
где
![]()
– гомотетия,
![]()
– движение. Запишем их формулы. Начнем
с гомотетии, общие формулы которой у
нас есть.
 .
.
Теперь найдем формулы движения
![]() .
.
Для этого умножим обе части равенства
![]()
справа на
![]() .
.
Получим
![]()
![]() .
.
Из этой записи мы видим, чтобы найти
формулы движения
![]() ,
,
нужно записать формулы гомотетии
![]()
, затем найти композицию
![]()
и
![]() .
.
 .
.
Чтобы найти композицию гомотетии и
подобия, введем другие обозначения для
переменных. Заметим, что гомотетия и
подобие действуют на точку в следующей
последовательности:
![]() .
.
Точка
![]()
является образом для точки
![]()
при гомотетии и исходной точкой для
подобия
![]() .
.
Тогда

и
 .
.
Движение
![]() ,
,
следовательно, в формулах нам надо
“избавиться” от переменных
![]() .
.
Подставим их из уравнений гомотетии в
уравнения подобия:
 .
.
Нам осталось только определить вид
движения по его формулам (см. §3). Это
движение 1 рода, имеющее единственную
инвариантную точку
![]() .
.
Это поворот вокруг точки
![]()
на угол
![]()
такой, что
![]() .
.
Задачи
к проверочной работе.
-
Построить
образ и прообраз точки, прямой, окружности
при гомотетии, заданной центром

и коэффициентом

( ).
). -
Составить
формулы гомотетии, заданной двумя
парами соответствующих точек
 .
. -
Построить
образ данной прямой при гомотетии,
заданной двумя парами прямых

( )
)
и коэффициентом
 .
.
-
Построить
образ данной прямой при гомотетии,
заданной двумя парами прямых

( )
)
и коэффициентом
 .
. -
Составить
формулы гомотетии с коэффициентом
 ,
,
при которой прямая

переходит в прямую
 ,
,
а прямая

– в прямую
 .
. -
Найти
образ окружности

при гомотетии с центром в точке

и переводящей прямую

в прямую
 .
. -
Написать
формулы гомотетии, при которой прямые

и

инвариантны, а образом прямой
 является
является
прямая
 .
. -
Написать
формулы гомотетии с положительным
коэффициентом, при которой окружность

переходит в окружность
 .
. -
Построить
образ и прообраз данной прямой при
гомотетии, переводящей данные прямые

и данные точки
 .
. -
Построить
прообраз данной окружности при гомотетии,
переводящей данные точки
 .
. -
Найти
уравнение прообраза прямой

при гомотетии с центром в точке
 ,
,
которая переводит прямую

в прямую
 .
. -
Построить
прообраз данной прямой при гомотетии,
заданной парой соответствующих точек

и инвариантной прямой
 .
. -
Даны
два параллельных отрезка
 .
.
Построить образ данной окружности при
гомотетии, переводящей один из данных
отрезков в другой. Сколько решений
имеет задача? -
Представить
подобие в виде композиции гомотетии с
тем же коэффициентом и движения.
Определить вид движения, если
1)
 ;
;
2)
 ;
;
3)
 .
. -
Представить
подобия предыдущей задачи в виде
композиции движения и гомотетии с
отрицательным коэффициентом и
произвольным центром. -
Представить
подобие

в виде композиции гомотетии с центром
в точке

и отрицательным коэффициентом и
движения. Определить вид движения. -
Подобие
задано парой реперов (нарисуйте
картинку!). Разложить его в композицию
гомотетии с положительным (отрицательным)
коэффициентом и движения. Определить
вид движения.
18*.
Составить формулы подобия первого рода,
переводящего отрезок с концами в точках
![]()
в отрезок с концами
![]() .
.
Сколько решений имеет задача?
19*.
Доказать, что квадрат подобия второго
рода есть гомотетия.
20*.
Доказать, что любые две равносторонние
гиперболы подобны.
21*.
Доказать, что две любые параболы подобны.
Чему равен коэффициент подобия?
22*.
Подобие задано парой реперов (нарисуйте
картинку!). Разложить его в композицию
гомотетии с положительным (отрицательным)
коэффициентом и движения с общей
инвариантной точкой. Определить вид
движения.
§ 6. Аффинные преобразования.
Определение.
Преобразование плоскости называется
аффинным, если оно любые три точки,
лежащие на одной прямой переводит в три
точки также лежащие на одной прямой и
при этом сохраняет простое отношение
трех точек.
Определение.
Нетождественное аффинное преобразование
называется перспективно-аффинным
(или родством), если оно имеет по
крайней мере две инвариантные точки А
и В.
При
этом вся прямая (АВ) состоит из инвариантных
точек. Она называется осью родства.
Свойства
родства.
-
Прямые,
соединяющие соответствующие точки
родства параллельны или совпадают. -
Если
прямая пересекает ось родства в некоторой
точке, то ее образ также пересекает ось
родства в этой же точке. Если прямая не
пересекает ось родства, то ее образ
также не пересекает ось родства.
Примеры
перспективно-аффинных преобразований.
|
Сдвиг
|
Косое сжатие
|
Косое
сжатие называется сжатием, если
![]() .
.
Задачи.
-
Сдвиг
(косое сжатие) задано осью и парой
соответствующих точек. Построить образ
и прообраз данной точки при этом
преобразовании.
Решение. Рисуем картинку для сдвига.
Нам даны ось
![]()
и пара соответствующих точек
![]() .
.
Так как мы рассматриваем сдвиг,
![]() .
.
Возьмем произвольную точку В плоскости
и построим ее образ
![]() .
.
Воспользуемся свойствами родства.
Во-первых,
![]()
по 1 свойству, то есть
![]()
принадлежит прямой
![]() ,
,
проходящей через точку В параллельно
прямой
![]() .
.
Во-вторых, если
![]() ,
,
то
![]()
по 2 свойству, то есть
![]() .
.
Тогда
![]() .
.
Прообраз произвольной точки
![]()
плоскости строится аналогично. Возьмем
произвольную точку
![]()
плоскости и построим ее прообраз
![]() .
.
Воспользуемся свойствами родства.
Во-первых,
![]()
по 1 свойству, то есть
![]()
принадлежит прямой
![]() ,
,
проходящей через точку
![]()
параллельно прямой
![]() .
.
Во-вторых, если
![]() ,
,
то
![]()
по 2 свойству, то есть
![]() .
.
Тогда
![]() .
.
В случае косого сжатия рассуждения
точно такие же.
-
Сдвиг
(косое сжатие) задано осью и парой
соответствующих точек. Построить образ
и прообраз данного квадрата при этом
преобразовании. Рассмотреть различное
расположение квадрата относительно
оси родства.
Решение. Достаточно построить образы
вершин квадрата и соединить их отрезками
(в результате этих действий мы получим
параллелограмм). Подумайте, как построить
образ квадрата проще.
-
Построить
образ точки при косом сжатии, заданном
инвариантной точкой С , парой
соответствующих параллельных
(пересекающихся) прямых

и направлением сжатия – прямой
 .
.
Решение. Рисуем картинку. Мы знаем, что
все инвариантные точки лежат на оси
родства
![]() ,
,
то есть
![]() .
.
Непараллельные соответствующие прямые
пересекаются на оси родства, то есть
![]() .
.
У нас появилась ось родства
![]() .
.
Нам осталось получить две соответствующие
точки
![]() ,
,
которые лежат на прямых
![]()
и
![]()
соответственно. Мы знаем, что все прямые,
соединяющие соответствующие точки
родства параллельны между собой. Это и
есть направление сжатия. Оно задается
прямой
![]() ,
,
то есть
![]() .
.
Кроме того,
![]() .
.
Следовательно,
![]() .
.
Теперь косое сжатие задано осью и парой
соответствующих точек. Дальше решение
такое же как в задаче 1.
-
Родство
задано двумя парами пересекающихся
соответствующих прямых

и
 .
.
Построить образ (прообраз) данной точки
при данном родстве.
Решение. Если мы построим ось родства
и пару соответствующих точек, то сможем
решить задачу по аналогии с задачей 1.
Мы знаем, что соответствующие прямые
пересекаются на оси родства, следовательно,
ось родства
![]() .
.
Найдем образ точки
![]() .
.
Тогда родство задано осью
![]()
и парой соответствующих точек
![]() .
.
Задачи
к проверочной работе.
-
Построить
образ (прообраз) данной трапеции при
косом сжатии, заданном осью и парой
соответствующих точек. -
Построить
образ данной прямой при сдвиге, заданном
осью и парой пересекающихся соответствующих
прямых. -
Сдвиг
задан парой соответствующих прямых

и инвариантной прямой
 .
.
Построить образ данного треугольника
(квадрата, параллелограмма) при данном
сдвиге. Сколько решений имеет задача? -
Построить
образ (прообраз) данной трапеции при
сдвиге, заданном парой соответствующих
точек

и инвариантной точкой В.
5.
Доказать, что любое аффинное преобразование
можно представить в виде композиции
родства и подобия.
6*.
Показать, что перспективно-аффинное
преобразование, вообще говоря, не
сохраняет величину угла. Но при этом
верно следующее утверждение: при всяком
перспективно-аффинном преобразовании
через каждую точку плоскости проходят
две взаимно перпендикулярные прямые,
образы которых при этом преобразовании
также взаимно перпендикулярны.
7*.
Доказать, что любое аффинное преобразование
можно представить в виде композиции
двух сжатий к взаимно перпендикулярным
прямым и движения.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
rotates points in the xy plane counterclockwise through an angle θ about the origin of a two-dimensional Cartesian coordinate system. To perform the rotation on a plane point with standard coordinates v = (x, y), it should be written as a column vector, and multiplied by the matrix R:
If x and y are the endpoint coordinates of a vector, where x is cosine and y is sine, then the above equations become the trigonometric summation angle formulae. Indeed, a rotation matrix can be seen as the trigonometric summation angle formulae in matrix form. One way to understand this is say we have a vector at an angle 30° from the x axis, and we wish to rotate that angle by a further 45°. We simply need to compute the vector endpoint coordinates at 75°.
The examples in this article apply to active rotations of vectors counterclockwise in a right-handed coordinate system (y counterclockwise from x) by pre-multiplication (R on the left). If any one of these is changed (such as rotating axes instead of vectors, a passive transformation), then the inverse of the example matrix should be used, which coincides with its transpose.
Since matrix multiplication has no effect on the zero vector (the coordinates of the origin), rotation matrices describe rotations about the origin. Rotation matrices provide an algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In some literature, the term rotation is generalized to include improper rotations, characterized by orthogonal matrices with a determinant of −1 (instead of +1). These combine proper rotations with reflections (which invert orientation). In other cases, where reflections are not being considered, the label proper may be dropped. The latter convention is followed in this article.
Rotation matrices are square matrices, with real entries. More specifically, they can be characterized as orthogonal matrices with determinant 1; that is, a square matrix R is a rotation matrix if and only if RT = R−1 and det R = 1. The set of all orthogonal matrices of size n with determinant +1 is a representation of a group known as the special orthogonal group SO(n), one example of which is the rotation group SO(3). The set of all orthogonal matrices of size n with determinant +1 or −1 is a representation of the (general) orthogonal group O(n).
In two dimensions[edit]

A counterclockwise rotation of a vector through angle θ. The vector is initially aligned with the x-axis.
In two dimensions, the standard rotation matrix has the following form:
This rotates column vectors by means of the following matrix multiplication,
Thus, the new coordinates (x′, y′) of a point (x, y) after rotation are
Examples[edit]
For example, when the vector
is rotated by an angle θ, its new coordinates are
and when the vector
is rotated by an angle θ, its new coordinates are
Direction[edit]
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. −90°). Thus the clockwise rotation matrix is found as
The two-dimensional case is the only non-trivial (i.e. not one-dimensional) case where the rotation matrices group is commutative, so that it does not matter in which order multiple rotations are performed. An alternative convention uses rotating axes,[1] and the above matrices also represent a rotation of the axes clockwise through an angle θ.
Non-standard orientation of the coordinate system[edit]

A rotation through angle θ with non-standard axes.
If a standard right-handed Cartesian coordinate system is used, with the x-axis to the right and the y-axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the y-axis down the screen or page.[2]
See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.
Common rotations[edit]
Particularly useful are the matrices
for 90°, 180°, and 270° counter-clockwise rotations.
A 180° rotation (middle) followed by a positive 90° rotation (left) is equivalent to a single negative 90° (positive 270°) rotation (right). Each of these figures depicts the result of a rotation relative to an upright starting position (bottom left) and includes the matrix representation of the permutation applied by the rotation (center right), as well as other related diagrams. See “Permutation notation” on Wikiversity for details.
Relationship with complex plane[edit]
Since
the matrices of the shape
form a ring isomorphic to the field of the complex numbers 
If one identifies 



As every rotation matrix can be written
the above correspondence associates such a matrix with the complex number
(this last equality is Euler’s formula).
In three dimensions[edit]
A positive 90° rotation around the y-axis (left) after one around the z-axis (middle) gives a 120° rotation around the main diagonal (right).
In the top left corner are the rotation matrices, in the bottom right corner are the corresponding permutations of the cube with the origin in its center.
Basic rotations[edit]
A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs. Notice that the right-hand rule only works when multiplying 
For column vectors, each of these basic vector rotations appears counterclockwise when the axis about which they occur points toward the observer, the coordinate system is right-handed, and the angle θ is positive. Rz, for instance, would rotate toward the y-axis a vector aligned with the x-axis, as can easily be checked by operating with Rz on the vector (1,0,0):
This is similar to the rotation produced by the above-mentioned two-dimensional rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.
General rotations[edit]
Other rotation matrices can be obtained from these three using matrix multiplication. For example, the product
represents a rotation whose yaw, pitch, and roll angles are α, β and γ, respectively. More formally, it is an intrinsic rotation whose Tait–Bryan angles are α, β, γ, about axes z, y, x, respectively.
Similarly, the product
represents an extrinsic rotation whose (improper) Euler angles are α, β, γ, about axes x, y, z.
These matrices produce the desired effect only if they are used to premultiply column vectors, and (since in general matrix multiplication is not commutative) only if they are applied in the specified order (see Ambiguities for more details). The order of rotation operations is from right to left; the matrix adjacent to the column vector is the first to be applied, and then the one to the left.[3]
Conversion from rotation matrix to axis–angle[edit]
Every rotation in three dimensions is defined by its axis (a vector along this axis is unchanged by the rotation), and its angle — the amount of rotation about that axis (Euler rotation theorem).
There are several methods to compute the axis and angle from a rotation matrix (see also axis–angle representation). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.
Determining the axis[edit]

A rotation R around axis u can be decomposed using 3 endomorphisms P, (I − P), and Q (click to enlarge).
Given a 3 × 3 rotation matrix R, a vector u parallel to the rotation axis must satisfy
since the rotation of u around the rotation axis must result in u. The equation above may be solved for u which is unique up to a scalar factor unless R = I.
Further, the equation may be rewritten
which shows that u lies in the null space of R − I.
Viewed in another way, u is an eigenvector of R corresponding to the eigenvalue λ = 1. Every rotation matrix must have this eigenvalue, the other two eigenvalues being complex conjugates of each other. It follows that a general rotation matrix in three dimensions has, up to a multiplicative constant, only one real eigenvector.
One way to determine the rotation axis is by showing that:
Since (R − RT) is a skew-symmetric matrix, we can choose u such that
The matrix–vector product becomes a cross product of a vector with itself, ensuring that the result is zero:
Therefore, if
then
The magnitude of u computed this way is ‖u‖ = 2 sin θ, where θ is the angle of rotation.
This does not work if R is symmetric. Above, if R − RT is zero, then all subsequent steps are invalid. In this case, it is necessary to diagonalize R and find the eigenvector corresponding to an eigenvalue of 1.
Determining the angle[edit]
To find the angle of a rotation, once the axis of the rotation is known, select a vector v perpendicular to the axis. Then the angle of the rotation is the angle between v and Rv.
A more direct method, however, is to simply calculate the trace: the sum of the diagonal elements of the rotation matrix. Care should be taken to select the right sign for the angle θ to match the chosen axis:
from which follows that the angle’s absolute value is
Rotation matrix from axis and angle[edit]
The matrix of a proper rotation R by angle θ around the axis u = (ux, uy, uz), a unit vector with u2
x + u2
y + u2
z = 1, is given by:[4]
A derivation of this matrix from first principles can be found in section 9.2 here.[5] The basic idea to derive this matrix is dividing the problem into few known simple steps.
- First rotate the given axis and the point such that the axis lies in one of the coordinate planes (xy, yz or zx)
- Then rotate the given axis and the point such that the axis is aligned with one of the two coordinate axes for that particular coordinate plane (x, y or z)
- Use one of the fundamental rotation matrices to rotate the point depending on the coordinate axis with which the rotation axis is aligned.
- Reverse rotate the axis-point pair such that it attains the final configuration as that was in step 2 (Undoing step 2)
- Reverse rotate the axis-point pair which was done in step 1 (undoing step 1)
This can be written more concisely as
where [u]× is the cross product matrix of u; the expression u ⊗ u is the outer product, and I is the identity matrix. Alternatively, the matrix entries are:
where εjkl is the Levi-Civita symbol with ε123 = 1. This is a matrix form of Rodrigues’ rotation formula, (or the equivalent, differently parametrized Euler–Rodrigues formula) with[nb 2]
In 
If the 3D space is right-handed and θ > 0, this rotation will be counterclockwise when u points towards the observer (Right-hand rule). Explicitly, with 
Note the striking merely apparent differences to the equivalent Lie-algebraic formulation below.
Properties[edit]
For any n-dimensional rotation matrix R acting on 
(The rotation is an orthogonal matrix)
It follows that:
A rotation is termed proper if det R = 1, and improper (or a roto-reflection) if det R = –1. For even dimensions n = 2k, the n eigenvalues λ of a proper rotation occur as pairs of complex conjugates which are roots of unity: λ = e±iθj for j = 1, …, k, which is real only for λ = ±1. Therefore, there may be no vectors fixed by the rotation (λ = 1), and thus no axis of rotation. Any fixed eigenvectors occur in pairs, and the axis of rotation is an even-dimensional subspace.
For odd dimensions n = 2k + 1, a proper rotation R will have an odd number of eigenvalues, with at least one λ = 1 and the axis of rotation will be an odd dimensional subspace. Proof:
Here I is the identity matrix, and we use det(RT) = det(R) = 1, as well as (−1)n = −1 since n is odd. Therefore, det(R – I) = 0, meaning there is a null vector v with (R – I)v = 0, that is Rv = v, a fixed eigenvector. There may also be pairs of fixed eigenvectors in the even-dimensional subspace orthogonal to v, so the total dimension of fixed eigenvectors is odd.
For example, in 2-space n = 2, a rotation by angle θ has eigenvalues λ = eiθ and λ = e−iθ, so there is no axis of rotation except when θ = 0, the case of the null rotation. In 3-space n = 3, the axis of a non-null proper rotation is always a unique line, and a rotation around this axis by angle θ has eigenvalues λ = 1, eiθ, e−iθ. In 4-space n = 4, the four eigenvalues are of the form e±iθ, e±iφ. The null rotation has θ = φ = 0. The case of θ = 0, φ ≠ 0 is called a simple rotation, with two unit eigenvalues forming an axis plane, and a two-dimensional rotation orthogonal to the axis plane. Otherwise, there is no axis plane. The case of θ = φ is called an isoclinic rotation, having eigenvalues e±iθ repeated twice, so every vector is rotated through an angle θ.
The trace of a rotation matrix is equal to the sum of its eigenvalues. For n = 2, a rotation by angle θ has trace 2 cos θ. For n = 3, a rotation around any axis by angle θ has trace 1 + 2 cos θ. For n = 4, and the trace is 2(cos θ + cos φ), which becomes 4 cos θ for an isoclinic rotation.
Examples[edit]
|
|
Geometry[edit]
In Euclidean geometry, a rotation is an example of an isometry, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave “handedness” unchanged. In contrast, a translation moves every point, a reflection exchanges left- and right-handed ordering, a glide reflection does both, and an improper rotation combines a change in handedness with a normal rotation.
If a fixed point is taken as the origin of a Cartesian coordinate system, then every point can be given coordinates as a displacement from the origin. Thus one may work with the vector space of displacements instead of the points themselves. Now suppose (p1, …, pn) are the coordinates of the vector p from the origin O to point P. Choose an orthonormal basis for our coordinates; then the squared distance to P, by Pythagoras, is
which can be computed using the matrix multiplication
A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties it can be shown that a rotation is a linear transformation of the vectors, and thus can be written in matrix form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, is stated as
or
Because this equation holds for all vectors, p, one concludes that every rotation matrix, Q, satisfies the orthogonality condition,
Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,
Equally important, it can be shown that any matrix satisfying these two conditions acts as a rotation.
Multiplication[edit]
The inverse of a rotation matrix is its transpose, which is also a rotation matrix:
The product of two rotation matrices is a rotation matrix:
For n > 2, multiplication of n × n rotation matrices is generally not commutative.
Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n × n rotation matrices form a group, which for n > 2 is non-abelian, called a special orthogonal group, and denoted by SO(n), SO(n,R), SOn, or SOn(R), the group of n × n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.
Ambiguities[edit]

Alias and alibi rotations
The interpretation of a rotation matrix can be subject to many ambiguities.
In most cases the effect of the ambiguity is equivalent to the effect of a rotation matrix inversion (for these orthogonal matrices equivalently matrix transpose).
- Alias or alibi (passive or active) transformation
- The coordinates of a point P may change due to either a rotation of the coordinate system CS (alias), or a rotation of the point P (alibi). In the latter case, the rotation of P also produces a rotation of the vector v representing P. In other words, either P and v are fixed while CS rotates (alias), or CS is fixed while P and v rotate (alibi). Any given rotation can be legitimately described both ways, as vectors and coordinate systems actually rotate with respect to each other, about the same axis but in opposite directions. Throughout this article, we chose the alibi approach to describe rotations. For instance,
- represents a counterclockwise rotation of a vector v by an angle θ, or a rotation of CS by the same angle but in the opposite direction (i.e. clockwise). Alibi and alias transformations are also known as active and passive transformations, respectively.
- Pre-multiplication or post-multiplication
- The same point P can be represented either by a column vector v or a row vector w. Rotation matrices can either pre-multiply column vectors (Rv), or post-multiply row vectors (wR). However, Rv produces a rotation in the opposite direction with respect to wR. Throughout this article, rotations produced on column vectors are described by means of a pre-multiplication. To obtain exactly the same rotation (i.e. the same final coordinates of point P), the equivalent row vector must be post-multiplied by the transpose of R (i.e. wRT).
- Right- or left-handed coordinates
- The matrix and the vector can be represented with respect to a right-handed or left-handed coordinate system. Throughout the article, we assumed a right-handed orientation, unless otherwise specified.
- Vectors or forms
- The vector space has a dual space of linear forms, and the matrix can act on either vectors or forms.
Decompositions[edit]
Independent planes[edit]
Consider the 3 × 3 rotation matrix
If Q acts in a certain direction, v, purely as a scaling by a factor λ, then we have
so that
Thus λ is a root of the characteristic polynomial for Q,
Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the axis of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is 2 cos θ (the negated linear term). This factorization is of interest for 3 × 3 rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the “complex conjugates” are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any n × n rotation matrix. If the dimension, n, is odd, there will be a “dangling” eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree n and thus n eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most n/2 of them.
The sum of the entries on the main diagonal of a matrix is called the trace; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for 2 × 2 and 3 × 3 rotation matrices that the trace reveals the angle of rotation, θ, in the two-dimensional space (or subspace). For a 2 × 2 matrix the trace is 2 cos θ, and for a 3 × 3 matrix it is 1 + 2 cos θ. In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any 3 × 3 rotation matrix a rotation axis and an angle, and these completely determine the rotation.
Sequential angles[edit]
The constraints on a 2 × 2 rotation matrix imply that it must have the form
with a2 + b2 = 1. Therefore, we may set a = cos θ and b = sin θ, for some angle θ. To solve for θ it is not enough to look at a alone or b alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent function.
Now consider the first column of a 3 × 3 rotation matrix,
Although a2 + b2 will probably not equal 1, but some value r2 < 1, we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to
zeroing b. This acts on the subspace spanned by the x– and y-axes. We can then repeat the process for the xz-subspace to zero c. Acting on the full matrix, these two rotations produce the schematic form
Shifting attention to the second column, a Givens rotation of the yz-subspace can now zero the z value. This brings the full matrix to the form
which is an identity matrix. Thus we have decomposed Q as
An n × n rotation matrix will have (n − 1) + (n − 2) + ⋯ + 2 + 1, or
entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of n × n rotation matrices, each of which has n2 entries, can be parameterized by 1/2n(n − 1) angles.
| xzxw | xzyw | xyxw | xyzw |
| yxyw | yxzw | yzyw | yzxw |
| zyzw | zyxw | zxzw | zxyw |
| xzxb | yzxb | xyxb | zyxb |
| yxyb | zxyb | yzyb | xzyb |
| zyzb | xyzb | zxzb | yxzb |
In three dimensions this restates in matrix form an observation made by Euler, so mathematicians call the ordered sequence of three angles Euler angles. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Cardano, Tait–Bryan, roll-pitch-yaw) to different sequences.
One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors, despite a similarity in appearance as a triplet of numbers.
Nested dimensions[edit]
A 3 × 3 rotation matrix such as
suggests a 2 × 2 rotation matrix,
is embedded in the upper left corner:
This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n + 1)-dimensional rotations, as subgroups. Each embedding leaves one direction fixed, which in the case of 3 × 3 matrices is the rotation axis. For example, we have
fixing the x-axis, the y-axis, and the z-axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then
where cθ = cos θ, sθ = sin θ, is a rotation by angle θ leaving axis u fixed.
A direction in (n + 1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sn. Thus it is natural to describe the rotation group SO(n + 1) as combining SO(n) and Sn. A suitable formalism is the fiber bundle,
where for every direction in the base space, Sn, the fiber over it in the total space, SO(n + 1), is a copy of the fiber space, SO(n), namely the rotations that keep that direction fixed.
Thus we can build an n × n rotation matrix by starting with a 2 × 2 matrix, aiming its fixed axis on S2 (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S3, and so on up through Sn−1. A point on Sn can be selected using n numbers, so we again have 1/2n(n − 1) numbers to describe any n × n rotation matrix.
In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n − 1 Givens rotations brings the first column (and row) to (1, 0, …, 0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1, 0, …, 0) fixed.
Skew parameters via Cayley’s formula[edit]
When an n × n rotation matrix Q, does not include a −1 eigenvalue, thus none of the planar rotations which it comprises are 180° rotations, then Q + I is an invertible matrix. Most rotation matrices fit this description, and for them it can be shown that (Q − I)(Q + I)−1 is a skew-symmetric matrix, A. Thus AT = −A; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, A contains 1/2n(n − 1) independent numbers.
Conveniently, I − A is invertible whenever A is skew-symmetric; thus we can recover the original matrix using the Cayley transform,
which maps any skew-symmetric matrix A to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.
In three dimensions, for example, we have (Cayley 1846)
If we condense the skew entries into a vector, (x,y,z), then we produce a 90° rotation around the x-axis for (1, 0, 0), around the y-axis for (0, 1, 0), and around the z-axis for (0, 0, 1). The 180° rotations are just out of reach; for, in the limit as x → ∞, (x, 0, 0) does approach a 180° rotation around the x axis, and similarly for other directions.
Decomposition into shears[edit]
For the 2D case, a rotation matrix can be decomposed into three shear matrices (Paeth 1986):
This is useful, for instance, in computer graphics, since shears can be implemented with fewer multiplication instructions than rotating a bitmap directly. On modern computers, this may not matter, but it can be relevant for very old or low-end microprocessors.
A rotation can also be written as two shears and scaling (Daubechies & Sweldens 1998):
Group theory[edit]
Below follow some basic facts about the role of the collection of all rotation matrices of a fixed dimension (here mostly 3) in mathematics and particularly in physics where rotational symmetry is a requirement of every truly fundamental law (due to the assumption of isotropy of space), and where the same symmetry, when present, is a simplifying property of many problems of less fundamental nature. Examples abound in classical mechanics and quantum mechanics. Knowledge of the part of the solutions pertaining to this symmetry applies (with qualifications) to all such problems and it can be factored out of a specific problem at hand, thus reducing its complexity. A prime example – in mathematics and physics – would be the theory of spherical harmonics. Their role in the group theory of the rotation groups is that of being a representation space for the entire set of finite-dimensional irreducible representations of the rotation group SO(3). For this topic, see Rotation group SO(3) § Spherical harmonics.
The main articles listed in each subsection are referred to for more detail.
Lie group[edit]
The n × n rotation matrices for each n form a group, the special orthogonal group, SO(n). This algebraic structure is coupled with a topological structure inherited from 
Lie algebra[edit]
The Lie algebra so(n) of SO(n) is given by
and is the space of skew-symmetric matrices of dimension n, see classical group, where o(n) is the Lie algebra of O(n), the orthogonal group. For reference, the most common basis for so(3) is
Exponential map[edit]
Connecting the Lie algebra to the Lie group is the exponential map, which is defined using the standard matrix exponential series for eA[7] For any skew-symmetric matrix A, exp(A) is always a rotation matrix.[nb 3]
An important practical example is the 3 × 3 case. In rotation group SO(3), it is shown that one can identify every A ∈ so(3) with an Euler vector ω = θu, where u = (x, y, z) is a unit magnitude vector.
By the properties of the identification 
According to Rodrigues’ rotation formula on matrix form, one obtains,
where
This is the matrix for a rotation around axis u by the angle θ. For full detail, see exponential map SO(3).
Baker–Campbell–Hausdorff formula[edit]
The BCH formula provides an explicit expression for Z = log(eXeY) in terms of a series expansion of nested commutators of X and Y.[8] This general expansion unfolds as[nb 4]
In the 3 × 3 case, the general infinite expansion has a compact form,[9]
for suitable trigonometric function coefficients, detailed in the Baker–Campbell–Hausdorff formula for SO(3).
As a group identity, the above holds for all faithful representations, including the doublet (spinor representation), which is simpler. The same explicit formula thus follows straightforwardly through Pauli matrices; see the 2 × 2 derivation for SU(2). For the general n × n case, one might use Ref.[10]
Spin group[edit]
The Lie group of n × n rotation matrices, SO(n), is not simply connected, so Lie theory tells us it is a homomorphic image of a universal covering group. Often the covering group, which in this case is called the spin group denoted by Spin(n), is simpler and more natural to work with.[11]
In the case of planar rotations, SO(2) is topologically a circle, S1. Its universal covering group, Spin(2), is isomorphic to the real line, R, under addition. Whenever angles of arbitrary magnitude are used one is taking advantage of the convenience of the universal cover. Every 2 × 2 rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2π. Correspondingly, the fundamental group of SO(2) is isomorphic to the integers, Z.
In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space, RP3. Its universal covering group, Spin(3), is isomorphic to the 3-sphere, S3. Every 3 × 3 rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group of SO(3) is isomorphic to the two-element group, Z2.
We can also describe Spin(3) as isomorphic to quaternions of unit norm under multiplication, or to certain 4 × 4 real matrices, or to 2 × 2 complex special unitary matrices, namely SU(2). The covering maps for the first and the last case are given by
and
For a detailed account of the SU(2)-covering and the quaternionic covering, see spin group SO(3).
Many features of these cases are the same for higher dimensions. The coverings are all two-to-one, with SO(n), n > 2, having fundamental group Z2. The natural setting for these groups is within a Clifford algebra. One type of action of the rotations is produced by a kind of “sandwich”, denoted by qvq∗. More importantly in applications to physics, the corresponding spin representation of the Lie algebra sits inside the Clifford algebra. It can be exponentiated in the usual way to give rise to a 2-valued representation, also known as projective representation of the rotation group. This is the case with SO(3) and SU(2), where the 2-valued representation can be viewed as an “inverse” of the covering map. By properties of covering maps, the inverse can be chosen ono-to-one as a local section, but not globally.
Infinitesimal rotations[edit]
The matrices in the Lie algebra are not themselves rotations; the skew-symmetric matrices are derivatives, proportional differences of rotations. An actual “differential rotation”, or infinitesimal rotation matrix has the form
where dθ is vanishingly small and A ∈ so(n), for instance with A = Lx,
The computation rules are as usual except that infinitesimals of second order are routinely dropped. With these rules, these matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals.[12] It turns out that the order in which infinitesimal rotations are applied is irrelevant. To see this exemplified, consult infinitesimal rotations SO(3).
Conversions[edit]
We have seen the existence of several decompositions that apply in any dimension, namely independent planes, sequential angles, and nested dimensions. In all these cases we can either decompose a matrix or construct one. We have also given special attention to 3 × 3 rotation matrices, and these warrant further attention, in both directions (Stuelpnagel 1964).
Quaternion[edit]
Given the unit quaternion q = w + xi + yj + zk, the equivalent pre-multiplied (to be used with column vectors) 3 × 3 rotation matrix is [13]
Now every quaternion component appears multiplied by two in a term of degree two, and if all such terms are zero what is left is an identity matrix. This leads to an efficient, robust conversion from any quaternion – whether unit or non-unit – to a 3 × 3 rotation matrix. Given:
we can calculate
Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates for 3 × 3 rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its w component is 1. For a 180° rotation around any axis, w will be zero, which explains the Cayley limitation.
The sum of the entries along the main diagonal (the trace), plus one, equals 4 − 4(x2 + y2 + z2), which is 4w2. Thus we can write the trace itself as 2w2 + 2w2 − 1; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: 2x2 + 2w2 − 1, 2y2 + 2w2 − 1, and 2z2 + 2w2 − 1. So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries:
Alternatively, use a single square root and division
This is numerically stable so long as the trace, t, is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose Qxx is the largest diagonal entry, so x will have the largest magnitude (the other cases are derived by cyclic permutation); then the following is safe.
If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric 4 × 4 matrix,
and find the eigenvector, (x, y, z, w), of its largest magnitude eigenvalue. (If Q is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix (Bar-Itzhack 2000) (Note: formulation of the cited article is post-multiplied, works with row vectors).
Polar decomposition[edit]
If the n × n matrix M is nonsingular, its columns are linearly independent vectors; thus the Gram–Schmidt process can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra, we convert M to an orthogonal matrix, Q, using QR decomposition. However, we often prefer a Q closest to M, which this method does not accomplish. For that, the tool we want is the polar decomposition (Fan & Hoffman 1955; Higham 1989).
To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, ‖Q − M‖F, squared, which is the sum of the squares of the element differences. Writing this in terms of the trace, Tr, our goal is,
- Find Q minimizing Tr( (Q − M)T(Q − M) ), subject to QTQ = I.
Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a 3 × 3 matrix, the orthogonality constraint implies six scalar equalities that the entries of Q must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers, assembled as a symmetric matrix, Y. Thus our method is:
- Differentiate Tr( (Q − M)T(Q − M) + (QTQ − I)Y ) with respect to (the entries of) Q, and equate to zero.
Consider a 2 × 2 example. Including constraints, we seek to minimize
Taking the derivative with respect to Qxx, Qxy, Qyx, Qyy in turn, we assemble a matrix.
In general, we obtain the equation
so that
where Q is orthogonal and S is symmetric. To ensure a minimum, the Y matrix (and hence S) must be positive definite. Linear algebra calls QS the polar decomposition of M, with S the positive square root of S2 = MTM.
When M is non-singular, the Q and S factors of the polar decomposition are uniquely determined. However, the determinant of S is positive because S is positive definite, so Q inherits the sign of the determinant of M. That is, Q is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an M with negative determinant has no uniquely defined closest rotation matrix.
Axis and angle[edit]
To efficiently construct a rotation matrix Q from an angle θ and a unit axis u, we can take advantage of symmetry and skew-symmetry within the entries. If x, y, and z are the components of the unit vector representing the axis, and
then
Determining an axis and angle, like determining a quaternion, is only possible up to the sign; that is, (u, θ) and (−u, −θ) correspond to the same rotation matrix, just like q and −q. Additionally, axis–angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent with atan2(sin θ, cos θ) equal to θ avoids the insensitivity of arccos; and in computing the axis magnitude in order to force unit magnitude, a brute-force approach can lose accuracy through underflow (Moler & Morrison 1983).
A partial approach is as follows:
The x-, y-, and z-components of the axis would then be divided by r. A fully robust approach will use a different algorithm when t, the trace of the matrix Q, is negative, as with quaternion extraction. When r is zero because the angle is zero, an axis must be provided from some source other than the matrix.
Euler angles[edit]
Complexity of conversion escalates with Euler angles (used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are θ1, θ2, θ3; physics and chemistry may interpret these as
while aircraft dynamics may use
One systematic approach begins with choosing the rightmost axis. Among all permutations of (x,y,z), only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us 3 × 2 × 2 = 12 variations; we double that to 24 by choosing static or rotating axes.
This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the zyz convention above; then we have the following equivalent pairs:
-
(90°, 45°, −105°) ≡ (−270°, −315°, 255°) multiples of 360° (72°, 0°, 0°) ≡ (40°, 0°, 32°) singular alignment (45°, 60°, −30°) ≡ (−135°, −60°, 150°) bistable flip
Angles for any order can be found using a concise common routine (Herter & Lott 1993; Shoemake 1994).
The problem of singular alignment, the mathematical analog of physical gimbal lock, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.
The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named the right-vector, up-vector and out-vector) instead of as angles. The singularities are also avoided when working with quaternions.
Vector to vector formulation[edit]
In some instances it is interesting to describe a rotation by specifying how a vector is mapped into another through the shortest path (smallest angle). In 

belongs to SO(n + 1) and maps x to y.[14]
Uniform random rotation matrices[edit]
We sometimes need to generate a uniformly distributed random rotation matrix. It seems intuitively clear in two dimensions that this means the rotation angle is uniformly distributed between 0 and 2π. That intuition is correct, but does not carry over to higher dimensions. For example, if we decompose 3 × 3 rotation matrices in axis–angle form, the angle should not be uniformly distributed; the probability that (the magnitude of) the angle is at most θ should be 1/π(θ − sin θ), for 0 ≤ θ ≤ π.
Since SO(n) is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group “translation”). This definition corresponds to what is called Haar measure. León, Massé & Rivest (2006) show how to use the Cayley transform to generate and test matrices according to this criterion.
We can also generate a uniform distribution in any dimension using the subgroup algorithm of Diaconis & Shashahani (1987). This recursively exploits the nested dimensions group structure of SO(n), as follows. Generate a uniform angle and construct a 2 × 2 rotation matrix. To step from n to n + 1, generate a vector v uniformly distributed on the n-sphere Sn, embed the n × n matrix in the next larger size with last column (0, …, 0, 1), and rotate the larger matrix so the last column becomes v.
As usual, we have special alternatives for the 3 × 3 case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. Arvo (1992) takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.
Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on S3. In practice: create a four-element vector where each element is a sampling of a normal distribution. Normalize its length and you have a uniformly sampled random unit quaternion which represents a uniformly sampled random rotation. Note that the aforementioned only applies to rotations in dimension 3. For a generalised idea of quaternions, one should look into Rotors.
Euler angles can also be used, though not with each angle uniformly distributed (Murnaghan 1962; Miles 1965).
For the axis–angle form, the axis is uniformly distributed over the unit sphere of directions, S2, while the angle has the nonuniform distribution over [0,π] noted previously (Miles 1965).
See also[edit]
- Euler–Rodrigues formula
- Euler’s rotation theorem
- Rodrigues’ rotation formula
- Plane of rotation
- Axis–angle representation
- Rotation group SO(3)
- Rotation formalisms in three dimensions
- Rotation operator (vector space)
- Transformation matrix
- Yaw-pitch-roll system
- Kabsch algorithm
- Isometry
- Rigid transformation
- Rotations in 4-dimensional Euclidean space
- Trigonometric Identities
- Versor
[edit]
- ^ Note that if instead of rotating vectors, it is the reference frame that is being rotated, the signs on the sin θ terms will be reversed. If reference frame A is rotated anti-clockwise about the origin through an angle θ to create reference frame B, then Rx (with the signs flipped) will transform a vector described in reference frame A coordinates to reference frame B coordinates. Coordinate frame transformations in aerospace, robotics, and other fields are often performed using this interpretation of the rotation matrix.
- ^ Note that
so that, in Rodrigues’ notation, equivalently,
- ^ Note that this exponential map of skew-symmetric matrices to rotation matrices is quite different from the Cayley transform discussed earlier, differing to the third order,
Conversely, a skew-symmetric matrix A specifying a rotation matrix through the Cayley map specifies the same rotation matrix through the map exp(2 artanh A).
- ^ For a detailed derivation, see Derivative of the exponential map. Issues of convergence of this series to the right element of the Lie algebra are here swept under the carpet. Convergence is guaranteed when ‖X‖ + ‖Y‖ < log 2 and ‖Z‖ < log 2. If these conditions are not fulfilled, the series may still converge. A solution always exists since exp is onto[clarification needed] in the cases under consideration.
Notes[edit]
- ^ Swokowski, Earl (1979). Calculus with Analytic Geometry (Second ed.). Boston: Prindle, Weber, and Schmidt. ISBN 0-87150-268-2.
- ^ W3C recommendation (2003). “Scalable Vector Graphics – the initial coordinate system”.
- ^ “Rotation Matrices” (PDF). Retrieved 30 November 2021.
- ^ Taylor, Camillo J.; Kriegman, David J. (1994). “Minimization on the Lie Group SO(3) and Related Manifolds” (PDF). Technical Report No. 9405. Yale University.
- ^ Cole, Ian R. (January 2015). Modelling CPV (thesis). Loughborough University. hdl:2134/18050.
- ^ Baker (2003); Fulton & Harris (1991)
- ^ (Wedderburn 1934, §8.02)
- ^ Hall 2004, Ch. 3; Varadarajan 1984, §2.15
- ^ (Engø 2001)
- ^ Curtright, T L; Fairlie, D B; Zachos, C K (2014). “A compact formula for rotations as spin matrix polynomials”. SIGMA. 10: 084. arXiv:1402.3541. Bibcode:2014SIGMA..10..084C. doi:10.3842/SIGMA.2014.084. S2CID 18776942.
- ^ Baker 2003, Ch. 5; Fulton & Harris 1991, pp. 299–315
- ^ (Goldstein, Poole & Safko 2002, §4.8)
- ^ Shoemake, Ken (1 July 1985). “Animating rotation with quaternion curves”. SIGGRAPH Comput. Graph. Association for Computing Machinery. 19 (3): 245–254. doi:10.1145/325334.325242. Retrieved 3 January 2023.
- ^ Cid, Jose Ángel; Tojo, F. Adrián F. (2018). “A Lipschitz condition along a transversal foliation implies local uniqueness for ODEs”. Electronic Journal of Qualitative Theory of Differential Equations. 13 (13): 1–14. arXiv:1801.01724. doi:10.14232/ejqtde.2018.1.13.
References[edit]
- Arvo, James (1992), “Fast random rotation matrices”, in David Kirk (ed.), Graphics Gems III, San Diego: Academic Press Professional, pp. 117–120, Bibcode:1992grge.book…..K, ISBN 978-0-12-409671-4
- Baker, Andrew (2003), Matrix Groups: An Introduction to Lie Group Theory, Springer, ISBN 978-1-85233-470-3
- Bar-Itzhack, Itzhack Y. (Nov–Dec 2000), “New method for extracting the quaternion from a rotation matrix”, Journal of Guidance, Control and Dynamics, 23 (6): 1085–1087, Bibcode:2000JGCD…23.1085B, doi:10.2514/2.4654, ISSN 0731-5090
- Björck, Åke; Bowie, Clazett (June 1971), “An iterative algorithm for computing the best estimate of an orthogonal matrix”, SIAM Journal on Numerical Analysis, 8 (2): 358–364, Bibcode:1971SJNA….8..358B, doi:10.1137/0708036, ISSN 0036-1429
- Cayley, Arthur (1846), “Sur quelques propriétés des déterminants gauches”, Journal für die reine und angewandte Mathematik, 1846 (32): 119–123, doi:10.1515/crll.1846.32.119, ISSN 0075-4102, S2CID 199546746; reprinted as article 52 in Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
- Diaconis, Persi; Shahshahani, Mehrdad (1987), “The subgroup algorithm for generating uniform random variables”, Probability in the Engineering and Informational Sciences, 1: 15–32, doi:10.1017/S0269964800000255, ISSN 0269-9648, S2CID 122752374
- Engø, Kenth (June 2001), “On the BCH-formula in so(3)”, BIT Numerical Mathematics, 41 (3): 629–632, doi:10.1023/A:1021979515229, ISSN 0006-3835, S2CID 126053191
- Fan, Ky; Hoffman, Alan J. (February 1955), “Some metric inequalities in the space of matrices”, Proceedings of the American Mathematical Society, 6 (1): 111–116, doi:10.2307/2032662, ISSN 0002-9939, JSTOR 2032662
- Fulton, William; Harris, Joe (1991), Representation Theory: A First Course, Graduate Texts in Mathematics, vol. 129, New York, Berlin, Heidelberg: Springer, ISBN 978-0-387-97495-8, MR 1153249
- Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
- Hall, Brian C. (2004), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 978-0-387-40122-5 (GTM 222)
- Herter, Thomas; Lott, Klaus (September–October 1993), “Algorithms for decomposing 3-D orthogonal matrices into primitive rotations”, Computers & Graphics, 17 (5): 517–527, doi:10.1016/0097-8493(93)90003-R, ISSN 0097-8493
- Higham, Nicholas J. (October 1, 1989), “Matrix nearness problems and applications”, in Gover, Michael J. C.; Barnett, Stephen (eds.), Applications of Matrix Theory, Oxford University Press, pp. 1–27, ISBN 978-0-19-853625-3
- León, Carlos A.; Massé, Jean-Claude; Rivest, Louis-Paul (February 2006), “A statistical model for random rotations”, Journal of Multivariate Analysis, 97 (2): 412–430, doi:10.1016/j.jmva.2005.03.009, ISSN 0047-259X
- Miles, Roger E. (December 1965), “On random rotations in R3“, Biometrika, 52 (3/4): 636–639, doi:10.2307/2333716, ISSN 0006-3444, JSTOR 2333716
- Moler, Cleve; Morrison, Donald (1983), “Replacing square roots by pythagorean sums”, IBM Journal of Research and Development, 27 (6): 577–581, doi:10.1147/rd.276.0577, ISSN 0018-8646
- Murnaghan, Francis D. (1950), “The element of volume of the rotation group”, Proceedings of the National Academy of Sciences, 36 (11): 670–672, Bibcode:1950PNAS…36..670M, doi:10.1073/pnas.36.11.670, ISSN 0027-8424, PMC 1063502, PMID 16589056
- Murnaghan, Francis D. (1962), The Unitary and Rotation Groups, Lectures on applied mathematics, Washington: Spartan Books
- Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
- Paeth, Alan W. (1986), “A Fast Algorithm for General Raster Rotation” (PDF), Proceedings, Graphics Interface ’86: 77–81
- Daubechies, Ingrid; Sweldens, Wim (1998), “Factoring wavelet transforms into lifting steps” (PDF), Journal of Fourier Analysis and Applications, 4 (3): 247–269, doi:10.1007/BF02476026, S2CID 195242970
- Pique, Michael E. (1990), “Rotation Tools”, in Andrew S. Glassner (ed.), Graphics Gems, San Diego: Academic Press Professional, pp. 465–469, ISBN 978-0-12-286166-6
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), “Section 21.5.2. Picking a Random Rotation Matrix”, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Shepperd, Stanley W. (May–June 1978), “Quaternion from rotation matrix”, Journal of Guidance and Control, 1 (3): 223–224, doi:10.2514/3.55767b
- Shoemake, Ken (1994), “Euler angle conversion”, in Paul Heckbert (ed.), Graphics Gems IV, San Diego: Academic Press Professional, pp. 222–229, ISBN 978-0-12-336155-4
- Stuelpnagel, John (October 1964), “On the parameterization of the three-dimensional rotation group”, SIAM Review, 6 (4): 422–430, Bibcode:1964SIAMR…6..422S, doi:10.1137/1006093, ISSN 0036-1445, S2CID 13990266 (Also NASA-CR-53568.)
- Varadarajan, Veeravalli S. (1984), Lie Groups, Lie Algebras, and Their Representation, Springer, ISBN 978-0-387-90969-1 (GTM 102)
- Wedderburn, Joseph H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2
External links[edit]
- “Rotation”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Rotation matrices at Mathworld
- Math Awareness Month 2000 interactive demo (requires Java)
- Rotation Matrices at MathPages
- (in Italian) A parametrization of SOn(R) by generalized Euler Angles
- Rotation about any point
Елена П.
16 ноября 2018 · 3,6 K
подумываю стать крутым программистом, но пока что просто пеку хлебушек · 17 нояб 2018
Воспользуемся правилом построения образа точки при повороте. Если у нас есть точка А, а поворот происходит около точки О на угол В:
1) проводим луч ОА
2) от луча ОА откладываем по часовой стрелке угол АОМ = В
3) на луче ОМ откладываем отрезок ОА1 = ОА, где точка А1 – искомая
При повороте все точки фигуры поворачиваются на один и тот же угол вокруг одной точки – центра поворота. Поэтому выполняем аналогичные действия с треугольником, делая поворот около одной из вершин.
3,5 K
Комментировать ответ…Комментировать…










![{displaystyle {begin{bmatrix}0&-1\[3pt]1&0\end{bmatrix}},quad {begin{bmatrix}-1&0\[3pt]0&-1\end{bmatrix}},quad {begin{bmatrix}0&1\[3pt]-1&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/049475f6bbfd9cfe4f0db0e7f063301e7acb774b)




![{displaystyle {begin{alignedat}{1}R_{x}(theta )&={begin{bmatrix}1&0&0\0&cos theta &-sin theta \[3pt]0&sin theta &cos theta \[3pt]end{bmatrix}}\[6pt]R_{y}(theta )&={begin{bmatrix}cos theta &0&sin theta \[3pt]0&1&0\[3pt]-sin theta &0&cos theta \end{bmatrix}}\[6pt]R_{z}(theta )&={begin{bmatrix}cos theta &-sin theta &0\[3pt]sin theta &cos theta &0\[3pt]0&0&1\end{bmatrix}}end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6821937d5031de282a190f75312353c970aa2df)






![{displaystyle [mathbf {u} ]_{times }=left(R-R^{mathsf {T}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f918d62cae11c81d33160177d9583d6e7efbe2d)
![{displaystyle left(R-R^{mathsf {T}}right)mathbf {u} =[mathbf {u} ]_{times }mathbf {u} =mathbf {u} times mathbf {u} =0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11848fee25bc229562a029195d181540a87e8597)





![{displaystyle R=(cos theta ),I+(sin theta ),[mathbf {u} ]_{times }+(1-cos theta ),(mathbf {u} otimes mathbf {u} ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5865faae48e2c8bca9a0780d52fec23a768e5354)

![{displaystyle mathbf {u} otimes mathbf {u} =mathbf {u} mathbf {u} ^{mathsf {T}}={begin{bmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\[3pt]u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\[3pt]u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}end{bmatrix}},qquad [mathbf {u} ]_{times }={begin{bmatrix}0&-u_{z}&u_{y}\[3pt]u_{z}&0&-u_{x}\[3pt]-u_{y}&u_{x}&0end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3ddca93f49b042e6a14d5263002603fc0738308)




































![{displaystyle Q_{3times 3}=left[{begin{matrix}Q_{2times 2}&mathbf {0} \mathbf {0} ^{mathsf {T}}&1end{matrix}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f439ce8b73f47040b70c9b64ab7fa89d91c46a6)
![{displaystyle {begin{aligned}Q_{mathbf {x} }(theta )&={begin{bmatrix}{color {CadetBlue}1}&{color {CadetBlue}0}&{color {CadetBlue}0}\{color {CadetBlue}0}&cos theta &-sin theta \{color {CadetBlue}0}&sin theta &cos theta end{bmatrix}},\[8px]Q_{mathbf {y} }(theta )&={begin{bmatrix}cos theta &{color {CadetBlue}0}&sin theta \{color {CadetBlue}0}&{color {CadetBlue}1}&{color {CadetBlue}0}\-sin theta &{color {CadetBlue}0}&cos theta end{bmatrix}},\[8px]Q_{mathbf {z} }(theta )&={begin{bmatrix}cos theta &-sin theta &{color {CadetBlue}0}\sin theta &cos theta &{color {CadetBlue}0}\{color {CadetBlue}0}&{color {CadetBlue}0}&{color {CadetBlue}1}end{bmatrix}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63ce9d4e595deed5ef5572d36ec99821e1b021e2)
![{displaystyle {begin{aligned}Q_{mathbf {u} }(theta )&={begin{bmatrix}0&-z&y\z&0&-x\-y&x&0end{bmatrix}}sin theta +left(I-mathbf {u} mathbf {u} ^{mathsf {T}}right)cos theta +mathbf {u} mathbf {u} ^{mathsf {T}}\[8px]&={begin{bmatrix}left(1-x^{2}right)c_{theta }+x^{2}&-zs_{theta }-xyc_{theta }+xy&ys_{theta }-xzc_{theta }+xz\zs_{theta }-xyc_{theta }+xy&left(1-y^{2}right)c_{theta }+y^{2}&-xs_{theta }-yzc_{theta }+yz\-ys_{theta }-xzc_{theta }+xz&xs_{theta }-yzc_{theta }+yz&left(1-z^{2}right)c_{theta }+z^{2}end{bmatrix}}\[8px]&={begin{bmatrix}x^{2}(1-c_{theta })+c_{theta }&xy(1-c_{theta })-zs_{theta }&xz(1-c_{theta })+ys_{theta }\xy(1-c_{theta })+zs_{theta }&y^{2}(1-c_{theta })+c_{theta }&yz(1-c_{theta })-xs_{theta }\xz(1-c_{theta })-ys_{theta }&yz(1-c_{theta })+xs_{theta }&z^{2}(1-c_{theta })+c_{theta }end{bmatrix}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87042389f5f93fc21a43beafc126d3ea5a9ee177)


![{displaystyle {begin{aligned}&{begin{bmatrix}0&-z&y\z&0&-x\-y&x&0end{bmatrix}}mapsto \[3pt]quad {frac {1}{1+x^{2}+y^{2}+z^{2}}}&{begin{bmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad82b169b68ec60349be493378761aab543c9cf8)






![{displaystyle Z=C(X,Y)=X+Y+{tfrac {1}{2}}[X,Y]+{tfrac {1}{12}}{bigl [}X,[X,Y]{bigr ]}-{tfrac {1}{12}}{bigl [}Y,[X,Y]{bigr ]}+cdots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18d3139eecb4a3799df3f187e78c1b3f0cb2f3bf)
![Z=alpha X+beta Y+gamma [X,Y],](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cdd2c4da063f9ec30359beaacd3767b962f3875)






















![{displaystyle mathbf {u} otimes mathbf {u} ={bigl (}[mathbf {u} ]_{times }{bigr )}^{2}+{mathbf {I} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dcf8163a3eb651f9af32eac4c5607585aadf524)
![{displaystyle mathbf {R} =mathbf {I} +(sin theta )[mathbf {u} ]_{times }+(1-cos theta ){bigl (}[mathbf {u} ]_{times }{bigr )}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/282727a43a016d243ecb74feb8a4dc864a961f17)

