Как найти образ вектора при отображении а

Как найти образ вектора при отображении а

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

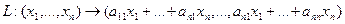
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 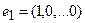, найдём его образ, это будет вектор 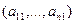. Для этого в формуле, задающей образ вектора, полагаем 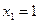, ,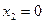…, 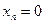. Аналогично находим образы для 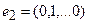,…, 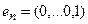. Из координат образа вектора 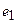составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

.

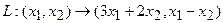Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

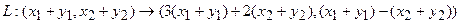Теперь каждую координату получившегося вектора можем преобразовать:

.

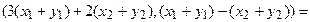
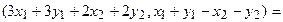
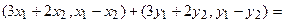
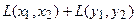Аналогично для умножения на константу:

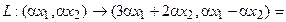
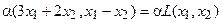
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

.

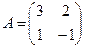Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .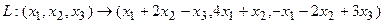

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

.

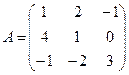2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

Если задана система 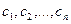из n векторов, образующих базис, и какая-нибудь произвольная система n векторов 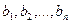(возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

Пусть 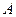– матрица оператора в базисе 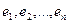. По условию, 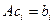для всех индексов 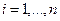. Данные n равенств можно записать в виде одного матричного равенства: 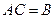, при этом столбцы матрицы 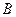– это векторы 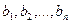, а столбцы матрицы 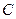– векторы 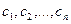. Тогда матрица 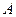может быть найдена в виде .

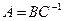Пример. Найти матрицу линейного оператора, отображающего базис

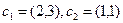в систему векторов .

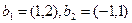Здесь 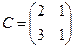, , 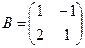, 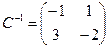и получаем:

.

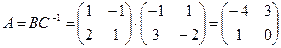Проверка осуществляется умножением получившейся матрицы на каждый вектор: .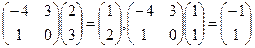

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 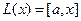и 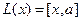. Построим матрицу одного из этих операторов, 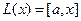. Для этого найдём образы всех трёх базисных векторов линейного пространства.

.

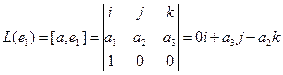Аналогично, ,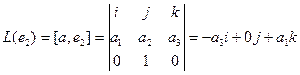

.

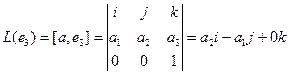Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .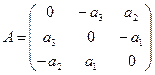

Аналогично можно построить матрицу линейного оператора :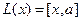

.

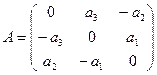Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .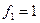

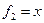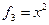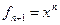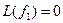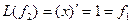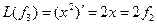, , , аналогично получим ,…, .

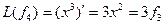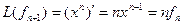Матрица этого линейного оператора:

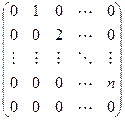
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

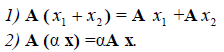
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 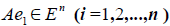, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

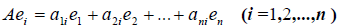
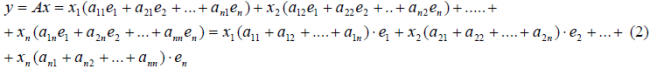
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

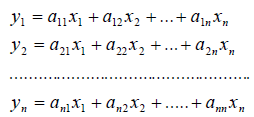
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

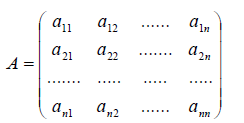
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

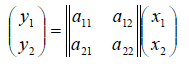
связывающее вектор-прообраз 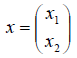с вектором-образом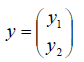

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

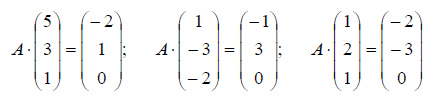
Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

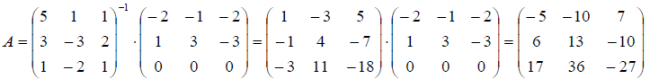
Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .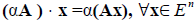

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

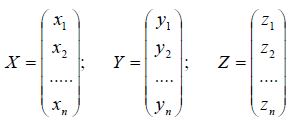
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 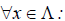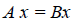. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 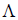он ставит в соответствие тот же самый элемент, то есть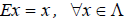

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 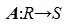, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

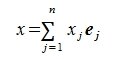(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

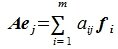(4)

где aij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

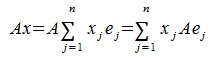
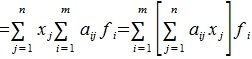
Сделаем следующее обозначение:

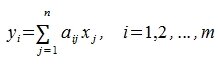(6)

Тогда равенство (5) примет следующий вид:

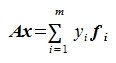(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами aij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору ej, тогда:

Cej= Aej+ Bej= n (aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица 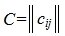,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 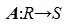, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

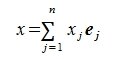(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

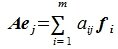(4)

где aij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

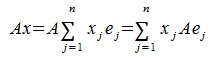
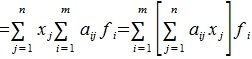
Сделаем следующее обозначение:

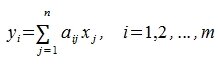(6)

Тогда равенство (5) примет следующий вид:

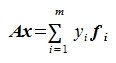(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами aij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору ej, тогда:

Cej= Aej+ Bej= n (aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица 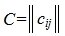,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya

http://matworld.ru/linear-algebra/linear-operator.php

[/spoiler]

Источник

Макеты страниц

1. Определение и простейшие свойства линейных преобразований. Пусть А — отображение векторного пространства U на векторное пространство V, ставящее в соответствие каждому вектору и пространства U вектор пространства V.

Определение 2. Отображение А называется линейным, если оно удовлетворяет следующим двум условиям («условиям линейности») :

1) Для любых двух векторов их и

2) Для любого вектора и и любого числа А имеем

Из условий 1), 2) сразу следует, что при линейном отображении всякая линейная комбинация каких-либо векторов пространства U переходит в линейиую комбинацию векторов пространства V с теми же коэффициентами .

Замечание. Линейные отображения векторного пространства в себя также называются линейными операторами, и это название является даже более употребительным. Мы будем его придерживаться в главах XXIV, XXV этих «Лекций».

Установим простейшие свойства линейных отображений.

1° При линейном отображении нулевой вектор пространства U переходит в нулевой вектор 0 пространства V:

В самом деле, (где и — произвольный вектор пространства U). Значит, . Отсюда непосредственно следует

2° Если векторы их, линейно зависимы, то и их образы также линейно зависимы («линейная зависимость векторов сохраняется при всяком линейном отображении»).

В самом деле, если их, линейно зависимы, то существуют такие числа не все равные , что

Но тогда, по только что доказанному, и

векторы линейно зависимы.

Следствие. Пусть – линейное отображение пространства U на пространство V и векторы образуют линейно независимую систему в V. Тогда в U существует линейно независимая система, состоящая из k векторов их, , отображающихся соответственно в :

В самом деле, для каждого вектора существует по крайней мере один такой вектор , что (ведь А — отображение на все пространство V). Поэтому можно найти в U такие векторы , что . Система линейно независима (в противном случае, в силу 2°, система была бы зависима).

Из доказанного вытекает, далее:

Если -мерное пространство U линейно отображено на -мерное пространство V, то . В самом деле, по предположению в V существует линейно независимая система, состоящая из векторов; но тогда такая система существует и в U, так что .

3° Пусть А есть взаимно однозначное линейное отображение векторного пространства U на векторное пространство V. Тогда определено обратное отображение пространства V на пространство .

Докажем, что оно также есть линейное отображение. Докажем, в самом деле, что преобразование удовлетворяет обоим условиям линейности.

— произвольные векторы из V, пусть . Надо доказать, что . Пусть . Тогда, вследствие линейности преобразования А, имеем

т. е. , но , значит, , что и требовалось доказать.

Положим . Тогда и, в силу линейности отображения А,

значит, , или, наконец (если подставить в это равенство ),

что и требовалось доказать.

Из доказанного следует, что взаимно однозначные линейные отображения одного векторного пространства на другое суть не что иное, как изоморфные отображения (изоморфизмы), рассмотренные нами в § 1 этой главы.

В частности, взаимно однозначные линейные отображения (изоморфизмы) векторного пространства U на себя называются линейными преобразованиями. Из доказанных в § 1 свойств изоморфизмов следует, что при линейном преобразовании всякая линейно независимая система векторов переходит в линейно независимую, а всякий базис пространства U переходит в базис этого пространства.

Замечание 1. Теперь мы видим, что всякое аффинное преобразование плоскости или трехмерного пространства порождает изоморфное преобразование многообразия всех свободных векторов плоскости (соответственно трехмерного пространства).

2. Матрица линейного преобразования. Умножение преобразований и умножение матриц. Пусть А есть линейное отображение -мериого векторного пространства U на -мерное векторное пространство V. Мы знаем, что тогда .

Пусть – какой-нибудь базис пространства U. При преобразовании А векторы переходят соответственно в векторы . Каждый вектор

переходит при преобразовании А в вектор

Таким образом, линейное преобразование А векторного пространства U полностью определено формулой если заданы образы векторов , образующих какой-нибудь базис пространства .

Если отображение А взаимно однозначно (т. е. является изоморфизмом), то векторы образуют базис пространства V и отображение А состоит в том, что каждому вектору

ставится в соответствие вектор

имеющий относительно базиса , те же самые координаты, которые вектор и имел относительно базиса . В частности, это имеет место в том случае, когда и А есть линейное преобразование пространства .

Этим важнейшим частным случаем мы сейчас только и займемся. Теперь векторы лежат в пространстве U, следовательно,

и невырождающаяся матрица

т. е. матрица перехода от базиса к базису , полностью определяет преобразование А: чтобы для каждого вектора . найти координаты вектора (относительно того же базиса ), надо только заметить, что вектор относительно «нового» базиса , имеет координаты , значит, относительно «старого» базиса его координаты вычисляются по формулам (3) из § 2 (с заменой в них на ) на на при , т. е.

Матрица

называется матрицей преобразования А относительно базиса эта матрица транспонирована к матрице перехода А от базиса к базису ,

Для простоты письма предполагаем . Записывая вектор не в виде строки , а в виде столбца

можем переписать формулы (4) в виде

Итак, образ вектора и, заданного своими координатами при преобразовании А, есть матрица (столбец), являющаяся произведением матрицы А на матрицу

Поэтому образ вектора при преобразовании с матрицей В есть произведение матрицы В на матрицу

Другими словами (помня ассоциативность умножения матриц),

Итак, при перемножении преобразований матрицы их также перемножаются: матрица преобразования (сначала А, потом ) есть ВА.

Отсюда вытекает, что матрица обратного преобразования к преобразованию А есть матрица . В самом деле, так как произведение преобразований А и (взятых в любом порядке) есть тождественное преобразование матрица которого, очевидно, есть единичная матрица Е, то произведение матриц преобразований А и есть Е, откуда и следует, что эти матрицы взаимно обратны.

Решим теперь следующую задачу. Дана матрица А линейного преобразования А относительно базиса . Дан второй базис с соответствующей матрицей перехода P (от базиса I к базису .

Требуется найти матрицу А преобразования относительно базиса .

Пусть — произвольный вектор; его координаты относительно базисов обозначим соответственно через , так что

Координаты вектора в базисах обозначим соответственно через . Тогда имеем для любого вектора

но

следовательно,

Внося в правую часть равенства (7) выражение (5), получим

Внося сюда первое выражение из (6), получаем окончательно

т. е.

Это и есть чрезвычайно важная формула, которую мы хотели получить.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
  • § 1. Отношение отрезков
  • § 2. Направленные отрезки (векторы); их отношение
  • § 3. Ось. Алгебраическое значение (координата) вектора на оси
  • § 4. Сложение векторов на прямой
  • § 5. Система координат на прямой
  • § 6. Деление отрезка в данном отношении
  • § 7. Пропорциональность пар чисел
  • § 8. Бесконечно удаленная точка прямой
  • § 9. Пропорциональность двух последовательностей, состоящих из и чисел
  • ГЛАВА II. ВЕКТОРЫ
  • § 1. Равенство векторов. Свободный вектор
  • § 2. Линейные операции над векторами (сложение и умножение на число)
  • § 3. Проекции
  • § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
  • § 5. Линейная зависимость и независимость векторов
  • § 6. Геометрический смысл линейной зависимости векторов
  • § 7. Векторные многообразия
  • ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
  • § 1. Определение аффинной системы координат
  • § 2. Перенос начала координат
  • § 3. Деление отрезка в данном отношении
  • ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
  • § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
  • § 2. Скалярное произведение векторов; угол между двумя векторами
  • § 3. Угол от одного вектора до другого на плоскости
  • § 4. Полярная система координат на плоскости
  • § 5. Полярная система координат в пространстве
  • ГЛАВА V. ПРЯМАЯ ЛИНИЯ
  • § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
  • § 2. Расположение двух прямых на плоскости
  • § 3. Частные случаи общего уравнения прямой
  • § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
  • § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
  • § 6. Две полуплоскости, определяемые данной прямой на плоскости
  • § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
  • § 8. Расстояние от точки до прямой (на плоскости)
  • § 9. Углы, образуемые двумя прямыми на плоскости
  • § 10. Прямая в пространстве, снабженном прямоугольной системой координат
  • ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
  • § 1. Парабола
  • § 2. Определение и каноническое уравнение эллипса
  • § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
  • § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
  • § 5. Определение гиперболы. Каноническое уравнение гиперболы
  • § 6. Основной прямоугольник и асимптоты гиперболы
  • § 7. Директрисы эллипса и гиперболы
  • § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
  • § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
  • ГЛАВА VII. ДЕТЕРМИНАНТЫ
  • § 1. Плошадь ориентированного параллелограмма и треугольника
  • § 2. Детерминант второго порядка. Матрицы
  • § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
  • § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
  • § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
  • § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
  • § 8. Правило Крамера для решений систем и уравнений с n неизвестными
  • § 9. Общее определение миноров матрицы. Теорема Лапласа
  • § 10. Умножение детерминантов
  • § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
  • ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
  • § 1. Переход от одной аффинной системы координат к другой
  • § 2. Перемножение матриц. Новое определение обратной матрицы
  • § 3. Переход от одной прямоугольной системы координат к другой
  • § 4. Действия над матрицами в общем случае
  • ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
  • § 1. Ориентация пространства (плоскости)
  • § 2. Углы Эйлера
  • § 3. Объем ориентированного параллелепипеда
  • § 4. Векторное произведение двух векторов
  • ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
  • § 1. Уравнения плоскости
  • § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
  • § 3. Взаимное расположение двух плоскостей
  • § 4. Прямая как пересечение двух плоскостей
  • § 5. Пучок плоскостей
  • § 6. Взаимное расположение двух прямых в пространстве
  • § 7. О двух полупространствах, определяемых данной плоскостью
  • § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
  • § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
  • § 10. Две задачи
  • ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
  • § 1. Определение движений и аффинных преобразований
  • § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
  • § 3. Аналитическое выражение аффинных преобразований
  • § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
  • § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
  • § 6. Движения как изометрические преобразования
  • § 7. Преобразования подобия
  • § 8. Классификация движений прямой и плоскости
  • ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
  • § 1. Определение векторного пространства
  • § 2. Размерность. Базис. Координаты
  • § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
  • § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
  • § 5. Алгебраическая (в частности, прямая) сумма подпространств
  • § 6. Линейные отображения векторных пространств
  • § 7. Теорема о ранге матрицы
  • § 8. Системы линейных однородных уравнения
  • ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
  • § 1. Линейные функции
  • § 2. Билинейные функции и билинейные формы
  • § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
  • § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
  • § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
  • ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
  • § 1. Определение n-мерного аффинного пространства
  • § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
  • § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
  • § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
  • § 5. Системы линейных уравнений
  • § 6. Аффинные преобразования n-мерного аффинного пространства
  • ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
  • § 1. Определение алгебраических линий и поверхностей
  • § 2. Преобразование многочлена второй степени при преобразовании координат
  • § 3. Аффинная эквивалентность линий и поверхностей
  • § 4. Комплексная плоскость
  • § 5. Прямая линия на комплексной плоскости
  • § 6. Замечание о действительных и мнимых линиях
  • § 7. Комплексное пространство
  • § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
  • § 9. Несколько заключительных замечаний о линиях и поверхностях
  • ГЛАВА XVI. Различные виды кривых второго порядка
  • § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
  • § 2. Инварианты многочлена второй степени
  • § 3. Центральный случай
  • § 4. Параболический случай
  • § 5. Аффинная классификация кривых второго порядка
  • § 6. Несколько заключительных замечаний
  • ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
  • § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
  • § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
  • § 3. Асимптотические направления кривых второго порядка
  • § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
  • § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
  • § 6. Центр кривой второго порядка
  • § 7. Диаметры кривой второго порядка
  • § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
  • § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
  • § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
  • § 11. Оси симметрии и главные направления кривой второго порядка
  • § 12. Основная теорема об аффинных преобразованиях
  • ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
  • § 1. Распадающиеся поверхности
  • § 2. Цилиндрические поверхности
  • § 3. Конусы второго порядка
  • § 4. Эллипсоиды и гиперболоиды
  • § 5. Параболоиды
  • § 6. Прямолинейные образующие
  • ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
  • § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
  • § 2. Пересечение поверхности второго порядка с плоскостью
  • § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
  • § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
  • § 5. Центр поверхности второго порядка
  • ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
  • § 1. Диаметральные плоскости. Особые направления
  • § 2. Диаметральные плоскости поверхностей различных видов
  • § 3. Сопряженные направления
  • § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
  • § 5. Теорема единственности
  • § 6. Главные направления
  • § 7. Приведение к каноническому виду уравнения поверхности второго порядка
  • § 8. Аффинная классификация поверхностей второго порядка
  • ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
  • § 1. Перспективное соответствие между плоскостью и связкой
  • § 2. Однородные координаты точек на плоскости и лучел в связке
  • § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
  • § 4. Принцип двойственности для проективной плоскости
  • § 5. Проективная система координат в связке и на проективной плоскости
  • § 6. Проективные преобразования и отображения проективной плоскости
  • § 7. Проективные координаты на прямой. Проективные отображения прямой
  • § 8. Двойное отношение
  • ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
  • § 1. Определение. Теорема единственности
  • § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
  • § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
  • § 4. Поляры и полюсы
  • § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
  • § 6. Диаметры как поляры несобственных точек
  • § 7. Автополярный треугольник
  • § 8. Проективная классификация кривых второго порядка
  • ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
  • § 1. Проективное пространство; его плоскости и прямые
  • § 2. Проективные координаты. Проективные преобразования.
  • § 3. Понятие об n-мерном проективном пространстве
  • § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
  • § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
  • § 6. Полюсы и полярные плоскости
  • § 7. Проективная классификация поверхностей второго порядка
  • § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
  • ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
  • § 1. Введение. Ортогональные матрицы
  • § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
  • § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
  • § 4. Неравенство Коши—Буняковского и его следствия. Углы
  • § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
  • ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
  • § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
  • § 2. Ортогональные преобразования n-мерного евклидова пространства
  • § 3. Движения трехмерного евклидова пространства
  • § 4. Преобразования подобия. Дальнейшие проблемы
  • § 5. Самосопряженные операторы
  • § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
  • § 7. Билинейные и квадратичные формы в евклидовых пространствах
  • § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
  • ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
  • § 1. Перестановки
  • § 2. Множества
  • § 3. Отображения или функции
  • § 4. Разбиение множества на подмножества. Отношение эквивалентности
  • § 5. Определение группы
  • § 6. Простейшие теоремы о группах
  • § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
  • ЗАДАЧИ
  • Задачи к главе IV
  • Задачи к главе V
  • Задачи к главе VI
  • Задачи к главе VIII
  • Задачи к главе IX
  • Задачи к главе X
  • Задачи к главе XI
  • Задачи к главе XII
  • Задачи к главе XIII
  • Задачи к главе XIV
  • Задачи к главе XV
  • Задачи к главам XVI и XVII
  • Задачи к главе XVIII
  • Задачи к главам XIX и XX
  • Задачи к главе XXI
  • Задачи к главе XXII
Источник

Содержание

Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом
ЛИНЕЙНОЕ ПРОСТРАНСТВО.

Линейное отображение

Линейным отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция (соответствие)
$$ mathcal A: mathbb V longmapsto mathbb W $$
(т.е. определенная на $ mathbb V_{} $, имеющая
значения в $ mathbb W_{} $), обладающая свойством линейности, которое описывается одним из двух эквивалентных представлений:
$$
mathcal A (X_1 +X_2)= mathcal A(X_1) boxplus mathcal A(X_2),quad mathcal A (alpha_1 X_1)=
alpha_1 mathcal A (X_1),
$$
или
$$
mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) boxplus alpha_2 mathcal A(X_2)
$$
указанные свойства должны быть выполнены для любых векторов $ X_1,X_2 $ пространства $ mathbb V_{} $ и любых скаляров $ alpha_1,alpha_ 2 $ (вещественных если оба пространства
вещественны, и комплексных если хотя бы одно из пространств комплексное).
Если $ Y=mathcal A(X) $, то говорят, что $ Y_{} $ — образ вектора $ X_{} $, а $ X_{} $ —
прообраз вектора $ Y_{} $ при отображении $ mathcal A_{} $. Пространство $ mathbb V_{} $ называется областью определения отображения $ mathcal A_{} $.

Образно говоря, свойство линейности отображения заключается в том, что при этом отображении образ суммы любых двух векторов совпадает с суммой образов этих векторов, а произвольное растяжение прообраза влечет за собой сообразное же растяжение образа1).

Примеры линейных отображений

П

Пример 1. Рассмотрим линейное пространство
полиномов степени не выше $ n_{} $:

$$ mathbb P_n={p(x) in mathbb R[x] mid deg p(x) le n } , ; $$
в это же множество включаем и тождественно нулевой полином (для которого степень не определяется). Операция нахождения частного и операция нахождения остатка от деления полинома $ p(x)_{} $ на заданный фиксированный полином $ g(x) in mathbb R[x], g(x) notequiv 0 $ являются линейными отображениями пространства $ mathbb P_{n} $: если

$$ p_1(x)equiv q_1(x)g(x)+r_1(x), p_2(x)equiv q_2(x)g(x)+r_2(x) $$
при $ deg r_j(x)<deg g(x) $
то
$$
(alpha_1p_1(x)+alpha_2p_2(x)) equiv
$$
$$
equiv
(alpha_1q_1(x)+alpha_2q_2(x)) g(x) + (alpha_1r_1(x)+alpha_2r_2(x)) . $$
Фактически, операция деления на $ g_{}(x) $ (с остатком) порождает два разных линейных отображения. Если $ deg g(x) = m $ при $ 0<mle n $, то операция нахождения остатка — это отображение $ mathbb P_{n} mapsto mathbb P_{m-1} $, а операция нахождения частного — это отображение $ mathbb P_{n} mapsto mathbb P_{n-m} $.

П

Пример 2. В том же линейном пространстве $ mathbb P_{n}^{} $ операция дифференцирования

$$ frac{d }{d, x}: p(x) {color{Red}{ longmapsto} } p'(x) $$
является отображением $ mathbb P_{n}^{} $ в $ mathbb P_{n-1}^{} $ линейным
поскольку
$$frac{d }{d, x} (alpha_1 p_1(x) + alpha_2 p_2(x))=
alpha_1 frac{d }{d, x} p_1(x) + alpha_2 frac{d }{d, x} p_2(x)
.
$$
Прообраз любого элемента $ mathbb P_{n-1}^{} $ неединствен:
$ frac{d }{d, x}(frac{1}{2} x^2 + const)=x $.

П

Пример 3. Операцию нахождения первообразной:

$$
int_{0}^{x}:
begin{array}{ccc}
p(x) & {color{Red}{ longmapsto} } & int_{0}^{x} p(t) d, t \
a_0x^n+a_1x^{n-1}+cdots+a_n & {color{Red}{ longmapsto} } &
displaystyle frac{a_0}{n+1}x^{n+1}+frac{a_1}{n}x^{n}+cdots+a_nx
end{array}
$$
тоже можно рассматривать как линейное отображение
$ mathbb P_n {color{Red}{ longmapsto} } mathbb P_{n+1} $. При этом прообраз каждого полинома из
$ mathbb P_{n+1} $ (если существует) будет единствен.

П

Пример 4. Линейная форма от переменных $ x_{1},dots,x_n $:

$$mathcal A(x_1,dots,x_n)=a_1x_1+dots+a_nx_n,quad {a_j }_{j=1}^{n}
subset mathbb R $$
является примером линейного отображения $ mathbb R^{n}_{} $ в $ mathbb R_{} $. Здесь тоже
прообразов у одного и того же элемента из $ mathbb W_{} $ может быть несколько:
$$mathcal A(x_1,x_2)=2x_1-x_2 mbox{ отображает вектора } X_1=[0,0]
mbox{ и } X_2=[1,2] mbox{ в } 0 .$$

П

Пример 5. Обобщением предыдущего примера является
отображение $ mathcal A: mathbb R^n longmapsto mathbb R^m $, задаваемое

$$
mathcal A
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n
end{array}
right)=
$$
$$
=
left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
$$
при произвольной вещественной матрице. Оно является линейным — в отличие от похожего на него отображения
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля. В самом деле, если записать последнее в матричном виде:
$$
tilde{mathcal A}(X)=Acdot X+ mathcal B,
$$
то
$$
tilde{mathcal A}(alpha X)=Acdot (alpha X)+ mathcal B ne alpha tilde{mathcal A}(X)=
alpha left(Acdot X+ mathcal B right).
$$
Для этого отображения свойство линейности не выполняется. Для отображений такого типа приходится расширять множество линейных отображений: см.

☟



AФФИННОЕ ОТОБРАЖЕНИЕ.

П

Пример 6. Предыдущим примерам
можно дать и геометрическую интерпретацию. Так, линейное отображение $ mathbb R^3 longmapsto mathbb R^3 $:

$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
left(begin{array}{c}
x \ y \ 0
end{array}
right)
$$
задает ортогональную проекцию вектора $ X=(x,y,z) $ на плоcкость $ z=0 $.
Можно рассматривать его и как отображение $ mathbb R^{3} longmapsto mathbb R^2 $.
Проецирование же на произвольное подпространство может быть задано
с помощью матрицы. Так, например, отображение
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
frac{1}{3} left(begin{array}{rrr}
2 & -1 & -1 \
-1& 2 & -1 \
-1 & -1 & 2
end{array}
right)
left(begin{array}{c}
x \ y \ z
end{array}
right)
$$
задает ортогональную проекцию вектора $ X_{} $ на многообразие $ x+y+z=0 $.

Общее выражение для отображения ортогонального проецирования на линейное подпространство в $ mathbb R^{n}_{} $

☞



ЗДЕСЬ.

П

Пример 7. В линейном пространстве $ mathbb R^{mtimes n} $ матриц порядка $ mtimes n_{} $ с вещественными элементами определим два отображения:

$$ X mapsto Acdot X quad u quad X mapsto X cdot B $$
умножения слева на фиксированную матрицу $ A_{elltimes m} $ и умножения справа на также фиксированную матрицу $ B_{ntimes k} $.
Оба отображения являются линейными. Линейным также будет и отображение
$$ X mapsto Acdot X cdot B . $$
При дополнительных условиях $ m=n=ell=k $ линейным будет и отображение
$$ X mapsto Acdot X + X cdot B . $$
Оно отображает пространство $ mathbb R^{ntimes n} $ в себя.

П

Пример 8. В пространстве полиномов с вещественными коэффициентами от $ m_{} $ переменных $ x_1,x_2,dots,x_{m} $ степени не выше $ n_{} $ рассмотрим отображение

$$ f(x_1,x_2,dots,x_m) mapsto operatorname{grad} (f)= left(frac{partial f}{partial x_1}, frac{partial f}{partial x_2}, dots, frac{partial f}{partial x_m}
right) .
$$
Здесь вектор $ operatorname{grad} (f) $ называется градиентом функции $ f_{} $. Это отображение будет линейным. Для его записи используют следующий формализм. Вводят в рассмотрение специальный вектор, называемый набла2)
$$ nabla = left(frac{partial }{partial x_1}, frac{partial }{partial x_2}, dots, frac{partial }{partial x_m} right) . $$
Умножение этого вектора на функцию $ f_{} $ имеет результатом именно градиент:
$$ nabla cdot f = operatorname{grad} (f) . $$
Умножение же этого вектора по правилу скалярного произведения на вектор $ F= (f_1,f_2,dots,f_m) $,
состоящий из $ m_{} $ полиномов, порождает отображение этого вектора в полином:
$$ operatorname{div} (F) = langle nabla, F rangle =frac{partial f_1 }{partial x_1}+ frac{partial f_2 }{partial x_2}+ dots+ frac{partial f_m }{partial x_m} ; $$
он называется дивергенцией вектора $ F_{} $. Это отображение
$$ F mapsto operatorname{div} (F) $$
также будет линейным.

?

В частном случае линейных форм:

$$ f_j=a_{j1}x_1+dots+a_{jn}x_m quad npu quad jin{1,dots,m} $$
получим связь $ operatorname{div} (F) $ с одним объектом матричного анализа. Каким именно?

?

Является ли линейным отображение

$$ X longmapsto operatorname{Sp} (X) , $$
определенное в пространстве квадратных матриц порядка $ n_{} $? Здесь $ operatorname{Sp} (X) $ — след матрицы $ X_{} $.

?

Про линейное отображение $ mathcal A $ пространства $ mathbb R^{3}_{} $ в пространство $ mathbb P_3^{} $ известно, что

$$ mathcal A(1,0,1)=1+3,x+x^3, mathcal A(1,-1,0)=-1+x-x^2 . $$
Найти $ mathcal A(-1,2,1) $.

Свойства линейных отображений

§

В настоящем пункте $ mathbb O_{} $ означает нулевой вектор пространства $ mathbb V_{} $,
а $ mathbb O’ $ — нулевой вектор пространства $ mathbb W_{} $.

Два линейных отображения $ mathcal A $ и $ mathcal B $ из
$ mathbb V_{} $ в $ mathbb W_{} $ называются равными если $ mathcal A(X)=mathcal B(X) $ для любого
$ Xin mathbb V $. Нулевое отображение определяется условием
$${mathcal O}(X)=mathbb O’ quad npu quad forall Xin mathbb V .$$

Т

Теорема 1. Для любого линейного отображения $ mathcal A(X) $:

а) $ mathcal A(mathbb O)=mathbb O’ $;

б) если система $ {X_1,dots,X_k} $ линейно зависима, то и система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно зависима;

в) если система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно независима, то и система
$ {X_1,dots,X_k} $ линейно независима.

Т

Теорема 2. Линейное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $.

Доказательство. Если
$$ mathbb M = X_0+mathcal L(X_1,dots,X_k)=
$$
$$
={X_0+alpha_1X_1+dots+ alpha_kX_k mid (alpha_1,dots,alpha_k)in mathbb R^k } ,
$$
то свойство линейности отображения $ mathcal A_{} $ дает:
$$
mathcal A( mathbb M) ={mathcal A(X_0)boxplus alpha_1mathcal A(X_1) boxplus dots boxplus alpha_kmathcal A(X_k) mid (alpha_1,dots,alpha_k)in mathbb R^k } =
$$
$$
=mathcal A(X_0) boxplus mathcal L(mathcal A(X_1),dots,mathcal A(X_k)) .
$$
Заметим, что в соответствии с теоремой 1, можно утверждать, что линейное отображение не увеличивает размерности отображаемого многообразия: $ dim mathcal A( mathbb M) le dim mathbb M $.

♦

=>

Линейное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.

?

Доказать, что линейное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.

Т

Теорема 3. Пусть $ {X_1,dots,X_n} $ — произвольный базис $ mathbb V_{} $,
а $ Y_1,dots,Y_n $ — произвольные векторы из $ mathbb W_{} $. Существует единственное линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $ такое, что$$ mathcal A(X_1)=Y_1,dots,mathcal A(X_n)=Y_n .$$

Иными словами: любое линейное отображение пространства $ mathbb V_{} $ в другое пространство однозначно определяется его заданием на базисных векторах пространства $ mathbb V_{} $.

Доказательство. Поскольку векторы $ X_1,dots,X_{n} $ — базисные, то существует
и единственно разложение любого $ Xin mathbb V_{} $: $ X=x_1X_1+cdots+x_nX_n $.
Зададим отображение $ mathcal A: mathbb V longmapsto mathbb W $ формулой
$$mathcal A(X) = x_1Y_1boxplus dots boxplus x_nY_n . $$
Легко проверить свойство его линейности. Кроме того:
$$mathcal A(X_j)=mathcal A(0cdot X_1+dots+1cdot X_j+dots+0cdot X_n)=
$$
$$
=0cdot Y_1 boxplus dots boxplus 1cdot Y_j boxplus dots boxplus 0cdot Y_n=Y_j,$$
т.е. оно удовлетворяет условиям теоремы.

Предположим теперь, что существует еще одно отображение $ mathcal B(X) $,
удовлетворяющее этим условиям: $ mathcal B(X_j)=Y_j $. Тогда
$$mathcal A(X)=x_1Y_1 boxplus cdots boxplus x_nY_n=
$$
$$
=x_1mathcal B(X_1) boxplus cdots boxplus x_nmathcal B(X_n)=mathcal B(X),$$
и, на основании определения, $ mathcal A(X)=mathcal B(X) $.

♦

Отображение $ {mathcal S}: mathbb V longmapsto mathbb W $ называется
суммой линейных отображений $ mathcal A $ и $ mathcal B $ если
$ mathcal S(X)=mathcal A(X) boxplus mathcal B(X) $ для $ forall Xin mathbb V_{} $. Отображение
$ mathcal F:mathbb V longmapsto mathbb W $ называется
произведением линейного отображения $ mathcal A_{} $ на число (скаляр)
$ lambda_{} in mathbb R $ если $ {mathcal F}(X)=lambda cdot mathcal A(X) $ для $ forall Xin mathbb V_{} $.

Т

Теорема 4. Отображения $ {mathcal S} $ и $ {mathcal F} $ — линейные.

П

Пример. В пространстве полиномов $ mathbb P_n $
операцию нахождения второй производной

$$ frac{d^2 }{d, x^2}:p(x) longmapsto p”(x)$$
тоже можно рассматривать как линейное отображение $ mathbb P_n longmapsto mathbb P_{n-1} $.
Линейным также будет и отображение
$$ frac{d^2 }{d, x^2}times Box + 2 frac{d}{d, x}times Box: p(x)
longmapsto p”(x)+2 p'(x) .$$

Т

Теорема 5. Множество $ {mathcal H}om(mathbb V,mathbb W) $ всех линейных
отображений из $ mathbb V_{} $ в $ mathbb W_{} $ образует линейное пространство и$$dim {mathcal H}om(mathbb V,mathbb W) = dim mathbb V cdot dim mathbb W .$$

Ядро и образ линейного отображения

Для линейного отображения $ mathcal A $ его ядром3) называется множество векторов из $ mathbb V_{} $, отображающихся в
$ mathbb O’ in mathbb W $:
$$mathcal{K}er (mathcal A)= left{Xin mathbb V big| mathcal A(X)=mathbb O’ right} ; $$
а его образом называется множество всех векторов из
$ mathbb W_{} $, для каждого из которых существует прообраз из $ mathbb V_{} $:
$$mathcal{I}m (mathcal A)= left{Yin mathbb W mid exists X in mathbb V, mathcal A(X)= Y
right} .$$

Фактически $ mathcal{I}m (mathcal A) $ можно назвать областью значений линейного отображения $ mathcal A_{} $.

Т

Теорема 1. $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ являются
линейными подпространствами соответствующих пространств.

Для линейного отображения $ mathcal A_{} $ его дефектом называется размерность ядра,
а его рангом — размерность образа:
$$ operatorname{dfc}(mathcal A )=dim (mathcal{K}er (mathcal A )) ,
operatorname{rank}(mathcal A )= dim (mathcal{I}m (mathcal A )) .
$$
Отображение называется невырожденным если $ operatorname{dfc}(mathcal A )=0 $.

Т

Теорема 2. Линейное отображение $ mathcal A $ невырождено тогда и только тогда, когда у каждого образа существует единственный прообраз.

Доказательство. Необходимость. Если $ mathcal A $ невырождено, то $ mathcal{K}er (mathcal A )={mathbb O} $, т.е. единственным вектором из $ mathbb V_{} $, отображающимся в $ mathbb O’ in mathbb W $ должен быть $ mathbb O_{} $. Если предположить неединственность прообраза для какого-то
$ Yin mathbb W $: $ Y=mathcal A (X_1)=mathcal A (X_2) $ при $ X_1ne X_2 $, то
$$mathbb O’=mathcal A (X_1)-mathcal A (X_2)=mathcal A (X_1-X_2)$$
и получаем противоречие с единственностью прообраза у $ mathbb O’ $.

Достаточность. Пусть $ mathcal A (X_1)ne mathcal A (X_2) $ для любых $ X_1ne X_2 $. Если бы $ mathcal{K}er (mathcal A ) $ имело ненулевую размерность, то существовал бы $ Xne mathbb O $ такой, что $ mathcal A (X)=mathbb O’ $, что противоречило бы предыдущей фразе: $ mathcal A (X)= mathcal A (mathbb O) $.

♦

Т

Теорема 3. Если $ {X_1,dots,X_{n}} $ — произвольный базис $ mathbb V_{} $,
то $ mathcal{I}m (mathcal A) $ совпадает с линейной оболочкой образов этих векторов$$ mathcal{I}m (mathcal A) ={mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$

Доказательство. Действительно, любой вектор $ Y in mathcal{I}m (mathcal A) $ является
образом какого-то вектора $ X=x_1X_1+cdots+x_nX_n $, тогда на основании
линейности отображения:
$$ Y=mathcal A (X)=x_1mathcal A (X_1) boxplus cdots boxplus x_n mathcal A (X_n) in
{mathcal L}left(mathcal A (X_1),dots, mathcal A(X_n) right) .$$
Таким образом
$$mathcal{I}m (mathcal A) subset
{mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$
Обратно, поскольку векторы $ mathcal A (X_1),dots, mathcal A (X_n) $ принадлежат
$ mathcal{I}m (mathcal A) $, то по теореме 1 и любая линейная комбинация
этих векторов должна принадлежать $ mathcal{I}m (mathcal A) $:
$${mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right)
subset mathcal{I}m (mathcal A) .$$
Из двух взаимных включений множеств следует их равенство.

♦

П

Пример. Найти ядро и образ отображения $ mathbb R^3 longmapsto mathbb R^4 $

$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right) .
$$

Решение. Для определения $ mathcal{K}er (mathcal A) $ найдем фундаментальную
систему решений системы уравнений
$$left{ begin{array}{rrr}
x_3 &=&0 \
0 &=&0 \
x_1+x_2+x_3 &=&0 \
x_1+x_2-x_3 &=&0
end{array} right. quad Longrightarrow
X_1= left(begin{array}{r}
-1 \ 1 \0
end{array}
right)
$$
Имеем $ operatorname{dfc}(mathcal A )=1 $ и $ mathcal{K}er (mathcal A)= mathcal L (X_1) $.

Теперь для нахождения $ mathcal{I}m (mathcal A) $ воспользуемся теоремой 3:
базис следует искать среди векторов
$$Y_1=mathcal A left(begin{array}{c}
1 \ 0 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
Y_2=mathcal A left(begin{array}{c}
0 \ 1 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
$$
$$
Y_3=mathcal A left(begin{array}{c}
0 \ 0 \1
end{array}
right)= left(begin{array}{r}
1 \ 0 \ 1 \ -1
end{array}
right) .
$$
Имеем: $ operatorname{rank}(mathcal A )=2 $ и $ mathcal{I}m (mathcal A) = mathcal L (Y_1,Y_3) $.

♦

П

Пример. Найти ядро и образ отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:

$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) – 6, p(x) . $$

Решение. Для начала проверим, что это отображение именно $ mathbb P_3 mapsto mathbb P_2 $, т.е. при таком отображении происходит понижение степени полинома, по крайней мере на $ 1_{} $. И действительно, если $ p(x)=a_0x^3+a_1x^2+a_2x+a_3 $, то
$$ x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x) equiv
$$
$$
equiv (-4,a_1+3,a_0)x^2+(2,a_1-6,a_2)x+(a_2-6,a_3) . $$
Теперь понятно, что $ mathcal{I}m (mathcal A) subset mathbb P_2 $, а, на самом деле, это включение может быть заменено на равенство. Действительно, в соответствии с теоремой 2, имеем:
$$ mathcal{I}m (mathcal A)= {mathcal L}left(mathcal A (1),mathcal A (x),mathcal A (x^2),mathcal A (x^3) right)=
$$
$$
= {mathcal L}left(-6,,-6,x+1 ,, -4,x^2+2,x ,, 3,x^2 right) = mathbb P_2 $$
поскольку три из четырех получившихся полиномов линейно независимы.

Теперь найдем $ mathcal{K}er (mathcal A) $, или, в альтернативной формулировке, подмножество решений дифференциального уравнения
$$ x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x)=0 $$
во множестве $ mathbb P_3 $ (полиномов степени не выше третьей). Воспользуемся уже выведенной выше формулой для образа произвольного полинома $ p(x) in mathbb P_3 $.
Этот образ будет тождественно равным нулю полиномом при выполнении условий
$$ -4,a_1+3,a_0=0, 2,a_1-6,a_2=0, a_2-6,a_3=0 . $$
Решаем эту систему:
$$ a_0=frac{4}{3} a_1, a_2=frac{1}{3} a_1, a_3=frac{1}{18} a_1 . $$
Таким образом,
$$ mathcal{K}er (mathcal A) = left{ lambda (24,x^3+18,x^2+6,x+1) mid lambda in mathbb R right} . $$


♦

Т

Теорема 4. Пусть $ {X_1,dots,X_{{mathfrak{r}}}} $ — относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal{A}) $. Тогда система $ {mathcal{A}(X_1),dots,mathcal {A}(X_{{mathfrak{r}}}) } $ образует базис $ mathcal{I}m (mathcal{A}) $.

Доказательство. Любой вектор $ Xin mathbb V $ представи́м в виде $ X=X_{ast}+alpha_1X_1+dots+ alpha_{{mathfrak{ r}}}X_{{mathfrak{r}}} $, где $ X_{ast} in mathcal{K}er (mathcal{A}) $. Тогда $ mathcal{A}(X) in mathcal{L} ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak {r}}})) $ и, следовательно,
$$ mathcal{I}m (mathcal{A}) = mathcal L ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak{r}}})) . $$
Если векторы $ mathcal{A}(X_1),dots,mathcal{A}(X_{{mathfrak{r}}}) $ удовлетворяют равенству:
$$ beta_1 mathcal{A}(X_1) boxplus dots boxplus beta_{{mathfrak{r}}} mathcal{A}(X_{{mathfrak{r}}})= mathbb O’ , $$
то $ beta_1 X_1 + dots + beta_{{mathfrak{r}}} X_{{mathfrak{r}}} in mathcal{K}er (mathcal{A}) $. На основании определения относительного базиса из такого равенства необходимо следует $ beta_1 = dots = beta_{{mathfrak{r}}}=0 $. Таким образом,
система $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak{r}}}) } $ л.н.з.

♦

Т

Теорема 5. Имеет место равенство:

$$ dim mathbb V=dim left( mathcal{K}er (mathcal A) right) + dim left( mathcal{I}m (mathcal A) right) = operatorname{dfc}(mathcal A )+ operatorname{rank}(mathcal A ) .$$

Доказательство

☞



ЗДЕСЬ.

Утверждение $ mathbb V= mathcal{K}er (mathcal A) oplus mathcal{I}m (mathcal A) $ (здесь $ oplus $ означает прямую сумму подпространств ),
вообще говоря, неверно!

Т

Теорема 6. Пусть $ mathbb V_1 $ — линейное подпространство $ mathbb V_{} $, а $ mathbb W_1 $ — линейное подпространство $ mathbb W $, причем

$$
dim mathbb V_1 + dim mathbb W_1 =dim mathbb V .
$$
Тогда существует линейное отображение
$ mathcal A : mathbb V longmapsto mathbb W $ такое, что
$$
mathcal{K}er (mathcal A ) =mathbb V_1 , quad mathcal{I}m (mathcal A )=mathbb W_1 .
$$

Определенные в настоящем пункте множества $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ позволяют полностью решить и следующую задачу:

Задача. Установить множество всех прообразов вектора $ Y ne mathbb O^{prime} $ при линейном отображении $ mathcal A_{} $ .

Т

Теорема 7. Если $ Y notin mathcal{I}m(mathcal A) $, то у вектора $ Y in mathbb W $ не существует прообраза в $ mathbb V_{} $. Если $ X_{0} in mathbb V $ — какой-то из прообразов вектора $ Y_{} $, то все множество прообразов этого вектора является линейным многообразием в $ mathbb V_{} $, а именно:
$$ X_0 + mathcal{K}er (mathcal A) . $$

Матрица линейного отображения

Рассмотрим линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $,
и пусть $ {X_1,dots,X_n} $ — базис $ mathbb V_{} $, а
$ {Y_1,dots,Y_m} $ — базис $ mathbb W_{} $. Найдем координаты векторов
$ mathcal A(X_1),dots,mathcal A(X_n) $ в базисе $ {Y_1,dots,Y_m} $:
$$
left{ begin{array}{ccr}
mathcal A(X_1)&=&{color{RubineRed} alpha }_{11}Y_1 boxplus {color{RubineRed} alpha }_{21}Y_2 boxplus dots boxplus {color{RubineRed} alpha }_{m1}Y_m, \
mathcal A(X_2)&=&{color{Green} alpha }_{12}Y_1 boxplus {color{Green} alpha }_{22}Y_2 boxplus dots boxplus {color{Green} alpha }_{m2}Y_m, \
dots & & dots, \
mathcal A(X_n)&=&alpha_{1n}Y_1 boxplus alpha_{2n}Y_2 boxplus dots boxplus alpha_{mn}Y_m.
end{array} right.
$$
Матрица
$$
{mathbf A}= left(begin{array}{cccc}
{color{RubineRed} alpha } _{11} & {color{Green} alpha }_{12}& dots & alpha_{1n} \
{color{RubineRed} alpha } _{21} & {color{Green} alpha }_{22}& dots & alpha_{2n} \
vdots & & & vdots \
{color{RubineRed} alpha } _{m1} & {color{Green} alpha }_{m2}& dots & alpha_{mn}
end{array}
right)_{mtimes n},
$$
по столбцам которой стоят координаты образов базисных векторов, называется матрицей линейного отображения $ mathcal A_{} $ в выбранных базисах.

Почему запись координат в матрицу производится по столбцам? Казалось бы, естественней ставить их по строкам :- Объяснение этому решению будет дано ниже.

Т

Теорема 1. Координаты произвольного вектора

$ X=x_1X_1+dots+x_nX_n $ и его образа $ mathcal A (X)=y_1Y_1 boxplus dots boxplus y_mY_m $
связаны формулой:
$$
left(begin{array}{l}
y_1 \ vdots \ y_m
end{array}
right) =
{mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) .
$$

Вот именно для этой последней формулы необходимо было «транспонировать» запись матрицы линейного отображения в начале настоящего пункта.

Доказательство. С помощью приведенных выше формул для $ mathcal A (X_1), dots, mathcal A (X_n) $ получаем:
$$
begin{array}{rcl}
mathcal A (X)&=&mathcal A (x_1X_1+dots+x_nX_n)=x_1mathcal A (X_1) boxplus dots boxplus
x_nmathcal A (X_n)= \
&=&x_1 (alpha_{11}Y_1 boxplus dots boxplus alpha_{m1}Y_m) boxplus dots boxplus
x_n(alpha_{1n}Y_1 boxplus dots boxplus alpha_{mn}Y_m)= \
&=&underbrace{(x_1alpha_{11} +dots+x_nalpha_{1n})}_{y_1}Y_1 boxplus dots boxplus
underbrace{(x_1alpha_{m1}+dots+x_nalpha_{mn})}_{y_m}Y_m,
end{array}
$$
откуда и следует утверждение теоремы.

♦

П

Пример. Найти матрицу линейного отображения

$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right)
$$
в стандартных базисах пространств
$$
overbrace{left{underbrace{left[ begin{array}{c} 1 \ 0 \ 0 end{array} right]}_{=mathfrak e_{_1}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 end{array} right]}_{=mathfrak e_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 end{array} right]}_{=mathfrak e_{_3}}
right}}^{mathbb R^3} quad u quad
overbrace{left{
underbrace{left[ begin{array}{c} 1 \ 0 \ 0 \ 0 end{array} right]}_{={mathfrak E_{_1}}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 \0 end{array} right]}_{=mathfrak E_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 \0 end{array} right]}_{=mathfrak E_{_3}} ,
underbrace{left[ begin{array}{c} 0 \ 0 \ 0 \1 end{array} right]}_{=mathfrak E_{_4}}
right}
}^{mathbb R^4}
$$

Решение.
$$ mathcal A(mathfrak e_1)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;quad mathcal A(mathfrak e_2)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;
$$
$$
mathcal A(mathfrak e_3)=
left[ begin{array}{r} 1 \ 0 \ 1 \ -1 end{array} right]=1cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}-1cdot mathfrak E_{_4} .
$$
Матрица отображения $ mathcal A_{} $ в выбранных базисах:
$$ mathbf A=
left(begin{array}{ccr}
0 & 0 & 1 \
0 & 0 & 0 \
1& 1 & 1 \
1 & 1 & -1
end{array}
right)
$$
совпадает с матрицей коэффициентов при переменных $ x_1,x_2,x_3 $ в выражениях координат вектора $ mathcal A(X) $.

♦

П

Пример. Найти матрицу линейного отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:

$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x) . $$
Базисом пространства $ mathbb P_3 $ выбран $ {1,x,x^2,x^3} $, а базис пространства
$ mathbb P_2 $ состоит из полиномов Лежандра
$$ {P_0(x)=1, P_1(x)= x, P_2(x)=frac{1}{2}(3,x^2-1) } .$$

Решение. В предыдущем ПУНКТЕ уже были получены выражения:
$$ mathcal A(1)=-6, mathcal A(x)=-6,x+1, mathcal A(x^2)=-4,x^2+2,x
, mathcal A(x^3)=3,x^2 .$$
Если бы базис пространства $ mathbb P_2 $ составляли полиномы, входящие в базис исходного пространства,
т.е. $ {1,x,x^2} $, то матрица линейного отображения построилась бы достаточно просто:
$$
mathbf B=
left(
begin{array}{rrrr}
-6 & 1 & 0 & 0 \
0 &-6 & 2 & 0 \
0 & 0 & -4 & 3 \
end{array}
right) .
$$
Однако базис пространства $ mathbb P_2 $ отличается от $ {1,x,x^2} $ в последнем полиноме: $ P_2(x) notequiv x^2 $. Координаты $ mathcal A(1) $ и $ mathcal A(x) $ остаются прежними, а вот $ mathcal A(x^2) $ и $ mathcal A(x^3) $ приходится переписывать под базис из полиномов Лежандра:
$$ -4,x^2+2,x equiv a_{13}cdot 1 + a_{23}cdot x + a_{33} cdot left( frac{1}{2}(3,x^2-1)
right) . $$
Откуда получаем: $ a_{13}=-4/3, a_{23}=2, a_{33}=-8/3 $. Аналогично
$$ 3,x^2equiv P_0(x)+2,P_2(x) $$
и, следовательно, матрица линейного отображения:
$$
mathbf A=
left(
begin{array}{rrrr}
-6 & 1 & -4/3 & 1 \
0 &-6 & 2 & 0 \
0 & 0 & -8/3 & 2 \
end{array}
right) .
$$


♦

Т

Теорема 2. Существует изоморфизм между линейным пространством $ {mathcal H}om(mathbb V,mathbb W) $ (линейных отображений из $ mathbb V_{} $ в $ mathbb W_{} $)
и линейным пространством матриц $ mathbb R^{mtimes n } $.

Фактически теоремы $ 1_{} $ и $ 2_{} $ сводят рассмотрение произвольного линейного отображения $ mathcal A_{} $ пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ к рассмотрению отображения арифметического пространства $ n_{} $-компонентных столбцов в арифметическое пространство $ m_{} $-компонентных столбцов
$$ Y=mathbf AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m ; $$
это отображение задается $ mtimes n_{} $-матрицей $ mathbf A_{} $. Получается, что для полного задания исходного линейного отображения достаточно знать только результат его действия на базисные векторы пространства $ mathbb V_{} $. После фиксирования базисов обоих пространств и установления матрицы линейного отображения, можно «забыть» о природе этих пространств и исследовать свойства отображения в «переводе на язык» умножения матрицы на столбец. В частности, «почти даром» получаем следующий результат:

Т

Теорема 3. Если $ A_{} $ — матрица линейного отображения $ mathcal A_{} $ в каких-то выбранных базисах пространств $ mathbb V_{} $ и $ mathbb W_{} $, то

$$operatorname{rank} (mathcal A)=operatorname{rank}( A ), operatorname{dfc} (mathcal A)=n-operatorname{rank}( A ) .$$

Ядро линейного отображения
$$ Y=AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m, quad A in mathbb R^{mtimes n } $$
часто называется ядром матрицы $ A_{} $ или нуль-пространством матрицы $ A_{} $ и также обозначается $ {mathcal K}er (A) $. Наряду с определением ядра матрицы через свойства отображения
$ AX $, можно дать ему и другую интерпретацию:

Т

Теорема 4. Если в пространстве $ mathbb R_{}^{n} $, рассматриваемом как пространство $ n_{} $-строк, ввести скалярное произведение формулой

$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=[x_1,x_2,dots,x_n], Y=[y_1,y_2,dots,y_n] , $$
то $ {mathcal K}er (A) $ образует ортогональное дополнение линейной оболочки строк этой матрицы в пространстве $ mathbb R_{}^{n} $:
$$ {mathcal K}er (A) bot mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ),
{mathcal K}er (A) oplus mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ) = mathbb R_{}^{n} .
$$

Дефектом матрицы4) $ A_{} $ будем называть размерность ядра этой матрицы, или, что то же, число элементов фундаментальной системы решений системы линейных однородных уравнений $ AX=mathbb O $. В соответствии с результатами, приведенными

☞



ЗДЕСЬ:
$$ operatorname{dfc}(A) = n – mathfrak r npu mathfrak r = operatorname{rank}(A) . $$

Вернемся теперь к общему случаю линейного пространства.

Задача. Как изменяется матрица линейного отображения $ mathcal A_{} $ при изменении
базисов?

Т

Теорема 5. Пусть $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ — новый базис пространства $ mathbb V_{} $, $ { {mathfrak Y}_1,dots,{mathfrak Y}_m } $— новый базис $ mathbb W_{} $, и в этих
базисах линейное отображение $ mathcal A $ имеет матрицу $ {mathbf B} $. Если $ C_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb V_{} $, а $ D_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb W_{} $, то

$$ {mathbf B}=D^{-1}cdot {mathbf A} cdot C . $$

Доказательство. Действительно, координаты произвольного вектора
$$ X=x_1X_1+dots+x_nX_n = {mathfrak x}_1 {mathfrak X}_1+dots+ {mathfrak x}_n {mathfrak X}_n ,$$
и его образа
$$ Y =mathcal A(X)=y_1Y_1 boxplus dots boxplus y_mY_m= {mathfrak y}_1{mathfrak Y}_1 boxplus dots boxplus {mathfrak y}_m{mathfrak Y}_m $$
связаны следующими соотношениями: с одной стороны, на основании теоремы 1,
$$
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right) = {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right), qquad
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) = {mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right) .
$$
с другой стороны, на основании результатов пункта

☞



ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ЗАМЕНЕ БАЗИСА,
$$
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right),
qquad
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right).
$$
Получаем цепочку равенств:
$$
{mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right)=
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) =D^{-1}left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D^{-1} {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=D^{-1} {mathbf A} C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right).
$$
Поскольку равенство справедливо для любого столбца координат, то оно справедливо и для столбцов
$$
left(begin{array}{c}
1 \ 0 \ vdots \ 0
end{array}
right) ,
left(begin{array}{c}
0 \ 1 \ vdots \ 0
end{array}
right)
,dots,
left(begin{array}{c}
0 \ 0 \ vdots \ 1
end{array}
right) .
$$
Объединяя полученные $ n_{} $ равенств в одно матричное, получаем $ {mathbf B}E = D^{-1} {mathbf A} C E $, где $ E_{} $ — единичная матрица порядка $ n_{} $. Отсюда и следует утверждение теоремы.

♦

Канонический вид матрицы линейного отображения

Задача. Подобрать базисы пространств $ mathbb V_{} $ и $ mathbb W_{} $ так, чтобы матрица заданного линейного отображения $ mathcal A $ имела наиболее простой вид.

Найдем относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal A) $, т.е. базис $ mathcal{K}er (mathcal A) $ дополним до базиса $ mathbb V_{} $:
$$
{X_1,dots,X_{{mathfrak r}}} gets mbox{ относительный базис }
mathbb V mbox{ над } mathcal{K}er (mathcal A)
$$
$$
{X_{{mathfrak r}+1},dots,X_{n} } gets mbox{ базис } mathcal{K}er (mathcal A)
$$
Было доказано (см.

☞



теорему 4 ), что $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}}) } subset mathbb W $ является базисом $ mathcal{I}m (mathcal A) $. Составим базис $ mathbb W_{} $ ее дополнением:
$$
{mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}})} gets
mbox{ базис } mathcal{I}m (mathcal A)
$$
$$
{ Y_{{mathfrak r}+1},dots,Y_{m}} gets mbox{ относительный базис }
mathbb W mbox{ над } mathcal{I}m (mathcal A)
$$

Т

Теорема. В выбранных базисах матрица линейного отображения $ mathcal A $ имеет следующий канонический вид:

$$
{mathbf B}=left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) .
$$
Здесь $ {mathfrak r}= operatorname{rank} (mathcal A) $.

Доказательство. Разложим образы базисных векторов $ {X_1,dots,X_n} $ по базису пространства $ mathbb W $:
$$
begin{array}{llllllll}
mathcal A(X_1) & = 1cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplusdots &boxplus 0cdot Y_m, \
mathcal A(X_2) & = 0cdot mathcal A(X_1) & boxplus 1 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m, \
dots & & & dots \
mathcal A(X_{mathfrak r}) & = 0cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 1cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m,
end{array}
$$
а $ mathcal A(X_{{mathfrak r}+1})=mathbb O^{prime},dots, mathcal A(X_{m})=mathbb O^{prime} $ по определению
$ mathcal{K}er (mathcal A) $.

♦

Матричный формализм

§

Настоящий пункт может быть пропущен при первоначальном чтении.

В частном случае отображения $ mathbb R^{n} $ в $ mathbb R^{m} $, задаваемого матрицей в стандартных базисах пространств, результат последнего пункта можно переформулировать в следующем виде.

Т

Теорема. Любую матрицу $ A_{mtimes n} $ ранга $ mathfrak r > 0 $ можно представить в виде произведения

$$ A=Dcdot A_d cdot tilde C $$
при
$$
A_d =left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) $$
и при невырожденных матрицах $ D_{mtimes m} $ и $ tilde C_{ntimes n} $.

Здесь матрица $ tilde C $ соответствует матрице $ C^{-1} $ из теоремы предыдущего пункта.

П

Пример. Представить матрицу

$$ A =
left(
begin{array}{rrr}
2 & – 1 & 0 \
-2/3 & 5/3 & 4/3 \
2 & – 1 & 0 \
-2/3 & 5/3 & 4/3
end{array}
right)
$$
в виде произведения из теоремы.

Решение. Здесь $ operatorname{rank} (A) =2 $, так что
$$
A_d=
left(begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 0 \
0 & 0 & 0
end{array}
right) , .
$$
Для нахождения матрицы $ C $ из теоремы предыдущего пункта ищем базис ядра отображения $ AX $, т.е. попросту говоря, фундаментальную систему решений системы уравнений $ AX=mathbb O $. Можно взять $ X=[1,2,-2]^{top} $. Этот столбец будет третьим столбцом матрицы $ C $. Первые два — любые линейно независимые с этим столбцом. Например
$$
C=
left(begin{array}{ccr}
1 & 0 & 1 \
0 & 1 & 2 \
0 & 0 & -2
end{array}
right) , .
$$
Теперь умножаем столбцы $ C_{[1]} $ и $ C_{[2]} $ на матрицу $ A $ (слева). Полученные столбцы
$$
D_{[1]}=left[2,-2/3,2,-2/3right]^{top}, D_{[2]}=left[-1,5/3,-1,5/3right]^{top}
$$
будут первыми столбцами искомой матрицы $ D $. Оставшиеся два выбираем произвольными линейно независимыми с уже найденными.
$$
D=
left(
begin{array}{rrrr}
2 & – 1 & 1 & 0 \
-2/3 & 5/3 & 0 & 1 \
2 & -1 & 0 & 0 \
-2/3 & 5/3 & 0 & 0
end{array}
right), quad tilde C= C^{-1} =
left(
begin{array}{rrr}
– 1 & 0 & 1/2 \
0 & 1 & 1 \
0 & 0 & -1/2
end{array}
right) , .
$$


♦

Разложение матрицы в произведение из теоремы не единственно. Так, например, матрицу $ tilde C $ можно выбрать в классе ортогональных матриц. Из этого замечания можно «перебросить мостик» к похожему разложению матрицы в произведение, известному как сингулярное разложение. Очень полезно в задачах обработки данных.

Линейный оператор

Линейное отображение векторного пространства $ mathbb V_{} $
в себя
$$ mathcal A : mathbb V longmapsto mathbb V $$
называется линейным преобразованием $ mathbb V_{} $ или линейным оператором на $ mathbb V_{} $. Подробнее

☞



ЗДЕСЬ.

Аффинное отображение

Линейные отображения пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ составляют подмножество более широкого класса отображений.

Рассмотрим пример $ 5_{} $

☞



ЗДЕСЬ. Отображение пространства $ mathbb R^{n}_{} $ в пространство $ mathbb R^{m} $, задаваемое соотношением
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
будет линейным отображением при условии, что $ b_1=0,dots, b_m=0 $ и не будет линейным отображением при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля.
Тем не менее, по своему внешнему виду отображение из $ mathbb R^{n}_{} $ в $ mathbb R^{m} $, задаваемое в матричном виде как $ A, X + mathcal B $ напоминает линейную функцию $ a, x+b $, действующую в $ mathbb R $. Кажется очень несправедливым лишать подобные отображения эпитета линейный, однако же именно это и произошло в линейной алгебре и геометрии.

Аффинным5) отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция вида
$$ mathcal A(X) boxplus_{} mathcal B npu X in mathbb V . $$
Здесь $ mathcal A $ — линейное отображение $ mathbb V_{} $ в $ mathbb W_{} $, а $ mathcal B $ — некоторый вектор пространства $ mathbb W_{} $.

Образно говоря, аффинное отображение может быть получено сдвигом некоторого линейного отображения. Фактически же определение содержит в себе объяснение той причины, по которой аффинные отображения изучаются менее подробно, чем линейные: первые сводятся ко вторым.

Основное геометрическое свойство аффинного отображения проявилось в

☞



ПУНКТЕ для отображения линейного.

Т

Теорема. Аффинное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $. Аффинное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.

=>

Аффинное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.

Почему рассматриваются только линейные отображения?

Почему во всех вузовских курсах алгебры не рассматриваются более сложные отображения, задаваемые, например, нелинейными полиномами:
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 – 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) ?
$$
— Да потому что про них мало что понятно. Попытки обобщения на нелинейный случай практически любого понятия, введенного для линейного отображения, приводят к нерешенной задаче. Так, для обобщения понятия ядра придется решить не решенную на настоящий момент 16-ю проблему Гильберта;
еще одна нерешенная проблема — проблема якобиана — связана с существованием обратного к полиномиальному отображению.

В одном частном случае нелинейные отображения сравнительно хорошо изучены — это отображения $ mathbb R^2 mapsto mathbb R^2 $, заданные условиями:
$$
left(
begin{array}{l}
x \
y
end{array}
right) mapsto
left(
begin{array}{l}
u(x,y) \
v(x,y)
end{array}
right) quad npu quad frac{partial u}{partial x}=frac{partial v}{partial y}, frac{partial u}{partial y}=-frac{partial v}{partial x} ;
$$
(функции $ u_{} $ и $ v_{} $ — не обязательно полиномы).
Последние два условия называются условиями Коши-Римана (Даламбера-Эйлера); из них следует, что каждая из функций $ u_{} $ и $ v_{} $ является гармонической функцией, т.е. удовлетворяет тождествам:
$$
frac{partial^2 u}{partial x^2}+frac{partial^2 u}{partial y^2}equiv 0,quad frac{partial^2 v}{partial x^2}+frac{partial^2 v}{partial y^2} equiv 0 .
$$
Подобные отображения рассматриваются в разделе математики, известном как КОМПЛЕКСНЫЙ АНАЛИЗ или теория функций комплексной переменной (ТФКП).

Как же исследовать нелинейные отображения в общем случае? — Ну, по крайней мере, можно попытаться свести их исследование к линейному случаю. Рассмотрим пример отображения из начала
пункта
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 – 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) =
$$
$$
=left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)
+
left(
begin{array}{c}
2, x_1 – 3,x_3 \
-x_1-5,x_2 \
x_3 \
x_1-2,x_2+6,x_3
end{array}
right)
+ dots
$$
В разложении каждого элемента вектора отбросим все члены степени выше первой. В результате мы получили отображение, которое можно представить в матричном виде
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
underbrace{left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)}_{=mathcal B}+
underbrace{left(
begin{array}{rrr}
2 & 0 & – 3 \
-1 & -5 & 0 \
0 & 0 & 1 \
1 & -2 & 6
end{array}
right)}_{=A}
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) .
$$
Это новое отображение является аффинным отображением пространства $ mathbb R^{3} $ в пространство $ mathbb R^{4} $. Таким образом, исходное, существенно нелинейное, отображение $ mathcal F(X) $ фактически заменили аффинным $ tilde{mathcal A}(X)=AX+mathcal B $. Насколько такая замена оправдана? — Ну, по крайней мере, в одной точке эти отображения совпадают: $ mathcal F(mathbb O) = tilde {mathcal A}(mathbb O) $. Трудно ожидать, что они будут совпадать еще где-нибудь. Однако же, в малой окрестности точки $ mathbb O $ значения этих двух функций оказываются близкими!
$$
begin{array}{lll}
mathcal F left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000994 \
2.090000000 \
-5.930006860 \
-32.53000000
end{array}
right); &
mathcal F left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.47907577 \
1.349999642 \
-6.140329280 \
-34.03000000
end{array}
right); & mathcal F left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.82475143 \
1.049938741 \
-6.243456000 \
-35.24000000
end{array}
right) ; dots
\
tilde{mathcal A}
left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000000 \
2.090000000 \
-5.930000000 \
-32.53000000
end{array}
right) ; &
tilde{mathcal A}
left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.48000000 \
1.350000000\
-6.140000000 \
-34.03000000
end{array}
right) &
tilde{mathcal A} left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.88000000 \ 1.050000000 \ -6.240000000 \ -35.24000000
end{array}
right); dots
end{array}
$$
Иными словами, в некоторой достаточно малой окрестности6) точки $ X_0=mathbb O_{} $ нелинейное отображение аппроксимируется аффинным. А чем аппроксимировать за пределами этой окрестности, скажем, в окрестности вектора $ X_0=[1,-1,1]^top $? — Для этого придется привлекать аппарат разложения нелинейных функций нескольких переменных в ряды Тейлора. К счастью, функции нашего примера являются полиномиальными, поэтому этот ряд не будет содержать бесконечного числа членов. Воспользовавшись материалом пункта

☞



ФОРМУЛА ТЕЙЛОРА, получим:
$$
mathcal F left(
begin{array}{r}
x_1 \
x_2\
x_3
end{array}
right)
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{rrr}
(6-2,sqrt{2})(x_1-1) &+ 85, (x_2+1) & +(-sqrt{2}-3)(x_3-1)\
&-34,(x_2+1) & +6,(x_3-1) \
&(x_2+1) & -2,(x_3-1)\
(x_1-1) &- 2,(x_2+1) & +6,(x_3-1)
end{array}
right)+ dots
$$
Перепишем второе слагаемое в матричном виде:
$$
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{ccc}
6-2,sqrt{2} &85& -sqrt{2}-3\
0 &-34 & 6 \
0&1& -2\
1 &- 2 & 6
end{array}
right)left(
begin{array}{c}
x_1-1 \
x_2+1 \
x_3-1
end{array}
right) + dots
$$
В общем же случае, если
$$
mathcal{F} left(
begin{array}{l}
x_1 \
x_2\
vdots \
x_n
end{array}
right)=
left(
begin{array}{c}
f_1(x_1,dots,x_n) \
vdots \
f_m(x_1,dots,x_n)
end{array}
right),
$$
то, в окрестности вектора $ X_0= (x_{01},x_{02},dots,x_{0n})^{top} $ его можно аппроксимировать аффинным отображением
$$
tilde{mathcal A} left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)=
underbrace{left(
begin{array}{c}
f_1(x_{01},dots,x_{0n}) \
vdots \
f_m(x_{01},dots,x_{0n})
end{array}
right)}_{=mathcal F(X_0)}+
underbrace{left(
begin{array}{cccc}
{partial f_1}/{partial x_1} & {partial f_1}/{partial x_2} & dots & {partial f_1}/{partial x_n} \
{partial f_2}/{partial x_1} & {partial f_2}/{partial x_2} & dots & {partial f_2}/{partial x_n} \
dots & && dots \
{partial f_m}/{partial x_1} & {partial f_m}/{partial x_2} & dots & {partial f_m}/{partial x_n}
end{array}
right)}_{mathbf J}left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right) ,
$$
которое рассматривается в окрестности $ Y_0=mathbb O_{} $. Здесь все частные производные в матрице $ mathbf J $ вычисляются в точке $ X_{0} $. Матрица
$$
mathbf J = left[ frac{partial f_j}{partial x_k} right]_{j=1,dots,m, atop k=1,dots,n}
$$
называется матрицей Якоби системы из $ m_{} $ функций $ {f_1(x_1,dots,x_n),dots,f_m(x_{1},dots,x_n)} $ по переменным $ x_1,dots,x_{n} $. Линейное отображение
$$
mathbf J left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)
$$
известно как дифференциал (первого порядка) функции $ mathcal F(X) $ в точке $ X_0 $.

Подводя итог, можно сказать, что линейные (аффинные) отображения служат основой анализа отображений нелинейных — но этот анализ носит локальный характер: линеаризация адекватно приближает исходное нелинейное отображение лишь в малых областях значений аргументов.

Задачи

Источник

  1. Ортогональные преобразования.

    Начать изучение

  2. Определение линейных преобразований.

    Начать изучение

  3. Произведение линейных преобразований.

    Начать изучение

  4. Образ вектора при линейном преобразовании.

    Начать изучение

Ортогональные преобразования.

Определение.

Ортогональными называются такие преобразования плоскости, которые не меняют расстояния между любыми двумя точками, то есть преобразования (f) ортогональное, если для любых точек (A) и (B) выполнено (|AB|=|f(A)f(B)|).

Основными примерами ортогональных преобразований служат параллельный перенос, поворот и осевая симметрия.

Получим координатную запись ортогонального преобразования в декартовой прямоугольной системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Обозначим через (A) и (B) концы базисных векторов: (boldsymbol{e}_{1}=overrightarrow{OA}), (boldsymbol{e}_{2}=overrightarrow{OB}) (рис. 12.1). При ортогональном преобразовании равнобедренный прямоугольный треугольник (OAB) перейдет в равный ему треугольник (O^{*}A^{*}B^{*}). Рассмотрим произвольную точку (M(x, y)). Она перейдет в точку (M^{*}) с координатами ((x^{*}, y^{*})). Нам надо выразить ((x^{*}, y^{*})) через ((x, y)).

ортогональное преобразование

Рис. 12.1. Ортогональное преобразование.

По определению координат (overrightarrow{OM}=xoverrightarrow{OA}+yoverrightarrow{OB}). Отсюда следует, что (overrightarrow{O^{*}M^{*}}=xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}). Действительно, векторы (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) взаимно перпендикулярны и по длине равны 1, а потому компоненты (overrightarrow{O^{*}M^{*}}) по этим векторам равны его скалярным проекциям на них. Эти проекции равны проекциям (overrightarrow{OM}) на (boldsymbol{e}_{1}, boldsymbol{e}_{2}), что видно из равенства соответствующих треугольников. Теперь мы можем написать
$$
overrightarrow{OM^{*}}=overrightarrow{OO^{*}}+overrightarrow{O^{*}M^{*}}=overrightarrow{OO^{*}}+xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}.label{ref1}
$$

Обозначим через (varphi) угол между (overrightarrow{O^{*}A^{*}}) и (boldsymbol{e}_{1}). Поскольку (|overrightarrow{O^{*}A^{*}}|=1), координаты этого вектора в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}) равны ((cos varphi, sin varphi)). Тогда перпендикулярный вектор единичной длины (overrightarrow{O^{*}B^{*}}) имеет координаты ((mp sin{y}, pm cos{y})), причем верхние знаки берутся в том случае, когда пара векторов (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) ориентирована так же, как (boldsymbol{e}_{1}, boldsymbol{e}_{2}). Координаты точки (O^{*}) обозначим через ((c_{1}, c_{2})).

Теперь мы можем разложить все члены равенства eqref{ref1} по базису:
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}label{ref2}
$$

Итак, мы доказали следующее утверждение.

Утверждение 1.

Произвольное ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами eqref{ref2}, где (varphi) — угол, на который поворачивается первый базисный вектор, a (c_{1}) и (c_{2}) — координаты образа начала координат. При этом выбираются верхние знаки, если образы базисных векторов ориентированы так же, как и сами эти векторы, и нижние знаки в противоположном случае.

Пример 1.

Параллельный перенос на вектор с сопоставляет точке (M) с координатами ((x, y)) в некоторой декартовой системе координат точку (M^{*}) с координатами
$$
x^{*}=x+c_{1}, y^{*}=y+c_{2},nonumber
$$
где (c_{1}) и (c_{2}) — координаты (c).

Пример 2.

Напишем уравнения поворота плоскости на угол (varphi) вокруг некоторой точки, приняв эту точку за начало декартовой прямоугольной системы координат. В этом случае (O=O^{*}) и, следовательно, (c_{1}=c_{2}=0). Должны быть выбраны верхние знаки. Итак
$$
x^{*}=x cos{varphi}-y sin{varphi}, y^{*}=x sin{varphi}+y cos{varphi},nonumber
$$

Пример 3.

Рассмотрим осевую симметрию относительно некоторой прямой. Примем ось симметрии за ось абсцисс декартовой прямоугольной системы координат. Тогда точка (M(x, y)) переходит в точку (M^{*}) с координатами
$$
x^{*}=x, y^{*}=-y.nonumber
$$
Здесь (c_{1}=c_{2}=0) и (varphi=0) при нижних знаках в формулах eqref{ref2}.

Определение линейных преобразований.

Основным объектом для нас будет более широкий класс преобразований, включающий в себя ортогональные преобразования.

Определение.

Преобразование (f) плоскости (P) называется линейным, если на (P) существует такая декартова система координат, в которой (f) может быть записано формулами
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}label{ref3}
$$
Взаимно однозначное линейное преобразование называется аффинным преобразованием.

Подчеркнем, что в определении линейного преобразования, вовсе не требуется, чтобы коэффициенты в формулах eqref{ref3} не обращались в нуль одновременно. Они могут быть любыми. Докажем следующее утверждение.

Утверждение 2.

Для того чтобы преобразование, задаваемое формулами eqref{ref3}, было взаимно однозначным, необходимо и достаточно,
$$
begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix} neq 0.label{ref4}
$$

Таким образом, аффинное преобразование определяется формулами eqref{ref3} при условии eqref{ref4}.

Доказательство.

Наше утверждение вытекает по существу из утверждения о существовании решения системы линейных уравнений. Нам нужно узнать, при каком условии каждая точка плоскости имеет единственный прообраз. Формулы eqref{ref3} связывают координаты ((x^{*}, y^{*})) точки (M^{*}) и координаты ((x, y)) ее прообраза. Их можно рассматривать как систему линейных уравнений для нахождения (x) и (y), и эта система имеет единственное решение при любых свободных членах (x^{*}-c_{1}) и (y^{*}-c_{2}) (а значит, при любых (x^{*}) и (y^{*})) тогда и только тогда, когда выполнено условие eqref{ref4}.

Как видно из доказанного утверждения, ортогональные преобразования являются линейными. Проверка условия eqref{ref4} показывает, что они аффинные. Рассмотрим другие примеры.

Пример 4.

Рассмотрим сжатие к прямой и примем эту прямую за ось абсцисс декартовой прямоугольной системы координат. Легко видеть, что в такой системе координат сжатие с коэффициентом (lambda) записывается формулами
$$
x^{*}=x, y^{*}=lambda y.nonumber
$$
Сжатие к прямой — аффинное преобразование.

Пример 5.

Проектирование на прямую в такой декартовой прямоугольной системе координат, для которой эта прямая — ось абсцисс, записывается формулами
$$
x^{*}=x, y^{*}=0.nonumber
$$
Это — линейное, но не аффинное преобразование.

Пример 6.

Для записи уравнений гомотетии не существенно, чтобы система координат была прямоугольной, но уравнения проще, если начало координат поместить в центр гомотетии. По определению гомотетии с коэффициентом (lambda) вектор (overrightarrow{OM}) переходит в вектор (overrightarrow{OM^{*}}=lambdaoverrightarrow{OM}). Если (O) — начало координат, координаты точек (M) и (M^{*}) будут связаны равенствами
$$
x^{*}=lambda x, y^{*}=lambda y.nonumber
$$
Гомотетия — аффинное преобразование.

Пример 7.

Преобразование, сопоставляющее каждой точке плоскости одну и ту же точку (C), записывается формулами (x^{*}=c_{1}), (y^{*}=c_{2}), где (c_{1}) и (c_{2}) — координаты точки (C). Оно линейное, но не аффинное.

Определение аффинного преобразования содержит упоминание о некоторой определенной системе координат, и заранее не известно, будет ли преобразование записываться формулами вида eqref{ref3} в какой-либо другой системе координат. Давайте докажем следующее утверждение.

Утверждение 3.

В любой декартовой системе координат, линейное преобразование задается формулами вида eqref{ref3}, то есть:
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}nonumber
$$

Доказательство.

Пусть преобразование задано равенствами eqref{ref3} в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Перейдем к системе координат (O’, boldsymbol{e}’_{1}, boldsymbol{e}’_{2}). Как мы знаем, старые координаты точки (M(x, y)) выражаются через новые координаты ((x’, y’)) по следующим формулам:
$$
x=alpha_{1}x’+beta_{1}y’+gamma_{1}, y=alpha_{2}x’+beta_{2}y’+gamma_{2}.label{ref5}
$$
Для образа (M^{*}) точки (M) нам нужно будет, наоборот, выразить новые координаты ((x’^{*}, y’^{*})) через его старые координаты ((x^{*}, y^{*})). Они выражаются такими же формулами, разумеется, с другими коэффициентами:
$$
x’^{*}=lambda_{1}(x^{*})+mu_{1}y^{*}+nu_{1}, y’^{*}=lambda_{2}x^{*}+mu_{2}y^{*}+nu_{2}.label{ref6}
$$

Нам требуется найти выражение новых координат ((x’^{*}, y’^{*})) точки (M^{*}) через новые координаты ((x’, y’)) точки (M). С этой целью подставим в равенства eqref{ref6} значения (x^{*}) и (y^{*}) из формул eqref{ref3}:
$$
begin{array}{cc}
& x’^{*}=lambda_{1}(a_{1}x+b_{1}y+c_{1})+mu_{1}(a_{2}x+b_{2}y+c_{2})+nu_{1},\
& y’^{*}=lambda_{2}(a_{1}x+b_{1}y+c_{1})+mu_{2}(a_{2}x+b_{2}y+c_{2})+nu_{2}.
end{array}nonumber
$$

Для нас важно, что правые части этих равенств — многочлены степени не выше 1 относительно (x) и (y):
$$
x’^{*}=A_{1}x+B_{1}y+C_{1}, y’^{*}=A_{2}x+B_{2}y+C_{2}.label{ref7}
$$
Подставив сюда выражения (x) и (y) по формулам eqref{ref5}, мы найдем искомую зависимость:
$$
begin{array}{cc}
& x’^{*}=A_{1}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{1}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{1},\
& y’^{*}=A_{2}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{2}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{2}.
end{array}nonumber
$$
Мы видим, что правые части этих равенств — многочлены степени не выше 1 относительно (x’) и (y’). Это нам и требовалось доказать.

Заметим, что аффинные преобразования выделяются из линейных требованием взаимной однозначности, которое не зависит от системы координат. Поэтому без дополнительных проверок мы можем быть уверены, что формулы, задающие аффинное преобразование в новой системе координат, удовлетворяют условию eqref{ref4}.

Произведение линейных преобразований.

Доказательство  последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.

Утверждение 4.

Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.

Доказательство.

Пусть заданы линейные преобразования (f) и (g) и выбрана система координат. Тогда координаты точки (f(M)) выражаются через координаты точки (M) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}.label{ref8}
$$
а координаты точки (g(f(M))) через координаты точки (f(M)) формулами
$$
x^{**}=d_{1}x^{*}+e_{1}y^{*}+f_{1}, y^{**}=d_{2}x^{*}+e_{2}y^{*}+f_{2}.label{ref9}
$$
Подстановка равенств eqref{ref9} в eqref{ref8} выражает координаты g(f(M)) через координаты (M). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.

Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного утверждения произведение двух взаимно однозначных преобразований взаимно однозначно.

Утверждение 5.

Преобразование, обратное аффинному преобразованию, также является аффинным.

Если преобразование (f) записано уравнениями eqref{ref3}, то координатная запись его обратного преобразования получается решением уравнений eqref{ref3} относительно (x) и (y). Для того чтобы решить эти уравнения, умножим первое из них на (b_{2}), второе — на (b_{1}) и вычтем одно уравнение из другого. Мы получим ((a_{1}b_{2}-a_{2}b_{1})x=b_{2}(x^{*}-c_{1})-b_{1}(y^{*}-c_{2})). Из условия eqref{ref4} следует, что (x) — линейный многочлен от (x^{*}) и (y^{*}). Выражение для (y) получается аналогично.

Образ вектора при линейном преобразовании.

Рассмотрим вектор (overrightarrow{M_{1}M_{2}}). Если координаты точек (M_{1}) и (M_{2}) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) обозначить соответственно (x_{1}, y_{1}) и (x_{2}, y_{2}), то компоненты вектора будут равны (x_{2}-x_{1}) и (y_{2}-y_{1}). Пусть формулы eqref{ref3} задают преобразование (f) в выбранной системе координат. Тогда образы (M_{2}^{*}) и (M_{1}^{*}) точек (M_{2}) и (M_{1}) имеют абсциссы
$$
x_{2}^{*}=a_{1}x_{2}+b_{1}y_{2}+c_{1}, x_{1}^{*}=a_{1}x_{1}+b_{1}y_{1}+c_{1}.nonumber
$$
Следовательно, первая компонента вектора (overrightarrow{M_{1}^{*}M_{2}^{*}}) равна
$$
x_{2}^{*}-x_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{1}(y_{2}-y_{1}).nonumber
$$
Аналогично находим вторую компоненту этого вектора
$$
y_{2}^{*}-y_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{2}(y_{2}-y_{1}).nonumber
$$

Обратим внимание на то, что компоненты (overrightarrow{M_{1}^{*}M_{2}^{*}}) выражаются только через компоненты (overrightarrow{M_{1}M_{2}}), а не через координаты точек (M_{1}) и (M_{2}) по отдельности. Два равных вектора имеют одинаковые компоненты и, следовательно, при линейном преобразовании перейдут в векторы, компоненты которых также одинаковы. Итак, мы получаем ещё одно утверждение.

Утверждение 6.

При линейном преобразовании равные векторы переходят в равные векторы. Компоненты (alpha_{1}^{*}), (alpha_{2}^{*}) образа вектора выражаются через его компоненты (alpha_{1}), (alpha_{2}) формулами
$$
begin{array}{cc}
& alpha_{1}^{*}=a_{1}alpha_{1}+b_{1}alpha_{2},\
& alpha_{2}^{*}=a_{2}alpha_{1}+b_{2}alpha_{2}.
end{array}label{ref10}
$$

Если быть точным, говорить об образе вектора при преобразовании (f) неправильно: преобразование отображает точки, а не векторы. Точнее было бы сказать, что (f) порождает преобразование (tilde{f}) множества векторов. Но ниже мы, тем не менее, будем придерживаться не совсем точной, но более удобной и общепринятой терминологии — говорить, что преобразование (f) переводит вектор (boldsymbol{a}) в вектор (boldsymbol{a}^{*}) и обозначать последний через (f(boldsymbol{a})).

Из формул eqref{ref10} вытекает, что для линейного преобразования (f) при любых векторах (boldsymbol{a}) и (boldsymbol{b}) и любом числе (lambda)
$$
begin{array}{cc}
& f(boldsymbol{a}+boldsymbol{b})=f(boldsymbol{a})+f(boldsymbol{b}),\
& f(lambdaboldsymbol{a})=lambda f(boldsymbol{a}).
end{array}label{ref11}
$$

Докажем, например, первое из этих равенств. Пусть (gamma_{1}^{*}) и (gamma_{2}^{*}) — компоненты вектора (f(boldsymbol{a}+boldsymbol{b})). Тогда
$$
gamma_{1}^{*}=a_{1}(alpha_{1}+beta_{1})+b_{1}(alpha_{2}+beta_{2}), gamma_{2}^{*}=a_{2}(alpha_{1}+beta_{1})+b_{2}(alpha_{2}+beta_{2}),nonumber
$$
где (alpha_{1}, alpha_{2}) и (beta_{1}, beta_{2}) — компоненты векторов (boldsymbol{a}) и (boldsymbol{b}). Отсюда
$$
begin{array}{cc}
& gamma_{1}^{*}=(a_{1}alpha_{1}+b_{1}alpha_{2})+(a_{1}beta_{1}+b_{1}beta_{2})=alpha_{1}^{*}+beta_{1}^{*},\
& gamma_{2}^{*}=(a_{2}alpha_{1}+b_{2}alpha_{2})+(a_{2}beta_{1}+b_{2}beta_{2})=alpha_{2}^{*}+beta_{2}^{*}.
end{array}nonumber
$$
Это — координатная запись доказываемого равенства. Второе из равенств eqref{ref11} доказывается аналогично.

Из равенств eqref{ref11} следует, что при линейном преобразовании (f) линейно зависимые векторы переходят в линейно зависимые. Действительно, как легко видеть, (f(boldsymbol{0})=boldsymbol{0}). Тогда любое соотношение вида (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}) влечет за собой (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}).

Если преобразование аффинное, то линейно независимые векторы переходят в линейно независимые. В самом деле, в противном случае из равенства (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}), (lambda^{2}+mu^{2} neq 0), при обратном преобразовании мы получили бы (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}).

Следующее утверждение устанавливает геометрический смысл коэффициентов в формулах, задающих линейное преобразование.

Утверждение 7.

Пусть преобразование (f) записано в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) формулами eqref{ref3}. Тогда (c_{1}) и (c_{2}) — координаты точки (f(O)), a (a_{1} a_{2}) и (b_{1}, b_{2}) — компоненты векторов (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).

Доказательство.

Для доказательства подставим в формулы eqref{ref3} значения (x=0) и (y=0) координат точки (O) и увидим, что координаты (f(O)) равны (c_{1}) и (c_{2}).

Подставим в формулы eqref{ref10} координаты вектора (boldsymbol{e}_{1}) (alpha_{1}=1), (alpha_{2}=0) и найдем (a_{1}^{*}=a_{1}), (a_{2}^{*}=a_{2}). Следовательно, (f(boldsymbol{e}_{1})) имеет компоненты (a_{1}) и (a_{2}). Так же доказывается, что компоненты (f(boldsymbol{e}_{2})) равны (b_{1}) и (b_{2}).

Утверждение 8.

Каковы бы ни были три точки (L), (M), (N), не лежащие на одной прямой, и три точки (L^{*}), (M^{*}) и (N^{*}), существует единственное линейное преобразование (f) такое, что (L^{*}=f(L)), (M^{*}=f(M)) и (N^{*}=f(N)). Это преобразование аффинное тогда и только тогда, когда точки (L^{*}), (M^{*}) и (N^{*}) также не лежат на одной прямой.

Доказательство.

Векторы (overrightarrow{LM}) и (overrightarrow{LN}) не коллинеарны. Следовательно, (L), (overrightarrow{LM}), (overrightarrow{LN}) — декартова система координат. Пусть (c_{1}, c_{2}) — координаты (L^{*}), а (a_{1}, a_{2}) и (b_{1}, b_{2}) — компоненты векторов (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) в этой системе координат. Формулы
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}nonumber
$$
определяют линейное преобразование (f), которое, как легко видеть, обладает требуемым свойством. При этом согласно предложению 7, коэффициенты в формулах однозначно определены.

Условие eqref{ref4}, равносильное аффинности преобразования, необходимо и достаточно для того, чтобы векторы (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) были не коллинеарны, то есть (L^{*}), (M^{*}) и (N^{*}) не лежали на одной прямой. Предложение доказано.

Заметим, что в том случае, когда преобразование (f) аффинное, точка (f(O)) и векторы (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) могут быть использованы как система координат. Для этой системы координат имеет место ещё одно утверждение.

Утверждение 9.

При аффинном преобразовании (f) образ (M^{*}) точки (M) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})) имеет те же координаты, что и точка (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).

Доказательство.

Равенство (overrightarrow{OM}=x boldsymbol{e}_{1}+y boldsymbol{e}_{2}) означает, что (x), (y) — координаты (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Подействовав преобразованием (f) на обе части этого равенства, мы получаем (overrightarrow{f(O)f(M)}=x f(boldsymbol{e}_{1})+y f(boldsymbol{e}_{2})), которое означает, что (x) и (y) — координаты (M^{*}) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})).

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 октября 2022 года; проверки требует 1 правка.

У этого термина существуют и другие значения, см. Оператор.

Лине́йное отображе́ние — обобщение линейной числовой функции (точнее, функции y=kx) с вещественных чисел на евклидовы пространства более высокой размерности, а также на произвольные векторные пространства. Является центральным понятием линейной алгебры.

Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

Являются частным случаем гомоморфизмов модулей. Линейные отображения из пространства в себя обычно называются линейными операторами или линейными преобразованиями[1].

Определение[править | править код]

Линейным отображением векторного пространства V над полем K в векторное пространство W над тем же полем называется отображение

{displaystyle fcolon Vto W},

удовлетворяющее условиям линейности[2]

  1. f(x+y)=f(x)+f(y)
  2. f(alpha x)=alpha f(x)

для всех {displaystyle x,yin V} и alpha in K.

Если {displaystyle W=V}, то f называется линейным оператором или линейным преобразованием пространства V. Если выполняется только первое свойство, то отображение f называется аддитивным.

Пространство линейных отображений[править | править код]

Если определить операции сложения и умножения на скаляр из основного поля K как

  • {displaystyle (f+g)(x)=f(x)+g(x)quad forall xin V}
  • {displaystyle (kf)(x)=kf(x)quad forall xin V,forall kin K}

то множество всех линейных отображений из V в W представит собой векторное пространство, которое обычно обозначается как {displaystyle {mathcal {L}}(V,W)}.

Ограниченные линейные операторы. Норма оператора[править | править код]

Если векторные пространства V и W являются линейными топологическими пространствами, то есть на них определены топологии, относительно которых операции этих пространств непрерывны, то можно определить понятие ограниченного оператора: линейный оператор называется ограниченным, если он переводит ограниченные множества в ограниченные (в частности, все непрерывные операторы ограничены). В частности, в нормированных пространствах множество ограничено, если норма любого его элемента ограничена, следовательно, в этом случае оператор называется ограниченным, если существует число N такое что {displaystyle forall xin V,|Ax|_{W}leqslant N|x|_{V}}. Можно показать, что в случае нормированных пространств непрерывность и ограниченность операторов эквивалентны. Наименьшая из постоянных N, удовлетворяющая указанному выше условию, называется нормой оператора:

|A|=sup _{{|x|not =0}}{frac {|Ax|}{|x|}}=sup _{{|x|=1}}{|Ax|}.

Введение нормы операторов позволяет рассматривать пространство линейных операторов как нормированное линейное пространство (можно проверить выполнение соответствующих аксиом для введённой нормы). Если пространство W — банахово, то и пространство линейных операторов тоже банахово.

Обратный оператор[править | править код]

Оператор A^{{-1}} называется обратным линейному оператору A, если выполняется соотношение:
A^{{-1}}A=AA^{{-1}}=1

Оператор A^{{-1}}, обратный линейному оператору A, также является линейным оператором. Если A — линейный непрерывный оператор, отображающий одно банахово пространство (или F-пространство) в другое, то и обратный оператор тоже является линейным непрерывным оператором.

Матрица линейного отображения[править | править код]

Матрица линейного отображения — матрица, выражающая линейное отображение в некотором базисе. Для того, чтобы её получить, необходимо подействовать отображением на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица отображения аналогична координатам вектора. При этом действие отображения на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис {mathbf {e}}_{k}. Пусть mathbf {x} — произвольный вектор. Тогда его можно разложить по этому базису:

{mathbf {x}}=x^{k}{mathbf {e}}_{k},

где x^{k} — координаты вектора mathbf {x} в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть mathbf {A} — произвольное линейное отображение. Подействуем им на обе стороны предыдущего равенства, получим

{mathbf {Ax}}=x^{k}{mathbf {Ae}}_{k}.

Вектора {mathbf {Ae}}_{k} также разложим в выбранном базисе, получим

{mathbf {Ae}}_{k}=a_{k}^{j}{mathbf {e}}_{j},

где a_{k}^{j} — j-я координата k-го вектора из {mathbf {Ae}}_{k}.

Подставим разложение в предыдущую формулу, получим

{mathbf {Ax}}=x^{k}a_{k}^{j}{mathbf {e}}_{j}=(a_{k}^{j}x^{k}){mathbf {e}}_{j}.

Выражение a_{k}^{j}x^{k}, заключённое в скобки, есть не что иное, как формула умножения матрицы на столбец, и, таким образом, матрица a_{k}^{j} при умножении на столбец x^{k} даёт в результате координаты вектора {mathbf {Ax}}, возникшего от действия оператора mathbf {A} на вектор mathbf {x} , что и требовалось получить.

(!) Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов {mathbf {e}}_{k}. Иными словами, порядок базисных элементов предполагается строго упорядоченным.

Пример преобразования[править | править код]

Векторы представлены как матрица 2 x 2, образованная сторонами соответствующего единичного квадрата, трансформируемого в параллелограмм.

Рассмотрим в качестве примера матрицу размера 2×2 следующего вида

{mathbf A}={begin{bmatrix}a&c\b&dend{bmatrix}},

может быть рассмотрена как матрица преобразования единичного квадрата в параллелограмм с вершинами (0, 0), (a, b), {displaystyle (a+c,b+d)}, и {displaystyle (c,d)}.
Параллелограмм, показанный на рисунке справа получается путём умножения матрицы A на каждый вектор-столбец {begin{bmatrix}0\0end{bmatrix}},{begin{bmatrix}1\0end{bmatrix}},{begin{bmatrix}1\1end{bmatrix}} и {begin{bmatrix}0\1end{bmatrix}}. Эти векторы соответствуют вершинам единичного квадрата.

В следующей таблице приведены примеры матриц 2 × 2 над вещественными числами с соответствующими им линейными преобразованиями R2. Синим цветом обозначена исходная координатная сетка, а зелёным — трансформированная. Начало координат (0, 0) обозначено чёрной точкой.

Горизонтальный сдвиг[en] (m=1.25) Горизонтальное отражение Сжатие[en][] (r=3/2) Гомотетия (3/2) Поворот (π/6R = 30°)
{begin{bmatrix}1&1.25\0&1end{bmatrix}} {begin{bmatrix}-1&0\0&1end{bmatrix}} {begin{bmatrix}3/2&0\0&2/3end{bmatrix}} {begin{bmatrix}3/2&0\0&3/2end{bmatrix}} {begin{bmatrix}cos(pi /6^{{R}})&-sin(pi /6^{{R}})\sin(pi /6^{{R}})&cos(pi /6^{{R}})end{bmatrix}}
VerticalShear m=1.25.svg Flip map.svg Squeeze r=1.5.svg Scaling by 1.5.svg Rotation by pi over 6.svg

Важные частные случаи[править | править код]

  • Линейная форма — линейное отображение, для которого {displaystyle W=K}:
        {displaystyle fcolon Vto K}
  • Линейный эндоморфизм — линейное отображение, для которого {displaystyle V=W}(оператор):
        fcolon Vto V
  • Тождественный оператор (единичный оператор)— оператор xmapsto x, отображающий каждый элемент пространства в себя; норма такого оператора равна единице (для нормированных пространств)
  • Нулевое отображение — оператор, переводящий каждый элемент V в нулевой элемент W.
  • Проектор — оператор сопоставляющий каждому x его проекцию на подпространство.
  • Сопряжённое отображение к отображению Ain L(V) — отображение A^{*} на V^*, заданное соотношением A^*f(x) := f(Ax).
  • Самосопряжённый оператор — оператор на гильбертовом пространстве, совпадающий со своим сопряжённым оператором. Иногда такие операторы называют гипермаксимальными эрмитовыми.
  • Эрмитов (или симметрический) оператор — такой оператор A, определённый на подпространстве гильбертова пространства, что (Ax,y)=(x,Ay) для всех пар x,y из области определения A. Для всюду определённых операторов данное свойство совпадает с самосопряжённостью.
  • Унитарный оператор — оператор, область определения и область значений которого — всё пространство, сохраняющий скалярное произведение (Ax,Ay)=(x,y); в частности, унитарный оператор сохраняет норму любого вектора |Ax|={sqrt {(Ax,Ax)}}={sqrt {(x,x)}}=|x|. Оператор, обратный унитарному, совпадает с сопряжённым оператором A^{{-1}}=A^{*}; норма унитарного оператора равна 1; в случае вещественного поля К унитарный оператор называют ортогональным.

Связанные понятия[править | править код]

Ядро линейного отображения образует подпространство в линейном пространстве V.
Образ линейного отображения образует подпространство в линейном пространстве W.
где L — линейный оператор, а v — вектор.
Критерий инвариантности. Пусть Msubset X — подпространство,такое что X разлагается в прямую сумму: X=Moplus N. Тогда M инвариантно относительно линейного отображения A тогда и только тогда, когда P_{M}AP_{M}=AP_{M}, где P_{M} — проектор на подпространство M.

Примеры[править | править код]

Примеры линейных однородных операторов:

Примеры линейных неоднородных операторов:

где varphi (t), varphi _{1}(t), varphi _{2}(t) — вполне определённые функции, а x(t) — преобразуемая оператором функция.

Примечания[править | править код]

См. также[править | править код]

  • Линейный непрерывный оператор
  • Вполне непрерывный оператор
  • Интегральный оператор Фредгольма
  • Сопряжённый оператор
  • Спектр оператора
  • Оператор (математика)
  • Выпуклый функционал

Литература[править | править код]

  • Шилов Г.Е. Математический анализ. Специальный курс. — М.: Наука, 1961. — 436 с.
Источник

Добавить комментарий