В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.
Общее представление о делении с остатком
Ранее мы указывали, что сам процесс деления сводится к разъединению одного множества на два или несколько. Чаще всего мы встречаемся с делением на равные части, то есть множества, получившиеся в результате, будут одинаковыми. Но так разделить возможно далеко не всегда. К примеру, 8 конфет разделить поровну на троих детей не выйдет: у каждого будет по 2 конфеты, а две останутся лишними. В данном случае мы имеем остаток 2, то есть остались две конфеты. Этот пример отображает основной смысл деления с остатком. Запишем определение:
Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.
В чем состоит смысл деления с остатком?
В случае натуральных чисел деление с остатком имеет следующий смысл. Мы уже знаем, что понятие натурального числа тесно связано с количеством чего-либо. Допустим, у нас есть некое число предметов (обозначим его a), а после его деления образуется остаток, условно d. У нас остались числа b и c. Есть два основных подхода к их обозначению:
1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.
2) если b – это количество множеств, то c – это число предметов в каждом из них.
Поясним нашу мысль на конкретных числах. Допустим, натуральное число 13 было разделено на 4. В итоге мы имеем два числа – 3 и 1. Мы можем рассмотреть эту ситуацию с двух сторон:
1) тринадцать предметов были сгруппированы по 4. У нас получилось 3 группы, а в исходном множестве остался всего 1 предмет;
2) тринадцать предметов разложили по 4 группам. У нас получилось, что в каждой группе по 3 предмета, а остаток равен 1.
Если натуральное число a всегда можно разделить с остатком на любое натуральное b, то можно выделить следующие ситуации:
1. A можно разделить на b без остатка, то есть все предметы можно разделить на равные множества. При этом «лишних» у нас не останется, тогда d будет равно 0. Получается, что деление без остатка – это частный случай деления с остатком.
2. A может быть меньше b. Тогда ни одного требуемого множества мы из него составить не можем, и число c будет равно нулю, а остаток равен a (то есть числу предметов в исходном множестве).
3. A может делиться на b с остатком. Тогдазначения a, b, c и d будут натуральными числами.
Подводим итог:
Результат деления натуральных чисел a и b с остатком – это два числа c и d, которые либо оба являются натуральными, либо одно из них равно нулю.
Основные понятия, используемые при делении с остатком
Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.
То натуральное число, которое делят на части, принято называть делимым, а то, на которое делят – делителем. Получившиеся в результате два числа мы называем соответственно остатком и неполным частным. К примеру, если мы разделим 8 на 3, то в итоге неполным частным будет 2, и остатком тоже 2.
Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение «÷», смысл которого тот же самый. Так, числовое выражение 16:3 означает деление одного натурального числа на другое с остатком.
Обозначим неполное частное буквой с, остаток – d, исходное число – a, а делитель – b. Тогда суть процесса деления в буквенном виде мы можем выразить как a:b=c (ост. d).
Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).
Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.
Задачи, в которых используется деление с остатком
В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:
1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.
Например:
У нас есть 67 шаров, которыми мы будем наряжать елки. Если на каждую елку нужно 15 шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.
Другой пример:
У нас есть 162 книги, которые нужно упаковать в 40 ящиков. Число книг, которое мы будем класть в каждую коробку, можно определить в результате деления 162 на 40.
Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)
Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.
2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.
Например:
У нас есть 197 конфет, которые раскладываются по коробкам. Мы знаем число этих коробок – оно равно 20. Деление 197 на 20 подскажет нам, сколько конфет остались неупакованными.
Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.
Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления
Для установления этих связей сразу разберем конкретный пример.
У нас есть некоторое множество предметов, обозначим его буквой a. Распределим его по кучкам, количество которых равно b. Всего в каждой кучке у нас будет c предметов. Остаток обозначим d. В буквенном виде это выражение можно записать как a:b=c (ост. d). Теперь проанализируем связи, которые есть в этом равенстве.
Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.
Учитывая смысл умножения и сложения натуральных чисел, мы можем записать это в виде равенства c·b+d=a. А наличие у умножения и сложения переместительных свойств позволяет нам переформулировать его как a=b·c+d. Получается следующее правило:
Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.
Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:
Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.
Решение
Имеем b=7, c=11 и d=2. Это все данные, которые нам нужны для вычислений. Подставим нужные значения: b·c+d=7·11+2. Следуя правильному порядку выполнения математических действий, получим в итоге 7·11+2=77+2=79 (если нужно, повторите основы умножения и сложения натуральных чисел).
Ответ: делимое будет равно 79.
Если нужно проверить верность результата действия деления с остатком, то для этого мы также проверяем справедливость равенства a=b·c+d.
Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.
Вспомним, что остаток от деления, который мы выше договорились обозначить буквой d, представляет собой число элементов, оставшееся в исходном множестве после его разделения на равные части. Значит, d=a−b·c. Записать это равенство мы можем благодаря свойствам умножения и вычитания натуральных чисел. Сформулируем определение:
Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.
У нас получилось буквенное выражение d=a−b·c, которое будет нам полезно при нахождении остатка от деления. Разберем такую задачу.
Мы разделили 67 на 15 и получили неполное частное 4. Вычислите остаток от деления.
Решение
Имеем a=67, b=15, c=4. Если мы подставим в выражение a−b·c исходные значения, то сможем подсчитать остаток: 67−15·4. Поскольку 15·4=60, то 67−15·4=67−60=7.
Ответ: остаток от деления равен 7.
Мы также можем найти неполное частное, если знаем значение делимого, делителя и остатка. Исключим из исходного множества те элементы, которые образуют остаток. Благодаря свойствам вычитания натуральных чисел количество элементов в множестве мы теперь можем записать как a−d. После этого уже можно произвести деление без остатка, в результате которого получится b множеств по c элементов в каждом. Мы получили равенство (a−d):b=c. Его также можно записать в виде c=(a−d):b.
Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.
Мы разделили 221 на 52 и получили остаток 13. Вычислите неполное частное.
Решение
Отнимем остаток от делимого и результат разделим на делитель. Считаем: (221−13):52=208:52=4 (для подсчета мы использовали метод подбора частного).
Ответ: неполное частное равно 4.
Осталось разобрать последний случай: как быть, если нужно найти делитель при известных значениях делимого, остатка и неполного частного? Начнем опять же с исключения остатка из делимого, то есть запишем a-d. Вспомнив смысл деления одного натурального числа на другое, запишем следующее равенство: (a−d):c=b. Также будет верно b=(a−d):c. Сформулируем правило:
Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.
Возьмем пример решения такой задачи.
Было выполнено деление 877 на некоторое число с остатком 2, неполное частное при этом составило 35. Найдите значение делителя.
Решение
Вычтем остаток из делимого и получим 875. Результат нужно разделить на известное нам неполное частное 35. В итоге получится нужное нам значение делителя. Вычислим столбиком:
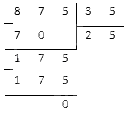
Ответ: делитель равен 25.
Циклические
коды позволяют обнаруживать и исправлять
групповые ошибки. В циклических кодах
широко используется операция циклической
перестановки (самый старший разряд
переставляется в конец кодовой комбинации,
а остальные сдвигаются влево или,
наоборот, младший разряд переставляется
в начало, остальные сдвигаются вправо).
При
формировании циклических кодов происходит
деление на образующий полином.
Представление
кодовой комбинации в виде полинома.
Q(x)=111111=x5+x4+x3+x2+x1+x0
xi
– двоичный разряд. x1=x,
x0=1
Если
какой-либо разряд xi
= 0 в составе полинома, то его опускают.
Q(x)=1100110=x6+x5+x2+x
Образующий
полином
– это полином,
который является простым числом: (11)10,
(13)10,
(17)10,
(19)10
и т.д. Он выбирается заранее как делитель,
позволяющий выполнять обнаружение и
исправление ошибки.
P(x)=(11)10=(1011)2=x3+x+1
Степень образующего полинома – к.
(к=3)
Операция
деления полинома на полином.
Деление
сходно с алгебраическим, но есть отличие:
-
операция
вычитания заменяется суммированием
по модулю 2; -
деление
заканчивается, если наивысшая степень
у остатка меньшей таковой у делителя; -
интерес
представляет не частное от деления, а
остаток.
Рассмотрим
пример деления.
Пусть
Q (x) = x 5
+ x 3
+ x – делимое
P
(x) = x 3
+ x + 1 – делитель
-
x



5
+ x
3
+ xx
3
+ x
+ 1x

5
+ x
3
+ x
2x
2x
2
+ x
Остаток:
R
(x)
= x
2
+ x
= 110
Формирование
циклического кода.
Правило:
нужно исходную кодовую комбинацию (КК)
– Q(x)
разделить на образующий полином Р(х) и
дописать справа остаток от деления к
исходной КК. Обозначим F(x)
– комбинация циклического кода.
F(x)
= Q(x)
*x
k
![]() R(x)
R(x)
, где k
– степень образующего полинома.
Величина
k
показывает количество сдвигов влево,
которое Q(x)
должно претерпеть.
Пример:
Q(x)
= x
5
+ x
3
+ x
= 101010 – исходная КК,
Р(х)
= x
3
+ x
+ 1 = 1011 – образующий полином
R(x)
= x
2
+ x
= 110 – полученный остаток от деления,
F(x)
= 101010 110 – комбинация циклического кода,
где:
101010 – информационная часть,
110
– контрольная часть
Остаток
R(x)
называется синдромом..
Пусть
Q(x)
= 1110. Если k
=3, то Q(x)
X
k
= 1110 000
Проверка
правильности циклического кода.
Правильность
циклического кода проверяется с помощью
операции деления на образующий полином.
Если в результате деления остаток равен
нулю (R(x)=0),
то считается ,что комбинация циклического
кода ошибки не содержит. Если же при
делении получился остаток, то комбинация
содержит ошибку, которую можно исправить.
Процедура отыскания места ошибки
сводится к циклическим сдвигам КК F(х)
и деление ее на образующий полином.
W
– вес остатка (количество единиц в нем).
S
– кратность ошибки (количество ошибочных
разрядов в кодовой комбинации).
В
алгоритме используются циклические
сдвиги влево и вправо, количество которых
подсчитывается во время выполнения.
Cn
– счетчик
циклических сдвигов.
Соседние файлы в папке Метрология и ТМ
- #
- #
- #
Задачи на частичное разложение — это задачи, в которых исходное вещество распадается только частично, то есть часть исходного вещества остается. При разложении твердого вещества может образоваться новый твердый продукт, но также остается часть исходного реагента, который не разложился. Это необходимо учитывать при составлении химических реакций.
По сути, это одна из разновидностей задач на материальный баланс.
Рассмотрим несколько примеров решения задач на частичное разложение из реальных ЕГЭ по химии.
1. При нагревании образца нитрата алюминия часть вещества разложилась. При этом выделилось 10,08 л (в пересчёте на н.у.) смеси газов. Для полного растворения образовавшегося твёрдого остатка необходимо затратить 60 г 40%-ного раствора гидроксида натрия. При этом образовался тетрагидроксоалюминат натрия. Определите массу исходного образца нитрата алюминия.
Решение:
Реакция разложения нитрата алюминия:
4Al(NO3)3 = 2Al2O3 + 12NO2 + 3O2
Из условия известно, что распалась только часть исходного вещества.
Количество вещества смеси газов:
nсм = V/Vm = 10,08 л/22,4 л/моль = 0,45 моль
Примем количество образовавшегося кислорода за х моль:
n(О2) = x моль
тогда количество вещества оксида азота (IV) равно 4х моль:
n(NО2) = 4x моль
Получаем уравнение:
х + 4х = 0,45
5х = 0,45
х = 0,09 моль
Количество образовавшегося оксида алюминия:
n(Al2О3) = 0,06 моль
Количество и масса разложившегося нитрата алюминия:
nразлож(Al(NО3)3) = 0,12 моль
mразлож(Al(NО3)3) = n·M = 0,12 моль · 213 г/моль = 25,56 г
С гидроксидом натрия реагирует и образовавшийся оксид алюминия, и остаток нитрата алюминия:
Al(NO3)3 + 4NaOH = Na[Al(OH)4] + 3NaNO3
Al2O3 + 2NaOH + 3H2O = 2Na[Al(OH)4]
Определим массу и количество вещества гидроксида натрия:
m(NaOH) = ω(NaOH)·mр-ра(NaOH) = 0,40 ·60 г = 24 г
n(NaOH) = m(NaOH)/M(NaOH) = 24 г/40 г/моль = 0,6 моль
Определим количество гидроксида натрия, который потребуется для растворения оксида алюминия во второй реакции:
n2(NaOH) = 2n(Al2О3) = 2·0,06 моль = 0,12 моль
Тогда в первой реакции будет израсходовано:
n1(NaOH) = n(NaOH) – n2(NaOH) = 0,6 моль – 0,12 моль = 0,48 моль
Количество неразложившегося нитрата алюминия, который затем растворится в щелочи в первой реакции:
nнеразлож.(Al(NО3)3) = 1/4·n1(NaOH) = 1/4·0,48 моль = 0,12 моль
Масса этого неразложившегося нитрата алюминия:
mнеразлож.(Al(NО3)3) = nнеразлож.(Al(NО3)3)·M = 0,12 моль·213 г/моль = 25,56 г.
Масса исходного нитрата алюминия:
m(Al(NО3)3) = mразлож.(Al(NО3)3) + mнеразлож.(Al(NО3)3) = 25,56 г + 25,56 г = 51,12 г
Ответ: m(Al(NO3)3) = 51,12 г
2. При нагревании карбоната магния часть вещества разложилась. При этом выделилось 5,6 л газа и образовалось 18,4 г твёрдого остатка. Остаток растворили в 365 г соляной кислоты, при этом массовая доля кислоты в конечном растворе составила 2,9%. Вычислите массовую долю соляной кислоты в исходном растворе.
MgCO3 = MgO + CO2
MgCO3 + 2HCl = MgCl2 + CO2 + H2O
MgO + 2HCl = MgCl2 + H2O
Ответ: w(HCl) = 10%
3. При нагревании хлората калия (KClO3) в присутствии катализатора часть вещества разложилась. При этом выделилось 6,72 л (н.у.) газа и образовался твёрдый остаток массой 16 г. К остатку добавили 170 г 30%-ного раствора нитрата серебра. Определите массовую долю нитрата серебра в полученном растворе. (KClO3 и AgClO3 растворимы в воде.)
2KClO3 = 2KCl + 3O2
KCl + AgNO3 = AgCl + KNO3
Ответ: w(AgNO3) = 10,8%
4. При нагревании образца нитрата магния часть вещества разложилась. При этом выделилось 10,08 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 69,36 г. К этому остатку последовательно добавили 100 мл воды и 240 г 20%-ного раствора гидроксида натрия. Определите массовую долю гидроксида натрия в образовавшемся растворе.
2Mg(NO3)2 = 2MgO + 4NO2 + O2
Mg(NO3)2 + 2NaOH = Mg(OH)2 + 2NaNO3
Ответ: w(NaOH) = 3,8%
5. При нагревании образца нитрата меди(II) часть вещества разложилась. При этом образовался твёрдый остаток массой 50,8 г. К остатку добавили 150 г 20%-ного раствора гидроксида натрия. При этом образовался раствор с массой 159 г и массовой долей гидроксида натрия 13,84%. Определите объём смеси газов (в пересчёте на н.у.), выделившихся в результате частичного разложения нитрата меди(II).
2Cu(NO3)2 = 2CuO + 4NO2 + O2
Cu(NO3)2 + 2NaOH = Cu(OH)2 + 2NaNO3
Ответ: V(смеси газов) = 22,4 л
6. При нагревании образца нитрата серебра часть вещества разложилась. При этом образовался твёрдый остаток массой 88 г. К этому остатку добавили 200 г 20%-ного раствора соляной кислоты. При этом образовался раствор массой 205,3 г с массовой долей соляной кислоты 15,93%. Определите объём смеси газов (в пересчёте на н.у.), выделившихся в результате частичного разложения нитрата серебра.
2AgNO3 = 2Ag + 2NO2 + O2
AgNO3 + HCl = AgCl + HNO3
Ответ: V(смеси газов) = 16,8 л
7. При нагревании образца карбоната бария часть вещества разложилась. При этом выделилось 1,12 л (н.у.) газа. Масса твёрдого остатка составила 27,35 г. Этот остаток добавили к 73 г 30%-ного раствора соляной кислоты. Определите массовую долю кислоты в полученном растворе.
BaCO3 = BaO + CO2
BaCO3 + 2HCl = BaCl2 + CO2 + H2O
BaO + 2HCl = BaCl2 + H2O
Ответ: w(HCl) = 11,4%
8. При нагревании образца нитрата цинка часть вещества разложилась. При этом выделилось 5,6 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 64,8 г. Остаток полностью растворили в минимальном объёме 28%-ного раствора гидроксида натрия. Определите массовую долю нитрата натрия в полученном растворе.
2Zn(NO3)2 = 2ZnO + 4NO2 + O2
Zn(NO3)2 + 4NaOH = Na2[Zn(OH)4] + 2NaNO3
ZnO + 2NaOH + H2O = Na2[Zn(OH)4]
Ответ: w(NaNO3) = 19,26%
9. При нагревании образца нитрата серебра часть вещества разложилась. При этом выделилось 6,72 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 25 г. К этому остатку последовательно добавили 50 мл воды и 18,25 г 20%-ного раствора соляной кислоты. Определите массовую долю соляной кислоты в полученном растворе.
2AgNO3 = 2Ag + 2NO2 + O2
AgNO3 + HCl = AgCl + HNO3
Ответ: w(HCl) = 4,2%
10. При нагревании образца нитрата меди(II) массой 94 г часть вещества разложилась. При этом выделилось 11,2 л (в пересчёте на н.у.) смеси газов. К полученному твёрдому остатку добавили 292 г 10%-ного раствора соляной кислоты. Определите массовую долю соляной кислоты в полученном растворе.
2Cu(NO3)2 = 2CuO + 4NO2 + O2
CuO + 2HCl = CuCl2 + H2O
Ответ: w(HCl) = 4%
11. При нагревании образца нитрата магния часть вещества разложилась. При этом образовался твёрдый остаток массой 15,4 г. Этот остаток прореагировал с 20 г 20%-ного раствора гидроксида натрия. Определите массу исходного образца нитрата магния и объём смеси газов (в пересчёте на н.у.), выделившихся при частичном разложении нитрата магния.
2Mg(NO3)2 = 2MgO + 4NO2 + O2
Mg(NO3)2 + 2NaOH = Mg(OH)2 + 2NaNO3
Ответ: m(Mg(NO3)2) = 37 г, V(смеси газов) = 11,2 л
12. При нагревании образца карбоната бария часть вещества разложилась, при этом выделилось 4,48 л (н.у.) газа. К образовавшемуся твёрдому остатку последовательно добавили 100 мл воды и 200 г 20%-ного раствора сульфата натрия. Вычислите массовую долю гидроксида натрия в полученном растворе.
BaCO3 = BaO + CO2
BaO + H2O = Ba(OH)2
Ba(OH)2 + Na2SO4 = BaSO4 + 2NaOH
Ответ: w(NaOH) = 5,6%
13. Оксид меди(II) массой 16 г нагрели в присутствии водорода объёмом 3,36 л (н.у.). При этом водород прореагировал полностью. Полученный твёрдый остаток растворили в 535,5 г 20%-ного раствора азотной кислоты, при этом наблюдали выделение бесцветного газа. Определите массовую долю азотной кислоты в образовавшемся растворе.
CuO + H2 = Cu + H2O
3Cu + 8HNO3 = 3Cu(NO3)2 + 2NO + 4H2O
CuO + 2HNO3 = Cu(NO3)2 + H2O
Ответ: w(HNO3) = 13,84%
14. При нагревании образца нитрата железа(III) часть вещества разложилась. При этом образовалось 88,6 г твёрдого остатка. Этот остаток может прореагировать с 225 г 16%-ного раствора гидроксида натрия. Определите массу исходного образца нитрата железа(III) и объём выделившейся смеси газов (в пересчёте на н.у.).
4Fe(NO3)3 = 2Fe2O3 + 12NO2 + 3O2
Fe(NO3)3 + 3NaOH = Fe(OH)3 + 3NaNO3
Ответ: m(Fe(NO3)3) = 121 г, V(смеси газов) = 16,8 л
15. При нагревании образца гидрокарбоната натрия часть вещества разложилась. При этом выделилось 0,448 л (н.у.) углекислого газа и образовалось 4,64 г твёрдого безводного остатка. Остаток добавили к 0,15%-ному раствору гидроксида кальция. При этом в полученном растворе не осталось ионов кальция и карбонат-анионов. Определите массовую долю гидроксида натрия в конечном растворе.
2NaHCO3 = Na2CO3 + CO2 + H2O
NaHCO3 + Ca(OH)2 = CaCO3 + H2O + NaOH
Na2CO3 + Ca(OH)2 = CaCO3 + 2NaOH
Ответ: w(NaOH) = 0,11%
16. При нагревании образца карбоната кальция часть вещества разложилась. При этом выделилось 4,48 л (н.у.) углекислого газа. Масса твёрдого остатка составила 41,2 г. Этот остаток добавили к 465,5 г раствора соляной кислоты, взятой в избытке. Определите массовую долю соли в полученном растворе.
CaCO3 = CaO + CO2
CaCO3 + 2HCl = CaCl2 + CO2 + H2O
CaO + 2HCl = CaCl2 + H2O
Ответ: w(CaCl2) = 11,2%
17. При нагревании образца нитрата магния массой 44,4 г часть вещества разложилась. При этом выделилось 13,44 л (в пересчёте на н.у.) смеси газов. К полученному твёрдому остатку добавили 124,1 г 20%-ного раствора соляной кислоты. Определите массовую долю соляной кислоты в полученном растворе.
2Mg(NO3)2 = 2MgO + 4NO2 + O2
MgO + 2HCl = MgCl2 + H2O
Ответ: w(HCl) = 5,1%
18. При нагревании образца нитрата меди(II) часть вещества разложилась. При этом выделилось 5,6 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 26,8 г. К этому остатку последовательно добавили 50 мл воды и 10%-ный раствор гидроксида натрия в количестве, необходимом для полного осаждения ионов меди. Определите массовую долю нитрата натрия в образовавшемся растворе.
2Cu(NO3)2 = 2CuO + 4NO2 + O2
Cu(NO3)2 + 2NaOH = Cu(OH)2 + 2NaNO3
Ответ: w(NaNO3) = 12,2%
19. При нагревании образца нитрата меди(II) часть вещества разложилась. При этом выделилось 2,8 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 32,2 г. К этому остатку последовательно добавили 50 мл воды и 160 г 10%-ного раствора гидроксида натрия. Определите массовую долю гидроксида натрия в образовавшемся растворе.
2Cu(NO3)2 = 2CuO + 4NO2 + O2
Cu(NO3)2 + 2NaOH = Cu(OH)2 + 2NaNO3
Ответ: w(NaOH) = 1,8%
20. При нагревании образца нитрата алюминия часть вещества разложилась. При этом выделилось 6,72 л (в пересчёте на н.у.) смеси газов. Масса твёрдого остатка составила 25,38 г. Остаток полностью растворили в необходимом для реакции минимальном объёме 24%-ного раствора гидроксида натрия. При этом образовался тетрагидроксоалюминат натрия. Определите массовую долю нитрата натрия в полученном растворе.
4Al(NO3)3 = 2Al2O3 + 12NO2 + 3O2
Al(NO3)3 + 4NaOH = Na[Al(OH)4] + 3NaNO3
Al2O3 + 2NaOH + 3H2O = 2Na[Al(OH)4]
Ответ: w(NaNO3) = 24,2%
21. При нагревании образца гидрокарбоната натрия часть вещества разложилась. При этом выделилось 4,48 л (н.у.) газа и образовалось 63,2 г твёрдого безводного остатка. К полученному остатку добавили минимальный объём 20%-ного раствора соляной кислоты, необходимый для полного выделения углекислого газа. Определите массовую долю хлорида натрия в конечном растворе.
2NaHCO3 = Na2CO3 + CO2 + H2O
NaHCO3 + HCl = NaCl + CO2 + H2O
Na2CO3 + 2HCl = 2NaCl + CO2 + H2O
Ответ: w(NaCl) = 26,8%
22. При нагревании образца нитрата магния часть вещества разложилась. При этом образовался твёрдый остаток массой 53,6 г. К остатку добавили 200 г 24%-ного раствора гидроксида натрия. При этом образовался раствор с массой 206,4 г и массовой долей гидроксида натрия 15,5%. Определите объём смеси газов (в пересчёте на н.у.), выделившихся в результате частичного разложения нитрата магния.
2Mg(NO3)2 = 2MgO + 4NO2 + O2
Mg(NO3)2 + 2NaOH = Mg(OH)2 + 2NaNO3
Ответ: V(смеси газов) = 33,6 л
23. При нагревании образца карбоната бария часть вещества разложилась. При этом выделилось 4,48 л (н.у.) газа и образовалось 50 г твёрдого остатка. К остатку последовательно добавили 100 мл воды и 200 г 20%-ного раствора сульфата натрия. Вычислите массовую долю гидроксида натрия в полученном растворе.
BaCO3 = BaO + CO2
BaO + H2O = Ba(OH)2
Ba(OH)2 + Na2SO4 = BaSO4 + 2NaOH
Ответ: w(NaOH) = 5,6%
25. При нагревании образца нитрата железа(III) часть вещества разложилась. В результате образовался твёрдый остаток, который разделили на две части. Первую часть массой 58 г обработали 267 г 20%-ного раствора гидроксида натрия. При этом массовая доля щёлочи в растворе уменьшилась вдвое. Вторую часть массой 29 г растворили в 126 г 10%-ного раствора азотной кислоты. Вычислите массовую долю соли в образовавшемся растворе.
4Fe(NO3)3 = 2Fe2O3 + 12NO2 + 3O2
Fe(NO3)3 + 3NaOH = Fe(OH)3 + 3NaNO3
Fe2O3 + 6HNO3 = 2Fe(NO3)3 + 3H2O
Ответ: w(Fe(NO3)3) = 25%
26. При нагревании образца нитрата меди(II) часть вещества разложилась. В результате образовался твёрдый остаток, который разделили на две части. Первую часть массой 59 г обработали 127,5 г 25,1%-ного раствора гидроксида натрия. При этом образовался раствор с массовой долей щёлочи 8%. Вторую часть массой 23,6 г растворили в 245 г 10%-ного раствора серной кислоты. Вычислите массовую долю кислоты в образовавшемся растворе
2Cu(NO3)2 = 2CuO + 4NO2 + O2
Cu(NO3)2 + 2NaOH = Cu(OH)2 + 2NaNO3
CuO + H2SO4 = CuSO4 + H2O
Ответ: w(H2SO4) = 6,9%
27. При нагревании образца нитрата цинка часть вещества разложилась. В результате образовался твёрдый остаток, который разделили на две части. Первую часть массой 27 г обработали 87,2 г 20%-ного раствора сульфида натрия. При этом массовая доля сульфида натрия в растворе уменьшилась вдвое. Вторую часть массой 81 г добавили к 202,5 г 40%-ного раствора бромоводородной кислоты. Вычислите массовую долю бромоводородной кислоты в образовавшемся растворе.
2Zn(NO3)2 = 2ZnO + 4NO2 + O2
Zn(NO3)2 + Na2S = ZnS + 2NaNO3
ZnO + 2HBr = ZnBr2 + H2O
Ответ: w(HBr) = 11,4%
28. При нагревании образца нитрата алюминия часть вещества разложилась. В результате образовался твёрдый остаток, который разделили на две части. Первую часть массой 73,2 г добавили к 663,6 г 15%-ного раствора карбоната натрия. При этом массовая доля соды в растворе уменьшилась в полтора раза. Вторую часть массой 24,4 г растворили при нагревании в 245 г 20%-ного раствора серной кислоты. Вычислите массовую долю кислоты в образовавшемся растворе.
4Al(NO3)3 = 2Al2O3 + 12NO2 + 3O2
2Al(NO3)3 + 3Na2CO3 + 3H2O = 2Al(OH)3 + 3CO2 + 6NaNO3
Al2O3 + 3H2SO4 = Al2(SO4)3 + 3H2O
Ответ: w(H2SO4) = 7,3%
29. При нагревании образца карбоната кальция часть вещества разложилась. При этом масса карбоната кальция в образовавшемся твёрдом остатке оказалась в 1,4 раза больше массы оксида кальция. Остаток добавили к 640 г 25%-ной соляной кислоты. В результате массовая доля кислоты в растворе уменьшилась вдвое. Вычислите объём газа (в пересчёте на н.у.), выделившегося в результате частичного разложения карбоната кальция.
CaCO3 = CaO + CO2
CaO + 2HCl = CaCl2 + H2O
CaCO3 + 2HCl = CaCl2 + CO2 + H2O
Ответ: V(CO2) = 12,544 л
При взаимодействии основных оксидов с водой получаются основания. А вот при взаимодействии с водой кислотных оксидов получаются кислоты.
Кислоты – это большой класс химических соединений, в которых есть атом водорода и так называемый кислотный остаток.
Правильно определять кислотные остатки и понимать, как определяется их валентность, просто необходимо, иначе будет сложно составлять формулы солей. Ниже мы поговорим о классификации кислот и узнаём побольше о кислотных остатках.
Классификация кислот
Делить кислоты на группы можно по разным признакам, но нас сейчас будут интересовать два: содержание кислорода и основность.
Классификация кислот по содержанию кислорода
Тут всё просто: в составе некоторых кислот кислород есть (и они называются кислородсодержащими), в составе других кислорода нет (и эти кислоты называют бескислородными).
Примеры кислородсодержащих кислот: серная Н2SO4, фосфорная H3PO4, азотная HNO3.
Примеры бескислородных кислот: сероводородная H2S, соляная HCl, плавиковая HF.
Классификация кислот по основности
Тут мы должны остановиться более подробно.
Основность определяется числом атомов водорода в составе кислоты.
Для того, чтобы узнать основность, нужно взглянуть на формулу. Например, соляная кислота HCl одноосновная, потому что здесь только один атом водорода, сернистая кислота H2SO3 – двухосновная (здесь два атома водорода), а фосфорная H3PO4 – трёхосновная (в формуле три атома водорода). Запомните, как определять основность, тогда вам будет значительно проще составлять формулы солей при составлении химических уравнений.
Теперь давайте уделим внимание второй составной части кислоты – кислотному остатку.
Кислотный остаток – это то, что останется от кислоты, если убрать водород.
То есть, в азотной кислоте HNO3 кислотный остаток -NO3, в сероводородной Н2S кислотный остаток -S, в фосфорной кислоте H3PO4 кислотный остаток – PO4. Обратите внимание, что в кислородсодержащей кислоте остаток кислород содержит, а в бескислородной не содержит.
Валентность кислотного остатка
Говорить о валентности кислотного остатка не совсем корректно, поскольку валентность – это способность атомов образовывать химические связи. Если же речь идёт о кислотном остатке кислородсодержащей кислоты, то у нас имеется группа атомов (например, кислотный остаток –NO3). Но мы всё равно будем говорить о валентности, чтобы проще было составлять формулы.
Итак,
валентность кислотного остатка определяется числом атомов водорода.
Фактически валентность равна основности. Например, у двухосновной серной кислоты H2SO4 есть кислотный остаток –SO4, валентность которого II. И для чего же нам нужно это знание? Давайте рассмотрим примеры.
Пример 1.
Составьте формулу сульфида натрия.
Натрий – металл первой группы с валентностью I. Сульфид – соль сероводородной кислоты H2S. Когда образуется соль (в данной ситуации сульфид натрия), металл замещает водород в кислоте, то есть соль состоит из металла и кислотного остатка. Тогда в сульфиде натрия будут натрий и сера. Сероводородная кислота – двухосновная, поскольку в ней два атома водорода. Следовательно, у кислотного остатка –S валентность II. Составляем формулу, используя знания о валентности:
Ответ: формула сульфида натрия H2S.
Пример 2.
Составьте формулу сульфита калия.
Этот пример посложнее: в нём фигурирует кислородсодержащая двухосновная сернистая кислота H2SO3. Из формулы видно, что валентность кислотного остатка –SO3 будет II. Калий же – металл первой группы, его валентность I. Составляем формулу:
Ответ: формула сульфита калия К2SO3.
Пример 3.
Составьте формулу нитрата кальция.
Итак, нитрат – соль азотной кислоты HNO3. Это одноосновная кислота, поэтому кислотный остаток -NO3 имеет валентность I. Кальций – металл второй группы с валентностью II. Составляем формулу:
Ответ: формула нитрата кальция Ca(NO3)2.
Обратите внимание на очень важный момент! Мы взяли кислотный остаток NO3 в скобки и внизу поставили индекс 2. Это показывает, что в формуле два кислотных остатка! Не забывайте ставить скобки, иначе это будет ошибкой. Фактически в соединении Ca(NO3)2 один атом кальция, два атома азота и шесть атомов кислорода (если раскрыть скобки), но написание CaN2O6 ничего не показывает, а вот из формулы Ca(NO3)2 сразу видно, что у нас имеется атом кальция и два кислотных остатка азотной кислоты.
Пример 4.
В заключение самый сложный пример от репетитора по химии. Нужно составить формулу фосфата магния.
Магний – металл второй группы, его валентность II. Фосфат – соль фосфорной кислоты H3PO4. Здесь кислотный остаток PO4 и его валентность III. Составляем формулу:
Формула выглядит громоздко, но она всё предельно точно рассказывает о составе вещества: в фосфате магния имеется три атома магния и два кислотных остатка фосфорной кислоты.
Ответ: формула фосфата магния Мg3(PO4)2.
Кстати, кислоты реагируют с металлами, но не всеми. Об этом читайте в тексте «Химические свойства кислот».
Пишите, пожалуйста, в комментариях, что осталось непонятным, и я обязательно дам дополнительные пояснения. Жалуйтесь на сложности в изучении школьного курса и говорите, что вас испугало в учебнике химии. И тогда следующая статья будет рассказывать именно об этой проблеме.
Подсчет остатка от деления большого числа
Для проверки на всякие чек-суммы, иногда нужно делить что-то вроде 6796573475894375894375893479583745897943759830 на какой-нибудь 73 или 97.
Далеко не все языки программирования на это рассчитаны. Есть, конечно и примочки в виде классов типа BigInt и т.п., но есть способ похитрее.
(A*B) mod N = ((A mod N) * (B mod N)) mod N
(A+B) mod N = ((A mod N) + (B mod N)) mod N
Другими словами, есть представить число 43517 как 7 + 10 + 500 + 3000 + 40000, т.е. 7*10^-1 + 1 * 10^1 + 5 * 10^2 + 3 * 10^3 + 4 * 10^4, то многое упрощается.
Остаток от деления цифры это легко, а если делитель больше 9, то и вовсе равняется самой цифре.
Что же касается степеней десятки, то тут, кажется, ничего не изменилось, ведь все равно нужно посчитать остаток от деления 10000000000000000000000000000 на 73.
Ан нет! Мы знаем, что 10^2 это 10*10, 10^3 это 10*10^2, а 10^N это 10*10^(N-1),
Из этого и нашей формулы следует, что (10^N) mod M = ((10^(N-1) mod M) * 10) mod M.
Таким образом, можно этот остаток вычислять итеративно, на каждом шаге, начиная с младшей цифры и до старшей, каждый раз берем остаток из предыдущего шага, умножаем на 10 и вычисляем остаток.
Вот так можно его и посчитать.
Пример.
Остаток от деления 1275436137 на 97.
Вначале, напишем наши цифры 7 3 1 6 3 4 5 7 2 1.
Посчитаем остатки от деления степеней 10-ки на 97. (При программировании, если делитель встречается часто, лучше всего эти результаты закешировать для более быстрых расчетов, подгружая массив в память, когда это нужно.)
1 mod 97 — 1, без вопросов.
(1 * 10) mod 97 — 10
(10 * 10) mod 97 — 3
(3 * 10) mod 97 — 30
(30 * 10) mod 97 — 9
(9 * 10) mod 97 — 90
(90 * 10) mod 97 — 27
(27 * 10) mod 97 — 76. и дальше 81, 34.
Перемножаем пары, складываем. У нас все цифры имеют ровно такие же остатки, так что
7 * 1 + 3 * 10 + 1 * 3 + 6 * 30 + 3 * 9 + 4 * 90 + 5 * 27 + 7 * 76 + 2 * 81 + 1 * 34 = 1470
1470 mod 97 = 15
Ответ. 1275436137 mod 97 = 15, что можно проверить на виндошном калькуляторе.
В псевдокоде
s <- 0
a <- 1
for i = LastDigitIndex to 1
s <- s + a * digits[i]
a <- (a * 10) mod n
endfor
result <- s mod n
Остаток от деления числа в большой степени
Как можно быстро вычислить (x^n)mod y. Уже когда-то копал этот вопрос и обнаружил теорему Эйлера (теория чисел).
Не относится к вопросу: Но вся проблема в том, что я учусь в школе, и мы не проходили еще подобных выражений, найденных мною на wiki, и теории чисел. Объясните пожалуйста:
- Как использовать эту теорему на практике(например, реализация на C).
- (Не так важно, но просто интересно)Кратко значение формулировки на
wiki. Буду рад какой-нибудь статье, etc для тех, кто еще не знаком с теорией чисел и математикой >9 классов.
Наприклад ми хочемо обчислити 7 222 (mod 10). Маємо, що 7 і 10 є взаємно простими і φ(10) = 4 . Одже згідно з теоремою Ейлера 7 4 ≡ 1 (mod 10) і як наслідок
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Моя попытка перевода:
Например мы хотим вычислить “7 222 (mod 10)”. 7 и 10 являются взаимно-простыми и φ(10) = 4 (это число натуральных чисел не больших чем 10 и являющихся взаимнопростыми по отношению к 10 . Это следующие числа: 1,3,7,9 и всего их 4 ).
Следовательно согласно теореме Эйлера 7 4 ≡ 1 (mod 10) и как следствие:
7 222 ≡ 7 4×55 + 2 ≡ (7 4 ) 55 x 7 2 ≡ 1 55 x 7 2 ≡ 49 ≡ 9 (mod 10).
Следствия из теоремы:
если a φ(n) ≡ 1 (mod n), то и (a φ(n) ) k ≡ 1 (mod n) для любого положительного k , т.к.
(a φ(n) ) k ≡ a φ(n) mod n * (a φ(n) ) k — 1 mod n ≡ (a φ(n) ) k — 1 (mod n) и т.д.
Остаток от деления больших чисел
числа по модулю образуют кольцо (а по простому — даже поле), то есть — нормальную арифметику. Модуль можно брать на любом этапе.
конечно, посчитать сначала 18^180, а потом взять (mod 13) — это долго (хотя на компе вполне реально, до нескольких миллионов знаков длинная арифметика считается несложно). Но можно брать модуль на каждом шаге!
например, 18^180 mod 13 = (18mod 13)^180 mod 13=5^180 mod 13.
теперь, как возводить в высокую степень (не обязательно по мудулю):
a^180=a^(4+16+32+128)
считаем и запоминаем промежуточные результаты
a^2=a*a
a^4=(a^2)(a^2)
a^8=(a^4)(a^4)
a^16=(a^4)(a^4)
a^32=(a^16)(a^16)
a^64=(a^32)(a^32)
a^128=(a^64)(a^64)
итого a^180=a^4 * a^16 * a^32 * a^128
если надо считать по модулю 13 — делаем каждую операцию по модулю 13, все числа — небольшие, не больше 12.
если немного подумать, то разложение a^180=a^(4+16+32+128) — это просто двоичное представление числа, 4,16,32,128 — единички, остальные — нули.
