как найти образующую конуса если узнаем радиус и угол между образующей и основанием конуса
Профи
(570),
на голосовании
8 лет назад
Голосование за лучший ответ
Александр Омелаенко
Мыслитель
(5485)
8 лет назад
если посмотреть на эту картинку “со стороны”, то увидим равнобедренный треугольник с основанием 2R, боковой стороной = образующей и углом при основании = углом между образующей и основанием.
проводим высоту и видим прямоугольный треугольник. из которого:
образующая = R / cos (alfa)
кстати, тут же высота конуса = R * tg (alfa)
Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.
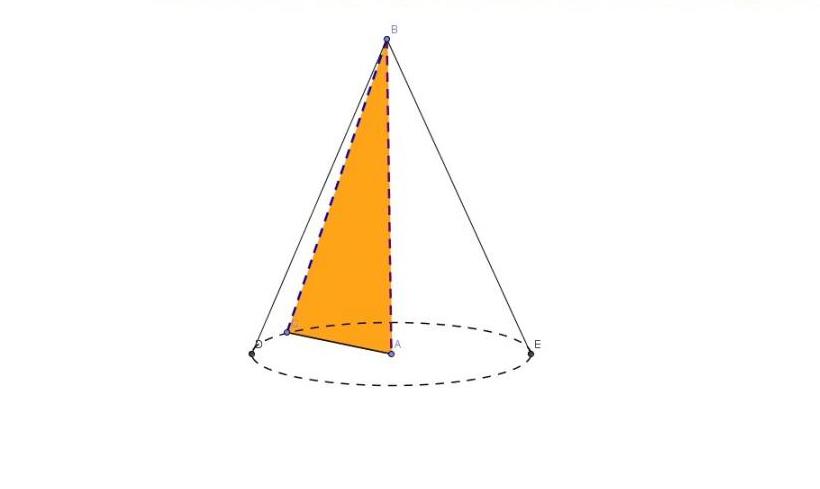
Полученная пространственная фигура имеет следующие характеристики:
- Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.
- Сторона AC треугольника – это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.
- Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.
- Вершина B треугольника – это вершина конуса.
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
g = √(r2 + h2)
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
g = h/sin(φ);
g = r/cos(φ)
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
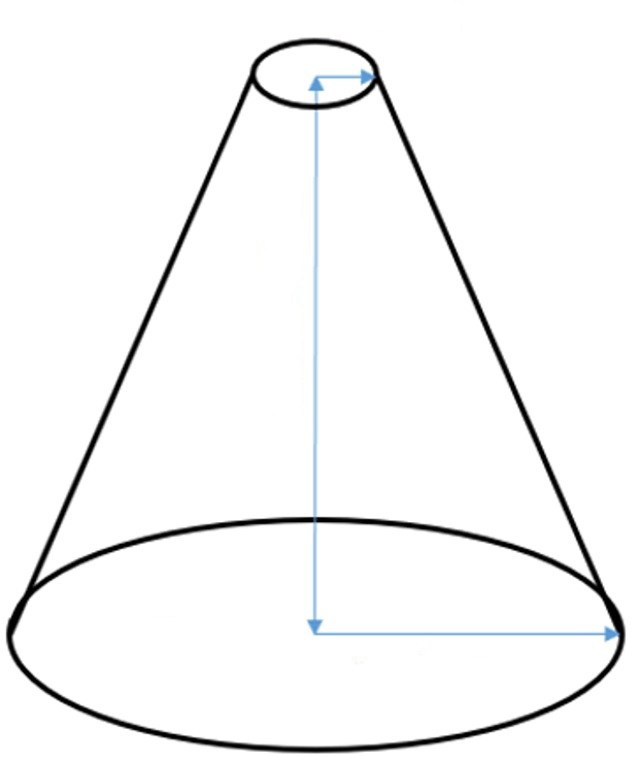
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок – это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
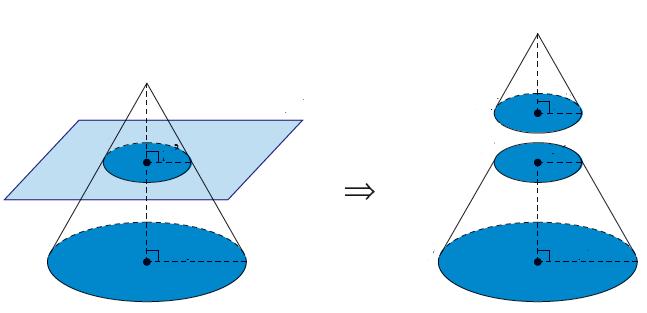
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
g = √((r1 – r2)2 + h2)
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
g = h/sin(φ1);
g = (r1 – r2)/cos(φ1)
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
g = h/sin(φ2);
g = (r2 – r1)/cos(φ2)
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.

Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.

Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.

Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.

Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.

Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
- Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
- Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
- Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
- На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:
- Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
- В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
- При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
- Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.
Построение уклона и конусности
Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:
- Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
- В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
- С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.
На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:
- Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
- Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
- Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
- Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
- Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:
- Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
- Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
- Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
- Есть возможность провести замер всех показателей при применении соответствующих инструментов.
- Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.
Построение развертки конуса на бумаге

Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Как сделать конус из картона
Вы узнали, как сделать конус из простой бумаги А4, но, если вам нужна плотная поделка, лучше воспользоваться картоном. Материалы и инструменты остаются теми же, что и в предыдущих поделках. Различие заключается только в оттенке картона, его подбираем исходя из предназначения.
Будущий конус будет достаточно прочным за счет чего, его применение может быть широким. Подобную методику работы мы уже рассмотрели выше, но это изготовление все же отличается.
Плотный конус готов. Если вам нужна не одна геометрическая фигура, а несколько, первый полученный круг, в котором уже вырезана одна четверть, можно использовать в качестве шаблона.
Инструкция изготовления простого конуса
Сделать конус в основе которого лежит бумага очень просто. На всю работу уходит до пяти минут. Достаточно перед работой изготовить верный чертеж и свернуть материал правильным образом.
Простой конус схема
Для первой работы потребуется:
Как сделать конус из бумаги пошагово:
Конус готов. Готовую фигуру можно использовать для разнообразных поделок. А если добавить к нашей фигуре шар, то получится поделка для выставки на геометрическую тематику.
Особенности построения уклона и конусности
Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Методы и средства контроля и измерения углов и конусов
- Контроль и измерение углов и конусов выполняется с использованием строгих примерных измерений, тригонометрии и абсолютных методов. К жестким примерным шкалам относятся угловые шкалы (плитки и многогранники), квадраты, узоры и калибр. Измерения угловых призм используются для хранения и переноса единиц измерения плоских углов.
Они используются, чтобы проверить образец и угловой размер различных продуктов. Для градуировки гониометра и прямого измерения. Угловые измерения, предназначенные для проверки гониометров и измерений движения, называются образцами.
В процессе сборки и эксплуатации детали неизбежны сглаживание микротрещин, морщин и износ, что приводит к дополнительным отклонениям в размерах и форме детали. Людмила Фирмаль
Защита углов выполняется по следующим видам ГОСТ 2875-75: I-1 Угловая плитка с одним рабочим углом и обрезанным верхом (рис. 14.1, а). II-угловая плитка с одним рабочим углом — острый угол (рис. 14.1, б); III — угловая плитка с четырьмя рабочими углами Рисунок 14.2. (Рис. 14.1, в); IV-шестиугольная призма с неравномерным угловым шагом. V-многогранная призма с равномерным угловым шагом (8 и 12 граней). Угловые меры создаются в виде набора плиток толщиной 5 мм, так что блок 10-90 состоит из трёх мер.
В зависимости от отклонения фактического значения рабочего угла от номинального значения и отклонения плоскостности измерительной поверхности измерения угла производятся в трёх классах точности (0, 1, 2). В зависимости от точности сертификации угловой точности для плиток первого класса 10 и второго класса 30, примерные измерения углов делятся на четыре категории (1, 2, 3, 4). Предельная погрешность при сертификации рабочего угла не должна превышать измеренное значение первой категории 0,5, а второй 1.
Третий угол 3 дюйма; четвертый угол 6 дюймов собираются в блоки с использованием специальных держателей. Контроль угла по углу. Согласно ГОСТ 3749-77, квадраты генерируют шесть типов (рисунок 14.2). Угол контролируется квадратом и зазором между квадратом и контролируемым Используйте разрез модели, созданный с использованием окончательного измерения длины и линейки.
При использовании больших квадратов зазор оценивается с помощью зонда, используя следующую зависимость для расчёта углового отклонения. Угол на длине 200 мм даёт просвет 1 мкм. Ошибка проверки угла Рисунок 14.3 С помощью квадрата это зависит от ошибки самого квадрата, длины стороны угла, где производится проверка, и других факторов. Триангуляция угла или косвенное измерение приводит к измерению отрезка прямой линии, после которого треугольное соотношение определяет желаемый угол.
- Используется специальное оборудование и измерительные приборы различных конструкций и концевых мер, линейки и контрольные шайбы и шишки. В современной технике часто необходимо контролировать прямые углы с допусками в несколько минут. Не обеспечивает оценку отклонения угла просвета Точно определяет угол наклона и сильно зависит от опыта работы контроллера.
В таких случаях рекомендуется проверять угол, используя косвенный метод, используя квадраты и измерительные ролики с различными диаметрами и Lg порядка сотых долей миллиметра (Рисунок 14.3). Рисунок 14.4 Рисунок 14.6 Ролики монтируются с помощью концевых блоков на определенной высоте L. Критический размер и высота L измерительного ролика рассчитываются в соответствии с максимальным отклонением угла контролируемой детали, указанной на чертеже, да. Измерительный ролик и измерительный шарик также используются для управления внешним (рис. 14.4, а, б) и внутренним (рис. 14.4, в) конусами.
Несопряженная или свободная поверхность-это конструктивно необходимая поверхность, которая не предназначена для соединения с поверхностью других деталей. Людмила Фирмаль
При контроле внешнего конуса сначала измерьте размер 4 по диаметру ролика 3 (рис. 14.4, а). Затем поместите конец 4 измерительного блока того же размера A под валиком и измерьте размер 2 (рис. 14.4, б). Конусность определяется по формуле 2a = (2-4) L (14,1) При измерении внутреннего конуса используются два шарика известного диаметра. Поместите гильзу 1 (Рис.14.4, c) на пластину 2, поместите в нее d-шарик небольшого диаметра и измерьте глубиномер (микрометр или индикатор) размером 4.
Затем поместите шарик большого диаметра O и измерьте размер 2. Конус рукава определяется по формуле 2 (С-4) 2 (1-12) (С-4) 2 51p a = (14-2) Синусоидальная линейка часто используется для измерения углов и конусов (рис. 14.5). Это стальной стол 2, оснащенный двумя цилиндрическими роликами одинакового диаметра. Ролики расположены на строго определенном расстоянии друг от друга, обычно 100 мм или 200 мм между центрами роликов.
Таблица 2 установлена под испытательной пластиной 4. Установите угол, используя конец блока 3. Соотношение между размером L элемента мозаичного изображения и углом синусоидальной линейки определяется из соотношения. 51pa = L b. (14.3) Например, угловое отклонение датчика конической пробки определяется разницей между показаниями прибора 1 в точке 1 и точке 2 и называется расстоянием I между этими точками. Если показания прибора равны в точках a и b, угол конуса по высоте блока L может быть найден. Погрешность измерения синусоиды составляет 3 52, в зависимости от расстояния b и угла измерения.
В абсолютных измерениях угол определяется непосредственно в угловых единицах с помощью гониометра, разделенной головки, микроскопа и другого оборудования. Наиболее распространённым является гониометр Нониуса (рис. 14.6). Они состоят из фиксированной линейки, прикрепленной к полудиску 2, к которой применяется угловое деление от 0 до 120, и подвижной линейки 5, неподвижно соединенной с нониусным сектором 3. Этот гониометр может измерять углы от 0 до 180. Для измерения углов от 0 до 90 съемный квадрат 6 приккреплён к подвижной линейке 5 с помощью зажима 4.
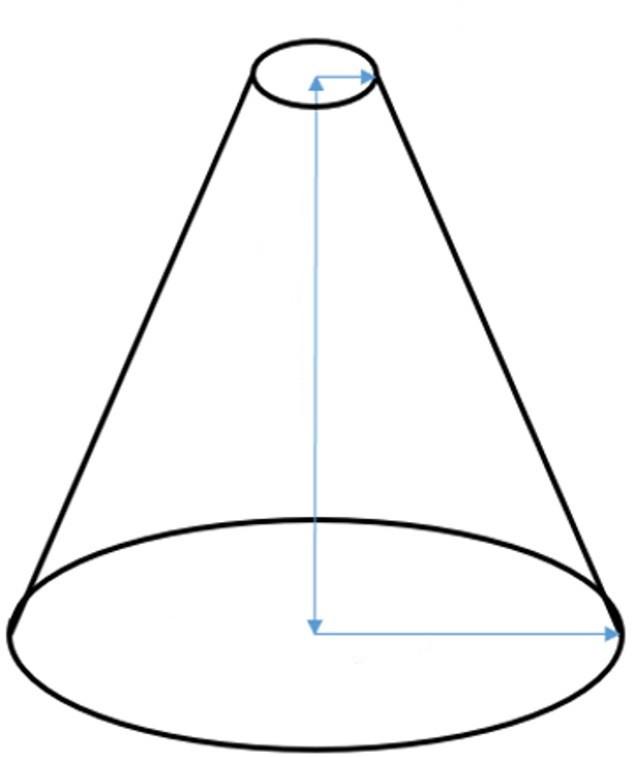
Через угол раствора можно найти угол между образующей и основанием, отняв от 180 градусов величину угла и разделив полученное значение на два. Через угол с основанием можно найти высоту и радиус конуса, используя тригонометрические отношения в прямоугольном треугольнике. (рис. 40.2, 40.1)
β=(180°-α)/2
h=sinβ l
r=cosβ l
Таким образом, через значение радиуса можно найти диаметр, периметр и площадь окружности, которая находится в основании конуса, подставляя в формулы вместо радиуса произведение косинуса известного угла на образующую.
d=2r=2 cosβ l
P=2πr=2π cosβ l
S_(осн.)=πr^2=πl^2 cos^2β
Площадь боковой поверхности конуса равна произведению радиуса на образующую и число π, а если прибавить в ней произведение числа π на квадрат радиуса, то получим площадь полной поверхности конуса.
S_(б.п.)=πrl=π cosβ l^2
S_(п.п.)=S_(б.п.)+S_(осн.)=πr(r+l)=π cosβ l^2 (cosβ+1)
Чтобы найти объем конуса необходимо площадь основания умножить на треть высоты, используя тригонометрические отношения через образующую для радиуса и высоты.
V=(hS_(осн.))/3=(πl^3 sinβ cos^2β)/3
Для расчетов радиуса вписанной и описанной около конуса сфер существуют специальные формулы с применением значений угла между образующей и основанием и угла раствора конуса. (рис.40.3, 40.4)
r_1=r tan〖β/2〗=l cosβ tan〖β/2〗
R=r/sinα =(l cosβ)/sinα
Радиус и образующая конуса

Свойства
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cosβ=r/l α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h
Как найти образующую конуса обычного и усеченного. Формулы
Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.
 Вам будет интересно: Развивающая функция обучения: цель, основные принципы
Вам будет интересно: Развивающая функция обучения: цель, основные принципы
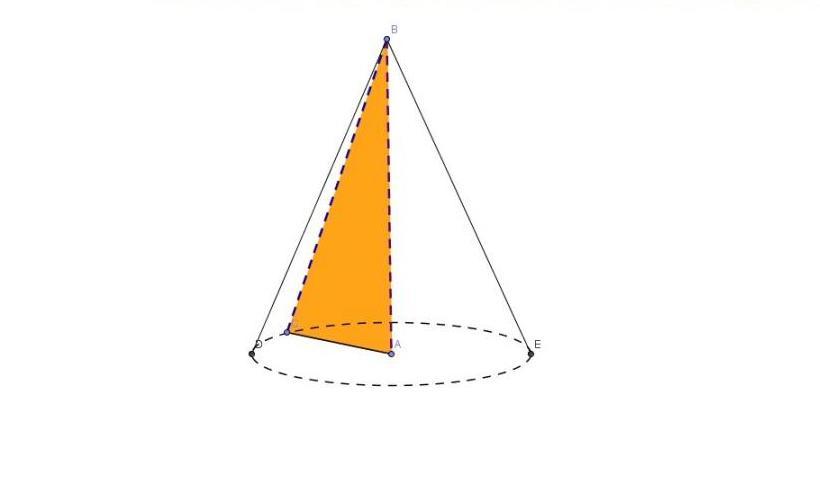
Полученная пространственная фигура имеет следующие характеристики:
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
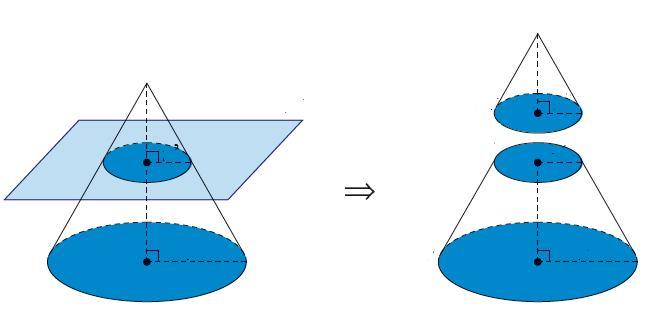
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок – это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Узнать ещё
Знание — сила. Познавательная информация
Конус, вписанный в шар
Решение задач на конус, вписанный в шар (конус, вписанный в сферу) сводится к рассмотрению одного или нескольких треугольников.
Конус вписан в шар, если его вершина и окружность основания лежат на поверхности шара, то есть на сфере. Центр шара лежит на оси конуса.
При решении задач на конус, вписанный в шар, удобно рассматривать сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара. Сечение представляет собой большой круг шара (то есть круг, радиус которого равен радиусу шара) с вписанным в него равнобедренным треугольником — осевым сечением конуса. Боковые стороны этого треугольника — образующие конуса, основание — диаметр конуса.
Если угол между образующими острый, центр описанного круга лежит внутри треугольника (соответственно, центр описанного около конуса шара — внутри конуса).
Если угол между образующими прямой, центр круга лежит на середине основания треугольника (центр шара совпадает с центром основания конуса).
Если угол между образующими тупой, центр круга лежит вне треугольника (центр описанного шара — вне конуса).
Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
Рассмотрим конуса и описанного около него шара плоскостью, проходящей через ось конуса и центр шара. Здесь SO=H — высота конуса, SB=l — образующая конуса,SO1=O1B=R — радиус шара, OB=r — радиус основания конуса, ∠OSB=α — угол между высотой и образующей конуса.
Треугольник SO1B — равнобедренный с основанием SB (так как SO1=O1B=R). Значит, у него углы при основании равны: ∠OSB=∠O1BS=α, и O1F — медиана, высота и биссектриса. Отсюда SF=l/2.
При решении задач на конус, вписанный в шар, можно рассмотреть прямоугольные треугольники SFO1 и SOB. Они подобны (по острому углу S). Из подобия треугольников
В прямоугольном треугольнике SOB ∠OBS=90º — ∠OSB=90º-α. По теореме Пифагора
В прямоугольном треугольнике O1OB ∠OBO1=90º — ∠O1BS=90º — α — α=90º — 2α.
Если продлить SO до пересечения с окружностью, получим прямоугольный треугольник SBM (∠SBM=90º как вписанный угол, опирающийся на диаметр SM). В нем BO- высота, проведенная к гипотенузе. По свойствам прямоугольного треугольника
[spoiler title=”источники:”]
http://1ku.ru/obrazovanie/45666-kak-najti-obrazujushhuju-konusa-obychnogo-i-usechennogo-formuly/
[/spoiler]
