
Давление равно отношению силы давления к площади. Это универсальное определение относится к твердым телам, жидкости, газу. Способы увеличения давления: увеличить силу; уменьшить площадь. Давление в твердых телах передается в том же направлении, в котором действует сила. При решении задач (например, тело на наклонной плоскости) рассматриваются проекции сил – давление тела на плоскость и реакция опоры – на оси координат. Направление движения тела, при действии несколкиз сил, не совпадает с направлением силы давления на тело. Гидростатика. Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково. Это связано с подвижностью молекул в жидком и газообразном состояниях. Давление столба жидкости: Р = ρgh(ро же аш), где ρ – плотность жидкости, g – ускорение свободного падения. h – высота столба жидкости или глубина, на котороей измеряется давление. Сила давления: F = p S Используя две формулы, находим силу давления на дно сосуда, на боковую грань аквариума и т.п. Экзаменационные задачи на эту тему простые; вычисляйте всё в системе СИ.

Гидростатический парадокс (следствие закона Паскаля): давление на дно сосуда определяется только высотой столба жидкости. И не только на дно, но и вообще на данной глуибне. Независимо от фомы сосуда и его размеров (см. формулу выше). Поэтому в трех сосудах давление на дно одинаково.
Но сила давления разная – не путаем понятия!
Сообщающиеся сосуды
Сообщающиеся сосуды – сосуды, соединенные между собой (трубкой) или имеющие общее дно. Уровень жидкости в сообщающихся сосудах располагается горизонтально, если: • поверхности жидкости открыты; • в сосуды налита однородная жидкость; • ни один из сосудов не является капилляром; • в жидкостях нет пузырьков с воздухом. Давление столбов жидкости на одном горизонтальном уровне одинаково: Гидравлический пресс – простой механизм, дающий выигрыш в силе. Он представляет собой сообщающиеся сосуды разного сечения. В основе его действия лежит закон Паскаля.

Внешняя сила, действующая на малый поршень, совершает работу. Давление в жидкости одинаково. (Высота столбов жидкостей в цилиндрах пресса меняется, но в задачах это не учитывается. Такой пресс может работать в любом положении и в невесомости.) Сила давления жидкости, действующая на большой поршень совершает полезную работу. Из меньшего цилиндра в больший перемещается некоторый объем жидкости – при этом перемещение меньшего поршня больше. Выигрыш в силе аналогичен действию рычага. Затрачиваемая и совершаемая работы одинаковы (если КПД 100%). Далее: Атмосферное давление
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.

Рис. 1. Сообщающиеся сосудыЗакон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
ρ/ρ=h/hГде:

- ρ – плотность жидкости;
- h – высота столба.
Также для сообщающихся сосудов важной является формула: p=gρhГде:
- g – ускорение свободного падения;
- ρ – плотность жидкости (кг/куб.м);
- h – глубина (высота столба жидкости).
Этой формулой определяется давление жидкости на дно сосуда. Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз. В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.

В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты.
Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору.

И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению.
И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).
Рис. 2. ШлюзИз этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.

Средняя оценка: 4.2. Всего получено оценок: 497.
Page 2
ОбразовакаФизика
- МанометрТест
- Закон ГукаТест
- Закон ПаскаляТест
- Сообщающиеся сосудыТест

СодержаниеСообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
[custom_ads_shortcode1]
Закон сообщающихся сосудов
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:

Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление. Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики.
None ρgh – сила тяжести (вес призмы).

Звучит уравнение так: Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости.
[custom_ads_shortcode2]
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2. Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики P = P1 + ρgh1если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образомP = P2 + ρgh2где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2P1 + ρ1gh1 = P2 + ρ2gh2В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеемρ1h1 = ρ2h2или ρ1 / ρ2 = h2 / h1т.е. закон сообщающихся сосудов состоит в следующем.

В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов. Можно.
С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.

Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой. В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0. Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.

Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости. Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.

Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения. В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее. В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
![[T =-P_0 cdot S_1]](https://fizikinfo.ru/wp-content/uploads/2019/07/Davlenie-gaza-v-dvuh-raznyh-soobschajuschihsja-sosudah15.png)
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого. В дополнение к статье “Закон сообщающихся сосудов и его применение.” Вам может быть интересно:
Каждое утро мы умываемся. А знаете ли вы, почему течет вода из крана, когда мы его открываем? А почему выливается вода из носика чайника, если чайник наклонить?

А как «работает» артезианский колодец? Может, кто-то из вас уже знает, что все эти устройства являются сообщающимися сосудами. Именно о сообщающихся сосудах, их свойствах и применении будет идти речь в этом параграфе.
исследуем сообщающиеся сосудыСообщающиеся сосуды — это сосуды, которые соединены между собой так, что между ними может перетекать жидкость.
Простейшие сообщающиеся сосуды — это две соединенные между собой трубки. Если в одну из трубок наливать воду, то вода будет перетекать в другую трубку. Когда движение воды прекратится, вода в обеих трубках (обоих коленах сообщающихся сосудов) установится на одном уровне (рис.

26. 1, а). Если наклонить или поднять одно из колен, то вода будет перетекать из колена, расположенного выше, пока уровни воды в обоих коленах не сравняются (рис.
26. 1, б).
Итак, мы определили основное свойство сообщающихся сосудов: В открытых сообщающихся сосудах свободные поверхности однородной неподвижной жидкости располагаются на одном уровне.

Обратите внимание! Свободные поверхности жидкости устанавливаются на одном уровне не только в двух, но и в любом количестве сообщающихся сосудов — независимо от того, какую форму они имеют и как расположены в пространстве (рис. 26.2).
А вот если в правое и левое колена сообщающихся сосудов налить жидкости, которые не смешиваются и имеют разные плотности, например керосин и воду, результат будет иным. Рассмотрим рис. 26.
3. На уровне CD давление столбов жидкостей в сосудах одинаково:

Отсюдаимеем еще одно свойство сообщающихся сосудов:
В открытых сообщающихся сосудах столб неподвижной жидкости, имеющей меньшую плотность, будет выше, чем столб неподвижной жидкости, имеющей большую плотность. для двух открытых сообщающихся сосудов соотношение высот столбов жидкостей и плотностей этих жидкостей имеет вид:
![]()
Сообщающиеся сосуды широко применяют в быту, медицине, технике, строительстве. Шлюзы на каналах и реках, водопроводы, водомерные трубки на паровых котлах, артезианские колодцы, фонтаны, чайники, воронки, капельницы — все это примеры сообщающихся сосудов.
Рассмотрите рис. 26.4 и попробуйте объяснить принцип действия некоторых устройств.
Изготовляем открытый жидкостный манометрНа правое колено и-образной трубки, в которую налита однородная жидкость, наденем резиновую грушу. Слегка сожмем грушу — жидкость в трубке установится таким образом, что высота столба жидкости в правом колене будет меньше, чем в левом, на h (рис. 26.5).

Определим давление воздуха рв в правом колене трубки. На уровне АВ давление в жидкости одинаково (рА = рВ). В точке В это будет давление рв — давление воздуха в груше, в точке А — атмосферное давление ратм плюс гидростатическое давление столба жидкости высотой h. Получаем:
Итак, с помощью и-образной трубки, заполненной однородной жидкостью (известной плотности р), и линейки, позволяющей измерить разность уровней жидкости в коленах трубки (И), можно определить, на сколько давление газа в груше отличается от атмосферного. Соответствующий прибор называют открытый жидкостный манометр (рис. 26.6).
Манометр — это прибор для измерения давления жидкостей и газов.
Открытый жидкостный манометр (рис. 26. 6, а) состоит из линейки 1, к которой присоединена ^образная трубка 2.
Трубка заполнена подкрашенной жидкостью 3 так, что уровень жидкости расположен на отметке 0. При измерениях (рис. 26.
Например, на рис. 26.6, б разность уровней подкрашенной жидкости в сообщающихся сосудах составляет 10 см (h = 01 м). Если в трубке находится подкрашенная вода, то давление газа в колбе 5 меньше атмосферного давления на 980 Па:

Заменяем жидкостный манометр металлическимЖидкостный манометр не всегда удобен в использовании: необходимо доливать жидкость до нужного уровня, осуществлять дополнительные вычисления. Поэтому, как правило, используют металлические деформационные манометры (рис. 26.7).
Основной элемент металлического деформационного манометра — гибкая дугообразная трубка 1, один конец которой (А) запаян. Второй конец трубки (Б) соединен с резервуаром, в котором нужно измерить давление. Принцип действия таких манометров следующий. Если давлениегаза внутри трубки больше атмосферного, то гибкая трубка распрямляется и ее движение передается через механизм 2 к стрелке 3, движущейся вдоль шкалы 4 прибора. После уменьшения давления газа до атмосферного трубка возвращается в начальное (недеформированное) положение, а стрелка останавливается на отметке 0. Шкала металлического манометра проградуирована в атмосферах или паскалях.
Обратите внимание! Металлический деформационный манометр показывает, на сколько измеренное давление больше или меньше атмосферного. Учимся решать задачиЗадача.

В правое колено открытой ^образной трубки, содержащей воду, налили слой керосина высотой 12,5 см (см. рисунок). Определите разность уровней воды и керосина в коленах трубки.
Анализ физической проблемы. В однородной жидкости давление на одном горизонтальном уровне одинаково. В обоих коленах на уровне ЛБ и ниже находится вода, значит, на уровне ЛБ давления, создаваемые атмосферой и жидкостями, одинаковы.
Чтобы определить гидростатические давления жидкостей, нужно знать их плотности. Плотности воды и керосина узнаем из таблицы плотностей (с. 249).
Подводим итогиСообщающиеся сосуды — это сосуды, которые соединены между собой так, что между ними может перетекать жидкость.
В открытых сообщающихся сосудах разных форм и размеров свободная поверхность однородной неподвижной жидкости располагается на одном уровне; если плотности жидкостей в сосудах различны, то столб жидкости, имеющей меньшую плотность, выше, чем столб жидкости, имеющей большую плотность.
Манометры — это приборы для измерения давления жидкостей и газов. В открытом жидкостном манометре давление газа рг в сосуде определяется по разности h уровней жидкости в коленах прибора:

На практике широко используют металлические деформационные манометры.
Контрольные вопросы1. Приведите примеры сообщающихся сосудов. 2. Сформулируйте основное свойство сообщающихся сосудов. 3. Как ведут себя жидкости разной плотности, налитые в сообщающиеся сосуды? 4. Что такое манометр? 5. Как работает открытый жидкостный манометр? 6. Опишите строение и принцип действия металлического деформационного манометра.
None 2. На сколько отличается давление в баллоне (см. задание 1) от атмосферного?

3. В некоторых храмах Древней Греции стояла так называемая «неисчерпаемая чаша» (рис. 2).
Объясните, опираясь на рисунок, как работало это «чудо». 4. В жидкостном манометре (рис.
3) находится ртуть. Левое колено манометра открыто в атмосферу. Определите давление в баллоне, если атмосферное давление равно 100 кПа.
5. Составьте задачу, обратную задаче в § 26, и решите ее.
6. Определите давление газа в колбе В (рис. 4), если давление газа в колбе Аравно 100 гПа.
7. Воспользуйтесь дополнительными источниками информации и узнайте о принципе работы шлюзов. Представьте себе, что вы оператор соответствующей службы.
Составьте систему команд для проведения судна через камеры шлюза (рис. 5). Разрешается использовать такие команды: открыть (закрыть) ворота (1, 2, 3, 4); спустить воду из камеры (І, ІІ, ІІІ); запустить воду в камеру (І, ІІ, ІІІ); перейти в камеру (І, ІІ, ІІІ).
8. Речное судно получило в днище пробоину площадью 200 см. Матрос массой 80 кг перекрыл доступ воды, накрыв отверстие пластиной и встав на нее. Определите осадку судна. Массу пластины не учитывайте.
Экспериментальное задание«Манометр своими руками».Воспользовавшись прозрачной эластичной трубкой и линейкой, изготовьте манометр, который будет измерять разность давлений в атмосфере и бутылке (см. рисунок). Проследите изменение разности давлений в течение недели; сделайте вывод.

Физика и техника в УкраинеКаскад из шести гидроэлектростанций (ГЭс) на днепре является выжным элементом энергосистемы Украины. Возведение этих ГЭс обеспечило энергией заводы-гиганты, принесло электрический свет в тысячи домов запорожья, Кривого Рога и других городов Украины. После того как высокие дамбы перегородили днепр, глубина реки значительно увеличилась. Это обеспечило судоходство по всей длине днепра. А чтобы суда могли плыть и дальше, к Черному морю, в конструкции плотин инженеры предусмотрели специальные узлы — шлюзы.
Шлюз представляет собой систему последовательно расположенных «комнат», которые называют камерами. В каждой камере с двух сторон есть «двери», но нет «крыши». Размеры камер огромны — каждая из них способна вместить одновременно несколько теплоходов.
Работает шлюз следующим образом. судно входит в первую камеру, ее внешние двери за ним закрываются, и происходит выравнивание уровня воды со второй камерой через систему сообщающихся труб (по принципу сообщающихся сосудов). Потом открываются двери между первой и второй камерами — судно переходит во вторую камеру и т.

Это материал учебника Физика 7 класс Барьяхтар, Довгий
Источники:
- kiselevich.ru
- obrazovaka.ru
- www.nektonnasos.ru
- narodna-osvita.com.ua
Ответы Mail.ru
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Вопросы – лидеры.
Помогите пожалуйста! СРОЧНО!!!!!
Сделайте развёрнуто и кратко.
1 ставка
Решите пожалуйста задачу
1 ставка
Просьба оказать помощь в решении задачи
1 ставка
Помогите пожалуйста,очень срочно нужно выполнить
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
если в сосуд налиты две жидкости с разными плотностями как найти их общее давление на дно сосуда?
Нина Гурова
Ученик
(136),
закрыт
11 лет назад
Лучший ответ
Владимир Соколов
Искусственный Интеллект
(212258)
11 лет назад
Жди отстоя, измеряй уровень каждой жидкости и Суммируй давления согласно формулы P=pж*g*h
Остальные ответы
Похожие вопросы
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж — плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
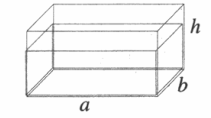
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
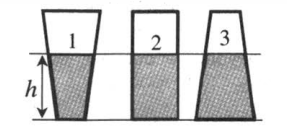
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
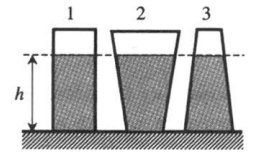
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22709
Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18804
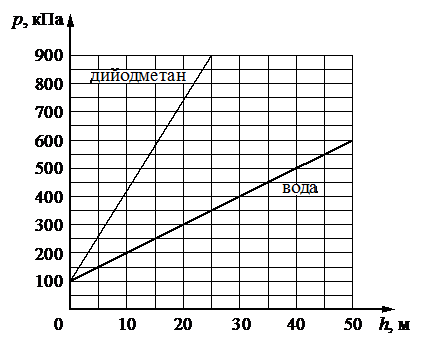
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.3k
Формула давления жидкости отличается от формулы, с помощью которой можно рассчитать давление твердого тела. Потому, что давление жидкости не зависит от площади поверхности, на которую жидкость давит.
Закон Паскаля
Французский физик, Блез Паскаль, в 1653 году сформулировал закон: «Давление, которое мы оказываем на жидкость (или газ), она без изменения передаст в любую точку и во всех направлениях».
Мы немного упростим формулировку:
Жидкость (или газ) передает давление, оказанное на нее, одинаково и без изменений во все стороны.
Это значит, что на одной и той же глубине жидкость будет одинаково давить и на дно, и на стенки сосуда.

Рис. 1. Чем глубже, тем больше давление жидкости, но в любой точке жидкость передает это давление одинаково во все стороны
На рисунке 1 изображен сосуд, наполненный жидкостью. Высоту столбика жидкости – то есть, глубину, отсчитываем от поверхности жидкости.
Видно, что на разных глубинах давление отличается.
[ large begin{cases} h_{1} < h_{2} < h_{3} \ P_{1} < P_{2} < P_{3} end{cases} ]
Чем глубже, тем больше давление жидкости. Но в любой точке оно одинаково передается во все стороны.
Формула давления жидкости
Формула, по которой можно посчитать давление жидкости:
[ large boxed{ P = rho_{text{ж}} cdot g cdot h }]
( P left(text{Па}right) ) – давление жидкости;
( displaystyle rho_{text{ж}} left(frac{text{кг}}{text{м}^3} right) ) – плотность жидкости;
( displaystyle g left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения;
Для большинства школьных задач можно принимать ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) );
( h left(text{м}right) ) – высота столбика жидкости.
В формулу для давления жидкости не входит площадь S поверхности, на которую эта жидкость давит.
Поэтому, давление жидкости не зависит от площади. А давление твердого тела рассчитывают по другой формуле.
В некоторых задачах указывают объем используемой жидкости. И иногда просят рассчитать силу давления. Чтобы получить правильный ответ для таких задач, нужно уметь переводить площади и объемы в единицы системы СИ.
Сообщающиеся сосуды
Сообщающиеся сосуды – это емкости, расположенные на плоской горизонтальной поверхности, у дна они соединяются трубками.
Если в один из сосудов начать наливать жидкость, то она будет распределяться по всем сосудам, так, что ее уровень будет одинаковым во всех сосудах (рис. 2).

Рис. 2. В сообщающихся сосудах уровень жидкости будет одинаковым
Неважно, какую форму имеет сосуд. Давление жидкости во всех сосудах будет одинаковым. Поэтому одинаковой будет высота h столбика жидкости во всех сосудах.
U-образное колено – это два сообщающихся сосуда, диаметры сосудов одинаковые.
Жидкости, которые заливают в колено, не должны смешиваться (рис. 3). Например, можно залить в оду трубку воду, а в другую — масло.

Рис. 3. Два сообщающихся сосуда одинакового диаметра образуют U-образное колено
Запишем формулы для расчета давления в левом (P_{1}) и правом (P_{2}) частях колена.
[ large boxed{begin{cases} P_{1} = rho_{1} cdot g cdot h_{1} \ P_{2} = rho_{2} cdot g cdot h_{2} end{cases}} ]
Чем больше разница плотностей двух жидкостей, тем больше отличаются высоты их столбиков.
При решении задач общую нижнюю часть колена не учитываем. На рисунке 3 она отделена от верхней части горизонтальной линией.
Давление столбиков, оставшихся в верхней части, будет одинаковым.
( P_{1} ) – давление жидкости в левой части колена;
( P_{2} ) – давление жидкости в правой части колена.
[ large begin{cases} P_{1} = P_{2} \ rho_{1} cdot g cdot h_{1} = rho_{2} cdot g cdot h_{2} end{cases} ]
Обе части последнего уравнения разделим на ускорение свободно падения. Тогда получим соотношение для высот столбиков жидкости и их плотностей:
[ large boxed{ rho_{1} cdot h_{1} = rho_{2} cdot h_{2} }]
Высоты столбиков можно измерить линейкой. Зная плотность одной из жидкостей, можно найти плотность второй жидкости.
Примечание: Давление жидкостей часто измеряют в миллиметрах ртутного столба или метрах водяного столба. Переходите по ссылке, чтобы узнать, как связаны эти единицы измерения и как давление переводить в систему СИ.
Гидравлический пресс
Молекулы жидкости плотно упакованы, они прилегают друг к другу. Поэтому жидкости не сжимаемы! Это свойство жидкостей используют в гидравлическом прессе.
Гидравлический пресс – это два сообщающихся сосуда. Их называют цилиндрами. Диаметры цилиндров отличаются. Внутри каждого цилиндра вверх и вниз может свободно перемещаться поршень (рис. 4). Поршень плотно прилегает к стенкам цилиндра, чтобы жидкость из цилиндра не просачивалась наружу.

Рис. 4. Гидравлический пресс – это два сообщающихся сосуда различных диаметров, по сосудам могут без трения перемещаться поршни
Перемещаясь, поршень из цилиндра вытесняет жидкость в соседний цилиндр. Объем жидкости, вытесненной из одного цилиндра, совпадает с объемом, перешедшим в другой цилиндр, так как жидкость не проливается наружу.
[ large Delta V_{1} = Delta V_{2} ]
( Delta V_{1} left(text{м}^{3}right) ) – объем жидкости, вытесненной из первого цилиндра;
( Delta V_{2} left(text{м}^{3}right) ) – объем жидкости, перешедшей во второй цилиндр.
Из геометрии известно, объем цилиндрической фигуры можно найти по формуле:
[ large boxed{ Delta V = Delta h cdot S }]
( Delta h left(text{м}right) ) – высота столбика вытесненной жидкости;
( S left(text{м}^{2}right) ) – площадь поршня (или основания цилиндра);
Так как объемы вытесненной и перешедшей в другой цилиндр жидкостей равны, можем записать
[ large Delta h_{1} cdot S_{1} = Delta h_{2} cdot S_{2} ]
То есть, высоты столбиков отличаются во столько же раз, во сколько отличаются площади поршней.
Площадь поверхности поршня и его диаметр связаны соотношением:
[ large boxed{ S_{text{круга}} = pi cdot frac{d^{2}}{4} }]
( S left(text{м}^{2}right) ) – площадь поршня;
( d left(text{м}right) ) – диаметр поршня;
Давления в цилиндрах будут равны.
[ large P_{text{общ.лев}} = P_{text{общ.прав}} ]
Поршни в цилиндрах не двигаются – т. е. находятся в равновесии. Запишем условия равновесия для поршней:
[ large boxed{ frac{F_{1}}{S_{1}} + rho_{1} cdot g cdot h_{1} = frac{F_{2}}{S_{2}} + rho_{2} cdot g cdot h_{2} } ]
Здесь дробью вида (displaystylelarge frac{F}{S}) обозначено давление твердого тела (ссылка) — поршня.
Назовем цилиндр большого диаметра большим цилиндром, а цилиндр малого диаметра – малым. Сформулируем принцип действия гидравлического пресса:
С помощью малой силы в малом цилиндре мы можем создавать большую силу в большом цилиндре.
Давление жидкостей и газов. Закон Паскаля
- Особенности давления жидкостей и газов
- Закон Паскаля
- Давление столба жидкости
- Давление столба газа
- Задачи
п.1. Особенности давления жидкостей и газов
Давление жидкостей и газов отличается от давления твердых тел. Причина – в особенностях поведения частиц вещества в разных агрегатных состояниях (см. §16 данного справочника).
В отличие от твердых тел, молекулы жидкостей и газов подвижны.
Жидкость принимает форму сосуда, который предохраняет её от растекания. Поэтому жидкость в сосуде оказывает давление не только на дно, но и на стенки. Верхние слои жидкости давят на нижние, и давление растет с глубиной (с увеличением столба жидкости).
Газ заполняет весь предоставленный ему объем. В закрытом сосуде хаотически движущиеся молекулы газа будут сталкиваться с дном, стенками и крышкой сосуда. Таким образом, газ будет оказывать давление во все стороны: вниз, по бокам и даже вверх.
Давление газа также растет с увеличением высоты столба. Однако за счет малой плотности газов этот рост менее заметен по сравнению с жидкостями. В небольшом сосуде давление газа можно считать постоянным во всем объеме сосуда.
п.2. Закон Паскаля
При давлении на жидкость или газ в определенной области происходит сжатие; расстояние между молекулами становится меньше, начинают сильнее действовать силы отталкивания. В результате молекулы перемещаются из области сжатия с большим давлением в области с меньшим давлением. Это происходит достаточно быстро; например, у кислорода при 0°С средняя скорость молекул 425 м/с, у паров воды – 570 м/с. Поэтому в течение небольшого времени давление в сосуде выравнивается.
Закон Паскаля
Жидкости и газы передают давление по всем направлениям одинаково.
Для подтверждения закона Паскаля можно провести следующие эксперименты.
п.3. Давление столба жидкости
Как было замечено выше, давление жидкостей заметно увеличивается с глубиной. Это объясняется тем, что верхние слои давят на нижние.
Найдем давление столба жидкости высотой (h)
Согласно закону Паскаля, давление в жидкости передается во всех направлениях одинаково. Поэтому на данной глубине (h) в каждой точке уровня давление будет постоянно.
 |
Рассмотрим сосуд в форме прямоугольного параллелепипеда. Пусть в его основании – прямоугольник с длиной (a) и шириной (b). Нальем в этот сосуд воду до отметки высотой (h). Нас интересует давление воды на дно сосуда. Сила давления на дно направлена вертикально вниз и равна силе тяжести: $$ F=mg=rho Vg $$ Объем воды в сосуде: $$ V=abh $$ |
Получаем: $$ F=rhocdot abhcdot g $$ Давление на дно сосуда равно отношению силы давления к площади дна: $$ p=frac FS=frac{rhocdot abh cdot g}{ab}=rho gh $$
Давление столба жидкости
На глубине (h) давление жидкости равно $$ p=rho gh $$
Давление не зависит от площади дна, и, следовательно, не зависит от его формы.
Полученное выражение будет справедливо для вертикального столба жидкости высотой (h) с любым сечением (квадратным, круглым, треугольным, совершенно фантазийным).
Это интересно
 |
Давление не зависит ни от формы, ни от размеров сечения столба жидкости, зато резко увеличивается с высотой. Это свойство использовал Паскаль, продемонстрировав своим современникам забавный эксперимент. Он взял прочную дубовую бочку, наполнил ее доверху водой, плотно закрыл и вставил очень узкую, но очень длинную трубку (около 4 м). Затем он поднялся на второй этаж и вылил в трубку кружку воды. Бочка тут же …лопнула. Действительно, ведь давление в бочке увеличилось на (p=1000cdot 10cdot 4=40 text{кПа}): её будто «придавило» четырьмя тоннами воды, хотя понадобилась всего лишь кружка. Тем не менее, результат этого фокуса всегда кажется неожиданным. |
п.4. Давление столба газа
Газы, как и жидкости, также имеют некоторую плотность. Поэтому, рассматривая давление столба газа по аналогии с жидкостью, можно прийти к тем же результатам.
Давление столба газа
Давление столба газа высотой (h) равно $$ p=rho gh $$
Понимание того, что газ также оказывает разное давление в разных слоях, возникло не сразу. Это объясняется небольшой плотностью газов по сравнению с жидкостями.
 |
Для иллюстрации рассчитаем давление столба воды и столба воздуха высотой (h=1 text{м}). Плотность воды (rho_text{воды}=1000 text{кг/м}^3), плотность воздуха при 20°C (rho_text{возд}=1,2 text{кг/м}^3). Получаем: begin{gather*} p_text{вода}= rho_text{вода}ghapprox 1000cdot 10cdot 1=10000 (text{Па})\[7pt] p_text{возд}= rho_text{возд}ghapprox 1,2cdot 10cdot 1=12 (text{Па}) end{gather*} Из-за разности в плотности, давление отличается почти в 1000 раз, ведь масса кубометра воды – 1 тонна, а масса кубометра воздуха – всего 1,2 кг. |
Поэтому при изучении процессов в небольших сосудах разность в давлении газа в верхних и нижних слоях практически не заметна.
С другой стороны, если рассматривать значительные по высоте «столбы» газов, например, атмосферу планеты, давление становится существенной величиной. Так, на поверхности Земли атмосферное давление составляет около 100 000 (Па). Подробней этот вопрос будет рассмотрен в §31 данного справочника.
В итоге, для открытого сосуда с жидкостью, где на поверхность дополнительно оказывает давление атмосфера, давление жидкости на глубине h равно сумме: $$ p=p_text{атм}+rho gh $$
п.5. Задачи
Задача 1. Пятый этаж расположен выше первого на 15 м.
На каком этаже давление в трубах водопровода больше и на сколько?
Дано:
(h=15 text{м})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(Delta p-?)
Давление в водопроводе на первом этаже $$ p_1=p_text{внеш}+rho gh, $$ где (p_text{внеш}) – давление, связанное с действием внешних сил (атмосфера, водонапорная башня, насос и т.п.), второе слагаемое – давление вертикального столба жидкости в трубе в доме.
Давление в водопроводе на пятом этаже (p_5=p_text{внеш}).
Давление больше на первом этаже.
Разность давлений $$ Delta p=p_1-p_5= p_text{внеш}+rho gh -p_text{внеш}=rho gh $$ Получаем: $$ Delta p=1000cdot 10cdot 15=150 000 (text{Па})=150 (text{кПа}) $$ Ответ: на первом; на 150 кПа
Задача 2. Давление в трубах водопровода (4cdot 10^5 text{Па}). На какую максимальную высоту можно достать струей воды в случае пожара, если подключить оборудование к пожарному гидранту на поверхности земли? Атмосферное давление примите равным (1cdot 10^5 text{Па})
Дано:
(p=4cdot 10^5 text{Па})
(p_text{атм}=1cdot 10^5 text{Па})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
При подключении на струю воды, направленную вертикально вверх, будет действовать снизу давление водопровода, сверху атмосферное давление.
Под действием разности этих давлений вода может подняться на высоту $$ h=frac{p-p_text{атм}}{rho g} $$ Получаем: $$ h=frac{(4-1)cdot 10^5}{1000cdot 10}=30 (text{м}) $$ Ответ: 30 м
Задача 3. Рассчитайте, какую силу давления воды должен выдерживать жесткий водолазный скафандр, предназначенный для глубоководных работ на глубине до 365 м, если общая поверхность скафандра составляет 2,5 м2?
(Плотность морской воды 1010 кг/м3, g=9,8 м/с2). Ответ округлите до меганьютонов.
Дано:
(rho=1010 text{кг/м}^3)
(g=9,8 text{м/с}^2)
(h=365 text{м})
(S=2,5 text{м}^2)
__________________
(F-?)
Давление воды на максимальной глубине $$ p=rho gh $$ Сила давления $$ F=pS=rho ghS $$ Получаем: $$ F=1010cdot 9,8cdot 365cdot 2,5approx 9,03cdot 10^6 (text{Н})=9 (text{МН}) $$ Ответ: ≈9 МН
Задача 4*. В цилиндрический сосуд налиты ртуть и вода. Общая высота столба жидкости 20 см. Чему равно давление, создаваемое жидкостями на дно сосуда, если:
а) объемы жидкостей одинаковы; б массы жидкостей одинаковы?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(H=20 text{см}=0,2 text{м})
(gapprox 10 text{м/с}^2)
(text{а)} V_1=V_2; text{б)} m_1=m_2)
__________________
(p-?)
Ответ: а) 14,6 кПа; б) 3,7 кПа
