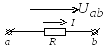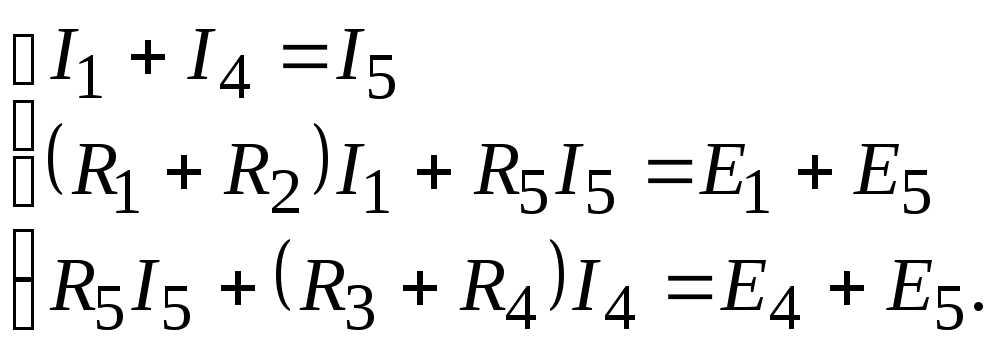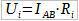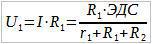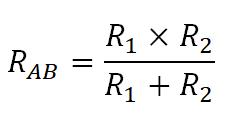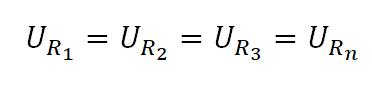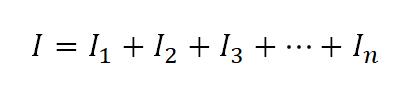Содержание
- Электрическая цепь с двумя источниками
- Электродвижущая сила (ЭДС) источника энергии
- Закон Ома для полной цепи
- Идеальный источник ЭДС
- Внутреннее сопротивление источника ЭДС
- Закон Ома для полной цепи
- Просадка напряжения
- Как найти внутреннее сопротивление источника ЭДС
- Вывод
Электрическая цепь с двумя источниками
Электрическая цепь может содержать несколько источников или приемников электроэнергии. Такие цепи называются сложными, для расчетов основных величин в таких цепях применяют специальные методы.
На рисунке 1 приведена схема с двумя источниками ЭДС: E1 и E2. Источники имеют внутренние сопротивления r1 и r2. Нагрузка условно обозначена резистором с сопротивлением R. Так как в цепи отсутствуют разветвления, то ток во всех ветвях будет одинаков и равен I

Для расчета сложных электрических цепей наряду с законом Ома применяются два закона Кирхгофа.
Одним из наиболее простых способов расчета цепи с двумя источниками ЭДС является метод наложения токов. Данный метод основан на аддитивном свойстве токов, согласно которому ток в цепи равен алгебраической сумме токов, создаваемых каждым источником питания независимо друг от друга. Это правило применимо для расчета любой линейной цепи (то есть цепи, в которой сопротивления всех участков постоянны).
Пусть в электрической цепи действует только один источник ЭДС E1, тогда ток в цепи будет равен
Теперь положим обратную ситуацию: в электрической цепи действует только один источник ЭДС E2, а источник E1 присутствует, но не производит ток. Тогда ток в цепи будет равен
Два источника ЭДС в цепи направлены встречно, следовательно, суммарный ток I будет равен разности токов I1 и I2
Из свойства аддитивности токов можно сделать немаловажный вывод: если ЭДС E1 и E2 имеют встречное направление, и равны, то ток в цепи будет равен нулю
Если значения E1 и E2 различны, то в цепи возникает ток, направление которого совпадает с током, создаваемой «большим» ЭДС. Иными словами, если E1 > E2, то направление тока совпадает с ЭДС E1, если E1 E2).
Электродвижущая сила E2, направленная в противоположную току I сторону, называется встречной или противо-ЭДС.
Рассмотрим процессы и запишем основные зависимости, которые соответствуют каждому из участков цепи.
На участке ab имеется сопротивление источника ЭДС r1, а действие самого источника совпадает с направлением тока I. Следовательно указанный источник работает в режиме генератора (источника энергии). Таким образом, ЭДС источника равна сумме напряжения на его выводах и внутреннего падения напряжения
Согласно записанному выше выражению,
Иными словами, напряжение на выводах источника, отдающего энергию в цепь, равно разности ЭДС источника и внутреннего падения напряжения.
Согласно закону Ома, на участке bc падение напряжения равно
Кроме того, следует отметить, что на участке bc электрическая энергия преобразуется в тепловую, при этом происходит выделение мощности, равной
На последнем рассматриваемом участке ca источник ЭДС E2 действует против направления тока I. Источник имеет сопротивление r2. На данном участке имеется потеря мощности (нагрев), равная r2 ⋅ I 2 . Кроме того, источник ЭДС создает собственную мощность E2⋅ I, направленную на преодоление сил встречной ЭДС. Получается, что источник с противо-ЭДС работает в цепи как потребитель (приемник).
Мощность, выделяемая на участке ca равна
Cледовательно, напряжение на этом участке равно
На основании записанного выше выражения можно сделать вывод, что напряжение на вывод источника, работающего в режиме противо-ЭДС равно сумме самого ЭДС и внутреннего падения напряжения на нем.
Источник
Электродвижущая сила (ЭДС) источника энергии
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока).
Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника. Иногда говорят, что ЭДС создает электрический ток в цепи. Нужно помнить об условности такого определения, так как выше мы уже установили, что причина возникновения и существования электрического тока — электрическое поле.
Источник электрической энергии производит определенную работу, перемещая электрические заряды по всей замкнутой цепи..
Определение: Работа, совершаемая источником электрической энергии при переносе единицы положительного заряда по всей замкнутой цепи, называется ЭДС источника
За единицу измерения электродвижущей силы принят вольт (сокращенно вольт обозначается буквой В или V — «вэ» латинское).
ЭДС источника электрической энергии равна одному вольту, если при перемещении одного кулона электричества по всей замкнутой, цепи источник электрической энергии совершает работу, равную одному джоулю:
В практике для измерения ЭДС используются как более крупные, так и более мелкие единицы, а именно:
1 киловольт (кВ, kV), равный 1000 В;
1 милливольт (мВ, mV), равный одной тысячной доле вольта (10-3 В),
1 микровольт (мкВ, μV), равный одной миллионной доле вольта (10-6 В).
Очевидно, что 1 кВ = 1000 В; 1 В = 1000 мВ = 1 000 000 мкВ; 1 мВ= 1000 мкВ.
В настоящее, время существует несколько видов источников электрической энергии. Впервые в качестве источника электрической энергии была использована гальваническая батарея, состоящая из нескольких цинковых и медных кружков, между которыми была проложена кожа, смоченная в подкисленной воде. В гальванической батарее химическая энергия превращалась в электрическую (подробнее об этом будет рассказано в главе XVI). Свое название гальваническая батарея получила по имени итальянского физиолога Луиджи Гальвани (1737—1798), одного из основателей учения об электричестве.
Многочисленные опыты по усовершенствованию и практическому использованию гальванических батарей были проведены русским ученым Василием Владимировичем Петровым. Еще в начале прошлого века он создал самую большую в мире гальваническую батарею и использовал ее для ряда блестящих опытов.
Источники электрической энергии, работающие по принципу преобразования химической энергии в электрическую, называются химическими источниками электрической энергии.
Другим основным источником электрической энергий, получившим широкое применение в электротехнике и радиотехнике, является генератор. В генераторах механическая энергия преобразуется в электрическую.
На электрических схемах источники электрической энергии и генераторы обозначаются так, как это показано на рис. 1.
Рисунок 1. Условные обозначения источников электрической энергии: а — источник ЭДС, общее обозначение, б — источник тока, общее обозначение; в — химический источник электрической энергии; г — батарея химических источников; д — источник потоянного напряжения; е — источник переменного нарияжения; ж — генератор.
У химических источников электрической энергии и у генераторов электродвижущая сила проявляется одинаково, создавая на зажимах источника разность потенциалов и поддерживая ее длительное время. Эти зажимы называются полюсами источника электрической энергии. Один полюс источника электрической энергии имеет положительный потенциал (недостаток электронов), обозначается знаком плюс ( + ) и называется положительным полюсом. Другой полюс имеет отрицательный потенциал (избыток электронов), обозначается знаком минус (—) и называется отрицательным полюсом.
От источников электрической энергии электрическая энергия передается по проводам к ее потребителям (электрические лампы, электродвигатели, электрические дуги, электронагревательные приборы и т. д.).
Определение : Совокупность источника электрической энергии, ее потребителя и соединительных проводов называется электрической цепью.
Простейшая электрическая цепь показана на рис. 2.
Рисунок 2. Простейшая электрическая цепь: Б — источник электрической энергии; SA — выключатель; EL — потребитель электрической энергии (лампа).
Для того чтобы по цепи проходил электрический ток, она должна быть замкнутой. По замкнутой электрической цепи непрерывно проходит ток, так как между полюсами источника электрической энергии существует некоторая разность потенциалов. Эта разность потенциалов называется напряжением источника и обозначается буквой U. Единицей измерения напряжения служит вольт. Так же как и ЭДС, напряжение может измеряться в киловольтах, милливольтах и микровольтах.
Для измерения величины ЭДС и напряжения применяется прибор, называемый вольтметром. Если вольтметр подключить непосредственно к полюсам источника электрической энергии, то при разомкнутой электрической цепи он покажет ЭДС источника электрической энергии, а при замкнутой — напряжение на его зажимах: (рис. 3).
Рисунок 3. Измерение ЭДС и напряжения источника электрической энергии: а— измерение ЭДС источника электрической энергии; б — измерение напряжения на зажимах источника электрической энергии..
Заметим, что напряжение на зажимах источника электрической энергии всегда меньше его ЭДС.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Закон Ома для полной цепи
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Источник
§ 17. Последовательное и параллельное соединение источников
При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.
При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.
В схеме на рис. 17.1 $$ {mathcal{E}}_{1}=12$$ В, $$ {mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
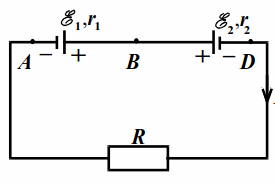 |
| Рис. 17.1 |
Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {varphi }_{A}-{varphi }_{B}$$ и $$ {varphi }_{B}-{varphi }_{D}$$.
ЭДС батареи последовательно соединённых источников:
$$ mathcal{E}={mathcal{E}}_{1}-{mathcal{E}}_{2}=9$$ B.
Причём, полярность батареи совпадает с полярностью источника $$ {mathcal{E}}_{1}$$ т. к. $$ {mathcal{E}}_{1}>{mathcal{E}}_{2}$$.
Ток по закону Ома для замкнутой цепи $$ I=mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:
$$ {varphi }_{A}-{varphi }_{B}+{mathcal{E}}_{1}=I{r}_{1,}$$, $$ {varphi }_{B}-{varphi }_{D}-{mathcal{E}}_{2}=I{r}_{2}$$.
Отсюда $$ {varphi }_{A}-{varphi }_{B}=I{r}_{1}-{mathcal{E}}_{1}=-11$$ B, $$ {varphi }_{B}-{varphi }_{D}=I{r}_{2}+{mathcal{E}}_{2}=5$$ B.
Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.
Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {mathcal{E}}_{1}=mathcal{E}$$, $$ {r}_{1}=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal{E}$$ и $$ {mathcal{E}}_{1}$$:
$$ {mathcal{E}}_{0}=3mathcal{E}-{mathcal{E}}_{1}=3mathcal{E}-mathcal{E}=2mathcal{E}$$,
$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.
Ток $$ I={displaystyle frac{{mathcal{E}}_{0}}{R+{r}_{0}}}={displaystyle frac{6mathcal{E}}{3R+11r}}$$.
6
ЛЕКЦИЯ №2
1.3.
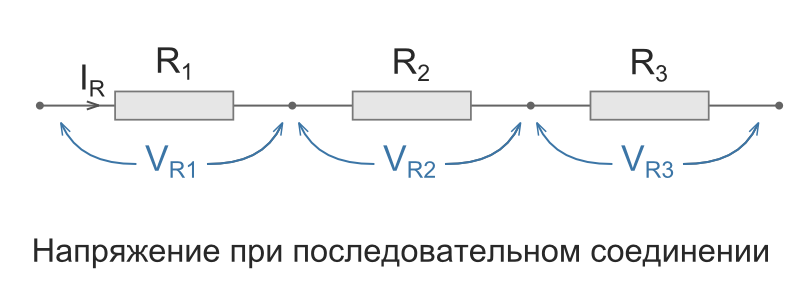
Напряжение на участке цепи
Под
напряжением на некотором участке
электрической цепи понимают разность
потенциалов между крайними точками
этого участка.
Рассмотрим
участок цепи с одним сопротивлением
(рис. 1.4).
Рис. 1.4. Схема
участка цепи
,
или
.
(1.1)
Эта
формула является законом Ома для участка
цепи без ЭДС.
Положительное
направление падения напряжения на
каком-либо участке цепи, указываемое
на схеме стрелкой, всегда совпадает с
положительным направлением отсчета
тока, протекающего по данному сопротивлению.
Если
цепь содержит ЭДС (рис. 1.5), то закон Ома
для участка цепи можно записать:
для
первого участка
;
для
второго участка
.
Отсюда
вытекает, что
. (1.2)
Это
формула закона Ома для участка цепи с
ЭДС (обобщенный закон Ома).
1.4.
Законы Кирхгофа. Составление уравнений
для расчета токов
с
помощью законов Кирхгофа
Для
расчета сложной разветвленной
электрической цепи существенное значение
имеет число ветвей и узлов.
Ветвью
называется участок электрической цепи,
состоящий только из последовательно
включенных источников ЭДС и приемников.
Узлом называется место или точка
соединения трех или более ветвей. При
обходе по соединенным в узлах ветвям
можно получить замкнутый контур
электрической цепи.
Все
электрические цепи подчиняются двум
законам Кирхгофа.
Первый
закон имеет две формулировки:
1)
алгебраическая сумма токов в узле равна
нулю;
2) сумма
токов, притекающих к любому узлу, равна
сумме токов, вытекающих из него
(1.3)
Физически
I закон Кирхгофа означает, что движение
зарядов в цепи происходит так, что ни в
одном из узлов (участков схемы) они не
накапливаются.
Второй
закон Кирхгофа гласит:
алгебраическая
сумма падений напряжений в любом
замкнутом контуре равна алгебраической
сумме ЭДС вдоль того же контура
(1.4)
где
m
– число сопротивлений в контуре;
n
– число ЭДС в контуре.
Если
направления падений напряжений и ЭДС
совпадают с направлением обхода контура,
то они входят в сумму со знаком « + ».
Законы
Кирхгофа используют для определения
токов в ветвях схемы.
Обозначим
число ветвей схемы – b,
число узлов – y,
число ветвей, содержащих источники тока
– bит.
В каждой ветви протекает свой ток.
Так
как токи в ветвях с источниками тока
известны, то число неизвестных токов
равно b
– bит.
Перед
составлением уравнений необходимо:
1)
произвольно выбрать положительные
направления токов в ветвях;
2)
выбрать положительные направления
обхода контуров для составления уравнений
по II закону Кирхгофа (с целью единообразия
рекомендуется для всех контуров выбирать
одно направление, например, по часовой
стрелке).
Для
получения линейно независимых уравнений
по I закону Кирхгофа составляют (y
– 1) уравнение, а по II закону – недостающие
(b
– bит)
– (y
– 1) уравнения. Составляя уравнения по
II закону Кирхгофа, необходимо охватить
все ветви схемы, исключая ветви с
источниками тока. При этом в каждый
контур должна входить хотя бы одна
ветвь, не вошедшая в предыдущий контур.
Такие контуры называются независимыми.
Это условие является необходимым и
достаточным для однозначного определения
токов.
Рассмотрим
уравнения для расчета токов на примере
схемы, изображенной на рис. 1.6.
2
y
II
– 1 = 2
b
J
– bит
= 4
п
о I закону – 2 уравнения
п
I
о II закону – 2 уравнения
1
3
Рис. 1.6. Пример
расчетной схемы
Узел
2 .
Узел
3 .
Контур
I .
Контур
II .
1.5.
Энергетический баланс в электрических
цепях
При
протекании токов по сопротивлениям
электрическая энергия преобразуется
в тепловую. На основании закона сохранения
энергии количество тепла, выделяющегося
в единицу времени в сопротивлениях
электрической цепи, равняется энергии,
доставляемой за то же время источниками
питания.
Если
направление тока I,
протекающего через источник ЭДС E,
совпадает с направлением ЭДС, то источник
ЭДС доставляет в цепь в единицу времени
энергию (его мощность), равную EI,
которая с положительным знаком входит
в уравнение энергетического баланса.
Уравнение
энергетического баланса
,
(1.5)
где
UabJk
– мощность, доставляемая в цепь источником
тока (a
– узел, к которому притекает ток Jk,
b
– узел, из которого этот ток вытекает).
1.6.
Метод пропорциональных величин
В
самой удаленной части схемы (ветви),
которую называют исходной, произвольно
задаются некоторым током, например, 1
А. Далее, продвигаясь от конца схемы к
началу, находят токи в ветвях и напряжения
на различных участках схемы. В результате
расчета получают значение напряжения
в начале схемы и токов в ветвях, если бы
в исходной ветви протекал ток 1 А.
Так
как найденное напряжение в начале схемы
в общем случае не будет равно ЭДС
источника, то следует во всех ветвях
изменить токи, умножив их на коэффициент,
равный отношению ЭДС источника к
найденному значению напряжения в начале
схемы.
Этот
метод применим только для расчета цепей,
состоящих из сопротивлений, соединенных
параллельно и последовательно, и одного
источника ЭДС.
1.7.
Метод контурных токов
В
основу метода положено два предположения:
1)
в каждом независимом контуре протекает
свой контурный ток;
2)
токи в ветвях схемы равны алгебраической
сумме контурных токов, протекающих
через данную ветвь.
Согласно
с этим методом неизвестными являются
контурные токи, поэтому число уравнений
для решения снижается до числа независимых
контуров, т.е. до числа уравнений
составленных по II закону Кирхгофа.
Рассмотрим
двухконтурную электрическую цепь (рис.
1.7).
Составим
уравнения по законам Кирхгофа
Подставим
в последние уравнения ток I5
Эти
уравнения можно записать в виде
где
и
– полные или собственные сопротивления
I
и II
контуров;
– сопротивление смежной ветви между
контурами I
и II;
и
– контурные ЭДС I
и II
контуров.
Сопротивление
смежной ветви входит в уравнение со
знаком « + », если направление смежного
контурного тока в нем совпадает с
направлением собственного контурного
тока.
Если
в электрической схеме имеются источники
тока, то их можно заменить источниками
напряжения. Если проводимости источников
тока равны нулю, то в этом случае
целесообразно выбрать заданные токи
источников тока в качестве контурных.
При этом число уравнений сократится на
число заданных источников тока.
Если
в схеме n
контуров, то уравнения запишутся

В
матричной форме можно записать
,
где


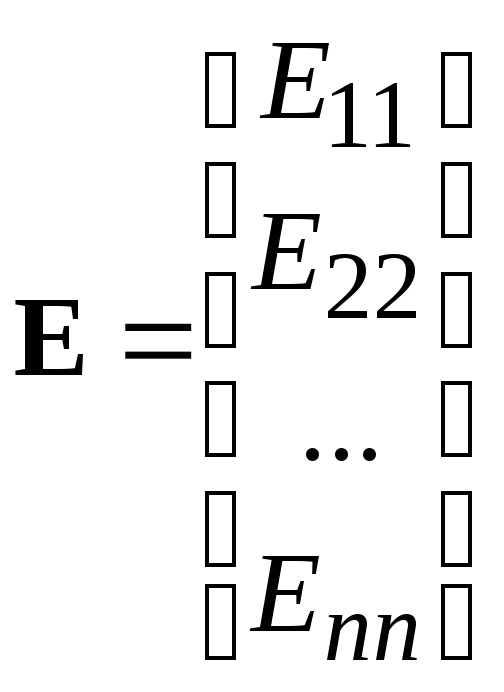
Общее
решение системы n
уравнений с n
неизвестными:
,
(1.7)
где
– определитель системы (1.6).
Алгебраическое
дополнение km
получено из
путем вычеркивания k-ого
столбца и m-й
строки и умножения полученного
определителя на
.
Относительно
главной диагонали определитель делится
на две части, являющиеся зеркальным
отображением друг друга. Это свойство
называется симметрией относительно
главной диагонали. Отсюда
.
Формула
(1.7) используется как исходная при
рассмотрении таких вопросов теории
линейных цепей как определение входных
и взаимных проводимостей ветвей, принцип
взаимности, метод наложения и линейные
соотношения в электрических цепях.
Соседние файлы в папке ТОЭ 1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрическая цепь — это совокупность элементов и устройств, предназначенных для протекания электрического тока, электромагнитные процессы в которых, могут быть описаны с помошью понятий сила тока и напряжение .
Электрическая схема — это документ, составленный в виде изображения, на котором с помощью условных обозначений показаны элементы электрической цепи и их взаимодействие.
Рассмотрим два основных элемента электрической цепи: источник ЭДС и резистор .
Резистор — это элемент электрической цепи, обладающий определенным или переменным значением омического сопротивления, предназначенный для линейного преобразования силы тока в напряжение, напряжения в силу тока, ограничения тока и поглащения электрической энергии. На электрических схемах, резистор обозначается: 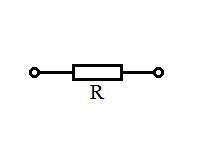
Далее, рассмотрим основные характеристи и параметры реальных резистров:
20 градусов цельсия).

Пусть по некоторому участку цепи A-B, являющегося последовательным только соединением резисторов R1. Rk, течет электрический ток I. Необходимо определить падение напряжения на данном участке цепи и общее электрическое сопротивление данного участка.
В начале, найдем падение напряжения на участке A-B. Т.к. в цепи нет источников ЭДС, то согласно закону ома, падение напряженя на i-м участке цепи равно: 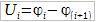
Просуммировав падение напряжения на всех участках (на всех резистрах), получим: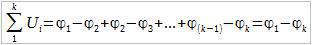
Заметим, что Ф1 = Фa, а Фk = Фb, тогда: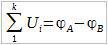
Разность потенциалов точек A и B по определению (с учетом того, что ЭДС на участке A-B равна нулю) является падением напряжения на участке A-B.
Имеем, что: 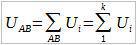
Теперь, определим суммарное сопротивление участка цепи A-B.
Запишим закон Ома для участка A-B: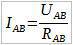
Из этой формулы выразим сопротивление Rab: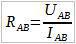
Далее, вспомним, что падение напряжения на участке A-B равно сумме падений напряжений на каждом из резисторов: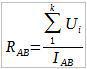
Теперь, для каждого резистра запишем закон Ома для однородного участка цепи: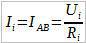
Отсюда:
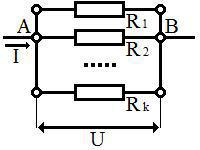
Перед тем, как переходить к условию задачи, введем дополнительное определение:
Узел — участок электрической цепи в котором сходятся более двух проводников.
Пусть в узел A втекакет ток I (из закона сохранения зарядов следует, что из узла B вытекает точно такой-же по величине ток). Необходимо определить эквивалентное сопротивление участка цепи A-B.
Вспомним, что: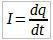
Рассмотрим достаточно малый промежуток времени, на котором ток можно считать постоянным, тогда: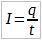
Ток через участок A-B равен отношению суммарного заряда q, прошедшего через данный участок цепи за время t к этому времени.
В узле A произойдет разделение тока на k — путей. Заряды будут перемещаться через каждый резистор. Пусть за время t через резистор R1 пройдет заряд q1, через R2 — q2, . , Rk — qk. Поскольку, выполняется закон сохранения заряда: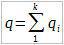
Разделим оба выражения на t, получим: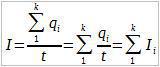
Получаем, что ток втекающий в узел равен сумме токов, вытекающих из этого узла. Более точно данное правило формулируется так: Алгебраическая сумма токов сходящихся в каждом узле любой цепи равна нулю — первое правило Кирхгофа.
Далее, применем закон Ома для однородного участка цепи: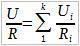
Заметим, что напряжения на всех резистрах одинаковы и равны U, т.к. Ui = Фa — Фb. Получаем: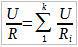
Далее разделим уравнение на U: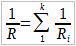
В результате, мы получили закон для поиска эквивалентного сопротивления при параллельном соединении резисторов.
Источник ЭДС (идеальный источник напряжения) — это элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока. ЭДС источника м.б. задана либо как постоянная величина, либо как функция от врмени или внешнего управления. Идеальный источник ЭДС имеет следующее графическое обозначение на электрических схемах: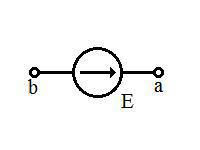
На практике, идеальных источников ЭДС не существует. Попробуем убедится в этом: Запишем закон Ома для полной цепи: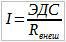
Заметим, что при уменьшении внешнего сопротивления до нуля, получим бесконечный рост силы тока, что физически невозможно. По этой причине вводят понятие реального источника напряжения
Реальный источник напряжения — это элемент электрической цепи, имеющий сопротивление r, на котором действует ЭДС. Обозначается: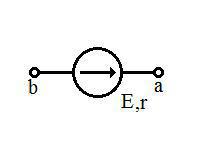
Реальный источник напряжения м.б. представлен как последовательное соединение источника ЭДС и резистра r: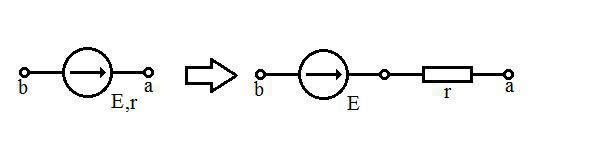
// тут нужно дописать о выборе направления ЭДС //
Делитель напряжения — это устройство входное и выходное напряжение связаны коэффиентом передачи a, 0
Рассмотрим устройство резистивного делителя напряжения:
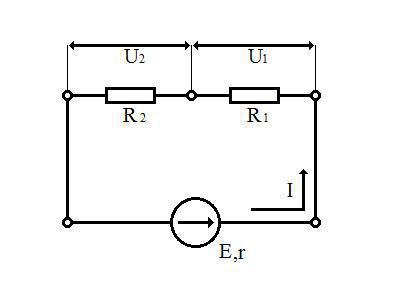
Пусть электрисеская цепь состоит из источника ЭДС (E,r) и двух резистров R1 и R2. По ней течет электрический ток, I. Необходимо найти отношение падений напряжения на резистрах и их сумму.
Запишем закон Ома для полной цепи: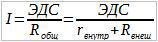
Сопротивление источника ЭДС нам известно, оно равно r. Резистры R1 и R2 образуют последовательное соединение, по этому их сопротивления складываются: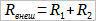
Ток I, протекающий через цепь равен: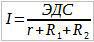
Теперь, применим закон Ома для участка цепи к R1 и R2: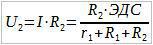
Разделим U1 на U2: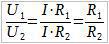
Отношение напряжений U1 к U2 равно отношению сопротивлений R1 к R2.
Далее, сложим U1 и U2. Получим U12 — падение напряжения на внешнем участке цепи: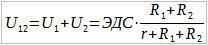
Если r достаточно мало, то падение напряжения на внешнем участке цепи практически равно ЭДС.
1) Подключите лабораторный блок питания (далее, БП) к вольтметру (рисунок ниже). С помошью ручки регулятора (располагается на блоке питания) изменяйте напряжение на вольтметре пока он не покажет значение 9 Вольт. Поскольку, внутреннее сопротивление блока питаия мало ( После установки сопротивления для каждого из вариантов А), Б), В), необходимо отключа ть мультимет р, используемый для измерения сопротивления.
4)Далее, необходимо:
Замкнуть ключ K. С помощью вольтметра измерить падение напряжения на резистре R для случаев A, Б и B. Проанализировать полученные результаты, на основании замеров сделать вывод о внутреннем сопротивлении источников питания.
5)Сфотографируйте и разместите этапы сборки.
6)Заполните таблицу падений напряжения для случаев А,Б,В.
Ход работы:
1)Соберите электрическую цепь, состоящую из источника ЭДС, двух последовательно соединенных резисторов R1, R2 и вольтметра (мультиметр в ежиме измерения напряжения) согласно схеме: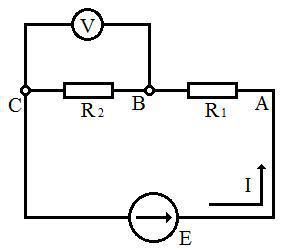
В качестве источника ЭДС возьмите лабораторный БП (установите на 15 вольт).
Используйте резистры R1 и R2 сопротивлениями:
А) 1КОм, 1КОм.
Б) 1КОм, 2КОм.
В) 1КОм, 5КОм.
Г) 1КОм, 10КОм.
2)Для всех вариантов А-Г с помощью мультиметра измерьте падение напряжения на участке С-B. Проанализируйте полученные результаты. В каких отношениях резистры делят напряжение?
3)Сфотографируйте и разместите этапы сборки.
4)Заполните таблицу падений напряжения для случаев А-Г.
При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.
При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.
Найти напряжения на зажимах источников, т. е. разность потенциалов $$ <varphi >_-<varphi >_$$ и $$ <varphi >_—<varphi >_$$.
ЭДС батареи последовательно соединённых источников:
Причём, полярность батареи совпадает с полярностью источника $$ <mathcal>_<1>$$ т. к. $$ <mathcal>_<1>><mathcal>_<2>$$.
Ток по закону Ома для замкнутой цепи $$ I=mathcal/(R+_<1>+_<2>)=1$$ A. По закону Ома для участков цепи `AB` и `BD`:
Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.
Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ <mathcal>_<1>=mathcal$$, $$ _<1>=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal$$ и $$ <mathcal>_<1>$$:
Источник
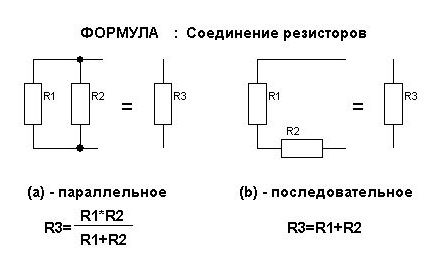
Последовательное и параллельное соединение резисторов
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
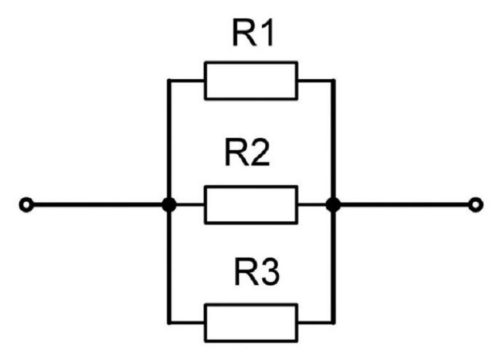
Понятие параллельного подключения резисторов
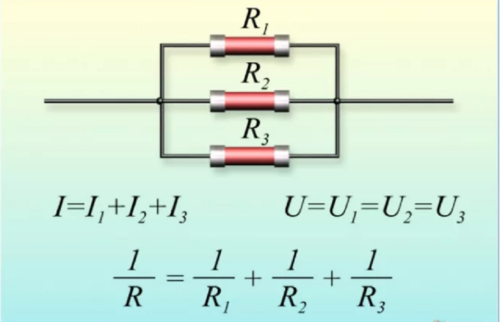
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Последовательное и параллельное соединение резисторов
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Последовательное подключение
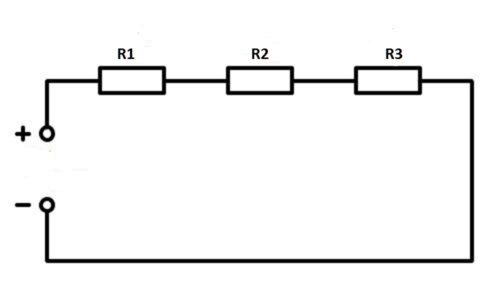
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
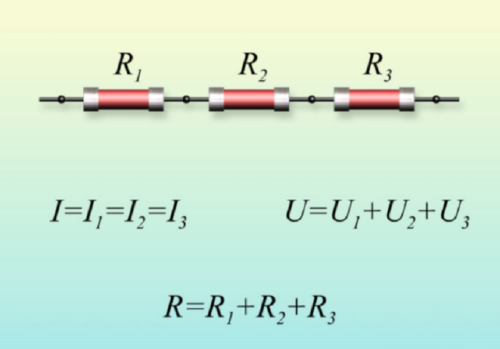
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Будет интересно➡ SMD резисторы: что это такое и для чего используются?
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
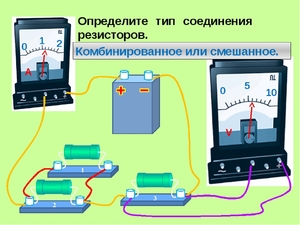
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Урок 11. ВСЕ Способы соединения резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
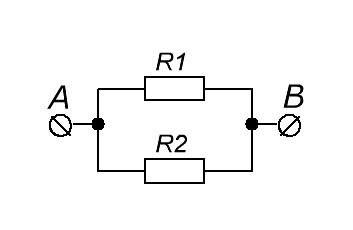
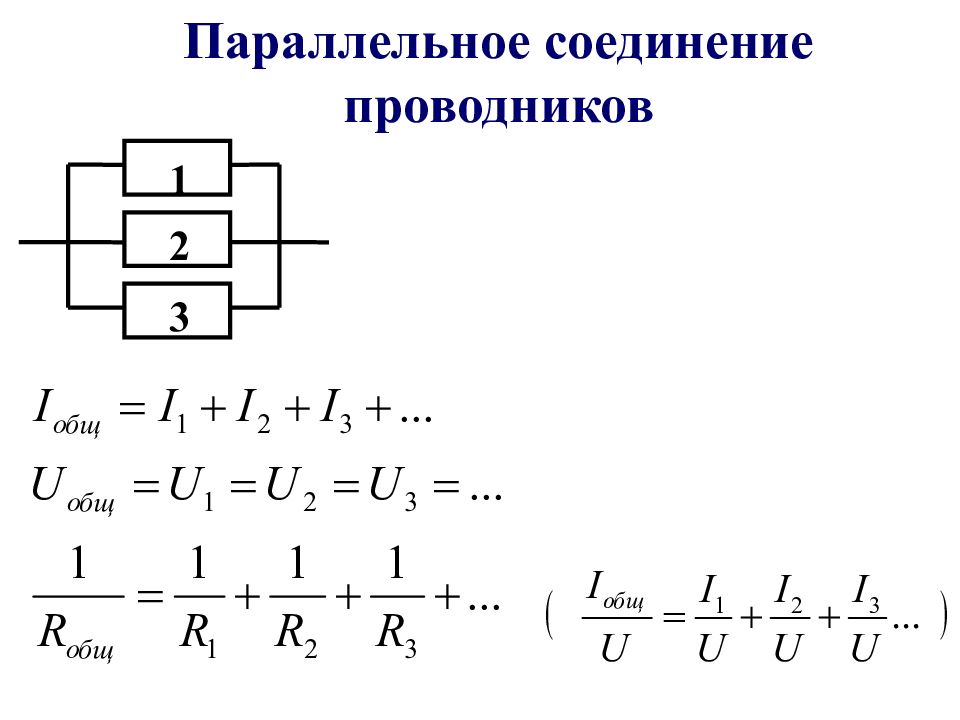
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
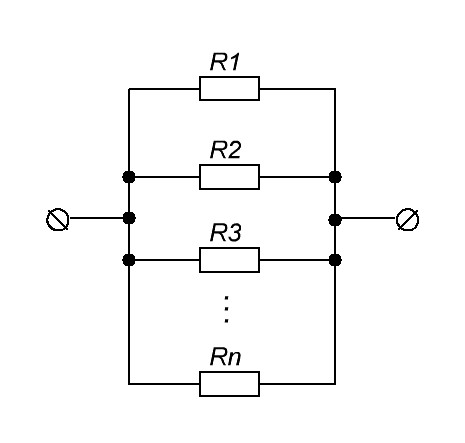
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
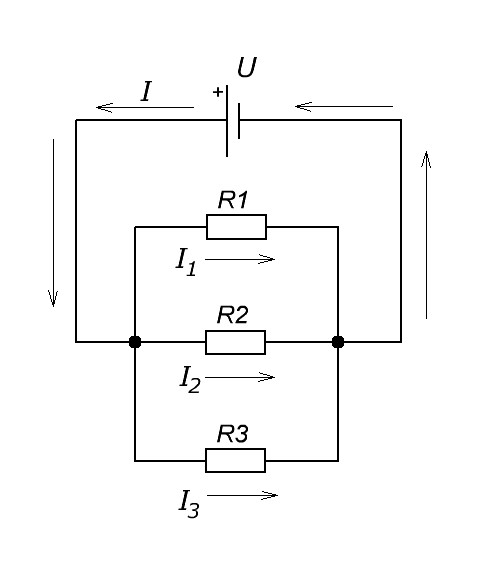
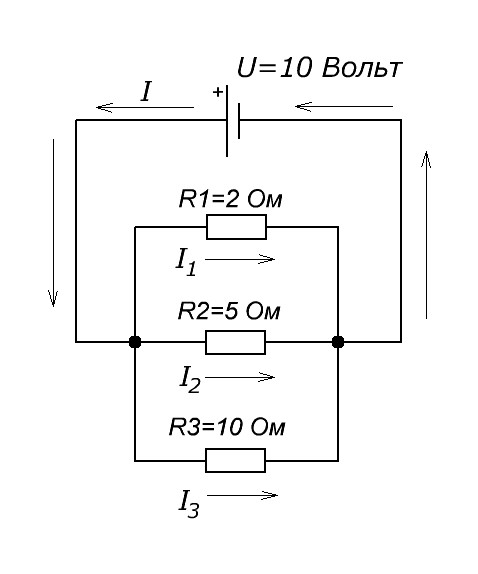
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
последовательное и параллельное соединение резисторов
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
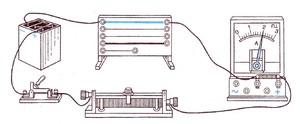
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Урок 11. ВСЕ Способы соединения резисторов
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a
Стандартная формула напряжения
Формула для вычисления напряжения
При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.
При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.
Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:
U = U1 = U2 = … = Uобщ.
Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.
Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.
Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп
В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.
ЧТО ТАКОЕ ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Отличия между двумя видами подключений
Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.
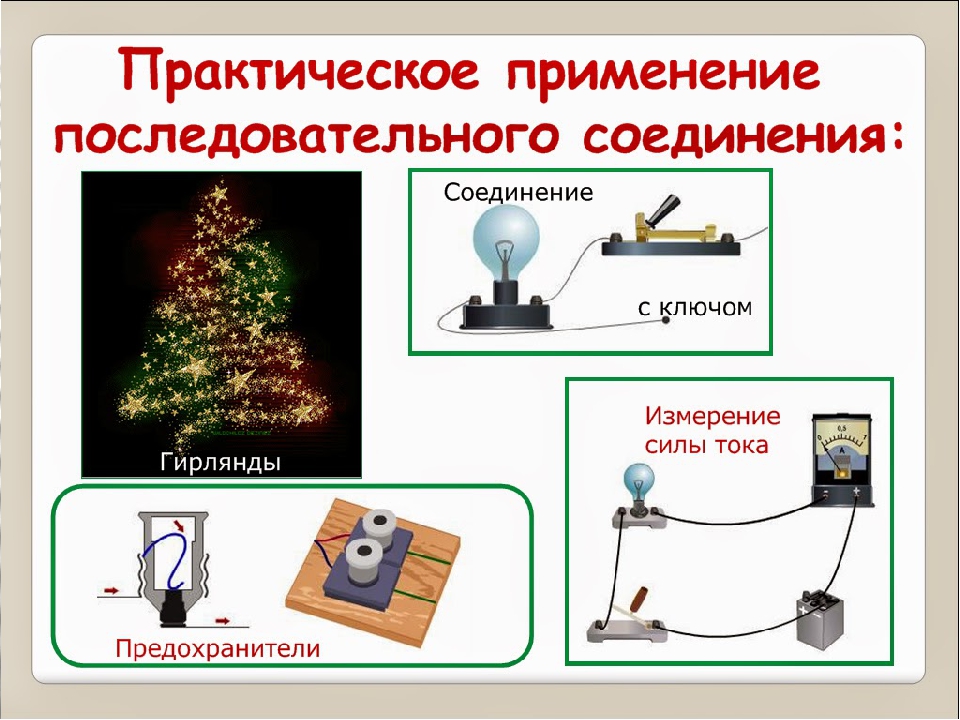
Пример подключения с предохранителем
Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.
Как рассчитать сложные схемы соединения резисторов
Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.
- источник постоянного тока 12V;
- сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.
- основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
- подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
- эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
- ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.
По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.
Расчет 1 (последовательное и параллельное соединение):
- для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
- эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
- второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
- общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
- Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.
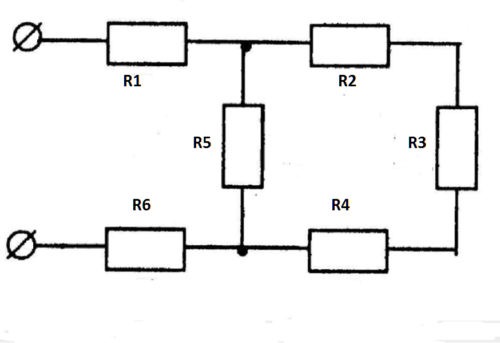
Расчет 2 (сложное параллельное соединение):
- в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
- Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
- суммарное значение для цепи: R1 + R2 = 20 Ом;
- по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
- после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
- делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.
В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).
В этом случае разница потенциалов на шестом резисторе составит:
U6 = I *R6 = 1,2 * 7,5 = 9 В.
Соответственно, изменится напряжение между контрольными точками:
Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.
Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип — U6).
Источник
Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;