Как найти общее напряжение на участке цепи

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Источник

Задачи на параллельное и последовательное соединение проводников с подробными решениями

Что бы ни происходило в мире, учиться надо всегда. Кстати, для тех, кто не знает, как организовать учебу на удаленке, мы подготовили отдельную статью. А сегодня займемся решением задач на последовательное и параллельное соеднинение проводников. Решение задач – отличный способ, чтобы успокоить нервы и не поддаваться панике.

Присоединяйтесь к нам в телеграме: там вас ждут актуальные новости и приятные скидки.

Последовательное и параллельное соединение проводников: решение задач

Как решать задачи с параллельным и последовательным соединением проводников? Для начала повторите теорию, вспомните общую памятку по решению физических задач и на всякий случай держите под рукой формулы.

Задача №1 на последовательное соединение проводников

Проводники сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника равно 12 В. Определите напряжение, сопротивление и силу тока в цепи на втором проводнике, а также полное напряжение.

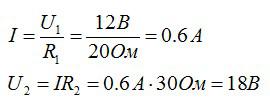
Для последовательного соединения проводников:

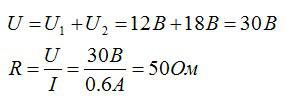
Ответ: 50 Ом; 18 В; 0,6 А; 30 В.

Задача №2 на параллельное соединение проводников

Два проводника соединены параллельно. Сила тока в первом проводнике равна 0,5 А, во втором — 1 А. Сопротивление первого проводника составляет 18 Ом. Определите сопротивление второго проводника и силу тока на всем участке цепи.

Для параллельного соединения:

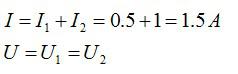
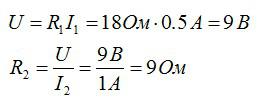
При решении задач не забывайте проверять размерности величин и при необходимости переводить их в систему СИ.

Ответ: 1,5 А; 9 Ом.

Задача №3 на последовательное и параллельное соединение проводников

Электрогрелка состоит из трех одинаковых секций. Во сколько раз быстрее грелка будет нагревать некоторое количество воды от 10 до 100 градусов Цельсия при параллельном включении всех секций, нежели при последовательном их включении?

Пусть сопротивление каждой секции равно R. Тогда при параллельном включении их в сеть напряжение на каждой секции равно напряжению в сети (U), и на трех секциях будет выделяться тепло:

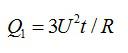
При последовательном соединении суммарное сопротивление цепи равно 3R, а выделяющееся количество теплоты:

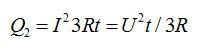
Как видим, выделяющееся тепло для первой схемы в 9 раз больше, так что и скорость нагрева воды будет в 9 раз выше.

Ответ: в 9 раз.

Задача №4 на смешанное соединение проводников

Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Определите силу тока во всей электрической цепи.

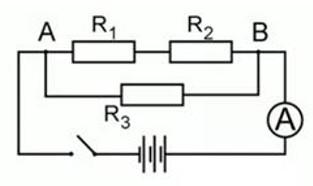
Согласно схеме, искомая сила тока – это сила тока, протекающая через амперметр.

Резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним.

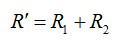
Резисторы 1 и 2 можно заменить эквивалентным сопротивлением R со штрихом и перерисовать схему в упрощенном виде:

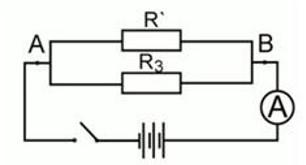
Сопротивления R3 и R со штрихом соединены параллельно, можно найти общее сопротивление электрической цепи по формуле для параллельного соединения:

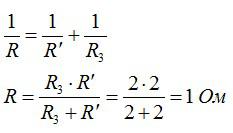
Теперь цепь можно перерисовать в еще более упрощенном виде и рассчитать силу тока по закону Ома:

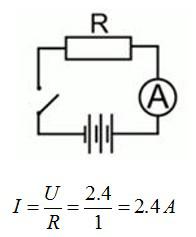
Ответ: 2.4 А.

Задача №5 на закон Кирхгофа

Три сопротивления R1 = 5 Ом, R2 = 1 Ом, R3 = 3 Ом и два источника тока соединены так, как показано на рисунке. Внутренними сопротивлениями источников тока можно пренебречь. ЭДС первого источника тока равна 1,4 В, и сила тока, текущего через сопротивление R3, равна I3= 1 А. Определите ЭДС второго источника тока.

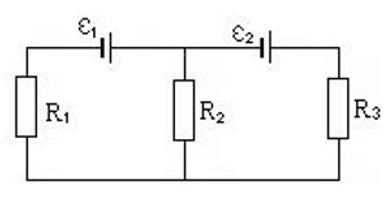
Выберем направление обхода контуров по часовой стрелке и запишем закон Кирхгофа для точки A (расположим ее между двумя источниками и сопротивлением R2) и двух контуров:

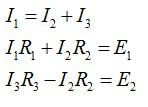
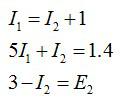
Решая систему уравнений, получаем ответ: Е2=3.6 В.

Ответ: 3.6 В.

Вопросы на параллельное и последовательное соединение проводников

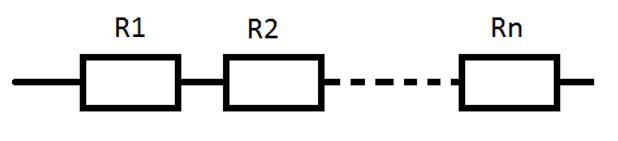
Вопрос 1. Схематически изобразите последовательное соединение проводников

Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:

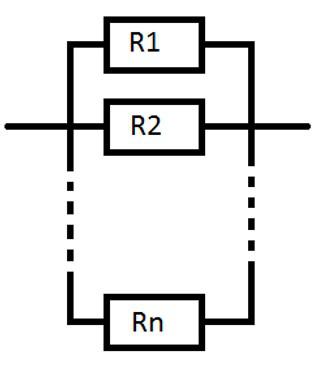
Вопрос 2. Схематически изобразите параллельное соединение проводников

Ответ. На рисунке ниже изображено параллельное соединение проводников:

Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.

Ответ. При последовательном соединении:

Сила тока во всех проводниках одинакова.

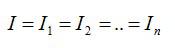
Общее напряжение равно сумме напряжений на каждом проводнике.

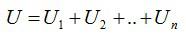
Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

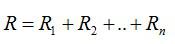
Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.

Ответ. Для параллельного соединения проводников:

Напряжение на всех проводниках одинаково.

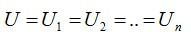
Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.

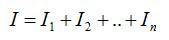
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

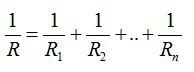
Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?

Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.

Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

«Не знаешь Ома – сиди дома» — пословица старых электриков. Действительно, этот закон очень важен для понимания того, как связаны напряжение, ток и сопротивление, или проще говоря — от чего зависит ток и мощность нагрузки и как их рассчитать.

Для понимания этих базовых вещей нужно знать закон Ома для участка цепи и закон Ома для полной цепи. Главное различие между ними, что первый распространяется на отдельный участок или элемент и учитывает только его сопротивление и приложенное к нему напряжение, а второй учитывает и внутреннее сопротивление источника питания. Давайте разберёмся подробнее.

Закон Ома для участка цепи

Самый простой и всем известный со школы вариант — закон Ома для участка цепи. Его определение звучит следующим образом:

В виде формулы это выглядит так:

I=U/R,

где I — ток, U — напряжение, R— сопротивление.

То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.

Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:

U=IR

Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:

R=U/I

К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».

Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.

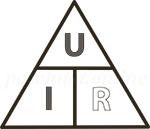
Как запомнить эти формулы?

В виде формулы это выглядит так:

I=U/R,

где I — ток, U — напряжение, R— сопротивление.

То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.

Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:

U=IR

Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:

R=U/I

К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».

Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.

Как запомнить эти формулы?

Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.

Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.

Как пользоваться треугольником? Всё просто — закройте пальцем величину, которую нужно найти, а оставшиеся не закрытыми буквы нужно умножить или разделить друг на друга, что подробно проиллюстрировано ниже.

Есть еще одна шпаргалка в виде круга разделенного на сегменты, где перечислены все необходимые формулы, кроме перечисленных выше, добавлены и формулы для вычисления мощности.

Примеры

Итак, чтобы научиться рассчитывать напряжение на участке цепи, решим простенькую задачу. У нас есть цепь, состоящая из 3 резисторов и идеального источника с напряжением 12В постоянного тока. Пусть участком цепи у нас будет резистор R2, найдём напряжение на нём.

Дано:

U= 12 В;

R1= 1 кОм;

R2= 2 кОм;

R3= 3 кОм;

Найти:

I — ?;

U(R2) — ?;

По закону Ома чтобы найти напряжение нужно знать ток через участок цепи и его сопротивление.

U=IR

Последнее у нас известно, поэтому нужно найти ток в цепи, элементы соединены последовательно, поэтому ток через каждый из них одинаков, и чтобы найти его силу — нужно сначала найти общее сопротивление всех элементов, но сначала переведём его в Омы:

R1 = 1 кОм = 1000 Ом; R2 = 2 кОм = 2000 Ом; R3 = 3 кОм = 3000 Ом.

Теперь найдём общее сопротивление:

Rобщ=R1+R2+R3=1000+2000+3000= 6000 Ом

Тогда ток в цепи равен:

I= U/R = 12/6000 = 0,002 А

И наконец падение напряжения на резисторе R2:

U(R2) = I*U(R2) = 0,002*2000=4В

Итого, на выводах резистора R2 будет 4 вольта.

Закон Ома для полной цепи

Определение закона Ома для полной цепи вы видите ниже, жирным выделено основное отличие от закона для участка цепи.

В формуле добавляется внутреннее сопротивление источника питания, а напряжение заменяется на ЭДС:

I=E/(R+r),

где I – ток, E – ЭДС, R – сопротивление, r- внутреннее сопротивление источника.

Внутреннее сопротивление источника обуславливается его устройством, например, сечением вторичной обмотки трансформатора, химическим составом, степенью заряда и состоянием электродов аккумуляторов и батареек и так далее. На схеме условно рисуется в виде резистора внутри источника, но на самом деле никакого «внутреннего» или «скрытого» сопротивления там нет, как было отмечено выше.

Почему важно учитывать внутреннее сопротивление источника? Всё очень просто — вы замечали, как погасают лампочки в автомобиле, когда стартер запускает двигатель? Это происходит из-за просадок на проводах и в аккумуляторе от высоких пусковых токов. В принципе, подобное мы наблюдаем, когда лампы накаливания «просаживаются» по яркости во время пуска мощной нагрузки, например, электродвигателей.

Примеры

Давайте проанализируем, как влияет внутреннее сопротивление источника на напряжение нагрузки. Допустим, что у нас есть какой-то источник с внутренним сопротивлением (r) в 1 Ом и ЭДС (E) в 12 Вольт. И есть 3 разных нагрузки, с сопротивлением (R) каждой из них: 10, 5 и 1 Ом соответственно. Нагрузку будем подключать по очереди, по одной для каждого расчета.

Рассчитаем ток первой нагрузки:

I1=E/(R1+r)=12/(10+1)=1.09 А

Рассчитаем напряжение на нагрузке:

U1=I1*R1=1.09*10=10.9 В

Сразу видим, что на нагрузке уже не 12, а 10 вольт, посчитаем другие варианты:

Рассчитаем ток второй нагрузки:

I2=E/(R2+r)=12/(5+1)=2 А

Рассчитаем напряжение на нагрузке:

U2=I2*R2=2*5=10 В

Рассчитаем ток третей нагрузки:

I3=E/(R3+r)=12/(1+1)=6 А

Рассчитаем напряжение:

U3=I3*R3=6*1=6 В

Как вы можете видеть на внутреннем сопротивлении падает какое-то напряжение, и падение напряжение прямо пропорционально току нагрузки. При этом до нагрузки доходит всё меньше и меньше напряжения.

Сделаем то же самое, но для источника с внутренним сопротивлением 0.1 Ома. Рассчитаем ток первой нагрузки:

I1=E/(R1+r)=12/(10+0,1)=1.18 А

Рассчитаем напряжение:

U1=I1*R1=1.18*10=11.8 В

Ток второй нагрузки:

I2=E/(R2+r)=12/(5+0,1)=2,35 А

Рассчитаем напряжение на нагрузке:

U2=I2*R2=2,35*5=11.75 В

Рассчитаем ток третей нагрузки:

I3=E/(R3+r)=12/(1+0,1)=10,9 А

Рассчитаем напряжение:

U3=I3*R3=10,9*1=10,9 В

Для удобства соберем все результаты расчётов в одну таблицу.

Из таблицы мы видим, что чем меньше внутреннее сопротивление источника — тем меньше просаживается напряжение под нагрузкой.

Заключение

Георг Симон Ом жил в 1786-1854 годах, в 1826 году вывел теоретически и подтвердил с помощью опытов закон выражающий связь напряжения, тока и сопротивления. Этот закон назвали в честь открывателя — законом Ома, а также единицу измерения электрического сопротивления.

Закон Ома — один из важнейших и основополагающих в электротехнике, он широко используется при расчетах электрических схем.

Пишите в комментариях, понравился ли вам такой формат теоретической статьи и какие статьи хотите увидеть в будущем?

Закон Ома

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока

Найти напряжение

Найти сопротивление

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

Найти ЭДС

Найти внутреннее сопротивление источника напряжения

Найти сопротивление всех внешних элементов цепи

См. также

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Схемы со смешанным соединением сопротивлений

• 

  2 слайд

  Закон ома

  I = U/R

  Сила тока на участке цепи прямо пропорциональна напряжению этого участка и обратно пропорциональна сопротивлению этого участка.

• 

  3 слайд

  Способы соединения потребителей
  Последовательное соединение

  Iвх=I1=I2=I3
  Uвх=U1+U2+U3
  Rвх=R1+R2+R3

• 

  4 слайд

  Способы соединения потребителей
  Параллельное соединение

  Iвх=I1+I2+I3
  Uвх=U1=U2=U3
  1/Rвх=1/R1+1/R2+1/R3

  Rвх= (R1*R2)/(R1+R2)

• 

  5 слайд

  R1
  R2
  R3
  R4
  R5
  E
  Ri
  Дано: Найти:
  Ri = 1,2 Ом I1-5, Iвх, U1-5, Uвх.
  R1 = 64 Ом
  R2 = 40 Ом
  R3 = 60 Ом
  R4 = 24 Ом
  R5 = 24 Ом
  Е = 52,2 В

• 

  6 слайд

  R1
  R2
  R3
  R4
  R5
  E
  Ri
  R2 x R3
  R2 + R3

  = R23
  R23
  R234
  R23 + R4 = R234

  R2345
  R234 x R5
  R234 + R5 = R2345

  Rэкв
  R2345 x R1
  R2345 + R1 = Rэкв

  Расчет сопротивлений:

• 

  7 слайд

  R2
  R1
  R3
  R5
  R1
  R3,4,5
  R3,4
  R2
  Rвх
  R4
  R5
  A5
  R2
  R1
  R2,3,4,5
  R1
  R3 + R4
  R3,4 =
  R3,4,5 =
  R3,4 х R5
  R2,3,4,5 =
  R2 х R3,4,5
  R2 + R3,4,5
  Rвх =
  R1 + R2,3,4,5
  R3 х R4
  R3,4 + R5

• 

  8 слайд

  R2
  R2
  R3
  R5
  R1
  R3,4
  R1
  R2,3,4,5
  R4
  R5
  R1
  R2
  R3,4,5
  R1
  Rвх
  R3 х R4
  R3 + R4
  R3,4 =
  R3,4,5 =
  R3,4 + R5
  R2,3,4,5 =
  R3,4,5 х R2
  R3,4,5 + R2
  Rвх =
  R2,3,4,5 + R1

• 

  9 слайд

  Пример решения задачи
  Дано:
  Ri = 1 Ом
  R1 = 3 Ом
  R2 = 20 Ом
  R3 = 6 Ом
  R4 = 40 Ом
  R5 = 60 Ом
  I2 = 2, 4 А

  Найти:
  I1,I3,I4,I5
  U1, U2, U3,U4,U5
  E, Iвх, Uвх
  Составить баланс мощностей

  E

• 

  10 слайд

  Решение
  Вычисляем входное сопротивление (Rвх):

  R4 параллельно R5, значит
  R4,5 = (R4*R5) / (R4+R5) = (40*60) / (40+60) = 24 Ом

  2) R3 соединено последовательно с R4,5, значит
  R3,4,5 = R3 + R4,5 = 6 +24 = 30 Ом

  3) R2 параллельно R3,4,5, значит
  R2,3,4,5 = (R2*R3,4,5)/ (R2+R3,4,5) = (20*30)/(20+30) = 12 Ом

  4) R1 соединено последовательно с R2,3,4,5, значит
  Rвх = R1 + R2,3,4,5, = 15 Ом
  E

• 

  11 слайд

  5) Находим напряжение по закону Ома для участка цепи
  U2 = I2 * R2 = 2,4 А * 20 Ом = 48 В
  6) Т.к. R2 параллельно R3,4,5 ,то
  U2 = U3,4,5 = U2,3,4,5 = 48 В
  7) Находим силу тока по закону Ома для участка цепи
  I3,4,5 = (U3,4,5) / (R3,4,5) = 48 Ом / 30 Ом = 1,6 А
  9) Т.к. R3 последовательно соединено с R4,5
  I3,4,5 = I3 = I4,5 = 1,6 А
  10) Находим силу тока по закону Ома для участка цепи
  I2,3,4,5 = U2,3,4,5 / R2,3,4,5 = 48 Ом / 12 В = 4 А
  11) Т.к. R2.3.4.5 последовательно с R1 и Rвх
  I2.3.4.5 = I1 = Iвх = 4 А
  12) Находим напряжение по закону Ома для участка цепи
  U3 = I3 * R3 = 1,6 А * 6 Ом = 9,6 В

  E

• 

  12 слайд

  13) Находим напряжение по закону Ома для участка цепи
  U4,5 = I4,5 * R4,5 = 38,4 А
  14) Т.к. R4 параллельно R5 то
  U4 = U5 = U4,5 = 38,4 В
  15) Находим силу тока по закону Ома для участка цепи
  I4 = U4 / R4 = 38,4 В/ 40 Ом = 0,96 А
  13) Находим напряжение по закону Ома для участка цепи
  U1 = I1 * R1 = 4 А * 3 Ом = 12 В
  14) Находим силу тока по закону Ома для участка цепи
  I5 = U5 / R5 = 38,4 В / 60 Ом = 0,64 А
  15) Находим напряжение по закону Ома для участка цепи
  Uвх = Iвх * Rвх = 4 * 15 = 60 В

  E

• 

  13 слайд

  Баланс Мощностей
  Pист = E * Iвх
  Рнагр = P1 + P2 + P3 + P4 + P5 + Pi

  Pист = 64 * 4 = 256 Вт
  Рнагр = (I12 * R1) + (I22 * R2) + (I32 * R3) + (I42 * R4) + (I52*R5) + (Iвх2 * Ri) = (42*3) + (2,42*20) + (1,62*6) + (0,962*40) + (0,642*60) + (42*1) = 256 Вт
  Pист = Pнагр
  Задача решена верно.
  16) Находим E по закону для полной цепи
  Iвх= E/(Rn+Ri) E = Iвх * (Rn+Ri) = 4 * 16 = 64 В

Краткое описание документа:

Данная презентация предназначена для преподавателей, объясняющих способы расчета задач с помощью законов Ома. В презентации дана краткая теория, основные формулы. Представлена схема удачно показывающая с помощью анимации “сворачивание” схем. Даны примеры расчета входного сопротивления с анимацией. Представлено решение задачи с акцентом на логику решения. Составлен баланс мощностей. Применение данной презентации упрощает объяснение данной темы, способствует лучшему усвоению материала, вызывает у студентов интерес, активизируется работа группы. Надеюсь, данная презентация пригодится и вам.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 257 212 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вы уже знаете, что есть два типа соединения элементов электрической цепи: последовательный и параллельный. Последовательно мы подключали в цепь амперметр, а параллельно — вольтметр.

На данном уроке мы более подробно рассмотрим последовательное соединение. Мы будем использовать сразу несколько потребителей электроэнергии и узнаем, каким закономерностям подчиняются уже известные нам величины (сила тока, сопротивление и напряжение) при таком соединении элементов в цепи.  

Последовательное включение элементов в электрическую цепь

Соберем электрическую цепь. Последовательно соединим две электролампы, два источника тока и ключа (рисунок 1).

Обратите внимание, что при таком подключении аккумуляторов соблюдается определенная полярность подключения: провод, идущий от положительного полюса одного аккумулятора необходимо соединить с отрицательным полюсом другого аккумулятора. И, наоборот, провод идущий от отрицательного полюса одного аккумулятора соединяется с положительным полюсом другого.

Если в такой цепи попытаться выключить только одну лампу, то погаснет и вторая.

Схема этой электрической цепи показана на рисунке 2.

В такую цепь мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества последовательно подключенных в цепь проводников.

Сила тока в цепи при последовательном соединении проводников

При изучении силы тока мы измеряли ее на различных участках электрической цепи (рисунок 3). Полученные с помощью амперметра значения силы тока были одинаковы.

При этом все элементы у нас были соединены последовательно. Сделаем вывод.

При последовательном соединении сила тока в любых частях цепи одна и та же:
$I = I_1 = I_2 = … = I_n$.

Сопротивление в цепи при последовательном соединении проводников

Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?

Давайте порассуждаем. В цепи был один проводник с определенным сопротивлением. Мы последовательно подключаем второй. Представим эти два проводника в виде одного элемента цепи. Тогда получается, что, подсоединив второй проводник, мы увеличили длину первого.

Сопротивление же зависит от длины проводника. Поэтому суммарное сопротивление цепи будет точно больше сопротивления одного проводника.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
$R = R_1 + R_2 + … + R_n$.

На схемах электрических цепей последовательное соединение нескольких проводников изображается так, как показано на рисунке 4.

Напряжение в цепи при последовательном соединении проводников

Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков:
$U_1 = IR_1$,
$U_2 = IR_2$,
…
$U_n = IR_n$.

Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.

Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
$U = U_1 + U_2 + … + U_n$.

Полное напряжение в цепи и закон сохранения энергии

Давайте вспомним, что напряжение определяется работой электрического тока. Эта работа совершается при прохождении по участку цепи электрического заряда, равного $1 space Кл$:
$U = frac{A}{q}$.

За счет чего совершается эта работа? Мы уже говорили, что электрическое поле обладает некоторой энергией. Именно за счет нее и идет совершение работы.

Такая работа совершается на каждом участке цепи, которую мы рассматриваем. Пользуясь законом сохранения энергии, мы можем сделать следующий вывод.

Энергия, израсходованная на всей цепи, равна сумме энергий, которые расходуются на отдельных ее участках (проводниках).

Пример задачи

Два проводника сопротивлением $R_1 = 2 space Ом$ и $R_2 = 3 space Ом$ соединены последовательно. Сила тока в цепи равна $1 space А$. Определите сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Так как проводники соединены последовательно, мы будем использовать формулы, полученные на данном уроке.

Дано:
$R_1 = 2 space Ом$
$R_2 = 3 space Ом$
$I = 1 space А$

$R — ?$
$U_1 — ?$
$U_2 — ?$
$U — ?$

Решение:

Общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников:
$R = R_1 + R_2$.

Рассчитаем его:
$R = 2 space Ом + 3 space Ом = 5 space Ом$.

Сила тока на всех участках цепи будет одинакова и равна $1 space А$.

Запишем закон Ома для участка цепи с первым проводником и выразим из него напряжение на концах первого проводника:
$I = frac{U_1}{R_1}$,
$U_1 = IR_1$.

Рассчитаем его:
$U_1 = 1 space А cdot 2 space Ом = 2 space В$.

Так же рассчитаем напряжение на концах второго проводника:
$I = frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 1 space А cdot 3 space Ом = 3 space В$.

При последовательном соединении проводников полное напряжение в цепи мы можем рассчитать двумя способами.

Способ №1
Напряжение на всей цепи равно сумме напряжений на концах проводников в этой цепи:
$U = U_1 + U_2$,
$U = 2 space В + 3 space В = 5 space В$.

Способ №2
Мы уже знаем общее сопротивление двух проводников. Получается, что эти два проводника мы можем представить как один целый. Используем закон Ома для участка цепи:
$I = frac{U}{R}$,
$U = IR$,
$U = 1 space А cdot 5 space Ом = 5 space В$.

Ответ: $R = 5 space Ом$, $U_1 = 2 space В$, $U_2 = 3 space В$, $U = 5 space В$.

Упражнения

Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$

$I = 0.2 space А$

$U_1 — ?$
$U_2 — ?$
$U — ?$

Показать решение и ответ

Скрыть

Такие лампы можно соединить последовательно в одну цепь. Главное, чтобы их суммарное напряжение не превышало общее. Рассчитаем количество таких ламп, которое мы можем включить в цепь.

Дано:
$U = 3000 space В$
$U_1 = 50 space В$

$n — ?$

Показать решение и ответ

Скрыть

Дано:

$U = 220 space В$

$U_1 — ?$
$U_2 — ?$

Показать решение и ответ

Скрыть

Схема такой цепи изображена на рисунке 5.

Дано:
$U = 6 space В$
$R_1 = 13.5 space Ом$
$R_2 = 3 space Ом$
$R_3 = 2 space Ом$

$I — ?$
$U_1 — ?$
$U_2 — ?$
$U_3 — ?$

Показать решение и ответ

Скрыть