Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.
Найти решение системы дифференциальных уравнений
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия
- Метод исключения
-
- Пример 1
- Пример 2
- Пример 3
- Метод Эйлера
-
- Пример 4
Основные понятия
В данной статье рассмотрим линейные системы дифференциальные уравнений, которые делятся на два вида: однородные и неоднородные. В общем виде они записываются следующим образом $$begin{cases} frac{dx}{dt} = a_1 x(t) + b_1 y(t) + f_1(t) \ frac{dy}{dt} = a_2 x(t) + b_2 y(t) + f_2(t) end{cases},$$где $a_1, b_1, c_1, a_2$ коэффициенты, функции $f_1(t)$ и $f_2(t)$ могут отсутствовать, либо быть константами, $x(t),y(t)$ неизвестные функции, которые требуется найти в качестве решения системы ДУ. Напоминаем, что аналогичная запись $frac{dx}{dt} = x'(t)$ и $frac{dy}{dt} = y'(t)$.
Если хотя бы один из коэффициентов $f_1(t)$ или $f_2(t)$ не равен нулю, то система называется неоднородной. Если $f_1(t) = f_2(t) = 0$, то система однородная.
Решением системы дифференциальных уравнений называется пара функций $y(t), x(t)$, подстановка которых в систему обращает её в тождество.
Разберём два основных способа решения линейных систем дифференциальных уравнений: метод исключения и метод Эйлера.
Метод исключения
Суть метода в том, что два уравнения сводятся к одному линейному дифференциальному уравнению. Для этого есть примерный алгоритм:
- Находим производную одного из уравнений системы, например, $y”_t$
- В получившейся производной исключаем всё что связано с $x$
- Решаем линейное дифференциальное уравнение относительно $y(t)$
- Подставляем получившийся $y(t)$ в одно из уравнений системы, чтобы найти $x(t)$
| Пример 1 |
| Решить систему дифференциальных уравнений методом исключения $$begin{cases} frac{dx}{dt} =y-7 \ frac{dy}{dt} = -2x – 3y end{cases}.$$ |
| Решение |
|
Применим метод исключения, чтобы из двух уравнений получить одно. Берем первое уравнение и дифференцируем его по $t$. $$frac{d^2 x}{dt^2} = frac{dy}{dt}$$ В получившееся уравнения вместо $frac{dy}{dt}$ подставим второе уравнение системы. $$frac{d^2 x}{dt^2} = -2x – 3y$$ Теперь нужно избавиться от $y$, чтобы остались только $x$, и тогда можно будет решить дифференциальное уравнение относительно $x(t)$. Для этого берём первое уравнение системы и получаем из него $$y = frac{dx}{dt}+7.$$ Продолжаем решение с учётом полученного $y$ $$frac{d^2 x}{dt^2} = -2x – 3 (frac{dx}{dt}+7).$$ После раскрытия скобок и преобразований получаем уравнение $$frac{d^2 x}{dt^2} + 3frac{dx}{dt} + 2x = 21.$$ Это линейное неоднородное дифференциальное уравнение второго порядка. Решение его будем искать в виде $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Сначала находим общее решение однородного уравнения $x_text{о.о.}$. Для этого отбрасываем правую часть уравнения и составляем характеристический многочлен и находим его корни. $$lambda^2 + 3lambda + 2 = 0,$$ $$lambda_{1,2} = frac{-3pm sqrt{9-4cdot 1 cdot 2}}{2} = frac{-3pm 1}{2},$$ $$lambda_1 = -1, lambda_2 = -2.$$ Итак, записываем $$x_text{о.о.} = C_1 e^{-t} + C_2 e^{-2t}.$$ Искать частное решение $x_text{ч.н.}$ будем искать методом подбора правой части исходного неоднородного линейного дифференциального уравнения. В данном случае в правой части стоит константа, значит подбор будет в виде $x_text{ч.н.} = A$. Находим первую и вторую производную и подставляем в исходное решаемое уравнение. $$x’_text{ч.н.} = 0, x”_text{ч.н.} = 0$$ $$0 + 3 cdot 0 + 2 A = 21 Rightarrow A = frac{21}{2}.$$ Значит, $x_text{ч.н.} = frac{21}{2}$. Записываем окончательно, что $$x(t) = x_text{о.н.} = x_text{о.о.} + x_text{ч.н.} = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2}$$ Теперь зная $x(t)$ можно получить $y(t)$. Для этого нужно вернуться к началу решения и вспомнить, что мы выражали $y = frac{dx}{dt}+7$. Таким образом осталось в него подставить полученное решение $x(t)$ $$y(t) = (C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2})’ + 7 = -C_1 e^{-t} – 2C_2 e^{-2t} + 7$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$begin{cases} x(t) = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2} \ y(t) = -C_1 e^{-t} – 2C_2 e^{-2t} + 7 end{cases}$$ |
| Пример 2 |
| Найти решение системы дифференциальных уравнений $$begin{cases} x’ = -2y+3t \ y’ = 2x+4 end{cases},$$ где $x(t),y(t)$ – искомые функции, $t$ – независимая переменная. |
| Решение |
|
Решаем методом исключения, то есть два уравнения приводим к одному. Берем производную первого уравнения по $t$. $$x” = (-2y+3t)’_t = -2y’+3$$ Знаем чему равен $y’$ из второго уравнения системы и поэтому его подставляем в получившееся последнее уравнение. $$x” = -2(2x+4)+3 = -4x – 8 + 3 = -4x – 5$$ Переписываем последнее получившееся уравнение в форме линейного неоднородного дифференциального уравнения второго порядка. $$x” + 4x = -5$$ Общее решение этого уравнения найдем в качестве суммы общего решения однородного уравнения и частного решения неоднородного $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Итак, составляем характеристический многочлен и находим его корни. $$lambda^2 + 4 = 0$$ $$lambda_1 = -2i, lambda_2 = 2i.$$ Так как получились комплексные корни, то общее решение записывается следующим образом $$x_text{о.о.} = C_1cos 2t + C_2 sin 2t.$$ Осталось найти $x_text{ч.н.}$. Для этого воспользуемся методом подбора правой части. Так как она представляет собой константу, то значит $x_text{ч.н.} = A$. Отсюда следует, что $x”_text{ч.н.} = 0$. Подставляя эти данные в дифференциальное уравнение получаем значение $A$. $$0 + 4A = -5,$$ $$A = -frac{5}{4}.$$ Таким образом можно записать, что $$x(t) = x_text{о.о.} + x_text{ч.н.} = C_1cos 2t + C_2 sin 2t -frac{5}{4}.$$ Осталось найти функцию $y(t)$. Для этого выразим её из первого уравнения и подставим ранее полученный $x(t)$. $$y = frac{3}{2}t – frac{x’}{2},$$ $$y = frac{3}{2}t – frac{1}{2}(C_1cos 2t + C_2 sin 2t -frac{5}{4})’ = $$ $$ = frac{3t}{2} + C_1 sin 2t – C_2 cos 2t.$$ |
| Ответ |
| $$begin{cases} x(t) = C_1cos 2t + C_2 sin 2t -frac{5}{4} \ y(t) = frac{3t}{2} + C_1 sin 2t – C_2 cos 2t end{cases}$$ |
| Пример 3 |
| Найти общее и частное решение системы дифференциальных уравнений $$begin{cases} frac{dx}{dt} = 2x+y \ frac{dy}{dt} = x+2y end{cases}, x(0)=1, y(0)=3$$ |
| Решение |
|
Берем второе уравнение и находим его производную по $t$. $$frac{dy^2}{dt^2} = frac{dx}{dt}+2frac{dy}{dt}$$ В полученное равенство вместо frac{dx}{dt} подставим первое уравнение системы. $$frac{dy^2}{dt^2} = 2x+y + 2frac{dy}{dt}$$ Осталось избавиться от $x$. Для этого выразим его из второго уравнения системы и подставим в последнее полученное уравнение. $$frac{dy^2}{dt^2} = 2(frac{dy}{dt} – 2y) + y + 2frac{dy}{dt}$$ Раскроем скобки и перенесем всё в левую сторону. Затем запишем для удобства $frac{dy}{dt} = y’$. $$y” – 4y’ + 3y = 0$$ Получившееся дифференциальное уравнение называется однородным линейным ду второго порядка. Для его решения составляем характеристический многочлен и находим его корни. $$lambda^2 – 4lambda + 3 = 0,$$ $$lambda_{1,2} = frac{4pm sqrt{16 – 4 cdot 1 cdot 3}}{2} = frac{4pm 2}{2},$$ $$lambda_1 = 1, lambda_2 = 3.$$ Общее решение такого уравнения записывается в виде $$y = C_1 e^{3t} + C_2e^{t}.$$ Так как мы нашли $y(t)$, то теперь можем найти $x(t)$. Для этого подставляем $y(t)$ во второе уравнение системы и выражаем $x(t)$. $$x(t) = frac{dy}{dt} – 2y = (C_1 e^{3t} + C_2e^{t})’ – 2(C_1 e^{3t} + C_2e^{t})$$ После раскрытия скобок и упрощения остаётся $$x(t) = 3C_1 e^{3t} + C_2 e^t – 2C_1 e^{3t} – 2C_2 e^t = C_1 e^{3t} – C_2 e^t.$$ Вот таким образом находится общее решение системы дифференциальных уравнений $$begin{cases} x(t) = C_1 e^{3t} – C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}.$$ По условию задания необходимо кроме общего найти частное решение. Для этого берем дополнительные условия из задачи $x(0)=1, y(0)=3$ и подставляем в полученное общее решение, чтобы вычислить константы $C_1$ и $C_2$. $$begin{cases} x(0) = C_1e^{0}-C_2e^0 = 1 \ y(0) = C_1 e^0 + C_2 e^0 = 3 end{cases},$$ $$ begin{cases} C_1-C_2 = 1 \ C_1 + C_2 = 3 end{cases} Rightarrow begin{cases} C_1 = 2 \ C_2 = 1 end{cases}.$$ Теперь зная постоянные можно записать частное решение системы дифференциальных уравнений $$begin{cases} x(t) = 2e^{3t} – e^t \ y(t) = 2e^{3t} + e^t end{cases}.$$ |
| Ответ |
| $$begin{cases} x(t) = C_1 e^{3t} – C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}, begin{cases} x(t) = 2e^{3t} – e^t \ y(t) = 2e^{3t} + e^t end{cases}$$ |
Метод Эйлера
Примерный алгоритм решения по данному методу следующий:
- Построить матрицу $A$ из коэффициентов дифференциальных уравнений
- Найти собственные значения $lambda$ и векторы матрицы $overline{x}$
- Записать общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 $$
Рассмотрим данный метод решения на конкретном примере, так как практика учит лучше, чем теория.
| Пример 4 |
| Решить систему дифференциальных уравнений методом эйлера $$begin{cases} x’ = 2x+y \ y’ = 3x+4y end{cases}.$$ |
| Решение |
|
Первым делом нужно составить матрицу, элементы которой равны коэффициентам из правой части системы дифференциальных уравнений. $$A = begin{pmatrix} 2&1 \ 3&4 end{pmatrix}$$ Далее нужно найти собственные значения матрицы. Для этого необходимо составить характеристический многочлен и вычислить его корни. $$|A-lambda E| = 0 Rightarrow begin{vmatrix} 2 – lambda & 1 \ 3 & 4-lambda end{vmatrix} = 0$$ Раскрываем определитель два на два и решаем квадратное уравнение. $$(2-lambda)(4-lambda)-3 = 0,$$ $$8-2lambda -4lambda+lambda^2 – 3 = 0,$$ $$lambda^2 – 6lambda + 5 = 0,$$ $$lambda_{1,2} = frac{6pm sqrt{36-4 cdot 5}}{2} = frac{6pm 4}{2},$$ $$lambda_1 = 1, lambda_2 = 5.$$ Зная собственные значения матрицы получим собственные векторы матрицы по формуле $(A-lambda E)overline{x} = 0$. 1) Для $lambda_1 = 1$ имеем $$(A-lambda_1 E)overline{x}_1 = 0 Rightarrow begin{cases} x_1 + x_2 = 0 \ 3x_1 + 3x_2 = 0 end{cases}$$ Видим, что после сокращения второго уравнения на 3 получится, что первое уравнение равно второму. $$x_1 + x_2 = 0 Rightarrow x_1 = -x_2$$ Так как $x_2$ свободный, то положим его $x_2 = 1$. Тогда $x_1 = -1$. Отсюда следует, что первый собственный вектор равен $$overline{x}_1 = begin{pmatrix} -1 \ 1 end{pmatrix}.$$ 2) Для $lambda_2 = 5$ имеем $$(A-lambda_2 E)overline{x}_2 = 0 Rightarrow begin{cases} -3x_1 + x_2 = 0 \ 3x_1 – x_2 = 0 end{cases}$$ Замечаем, что первое уравнение одно и тоже что второе, если домножить на (-1) одно из них. $$3x_1 – x_2 = 0 Rightarrow x_1 = frac{x_2}{3}$$ Так как $x_2$ свободный, то зададим его $x_2 = 3$. Таким образом $x_1 = 1$. Из этих значений получаем второй собственный вектор $$overline{x}_2 = begin{pmatrix} 1 \ 3 end{pmatrix}.$$ Находим общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 = $$ $$ = C_1 e^t begin{pmatrix} -1 \ 1 end{pmatrix} + C_2 e^{5t} begin{pmatrix} 1\3 end{pmatrix} = begin{pmatrix} -C_1 e^t \ C_1e^t end{pmatrix} + begin{pmatrix} C_2 e^{5t} \ 3C_2 e^{5t} end{pmatrix} = $$ $$ = begin{pmatrix} -C_1 e^t + C_2 e^{5t} \ C_1 e^t + 3C_2 e^{5t} end{pmatrix} Rightarrow begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$ |
| Ответ |
| $$begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$ |
Этот раздел мы решили посвятить тому, как решать систему дифференциальных уравнений (ду) простейшего вида dxdt=a1x+b1y+c1dydt=a2x+b2y+c2, в которых a1, b1, c1, a2, b2, c2 – некоторые действительные числа. Наиболее эффективным в решении систем ду и основным является метод интегрирования. Также рассмотрим решение примера по теме – научимся дифференцировать.
Как решить систему дифференциальных уравнений? Решением системы ДУ будет являться пара функций x(t) и y(t), которая способна обратить в тождество оба уравнения системы.
Рассмотрим правило или метод интегрирования системы ДУ dxdt=a1x+b1y+c1dydt=a2x+b2y+c2. Выразим х из 2-го уравнения системы для того, чтобы исключить неизвестную функцию x(t) из 1-го уравнения:
dydt=a2x+b2y+c2⇒x=1a2dydt-b2y-c2
Выполним дифференцирование 2-го уравнения по t и разрешим его уравнение относительно dxdt:
d2ydt2=a2dxdt+b2dydt⇒dxdt=1a2d2ydt2-b2dydt
Теперь подставим результат предыдущих вычислений в 1-е уравнение системы:
dxdt=a1x+b1y+c1⇒1a2d2ydt2-b2dydt=a1a2dydt-b2y-c2+b1y+c1⇔d2ydt2-(a1+b2)·dydt+(a1·b2-a2·b1)·y=a2·c1-a1·c2
Так мы исключили неизвестную функцию x(t) и получили линейное неоднородное ДУ 2-го порядка с постоянными коэффициентами. Найдем решение этого уравнения y(t) и подставим его во 2-е уравнение системы. Найдем x(t). Будем считать, что на этом решение системы уравнений будет закончено.
Также выделяют жесткую систему ду в классификации уравнений: ее решение явными методами или способами будет неудовлетворительным ввиду резкого увеличения количества вычислений (в случае малого шага интегрирования) и погрешности (в случае недостаточно малого шага).
Найдите общее решение системы дифференциальных уравнений dxdt=x-1dydt=x+2y-3
Решение
Поиск начнем с первого уравнения системы линейных дифференциальных уравнений. Разрешим его относительно x:
x=dydt-2y+3
Теперь выполним дифференцирование 2-го уравнения системы оду, после чего разрешим его относительно dxdt: d2ydt2=dxdt+2dydt⇒dxdt=d2ydt2-2dydt
Полученный в ходе вычислений результат мы можем подставить в 1-е уравнение дифсистемы:
dxdt=x-1d2ydt2-2dydt=dydt-2y+3-1d2ydt2-3dydt+2y=2
В результате преобразований мы получили линейное неоднородное диф-е уравнение 2-го порядка с постоянными коэффициентами d2ydt2-3dydt+2y=2 (линеаризация дифференциальных уравнений, линеаризованное уравнение). Если мы найдем его общее решение, то получим функцию y(t).
Общее решение соответствующего ЛОДУ y0 мы можем найти общее решение системы дифференциальных уравнений путем вычислений корней характеристического уравнения k2-3k+2=0:
D=32-4·2=1k1=3-12=1k2=3+12=2
Корни, которые мы получили, являются действительными и различными. В связи с этим общее решение ЛОДУ будет иметь вид y0=C1·et+C2·e2t.
Теперь нам нужно находить частное решение линейного неоднородного ДУ y~:
d2ydt2-3dydt+2y=2
Правая часть записи уравнения представляет собой многочлен нулевой степени. Это значит, что частное решение будем искать в виде y~=A, где А – это неопределенный коэффициент.
Определить неопределенный коэффициент мы можем из равенства d2y~dt2-3dy~dt+2y~=2:
d2(A)dt2-3d(A)dt+2A=2⇒2A=2⇒A=1
Таким образом, y~=1 и y(t)=y0+y~=C1·et+C2·e2t+1. Одну неизвестную функцию мы нашли.
Теперь подставим найденную функцию во 2-е уравнение системы ДУ и разрешим новое уравнение относительно x(t):
d(C1·et+C2·e2t+1)dt=x+2·(C1·et+C2·e2t+1)-3C1·et+2C2·e2t=x+2C1·et+2C2·e2t-1x=-C1·et+1
Так мы вычислили вторую неизвестную функцию x(t)=-C1·et+1.
Ответ: x(t)=-C1·et+1y(t)=C1·et+C2·e2t+1
Теперь вы знаете, как решать системы дифференциальных уравнений на этом примере.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции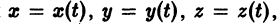 
выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид
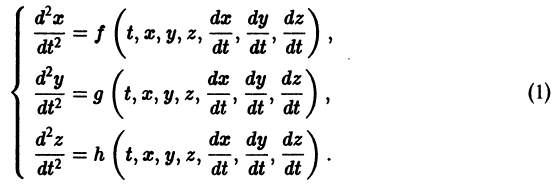
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями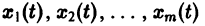 
аргумента t, назовем канонической систему вида
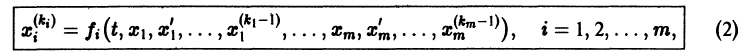
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
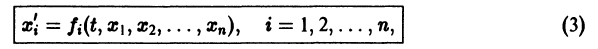
называется нормальной.
Если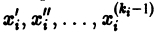 
в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из 
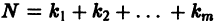уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение
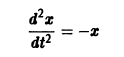
является мастным случаем канонической системы. Положив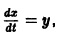 
в силу исходного уравнения будем иметь
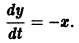
В результате получаем нормальную систему уравнений
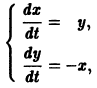
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
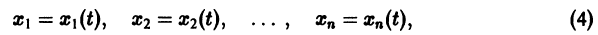
дифференцируемых на интервале а < t < b, обращающая уравнения системы (3) в тождества по t на интервале (а, b).
Задача Коши для системы (3) формулируется так: найти решение (4) системы, удовлетворяющее при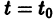 
начальным условиям
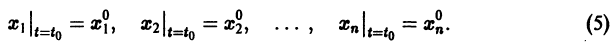
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
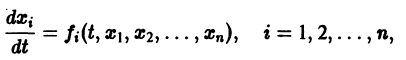
и пусть функции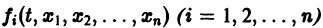 
определены в некоторой (n + 1) — мерной области D изменения переменных 
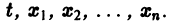Если существует окрестность 
точки 
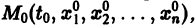в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным 
то найдется интервал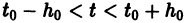 
изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям
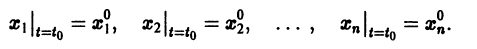
Определение:
Система n функций
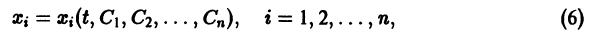
зависящих от t и n произвольных постоянных 
называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если
1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,
2) в области функции (6) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат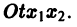 
Решение
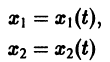
системы (7), принимающее при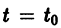 
значения 
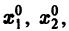определяет в пространстве некоторую линию, проходящую через точку 
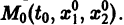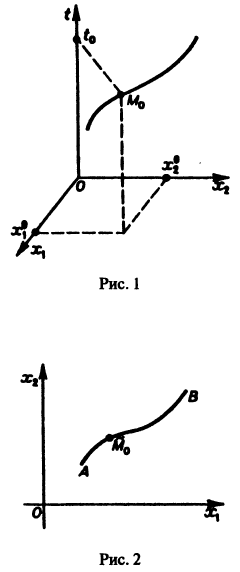
Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку 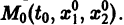(рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
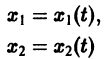
системы — как параметрические уравнения кривой на плоскости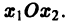 
Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение 
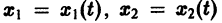системы (7), принимающее при t = to начальные значения 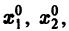изображается кривой АВ, проходящей через точку 
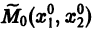(рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
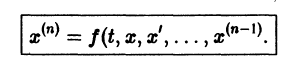
Введя новые функции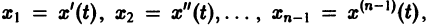 
заменим это уравнение следующей нормальной системой n уравнений:
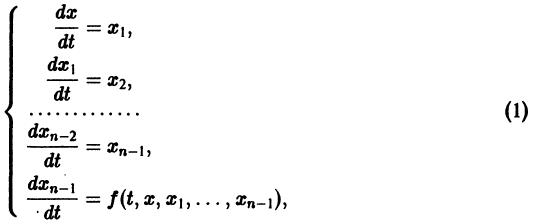
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
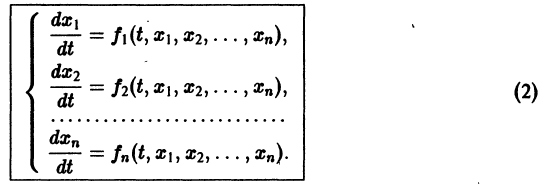
Продифференцируем первое из уравнений (2) по t. Имеем
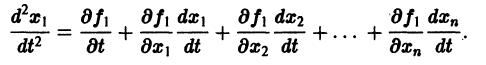
Заменяя в правой части производные 
их выражениями 
получим
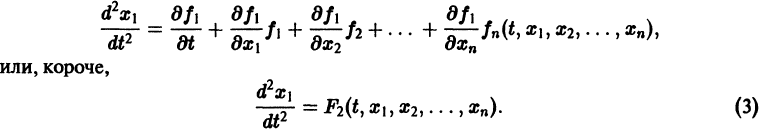
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
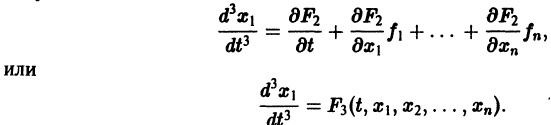
Продолжая этот процесс, найдем
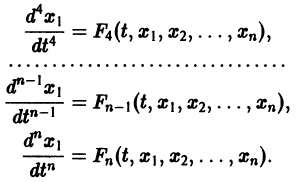
Предположим, что определитель
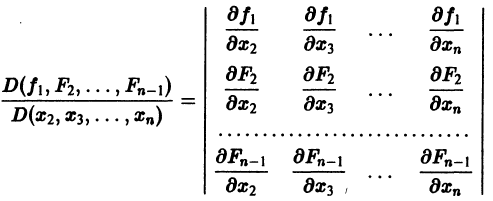
(якобиан системы функций 
отличен от нуля при рассматриваемых значениях 
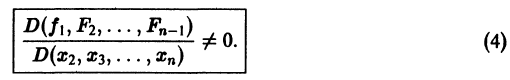
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
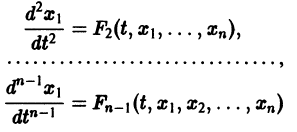
будет разрешима относительно неизвестных 
При этом выразятся через 
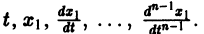
Внося найденные выражения в уравнение
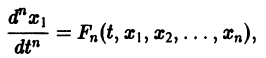
получим одно уравнение n-го порядка
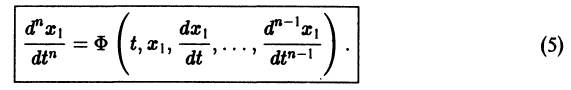
Из самого способа его построения следует, что если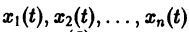 
есть решения системы (2), то функция х1(t) будет решением уравнения (5).
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим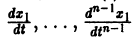 
и подставим найденные значения как известные функции
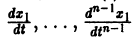
от t в систему уравнений
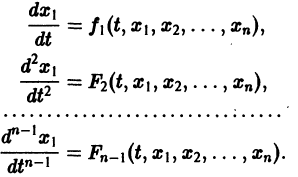
По предположению эту систему можно разрешить относительно т. е найти как функции от t.
Можно показать, что так построенная система функций
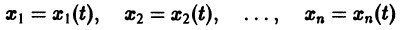
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
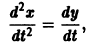
откуда, используя второе уравнение, получаем
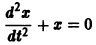
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
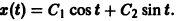
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
Функции x(t), y(t) можно представить в виде
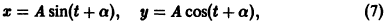
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом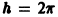 
и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).
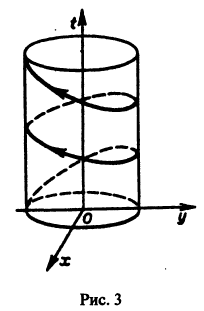
Исключая в формулах (7) параметр t, получаем уравнение
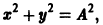
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 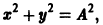нельзя выразить через 
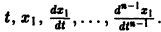Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений
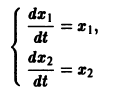
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
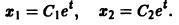
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
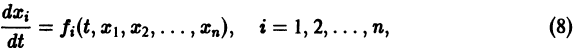
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Проинтегрировать систему
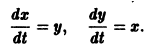
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
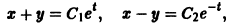
из которых легко определяется общее решение системы:
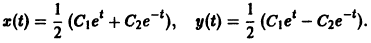
Одна интегрируемая комбинация дает возможность получить одно уравнение
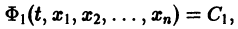
связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция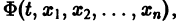 
не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
отличен от нуля:
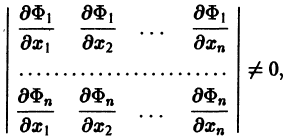
то задача интефирования системы (8) решена (так как из системы
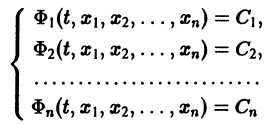
определяются все неизвестные функции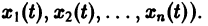 
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
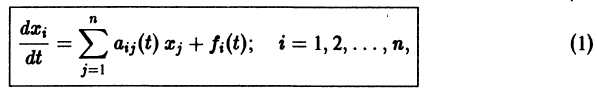
или, в матричной форме,
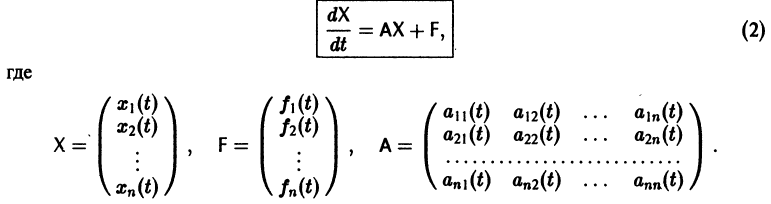
Теорема:
Если все функции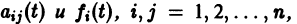 
непрерывны на отрезке 
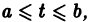то в достаточно малой окрестности каждой точки 
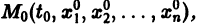где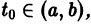 
выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по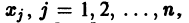 
ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам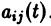 
Введем линейный оператор
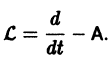
Тогда система (2) запишется в виде
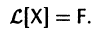
Если матрица F — нулевая, т. е.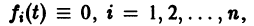 
на интервале (а,b), то система (2) называется линейной однородной и имеет вид
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
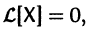
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
Сумма
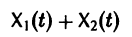
двух решений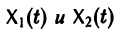 
однородной линейной системы уравнений является решением той же системы.
Следствие:
Линейная комбинация
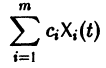
с произвольными постоянными коэффициентами сi решений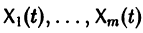 
линейной однородной системы дифференциальных уравнений
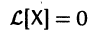
является решением той же системы.
Теорема:
Если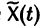 
есть решение линейной неоднородной системы
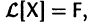
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы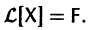 
Действительно, по условию,
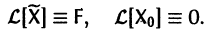
Пользуясь свойством аддитивности оператора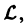 
получаем
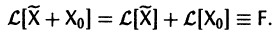
Это означает, что сумма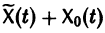 
есть решение неоднородной системы уравнений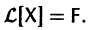
Определение:
Векторы
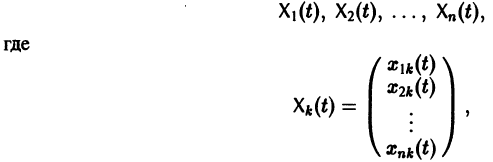
называются линейно зависимыми на интервале a < t < b, если существуют постоянные числа 
, такие, что
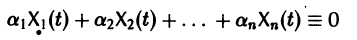
при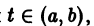 
причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при 
то векторы 
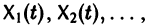
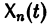называются линейно независимыми на (а, b).
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
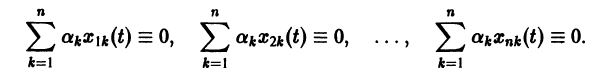
Определитель
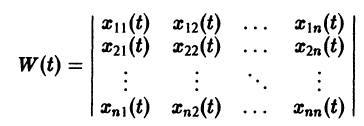
называется определителем Вронского системы векторов 
Определение:
Пусть имеем линейную однородную систему
где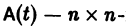 
матрица с элементами 
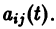Система n решений
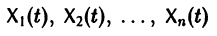
линейной однородной системы (6), линейно независимых на интервале а < t < Ь, называется фундаментальной.
Теорема:
Определитель Вронского W(t) фундаментальной на интервале а < t < b системы решений линейной однородной системы (6) с непрерывными на отрезке 
коэффициентами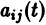 
отличен от нуля во всех точках интервала (а, Ь)
Теорема:
О структуре общего решения линейной однородной системы. Общим решением в области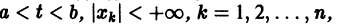 
линейной однородной системы
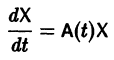
с непрерывными на отрезке коэффициентами 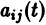является линейная комбинация п линейно независимых на интервале а < t < b решений 
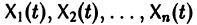системы (6) :
(
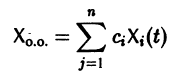
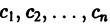) — произвольные постоянные числа).
Пример:
Система
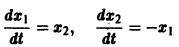
имеет, как нетрудно проверить, решения
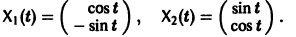
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
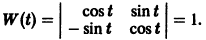
Общее решение системы имеет вид
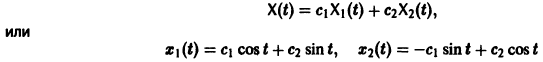
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
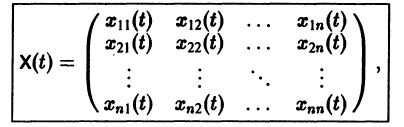
столбцами которой являются линейно независимые решения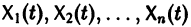 
системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению
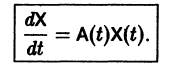
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
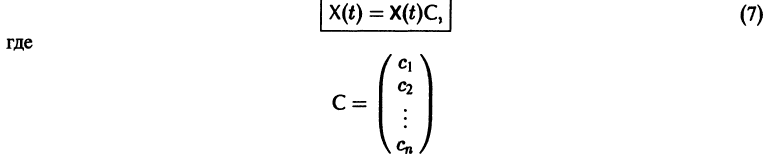
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
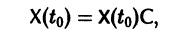
откуда
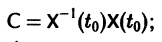
следовательно,
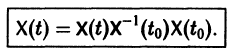
Матрица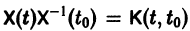 
называется матрицей Коши. С ее помощью решение системы (6) можно представить так:
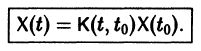
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области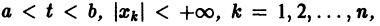 
линейной неоднородной системы дифференциальных уравнений
с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения
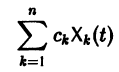
соответствующей однородной системы и какого-нибудь частного решения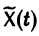 
неоднородной системы (2):
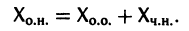
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
Пусть
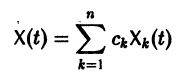
есть общее решение однородной системы (6), тогда
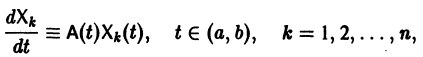
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
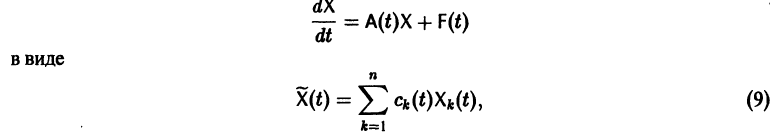
где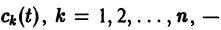 
неизвестные функции от t. Дифференцируя 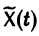по t, имеем
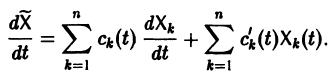
Подставляя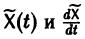 
в (2), получаем
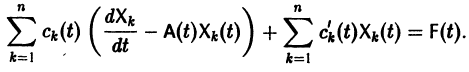
Так как
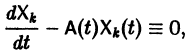
то для определения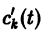 
получаем систему
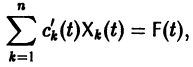
или, в развернутом виде,
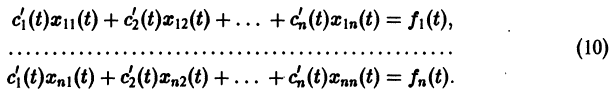
Система (10) есть линейная алгебраическая система относительно 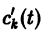определителем которой является определитель Вронского W(t) фундаментальной системы решений 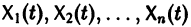. Этот определитель отличен от нуля всюду на интервале a < t < Ь, так что система (10) имеет единственное решение
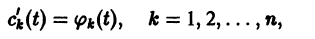
где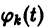 
— известные непрерывные функции. Интегрируя последние соотношения, находим
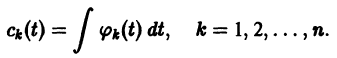
Подставляя эти значения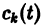 
в (9), находим частное решение системы (2)
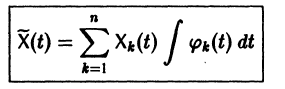
(здесь под символом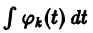 
понимается одна из первообразных для функции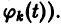 
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
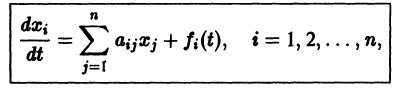
в которой все коэффициенты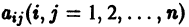 
— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
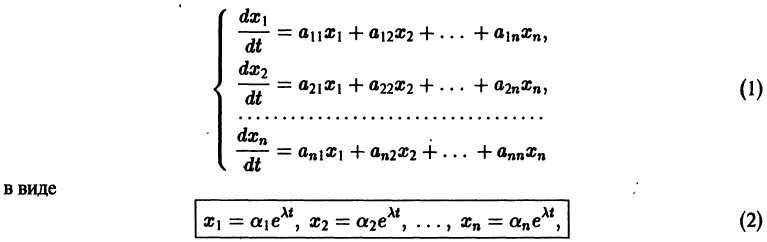
где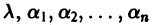 
— постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на 
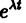и перенося все члены в одну часть равенства, получаем систему
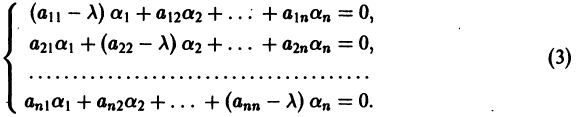
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
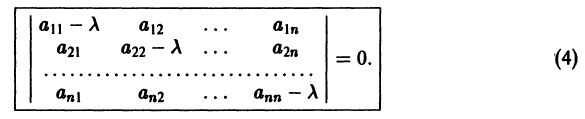
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 
степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни 
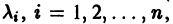характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения 
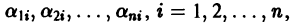этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
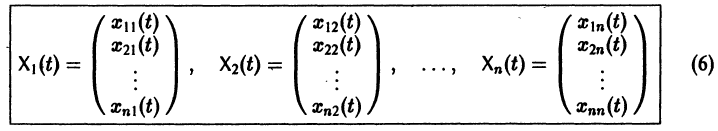
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
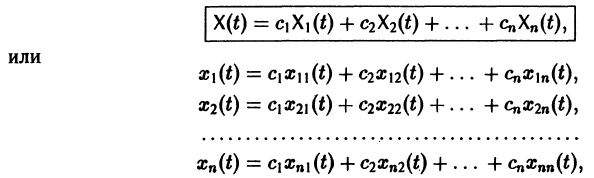
где 
произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Решить систему
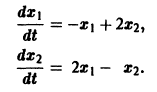
Ищем решение в виде
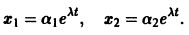
Характеристическое уравнение
имеет корни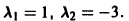 
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*)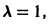 
получаем
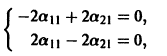
откуда а21 = а11. Следовательно,
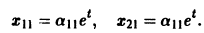
Полагая в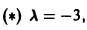 
находим a22 = — a12, поэтому
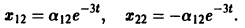
Общее решение данной системы:
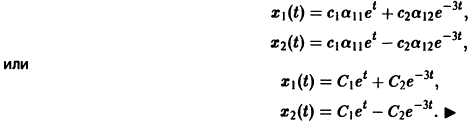
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде
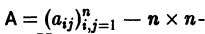матрица с постоянными действительными элементами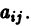 
Напомним некоторые понятия из линейной алгебры. Вектор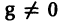 
называется собственным вектором матрицы А, если
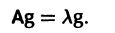
Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения
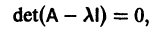
где I — единичная матрица.
Будем предполагать, что все собственные значения 
матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует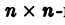 
матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что
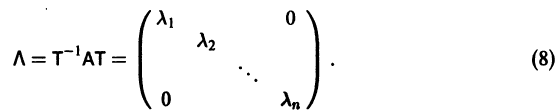
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 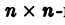матрица, элементы 
которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на 
, если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы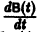 
называется матрица, элементами которой являются производные 
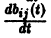у соответствующих элементов матрицы В(t).
Пусть B(t) — n х n-матрица,
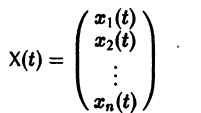
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
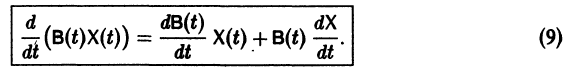
В частности, если В — постоянная матрица, то
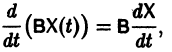
так как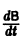 
есть нуль-матрица.
Теорема:
Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид
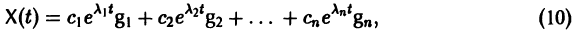
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
произвольные постоянные числа.
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
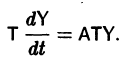
Умножая обе части последнего соотношения слева на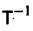 
и учитывая, что 
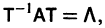придем к системе
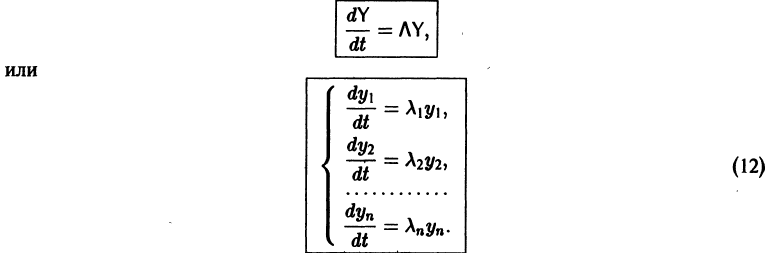
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
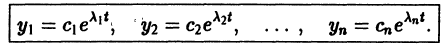
Здесь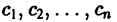 
— произвольные постоянные числа.
Вводя единичные n-мерные векторы-столбцы
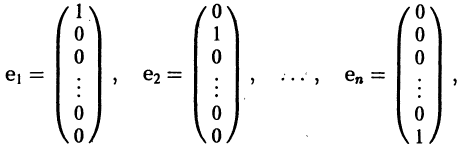
решение Y(t) можно представить в виде
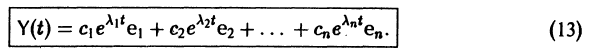
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы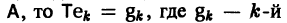 
собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):
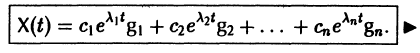
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения матрицы как корни алгебраического уравнения
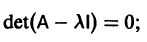
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Решить систему
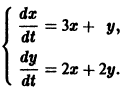
Матрица А системы имеет вид
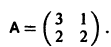
1) Составляем характеристическое уравнение
Корни характеристического уравнения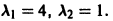 
2) Находим собственные векторы
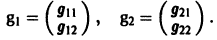
Для = 4 получаем систему
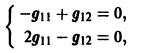
откуда g11 = g12, так что
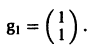
Аналогично для = 1 находим
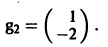
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
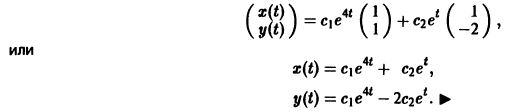
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 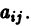системы (7) действительные, то характеристическое уравнение
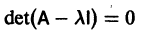
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.
При комплексном решение
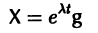
системы (7) также будет комплексным. Действительная часть
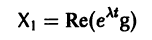
и мнимая часть
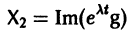
этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.
Пусть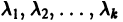 
— действительные собственные значения,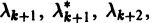 
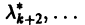— комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид
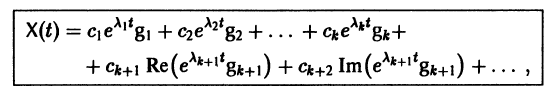
где сi — произвольные постоянные.
Пример:
Решить систему
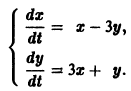
Матрица системы
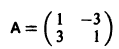
1) Характеристическое уравнение системы
Его корни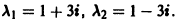 
2) Собственные векторы матриц
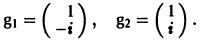
3) Решение системы
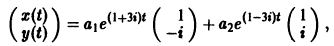
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
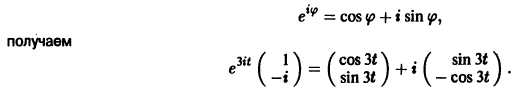
Следовательно, всякое действительное решение системы имеет
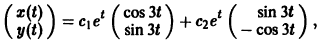
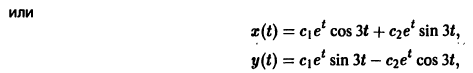
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений
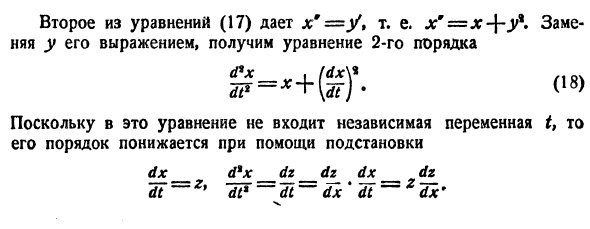
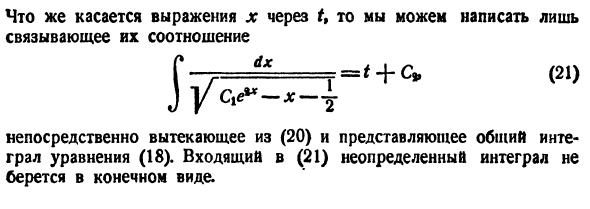
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
