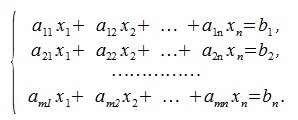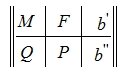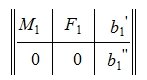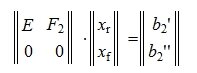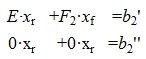Как найти общее решение слу

Как найти общее решение слу

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Метод Гаусса

  1. Метод Гаусса
    1. Пример 1
    2. Пример 2
  2. Несовместность системы (нет решений)
    1. Пример 3
  3. Общее и частное решение системы (бесконечное множество решений)
    1. Пример 4

Пусть задана система линейных алгебраических уравнений: $$begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = b_1 \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = b_2 \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = b_3 end{cases}. $$

  1. Запишем систему уравнений в виде расширенной матрицы, состоящей из коэффициентов и столбца свободных членов. Вертикальная черта используется для удобства оформления. $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ a_{21} & a_{22} & a_{23} & | & b_2 \ a_{31} & a_{32} & a_{33} & | & b_3 end{pmatrix} $$
  2. С помощью элементарных преобразований матрицы (вычитание одной строки из другой, умноженной на коэффициент, удаление одинаковых и нулевых строк, деление строки на число отличное от нуля) получаем нули под главной диагональю $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ 0 & a_{22} & a_{23} & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
  3. Используя элементарные преобразования, изложенные в пункте 2, приводим матрицу к виду содержащему нули везде, кроме главной диагонали $$ begin{pmatrix} a_{11} & 0 & 0 & | & b_1 \ 0 & a_{22} & 0 & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
Пример 1
Решить систему уравнений методом Гаусса $$begin{cases} x_1 + 2 x_2 + x_3 = 5 \ -x_1 + 3 x_2 -2 x_3 = 3 \ – x_1 -7 x_2 + 4 x_3 = -5 end{cases}. $$
Решение

Запишем расширенную матрицу, состоящую из коэффициентов при неизвестных $x_1, x_2, x_3$ и отдельно столбец свободных членов $b_1, b_2, b_3$. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ -1 & 3 & -2 & | & 3 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$

Приведем матрицу к нижнетреугольному виду (под главной диагональю должны быть нули) с помощью элементарных преобразований.

Прибавим ко второй строке первую. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$

Далее прибавляем к третьей строке первую. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & -5 & 5 & | & 0 end{pmatrix}$$

Теперь осталось к третьей строке прибавить вторую строку, чтобы под главной диагональю были только нули. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 4 & | & 8 end{pmatrix}$$

Замечаем, что в третьей строке стоят числа, которые можно сократить на четыре. Для этого выполняем деление всей третьей строки на 4. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Теперь выполняем обратный ход Гаусса снизу вверх. Прибавляем ко второй строке третью строку. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & 0 & | & 10 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Сразу замечаем, что вторую строку можно сократить на 5. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Продолжаем обратный ход, вычитаем третью строку из первой. $$begin{pmatrix} 1 & 2 & 0 & | & 3 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Осталось из первой строки вычесть вторую строку, умноженную на 2, для того, чтобы в первой строке появился ноль. $$begin{pmatrix} 1 & 0 & 0 & | & -1 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Теперь перепишем получившуюся матрицу в виде системы уравнений, чтобы в дальнейшем получить чему равны неизвестные $x_1, x_2, x_3$. $$begin{cases} x_1 = -1 \ x_2 = 2 \ x_3 = 2 end{cases}$$
Ответ
$$x_1 = -1, x_2 = 2, x_3 = 2$$
 

Пример 2
Решить систему линейных алгебраических уравнений методом Гаусса $$begin{cases} 2x_1 + 5 x_2 + 4x_3 + x_4 = 20 \ x_1 + 3 x_2 + 2x_3 +x_4 = 11 \ 2x_1 +10 x_2 + 9 x_3 + 7x_4 = 40 \ 3x_1 + 8x_2 + 9x_3 + 2x_4 = 37 end{cases}. $$
Решение

Записываем расширенную матрицу $$ begin{pmatrix} 2&5&4&1&|&20 \ 1&3&2&1&|&11 \ 2&10&9&7&|&40 \ 3&8&9&2&|&37 end{pmatrix}.$$

Умножаем вторую строку на 2 и вычитаем из неё первую строчку. Из третьей строки просто вычитаем первую. Умножаем четвертую строку на 2 и вычитаем из неё первую строку, умноженную на 3. Получаем матрицу $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&5&5&6&|&20 \ 0&1&6&1&|&14 end{pmatrix}.$$

Берем вторую строку, умноженную на 5 и вычитаем из третьей. Затем вторую строку вычитаем из четвертой. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&6&0&|&12 end{pmatrix}$$

Теперь умножаем третью строку на 6 и вычитаем её из четвертой строки, умноженной на 5. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&-6&|&0 end{pmatrix}$$

Получили нижнетреугольную матрицу, то есть ниже главной диагонали расположены нули. Теперь проделываем элементарные преобразования снизу вверх, так называемый обратный ход Гаусса. Но прежде замечаем, что появилась строка, в которой можно выполнить сокращение. А именно в четвертой строке можно разделить все числа на (-6). И получаем $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Вот теперь вычитаем четвертую строчку из третьей, второй и первой. $$begin{pmatrix} 2&5&4&0&|&20 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Из второй строки мы не будем вычить третью, потому что там итак стоит ноль, ради которого мы проводим элементарные преобразования, поэтому пропускаем этот шаг. 

Умножаем на 4 третью строку и вычитаем её из первой, умноженной на 5. $$begin{pmatrix} 10&25&0&0&|&60 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Замечаем, что в первой строке можно все числа сократить на 5. $$begin{pmatrix} 2&5&0&0&|&12 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Теперь остался последний шаг это умножить вторую строку на 5 и вычесть из первой. $$begin{pmatrix} 2&0&0&0&|&2 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Замечаем, что первую строку можно сократить на 2, а третью строку на 5. $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix}$$

Переписываем матрицу в виде привычной системы уравнений и получаем ответ $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix} sim begin{cases} x_1 = 1 \ x_2 = 2 \ x_3 = 2 \ x_4 = 0 end{cases}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$x_1 = 1, x_2 = 2, x_3 = 2, x_4 = 0$$

Несовместность системы (нет решений)

Если в результате элементарных преобразований появилась нулевая строка вида $$begin{pmatrix} 0&0&0&|&b end{pmatrix} text{ где } b neq 0,$$то система уравнений не имеет решений. На этом алгоритм Гаусса заканчивает свою работу и можно записывать ответ, что система несовместна, то есть нет решений. 

Пример 3
Найти решение системы линейных уравнений методом Гаусса $$begin{cases} 7x_1 – 2x_2 – x_3 = 2 \ 6x_1 – 4x_2 – 5x_3 = 3 \ x_1 + 2x_2 + 4x_3 = 5 end{cases}.$$
Решение

Как обычно пишем расширенную матрицу по коэффициентам при неизвестных переменных и столбцу свободных членов $$begin{pmatrix} 7&-2&-1&|&2 \ 6&-4&-5&|&3 \ 1&2&4&|&5 end{pmatrix}.$$

Запускаем алгоритм Гаусса. Идём сверху вниз. Умножаем вторую строку на 7 и вычитаем из неё первую строчку умноженную на 6. Затем первую строку вичитаем из третьей, умноженной на 7. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&16&29&|&33 end{pmatrix}$$

Далее по алгоритму прибавляем вторую строку к третьей. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&0&0&|&42 end{pmatrix}$$

Видим, что в результате элементарных преобразований появилась строка в которой все нули, кроме свободного члена. Это означает, что система несовместа, то есть у системы уравнений нет решения.
Ответ
Нет решений, так как система несовместна.

Общее и частное решение системы (бесконечное множество решений) 

Часто после элементарных преобразований в расширенной матрице появляются нулевые строки вида $$begin{pmatrix} 0&0&0&|&0 end{pmatrix}.$$ Такую строку нужно вычеркивать из матрицы и система уравнений будет иметь бесконечное множество решений. Разберем это на практике.

Пример 4
Найти общее и два частных решения системы линейных алгебраических уравнений методом Гаусса $$begin{cases} x_1+x_2-x_3=4 \ 3x_1+2x_2-5x_3=7 \ 3x_1+x_2-7x_3=2 end{cases}.$$
Решение

Составляем расширенную матрицу $$begin{pmatrix} 1&1&-1&|&4 \ 3&2&-5&|&7 \ 3&1&-7&|&2 end{pmatrix}.$$

Из второй и третьей строки вычетаем первую, умноженную на 3. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&-2&-4&|&-10 end{pmatrix}$$

Из третьей строки вычитаем вторую, домноженную на 2. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$

Теперь согласно обратному ходу Гаусса вторую строку прибавляем к первой. $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$

По окочанию элементарных преобразований получилась строка, в которой все элементы равны нулю. Значит, система имеет бесконечное множество решений. Для его записи понадобится отличать базисные и свободные переменные. Обычно за базисные берут переменные, которые стоят на главной диагонали, а остальные свободные. В нашем случае базисными будут $x_1, x_2$, а свободной $x_3$.

Переписываем матрицу в виде системы $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix} sim begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases}.$$

Так как $x_1, x_2$ являются базисными переменными, то их переносим в левую часть равенства, а всё остальное в правую часть. Получившееся называют общим решением решением системы уравнений $$begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases} sim begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$

Чтобы получить частное решение системы уравнений нужно вместо свободного $x_3$ подставить любое число, например $x_3 = 0$. Тогда получаем, что $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}.$$ Возьмем ещё например $x_3 = 1$ и получаем $$begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$

Можно брать различные числа вместо $x_3$ и получать бесконечное множество решений.
Ответ

Общее решение системы уравнений $$begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$

Частные решения системы уравнений $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}, begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$
Источник

Пусть
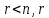переменных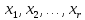называются основными (или базисными),
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальныепеременных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний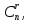то
и базисных решений имеется не более

Совместная
система
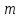линейных уравнений с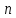переменными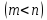имеет
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее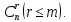

Достоинства
метода Гаусса по сравнению с другими:

–
менее трудоемкий метод;

–
позволяет однозначно установить,
совместна система или нет и в случае
совместности найти ее решение;

–
дает возможность найти максимальное
число линейно независимых уравнений –
ранг матрицы системы.

Рассмотрим
пример. Найти
решение системы линейных алгебраических
уравнений

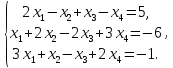
Составим
расширенную матрицу по данной системе

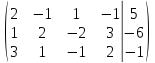
поменяем
местами первую и вторую строку

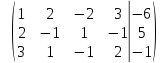
умножим
первую строку на
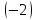и сложим со второй строкой; умножим
первую строку наи сложим с третьей строкой

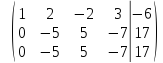
умножим
вторую строку на
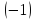и сложим с третьей строкой

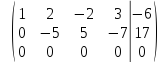
последняя
строка вычеркивается, так как все ее
элементы равны нулю

Ранг
основной матрицы
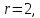ранг
расширенной матрицы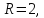следовательно, система совместна. Число
строк в основной матрице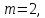число
столбцов в основной матрице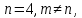следовательно, система имеет множество
решений.

Выявим
базисные переменные

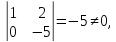
следовательно,
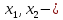базисные
переменные, тогда

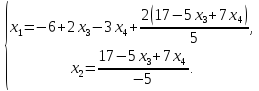
3.4. Однородные системы линейных алгебраических уравнений

Система
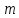линейных уравнений с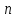переменными называетсясистемой
линейных однородных уравнений,
если все их свободные члены равны нулю.

Системы
линейных однородных уравнений:

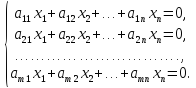
Система
линейных однородных уравнений всегда
совместна, так как имеет, по крайней
мере, нулевое решение

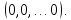
Если
в однородной системе
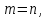а
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.

Система
линейных однородных уравнений имеет
ненулевое решение тогда и только тогда,
когда ранг ее матрицы коэффициентов
при переменных меньше числа переменных,
т.е. при

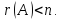
Рассмотрим
пример. Найти
решение системы линейных алгебраических
уравнений

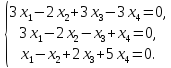
Составим
по данной системе расширенную матрицу

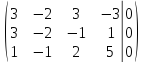
поменяем
местами первую и третью строки

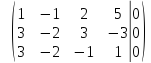
умножим
первую строку на
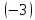и сложим со второй строкой, а затем с
третьей строкой, получим

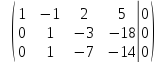
умножим
вторую строку на
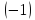и сложим с третьей строкой

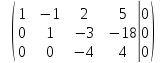
разделим
последнюю строку на

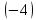
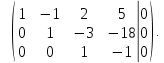
Таким
образом, ранг расширенной матрицы и
ранг основной матрицы равны
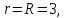следовательно,
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные

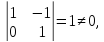
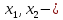базисные
переменные.

Перейдем
от матрицы к системе, выразим переменные
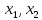через другие переменные

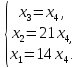
Контрольные
вопросы

  1. Сформулировать
    теорему Кронекера
    – Капелли.

  2. Сформулировать
    Метод Гаусса решения систем m
    линейных
    уравнений с n
    неизвестными.

  3. Дать
    определение базисному решению систем
    линейных алгебраических уравнений.

  4. Какие
    системы линейных алгебраических
    уравнений называют однородными?

Лекция
№4. Векторы

4.1.
Векторы в науке и технике. Понятие
вектора. Координаты вектора.

4.2.
Линейные операции над векторами.

4.3.
Декартова система координат. Базис
векторного пространства.

4.4.
Скалярное произведение векторов,
основные свойства и выражение в
координатной форме.

4.5.
Векторное произведение векторов.
Основные свойства векторного произведения
векторов и выражение в координатной
форме.

4.6.
Применение векторного произведения
векторов к решению задач.

4.7.
Смешанное произведение векторов.
Основные свойства смешанного произведения
векторов и выражение в координатной
форме.

4.8.
Применение смешанного произведения
векторов к решению задач.

    1. Векторы
      в науке и технике. Понятие вектора.
      Координаты вектора

В
физике и математике вектор – это
величина, которая характеризуется
численным значением и направлением. В
физике встречается немало важных
величин, которые характеризуются
направлением. Например, сила, скорость,
ускорение, вращающий момент, импульс,
напряженность электрического и магнитного
полей. Их можно противопоставить другим
величинам, таким как масса, объем,
давление, температура, плотность, которые
можно описать обычным числом и называются
они скалярными величинами.

Векторная
запись используется при работе с
величинами, которые невозможно задать
полностью с помощью обычных чисел.
Например, необходимо описать положение
предмета, но полностью определить
местоположение предмета невозможно,
пока не будет известно направление, в
котором он находится. Таким образом,
местонахождение предмета характеризуется
численным значением (расстоянием в
километрах) и направлением.

При
изучении и расчете цепей переменного
тока удобно пользо­ваться векторными
диаграммами, на которых синусоидальные
напряжения и токи условно изображают
с помощью векто­ров. Применение этих
диаграмм упрощает изучение и расчет
цепей и вносит наглядность в рассматриваемые
соотношения.

Вектором
на плоскости называется
направленный отрезок

с начальной точкой
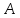и конечной точкой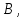который
можно перемещать параллельно самому
себе.

Рис.
1

Вектор
на плоскости

От
любой точки можно отложить вектор,
равный данному, и притом только один,
используя параллельный перенос. При
параллельном переносе точки смещаются
по параллельным или совпадающим прямым
на одно и тоже расстояние.

Нулевой
вектор – точка
в пространстве. Начало и конец нулевого
вектора совпадают, и он не имеет длины
и направления.

Абсолютной
величиной или модулем вектора называется
длина отрезка, изображающего вектор.
Другими словами длина
вектора есть
расстояние между началом и концом
вектора

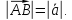
Векторы
называются коллинеарными,
если они
расположены на одной или на параллельных
прямых. Нулевой вектор коллинеарен
любому вектору. Если векторы
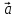и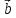коллинеарны и их лучи сонаправлены, то
векторы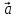и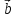называютсонаправленными.
Обозначают
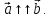Если векторы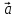иколлинеарны,
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают
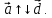Нулевой вектор условились считать
сонаправленным с любым вектором.

Рис.2

Коллинеарные
вектора

Свойство
коллинеарных векторов.

Если
векторы
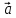и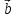коллинеарны и,
то существует число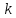такое,
что.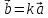
Причем, если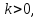то векторы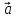и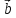сонаправленные, если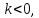то
противоположно направленные.

Векторы
называются компланарными,
если при
откладывании их от одной и той же точки
они будут лежать в одной плоскости.
Любые два вектора компланарны. Коллинеарные
векторы всегда компланарны, но не все
компланарные векторы коллинеарны.

Признак
компланарности трех векторов.

Если
вектор
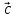можно разложить по векторам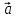и,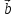
т.е. представить в виде,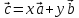
где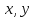-некоторые
числа, то векторы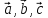-компланарны.

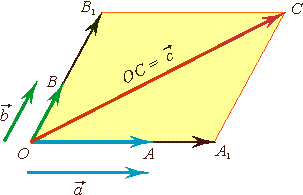
Рис.3

Компланарные
вектора

,
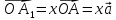где
;

,
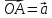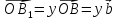где

,
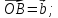
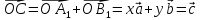где

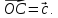
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Система линейных уравнений. Общее решение

Система линейных уравнений (СЛУ) может быть записана в виде

 (1)

где m, n натуральные числа, aij (i=1,2, …m, j=1,2,…n) называются коэффициентами, bi (i=1,2,…m) называются свободными членами, xi (i=1,2,…n) называются неизвестными.

Систему линейных уравнений (1) можно записать в виде

где A матрица порядка m×n , x – вектор порядка n (x∈Rn), b – вектор порядка m (b∈Rm).

Решением системы (2) называется выбор такого вектора x’, что выполнено равенство

Ax’≡b.

Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.

Если СЛУ не имеет решения, то СЛУ называется несовместным.

Если СЛУ имеет единственное решение, то СЛУ называется определенным.

Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.

 Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.

Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.

Нахождение общего решения системы линейных уравнений

Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.

Пусть A m×n – матрица rankA=r. В общем случае можем предположить что r<n, r<m. Тогда r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Запишем систему (2) в блочном виде:

 (3)

где M – r×r – матрица, Q -m-r×r – матрица, F – n-r×r – матрица, P – m-r×n-r – матрица, .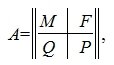

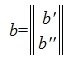Применяя метод исключения Гаусса для системы (3), получим:

 (4)

где M1 верхняя треугольная матрица, 0 – нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

 (5)

где E – единичная матрица порядка r×r.

Запишем (5) в виде системы линейных уравнений:

 (6)

где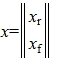

Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:

 (7)

Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b2”≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора xr:

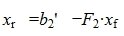(8)

Таким образом первые r координаты вектора x 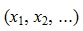выражены через остальные координаты 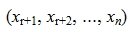. 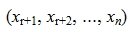– свободные координаты, т.е. могут принимать любые значения.

Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).

Рассмотрим множество всех векторов х, удовлетворяющих условию

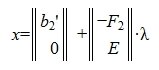(9)

где λ – произвольный вектор-столбец длины n-r.

Подставляя (9) в (6) получим:

Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор 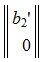является частным решением неоднородной системы линейных уравнений Ax=b, а 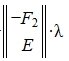является общим решением однородной системы линейных уравнений Ax=0;

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы

Обозначим через R(A) пространство столбцов матрицы A, т.е.

R(A)={z: z=Ax, ∀x∈Rn}.

1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A-1, и следовательно единственное решение СЛУ (2) примет вид:

x’=A−1b.

(10)

Действительно, подставляя (3) в (2) имеем:

Ax’=AA−1b=Eb=b,

где E − единичная матрица.

2. Пусть A m×n − матрица, rank(A)=r.

Вычислим следующий вектор:

x’=A+b.

(11)

где A+ – псевдообратная к A матрица.

Подставляя (11) в (2), имеем:

AA+b=b.

(12)

Из равенства (12) следует, что для того, чтобы система линейных уравнений (2) имела решение, должно выполняться условие

b∈R(A).

Если СЛУ совместна, т.е. если AA+b=b, то x’=A+b является решением СЛУ (2).

Общее решение системы линейных уравнений является суммой частного решения неоднородной системы линейных уравнений и множества всех решений соответствующей однородной системы линейных уравнений.

Общее решение системы линейных уравнений (2) имеет следующий вид:

x=x*+(E−A+A)z, ∀z∈Rn. (13)

где x* – один из решений неоднородной системы (2) (например (4)), (E−A+A) образует ядро (нуль пространство) матрицы A.

Сделаем скелетное разложение матрицы (E−A+A):

E−A+A=Q·S

где Q n×n−r – матрица rank(Q)=n−r, S n−r×n-матрица rank(S)=n−r.

Тогда (13) можно записать в следующем виде:

x=x*+Q·k,   ∀k∈Rn-r.

где k=Sz.

Итак, процедура нахождения общего решения системы линейных уравнений с помощью псевдообратной матрицы можно представить в следующем виде:

  1. Вычисляем псевдообратную матрицу A+.
  2. Вычисляем частное решение неоднородной системы линейных уравнений (2): x*=A+b.
  3. Проверяем совместность системы. Для этого вычисляем AA+b. Если AA+b≠b, то система несовместна. В противном случае продолжаем процедуру.
  4. Высисляем E−A+A.
  5. Делаем скелетное разложение E−A+A=Q·S.
  6. Строим решение

x=x*+Q·k,   ∀k∈Rn-r.

Решение системы линейных уравнений онлайн

Онлайн калькулятор позволяет найти обшее решение системы линейных уравнений с подробными объяснениями.

Источник

Структура общего решения системы уравнений

Однородная система линейных уравнений

begin{cases}a_{11}x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+a_{22}x_2+ldots+ a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{m1}x_1+a_{m2}x_2+ldots+a_{mn}x_n=0,end{cases} или Ax=o

всегда совместна, так как имеет тривиальное решение x_1=x_2=ldots=x_n=0~(x=o). Если ранг матрицы системы равен количеству неизвестных (operatorname{rg}A=n), то тривиальное решение единственное. Предположим, что r=operatorname{rg}A&lt;n. Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица (Amid o) однородной системы при элементарных преобразованиях строк приводится к упрощенному виду (A'mid o), т.е. b'_1=b'_2=ldots=b'_r=0. Поэтому из (5.11) получаем общее решение однородной системы уравнений:

begin{cases}x_1=-a'_{1,r+1}x_{r+1}-ldots-a'_{1n}x_n,\phantom{ x_1=-a'_{1,r+1}}vdots\ x_r=-a'_{r,r+1}x_{r+1}-ldots-a'_{rn}x_n.end{cases}

(5.13)

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы varphi_1,varphi_2,ldots,varphi_k — решения однородной системы уравнений, то любая их линейная комбинация alpha_1varphi_1+alpha_2varphi_2+ ldots+alpha_kvarphi_k также является решением однородной системы.

В самом деле, из равенств Avarphi_1=o,~ Avarphi_2=o,~ldots,~ Avarphi_k=o следует, что

Acdot! begin{pmatrix}alpha_1cdotvarphi_1+ alpha_2cdotvarphi_2+ ldots+alpha_kcdotvarphi_k end{pmatrix}= alpha_1cdot Acdotvarphi_1+ alpha_2cdot Acdotvarphi_2+ ldots+alpha_kcdot Acdotvarphi_k=o,

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен r, то система имеет (n-r) линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем (n-r) частных решений varphi_1,varphi_2,ldots,varphi_{n-r}, придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

begin{aligned} mathsf{1)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=0colon~~ varphi_1= begin{pmatrix}-a'_{1,r+1}&cdots&-a'_{r,r+1}&1&0&cdots&0end{pmatrix}^T;\[5pt] mathsf{2)}&quad x_{r+1}=0,~x_{r+2}=1,~ldots,~x_n=0colon~~ varphi_2= begin{pmatrix}-a'_{1,r+2}&cdots&-a'_{r,r+2}&0&1&cdots&0end{pmatrix}^T;\[5pt] mathsf{n-r)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=1colon~~ varphi_{n-r}= begin{pmatrix}-a'_{1n}&cdots&-a'_{rn}&0&0&cdots&1end{pmatrix}^T. end{aligned}

Получим (n-r) решений

varphi_1= begin{pmatrix}-a'_{1,r+1}\vdots\-a'_{r,r+1}\1\0\vdots\0end{pmatrix}!,quad varphi_2= begin{pmatrix}-a'_{1,r+2}\vdots\-a'_{r,r+2}\0\1\vdots\0end{pmatrix}!,quad ldots,quad varphi_{n-r}= begin{pmatrix}-a'_{1n}\vdots\-a'_{rn}\0\0\vdots\1end{pmatrix}!.

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние (n-r) ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних (n-r) строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен (n-r). Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность (n-r) линейно независимых решений varphi_1,varphi_2,ldots,varphi_{n-r} однородной системы называется фундаментальной системой (совокупностью) решений.

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества (n-r) линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если varphi_1,varphi_2,ldots,varphi_{n-r} — фундаментальная система решений однородной системы уравнений (5.4), то столбец

x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}

(5.14)

при любых значениях произвольных постоянных C_1,C_2,ldots,C_{n-r} также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных C_{1},C_{2},ldots,C_{n-r}, при которых это решение x удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение x можно представить в виде (5.14). Для этого составим матрицу H, приписав к столбцам фундаментальной системы решений столбец x:

H=begin{pmatrix}varphi_1&cdots&varphi_{n-r}&xend{pmatrix}= begin{pmatrix}varphi_{11}&cdots&varphi_{1,n-r}&x_1\ vdots&ddots&vdots&vdots\ varphi_{r1}&cdots&varphi_{r,n-r}&x_r\ varphi_{r+11}&cdots&varphi_{r+1,n-r}&x_{r+1}\ vdots&ddots&vdots&vdots\ varphi_{n1}&cdots&varphi_{n,n-r}&x_n end{pmatrix}!.

Найдем ранг этой матрицы. Так как первые (n-r) столбцов линейно независимы, то operatorname{rg}Hgeqslant n-r. Так как каждый из столбцов матрицы H является решением системы A'x=o, то по первой формуле из (5.13) получаем

begin{aligned} varphi_{11}&= -a'_{1,r+1}varphi_{r+11}-ldots- a'_{1n}varphi_{n1},\ cdots & cdotscdotscdotscdots\[2pt] varphi_{1,n-r}&= -a'_{1,r+1}varphi_{r+1,n-r}-ldots- a'_{1n}varphi_{n,n-r},\[2pt] x_1&= -a'_{1,r+1}x_{r+1}-ldots- a'_{1n}x_n. end{aligned}

Следовательно, первая строка матрицы H является линейной комбинацией последних (n-r) строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы H является линейной комбинацией последних (n-r) строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы H является линейной комбинацией последних (n-r) строк этой матрицы. Значит, первые r строк матрицы H можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, operatorname{rg}Hleqslant n-r, так как после вычеркивания в матрице H будет всего (n-r) строк. Таким образом, operatorname{rg}H=n-r. Значит, есть базисный минор матрицы H, который расположен в первых (n-r) ее столбцах, а столбец x не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа C_1,C_2,ldots,C_{n-r}, что

x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}.

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг r матрицы системы равен числу n неизвестных (r=operatorname{rg}A=n), то система имеет единственное тривиальное решение x-o и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных (operatorname{rg}A&lt;n), то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему varphi_1, varphi_2, ldots,varphi_{n-r} решений однородной системы. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

Замечания 5.3

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица Phi=begin{pmatrix}varphi_1&varphi_2&cdots&varphi_{n-r} end{pmatrix} столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

x=Phicdot c, где c=begin{pmatrix}C_1&cdots&C_{n-r} end{pmatrix}^T — столбец произвольных постоянных.

3. Если базисный минор матрицы A расположен в левом верхнем углу (в первых r строках и первых r столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&0\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&0\ 0&0&cdots&0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix} E_r!!&vline!!&A'_{rtimes(n-r)}!!&vline!!&o\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.

Тогда блочная матрица Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix} размеров ntimes(n-r) является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

begin{cases}x_1+x_2+2x_3+x_4=0,\[2pt] 2x_1+3x_2+x_4=0,\[2pt] 3x_1+4x_2+2x_3+2x_4=0. end{cases}

Решение. 1. Составляем расширенную матрицу системы

begin{pmatrix}Amid oend{pmatrix}= begin{pmatrix} 1&1&2&1!!&vline!!&0\ 2&3&0&1!!&vline!!&0\ 3&4&2&2!!&vline!!&0 end{pmatrix}!.

2-4. Используя элементарные преобразования над строками матрицы (Amid o), приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

begin{pmatrix}A'mid oend{pmatrix}= begin{pmatrix} 1&0&6&2!!&vline!!&0\ 0&1&-4&-1!!&vline!!&0\ 0&0&0&0!!&vline!!&0 end{pmatrix}!.

Пункт 3 метода Гаусса пропускаем.

5. Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные. Записываем формулу (5.13) общего решения однородной системы

begin{cases}x_1=-6x_3-2x_4,\x_2=4x_3+x_4.end{cases}

6. Находим фундаментальную систему решений. Так как n=4 и r=operatorname{rg}A=2, надо подобрать n-r=2 линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

1) если x_3=1,~x_4=0, то x_1=-6,~x_2=4;

2) если x_3=0,~x_4=1, то x_1=-2,~x_2=1.

В результате получили фундаментальную систему решений

varphi_1=begin{pmatrix}-6\4\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-2\1\0\1end{pmatrix}!.

7. Записываем общее решение однородной системы по формуле (5.14):

x=C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot!begin{pmatrix}-2\1\0\1end{pmatrix}!.

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, x_3=1,~x_4=2 и x_3=2,~x_4=3. Тогда получим другую фундаментальную систему решений

varphi_1=begin{pmatrix}-10\6\1\2end{pmatrix}!,quad varphi_2=begin{pmatrix}-18\11\2\3end{pmatrix} и общее решение системы x=C_1cdot! begin{pmatrix}-10\6\1\2end{pmatrix}+ C_2cdot! begin{pmatrix}-18\11\2\3end{pmatrix}!.

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему Ax=b и соответствующую ей однородную систему Ax=o. Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений x и y неоднородной системы есть решение однородной системы.

Действительно, из равенств Ax=b и Ay=b следует, что A(x-y)=Ax-Ay=b-b=o.

2. Пусть x^H — решение неоднородной системы. Тогда любое решение x неоднородной системы можно представить в виде

x=x^H+x^O, где x^O — решение однородной системы.

В самом деле, для любого решения x неоднородной системы разность x-x^H по свойству 1 является решением однородной системы, т.е. x^O=x-x^H — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть x^H — решение неоднородной системы, а varphi_1,varphi_2,ldots,varphi_{n-r} — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

x=x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2+ldots+ C_{n-r}cdotvarphi_{n-r}

(5.15)

при любых значениях [i]произвольных постоянных C_1,C_2,ldots,C_{n-r} является решением неоднородной системы, и, наоборот, для каждого решения x этой системы найдутся такие значения произвольных постоянных C_1,C_2,ldots,C_{n-r}, при которых это решение x удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение x^H неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему varphi_1,varphi_2,ldots,varphi_{n-r} ее решений. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

Замечания 5.4

1. Используя фундаментальную матрицу Phi однородной системы Ax=o, решение неоднородной системы Ax=b можно представить в виде

x=x^H+Phicdot c,

где x^H — частное решение неоднородной системы, а c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T — столбец произвольных постоянных.

2. Если базисный минор матрицы A расположен в левом верхнем углу (в первых r строках и первых r столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&b'_1\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&b'_2\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&b'_r\ 0&0&cdots& 0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots& vdots&ddots& vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix}E_r!!& vline!!&A'_{rtimes(n-r)}!!&vline!!&b'_{rtimes1}\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.

Тогда блочная матрица Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix} оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец x^H=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix} является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

x=x^H+Phicdot c=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}+begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}!cdot c,

(5.16)

где c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

begin{cases}x_1+ x_2+2x_3+x_4=1,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=1.end{cases}

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

begin{cases}x_1=3-6x_3-2x_4,\x_2=-2+4x_3+x_4.end{cases}

Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные.

6. Полагая x_3=0,~x_4=0, получаем частное решение неоднородной системы x^H=begin{pmatrix}3&-2&0&0end{pmatrix}^T.

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

varphi_1=begin{pmatrix}-6&4&1&0end{pmatrix}^T,qquad varphi_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T.

8. Записываем по формуле (5.15) общее решение неоднородной системы

x=x^H+C_1cdotvarphi_1+C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

begin{pmatrix}Amid bend{pmatrix}= begin{pmatrix}1&0&6&2!!&vline!!&3\ 0&1&-4&-1!!&vline!!&-2\ 0&0&0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} 1&0!!& vline!!&6&2!!&vline!!&3\ 0&1!!&vline!!&-4&-1!!&vline!!&-2\hline 0&0!!&vline!!& 0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} E_2!!&vline!!&A'_{2times2}!!& vline!!& b'_{2times1}\ O!!&vline!!&O!!&vline!!&o end{pmatrix}!.

Записываем частное решение неоднородной системы

x^H= begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}= begin{pmatrix}dfrac{b'_{2times1}}{o_{2times1}}end{pmatrix}= begin{pmatrix}3\-2\0\0 end{pmatrix}

и составляем фундаментальную матрицу:

Phi= begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}= begin{pmatrix}dfrac{-A'_{2times2}}{E_2}end{pmatrix}= begin{pmatrix}-6&-2\4&1\1&0\ 0&1end{pmatrix}= begin{pmatrix}varphi_1&varphi_2end{pmatrix}!.

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

x=x^H+Phicdot! begin{pmatrix}C_1\C_2end{pmatrix}= x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0 end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.

которое совпадает с ранее полученным.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Добавить комментарий