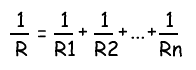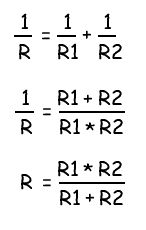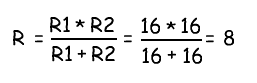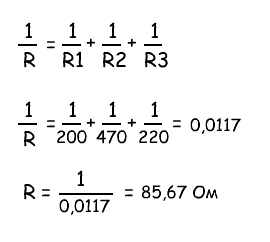В статье подробно рассмотрим, как параллельно соединять резисторы и научимся легко считать сопротивление тока в электрической цепи и узнаем, для чего вообще нужно параллельное соединение резисторов.
Понятие и определение
Параллельное соединение резисторов имеет некоторый принцип, согласно которому, выводы одного изделия подключены и работают с аналогичными выводами другого. Создаются подобные решения, чтобы специально формировать более трудные по своему составу и компоновке схемы.
Что ещё нужно учитывать
Параллельное соединение определяет принцип, согласно которому величина, установленная обратной общему показателю цепи, будет равна непосредственно сумме величин, обратных значению включённых проводников. Такая же ситуация будет отмечена при значительно большем количестве проводниковых элементов.
Особенности включения
Параллельное соединение резисторов предусматривает, что показатель напряжения везде будет одинаковым, но ток фиксируется пропорциональным.
Отличия от иных вариантов подключения
В данной схеме, исключается подключение к источнику различных наименований реактивных компонентов. Исключаются проблемные процессы колебания, сопряжённые ранее с фиксируемыми циклами смены уровня получения энергии в контексте подачи нагрузки.
Формула
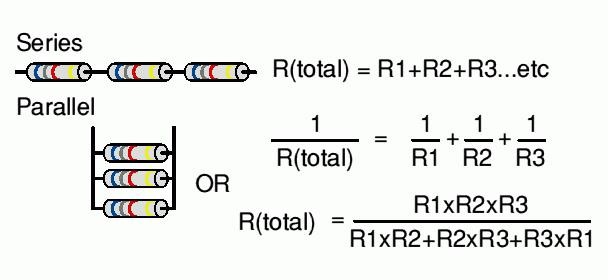
Формула, согласно которой проводится расчёт и составляется схема резисторов в параллельном соединении:
[ 1/Rобщ=1/R1+1/R2 ]
[ Rобщ=1/(1/R1+1/R2) ]
[ Rобщ=(R1*R2)/(R1+R2) ]
Онлайн-калькулятор расчета параллельного соединения резисторов
Как выполняется расчёт
Проводя расчёт сопротивления для рассматриваемого соединения резисторов, нужно учесть факт, общий параметр всегда будет несколько ниже, нежели параметр наименьшего в приведённом сочетании.
Пример №1
Потребуется включить резистор, имеющий сопротивление 8 Ом. Рассматривая номенклатуру изделий, отмечаем, резистор с подобным параметром в базовых наименованиях отсутствует. Необходимо использовать параллельную схему. В дальнейшем, расчёт выполняется:
[ 1/R=1/R1+1/R2 ]
[ 1/R=(R1+R2)/(R1*R2) ]
[ R=(R1*R2)/(R1+R2) ]
В данном случае можно увидеть, что если оба значения равны между собой, то итог будет соответствовать половине одного из используемых двух резисторов. Если ставится задача подобрать сопротивление 8 Ом, то значение 2*8=16 Ом.
[ R=(R1*R2)/(R1+R2)=(16*16)/(16+16)=8 ]
Таким образом, чтобы получить значение равное 8 Ом, соединяем два резистора по 16 Ом параллельно.
Пример расчёта №2
Есть три элемента: R1=200, R2=470, R=220
Общее значение выводится по формуле:
[ 1/R=1/R1+1/R2/1/R3 ]
[ 1/R=1/200+1/470+1/220=0,0117 ]
[ R=1/0,0117=85,67 Ом ]
Данный метод без проблем актуален для выполнения расчёта практически любой численности включённых в конструкцию элементов.
Ток в цепи параллельно соединенных резисторов
При параллельном соединении отмечается, что ток, приравнивается сумме из отдельных составляющих. Показатель в каждом ответвлении, не фиксируется идентичным значению в соседних ответвлениях. К отдельному резистору прикладывается идентичное напряжение.
Сила тока
Актуально выполнить расчёт для всех ветвей. Общий показатель силы тока составляет 8А, тогда предстоит распределить напряжения, показатель замеряется на отдельно рассмотренных участках.
[ U12=I*Rэкв1=0,8*((2*4)/(2+4))=0,8*1,3=1,04 V ]
[ I1=U12/R1=0,52 А ]
[ I2=U12/R2=0,26 А ]
Корректность выполненных вычислений определяется:
[ I=I1+I2=0,52+0,26≈0,8 А ]
Мощность
Для корректного выбора резисторов учитывается и мощность рассеивания. Данный показатель можно рассчитывать так:
[ P=U*I ]
U — напряжение, В
I — сила тока, А
Показатель косвенным образом определяет некоторое количество энергии, она будет потребляться на выделение тепла.
Как найти сопротивление
Определение сопротивления выполняется по формулам:
[ 1/G ]
[ U/I ]
[ U2/P ]
[ P/I2 ]
Выбор параллельного подключения резисторов определяется с учётом входных параметров. Стоит только помнить о том, что показатель напряжения и уровень тока в отдельных ответвлениях идентичны.
Примеры применения при параллельном соединении
Конструктивно, каждый резистор рассчитан на некоторый рабочий диапазон температурного воздействия. Увеличение порога вызовет разрушение места пайки, соединения, самой детали, даже расположенных соседних блоков. Стоит помнить, что существуют одновременные соединения резисторов, приведённая компоновка способна нарушить функциональность и исправное состояние.
Благодаря использованию автоматических схем определения рабочих показателей можно переставлять резисторы, устанавливать в конкретном месте различные светодиоды, корректировать уровень сигнала на выходе.
Видео
Главная » Справочник » Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Калькулятор параллельных сопротивлений
Параллельные (как и последовательные) схемы соединения резисторов, часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет и его необходимо подобрать.
Req
Эквивалентное сопротивление Req параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
Эквивалентное сопротивление группы параллельно соединенных резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе ,а добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Расчет сопротивления
Расчет эквивалентного сопротивления
Расчет при известном эквивалентном значении
Для расчета введите данные сопротивления резисторов и добавьте необходимое количество (max 8 шт.).
Для расчета введите данные эквивалентного сопротивления и одного из резисторов.
Поиск резистора на сайте
Для подбора резистора укажите необходимое напряжение
Внимание! Производители объединяют резисторы в серии или ряды: E6, E12, E24…
Для подбора компонента будет использована серия E24.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.
Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.
Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
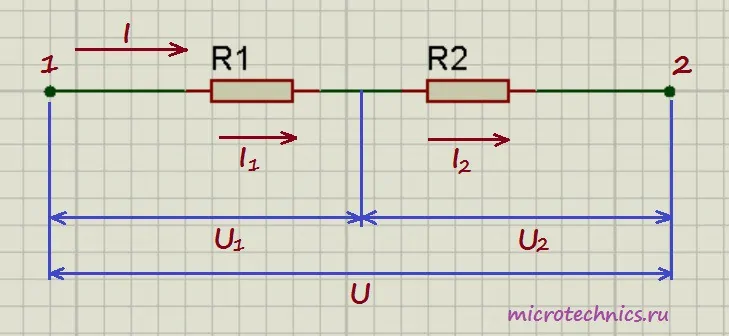
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжения также справедлив закон Ома:
Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например, для следующей цепи:
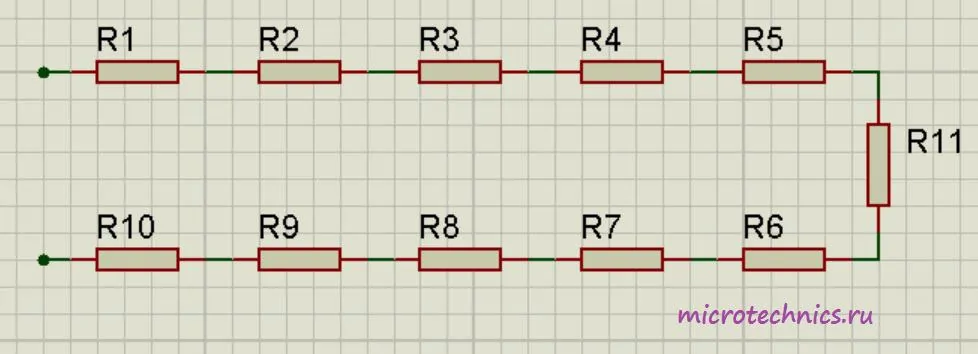
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:
В данной формуле n равно количеству элементов. С последовательным соединением резисторов разобрались, логичным образом переходим к параллельному.
Параллельное соединение резисторов.
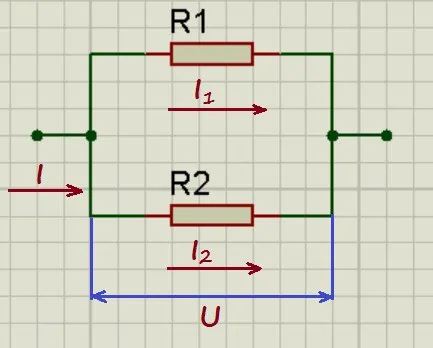
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
I_1 = frac{U_1}{R_1} = frac{U}{R_1}
I_2 = frac{U_2}{R_2} = frac{U}{R_2}
Подставим эти выражения в формулу общего тока:
I = frac{U}{R_1} + frac{U}{R_2} = Umedspace (frac{1}{R1} + frac{1}{R2})
А по закону Ома:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2}
Данную формулу можно записать и несколько иначе:
R_0 = frac{R_1R_2}{R_1 + R_2}
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
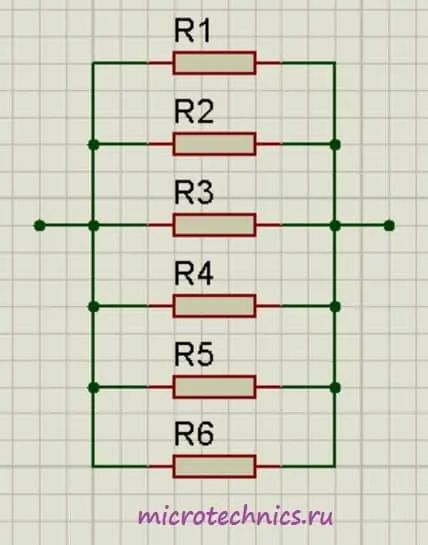
frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2} + frac{1}{R_3} + frac{1}{R_4} + frac{1}{R_5} + frac{1}{R_6}
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
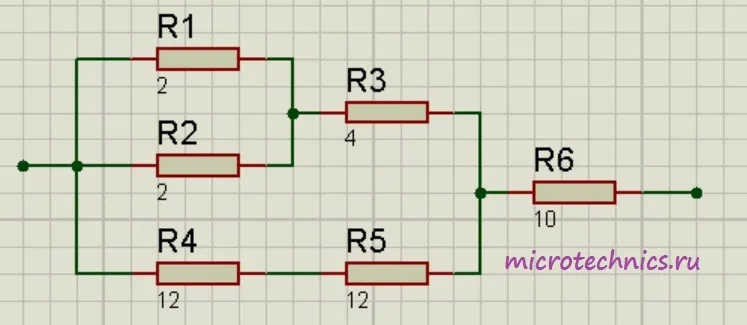
Давайте рассчитаем общее сопротивление. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:
R_{1-2} = frac{R1cdot R2}{R1 + R2} = 1
Теперь у нас образовались две группы последовательно соединенных резисторов:
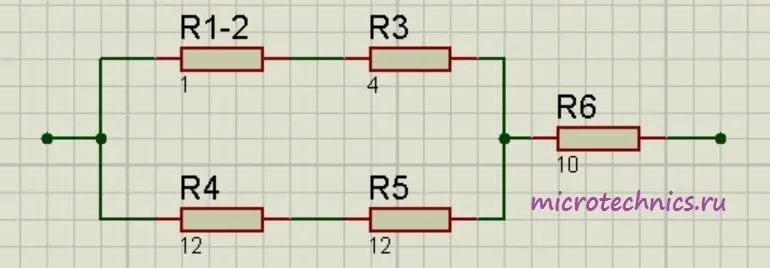
- R_{1-2} и R_3
- R_4 и R_5
Заменим эти две группы двумя резисторами, сопротивление которых равно:
R_{1-2-3} = R_{1-2} + R_3 = 5
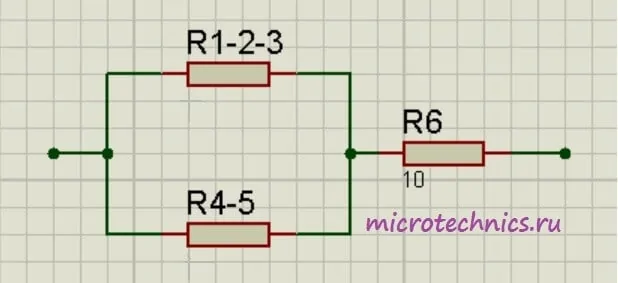
Как видите, схема стала уже совсем простой. Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:
R_{1-2-3-4-5}enspace = frac{R_{1-2-3}medspacecdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = frac{5cdot24}{5 + 24} = 4.14
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
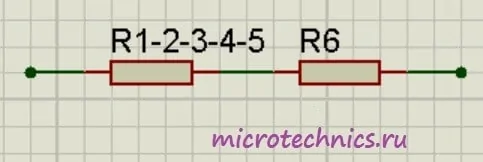
Общее сопротивление цепи получилось равным:
R_0 = R_{1-2-3-4-5}medspace +medspace R_6 = 4.14 + 10 = 14.14
Таким вот образом достаточно большая схема свелась к банальнейшему последовательному соединению двух резисторов. Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝