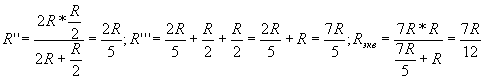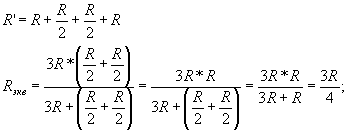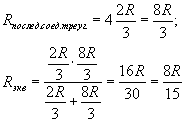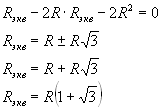Как найти общее сопротивление квадрата

Расчет сопротивлений сеток

Попались мне интересные задачки, близкие друг другу по стилю, что ли. В них нужно либо определить входное сопротивление схемы, либо потенциалы в точках. В каждой будем использовать хитрый метод на основе законов Кирхгофа. Только первые схемы простые, прозрачные, а последняя посложнее.

Задача. На рисунках изображены 4 схемы, составленные из проволок. В местах соединений проволоки спаяны. Определить: а) входное сопротивление между точками и схем 1 и 2, полагая сопротивление каждой проволоки ; б) входное сопротивление между точками и , и для схемы 3, полагая сопротивление каждой проволоки ; в) потенциалы точек схемы 4, полагая В, В. Считать сопротивление каждой проволоки для этой схемы равным 3 Ом.

Схема 1.

Рисунок 1

Схема имеет ось симметрии. Расставим токи в схеме так, чтобы симметрия сохранялась и чтобы при этом соблюдались первый и второй законы Кирхгофа. Поэтому начинать расставлять нужно от середины.

Рисунок 2

Чтобы соблюдался второй закон, расставим токи «внутри»

Рисунок 3

Теперь проследим за тем, чтобы соблюдался первый закон:

Рисунок 4

Наконец, сосчитаем входной ток:

Рисунок 5

Чтобы определить сопротивление схемы, надо пройти любым путем от точки до точки , считая по дороге падения напряжений и складывая их:

Рисунок 6

Разделим на входной (он же выходной) ток – и сопротивление схемы нам известно!

Ответ: .

Схема 2.

Рисунок 7

Схема имеет ось симметрии, поэтому действовать будем точно так же. Расставим токи в цепи, начав с середины и придерживаясь симметрии:

Рисунок 8

Чтобы соблюсти 2 закон, в центре токи будут по 1,5I:

Рисунок 9

Теперь опять следим за соблюдением первого закона Кирхгофа:

Рисунок 10

Расставляем последние и , наконец, входной:

Рисунок 11

Теперь выбираем произвольный путь от точки до точки , и «собираем» по дороге падения напряжений. Я пройду по правым ветвям:

Рисунок 12

Определяем сопротивление схемы, деля общее падение напряжения на общий (входной) ток:

Ответ: .

Схема 3. Действуем тем же манером. Расставляем токи, соблюдая симметрию и законы Кирхгофа. Через помеченные крестом ветви ток не потечет: на их концах точки, потенциалы которых равны.

Рисунок 13

Рисунок 14

Выходной ток – , сумма падений напряжений равна , сопротивление будет равно

Для определения сопротивления надо расставить токи по новой:

Рисунок 15

Теперь проходим от до , «собирая» падения напряжений:

И, чтобы найти сопротивление, делим на входной ток:

Ответ: , .

Схема 4. Здесь придется попотеть. Схема сложная, большая.

Рисунок 16

Начинаем расстановку токов с середины, причем я сделаю эти токи «четными» – просто для того, чтобы не пришлось возиться с дробями:

Рисунок 17

Так как схема, очевидно, симметрична, то точки , и другие, оказавшиеся на данной горизонтали – точки равного потенциала (учитывая данные задачи – нулевого). Поэтому в указанных перемычках ток не потечет. Также тока не будет в других помеченных крестами перемычках по тем же соображениям. Так как нужно, кроме симметрии, следить и за соблюдением законов Кирхгофа (и первого, и второго), то расстановку токов я сделала так:

Рисунок 18

Проходим любым путем, «собирая» падения напряжений:

Это напряжение равно 36 В: В.

Определим ток:

Тогда

Определяем потенциалы точек:

Ответ: B, B, B, B.

12 комментариев

Виталий
✉️
27.10.2021 05:30:01

Добрый день, поясните, пожалуйста для какого замкнутого контура рассматривается второй закон Кирхгофа в схеме 2 на этапе “Чтобы соблюсти 2 закон, в центре токи будут по 1,5I”.

Анна Валерьевна
✨
27.10.2021 05:43:46

Рыжий и синий токи в сумме – 2I, поэтому на той перемычке, где этот ток протекает (суммарный), будет создано падение напряжения 2IR. Далее рассматриваем второй ряд, квадратик слева. По левой стороне падение напряжения 3IR, значит, и по правой должно быть тоже 3IR. Отсюда ток, равный 1,5I – ведь он протекает через две перемычки сопротивлением R.

Виталий
✉️
30.10.2021 08:19:06

Спасибо за пояснение. Объясните, пожалуйста, как в 4 схеме был получен ток в 1I на горизонтальной перемычке. Если выбрать этот ток равным, например, 2I мы сможем расставить остальные токи в соответствии с двумя законами Кирхгофа, но ток на выходе будет другим, также будет отличаться суммарное падение напряжения при обходе

Анна Валерьевна
✨
30.10.2021 08:44:45

Всегда долго подбираю токи, все проверяю. Если сделать 2I, то в квадратике, диагональю которого является эта перемычка, второй закон не выполнится (в треугольнике под этой перемычкой).

АннА
✉️
09.12.2021 13:41:27

Здравствуйте, подскажите, а если в схеме на рис.2 выводы тока сделать из соседних вершин, этот метод работать не будет?

Анна Валерьевна
✨
09.12.2021 13:42:38

Почему же не будет, будет, конечно!

АннА
✉️
10.12.2021 06:15:24

Еще раз здравствуйте. Простите мою навязчивость,но очень хочется разобраться в теме!!!
У меня получились токи между соседними вершинами квадрата(где вход и выход цепи) 2i – 1i. В центре (перекрестие) 1i- 1i- 1i -1i , а между входом и выходом тока по дальним ребрам 2i-1i-1i-2i-2i-3i. Но если взять обходной ток (по ребру, кратчайшему пути между входом и выходом общее сопротивление получается 3/4, а если беру обходной ток по трем дальним ребрам, сопротивление-11/4).Что я делаю не так??? Помогите пожалуйста

АннА
✨
10.12.2021 06:21:19

Это если выводы тока в соседних вершинах

Анна Валерьевна
✨
11.12.2021 06:39:50

Присылайте полный текст задачи на почту.

Александр
✨
14.02.2022 10:29:49

Здравствуйте, а почему тогда также нельзя сказать про 3 схему 14 рисунок, верхний квадрат?

Александр
✨
14.02.2022 10:44:45

То есть почему мы не можем сказать тоже самое для верхней и нижней стороны, а говорим только для правой и левой

Анна Валерьевна
✨
16.02.2022 06:25:42

Все правильно: при обходе в любую сторону сумма падений напряжений в контуре равна нулю.

Источник

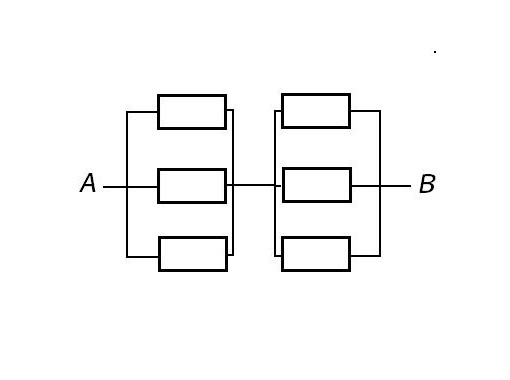
У тебя подозрительно разные обозначения для резисторов. Ну ладно, будем считать что это всё одинаковые резисторы. Тогда это параллельное соединение трёх сопротивлений: 16 Ом, 8 Ом и 16 Ом. А значит общее сопротивление = 1/(1/16+1/8+1/16) = 4 Ом

Общий ток составит 10/4 = 2.5 А

danilovamuurЗнаток (284)

4 года назад

спасибо, у меня те же ответы получились) решила проверить, правильно ли я вообще решила) если у двух людей правильно, значит это точно правильный ответ)

daybit
Высший разум
(146312)
“если у двух людей правильно, значит это точно правильный ответ)”

Ну строго говоря тезис неверный – вон взять двух любых плоскоземельщиков и послушать то, что они несут – будет примерно совпадать, но от этого их бред правильным не станет. )

Ну а если вернуться к задачке про резисторы – вроде подводных камней нет, так что вряд ли мы ошиблись.

Источник

Загрузить PDF

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

1

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.^[1] Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.
- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.^[2] Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи.
- Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.^[3]
4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R_O = 12 В / 8 А = 1,5 Ом.
Реклама

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
2

Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ , где R₁ – сопротивление первой ветви, R₂ – сопротивление второй ветви и так далее до последней ветви R_n.
3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.^[4] Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока.
- В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R_O = 9 В / 3 А = 3 Ом.
5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.^[5]
Реклама

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
2

Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ .
3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно: $R_{O}=1+1,5+1,875=4,375$ Ом.
5

Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.

Реклама

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).^[6] Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.^[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I²R.
- Обособьте переменную R: R = P / I².
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V²/R.
- Обособьте переменную R: R = V²/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама

Советы

Мощность измеряется в ваттах (Вт).
Напряжение измеряется в вольтах (В).
Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА = $1*10^{{-3}}$ A = 0,001 А.
В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: P_СР = VIcosθ, где cosθ – это коэффициент мощности цепи.^[8]

Об этой статье

Эту страницу просматривали 407 314 раз.

Была ли эта статья полезной?

Источник

Цели: обучающая: систематизировать
знания и умения учащихся решать задачи ан расчет
эквивалентных сопротивлений с помощью моделей,
каркасов и т.д.

Развивающая: развитие навыков логического
мышления абстрактного мышления, умений заменять
схемы эквивалентности, упрощать расчет схем.

Воспитательная: воспитание чувства
ответственности, самостоятельности ,
необходимости навыков приобретенных на уроке в
будущем

Оборудование: проволочный каркас куба,
тетраэдера, сетки бесконечной цепочки
сопротивлений.

ХОД УРОКА

Актуализация:

1. Учитель: “Вспомним последовательное
соединение сопротивлений”.

Учащиеся на доске зарисовывают схему.

и записывают

R_эк=n*R

U_об=U₁+U₂

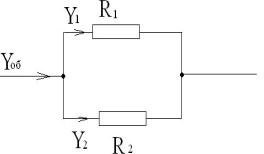
Y_об=Y₁=Y₂

Учитель: вспомним параллельное соединение
сопротивлений.

Учащийся на доске зарисовывает элементарную
схему:

U_об=U₁+U₂

Y_об=Y₁=Y₂

; длядля n равных

Учитель: А теперь будем решать задачи на расчет
эквивалентного сопротивления участок цепи
представлен в виде геометрической фигуры, либо
металлической сетки.

Задача № 1

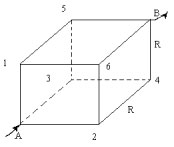
Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.

На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно
для последовательного соединения сопротивлений
имеем:

Задача № 2

Рассчитать R_ЭКВ.этого же куба, если куб
включён в цепь в точках 2 и 4.

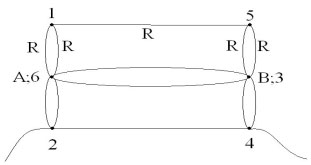
По тому же принципу потенциалы точек А и 6 равны,
В и 3 равны. Учащиеся совмещают эти точки на своей
модели и получают эквивалентную схему:

Расчёт эквивалентного сопротивления такой
цепи прост

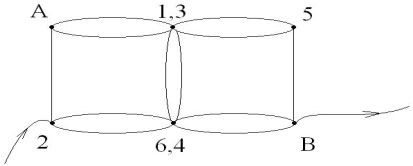
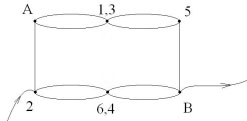
Задача № 3

Эта же модель куба, с включением в цепь между
точками 2 и В. Учащиеся соединяют точки с равными
потенциалами 1 и 3; 6 и 4. Тогда схема будет
выглядеть так:

Точки 1,3 и 6,4 имеют равные потенциалы, и ток по
сопротивлениям между этими точками не потечёт и
схема упрощается до вида; эквивалентное
сопротивление которой рассчитывается так:

Задача № 4

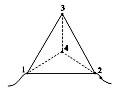
Равносторонняя треугольная пирамида, ребро
которой имеет сопротивление R. Рассчитать
эквивалентное сопротивление при включении в
цепь.

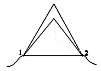
Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.

Тогда схема будет выглядеть так:

либо

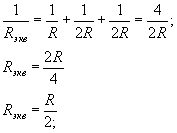
Эквивалентное сопротивление рассчитывается
так:

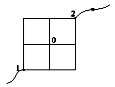
Задача № 5

Металлическая сетка с сопротивлением звена
равном R. Рассчитать эквивалентное сопротивление
между точками 1 и 2.

В точке 0 можно звенья отделить, тогда схема
будет иметь вид:

–
сопротивление одной половины симметричной по 1-2
точкам. Параллельно ей такая же ветвь, поэтому

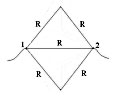
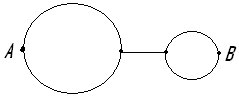
Задача № 6

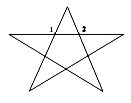
Рассчитать эквивалентное сопротивление
проволочной звезды с сопротивлением каждого
звена R, включённой в цепь между точками 1 и 2.

Звезда состоит из 5-и равносторонних
треугольников, сопротивление каждого.

Между точками 1 и 2 один треугольник параллелен
четырём, последовательно соединенным между
собой

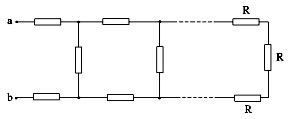
Имея опыт расчёта эквивалентного
сопротивления проволочных каркасов можно
приступить к расчету сопротивлений цепи,
содержащий бесконечное число сопротивлений.
Например:

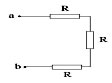
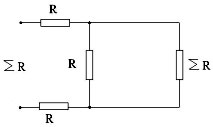
Если отделить звено

от общей схемы, то схема не изменится, тогда
можно представить ввиде

или ,

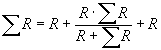
решаем данное уравнение относительно R_экв.

Итог урока: мы научились абстрактно
представлять схемы участков цепи, заменять их
эквивалентными схемами, которые позволяют легко
рассчитать эквивалентное сопротивление.

На дом:

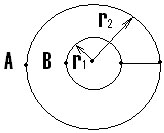
Рассчитать эквивалентное сопротивление
проволочного каркаса из двух окружностей с
радиусами r₁и r_2,r₂₌2r₁между
точками А и В. Сопротивление единицы длинны
проволоки?

Указание: Эту модель представить в виде:

Источник

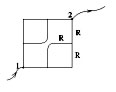
Найти сопротивление фигуры, включенной в цепь точками

#20904
2015-01-25 11:03 GMT

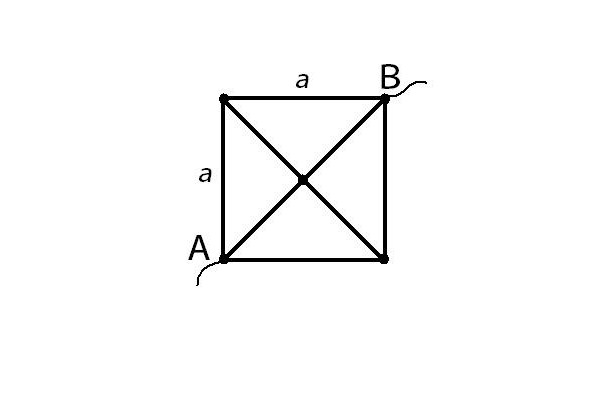
Из проволоки, площадь поперечного сечения которой постоянна, спаяна фигура. Длина стороны квадрата а, а сопротивление единицы длины ρ. Определите сопротивление R фигуры, включенной в церь точками А и В.

#20905
2015-01-25 16:26 GMT

И в чём трудность? Режем или рвём пересечение диагоналей и считаем.

Рвём хоть по вертикали, хоть по горизонтали.

Если ни то, ни другое, ни третье не помогает, прочтите, наконец инструкцию.

#20912
2015-01-25 19:22 GMT

В том-то и дело, что не могу разобраться, как именно эти диагонали разорвать и выгнуть. Туговато это идет мне.

#20913
2015-01-25 19:40 GMT

В силу симметрии фигуры относительно диагонали АВ вершины квадрата (которые не обозначены) находятся под одинаковым потенциалом и их можно соединить.

#20914
2015-01-25 20:52 GMT

Такая схема получится в итоге?

#20917
2015-01-26 10:25 GMT

отредактировал(а) iskander: 2015-01-26 12:17 GMT

#20919
2015-01-26 13:12 GMT

Источник

Расчет сопротивлений сеток

12 комментариев

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Найти сопротивление фигуры, включенной в цепь точками

Добавить комментарий Отменить ответ

Расчет сопротивлений сеток

12 комментариев

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Найти сопротивление фигуры, включенной в цепь точками

Вам также может понравиться

Как найти вещи zara на алиэкспресс

Как найти время работы математика

Если ребенок постоянно поворачивает голову в одну сторону как исправить

Добавить комментарий Отменить ответ