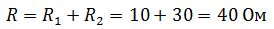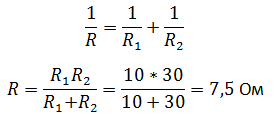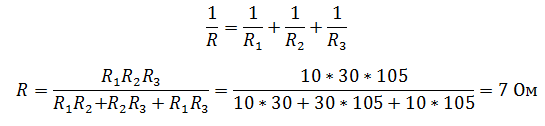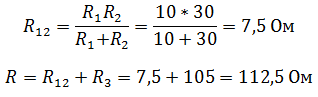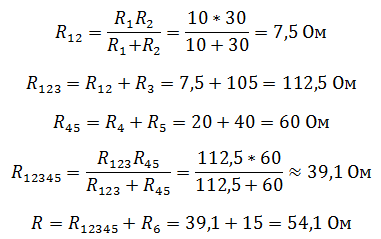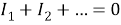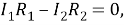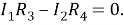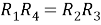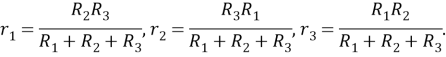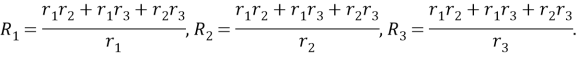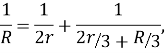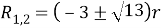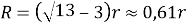Как найти общее сопротивление сложной цепи

Для школьников.

При расчётах сложных цепей постоянного тока можно применять следующие методы:

1. Если можно, то представляют электрические цепи в виде последовательных и параллельных соединений сопротивлений. Как находится общее сопротивление при таких соединениях нам известно, тогда сложная задача превращается в простую.

2. Пользуются законом Ома для неоднородного участка цепи (содержащего источник тока). Применение этого метода рассмотрим в следующей статье. (Неоднородным называется участок цепи, включающий в себя источник тока. Здесь надо учитывать, что ток, протекающий по участку, определяется не только разностью потенциалов между концами участка, но и ЭДС источника.)

3. Применяют метод узловых потенциалов.(Этот метод заключается в том, что потенциал одного узла в цепи приравнивают к нулю, а потенциалы других узлов сравнивают с ним. Учитывая, что алгебраическая сумма токов в узле равна нулю, находят токи, а затем потенциалы узлов).

4. Применяют правила Кирхгофа.(Первое правило: Алгебраическая сумма токов, сходящихся в узле, равна нулю. Второе правило: Алгебраическая сумма произведений тока на сопротивление участка контура равна алгебраической сумме ЭДС в контуре).

Применение этих методов будет рассмотрено в нескольких последующих статьях.

Начнём с первого метода, когда соединение сопротивлений в цепи можно свести к их последовательному и параллельному соединениям. Эти методом мы уже пользовались при решении задач. Здесь точки цепи, имеющие одинаковый потенциал собирают в узел, получают несколько узлов, то есть получают эквивалентную схему.

Таким образом, при использовании первого метода для решения задач, находят в цепи точки равного потенциала, соединяют их в узел, заменяя схему цепи эквивалентной схемой.

При этом учитывается, что сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла, то есть учитывается принцип непрерывности электрического тока.

Этот принцип означает, что ни в одной точке цепи нет скопления или убыли электронов или ионов, то есть сила тока во всех сечениях неразветвлённой цепи одинакова.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Опыты по демонстрации величины напряжения на зажимах источника тока. Короткое замыкание.

Следующая запись: Закон Ома для неоднородного участка цепи. Его применение к расчёту сложных цепей постоянного тока.

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.

Была ли эта статья полезной?

Расчет сопротивления цепи

Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью. 

Пример 1

 

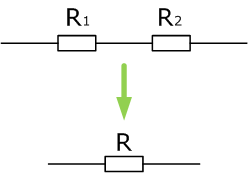
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.

Допустим, что R₁=10 Ом R₂=20 Ом, тогда 

Пример 2

 

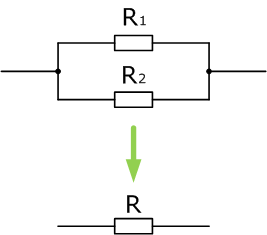
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R₁,R₂ такие же как и в примере 1) 

Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз. 

Пример 3

 

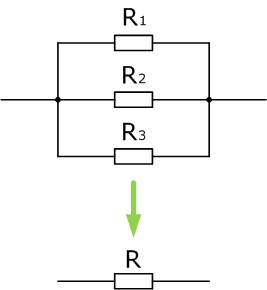
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R₁,R₂ прежние, R₃=105 Ом) 

Пример 4

 

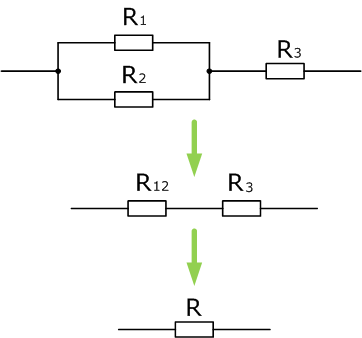
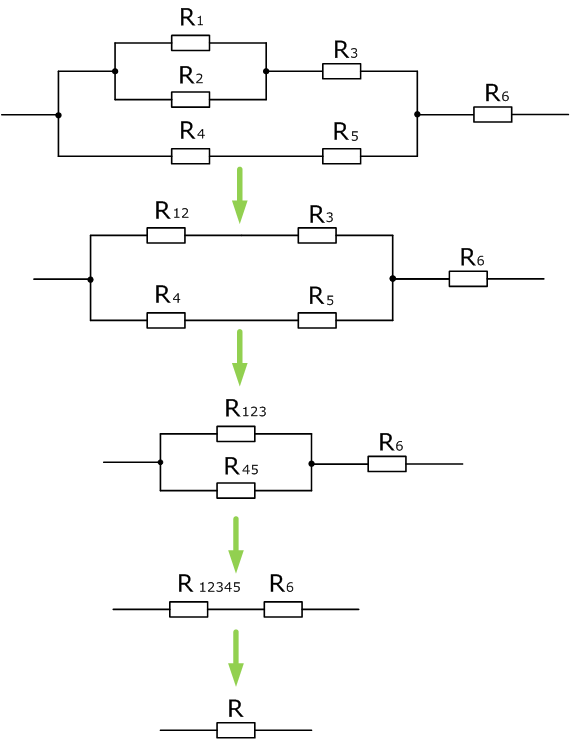
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R₁ и R₂ соединенных параллельно, а затем общее сопротивление, как сумму R₁₂ и R₃ соединенных последовательно. 

 Пример 5

Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.

R₄=20 Ом, R₅=40 Ом, R₆=15 Ом 

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.  

Просмотров: 89119



В учебных и олимпиадных задачах, связанных с расчетом параметров электрических цепей постоянного тока, зачастую требуется рассчитать общее сопротивление цепи. Для решения подобных задач электрические цепи

преобразовывают

, то есть исходную схему заменяют другой с тем же числом выводов. Причём замена должна осуществляться так, чтобы сопротивления между любыми двумя выводами новой схемы были такими же, как у старой. Токи, потребляемые новой схемой от источника, должны оставаться прежними. Общее сопротивление схемы, рассчитанное для подключения к источнику для каждой пары выводов, также не изменяется. Такие преобразования называются

эквивалентными

. Расчёт потребления тока и общего сопротивления при этом обычно упрощается.

Универсального метода преобразования электрических цепей нет. Некоторые методы изложены методических пособиях и задачниках, например [1–4]. Однако изложение не носит систематического характера — обычно суть метода излагается прямо по ходу решения той или иной задачи.

В настоящей статье мы попытались собрать и кратко изложить (в виде конспекта) методы преобразования электрических цепей с сопротивлениями, которые могут быть полезны при решении широкого круга задач. Конспект будет полезен школьникам 8–11 классов, преподавателям физики, тем, кто интересуется проблемами углубленного изучения физики и подготовки школьников к олимпиадам (в частности, к Всероссийской олимпиаде и вузовским олимпиадам).

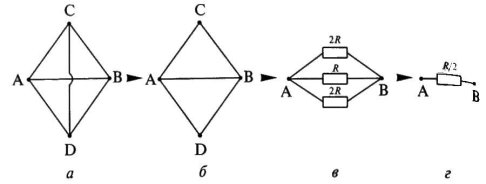
Метод простейших эквивалентных преобразований.

Простейшие примеры преобразования цепи — это 1) замена двух последовательно соединённых сопротивлений

r


₁

и

r


₂

одним сопротивлением

r


₁



+

r


₂

; 2) замена двух параллельно соединённых сопротивлений

r


₁



и

r


₂

одним сопротивлением

r


₁

·

r


₂

/(

r


₁



+

r


₂

). Эти две замены лежат в основе данного метода.

При решении задач в первую очередь необходимо установить, какие проводники соединены между собой последовательно, какие параллельно. Отдельные участки схемы с параллельно или последовательно соединенными резисторами заменяются одним эквивалентным резистором. Постепенным преобразованием участков схему упрощают и приводят к простейшей схеме, состоящей из одного резистора. При этом используются свойства последовательно и параллельно соединенных проводников.

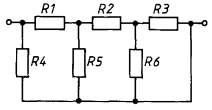
Задача 1.

Найти общее сопротивление цепи.

R


₁

=

R


₂

= 4 Ом,

R


₃

=

R


₄

=

R


₅

=

R


₆

= 8 Ом.

Решение


: В этой задаче часто неправильно определяют, какие сопротивления включены последовательно, а какие параллельно. Эквивалентная схема представлена на рисунке. Расчет по формулам дает ответ 4 Ом.

Ответ


: 4 Ом.

Для отработки метода можно использовать следующие задачи.

– Задачи 6,11–12 с разобранными решениями, а также 10.13–10.14, 10.21–10.28 для самостоятельного решения из главы 10 [1];

– 2.22–2.24 из [2];

– 19.2–19.6 из [3].

Использование правил Кирхгофа.

Правила Кирхгофа позволяют упростить расчеты параметров разветвленных электрических цепей. Этих правил два.

Первое правило Кирхгофа

: алгебраическая сумма токов, сходящихся в узле, равна нулю.

.

Второе правило Кирхгофа

: для любого замкнутого контура разветвленной электрической цепи алгебраическая сумма напряжений на сопротивлениях равна алгебраической сумме ЭДС, действующих в этом контуре.

Первое правило Кирхгофа является следствием закона сохранения заряда, второе — следствием закона Ома для неоднородного участка цепи.

Правила Кирхгофа в каждом конкретном случае позволяют написать полную систему алгебраических уравнений, из которых могут быть найдены неизвестные токи и напряжения. При расчете разветвленной цепи данным методом следует применять следующий порядок:

1. произвольно выбрать направления токов во всех участках разветвленной цепи, отметив их стрелками на чертеже;
2. при составлении уравнений для узлов токи считать положительными, если они втекают к узлу, и отрицательными, если они вытекают от узла;
3. следует помнить, что число независимых уравнений, составленных по первому правилу Кирхгофа, всегда на одно меньше числа узлов, имеющихся в данной цепи;
4. выбрать направление обхода контуров цепи;
5. написать уравнения, соответствующие второму правилу Кирхгофа, соблюдая правило знаков: токи, совпадающие с направлением обхода, записывать со знаками «+», обратные направлению обхода − со знаками «−». ЭДС считать положительными, если они повышают потенциал в направлении обхода (при обходе по контуру сначала встречается отрицательный полюс источника, затем положительный);
6. следует помнить, что число независимых уравнений, составленных по второму правилу Кирхгофа, равно наименьшему числу разрывов, которые следует сделать в цепи, чтобы нарушить все контуры. Если удается изобразить схему на плоскости без пересечений, то это число равно числу областей, ограниченных проводниками (числу «дырок» в графе схемы);
7. если в полученном ответе какой-либо ток будет иметь отрицательный знак, то это указывает на ошибочность первоначального выбора направления данного тока.

Для отработки метода можно использовать, например, задачи 4.4.29–4.4.32 из [5].

Важнейшим примером задачи на применение правил Кирхгофа является задача о согласованном мосте Уитстона.

Задача 2.

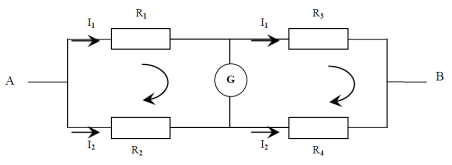
Определить, при каких условиях в мостовой схеме через перемычку моста не течет ток.

Решение


: Схема моста представлена на рисунке, в качестве перемычки выступает гальванометр G. Если мостик подключить к источнику току, то мы получим разветвленную электрическую цепь, содержащую 4 узла и 3 дырки. Значит, для расчета токов и напряжений можно составить систему 6 независимых уравнений: 3 уравнения для узлов и три уравнения для контуров. Мы ограничимся выводом условия, при котором ток через гальванометр G идти не будет. Такой мостик называется

согласованным

. В этом случае токи через сопротивления

R


₁

и



R


₃

будут одинаковы. На схеме эти токи обозначены

I


₁

. Одинаковыми будут токи и через сопротивления

R


₂

и



R


₄

. На схеме токи через

R


₂

и



R


₄

обозначены

I


₂

.

Из второго правила Кирхгофа получаем:

Преобразовав систему, получим искомое условие:

. Это соотношение очень полезно для решения задач. Из него, в частности, следует, что мост, собранный из одинаковых сопротивлений, всегда будет согласованным.

Ответ:

.

Если бы вместо гальванометра в схеме было бы сопротивление

R

, то удаление этого сопротивления не привело бы к изменению токов и потенциалов в цепи. Поэтому в тех частях электрических схем, где будут согласованные мосты, перемычку можно будет удалять.

Пример с мостом Уитстона вплотную подвёл нас к следующему методу расчёта сопротивления разветвлённой электрической цепи — к методу удаления сопротивления.

Метод удаления сопротивления.

Идея этого метода состоит в том, чтобы исключить участок цепи, через который не течет ток. Полученная схема будет эквивалентна исходной.

Задача 3.

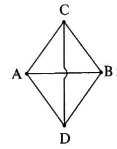
Найти сопротивление участка цепи между точками А и В, изображенного на рисунке.

Решение:


Узлы С и D симметричны относительно прямой АВ. Если повернуть схему на 180° вокруг прямой АВ, то схема на изменяется. Можно представить себе такую ситуацию: независимый наблюдатель следит за ходом измерений для данной схемы. Его попросили выйти из лаборатории. После этого отсоединили источник тока, несколько раз повернули схему вокруг АВ, затем подсоединили источник и пригласили наблюдателя. Из-за симметрии никакими экспериментами он не сможет определить, сколько раз повернули схему и где теперь находится точка С. Значит, между симметричными точками C и D ток течь не может — иначе бы наблюдатель измерил его направление и определил местонахождение точки C. Следовательно, перемычку CD можно удалить.

Удаление сопротивления CD можно обосновать и с использованием моста Уитстона. Заметим, что часть цепи A-C-B-D-A представляет из себя согласованный мост с перемычкой CD, которую, как мы ранее доказали, можно убрать.

После исключения участка CD получим эквивалентную цепь, сопротивление которой равно

R

/2.

Для отработки метода удаления сопротивления можно использовать следующие задачи:

– Каркасный тетраэдр: задача 8 из главы 10 [1], 19.15(3) из [3].

– N-полюсник: 19.18 из [3].

Метод эквипотенциальных узлов

. Эквипотенциальными называются узлы с равными потенциалами. Если в цепи, содержащей сопротивления, имеются эквипотенциальные узлы, то их можно рассматривать как один узел, проводя операцию склейки узлов.Поэтому данный метод еще называют

методом склейки узлов

.

Почему операция сведения в один узел правомочна? В электрических схемах соединительные провода, не имеющие сопротивления (их изображают на схемах тонкой линией), можно удлинять или укорачивать. Общее сопротивление цепи при этом не изменяется. Если узлы соединены накоротко (соединительный провод имеет сопротивление равное нулю), то соединительный провод можно укорачивать до тех пор, пока узлы не «склеятся», образуя один узел. Если узлы имеют одинаковые потенциалы и не соединены проводом, то электрические условия в этих точках не изменяются (а значит и сопротивление всей цепи) при соединении их проводником, не имеющим сопротивления. После чего можно провести операцию склейки.

Но есть ещё один случай, когда эквипотенциальные узлы соединены проводником с не равным нулю сопротивлением. Если при подключении цепи к источнику тока, по этому проводнику не идёт ток, то по закону Ома для однородного участка цепи разность потенциалов на концах этого проводника равна нулю. А, значит, узлы на концах проводника являются эквипотенциальными. В этом случае проводник с сопротивлением можно заменить на соединительный провод без сопротивления, после чего узлы также склеиваются.

Как найти эквипотенциальные точки в разветвленной электрической цепи? Общих правил нет. Нахождению эквипотенциальных точек часто помогает симметрия включения участков цепи. При этом граф схемы должен иметь ось симметрии или плоскость симметрии, проходящую через точки подключения. Можно мысленно повернуть или трансформировать граф таким образом, чтобы «кандидаты» в эквипотенциальные узлы поменялись местами. Если после обмена наименований точек получается исходная схема, значит, выбранные узлы эквипотенциальны.

Операция склейки приводит к уменьшению количества узлов. После этой операции схема обычно упрощается и к ней можно применить метод эквивалентных преобразований.

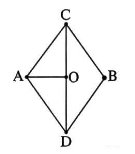
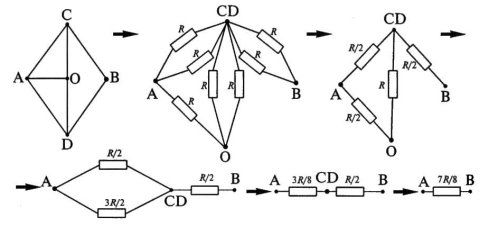
Задача 4.

Найти сопротивление участка цепи между точками А и В. Считать сопротивление каждого проводника равным

R.

Решение



:

Докажем, что точки С и D эквипотенциальны. Точки С и D симметричны относительно прямой, проходящей через точки А и В. Если повернуть четырёхугольник вокруг прямой АВ на 180°, точка С перейдёт в точку D и наоборот. Если после поворота на 180° заменить наименование точек С на D, а D на С, мы получим исходную схему. Следовательно, потенциалы ϕ

_С

и ϕ

_D

равны.

Соединив точки С и D в один узел, получим эквивалентную схему, которую можно разложить на элементы последовательного и параллельного соединений. Сопротивление между точками А и В рассчитываем, используя преобразования схемы.

Ответ



:


R

_АВ


=7

R

/8.

Метод эквипотенциальных узлов помогает решать задачи, которые предлагаются на некоторых олимпиадах. К таким задачам, в частности, относятся следующие.

– Каркасный куб: задача 7 и задачи 10.15–10.16 из главы 10 [1], 2.28 из [2], 19.15(5) из [3];

– Каркасный многоугольник: 2.27а из [2];

– Склейка узлов, к которым подсоединен идеальный амперметр: 19.20–19.21 из [3].

Метод разрезания узлов

.Чуть более сложный метод, который заключается в замене одного узла несколькими эквипотенциальными. Главное условие — чтобы при разрезании не нарушилось распределение токов в цепи.

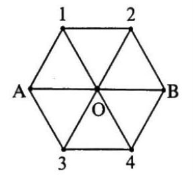
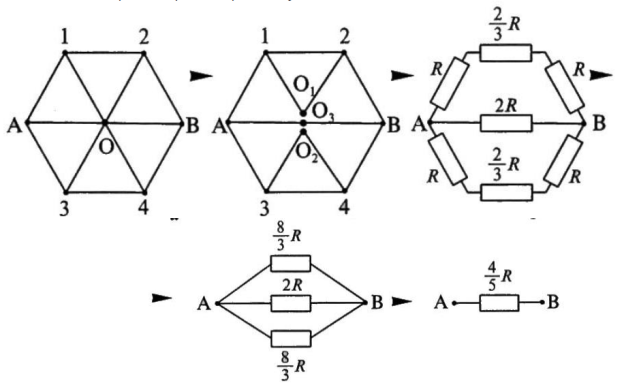
Задача 5.

Определить сопротивление участка цепи между точками А и В. Сопротивления отдельных участков одинаковы и равны

R



.

Решение


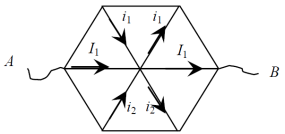
: Здесь нет ни одной пары проводников, соединенных между собой последовательно или параллельно. Поэтому необходимо обратить внимание на возможную симметрию цепи. Для применения метода разрезания узлов сначала надо провести анализ распределения токов в цепи.

Из симметрии схемы относительно прямой АВ следует, что токи в проводниках А-1 и А-3 будут равны между собой. А значит, в узлах 1 и 3 токи делятся в одинаковых пропорциях. Поэтому токи между узлами 1-О и 3-О также будут одинаковыми друг другу. Токи

I


_AO

=

I


_OB

=

I


₁

,

I


_1O

=

I


_O2

=

i


₁

,

I


_3O

=

I


_O4

=

i


₂

.

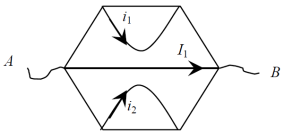
Следовательно, узел O можно разрезать так, чтобы не нарушалось протекание токов

I


₁

,

i


₁

и

i


₂

. После преобразований получаем окончательный ответ 4

R

/5.

Для отработки метода можно использовать следующие задачи: задачи 9 и 10.17 из главы 10 [1], 2.27в из [2], 19.15(1,2,4) и 19.16 из [3].

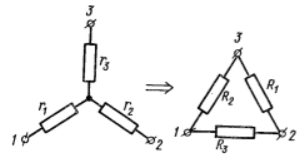
Метод замены «треугольника» на «звезду»

. Данный метод позволяет быстро рассчитать сопротивления участков цепи в том случае, когда не удается установить симметричного распределения токов. Метод замечательно изложен в статье А. Р. Зильбермана [6].

В основе этого метода лежит задача 19.13 из [3], разобрать которую мы предлагаем читателям самостоятельно. Выпишем только полученный результат.

Если в схеме к некоторым узлам подключены сопротивления

R


₁

,

R


₂

,

R


₃

в виде «треугольника», то его можно заменить на элемент «звезда» с сопротивлениями

r


₁

,

r


₂

,

r


₃

, которые рассчитываются по формулам

Результат легко запомнить, если заметить, что в знаменателе всегда стоит сумма сопротивлений «треугольника», в числителе — произведение сопротивлений с дополняющими номерами, причем индексы у

r


₁

,

R


₂

,

R


₃

в первой формуле можно менять по циклу 1–2–3–1 и таким образом получить остальные две формулы.

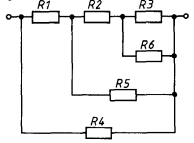
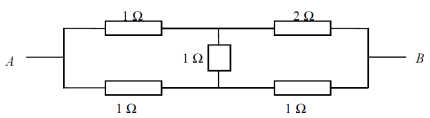
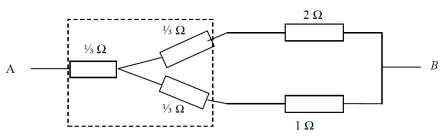
Задача 6.

В схеме, изображенной на рисунке, определить сопротивление между точками A и B.

Решение:


Данный мост не является согласованным, что легко проверить. Симметрия в схеме отсутствует. Однако левую половину моста (с сопротивлениями по 1 Ом) можно рассматривать как «треугольник». После замены на «звезду» получается схема с последовательным и параллельным соединениями, сопротивление которой предлагаем читателям подсчитать самостоятельно.

Ответ:


13/11 Ом.

Замена «треугольника» на «звезду» уменьшает на один количество контуров в схеме и увеличивает на один количество узлов. Если мы, напротив, хотим уменьшить число узлов в схеме, то можно провести обратную замену — «звезды» на «треугольник» по формулам [6]:

При удалении большего числа узлов можно использовать обобщенный метод, изложенный в статье Е. Соколова [7].

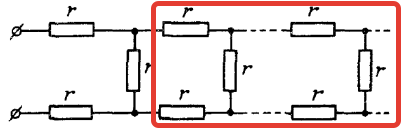
Расчет бесконечных цепей.

В олимпиадных задачах иногда встречаются электрические цепи, в которых повторяется одно и то же звено цепи до бесконечности. С практической точки зрения это означает, что число повторяющихся звеньев

N

очень велико и добавление очередного звена не приводит к сколько-нибудь значительному изменению общего сопротивления. С математической точки зрения

сопротивлением бесконечной цепиR

называется предельное значение сопротивления при

N

→ ∞.

Идея решения заключается в том, что при удалении первого звена сопротивление оставшейся части также будет равно

R

(ведь число элементов останется бесконечным. Значит, бесконечную цепь (без первого звена) можно заменить эквивалентным сопротивлением

R

, причем общее сопротивление также равно

R

. После этого составляется уравнение и находится его решение относительно

R

. Рисунок иллюстрирует сказанное применительно к задаче 19.19 из [3], которую мы предлагаем сделать читателям самостоятельно, как и задачу 2.26 из [2].

Повторяющиеся звенья цепи могут быть не в точности одинаковы, а быть подобны друг другу (т. е. все сопротивления в звеньях отличается в какое-то фиксированное количество раз). Такая схема, в частности, может быть реализована в виде

фрактала

, как это было в задаче № 6 для 8–11 кл. в Турнире Ломоносова 2015 г.

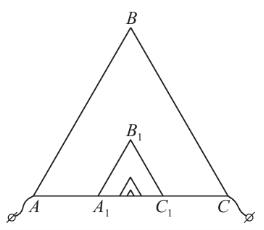
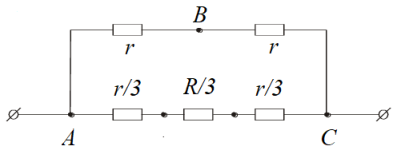
Задача 7.

Из однородной проволоки изготовлен равносторонний треугольник

ABC

, сторона которого равна

a

. К точкам

A


₁

и

C


₁

, делящим сторону

AC

на три равные части, прикреплены еще два куска проволоки — вместе с отрезком

A


₁

и

C


₁

они образуют равносторонний треугольник со стороной

a

/3. Внутри этого треугольника сделан еще один (в три раза меньший) и т. д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины

a

равно

r

.

Решение:


Обозначим искомое сопротивление за

R

.


Если разорвать куски проволоки

AA


₁

и

C


₁


C

, то оставшийся треугольник, как подобный исходному с коэффициентом 1/3, будет иметь сопротивление

R

/3, поскольку все сопротивления в нем (по сравнению с исходным) меньше в 3 раза. Эквивалентная схема показана на рисунке.

Вычисляя ее сопротивление, получим уравнение:

решения которого

. Один из корней отрицателен, другой положителен. Он и является ответом в задаче.

Ответ:

.

Напоследок предлагаем читателям еще одну задачу 3.52 из [4] с бесконечными цепями, содержащими подобные друг другу звенья.

Принцип суперпозиции

. Уравнения закона Ома и правил Кирхгофа линейны относительно токов. Это значит, что если в цепи есть несколько источников тока, то можно рассчитать, какой ток создаст в данном проводнике каждый источник в отдельности. А реальный ток через выбранный проводник будет равен сумме токов, создаваемых каждым источником в отдельности.

Задача 8

(задача 10 из главы 10 [1])

.

В каждое ребро бесконечной сетки с квадратными ячейками включено сопротивление

r =

20 Ом. Чему равно сопротивление сетки при подключении её соседними узлами?

Решение:


К узлам А и В подключается внешний источник тока. Он создаёт ток

I

, входящий через узел А, и такой же ток, выходящий через узел В. Будем измерять напряжение

U

между точками А и В идеальным вольтметром и ток

I

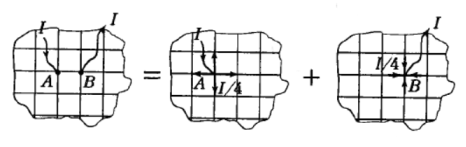
в измерительной цепи, содержащей источник тока и идеальный вольтметр. Во время измерений напряжение и ток в очень далёких от А и В узлах равны нулю. Поэтому, если соединить далёкие точки хорошо проводящим проводом, то ничего не изменится. Назовём этот провод «бесконечность». Его можно представить как провод, идущий по окружности очень большого радиуса.

Теперь возьмём два одинаковых источника тока. Первый подключим к точке А и «бесконечности» так, чтобы ток

I

, шёл по сетке от точки А к «бесконечности». При этом распределение тока по разным направлениям (по четырём проводникам, подключённым к узлу А) равномерно. Поэтому по каждому такому проводнику пойдёт ток

I

/4 от узла А.

Второй источник подключим к узлу В и «бесконечности» так, чтобы ток

I

, шёл по сетке от «бесконечности» к точки В (см. рис. 25 в). По каждому проводнику, подключённому к узлу В пойдёт ток

I

/4 в направлении к узлу В. В силу указанной выше линейности уравнений закона Ома на каждом участке бесконечной сетки ток в любом ребре сетки будет суммой токов этих двух источников. Причём, для каждого источника распределение тока симметрично относительно узла, к которому источник подключён.

От первого источника по ребру АВ течёт ток

I

/4 в направлении от А к В. Такой же ток в том же направлении протекает по ребру АВ от второго источника. Значит, по ребру АВ течет ток

I

/2.

Тогда напряжение, измеренное на этом ребре, будет равно

U =

(

I

/2)

r

. Сопротивление сетки

R

=

U/I

=

r

/2.

Ответ:


10 Ом.

Для отработки метода предлагаем сформулировать и решить две аналогичные задачи с бесконечной сеткой из шестиугольников (должен получиться ответ 2

r

/3) и треугольников (

r

/3), а также разобрать еще более сложную задачу 3.53 с треугольной сеткой из [4].

Работа выполнена на базе ГБОУ Школа № 1557 имени Петра Леонидовича Капицы в рамках проекта «Курчатовский проект в московской школе». Авторы благодарят администрацию ГБОУ Школа № 1557 за помощь и поддержку.

Литература:

1. Черноуцан А. И. Физика. Задачи с ответами и решениями: учебное пособие. 9-е изд. М.: КДУ, 2017. 352 с.

2. Сборник задач по физике с решениями и ответами. Часть III. Электричество и оптика / Под ред. А. Н. Долгова. М.: МИФИ, 2001. 188 с.

3. Гольдфарб Н. И. Сборник вопросов и задач по физике. 9-е изд. М.: Дрофа, 2005. 351 с.

4. Варламов С. Д. и др. Задачи Московских городских олимпиад по физике. 1986–2005 / Под ред. М. В. Семенова, А. А. Якуты. 2-е изд., исправл. М.: МЦНМО, 2007. 624 с.

5. Павленко Ю. Г. Физика. Избранные задачи. Кн. I. М.: Экзамен, 2008. 544 c.

6. Зильберман А. Р. Преобразование электрических цепей // Квант, 1971. № 3. С. 10–14.

7. Соколов Е. О простом и сложном // Квант, 2002. № 2. С. 7–12.