Загрузить PDF
Загрузить PDF
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
-

1
Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
-

2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.[1]
Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.[2]
Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи. - Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.[3]
- Сила тока в любых частях последовательной цепи одна и та же.[2]
-

4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: RO = 12 В / 8 А = 1,5 Ом.
Реклама
-

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
-

2
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления:
, где R1 – сопротивление первой ветви, R2 – сопротивление второй ветви и так далее до последней ветви Rn.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока. - В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
-

4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
-

5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
Реклама
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
-

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
-

2
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи:
.
-

3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
-

4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
Ом.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
-

5
Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.
Реклама
-

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).[6]
Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
-

2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I2R.
- Обособьте переменную R: R = P / I2.
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
-

3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V2/R.
- Обособьте переменную R: R = V2/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама
Советы
- Мощность измеряется в ваттах (Вт).
- Напряжение измеряется в вольтах (В).
- Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА =
A = 0,001 А.
- В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: PСР = VIcosθ, где cosθ – это коэффициент мощности цепи.[8]
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 408 213 раз.
Была ли эта статья полезной?
Общие сведения
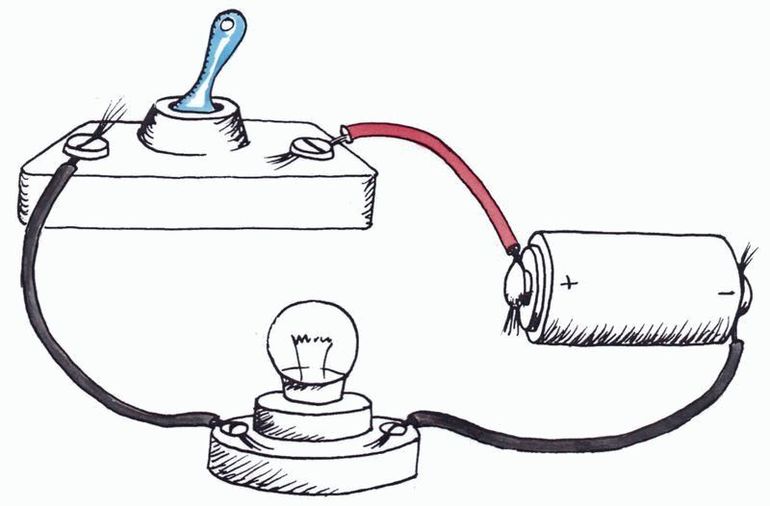
Прохождение электрического тока через проводник зависит от его проводимости. Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом. Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
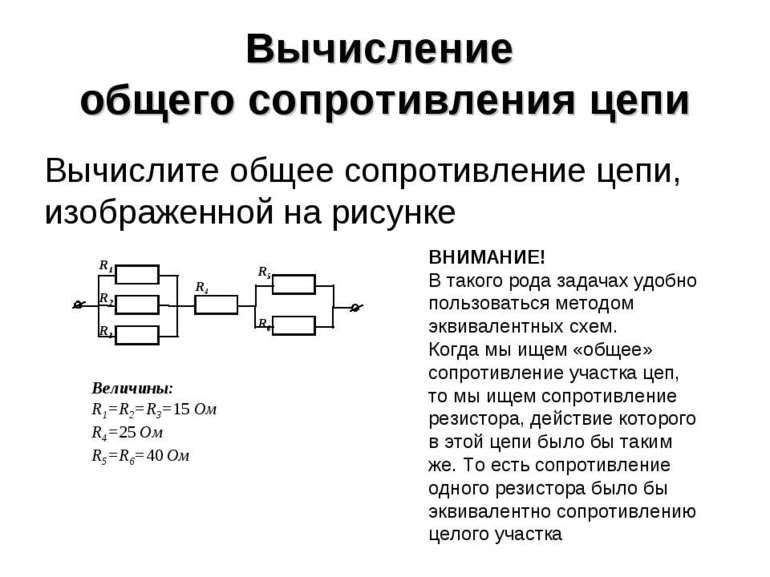
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.
Реальная замкнутая электрическая цепь состоит из множества активных и пассивных радиоэлементов. Каждый из них обладает каким-то значением сопротивления. В этом случае говорят о внутреннем сопротивлении прибора.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
Последовательное подключение
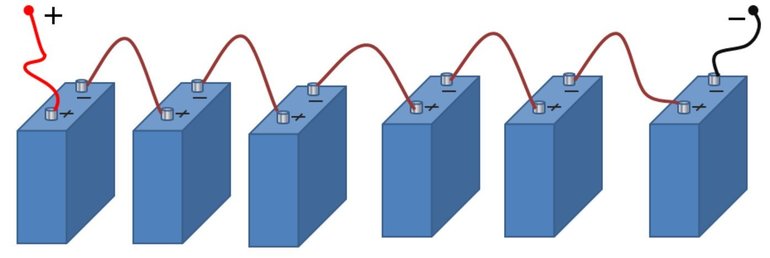
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.
При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
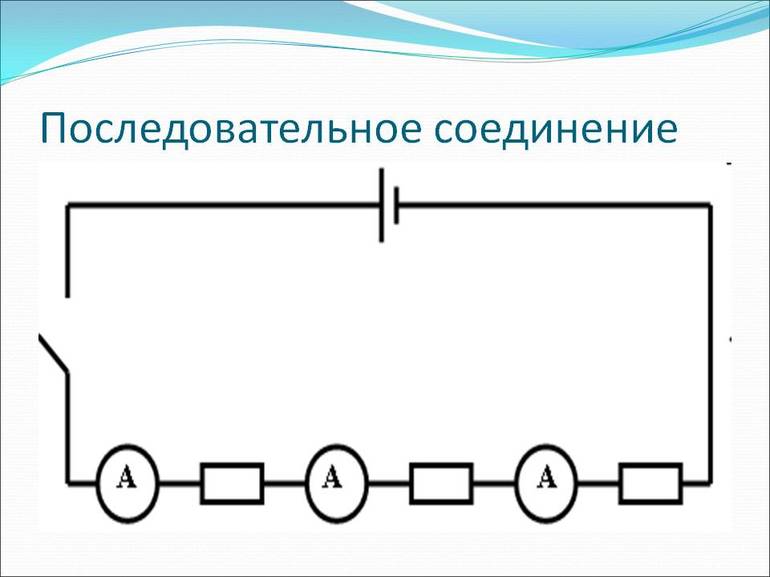
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.
Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:
- I = I 1 = I 2 = … = In;
- U = U1 + U2 + … +Un.
Эти равенства являются фундаментальными для нахождения параметров при повторении резисторов в цепи. Используя закон Ома, можно найти, чему будет равняться сопротивление цепи. Формула для его нахождения будет выглядеть так: Rпос = R 1 + R 2 +… + Rn.
Параллельное соединение
По распространённости такой вид соединения чаще встречается, чем последовательное подключение. При нём проводники соединены так, что начала всех резисторов сводятся в одну точку электрической цепи, а концы — в другую. Для того чтобы заменить разветвлённое подключение одним эквивалентным элементом, нужно знать, как правильно рассчитать ток и напряжение.
Пусть имеется цепь, состоящая из R1 + R2 + … +Rn параллельно включённых радиоэлементов. На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
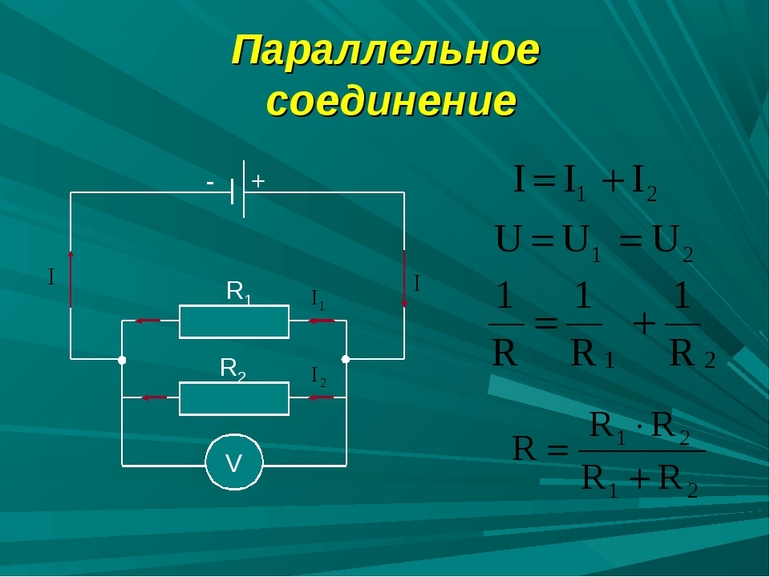
В результате через первую ветвь потечёт ток I1, вторую — I2, в энную — In. Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Электростатическое поле является потенциальным, то есть работа по перемещению заряда из одной точки в другую не зависит от траектории, по которой перемещается носитель. Следовательно, при переносе одного кулона по любой ветви нужно будет совершить одинаковую работу. Из приведённых рассуждений следует, что при параллельном соединении формулы, с помощью которых можно рассчитать характеристики электрической цепи, будут следующими:
- I = I1 + I2 + … +In;
- U1 = U2 = … = Un.
Таким образом, вычисление эквивалентного сопротивления, которым можно будет заменить всю цепь в соответствии с законом Ома, выполняется по формуле: 1 / R пар = 1 / R 1 + 1 / R 2 + … + 1 / Rn. Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу. Это позволяет в некоторых случаях упростить расчёт.
Согласно правилу сложения дробей c одинаковым знаменателем можно записать равенство: 1 / R1 + 1 / R2 + … + 1 / Rn = N / R1. Отсюда следует, что Rпар = R1 / N, где N равно числу резисторов. По аналогии можно посчитать общее сопротивление по упрощённой формуле для двух элементов: (1 / R1) + (1 / R2) = (R 2 + R 1) / R 1 * R 2. Это довольно удобные формулы для практического применения.
Решение задач

Для вычисления сопротивления любого смешанного соединения нужно запомнить всего две формулы — выражения для нахождения величины при последовательном и параллельном подключении. Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Например, пусть имеется параллельное подключение из четырёх резисторов. Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Из типовых задач, в которых необходимо найти сопротивление цепи, предлагающихся в школе на уроках физики, можно привести следующие:

- Найдите ток в цепи, если вольтметр, подключённый к одному из трёх последовательно соединённых проводников, показывает 100 В. Сопротивление элементов составляет: R1 = R2 = 5 Ом, R3 = 15 Ом. В задаче три резистора подключены в линию, значит, их полное сопротивление равно: R = R 1 + R 2 + R 3 = 25 Ом. У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A.
-
Каково будет сопротивление каждого из резисторов, если при их последовательном соединении ток равен 3A, а при параллельном — 16A. Напряжение в сети составляет 120 В. При первом способе соединения Iпосл = U / (R1 + R2), при втором Iпар = U / Rпар = U * (R1 + R2) / R1 * R2. Из первой формулы следует, что R1 + R2 = U / Iпос. Тогда: I пар = U 2 / Iпос * R 1 * R 2 → R 1 * R 2 = U 2 / I пар * I пос. Используя теорему Виета, можно составить квадратное уравнение. После его решения искомые величины будут равны: R 1 = 30 Ом, R 2 = 10 Ом.
Следует отметить, что приборы для измерения тока, напряжения и даже ёмкости используют особенности вычисления сопротивления цепи. Так, вольтметр имеет бесконечно большой внутренний импеданс, что позволяет подключать его параллельно к измеряемым точкам без внесения изменения в протекающий сигнал.
Амперметр же, наоборот, характеризуется пренебрежимо малой величиной внутреннего сопротивления, поэтому и подключают его в разрыв линии, на которой выполняют измерения.
Способы нахождения общего сопротивления цепи
Содержание
- 1 Определение сопротивления
- 2 Соединение параллельным и последовательным способом
- 2.1 Сопротивление при подключении проводников последовательно
- 2.2 Напряжение при подключении проводников последовательно
- 2.3 Параллельное подключение потребителей
- 2.4 Сопротивление при подключении проводников параллельно
- 2.5 Напряжение при подключении проводников параллельно
- 2.6 Сила тока при подключении проводников параллельно
- 3 Практическое применение
- 4 Комбинированное соединение
- 5 Видео по теме
Нередко при использовании электрооборудования бывает необходимо найти общее сопротивление цепи. С помощью данной величины определяют противодействие перемещению электричества в цепи или проводнике. В первый раз ее обосновали в законе Ома – трудах физика из Германии, ставившего опыты, связанные электричеством. По его имени и получила название единица сопротивления – Ом.

Определение сопротивления
Есть 2 вида напряжения – переменное и постоянное, а сопротивление электрической цепи может быть активным и реактивным. Дополнительно оно подразделяется на емкостное и индуктивное. Частоты в электросети не влияют на активное сопротивление. Этому параметру совершенно неважно, какой вид электроэнергии перемещается по проводам. А вот реактивная разновидность, наоборот, способна изменяться при перемене частоты. Дополнительно емкостные показатели в конденсаторах, а также индуктивные в трансформаторах проявляют себя по-разному.
Кроме сопротивления электрических приборов, работающих от сети, на ее общее состояние воздействуют промежуточные проводники, также способные сопротивляться электронапряжению. Чтобы правильно определить параметры электроцепи, необходимо понимать, что такое общее сопротивление, и по каким формулам осуществляется его расчет.
Необходимо учитывать, что индуктивный вид сопротивления при увеличении частоты электротока в сети также увеличивается. Его находят по формуле:

Емкостное сопротивление конденсатора с увеличением частоты электротока, наоборот, снижается. По этой причине принимается, что конденсатор при использовании постоянного тока имеет бесконечно большое сопротивление. Чтобы рассчитать емкостное сопротивление участка цепи, следует воспользоваться формулой:

Полное сопротивление включает в себя активную и реактивную составляющие. Графически оно выражается гипотенузой прямоугольного треугольника, катеты которого – активное и реактивное сопротивление.

Чтобы посчитать общее активное сопротивление, достаточно знать значение тока и напряжения в цепи, подключенной к определенному источнику питания. В данной ситуации достаточно воспользоваться законом Ома.

Но значение общего сопротивления в электроцепи зависит не только от используемых радиоэлементов и присутствующего в схеме вида сопротивления. Особое влияние в этом случае оказывает метод сборки электроцепи из отдельных элементов. На практике используется 2 способа подключения потребителей:
- Параллельный;
- Последовательный.
Соединение параллельным и последовательным способом
Эти способы часто используются в электротехнике и электронике, во многих случаях без них невозможна правильная работа оборудования или узла электроники. В первую очередь нужно понять, как функционируют простейшие цепи радиоэлектронных устройств — проводники.
По существу, проводник — особый материал, хорошо передающий электрический ток. Каждый из них обладает собственным сопротивлением. Вычисляют этот параметр для какого-либо проводника по следующей формуле:

По факту каждый проводник – это простейший резистор, имеющий собственное сопротивление.
Сопротивление при подключении проводников последовательно
При таком соединении к одному из проводников подключается следующий и таким образом соединяется цепочка из отдельных элементов. Подобная сборка электроцепи называется последовательной. Допустимо соединять в одну систему необходимое количество резисторов и прочих компонентов.
Узнать общее сопротивление схемы с последовательным подключением элементов совсем несложно. Для этого найдем, чему равна сумма сопротивлений всех использованных проводников. В результате получается формула для определения общего сопротивления цепи с последовательным подключением:

Например, соединяют последовательно в одну цепь 3 проводника. Один из них имеет сопротивление 3 Ома, следующий 4 Ома и последний 2 Ома. Для подсчета общего сопротивления нужно суммировать значение всех установленных элементов:
R цепи = R1 + R2 + R3 = 3 + 4 + 2 = 9 Ом.
Напряжение при подключении проводников последовательно
При соединении элементов цепи последовательно, через каждый из них проходит одинаковая сила тока. Но нужно понять, как определить напряжение и что с ним происходит на каждом участке цепи.
Следует вспомнить закон Ома и станет просто находить, чему равно реальное напряжение на каждом резисторе. Например, есть собранная система элементов с такими характеристиками как на рисунке:

В этой цепи, как выяснили выше, везде присутствует одинаковая сила тока. Но как узнать ее номинальное напряжение? Сперва нужно модифицировать систему, изменив ее как на изображении, представленном ниже. При этом принимаем сумму сопротивлений всех элементов системы, как RАВ:

В результате выходит по расчетам, что:
RАВ = R1 + R2 + R3 = 2 + 3 + 4 = 9 Ом.
По вычисленному RАВ с учетом закона Ома определяется сила тока, имеющаяся в цепи:
I = U/R = 9/9 = 1 Ампер.
После этого нужно найти напряжение на всех установленных резисторах. Точнее говоря, требуется вычислить значения, соответствующие UR1, UR2, UR3. Для их нахождения также следует воспользоваться законом Ома, согласно которому U = IR.
В результате выходит, что:
- UR1 = IR1= 1×2 = 2 В.
- UR2= IR2 = 1×3 = 3 В.
- UR3= IR3 = 1×4 = 4 В.
После этих вычислений если суммировать все найденные напряжения на отдельных участках, то в результате получится характеристика, равная 10 Вольтам. С учетом этого выходит, что U = UR1 + UR2 + UR3. В результате мы получили элементарный делитель напряжения.
Следовательно, при последовательном подключении сумма изменения напряжения на отдельных участках соответствует общему напряжению источника питания.

Параллельное подключение потребителей
Это соединение выполняется по-другому, пример показан на рисунке:

Сопротивление при подключении проводников параллельно
Общее сопротивление считают по формуле:

Если подсоединены параллельно только 2 компонента, то формулу можно сделать проще. Выглядеть она должна таким образом:

Напряжение при подключении проводников параллельно
С этим все просто. Благодаря тому, что все потребители подключаются параллельно, то они имеют равное напряжение. По этой причине выходит, что напряжение, которое можно получить на R1 не станет отличаться от показаний на всех других участках.
Сила тока при подключении проводников параллельно
Если все было просто с напряжением, то появляются сложности с силой тока. При соединении последовательным способом на всех проводниках одинаковая сила тока, а при параллельном все происходит наоборот. На установленные потребители будет поступать разная сила тока. Чтобы ее определить, придется еще раз воспользоваться законом Ома.
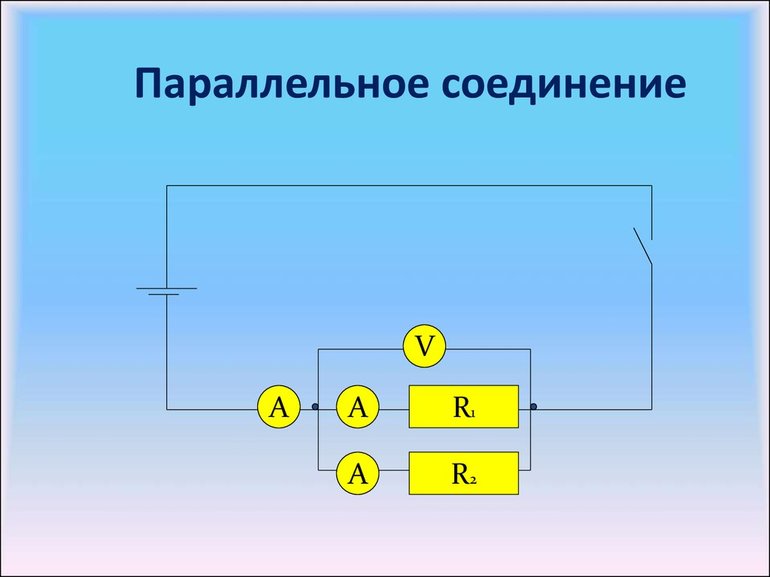
Проще разобраться в принципе работы и расчетов, на реальном примере. На изображении, расположенном ниже, 3 резистора соединены параллельно, и запитаны от источника U.

В любом из установленных устройств напряжение отличаться не будет, как выяснили ранее. Но на разных участках цепи будет собственная сила тока. Для каждого потребителя ее определяют по закону Ома, используя для этой цели соотношение I=U/R.
Таким образом получается:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
Если в системе присутствуют другие подключенные параллельно приборы, для них используют: In = U/Rn
В результате сила тока всей цепи определяется по формуле:

В электронике способ параллельного подсоединения потребителей называют дополнительно «делителем тока», причина в том, что в схемах резисторы поступающий ток делят между установленными элементами.

Практическое применение
Попробуем решить следующую задачу: найти проходящую через каждый резистор силу тока и определить общую силу тока при известных номиналах резисторов и напряжении питания.

Решение
Расчет проводится с помощью выше приведенных формул:
- I1 = U/R1
- I2 = U/R2
- I3 = U/R3
В результате получается:
- I1 = U/R1 = 10/2=5 Ампер
- I2 = U/R2 = 10/5=2 Ампера
- I3 = U/R3 = 10/10=1 Ампер
После этого используется формула расчета общего сопротивления цепи, позволяющая определить силу тока, проходящую по ней.
Следовательно, Iобщ = 5 + 2 + 1 = 8 Ампер.
В результате получается I=I1 + I2 + I3 = 5+2+1=8 Ампер
Комбинированное соединение
На практике используются довольно сложные электроцепи, состоящие и из последовательно подключенных сопротивлений, и из параллельно. Такую цепь следует разбить на отдельные участки, включающие элементы, соединенные только последовательным способом или только параллельным.
Расчет следует начинать с того участка цепи, который является наиболее удаленным от двух конечных выводов, выступающих в роли контактов общего сопротивления. Схему соединения элементов, называемую «треугольником» можно трансформировать в «звезду» и обратно.

Чтобы не напрягаться с различными расчетами, на практике очень часто используют онлайн-калькуляторы.
Видео по теме
Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.
Лучший ответ
АлчEноК
Высший разум
(289636)
11 лет назад
Общее сопротивление цепи при прямом соединении равно сумме сопротивлений, то есть R1+R2+R3+..+Rn.
сложить все сопротивления. /
последовательные по формуле R=R1+R2
параллельные по формуле R=R1R2/(R1+R2)
..удачи.. =)
Остальные ответы
Элина
Гений
(52643)
11 лет назад
Электрические цепи постоянного тока и методы их расчета http://zao-tehnolog.ru/page918222
—
если элементы соединены последовательно, то общее сопротивление цепи вычисляется сложением всех сопротивлений R=R1+R2
параллельно- R=R1R2/(R1+R2)
Юлия Новокрещенова
Ученик
(190)
7 лет назад
все легко -Вот формула для параллельного соединения R=R1*R2(R1+R2)
Scamp
Знаток
(402)
5 лет назад
Вот
