Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
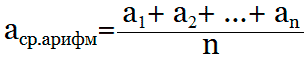
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Как считается среднее арифметическое?
Анонимный вопрос
30 октября 2018 · 98,0 K
Среднее арифметическое – это сумма всех чисел, подлежащих усреднению, деленная на их количество.
Для вычисления среднего арифметического необходимо выполнить следующие действия:
1. Сложить все числа, которые нужно усреднить.
2. Разделить полученную сумму на количество чисел.
Формула для вычисления среднего арифметического:
Среднее арифметическое = (a1 + a2 + … + an) / n
Где a1, a2, …, an – числа, которые нужно усреднить, а n – их количество.
387
Комментировать ответ…Комментировать…
Среднее арифметическое рассчитывается как сумма всех чисел, деленная на количество этих чисел. То есть, если у нас есть числа 1, 2, 3, то их среднее арифметическое будет (1+2+3)/3 = 2.
15,4 K
Спасибо большое за то что объяснили
Комментировать ответ…Комментировать…
> как читают средние арифметическое,Просто, берём числа 5, 7, 10
> мы их складываем
> 5+7+10 =22
> Потом умножаем на то количество цифер сколько их в уравнение, у нас их 3 значит
> 22 / 3 = 7 ,3
> Ответ:7,3 Читать далее
7,6 K
Комментировать ответ…Комментировать…
Мне интересны множество тем: от психологии до космоса…) · 31 окт 2018
Среднее арифметическое – самый простой, и потому часто используемый, показатель для сравнения данных, а также вычисления приемлимого значения.
Рассчитывается как частное от деления суммы значений массива данных на количество значений в массиве.
9,1 K
Комментировать ответ…Комментировать…
Найти среднее арифметическое можно таким способом:
например, у вас есть числа 5, 9 и 10. Для начала нам нужно сложить эти числа , всего получается 24. Всего у нас три числа, значит 24 нужно поделить на 3. Получается 8. (24:3=8)
2,7 K
Комментировать ответ…Комментировать…
Найти среднее арифметическое можно по такой схеме
Среднее арифметическое=сумма всех чисел:количество слагаемых.
Пример, найдем среднем арифметическое чисел 12,11 и 4
1.12+11+4=27=27:3(делим на три потому что у нас три слагаемых) =9
Среднее арифметическое равно 9
9,9 K
Комментировать ответ…Комментировать…
Что бы посчитать среднее арифметическое,нужно все числа сложить, а потом разделить на их численность.
Пример: 1,2,3
1)1+2+3=6
2)6:3=2.
Ответ:среднее арифметическое равно двум.
25,9 K
Комментировать ответ…Комментировать…
Среднее арифметическое значение можно вычилисть вот таким способом.
Допустим у вас есть три числа: 2, 8 и 12.
Нужно вычислить среднее арифметическое.
Сумма всех этих чисел равна 22.
Всего этих чисел три.
22 / 3 = 7,3 (это среднеарифметическое). Читать далее
471
22/3 не равно в точности 7,3. Получается, что и метод не объяснен, и пример неточный.
Комментировать ответ…Комментировать…
13 мая 2021 г.
Арифметика может помочь людям множеством способов, некоторые из которых более распространены, чем другие. Одной из наиболее распространенных форм арифметики является вычисление среднего значения, которое является средним значением набора чисел. Понимание того, что такое среднее значение, а также как его вычислить, может помочь вам проводить расчеты, такие как средние оценки, средние денежные значения и другие полезные числовые значения. В этой статье мы объясним, что такое среднее значение набора чисел, покажем вам, как вычислить среднее значение, и опишем ситуации, в которых может потребоваться вычисление среднего значения.
Какое значение?
Среднее значение — это среднее числовое значение набора чисел. Люди могут использовать среднее значение для расчета средней оценки из набора оценок за тест или затрат в месяц для личных бюджетов. В отличие от медианы или моды, среднее значение является более традиционным методом расчета среднего. Среднее значение не обязательно приводит к одному из заданных чисел, которое появляется в наборе, который вы вычисляете.
Почему важно знать среднее значение?
Знание того, как рассчитать среднее значение, важно, потому что вы можете использовать его во многих статистических, математических и часто встречающихся жизненных ситуациях. Вы можете взять среднее значение своих оценок, расходов или общих средних значений, найдя среднее значение. Знание среднего может помочь свести к минимуму ошибку при прогнозировании любого отдельного значения в ваших данных. Среднее также может применяться к нескольким типам и типам чисел, например к денежным значениям. Знание того, как вычислить среднее значение, гарантирует, что ваши данные непротиворечивы и точны.
Как рассчитать среднее значение?
Формула для вычисления среднего значения набора чисел выглядит следующим образом:
(Сложение чисел)/общее число в наборе = среднее
Например, среднее числового набора 1, 2, 3, 4 и 5 выглядит следующим образом:
1 + 2 + 3 + 4 + 5 = 15
(15)/5 = 3
Следовательно, среднее значение равно 3 для этого набора чисел.
В чем разница между средним и медианой?
Разница между средним значением и медианой заключается в формуле для каждого из них. Среднее значение — это среднее значение набора чисел, а медиана — это расчет, используемый для определения середины набора чисел. Преимущества нахождения медианы включают тот факт, что экстремальные выбросы в наборе данных не влияют на медиану так сильно, как на среднее значение. Если вы хотите найти среднее значение набора чисел, включающего один или несколько экстремальных выбросов, вы можете найти медиану вместо среднего для более точного результата.
Формула медианы выглядит следующим образом:
Либо: если общее количество чисел в наборе нечетное, среднее число в наборе является медианой.
Или: если общее количество чисел в наборе четное, возьмите два средних числа, сложите их и разделите это число на два.
Например, если вы хотите вычислить медиану набора 2, 3, 4, 5 и 6, вы должны просто извлечь среднее число, которое в данном случае равно 4.
Чтобы вычислить медиану набора 2, 3, 4 и 5, вы складываете два средних числа и делите это число на два:
(3 + 4)/2 = 3,5
Медиана = 3,5
Связанный: Как рассчитать операционный доход
Каковы некоторые примеры ситуаций, когда вы могли бы использовать среднее значение?
Есть много ситуаций, в которых вы бы использовали среднее значение набора чисел для вычисления чего-либо. Некоторые из этих ситуаций включают следующее:
Средние оценки
Джейкоб хочет, чтобы в его табеле успеваемости по математике за неделю было не менее 85 баллов. Чтобы понять общую оценку, которую он получил за последнюю неделю, он подсчитывал среднее значение своих баллов. Оценки, которые Джейкоб получил на прошлой неделе, были 87, 65, 93, 89 и 72.
Чтобы рассчитать средний балл Джейкоба за эту неделю, он воспользовался формулой среднего:
(87 + 65 + 93 + 89 + 72)/5 = Среднее
Среднее значение = 81,2
Это означает, что средняя оценка Джейкоба за неделю составляет 81,2. Джейкоб не достиг своей цели на этой неделе.
Статистические средние
Карл владеет кинотеатром и хочет рассчитать статистику количества положительных отзывов о конкретном фильме, оставленных людьми в течение недели, чтобы определить, следует ли ему продолжать смотреть этот фильм. Для этого он подсчитывает среднее количество положительных отзывов, которые люди оставили после просмотра фильма в его местном кинотеатре. Из 100 человек, зарегистрированных каждый день, 47 оставили положительный отзыв в понедельник, 26 оставили положительный отзыв во вторник, 59 оставили положительный отзыв в среду, 93 оставили положительный отзыв в четверг и 82 оставили положительный отзыв в пятницу.
Он вычисляет свою среднюю формулу следующим образом:
(47 + 26 + 59 + 93 + 82)/5 = Среднее
Среднее значение = 61,4
В среднем более половины зрителей оставили положительные отзывы об этом фильме, поэтому Карл продолжает показывать этот фильм в своем кинотеатре.
Результаты исследований
Венди — директор школы. Она провела опрос, который показал, что 73 из 100 учеников ее школы предпочитают использовать в классе учебники, а не планшеты. Тем не менее, она проводит опрос еще пять раз в этом году, чтобы убедиться, что ее результаты точны. Результаты были 89, 74, 62, 82 и 90. Чтобы вычислить среднее значение, она применяет следующую формулу:
(73 + 89 + 74 + 62 + 82 + 90)/6 = Среднее
Среднее значение = 78,3
Таким образом, среднее количество учеников, предпочитающих учебники, составляет 78,3 из 100. Венди решает отдать предпочтение обучению по учебникам, а не по планшетам в классах своей школы.
Средняя посещаемость
Барбара владеет местным театром, в котором недавно ставили спектакль в течение пяти вечеров, и она хочет знать, сколько людей в среднем посещало спектакль каждый вечер. В первый вечер пришло 200 человек, во второй — 340, в третий — 220, в четвертый — 345, а в последний вечер — 456 человек. Она применяет формулу среднего к этим данным следующим образом:
(200 + 340 + 220 + 345 + 456)/5 = Среднее
Среднее значение = 312,2
В результате среднего расчета Барбара обнаружила, что средняя посещаемость составляет чуть более 312 посетителей за ночь, что она считает успехом.
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Здесь для определения отрезка ![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)


Линейное преобразование[править | править код]
Линейно преобразованный набор данных 





Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:
$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.
Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент 
Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического

Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
- ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
- Среднее арифметическое взвешенное
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика



![{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)
