| Удельное электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
СИ:L3MT-3I-2 СГС:T |
| Единицы измерения | |
| СИ | Ом·метр |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле 

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[править | править код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения 
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Зависимость от температуры[править | править код]
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
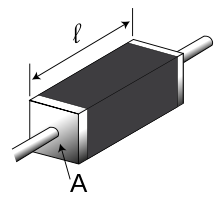
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля 


Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент 
В анизотропном, но однородном веществе тензор 
Тензор 



Как и для всякого симметричного тензора, для 
ортогональную систему декартовых координат, в которых матрица 






Величины 
Связь с удельной проводимостью[править | править код]
В изотропных материалах связь между удельным сопротивлением 

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления 

Из этого равенства и приведённого ранее соотношения для 
где 

Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
| Вещество | ρ, Ом·мм²/м |
|---|---|
| Сжиженные углеводородные газы | 0,84⋅1010 |
Тонкие плёнки[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», 

См. также[править | править код]
- Электрическое сопротивление
- Сверхпроводимость
- Закон Ома
- Удельная проводимость
- Отрицательное сопротивление
- Импеданс
- Температурный коэффициент электрического сопротивления
Примечания[править | править код]
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Литература[править | править код]
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
Что это такое
Удельным сопротивлением проводника называется физический вид величины, который показывает, что материал может препятствовать электротоку. По-другому, это такое сопротивление металлов, которое оказывает материал с единичным сечением сопротивление протекающему току. Отличается удельное сопротивление постоянному току тем, что оно вызывается током на проводник. Что касается переменного тока, то он появляется в проводнике под действием вихревого поля.

Важно также уточнить, что собой представляет удельная электрическая проводимость. Электропроводимость — это величина, которая обратна сопротивлению и называется электропроводностью. Это показатель, показывающий меру проводимости силы электротока.
Обратите внимание! Чем больше он, тем лучше способен проводник проводить электричество.

Формула
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.
Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.
Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Что такое общее сопротивление цепи
Если говорить простыми словами, общее сопротивление электрической цепи – это такое R, которое она оказывает на напряжение в ее проводниках и приборах. Существует два типа напряжения (исходя из силы тока) – постоянное и переменное. Так же и сопротивление делится на активное и реактивное, которое, в свою очередь, подразделяется на индуктивное и емкостное. Активный тип не зависит от частот сети. Также для него абсолютно не важно, какой ток протекает по проводникам. Реактивный же, наоборот, зависит от частоты, причем емкостная характеристика в конденсаторах и индуктивная в трансформаторах ведут себя по-разному.

Помимо сопротивления подключенных в сеть электроприборов, на общее состояние оказывают влияние даже промежуточные провода, также имеющие сопротивляемость напряжению.
Резистор – основной элемент сопротивляемости цепи
Какие существуют виды
Их немного, одно из которых мы уже разобрали:
- омическое;
- активное;
- индуктивное;
- ёмкостное.
Формулы расчёта электрического сопротивления для переменного тока
К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.

Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:
- R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
- I (сила тока). Латинская «I», как проводок, по которому идёт ток.
- U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.
Ну и, конечно, формула закона Ома для участка цепи.

- R=U/I т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).
- U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
- I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.
Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»

Представьте перед собой электрическую цепь, по которой проходит ток, напряжение и сопротивление. И встаёт вопрос, как понять где что и в каких размерах. Для этого вывели формулу.

Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».

Активного сопротивления
Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.
Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.

Подключим к нашей цепи проводник. Проводником может выступать лампа.

Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.
Мы ищем полное сопротивление. Обозначается большой буквой Z.

Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.
Формула, как рассчитать силу тока:
I=U/Z
Индуктивного сопротивления
Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».
Начнем с обозначения:
- XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
- f — частота, в Гц;
- сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
- единица СИ индуктивного сопротивления: [XL] = Ом;
- запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
- XL=2π×f×L;
- формула расчета мощности по напряжению: P = U×I;
- мощность электрического тока вычисляется в Ватах.
Емкостного
Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.
Единица измерения сопротивления неизменно остается Ом.

- Xc = 1/ωC;
- ω — циклическая частота;
- С — ёмкость.
Полного
Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.

Чтобы определить полное сопротивление цепи:
R = R1 +R2 (проводников может быть несколько).
Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.

Нахождение параметра
Найти сопротивление — значит, рассчитать потери тока. Существует 2 принципиально разных подхода к расчёту. В одном случае он ведётся для электрической цепи, а в другой — для материала. Если во втором случае всё предельно понятно, используется одна формула, в которую подставляют размеры тела и табличное значение удельной проводимости, то для электрической цепи не так всё просто.
В цепи может встречаться 3 вида соединения элементов:
- Параллельное. При таком соединении цепь разветвляется, то есть появляются ветви, по которым течёт ток. Ветви могут пересекаться между собой.
- Последовательное. Схема соединения представляет единую цепь, в которой нет разветвлений.
- Смешанное. Состоит из комбинированного соединения, включающего комбинации из параллельного и последовательного подключения.
Вычисление сопротивления для каждого типа соединения имеет особенности. При последовательном включении общее значение определяется путём простого складывания: R = r1 + r2 +…+ rn. При параллельном же соединении полное сопротивление цепи будет меньше самого малого из сопротивлений ветвей. Для такого включения верна формула: 1 / R = 1 / r1 + 1 / r2 +…+ 1 / rn.
Принцип расчёта смешанного соединения построен на группировке электрической цепи по виду подключения элементов. Определение параметра выполняют поочерёдно. Сначала высчитывают сопротивление одного узла, включающего однотипное соединение, затем к результату добавляют следующий элемент. Эту операцию повторяют до тех пор, пока не останется один элемент.
В радиотехнике деталь, применяющуюся в качестве сопротивления, называют резистором. С его помощью обозначают и так называемый эквивалентный параметр, используемый при расчётах электрических цепей. Его вводят, если нужно определить, например, мощность источника тока, выходное напряжение.
Таким образом, чтобы правильно посчитать сопротивление, нужно учитывать несколько факторов. При этом нужно помнить о единой системе измерений. Следует придерживаться СИ. Все величины, используемые в формулах, должны подставляться в стандартных единицах измерения. Почти во всех таблицах значение удельного сопротивления даётся в мм2/м, что связано с измерением площади.
Зависимость удельного сопротивления от температуры
Говоря об удельном сопротивлении, нельзя упомянуть о влиянии температуры окружающей среды на его значение. Однако, это влияние будет разным для каждого материала. Это объясняется одним важным параметром $α$ — температурным коэффициентом.
Температурный коэффициент используется в формула для расчета удельного сопротивления с учетом изменения температуры:
$ρ_t =ρ_0 • [1+α•(t-t_0)]$, где
- $ρ_0$ — удельное сопротивление при 20 С*,
- $α$ — температурный коэффициент,
- $t-t_0$ — разница температур.

Рассчитаем удельное сопротивление меди при -30 C и +30 C .
Пример 1
Для расчета удельного сопротивления при +30 C*, нужно взять первую формулу и подставить известные значения:
$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017• [1+0,0039•(30-20)]=0,017•[1+(0,0039•10)]=0,0176 $
Для расчета удельного сопротивления при -30 C*, нужно взять вторую формулу и выполнить аналогичный расчет:
$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017 • [1+(0,0039 • (– 30 – 20)=0,0136$
Исходя из расчетов можно сделать вполне логичный вывод, который заключается в следующем.
Замечание 2
Чем выше температура окружающей среды, тем выше удельное сопротивление.
Подробнее о проводимости и сопротивлении
Способность проводника проводить электрический ток характеризуется его удельным сопротивлением, которое можно найти через формулу удельного сопротивления, или удельной проводимостью, рассчитывающейся как обратное проводимости. Величина данных параметров определяется как химическими свойствами материала проводника, так и внешними условиями. В частности температурой окружающей среды.
Для большинства металлов удельное сопротивление при нормальной температуре пропорционально ей, то есть р ~ T. Однако при низких температурах наблюдаются отклонения. У большого ряда металлов и сплавов при температурах, близких к 0°К, расчет сопротивления показывал нулевые значения. Это явление получило название сверхпроводимости. Таким свойством обладают, например, ртуть, олово, свинец, алюминий и др. Для каждого металла существует свое критическое значение температуры Tk, при которой наблюдается явление сверхпроводимости.
Также отметим, что определение удельного сопротивления цилиндра можно обобщить для проводов, состоящих из одного материала. В таком случае площадь поперечного сечения из формулы удельного сопротивления будет равна сечению провода, а l — его длине.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ {displaystyle rho } и удельной проводимостью σ {displaystyle sigma } выражается равенством
ρ = 1 σ . {displaystyle rho ={frac {1}{sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {displaystyle rho _{ij}} и тензора удельной проводимости σ i j {displaystyle sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {displaystyle J_{i}({vec {r}})=sum _{j=1}^{3}sigma _{ij}({vec {r}})E_{j}({vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {displaystyle E_{i}({vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {displaystyle rho _{11}={frac {1}{det(sigma )}},} ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {displaystyle rho _{12}={frac {1}{det(sigma )}},}
где det ( σ ) {displaystyle det(sigma )} — определитель матрицы, составленной из компонент тензора σ i j {displaystyle sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов.
Удельное электрическое сопротивление
Экспериментальным методом было установлено, что сопротивление электрического тока проводника зависит от его размеров: длина, ширина, высота. А также от его формы (сфера, цилиндр) и материала, из которого он сделан. Таким образом, формула удельного сопротивления, например, однородного цилиндрического проводника будет: R = р*l/S.
Если в этой формуле положить s = 1 м2 и l = 1 м, то R численно будет равен р. Отсюда вычисляется единица измерения для коэффициента удельного сопротивления проводника в СИ — это Ом*м.

В формуле удельного сопротивления р — это коэффициент сопротивления, определяемый химическими свойствами материала, из которого изготовлен проводник.
Для рассмотрения дифференциальной формы закона Ома, необходимо рассмотреть еще несколько понятий.
Формулировка закона
Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.

Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.
Закон в простой форме
Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R. Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.

Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
I = ε/(R + r)
I — сила тока [A]
ε — ЭДС [В]
R — сопротивление [Ом]
r — внутреннее сопротивление источника [Ом]
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Как определить формулой общее сопротивление цепи
Из закона Ома исходит то, что общее сопротивление равно общему напряжению, деленному на общую силу тока в цепи. При параллельном подключении напряжение, как уже было сказано, равно везде, поэтому необходимо узнать его значение на любом участке цепи. С током все сложнее, так как на каждой ветке его значение свое и зависит от конкретного R.
Вам это будет интересно Особенности пайки
Также необходимо помнить, что могут быть параллельные подключения с нулевым значением R. Если в какой-либо ветке нет резистора или другого подобного элемента, но весь ток будет течь через нее и все общее значение для цепи станет нулевым. На практике это случается при выходе резистора из строя или при замыкании. Такая ситуация может навредить другим элементам из-за большой силы тока.

Как образуется сопротивление проводников
Современные воззрения говорят: свободные электроны перемещаются по проводнику со скоростью порядка 100 км/с. Под действием возникающего внутри поля дрейф упорядочивается. Скорость перемещения носителей вдоль линий напряженности мала, составляет единицы сантиметров в минуту. В ходе движения электроны сталкиваются с атомами кристаллической решетки, некая доля энергии переходит в тепло. И меру этого преобразования принято называть сопротивлением проводника. Чем выше, тем больше электрической энергии переходит в тепло. На этом основан принцип действия обогревателей.
Параллельно контексту идет численное выражение проводимости материала, которое можно увидеть на рисунке. Для получения сопротивления полагается единицу разделить на указанное число. Ход дальнейших преобразований рассмотрен выше. Видно, что сопротивление зависит от параметров – температурное движение электронов и длина их свободного пробега, что прямо приводит к строению кристаллической решётки вещества. Объяснение – сопротивление проводников отличается. У меди меньше алюминия.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Катушка индуктивности
Катушки индуктивности представляет собой устройство, главной частью которого является проводящий металл, скрученный в некое подобие колец либо обернутый вокруг диэлектрического сердечника. Если через такое устройство проходит электрический ток, то формируется местное магнитное поле. Это происходит из-за концентрации переменного магнитного поля.
Для вычислительной техники используется дроссель, который применяется для питания различного высокоточного оборудования. Устройство требуется для снижения колебаний переменного напряжения. С добавлением частоты сопротивление соответственно увеличивается. Технические параметры дросселя зависят от площади поперечного сечения проводящего материала, числа витков вокруг сердечника из диэлектрика.
Формула как найти
Согласно положению из любого учебного пособия по электродинамики, удельное сопротивление материала проводника формула равна пропорции общего сопротивления проводника на площадь поперечного сечения, поделенного на проводниковую длину
Важно понимать, что на конечный показатель будет влиять температура и степень материальной чистоты. К примеру, если в медь добавить немного марганца, то общий показатель будет увеличен в несколько раз

Интересно, что существует формула для неоднородного изотропного материала. Для этого нужно знать напряженность электрополя с плотностью электротока. Для нахождения нужно поделить первую величину на другую. В данном случае получится не константа, а скалярная величина.
Закон ома в дифференциальной форме
Есть другая, более сложная для понимания формула для неоднородного анизотропного материала. Зависит от тензорного координата.
Важно отметить, что связь сопротивления с проводимостью также выражается формулами. Существуют правила для нахождения изотропных и анизотропных материалов через тензорные компоненты
Они показаны ниже в схеме.

Электросопротивление других металлов
Кроме меди и алюминия, в электротехнике используются другие металлы и сплавы:
- Железо. Удельное сопротивление стали выше, но она прочнее, чем медь и алюминий. Стальные жилы вплетаются в кабеля, предназначенные для прокладки по воздуху. Сопротивление железа слишком велико для передачи электроэнергии, поэтому при расчёте сечения жилы не учитываются. Кроме того, оно более тугоплавкое, и из него изготавливаются вывода для подключения нагревателей в электропечах большой мощности;
- Нихром (сплав никеля и хрома) и фехраль (железо, хром и алюминий). Они обладают низкой проводимостью и тугоплавкостью. Из этих сплавов изготавливаются проволочные резисторы и нагреватели;
- Вольфрам. Его электросопротивление велико, но это тугоплавкий металл (3422 °C). Из него изготавливаются нити накала в электролампах и электроды для аргонно-дуговой сварки;
- Константан и манганин (медь, никель и марганец). Удельное сопротивление этих проводников не меняется при изменениях температуры. Применяются в претензионных приборах для изготовления резисторов;
- Драгоценные металлы – золото и серебро. Обладают самой высокой удельной проводимостью, но из-за большой цены их применение ограничено.
Удельное сопротивление различных металлов
Чтобы рассчитать потери, которые обеспечивает определенная длина проводника, удобно оперировать удельными параметрами. Базовая формула для вычисления электрического сопротивления:
R = p*(L/S),
где:
- L – длина в метрах;
- S – площадь поперечного сечения, мм кв.;
- p – удельное сопротивление кабеля, изготовленного из определенного материала, (Ом*мм кв.)/м.
При необходимости сечение можно вычислить по диаметру (D), применив известную формулу из геометрии:
S = (π * D2)/4.
Если микрометр отсутствует, применяют намотку провода на цилиндрический инструмент (отвертку, карандаш). Далее измеряют длину созданной катушки обычной линейкой, делят полученное значение на количество витков.
Измерение диаметра подручными средствами
Медь и алюминий
Для значительного изменения сопротивления провода достаточно минимального количества примесей. Однако даже при высокой степени очистки медь гораздо лучше проводит электрический ток, по сравнению с алюминием. Ниже приведены значения удельного сопротивления соответствующих материалов. С применением справочных сведений несложно проверить потери при выборе кабельной продукции для формирования трассы определенной длины:
- pм = 0,0175;
- pа = 0,028.
Другие металлы
Удельное сопротивление нихрома составляет от 1,04 до 1,42 (Ом*мм кв.)/метр. Большой разброс параметров объясняется пропорциональным изменением составляющих сплава. Такие материалы применяют для создания нагревательных элементов, так как целостность изделий сохраняется при высокой температуре. С учетом высокого сопротивления нихромовой проволоки на единицу длины этот кабель идеально подходит для создания «теплого пола».
Особенности других материалов (удельное сопротивление Ом*мм кв.)/м):
- золото (0,023) обеспечивает хорошую проводимость и устойчивость к окислению, но стоит дорого;
- ограниченное применение серебра (0,015) также объясняется высокой ценой;
- высокая температура (+3 422°C) плавления вольфрама (0,05) позволяет применять его для изготовления спиралей классических ламп накаливания;
- константан (0,5) применяют для создания резисторов.
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10-20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Медь
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м3. Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Таблица удельных сопротивлений проводников
| Проводник | Удельное сопротивление ρ | Температурный коэффициент α |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан | 0,5 | 0,05 |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин | 0,43 — 0,51 | 0,01 |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Где: удельное сопротивление ρ измеряется в Ом*мм 2 /м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 -3 *C -1 (или K -1 ) .
Пример из практики
Последовательно с источником освещения включен тестер. Напряжение осветительного прибора = 220 Вольт. Мощность неизвестна. На показателе амперметра указано 276 миллиампер тока. Какая величина у спирали лампы при последовательном включении в схему резисторов?
Формула нахождения сопротивления спирали
Электросопротивление представляет собой физическую величину, которая соответствует степени препятствия движению электрических частиц у каждого материала. Возможно измерить уровень величины мультиметром. В таком случае придется находить значение по формуле. Для предотвращения попадания электрического тока на непредназначенные для этого участки желательно заземлять линии передачи. Данная физическая величина используется во многих радиодеталях, например, светодиодах. В электрической цепи, чтобы узнать величину, требуется подключить к вольтметру фазу и ноль при известной силе тока, затем рассчитать по закону Ома.
Источники
- https://rusenergetics.ru/ustroistvo/udelnoe-soprotivlenie
- https://hmelectro.ru/poleznye_statyi/chto-takoe-soprotivlenie
- https://nauka.club/fizika/raschyet-soprotivleniya-provodnik%D0%B0.html
- https://tokzamer.ru/informaciya/formula-elektricheskogo-soprotivleniya-dlya-novichkov
- https://master-pmg.ru/cvetmet/kak-najti-udelnoe-soprotivlenie.html
- https://skysmart.ru/articles/physics/zakon-oma
- https://amperof.ru/elektroenergia/soprotivlenie-toka-formula.html
- https://PlazmoSvarka.ru/metally/soprotivlenie-medi.html
Калькулятор сопротивлений проводов
Движение электронов зависит от однородности вещества и его структуры, которые влияют на распределение
электронов в проводнике. При температурах жидкого гелия, которая равна (–273) градуса по Цельсию удельное
сопротивление металлов уменьшается почти до полного исчезновения. При таких условиях, возникает эффект
сверхпроводимости, структура металла не имеет тормозящего влияния на движение зарядов под действием
электрического поля. Наименьшим удельным сопротивлением обладает серебро и является лучшим проводником.
Сопротивление металлического проводника прямо пропорционально его длине,
удельному сопротивлению и обратно пропорционально площади его поперечного сечения.

ρ – удельное сопротивление (Ом × м),
L – длина проводника (м),
А – площадь поперечного сечения проводника (м2),
D – диаметр (м),
Расчёт сопротивлений проводов
Введите значение длины, материала а так же либо диаметр,
либо площадь поперечного сечения проводника
Справочные значения ρ-(удельного сопротивления) для основных металлов
Введите значения
Площадь поперечного сечения
А
![]()
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Удельное сопротивление металлов


4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
Величина удельного сопротивления характеризует способность вещества ограничивать электрический ток (оказывать сопротивление). Металлические проводники имеют самые низкие значения удельных сопротивлений, поэтому они используются и для передачи электроэнергии на большие расстояния, и в качестве соединительных проводов в электронных приборах, и соединительных дорожек на платах микросхем. Разберемся почему металлы обладают этим свойством и какие из них лучше всего подходят для этих целей.
Определение удельного сопротивления
Общая формула для вычисления удельного сопротивления ρ любого вещества выглядит следующим образом:
$ ρ = R * { S over L } $ (1),
где: R — сопротивление, S — площадь поперечного сечения, L — длина проводника. На основании экспериментальных данных, пользуясь законом Ома и этой формулой, определены удельные сопротивления большого числа материалов, которые приведены в справочниках и на специализированных интернет-ресурсах.
Единицы измерения удельного сопротивления
Из формулы (1) следует, что поскольку в Международной системе СИ сопротивление измеряется в омах, длина и площадь в метрах и метрах квадратных соответственно, то единицей измерения удельного сопротивления будет Ом*м:
$ [ρ] = {{[Oм]*[м^2]}over [м]} = [Oм]*[м] $ (2).
Для практических расчетов часто используется внесистемная единица Ом*мм2/м. Эта единица равна удельному сопротивлению вещества, из которого сделан проводник длиной 1 м и площадью поперечного сечения 1 мм2. Числовые значения для ρ становятся более комфортны для восприятия. Еще одна причина связана с тем, что величины сечений реальных проводов и кабелей составляют 1-10 мм2, и для вычисления их параметров внесистемная единица удобнее.
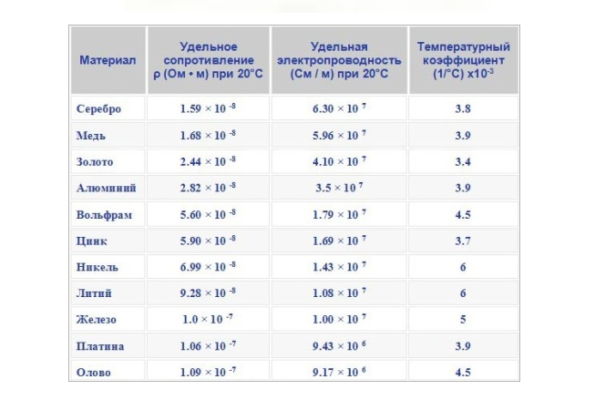
Почему у металлов самые низкие удельные сопротивления
Из приведенной таблицы видно, что самыми низкими значениями удельных сопротивлений обладают металлы: серебро, медь, золото, алюминий и др. Такое свойство металлов связано с большой концентрацией свободных электронов, “не привязанных” к конкретному атому, а блуждающих в пространстве кристаллической решетки. Напряжение, приложенное к концам проводника, создает электрическое поле, которое действует на электроны, заставляя их двигаться согласованно, в одном направлении.
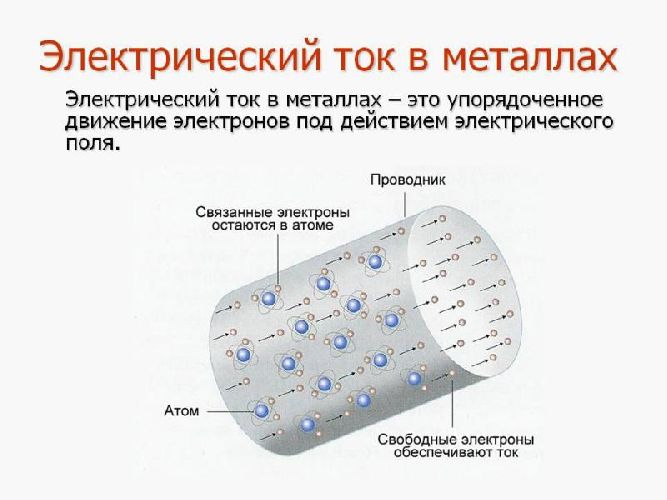
Самым низким значением ρ обладает серебро — 0,016 Ом*мм2/м. Но для повсеместного, массового, использования в сетях электроснабжения и оборудовании этот металл не используется в виду слишком большой цены. Серебро применяется для создания самых ответственных контактов в специальных электротехнических устройствах. В следующей таблице приведены величины удельных сопротивлений металлов и сплавов, часто используемых металлов в электротехнике:
Таблица
Удельные сопротивления металлов, Ом*мм2/м
(при Т = 200С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Наиболее популярными в электротехнике являются медь и алюминий. Медь и медные сплавы применяются для изготовления кабельной продукции и шунтов — деталей, ограничивающих большие токи через измерительные приборы.
Влияние температуры на удельное сопротивление
В справочниках значения ρ металлов приводятся при комнатной температуре 200С. Но эксперименты показали, что зависимость ρ(Т) имеет линейный характер и описывается формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (3),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α — температурный коэффициент сопротивления, который тоже имеет тоже индивидуален для каждого вещества. Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
- Серебро — 0,0035;
- Медь — 0,004;
- Алюминий — 0,004;
- Железо — 0,0066;
- Платина — 0,0032;
- Вольфрам — 0,0045.
Таким образом, при повышении температуры сопротивление металлов растет. Это объясняется тем, что с ростом температуры увеличивается число дефектов в кристаллической решетке из-за более интенсивных тепловых колебаний ионов, тормозящих электронный ток.
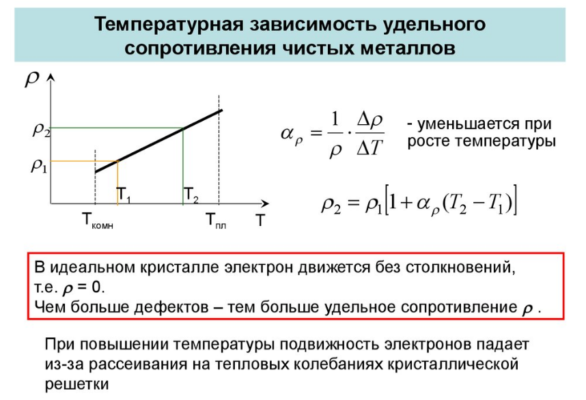
При приближении температуры металла к абсолютному нулю удельное сопротивление резко падает до нуля. Это явление называется сверхпроводимостью, а материалы, обнаруживающие такую способность, называются сверхпроводниками. Этот эффект открыл в 1911 г. голландский физик Камерлинг-Оннес. В его эксперименте удельное сопротивление ртути уменьшилось до нуля при 4,10К.

Что мы узнали?
Итак, мы узнали, что металлы обладают самыми низкими значениями удельного сопротивления среди проводников. Это свойство металлов используется для передачи электрической энергии с минимальными потерями. Алюминий, медь, сталь, серебро являются основными материалами для изготовления кабельной продукции. Удельное сопротивление металлов зависит от температуры. Таблица удельных сопротивлений металлов приведена для комнатной температуры — 200С.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 274.
А какая ваша оценка?
Удельное сопротивление
Содержание:
- Что такое удельное сопротивление
- Как образуется в материале проводимость
- Единицы измерения
- Формула расчета удельного сопротивления
-
От чего зависит сопротивление
- Связь с удельной проводимостью
- Удельное сопротивление различных материалов
Что такое удельное сопротивление
Удельное сопротивление (УС) — это свойство вещества оказывать сопротивление электротоку в момент прохождения через него.
Все вещества по способности проводить электрический ток делятся на:
- Проводники. Проводниками называют вещества, в которых находится большое количество свободных заряженных частиц — электронов. Благодаря наличию таких заряженных частиц, свободно перемещающихся по всему металлическому проводнику, электрическое поле внутри таких веществ отсутствует. Отличными проводниками, например, являются металлы.
- Полупроводники. Полупроводниками называют такие вещества, которые способны изменять удельное сопротивление в широких пределах и быстро уменьшать его значение с повышением температуры.
Как образуется в материале проводимость
Причина того, что вещества оказывают сопротивление электрическому току, кроется в том, что движению электрического тока, представляющему собой направленное движение электрических зарядов, мешают ионы кристаллической решетки вещества, движущиеся беспорядочно. Это препятствие или сопротивление электротоку влияет на его скорость — она уменьшается.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Единицы измерения
В физике символом р принято обозначать удельную проводимость вещества. Она характеризует то вещество, из которого выполнен проводник. Ее значение равняется сопротивлению проводника, длина которого составляет 1 метр, а площадь сечения — 1 (м^2.)
Единицами УС вещества в международной системе принято считать 10(м*1) (м^2 /1 м).
Так как площадь поперечного сечения часто измеряют в (мм^2), поэтому в учебниках по физике для удельного сопротивления можно встретить два варианта единиц измерения: (Ом*м) и (Ом*мм^2/м).
Формула расчета удельного сопротивления
Удельное сопротивление рассчитывается по формуле:
(p=frac{Rtimes S}l)
Где R — сопротивление проводника, S — площадь его поперечного сечения, l — его длина.
От чего зависит сопротивление
УС зависит от температуры в различных материалах. Но меняется оно по-разному:
- В проводниках p с повышением температуры увеличивается.
- В полупроводниках и диэлектриках p с повышением температуры уменьшается.
Температурный коэффициент электрического сопротивления — величина, которая учитывает изменение электрического сопротивления от температуры.
Связь с удельной проводимостью
Удельной электропроводностью называют величину, обратную удельному сопротивлению. Она обозначается символом k и измеряется в сименс/м.
Взаимосвязь двух величин выражает формула:
(p=frac1k)
Электрическое сопротивление является свойством проводника и зависит от материала, размеров и формы вещества.
Удельное электрическое сопротивление — это свойство только вещества.
Удельное сопротивление различных материалов
В таблице приведены значения УС некоторых веществ:
Опытным путём было установлено, что у металлов удельное сопротивление с повышением температуры увеличивается. Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.
Стекло и дерево имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток и являются изоляторами.
Насколько полезной была для вас статья?
Рейтинг: 2.00 (Голосов: 7)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так





![rho _{{11}}={frac {1}{det(sigma )}}[sigma _{{22}}sigma _{{33}}-sigma _{{23}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/08befe7409fd1685d379b9d3045f8b7d88b62e44)
![rho _{{12}}={frac {1}{det(sigma )}}[sigma _{{33}}sigma _{{12}}-sigma _{{13}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/023c28c36a33abc59ec81a040eeeee5d6040e007)
