Уравнения прямых в пространстве
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями
в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости
и
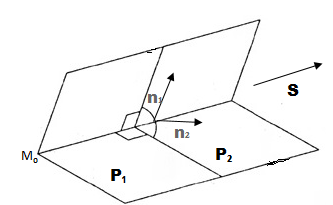
пересекаются (см. условие (4.25)), поскольку их нормали
и
неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений
(4.31)
Система (4.31) называется общим уравнением прямой в пространстве.
Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту
треугольника.
Решение. Прямая является линией пересечения двух плоскостей: плоскости
, треугольника
и плоскости
, проходящей через точку
перпендикулярно вектору
(рис.4.26). По формуле (4.21) составим уравнение плоскости
проходящей через три точки
По формуле (4.14) составим уравнение плоскости , проходящей через точку
перпендикулярно вектору
Следовательно, общее уравнение (4.31) прямой имеет вид
Параметрическое уравнение прямой в пространстве
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном пространстве заданы точка
и ненулевой вектор
(рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору
и проходящей через точку
.
Выберем на прямой произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.28).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы
и
коллинеарны. Запишем условие коллинеарности:
, где
— некоторое действительное число (параметр). Учитывая, что
, получим векторное параметрическое уравнение прямой в пространстве:
(4.32)
где — направляющий вектор прямой, а
— радиус-вектор заданной точки
принадлежащей прямой.
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где — координаты направляющего вектора
прямой. Параметр
в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина
пропорциональна расстоянию от заданной точки
до точки
. Физический смысл параметра
в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки
по прямой. При
точка
совпадает с заданной точкой
. При возрастании параметра
движение происходит в направлении направляющего вектора.
Каноническое уравнение прямой в пространстве
Выразим параметр из каждого уравнения системы (4.33):
, а затем исключим этот параметр:
(4.34)
Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.
Замечания 4.6.
1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:
а) каноническое уравнение — это уравнение
прямой, параллельной оси аппликат (рис.4.29,а);
б) каноническое уравнение — это уравнение
прямой, параллельной координатной плоскости
(рис.4.29,б).
2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор
, где
, также является направляющим вектором для той же прямой.
Переход от общего уравнение к каноническому
3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1) найти любое решение системы
определяя тем самым координаты точки
, принадлежащей прямой;
2) найти направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей:
3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):
6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки
, а коэффициентам
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
, т.е. совокупность всех прямых, проходящих через точку
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис. 4.30). Требуется:
а) составить каноническое уравнение прямой, содержащей высоту треугольника;
б) составить общее уравнение прямой, содержащей биссектрису треугольника.
Решение. а) Общее уравнение прямой получено в примере 4.13:
Перейдем от общего уравнения к каноническому.
1) Найдем любое решение системы, например,
(это координаты точки
).
2) Найдем направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей
3) Запишем каноническое уравнение (4.34): .
б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор
этой прямой. Учитывая, что диагональ ромба является биссектрисой,
, где
и
— единичные векторы, одинаково направленные с векторами
и
соответственно. Находим
Составляем каноническое уравнение прямой .
Записывая двойное равенство в виде системы, получаем общее уравнение прямой
Расстояние от точки до прямой в пространстве
Найдем расстояние от точки
до прямой
, заданной каноническим уравнением (рис.4.31)):
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, то есть.
(4.35)
Уравнение прямой, проходящей через две заданные точки
Пусть в координатном пространстве заданы две точки
и
. Требуется составить уравнение прямой, проходящей через заданные точки.
Как показано в разд., точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию (рис.4.32):
, где
— некоторое действительное число (параметр). Это уравнение, а также его координатную форму
(4.36)
будем называть аффинным уравнением прямой, проходящей через две точки и
.
Выражая параметр из каждого уравнения системы (4.36), получаем:
. Исключая параметр
, приходим к уравнению прямой, проходящей через две точки
и
:
(4.37)
Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор
т.е. подставляя
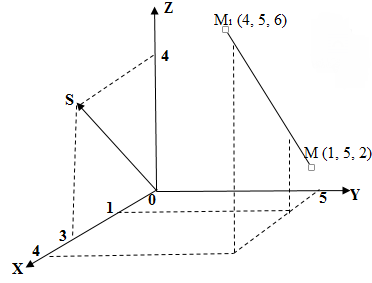
Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.33). Требуется:
а) составить уравнение прямой ;
б) составить уравнение прямой, содержащей медиану треугольника;
в) найти высоту треугольника, опущенную на сторону
.
Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки
б) Находим координаты середины стороны
. Составляем уравнение (4.37) прямой
в) Искомую высоту находим по формуле (4.35), полагая
и
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.
Уравнение прямой в пространстве: общие сведения
Уравнение прямой на плоскости в прямоугольной системе координат Oxy – это линейное уравнение с переменными x и y, которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.
Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x, y, z, которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение Ax+By+Cz+D=0, где x, y, z – переменные, а А, В, С и D – некоторые действительные числа (А, В, С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат Oxyz? Найдем ответ на этот вопрос в следующих пунктах темы.
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей
Вспомним аксиому:
Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.
Рассмотрим это утверждение в алгебраическом толковании.
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и задано, что прямая a – это линия пересечения двух плоскостей α и β, которые соответственно описываются уравнениями плоскости A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Поскольку прямая a – это множество общих точек плоскостей α и β, то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.
Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
Общее же решение системы уравнений _A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 определит координаты каждой точки прямой a, т.е. по сути задает саму прямую a.
Резюмируем: прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой уравнений двух плоскостей, которые пересекаются:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
Приведем пример описания прямой линии в пространстве при помощи системы уравнений:
x+3y-21z+113y+14z-2=0
Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.
Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.
Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.
Параметрические уравнения прямой в пространстве
x=x1+ax·λy=y1+ay·λz=z1+az·λ, где x1, y1, z1 – координаты некой точки прямой; аx, аy и az (одновременно не равны нулю) – координаты направляющего вектора прямой. а·λ – некий параметр, принимающий любые действительные значения.
Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел (x, y, z), соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ=0, тогда из параметрических уравнений прямой в пространстве получим координаты:
x=x1+ax·0y=y1+ay·0z=z1+az·0⇔x=x1y=y1z=z1
Рассмотрим конкретный пример:
Пусть прямая задана параметрическими уравнениями вида x=3+2·axy=-2·ayz=2+2·az.
Заданная прямая проходит через точку М1(3, 0, 2); направляющий вектор этой прямой имеет координаты2, -2, 2.
Ответ: 2, -2, 2,
Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.
Канонические уравнения прямой в пространстве
Если разрешить каждое из параметрических уравнений прямой
x=x1+ax·λy=y1+ay·λz=z1+az·λ относительно параметра λ, возможно просто перейти к каноническим уравнениям прямой в пространстве x-x1ax=y-y1ay=z-z1az.
Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М1(x1, y1, z1), и у которой направляющий вектор равен a→=(ax, ay, az). Например, задана прямая, описываемая каноническим уравнением x-11=y2=z+57. Эта прямая проходит через точку с координатами (1, 0, -5), ее направляющий вектор имеет координаты (1, 2, -7).
Отметим, что одно или два числа из чисел аx, аy и аz в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x-x1ax=y-y1ay=z-z1az является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:
x=x1+ax·λy=y1+ay·λz=z1+az·λ, где λ∈R.
Если одно из чисел аx, аy и az канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел аx, аy и az равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x+43=y-52=z+20, лежит в плоскости z=-2, параллельной координатной плоскости Oxy, а координатная ось Oy описывается каноническими уравнениями x0=y1=z0.
Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.
1. Общее уравнение прямой.
Прямая в пространстве
может быть задана как пересечение двух
плоскостей:

(1)
О1.
Геометрическое место точек пространства,
удовлетворяющих системе уравнений (1),
называется
прямой
в пространстве,
а
система уравнений (1) называется общим
уравнением прямой.
З1. Для того чтобы
система уравнений (1) определяла прямую
в пространстве необходимо и достаточно,
чтобы нормальные вектора плоскостей,
определяющих
прямую,
и
были неколлинеарными, т.е. выполняется
одно из неравенств:или
.
Пусть прямая
проходит через точку
параллельно вектору
,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:
.
(2)
З2. Если в уравнении
(2) одна из проекций направляющего вектора
равна 0, то это означает, что прямая
перпендикулярна соответствующей
координатной оси.
Пример 1.
Как расположена прямая
относительно координатных осей.
Согласно замечанию
2 эта прямая будет перпендикулярна осям
абсцисс и ординат (параллельна оси
аппликат) и будет проходить через точку
.
Приравняв каждую
дробь уравнения (2) параметру
,
получимпараметрическое
уравнение прямой:
Пример 2.
Записать уравнение прямой
в параметрическом виде.
Приравняем каждую
дробь к параметру
:
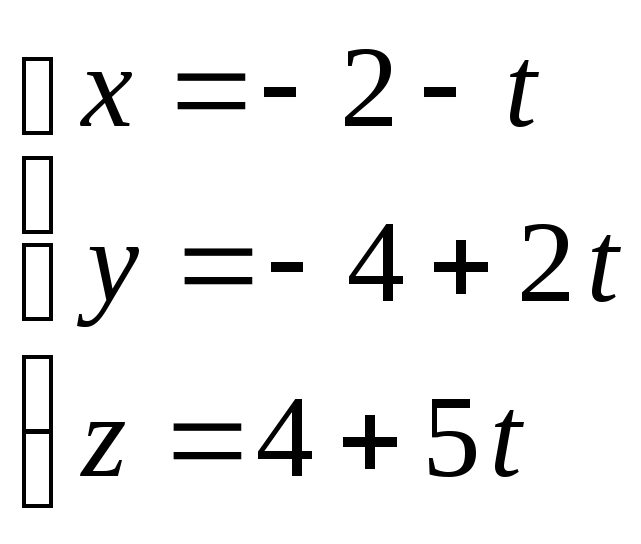
Если пря-
мая проходит через
две известные точки
и
,
то ее уравнение имеет вид (см.Лекцию
№ 7):
и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.
2. Основные задачи.
а) Переход
от общего уравнения прямой к каноническому.
Пусть прямая задана общим уравнением

Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:
– находят
координаты любой точки, удовлетворяющие
приведенной системе, для чего одну из
переменных величин, например
,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;
– направляющий
вектор
прямой находят как векторное произведение
нормальных векторов
и
:
;
– зная
точку, через которую проходит прямая,
и направляющий вектор прямой записывают
каноническое уравнение прямой.
Пример 3.
Записать уравнение прямой

Положив
,
получим СЛАУ
.
Подставив это значение переменнойво второе уравнение системы, по-лучим
.
Таким образом, прямая проходит через
точку
.
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:
б)
Угол
между пересекающимися прямыми.
Угол
между двумя пересека-ющимися прямыми
определяется как угол между их
направляющими векторами.
Если прямые
и
имеют направляющие вектора
и
,
соответственно,
то угол между прямыми определяется по
формуле:
.
Сл1.
Если
прямые перпендикулярны (),
тоусловием
перпен-дикулярности
прямых является
равенство:
.
Сл2.
Если прямые параллельны, то направляющие
вектора коллинеарны, следовательно,
условие
параллельности прямых:
.
в)
Координаты
точки пересечения прямой и плоскости.
Пусть прямая
задана общим уравнением
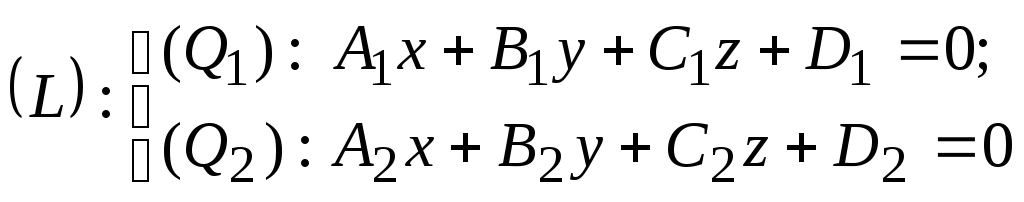
а плоскостьуравнением
.Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:

Если прямая
задана
каноническим уравнением,
а плоскость
уравнением
,
то поступают по следующей
схеме:
– переходят
от канонического уравнения прямой к
параметрическому, т.е. записывают
уравнение прямой в виде

– полученные
выражения подставляют в уравнение
заданной плоскости
и
находят параметр
:
.
Рассмотрим возможные
случаи:
1) если
выполняются условия

то прямая не пересекает плоскость
(прямая параллельна плоскости);
2) при
условиях

3) если
,
прямая пересекает плоскость в одной
точке.
– вычисляют
координаты точки пересечения, подставив
найденное значение
в параметрическое уравнение прямой

г)
Угол
между прямой и плоскостью.
Пусть дана плоскость
с нормальным вектором
и пересекающая ее прямая
с направляющим вектором
(Рис.
53).
Рис.
53.
Угол между
прямой
и
плоскостью.
Угол
является углом между прямой
и плоскостью
.
Угол между нормальным вектором плоскости
и прямой обозначим через.
Из рисунка видно, что.
Следовательно,
.
Сл1.
Если прямая
перпендикулярна плоскости (),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:
.
Сл2.
Если прямая
параллельна плоскости (),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (),
следовательно,условие
параллельности прямой и плоскости:
.
21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.
Параметрическое и каноническое уравнение прямой в пространстве
Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку
параллельно направляющему вектору
.
Пусть, – произвольная точка прямой, тогда векторы
и
коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:
(1)
это и есть канонические уравнения прямой.
Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:
(2)
Уравнение прямой в пространстве, которая проходит через две заданные точки
Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.
Итак, через две точки и
можно не только геометрично провести линию, но и сложить её уравнения.
За направляющий вектор возьмём , тогда по формуле (1) у нас получается:
(3)
уравнение прямой в пространстве, которые проходят через две заданные точки.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Общее уравнение прямой – переход к каноническому уравнению
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.
Пусть известны их уравнения:
(4)
Тогда система (4) называется общим уравнением прямой.
Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку
этой прямой.
Точку находим, как один из решений системы (4). Например, положив в (4)
находим
, тогда и точку
. Направляющий вектор
, который параллелен к каждой из плоскостей
и
и перпендикулярен к их нормальным векторам
и
, то есть
,
. (см. рис. 1). Поэтому вектор
можно найти при помощи векторного произведения
и
=
x
=
Найдены координаты и
подставим в каноническое уравнение (1).
Например, от общих уравнений прямой:
Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём
. Нормальные векторы
и
. Тогда направляющий вектор
Рис. 1
x
=
,
и канонические уравнения станут:
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Угол между двумя прямыми :
и
равен углу между их направляющими векторами и
, поэтому
=
(5)
Условия параллельности и перпендикулярности прямых соответственно запишутся:
и
.
(6)
Примеры решения задач
Давайте рассмотрим первый пример, где можно двумя способами построить прямую:
Задача
При точке и направляющем векторе
необходимо:
- составить каноническое уравнение прямой;
- построить эту прямую.
Решение
1) По формуле (1) запишем каноническое уравнение прямой :
=
.
2) Рассмотрим два способа построения прямой .
Первый способ
В системе координат строим вектор
и точку
и проводим через точку
прямую параллельную вектору
.
Второй способ
По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:
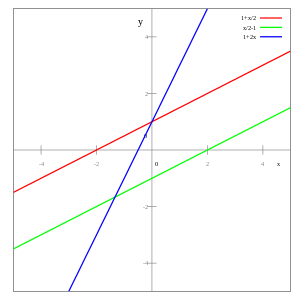
На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой
. Так при
находим координаты
. Через две точки
и
проводим прямую
.
Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:
Задача
Найти острый угол между прямыми:
,
(7)
Решение
По формуле (7) получаем:
=
=
=
Так как , тогда угол
тупой,
, а острый угол
.
Ответ
.
Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.
Задача
Составить уравнение прямой , которая проходит через точку
и параллельна прямой
.
Решение
От параметрического уравнения переходим к каноническому При условии параллельности прямых
то есть направляющим вектором новой прямой может служить известный вектор
и по формуле (1) у нас получается:
.
Ответ
.
Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий[1], их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии[2].
Прямая, наряду с окружностью, относится к числу древнейших геометрических фигур. Античные геометры считали эти две кривые «совершенными» и поэтому признавали только построения с помощью циркуля и линейки. Евклид описал линию как «длину без ширины», которая «равно лежит на всех своих точках»[3].
Аналоги прямых могут быть определены также в некоторых типах неевклидовых пространств. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то отрезок прямой можно определить как самую короткую кривую, соединяющую эти точки. Например, в римановой геометрии роль прямых играют геодезические линии, которые являются кратчайшими; на сфере кратчайшими являются дуги больших кругов[4].
Свойства прямой в евклидовой геометрии[править | править код]
Участки прямой, ограниченные двумя её точками, называются отрезками.
- Через любую точку можно провести бесконечно много прямых.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке[5], или являются параллельными (следует из предыдущего).
- В трёхмерном пространстве существуют три варианта взаимного расположения двух несовпадающих прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
- Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости[править | править код]
Способы задания прямой:
Общее уравнение прямой[править | править код]
Общее уравнение прямой линии на плоскости в декартовых координатах:
где 



При 



Вектор с координатами 
При 
Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом[править | править код]
Уравнение прямой линии, пересекающей ось 



Коэффициент 
В этом виде невозможно представить прямую, параллельную оси 
Получение уравнения прямой в отрезках
Уравнение прямой в отрезках[править | править код]
Уравнение прямой линии, пересекающей ось 



В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой[править | править код]
где 




Если прямая задана общим уравнением 









Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие 



Уравнение прямой, проходящей через две заданные несовпадающие точки[править | править код]
Если заданы две несовпадающие точки с координатами 

или
или в общем виде
Получение векторного параметрического уравнения прямой
Векторное параметрическое уравнение прямой[править | править код]
Векторное параметрическое уравнение прямой задается вектором 


Параметрические уравнения прямой[править | править код]
Параметрические уравнения прямой могут быть записаны в виде:
где 



Смысл параметра 
Каноническое уравнение прямой[править | править код]
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где 




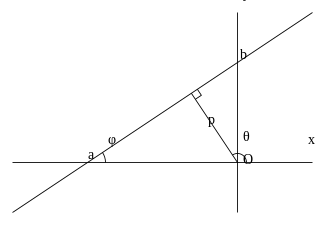
Уравнение прямой в полярных координатах[править | править код]
Уравнение прямой в полярных координатах 

или
Тангенциальное уравнение прямой[править | править код]
Тангенциальное уравнение прямой на плоскости:
Числа 

Уравнения прямой в пространстве[править | править код]
Векторное параметрическое уравнение прямой в пространстве:
где 



Параметрические уравнения прямой в пространстве:
где 
некоторой фиксированной точки 

Каноническое уравнение прямой в пространстве:
где 
некоторой фиксированной точки 

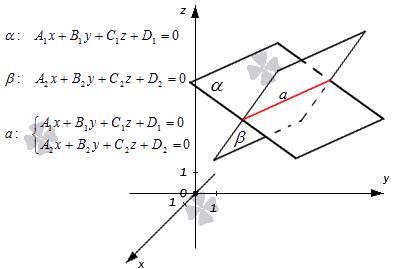
Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных плоскостей, заданных соответственно общими уравнениями:
и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[6]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой
на фиксированный направляющий вектор прямой
:
где фиксированный вектор 

Взаимное расположение точек и прямых на плоскости[править | править код]
Три точки 


Отклонение точки 

где знак перед радикалом противоположен знаку 
В пространстве расстояние от точки 
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент 
Взаимное расположение нескольких прямых на плоскости[править | править код]
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол 
При этом под 





Эти прямые параллельны, если 



Любую прямую, параллельную прямой с уравнением 

Если же уравнение прямой задано как 

Если знак перед радикалом противоположен 

Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если 



Некоторые специальные типы прямых[править | править код]
- Прямая Александрова
- Прямая Симсона
- Прямая Суслина[en]
- Прямая Эйлера
- Числовая прямая
Примечания[править | править код]
- ↑ Coxeter, 1969, p. 4
- ↑ Математическая энциклопедия, 1984, с. 721—722.
- ↑ Прокл Диадох. Комментарий к первой книге «Начал» Евклида / Университет Дмитрия Пожарского. — М., 2013. — С. 116. — 368 с.
- ↑ Норден А. П. Краткий курс дифференциальной геометрии. — М.: Физматгиз, 1958. — С. 214—215. — 244 с.
- ↑ Faber, Appendix B, p. 300.
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Литература[править | править код]
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике. — Выпуск 4. — Гостехиздат, 1952 г. — 32 стр.
- Прямая // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
- Coxeter, H.S.M (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 0-471-18283-4
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, ISBN 0-8247-1748-1
- Pedoe, Dan (1988), Geometry: A Comprehensive Course, Mineola, NY: Dover, ISBN 0-486-65812-0
- Wylie, Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, ISBN 0-07-072191-2
Ссылки[править | править код]
- Прямая на плоскости, справочник математических формул «Прикладная математика»
- Прямая в пространстве, справочник математических формул «Прикладная математика»

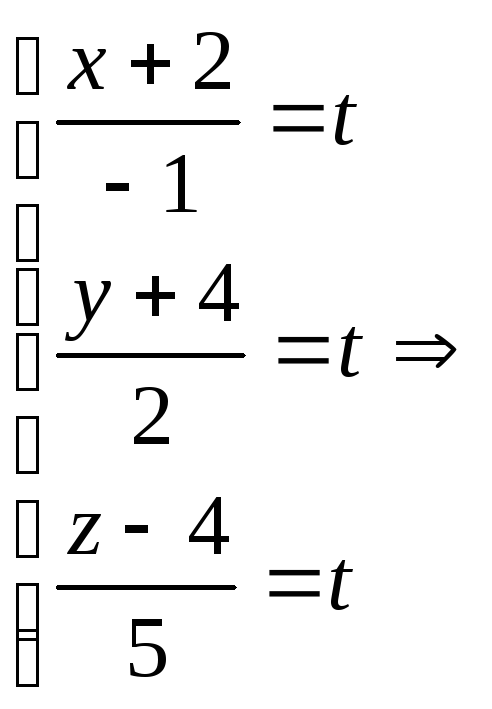


























![[{vec r},{vec a}]={vec M},](https://wikimedia.org/api/rest_v1/media/math/render/svg/940ec5302c287b63f2e45bbfb8501d3ec4133d15)












