Как найти общее время падения

Как найти время падения тела

Если пренебречь сопротивлением воздуха, время падения тела не зависит от его массы. Оно определяется только высотой и ускорением свободного падения. Если сбросить с одинаковой высоты два тела разной массы, упадут они одновременно.

Вам понадобится

• – калькулятор.

Инструкция

Высоту, с которой падает тело, переведите в единицы системы СИ – метры. Ускорение свободного падение дано в справочнике уже переведенным в единицы этой системы – метры, деленные на секунды в квадрате. Для Земли на средней полосе оно составляет 9,81 м/с². В условиях некоторых задач указаны другие планеты, например, Луна (1,62 м/с²), Марс (3,86 м/с²). Когда обе исходные величины заданы в единицах системы СИ, результат получится в единицах той же системы – секундах. А если в условии указана масса тела, игнорируйте ее. Это информация здесь лишняя, ее могут привести для того, чтобы проверить, насколько хорошо вы знаете физику.

Для вычисления времени падения тела умножьте высоту на два, поделите на ускорение свободного падения, а затем из результата извлеките квадратный корень:

t=√(2h/g), где t – время, с; h – высота, м; g – ускорение свободного падения, м/с².

Задача может требовать найти дополнительные данные, например, о том, какова была скорость тела в момент касания земли или на определенной высоте от нее. В общем случае скорость вычисляйте так:

v=√(2g(h-y))

Здесь введены новые переменные: v – скорость, м/с и y – высота, где требуется узнать скорость падения тела, м. Понятно, что при h=y (то есть, в начальный момент падения) скорость равна нулю, а при y=0 (в момент касания земли, перед самой остановкой тела) формулу можно упростить:

v=√(2gh)

После того, как касание земли уже произошло, и тело остановилось, скорость его падения снова равна нулю (если, конечно, оно не спружинило и не подпрыгнуло снова).

Для уменьшения силы удара после окончания свободного падения применяют парашюты. Вначале падение является свободным и происходит в соответствии с приведенными выше уравнениями. Затем парашют раскрывается, и происходит плавное замедление за счет сопротивления воздуха, которым теперь пренебрегать нельзя. Закономерности, описываемые приведенными выше уравнениями, больше не действуют, и дальнейшее уменьшение высоты происходит медленно.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Скорость, время и высота свободного падения

Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Скорость свободного падения

Расстояние и время свободного падения

Просто введите данные, и получите ответ.

Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.

Теория

Ускорение свободного падения

Как найти скорость свободного падения

Время свободного падения

Высота свободного падения

См. также

В статье собраны задачи, связанные с падением тел. При падении ускорение постоянно и равно 9,8 м/c. Свободно падающее тело – тело, падающее без начальной скорости, как оторвавшаяся сосулька.

Задача 1.

Свободно падающее тело в некоторый момент времени находилось на высоте м, а спустя время с – на высоте м над поверхностью земли. С какой высоты падало тело?

Итак, за 10 с тело прошло путь, равный м с известным ускорением, равным м/c. Тогда можно записать:

Здесь – скорость, которую тело приобрело к моменту, когда оно оказалось на высоте 1100 м. Эта скорость нам неизвестна, и ее можно определить из последнего уравнения. Так как тело падало свободно, следовательно, у него не было начальной скорости в самом начале падения. Тогда, узнав, какая скорость была им приобретена, мы легко установим, сколько оно пролетело до этого момента (до высоты 1100 м).

Изначально тело двигалось без начальной скорости:

Таким образом, тело всего падало c. Следовательно, за указанное время прошло путь

При этом тело не долетело до земли 120 м, а значит, падало оно с высоты м.

Ответ: 1222,5 м

Задача 2.

Тело свободно падает с высоты м. За какое время тело проходит первый и последний метр своего пути? Какой путь проходит тело за первую секунду своего движения? За последнюю секунду?

Тогда время прохождения первого метра:

Время прохождения первого метра – 0,45 с.

Чтобы найти время движения на последнем метре, придется найти общее время падения, а также время прохождения телом 99 метров пути, после чего вычесть из первого второе:

Время прохождения последнего метра – 0,01 с.

Путь, который тело проходит за первую секунду:

А за последнюю секунду… Найдем, сколько тело пролетело за время c:

Тогда оставшиеся 40 метров тело прошло за последнюю секунду.

Ответ: первый метр – за 0,45 с, последний – за 0,01 с, 4,9 м – за первую секунду полета, 40 м – за последнюю.

Задача 3.

С крыши дома сорвалась сосулька и за с пролетела мимо окна, высота которого м. С какой высоты относительно верхнего края окна  она оторвалась?

Эту задачу можно решить по-разному.

Первый способ.

Запишем путь, пройденный сосулькой до нижнего края окна:

Здесь – общее время полета сосульки с крыши до нижнего края окна.

Так как окно сосулька пролетела за 0,2 с, то до его верхнего края она летела c. Тогда искомая высота от верхнего края окна до крыши равно:

Разность этих двух расстояний – как раз высота окна:

Раскроем скобки и решим:

Решив уравнение, мы нашли общее время полета сосульки, которое дает нам возможность определить высоту, с которой она упала:

Вычтем высоту окна – и ответ готов: м.

Второй способ:

Найдем скорость, с которой сосулька подлетела к верхнему краю окна:

Здесь – время полета сосульки до окна.

Эта скорость будет служить нам начальной скоростью, когда мы будем рассматривать собственно пролет сосулькой окна. Тогда можно записать так:

Тогда искомое расстояние равно:

Ответ: от верхнего края окна до крыши 2,17 м.

Задача 4.

Мячик, отскочивший от поверхности земли вертикально вверх со скоростью м/c, пролетел мимо окна, высота которого м, за время с. На какой высоте относительно поверхности земли находится подоконник?

Решим эту задачу вторым способом (смотри предыдущую задачу). Пусть время полета от пола до подоконника – . Тогда мячик подлетел к окну со скоростью .

Высота окна может быть записана так:

Подставим :

Откуда

Тогда путь до подоконника равен:

Ответ: м

Задача 5.

Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время , а такой же последний – за время . Найти высоту, с которой падало тело.

Первый участок:

Пусть участков – штук. Тогда высота, с которой падало тело, равна , а общее время полета – .

Тело пролетело участков:

Подставим в последнее уравнение то, что записали выше:

Сокращаем и приводим подобные слагаемые:

– полное время падения, поэтому пройденный путь равен:

Откуда .

Ответ: или .

Задача 6.

Камень падает в ущелье. Через с слышен звук удара камня о землю. Определить глубину ущелья . Скорость звука м/с.

Сначала наш камень падает, а потом звук идет со дна ущелья до наблюдателя – из этих двух времен складывается . Скорость звука известна, поэтому время его распространения равно .

Найдем время падения камня.

Введем новую переменную: и решим получившееся квадратное уравнение:

Домножим на 330:

Тогда м

Ответ: 144 м.

Время свободного падения — характерное время, которое потребуется телу для коллапса под действием силы тяготения, если никакие другие силы не противодействуют коллапсу. Играет важную роль при определении временных шкал ряда астрофизических процессов, таких как звездообразование, вспышки сверхновых звёзд.

Вывод формул[править | править код]

Падение на точечный источник гравитации[править | править код]

Несложно вывести формулу для времени свободного падения, применяя третий закон Кеплера к движению объекта по вырожденной эллиптической орбите. Рассмотрим точку массы на расстоянии от точечного источника массы , на который падает точка по радиусу. Формула третьего закона Кеплера зависит от большой полуоси и не зависит от эксцентриситета. Радиальная траектория является примером вырожденного эллипса с эксцентриситетом 1 и большой полуосью, равной . Следовательно, время, которое потребуется телу для падения, поворота и возврата к изначальному положению, равно периоду обращения по круговой орбите радиуса :

Для того чтобы пояснить, почему большая полуось равна , исследуем свойства орбит при увеличении эллиптичности. Первый закон Кеплера утверждает, что орбита планеты является эллипсом с фокусом, расположенным в центре масс. В случае падения очень малой массы на очень большую массу центр масс системы расположен внутри тела массы . С увеличением эллиптичности фокус эллипса смещается всё дальше от центра системы. В предельном случае вырожденного эллипса с эксцентриситетом, равным единице, орбита превращается в отрезок от точки начального расположения объекта () до точки расположения массы . Другими словами, эллипс превращается в отрезок длины . Большая полуось является половиной длины эллипса вдоль длинной оси; в данном случае большая полуось равна .

Если бы падающее тело совершило полный оборот по орбите, то движение началось бы на расстоянии от тела , затем тело падало бы к телу , обогнуло его и вернулось к изначальному положению. В реальных системах точечный источник не является точкой и падающее тело испытает столкновение с поверхностью. Следовательно, падающее тело совершит только половину оборота по орбите. Поскольку часть орбиты, соответствующая падению, симметрична части орбиты, по которой происходит гипотетический возврат к начальной точке, то для получения времени свободного падения требуется разделить период обращения по полной орбите пополам:

.

Заметим, что в формуле является временем падения массы по орбите с большим эксцентриситетом, в рамках которой совершается быстрый поворот вокруг притягивающего центра почти на нулевом расстоянии от него, а затем происходит возврат в начальное положение на расстоянии , где снова происходит быстрый поворот. Подобная орбита соответствует почти прямолинейному движению от точки на расстоянии от притягивающего центра до точки расположения притягивающего центра. Как указано выше, большая полуось орбиты равна половине радиуса круговой орбиты, соответствующей расстоянию . Период орбиты соответствует прохождению пути, равного удвоенному значению . Тогда по третьему закону Кеплера с учётом того, что большая полуось является половиной радиуса круговой орбиты, получается, что период обращения по вытянутой орбите равен (1/2)^3/2 = (1/8)^1/2 периода обращения по круговой орбите, причем радиус круговой орбиты равен длине максимального радиус-вектора вытянутой орбиты.

Падение на сферически-симметричное распределение массы[править | править код]

Рассмотрим случай, когда представляет собой не точку, а протяженное сферически-симметричное тело, обладающее средней плотностью ,

,

где объём сферы равен

Предположим, что единственной действующей силой является сила тяготения. Тогда, как было показано ещё Ньютоном и может быть получено при применении формулы Остроградского-Гаусса, ускорение в точке на расстоянии от центра притягивающей массы зависит только от полной массы, содержащейся внутри сферы радиуса . Следствием является следующий факт: если разбить тело со сферически-симметричным распределением массы на сферические оболочки, то при коллапсе оболочки будут падать таким образом, что каждая последующая не будет при движении пересекать предыдущие. Также время падения точки нулевой массы с расстояния можно выразить в терминах полной массы внутри оболочки радиуса :^[1]

в последней формуле величины выражены в системе СИ.

Примечания[править | править код]

• Galactic dynamics Binney, James; Tremaine, Scott. Princeton University Press, 1987.

Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.

Ускорение свободного падения

Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.

Свободное падение тела

Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его. 

Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.

h=v0+gt22.

Так как начальна скорость равна нулю, перепишем:

h=gt22.

Отсюда находится выражение для времени падения тела с высоты h:

t=2hg.

Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:

v=2hg·g=2hg.

Движение тела, брошенного вертикально вверх

Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.

Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:

v=v0-gt.

Подставив v=0, найдем время подъема тела на максимальную высоту:

t=v0g.

Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.

 Максимальная высота подъема тела, брошенного вертикально:

h=v022g.

Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.

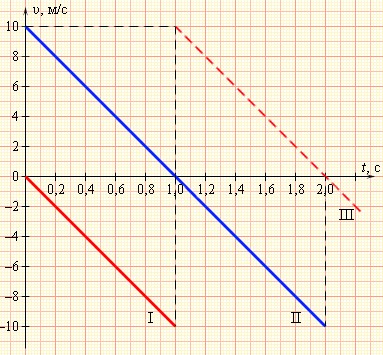
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.

Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.

Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.

Движение тела, брошенного под углом к горизонту

С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.

Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.

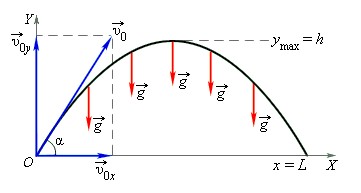
Условия для движения вдоль оси ОХ:

x0=0; v0x=v0cosα; ax=0.

Условия для движения вдоль оси OY:

y0=0; v0y=v0sinα; ay=-g.

Приведем формулы для движения тела, брошенного под углом к горизонту.

Время полета тела:

t=2v0sinαg.

Дальность полета тела:

L=v02sin2αg.

Максимальная дальность полета достигается при угле α=45°.

Lmax=v02g.

Максимальная высота подъема:

h=v02sin2α2g.

Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.