Задача 1.
Найти вторую производную от функции
![]()
Указание
Найдите вначале первую производную данной функции, а затем воспользуйтесь тем, что
![]()
Решение

Ответ: 
Задача 2.
Найти вторую производную от функции
![]()
При Х = 1.
Указание
Найдите вторую производную по формуле
![]()
А затем вычислите ее значение при Х = 1.
Решение


Ответ: ![]()
Задача 3.
Найти производную 4-го порядка от функции
![]()
Указание
Воспользуйтесь тем, что
![]()
Решение

Ответ: ![]()
Задача 4.
Найдите общее выражение для производной порядка П от функции
![]()
Указание
Воспользуйтесь тем, что
![]()
Решение
Вычислим подряд производные 1-го, 2-го, … порядка от данной функции и попробуем определить вид зависимости выражения для П-й производной от ее порядка.

Ответ: 
Задача 5.
Найдите общее выражение для производной порядка П от функции
![]()
Указание
Для упрощения воспользуйтесь формулами приведения:

Решение
![]()

Ответ: ![]()
Задача 6.
Найти вторую производную ![]() для функции, заданной параметрически:
для функции, заданной параметрически:

Указание
Воспользуйтесь формулой

Решение

Ответ: ![]()
Задача 7.
Найти D3Y для функции У = Х5.
Указание
Воспользуйтесь формулой
![]()
Решение

Ответ: ![]()
Задача 8.
Вычислите производную:
![]()
Указание
Воспользуйтесь формулой Лейбница:
![]()
Решение
Пусть
![]()
Тогда

Применяя формулу Лейбница, получим:

Ответ: ![]()
Задача 9.
Рассматриваются функции


Для какой из них выполнены все условия теоремы Ролля?
Указание
По условию теоремы Ролля функция Y = F(X)
4) непрерывна на отрезке [Ab];
5) дифференцируема во всех внутренних точках этого отрезка;
6) принимает равные значения на концах этого отрезка, то есть F(A) = F(B).
Решение
Проверим выполнение условий теоремы Ролля для каждой из функций:
![]()
Не выполнено 3-е условие теоремы Ролля;

Эта функция не дифференцируема при Х = 1, то есть не выполнено 2-е условие теоремы Ролля;
3) Х = 0 – точка разрыва данной функции, то есть не выполнено 1-е условие теоремы Ролля;
![]()
Функция Y = ln cos X определена и непрерывна на заданном отрезке;
![]()
Существует на всем отрезке;
![]()
Таким образом, все условия теоремы Ролля выполнены.
![]()
Функция не является непрерывной в точке Х = 1, не выполнено 1-е условие теоремы Ролля.
Ответ: 4.
| < Предыдущая | Следующая > |
|---|
Макеты страниц
Итак, для того, чтобы вычислить  производную от какой-либо функции, вообще говоря, нужно предварительно вычислить производные всех
производную от какой-либо функции, вообще говоря, нужно предварительно вычислить производные всех
водные всех предшествующих порядков. Однако в ряде случаев удаётся установить такое общее выражение для  производной, которое зависит непосредственно от
производной, которое зависит непосредственно от  и не содержит более обозначений предшествующих производных.
и не содержит более обозначений предшествующих производных.
При выводе таких общих выражений иногда бывают полезны формулы:

обобщающие на случай высших производных известные читателю правила I и II п° 97. Их легко получить последовательным применением этих правил.
1) Рассмотрим сначала степенную функцию  где (а — любое вещественное число. Имеем последовательно:
где (а — любое вещественное число. Имеем последовательно:

Легко усмотреть отсюда и общий закон:

но, строго говоря, он ещё подлежит доказательству. Для этого воспользуемся методом математической индукции. Допустив, что для некоторого значения  эта формула верна, продифференцируем её ещё раз. Мы придем к результату:
эта формула верна, продифференцируем её ещё раз. Мы придем к результату:

так что наша формула оказывается верной для  производной, если была верна для
производной, если была верна для  Отсюда и следует её справедливость при всех натуральных значениях
Отсюда и следует её справедливость при всех натуральных значениях 
Если, например, взять  то получим
то получим

а при 

Когда само  есть натуральное число
есть натуральное число  то
то  производная от
производная от  будет уже постоянным числом
будет уже постоянным числом  , а все следующие —
, а все следующие —
нулями. Отсюда ясно, что и для целого многочлена степени  имеет место аналогичное обстоятельство.
имеет место аналогичное обстоятельство.
2) Для несколько более общего выражения

столь же легко найдем:

В частности, получается, как и выше,

3) Пусть теперь  Прежде всего, имеем
Прежде всего, имеем

Возьмём отсюда производную  порядка по соответствующей формуле из 1), заменив в ней
порядка по соответствующей формуле из 1), заменив в ней  на
на  мы и получим тогда
мы и получим тогда

Общая формула

легко доказывается по методу математической индукции.
В частности, очевидно,

5) Положим  тогда
тогда

На этом пути найти требуемое общее выражение для  производной трудно. Но дело сразу упрощается, если переписать формулу для первой производной в виде
производной трудно. Но дело сразу упрощается, если переписать формулу для первой производной в виде  становится ясным, что при каждом дифференцировании к аргументу будет прибавляться у, так что
становится ясным, что при каждом дифференцировании к аргументу будет прибавляться у, так что

Аналогично получается и формула

6) Рассмотрим функцию  Представив её в виде
Представив её в виде

мы получаем возможность использовать пример 2) (и общие правила, указанные вначале). Окончательно,

7) В случае функции  мы употребим более искусственный приём. Именно, имеем
мы употребим более искусственный приём. Именно, имеем

если ввести вспомогательный угол  , определяемый условиями
, определяемый условиями

то выражение для первой производной можно переписать в виде:

Повторяя дифференцирование, легко установить общий закон

и обосновать его по методу математической индукции.
8) Остановимся ещё на функции  Поставим себе сначала задачей выразить
Поставим себе сначала задачей выразить  через у. Так как
через у. Так как  то
то

Дифференцируя вторично по х (и помня, что у есть функция от  получим
получим

Следующее дифференцирование дает 

Общая формула:

оправдывается по методу математической индукции.
Если (при  ) ввести угол
) ввести угол

то эта формула может быть переписана так:

или, наконец,

9) Установим в заключение, в виде упражнения, формулу

Справедливость её при  проверяется непосредственно. Допустим теперь, что она верна для всех значений
проверяется непосредственно. Допустим теперь, что она верна для всех значений  вплоть до некоторого
вплоть до некоторого  и докажем, что тогда она сохранит верность и при замене
и докажем, что тогда она сохранит верность и при замене  на
на  . С этой целью рассмотрим выражение
. С этой целью рассмотрим выражение

Пользуясь нашим допущением, можно переписать это выражение так:

Итак, формула верна для всех натуральных значений а.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:

Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:

Решение:

Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:

Пример:

Решение:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Конев В.В. Дифференцирование функций
![]()
![]()
Производные высших порядков (примеры)
![]()
![]()
-
Пусть
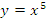 . Тогда
. Тогда
***
-
Получить общую формулу для производной n-го порядка от функции
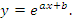
Решение.
Отметим, что полученная формула для производной n-го порядка оказывается справедливой и при n = 0:
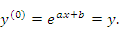
***
-
Вывести общую формулу для производной n-го порядка от функции

Решение.
При n = 0 эта формула дает правильное выражение для функции y.
***
-
Вывести общую формулу для производной n-го порядка от функции
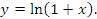
Решение.
Заметим, что полученная формула применима только при
 и, следовательно,
и, следовательно,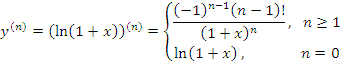
***
-
Вывести общую формулу для производной n-го порядка от функции

Решение. Представим предварительно эту функцию в виде алгебраической суммы простых дробей:
Используя формулу, полученную в примере 3, находим
***
-
Вывести общую формулу для производной n-го порядка от функции
 и вычислить эту производную в точке x = 0.
и вычислить эту производную в точке x = 0.
Решение.При каждом дифференцировании происходит сдвиг аргумента синуса на
 и, следовательно,
и, следовательно,
Очевидно, что
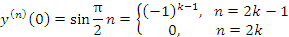
***
-
Аналогичным образом решается подобная задача для функции
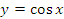 :
:

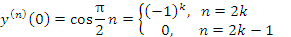
Правила вычисления производных
7 апреля 2011
- Скачать все правила
Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:
![]()
Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x
2 + (2x + 3) · e
x
· sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.
Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.
Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f(x) = C, C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем |
f(x) = x n |
n · x n − 1 |
| Синус | f(x) = sin x | cos x |
| Косинус | f(x) = cos x | − sin x (минус синус) |
| Тангенс | f(x) = tg x | 1/cos2 x |
| Котангенс | f(x) = ctg x | − 1/sin2 x |
| Натуральный логарифм | f(x) = ln x | 1/x |
| Произвольный логарифм |
f(x) = log a x |
1/(x · ln a) |
| Показательная функция |
f(x) = e x |
e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
(C · f)’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2x
3)’ = 2 · (x
3)’ = 2 · 3x
2 = 6x
2.
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Задача. Найти производные функций: f(x) = x
2 + sin x; g(x) = x
4 + 2x
2 − 3.
Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x
2 + sin x)’ = (x
2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x
4 + 2x
2 − 3)’ = (x
4 + 2x
2 + (−3))’ = (x
4)’ + (2x
2)’ + (−3)’ = 4x
3 + 4x + 0 = 4x · (x
2 + 1).
Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x
2 + 1).
Производная произведения
Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike“>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f(x) = x
3 · cos x; g(x) = (x
2 + 7x − 7) · e
x
.
Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x
3 · cos x)’ = (x
3)’ · cos x + x
3 · (cos x)’ = 3x
2 · cos x + x
3 · (− sin x) = x
2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x
2 + 7x − 7) · e
x
)’ = (x
2 + 7x − 7)’ · e
x
+ (x
2 + 7x − 7) · (e
x
)’ = (2x + 7) · e
x
+ (x
2 + 7x − 7) · e
x
= e
x
· (2x + 7 + x
2 + 7x −7) = (x
2 + 9x) · e
x
= x(x + 9) · e
x
.
Ответ:
f ’(x) = x
2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e
x
.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного
Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:
![]()
Неслабо, да? Откуда взялся минус? Почему g
2? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций:
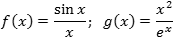
В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:
![]()
![]()
По традиции, разложим числитель на множители — это значительно упростит ответ:
![]()
Ответ:
![]()
Производная сложной функции
Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x
2 + ln x. Получится f(x) = sin (x
2 + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.
Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:
f ’(x) = f ’(t) · t ’, если x заменяется на t(x).
Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.
Задача. Найти производные функций: f(x) = e
2x + 3; g(x) = sin (x
2 + ln x)
Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e
x
. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e
t
. Ищем производную сложной функции по формуле:
f ’(x) = f ’(t) · t ’ = (e
t
)’ · t ’ = e
t
· t ’
А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:
f ’(x) = e
t
· t ’ = e
2x + 3 · (2x + 3)’ = e
2x + 3 · 2 = 2 · e
2x + 3
Теперь разберемся с функцией g(x). Очевидно, надо заменить x
2 + ln x = t. Имеем:
g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’
Обратная замена: t = x
2 + ln x. Тогда:
g ’(x) = cos (x
2 + ln x) · (x
2 + ln x)’ = cos (x
2 + ln x) · (2x + 1/x).
Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.
Ответ:
f ’(x) = 2 · e
2x + 3;
g ’(x) = (2x + 1/x) · cos (x
2 + ln x).
Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.
Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:
(x
n
)’ = n · x
n − 1
Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x
0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.
Задача. Найти производную функции:
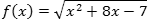
Для начала перепишем корень в виде степени с рациональным показателем:
f(x) = (x
2 + 8x − 7)0,5.
Теперь делаем замену: пусть x
2 + 8x − 7 = t. Находим производную по формуле:
f ’(x) = f ’(t) · t ’ = (t
0,5)’ · t ’ = 0,5 · t
−0,5 · t ’.
Делаем обратную замену: t = x
2 + 8x − 7. Имеем:
f ’(x) = 0,5 · (x
2 + 8x − 7)−0,5 · (x
2 + 8x − 7)’ = 0,5 · (2x + 8) · (x
2 + 8x − 7)−0,5.
Наконец, возвращаемся к корням:
![]()
Ответ:
![]()
Смотрите также:
- Вводный урок по вычислению производных степенной функции

- Уравнение касательной к графику функции

- Тест к параграфу «Что такое логарифм» (легкий)

- Комбинаторика в задаче B6: легкий тест

- Задача B2: лекарство и таблетки

- Задача B4 про шерсть и свитер

