Как найти общем шара – Сайт, где вы сможете решить свои вопросы

Объем шара через радиус

{V= dfrac{4}{3} pi R^3}

На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.

Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.

Содержание:

калькулятор объема шара
формула объема шара через радиус
формула объема шара через диаметр
формула объема шара через длину окружности
формула объема шара через площадь поверхности
примеры задач

Формула объема шара через радиус

Объем шара через радиус

{V = dfrac{4}{3} pi R^3}

R – радиус шара

Формула объема шара через диаметр

Объем шара через диаметр

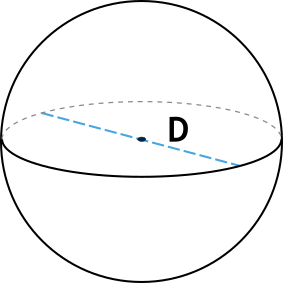
{V = dfrac{1}{6} pi D^3}

D – диаметр шара

Формула объема шара через длину окружности

Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}

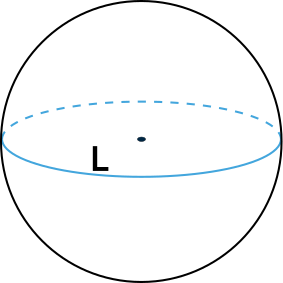
Объем шара через длину окружности

{V = dfrac{L^3}{6 pi^2}}

L – длина окружности

Формула объема шара через площадь поверхности

Объем шара через площадь поверхности

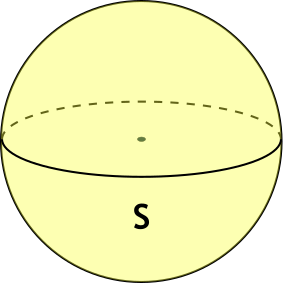
{V = sqrt{ dfrac{S^3}{36 pi}}}

S – площадь поверхности

Примеры задач на нахождение объема параллелепипеда

Задача 1

Найдите объем шара радиус которого равен 12см.

Решение

Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.

V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3

Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3

Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .

Задача 2

Найдите объем шара диаметр которого равен 12см.

Решение

В этой задаче воспользуемся формулой шара через диаметр.

V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3

Ответ: 288 pi : см^3 approx 904.77868 : см^3

И снова в проверке ответа нам поможет калькулятор .

Задача 3

Найдите объем шара диаметр которого равен 6см.

Решение

Эта задача аналогична задаче 2.

V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3

Ответ: 36 pi : см^3 approx 113.09734 : см^3

И снова в проверке ответа нам поможет калькулятор .

Источник

В данной публикации мы рассмотрим, как можно найти объем шара и разберем примеры решения задач для закрепления материала.

Формула вычисления объема шара
Примеры задач

Формула вычисления объема шара

1. Через радиус

Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.

Формула объема шара через радиус

Объем шара

Примечание: в расчетах значение числа π округляется до 3,14.

2. Через диаметр

Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:

Формула объема шара через диагональ

Примеры задач

Задание 1
Вычислите объем шара, если его радиус равняется 3 см.

Решение:
Применив первую формулу (через радиус) получаем:

Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.

Решение:
Используем вторую формулу, в которой задействован диаметр:

Источник

У этого термина существуют и другие значения, см. Шар (значения).

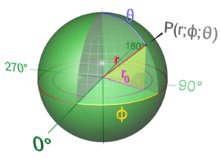
Поверхность шара — сфера
r — радиус шара

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Связанные определения[править | править код]

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Основные геометрические формулы[править | править код]

Площадь поверхности $S$ и объём $V$ шара радиуса $r$ (и диаметром $d = 2r$ ) определяются формулами:

$S= 4pi r^{2}$

$S= pi d^{2}$

$V={frac {4}{3}}pi r^{3}$

Доказательство

Возьмём четверть круга радиуса R с центром в точке $left(0;0right)$ . Уравнение окружности этого круга : $x^{2}+y^{2}=R^{2}$ , откуда $y^{2}=R^{2}-x^{2}$ .

Функция $y={sqrt {R^{2}-x^{2}}},xin (0;R)$ непрерывная, убывающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

${1 over 2}V=pi int limits _{0}^{R}(R^{2}-x^{2})dx=pi cdot {Bigl .}left(R^{2}x-{frac {x^{3}}{3}}right){Bigr |}_{0}^{R}=pi cdot (R^{3}-{frac {R^{3}}{3}})={frac {2}{3}}pi R^{3}$

Откуда $V={frac {4}{3}}pi R^{3}$ Ч. т. д.

$V={frac {pi d^{3}}{6}}$

Доказательство

$d=2r, V={4 over 3} pi r^3 = {4 over 3} pi left ( {d over 2} right )^3 = {4 over 3} pi frac {d^3} {8} = frac {pi d^3} {6}$ Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Определения[править | править код]

Пусть дано метрическое пространство $(X,rho)$ . Тогда

$B_{r}(x_{0})={xin Xmid rho (x,x_{0})<r}.$

$D_{r}(x_{0})={xin Xmid rho (x,x_{0})leqslant r}.$

Замечания[править | править код]

Шар радиуса $r$ с центром $x_{0}$ также называют $r$ -окрестностью точки $x_{0}$ .

Свойства[править | править код]

$B_{1}(x)={x},;overline {B_{1}(x)}={x},;D_{1}(x)=X.$

Объём[править | править код]

Объём n-мерного шара радиуса R в n-мерном евклидовом пространстве:^[1]

${displaystyle V_{n}(R)={frac {pi ^{n/2}}{Gamma ({frac {n}{2}}+1)}}R^{n},}$

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объёма n-мерного шара, которые не требуют гамма-функции:

${displaystyle V_{2k}(R)={frac {pi ^{k}}{k!}}R^{2k}}$ ,

${displaystyle V_{2k+1}(R)={frac {2^{k+1}pi ^{k}}{(2k+1)!!}}R^{2k+1}={frac {2(k!)(4pi )^{k}}{(2k+1)!}}R^{2k+1}}$ .

Знаком !! здесь обозначен двойной факториал.

Эти формулы также можно свести в одну общую:

${displaystyle V_{n}(R)={frac {2^{left[{frac {n+1}{2}}right]}pi ^{left[{frac {n}{2}}right]}}{n!!}}R^{n}}$ .

Обратная функция для выражения зависимости радиуса от объёма:

${displaystyle R_{n}(V)={frac {Gamma (n/2+1)^{1/n}}{sqrt {pi }}}V^{1/n}}$ .

Эта формула также может быть разделена на две: для пространств с чётным и нечётным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

${displaystyle R_{2k}(V)={frac {(k!V)^{1/2k}}{sqrt {pi }}}}$ ,

${displaystyle R_{2k+1}(V)=left({frac {(2k+1)!!V}{2^{k+1}pi ^{k}}}right)^{1/(2k+1)}}$ .

Рекурсия[править | править код]

Формулу объёма также можно выразить в виде рекурсивной функции. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объём n-мерного шара через объём шара размерности $n-2$ (при условии, что они имеют одинаковый радиус):

${displaystyle V_{n}(R)={frac {2pi R^{2}}{n}}V_{n-2}(R)}$ .

Также существует формула объёма n-мерного шара в зависимости от объёма (n−1)-мерного шара того же радиуса:

${displaystyle V_{n}(R)=R{sqrt {pi }}{frac {Gamma ({frac {n+1}{2}})}{Gamma ({frac {n}{2}}+1)}}V_{n-1}(R)}$ .

То же без гамма-функции:

${displaystyle {begin{aligned}V_{2k}(R)&=Rpi {frac {(2k-1)!!}{2^{k}k!}}V_{2k-1}(R)=Rpi {frac {(2k-1)(2k-3)cdots 5cdot 3cdot 1}{(2k)(2k-2)cdots 6cdot 4cdot 2}}V_{2k-1}(R),\V_{2k+1}(R)&=2R{frac {2^{k}k!}{(2k+1)!!}}V_{2k}(R)=2R{frac {(2k)(2k-2)cdots 6cdot 4cdot 2}{(2k+1)(2k-1)cdots 5cdot 3cdot 1}}V_{2k}(R).end{aligned}}}$

Пространства младших размерностей[править | править код]

Формулы объёма для некоторых пространств младших размерностей:

Кол-во измерений	Объём шара радиуса R	Радиус шара объёма V
1	${displaystyle 2R}$	${displaystyle V/2}$
2	$pi R^{2}$	${displaystyle {frac {V^{1/2}}{sqrt {pi }}}}$
3	${displaystyle {frac {4pi }{3}}R^{3}}$	${displaystyle left({frac {3V}{4pi }}right)^{1/3}}$
4	${displaystyle {frac {pi ^{2}}{2}}R^{4}}$	${displaystyle {frac {(2V)^{1/4}}{sqrt {pi }}}}$
5	${displaystyle {frac {8pi ^{2}}{15}}R^{5}}$	${displaystyle left({frac {15V}{8pi ^{2}}}right)^{1/5}}$
6	${displaystyle {frac {pi ^{3}}{6}}R^{6}}$	${displaystyle {frac {(6V)^{1/6}}{sqrt {pi }}}}$
7	${displaystyle {frac {16pi ^{3}}{105}}R^{7}}$	${displaystyle left({frac {105V}{16pi ^{3}}}right)^{1/7}}$
8	${displaystyle {frac {pi ^{4}}{24}}R^{8}}$	${displaystyle {frac {(24V)^{1/8}}{sqrt {pi }}}}$
9	${displaystyle {frac {32pi ^{4}}{945}}R^{9}}$	${displaystyle left({frac {945V}{32pi ^{4}}}right)^{1/9}}$
10	${displaystyle {frac {pi ^{5}}{120}}R^{10}}$	${displaystyle {frac {(120V)^{1/10}}{sqrt {pi }}}}$

Пространства старших размерностей[править | править код]

Объём гипершара размерности n единичного радиуса в зависимости от n.

При стремлении количества размерностей к бесконечности объём шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объёма.

Примеры[править | править код]

Пусть $mathbb{R}^d$ — евклидово пространство с обычным евклидовым расстоянием. Тогда

если $d=1$ (пространство — прямая), то

${displaystyle B_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|<r}=left(x_{0}-{r},x_{0}+{r}right),}$

${displaystyle D_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|leq r}=left[x_{0}-{r},x_{0}+{r}right].}$

— открытый и замкнутый отрезок соответственно.

— открытый и замкнутый диск соответственно.

— открытый и замкнутый стереометрический шар соответственно.

Тогда

См. также[править | править код]

Шаровой слой
Гиперсфера
Сферический слой

Примечания[править | править код]

↑ Equation 5.19.4, NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.6 of 2013-05-06.

Литература[править | править код]

Шар, геометрическое тело // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки на онлайн калькуляторы[править | править код]

Вычисление объема и площади шара. Дата обращения: 12 марта 2012. Архивировано из оригинала 8 августа 2011 года.
Онлайн-калькуляторы. Дата обращения: 2 июля 2019. Архивировано из оригинала 9 января 2019 года.
Математические этюды. Дата обращения: 20 октября 2011. Архивировано из оригинала 18 октября 2011 года. Мультфильм про объём шара

Источник

Определение шара

Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.

Онлайн-калькулятор объема шара

Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.

У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:

D=2⋅RD=2cdot R

Формула объема шара через его радиус

Объем шара вычисляется по следующей формуле:

Формула объема шара через радиус

V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3

RR — радиус данного шара.

Рассмотрим несколько примеров.

Задача 1

Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.

Решение

d=500d=sqrt{500}

Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):

d=a2+a2+a2d=sqrt{a^2+a^2+a^2}

d=3⋅a2d=sqrt{3cdot a^2}

d=3⋅ad=sqrt{3}cdot a

500=3⋅asqrt{500}=sqrt{3}cdot a

a=5003a=sqrt{frac{500}{3}}

a≈12.9aapprox12.9

Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:

R=12⋅aR=frac{1}{2}cdot a

R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4

Заключительный этап — нахождение объема шара по формуле:

V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3

Ответ

1097,5 см3.1097,5text{ см}^3.

Формула объема шара через его диаметр

Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:

D=2⋅RD=2cdot R

R=D2R=frac{D}{2}

Подставим это выражение в формулу для объема шара:

V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3

Объем шара через диаметр

V=π6⋅D3V=frac{pi}{6}cdot D^3

DD — диаметр данного шара.

Задача 2

Диаметр шара равен 15 см.15text{ см.} Найдите его объем.

Решение

D=15D=15

Сразу подставляем значение диаметра в формулу:

V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3

Ответ

1766.25 см3.1766.25text{ см}^3.

Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!

Тест по теме «Объем шара»

Источник

Нужно знать его радиус. Умножить 4/3 на число “пи” и на радиус шара в третьей степени. К примеру, объем шара с радиусом 2 метра будет: 4/3х3,14х8=33,5 куб.метра

автор вопроса выбрал этот ответ лучшим

Алиса в Стране
[363K]

5 лет назад

Все, что нам нужно для вычисления объема шара – это просто знать его радиус и нехитрую формулу для расчета. Формула вот такая:

Допустим, радиус нашего шара равен 10 сантиметрам, подставляем 10 см в нашу формулу и получаем: V = 4/3 х 3,14 х 1000 = 4187 кубических сантиметров.

Марина Вологда
[294K]

5 лет назад

Чтобы найти объем шара (сферы) следует знать его радиус или диаметр.

Если радиус шара (сферы) известен, применяем следующую формулу:

Где “r” – радиус шара.

Известно, что “Пи” всегда равно 3,14.

Так же иногда в задачах дается диаметр шара (сферы). Если известен диаметр шара, применяется следующая формула:

Где “d” – это диаметр.

Любопытство
[135K]

5 лет назад

В выпускном, одиннадцатом (насколько я помню) классе учат находить объём шара вот так: высчитывают его по формуле: 4/3 Пи Х радиус в кубе. Думаю, что значение Пи всем известно, но на всякий случай сообщаю: π = 3,14.

В Рокотов
[277K]

5 лет назад

Сначала определимся что такое шар – это точки пространства равноудаленные от центра шара. Чтобы найти объем шара, при известном значении пи (3,14), нужно знать значения его радиуса или половины радиуса -диаметра, при известном радиусе искомое можно получить по формуле:

Zolotynka
[550K]

5 лет назад

Для начала разберемся, что представляет собой такая геометрическая фигура как шар.

Итак, шар – это твердое тело, у которого есть особенность: любая точка на поверхности шара будет находиться на одном и том же расстоянии от его центра. Данное расстояние известно как радиус. Максимально прямое расстояние через центр шара принято называть диаметром. Диаметр -вдвое больше радиуса.

Теперь посмотрим, как найти объем шара?

Объем сферы равен четырем третям произведения числа pi и радиуса, возведенного в куб. Формула будет выглядеть следующим образом:

Число pi, в задачах принято сокращать до двух десятых- 3,14.

Ninaarc
[479K]

5 лет назад

Шар представляет собой часть пространства, которое ограничено сферой. Для определения объема шара имеется специальная формула, в которую следует подставить нужные значения. Формула для вычисления объема шара выглядит таким образом:

Из формулы становится ясно, что нам должен быть известен радиус шара (r), который затем потребуется возвести в третью степень. А число ПИ нам хорошо известно, оно в числовом значении выглядит так: π = 3,14.

Трибунька
[54.9K]

8 лет назад

Чтобы вычислить объем шара надо знать формулу, где R – радиус шара.

текст при наведении

Вот есть отличный сайт где можно онлайн высчитать объём шара. Этот сайт очень полезен для школьников, так как там много формул по геометрии, математике, физике и химии.

Кроме формул некоторые задачи можно решить сразу на сайте. Есть справочные таблицы. Сайт очень удобно и грамотно сделан, все легко и просто на нём искать.

Нахождение объема шара, тема урока по Геометрии, если я не ошибаюсь, одиннадцатого класса общеобразовательной школы.

Для нахождения объема геометрического тела Шар, нужно знать диаметр диаметр этого тела, разделив который на два получим его радиус. А далее подставляем это значение (радиус) в ниже приведенную формулу, и на выходе получаем объем шара.

РУДЬКО
[256K]

5 лет назад

Объём шара, это всем известная формула, которая на словах звучит как “четыре третьих пи эр в кубе”. То есть это проиизведение частного от 43 умноженное на число “Пи” и радиуса шара, возведённого в третью степень, то есть в “куб”.

vksvovko
[1.6K]

6 лет назад

4/3*Пи*радиус в кубе.

это и есть объем шара.

Есть ещё один интересный способ – опустить его в измерительную емкость с водой, и сколько он вытеснит воды столько и его объем. таким способом можно измерять любой предмет.

Знаете ответ?

Источник

Содержание:

Формула объема шара через радиус

Формула объема шара через диаметр

Формула объема шара через длину окружности

Формула объема шара через площадь поверхности

Примеры задач на нахождение объема параллелепипеда

Формула вычисления объема шара

Примеры задач

Связанные определения[править | править код]

Основные геометрические формулы[править | править код]

Определения[править | править код]

Замечания[править | править код]

Свойства[править | править код]

Объём[править | править код]

Рекурсия[править | править код]

Пространства младших размерностей[править | править код]

Пространства старших размерностей[править | править код]

Примеры[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки на онлайн калькуляторы[править | править код]

Онлайн-калькулятор объема шара

Формула объема шара через его радиус

Формула объема шара через его диаметр

Тест по теме «Объем шара»

Вам также может понравиться

Как найти евро в консультант плюс

Как найти собес по прописке

Как найти общую мощность тока в цепи

Добавить комментарий Отменить ответ