Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Перед тем как находить и считать определитель, дадим определение определителю матрицы.
Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A – символы, которыми обозначают определитель матрицы.
Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.
Определитель матрицы второго порядка можно вычислять по формуле:
А=1-231.
Решение матрицы:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:
- он может считаться по правилу треугольника;
- расчет также проводится по правилу Саррюса.
Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=13402115-1
Решение:
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
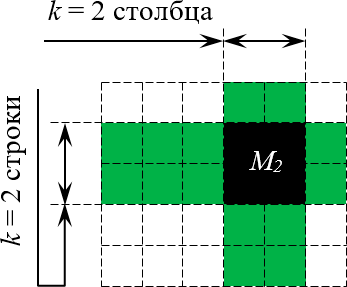
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя:
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
В рамках темы советуем обратиться к модулю определителя.
А=134021005
Решение:
det А=134021005=1×5×2=10
Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде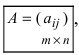
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой 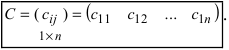
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом 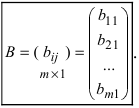
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы 
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы – на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной

Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной 
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю: 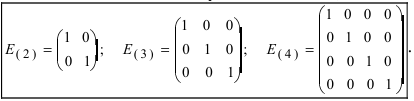
Действия над матрицами
1. Суммой (разностью) двух матриц  и
и 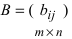 одинаковой структуры называется матрица той же размерности
одинаковой структуры называется матрица той же размерности 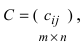 элементы которой вычисляются по формуле:
элементы которой вычисляются по формуле: 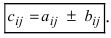
Пример:
Найти сумму (разность) матриц 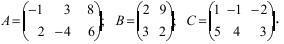
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
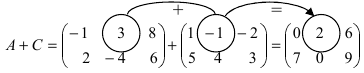
и разность этих матриц:
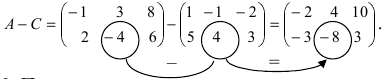
2. При умножении вещественного числа k на матрицу  все элементы матрицы умножаются на это число.
все элементы матрицы умножаются на это число.
Пример:
Умножить (-2) на матрицу 
Решение:
Результат умножения имеет вид 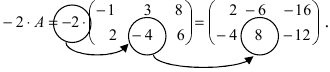
3. Произведением матриц 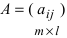 и
и 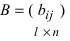 называется матрица
называется матрица 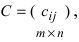 элементы которой вычисляются по формуле:
элементы которой вычисляются по формуле: 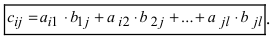
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
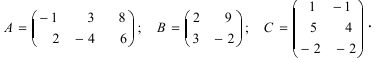
Решение:
Матрица А имеет структуру 2×3, матрица В – 2×2, матрица С – 3×2. Согласно определению можно найти произведения 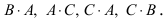 Не существуют произведения
Не существуют произведения 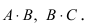 Вычислим произведение
Вычислим произведение 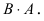 Прежде всего, определим структуру результирующей матрицы: имеем размерности
Прежде всего, определим структуру результирующей матрицы: имеем размерности 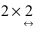 и
и 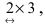 убирая подчеркнутые цифры, получим структуру результирующей матрицы 2×3. Вычислим ее элементы. Для того чтобы найти элементы возможных произведений, надо просуммировать произведения элементов строки первой матрицы на соответствующие элементы столбца второй матрицы:
убирая подчеркнутые цифры, получим структуру результирующей матрицы 2×3. Вычислим ее элементы. Для того чтобы найти элементы возможных произведений, надо просуммировать произведения элементов строки первой матрицы на соответствующие элементы столбца второй матрицы:
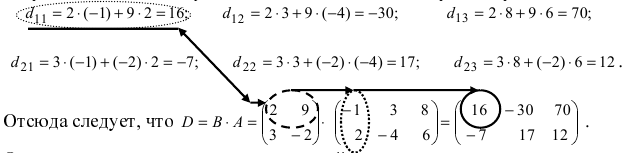
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.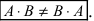
Определение: Обратной матрицей к исходной квадратной матрице 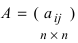 называется матрица
называется матрица 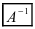 той же структуры, произведение которой с матрицей А коммутативно и равно единичной матрице, то есть
той же структуры, произведение которой с матрицей А коммутативно и равно единичной матрице, то есть 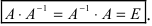
Рассмотрим схему построения обратной матрицы 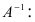
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице 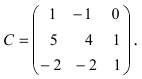
Решение:
Вычислим детерминант данной матрицы 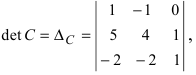 раскроем этот определитель по элементам первой строки:
раскроем этот определитель по элементам первой строки:
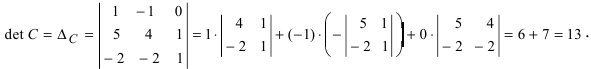
Вычислим алгебраические дополнения всех элементов определителя: 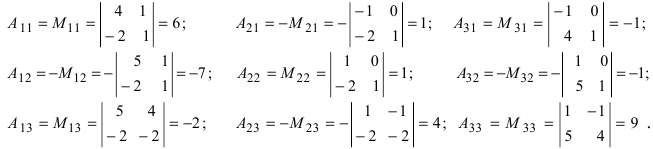 Запишем обратную матрицу
Запишем обратную матрицу 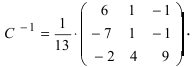
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
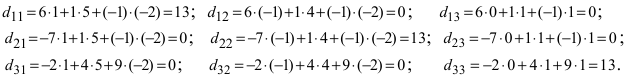
Таким образом, 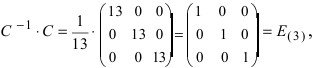 т.е. найдена верно.
т.е. найдена верно.
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 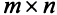 называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 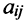 , где
, где 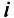 — номер строки,
— номер строки, 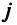 — номер столбца.
— номер столбца.
Например, матрица
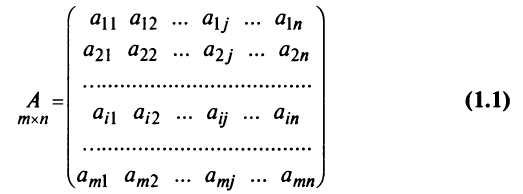
или, в сокращенной записи, 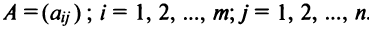
Например, 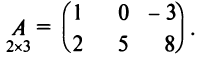 Наряду с круглыми скобками используются и другие обозначения матрицы:
Наряду с круглыми скобками используются и другие обозначения матрицы:
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 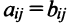 для любых
для любых 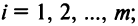
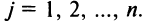
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.) 
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям: 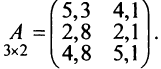
В этой записи, например, матричный элемент 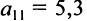 показывает, сколько электроэнергии потребляет промышленность, а элемент
показывает, сколько электроэнергии потребляет промышленность, а элемент 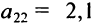 — сколько трудовых ресурсов потребляет сельское хозяйство.
— сколько трудовых ресурсов потребляет сельское хозяйство.
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 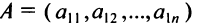 — матрица-строка;
— матрица-строка;
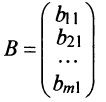 — матрица-столбец.
— матрица-столбец.
Матрица называется квадратной 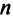 -го порядка, если число ее строк равно числу столбцов и равно
-го порядка, если число ее строк равно числу столбцов и равно 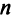 .
.
Например, 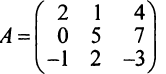 — квадратная матрица третьего порядка.
— квадратная матрица третьего порядка.
Элементы матрицы 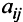 , у которых номер столбца равен номеру строки
, у которых номер столбца равен номеру строки 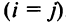 , называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы
, называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы 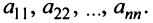
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
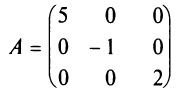 —диагональная матрица третьего порядка.
—диагональная матрица третьего порядка.
Если у диагональной матрицы  -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей
-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей  -го порядка, она обозначается буквой Е.
-го порядка, она обозначается буквой Е.
Например,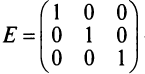 — единичная матрица третьего порядка.
— единичная матрица третьего порядка.
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:

Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.
Умножение матрицы на число
Произведением матрицы А на число 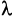 называется матрица
называется матрица 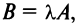 элементы которой
элементы которой 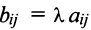 для
для 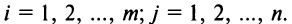
Например, если 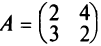 , то
, то 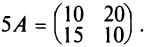
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например, 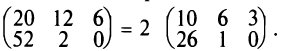
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е. 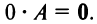
Сложение матриц
Суммой двух матриц А и В одинакового размера  называется матрица
называется матрица 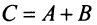 , элементы которой
, элементы которой 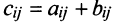 для
для 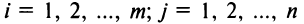 (т.е. матрицы складываются поэлементно).
(т.е. матрицы складываются поэлементно).
Например,
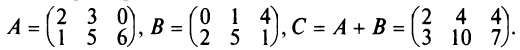 В частном случае A + 0 = A.
В частном случае A + 0 = A.
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции: 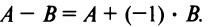
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй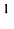 . Тогда произведением матриц
. Тогда произведением матриц 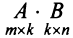 называется такая матрица
называется такая матрица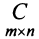 , каждый элемент которой
, каждый элемент которой 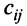 равен сумме произведений элементов
равен сумме произведений элементов  -й строки матрицы А на соответствующие элементы
-й строки матрицы А на соответствующие элементы 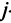 -го столбца матрицы В:
-го столбца матрицы В:
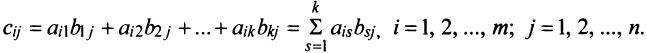
Пример №1
Вычислить произведение матриц 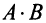 , где
, где

Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно): 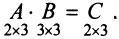
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
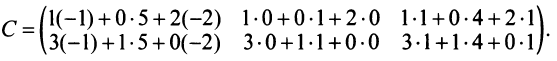
Получаем 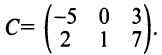 ►
►
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
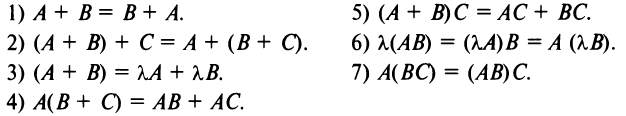
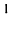 этом случае матрица А называется согласованной с матрицей В.
этом случае матрица А называется согласованной с матрицей В.
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 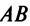 существует, то после перестановки сомножителей местами произведения матриц
существует, то после перестановки сомножителей местами произведения матриц 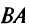 может и не существовать. Действительно, в примере 1.1 получили произведение матриц
может и не существовать. Действительно, в примере 1.1 получили произведение матриц 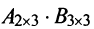 , а произведения
, а произведения 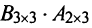 не существует, так как число столбцов первой матрицы не совпадает с числом строк второй матрицы.
не существует, так как число столбцов первой матрицы не совпадает с числом строк второй матрицы.
б)Если даже произведения 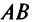 и
и 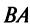 существуют, то они могут быть матрицами разных размеров.
существуют, то они могут быть матрицами разных размеров.
Пример №2
Найти произведения матриц 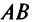 и
и 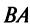 :
:
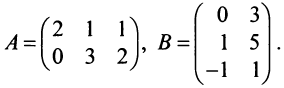
Решение:
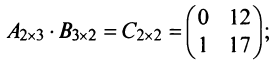
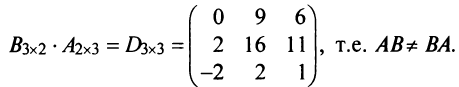 ► в) В случае, когда оба произведения
► в) В случае, когда оба произведения 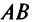 и
и 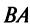 существуют и оба — матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.
существуют и оба — матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е.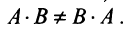
Пример №3
Найти произведения матриц 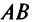 и
и 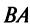 , где
, где 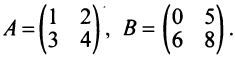
Решение:
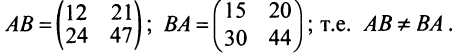 В частном случае коммутативным законом обладает произведение любой квадратной матрицы А
В частном случае коммутативным законом обладает произведение любой квадратной матрицы А 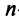 -гo порядка на единичную матрицу Е того же порядка, причем это произведение равно А:
-гo порядка на единичную матрицу Е того же порядка, причем это произведение равно А:
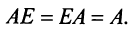
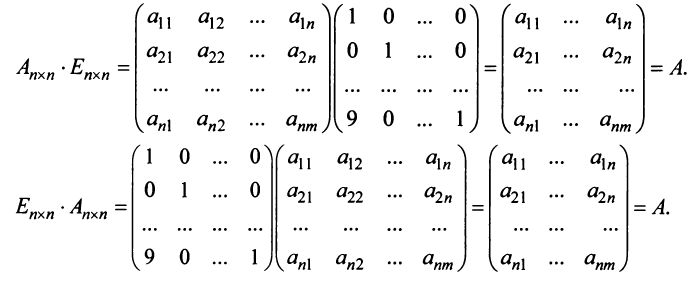
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 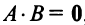 , не следует, что
, не следует, что 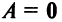 или,
или,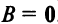 . Например,
. Например, 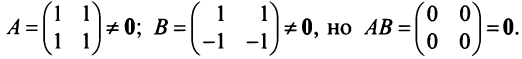
Возведение в степень
Целой положительной степенью 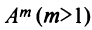 квадратной матрицы
квадратной матрицы 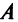 называется произведение
называется произведение 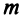 матриц, равных
матриц, равных 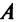 , т.е.
, т.е.
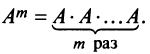
Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 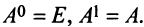 Нетрудно показать, что
Нетрудно показать, что 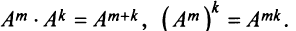
Пример №4
Найти 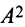 , где
, где 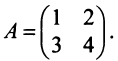
Решение:
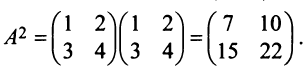
Обращаем внимание на то, что из равенства 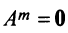 еще не следует, что матрица
еще не следует, что матрица 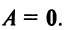 ►
►
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы  к матрице
к матрице 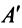 , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица
, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица 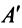 называется транспонированной относительно матрицы
называется транспонированной относительно матрицы 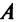 :
: 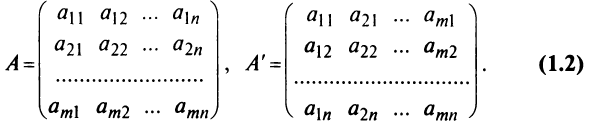 Из определения следует, что если матрица
Из определения следует, что если матрица 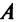 имеет размер
имеет размер 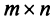 , то транспонированная матрица
, то транспонированная матрица 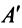 имеет размер
имеет размер 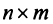 .
.
Например, 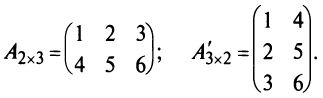
В литературе встречаются и другие обозначения транспонированной матрицы, например, 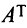 .
.
Свойства операции транспонирования:

Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 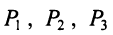 и использует сырье двух типов:
и использует сырье двух типов: 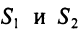 . Нормы расхода сырья характеризуются матрицей
. Нормы расхода сырья характеризуются матрицей 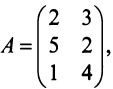
где каждый элемент 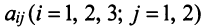 показывает, сколько единиц сырья
показывает, сколько единиц сырья
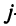 -го типа расходуется на производство единицы продукции
-го типа расходуется на производство единицы продукции 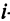 -го вида. План выпуска продукции задан матрицей-строкой
-го вида. План выпуска продукции задан матрицей-строкой 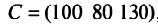 , стоимость единицы каждого типа сырья (ден. ед.) — матрицей-столбцом
, стоимость единицы каждого типа сырья (ден. ед.) — матрицей-столбцом 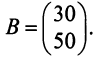
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 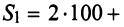
 ед. и 2-го —
ед. и 2-го — 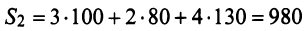 ед., поэтому матрица-строка затрат сырья
ед., поэтому матрица-строка затрат сырья 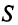 может быть записана как произведение
может быть записана как произведение 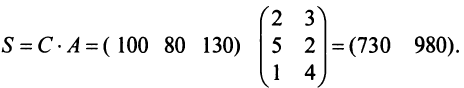
Тогда общая стоимость сырья 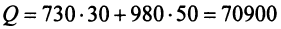 ден. ед. может быть записана в матричном виде
ден. ед. может быть записана в матричном виде 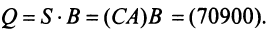 Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
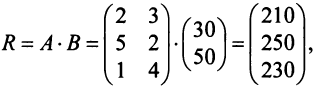 а затем общую стоимость сырья
а затем общую стоимость сырья
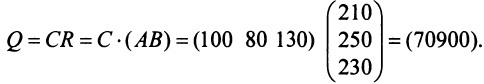

На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц: 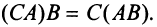
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 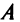 , — тесно связана с решением систем линейных уравнений (см. гл. 2). Определитель матрицы
, — тесно связана с решением систем линейных уравнений (см. гл. 2). Определитель матрицы 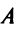 обозначается
обозначается 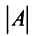 или
или 
Определителем матрицы первого порядка 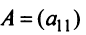 , или определителем первого порядка, называется элемент
, или определителем первого порядка, называется элемент 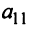 :
:
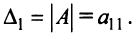 Например, пусть
Например, пусть 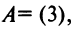 тогда
тогда 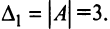
Определителем матрицы второго порядка 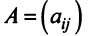 , или определителем второго порядка, называется число, которое вычисляется по формуле:
, или определителем второго порядка, называется число, которое вычисляется по формуле:
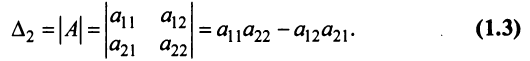
Произведения а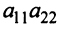 и
и 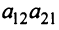 называются членами определителя второго порядка. Например, пусть
называются членами определителя второго порядка. Например, пусть 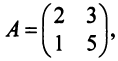 тогда
тогда
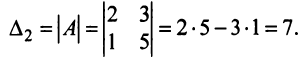
Пусть дана квадратная матрица третьего порядка:  Определителем матрицы третьего порядка
Определителем матрицы третьего порядка 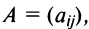 , или определителем третьего порядка, называется число, которое вычисляется по формуле:
, или определителем третьего порядка, называется число, которое вычисляется по формуле:
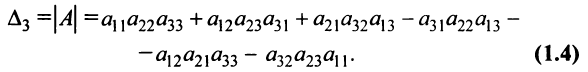
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.

Пример №6
Вычислить определитель третьего порядка
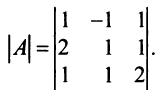
Решение:
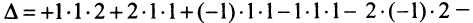
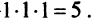 ►
►
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу  -гo порядка:
-гo порядка: 
Из общего числа 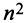 элементов этой матрицы выберем набор, содержащий
элементов этой матрицы выберем набор, содержащий 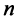 элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, набор элементов
элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, набор элементов 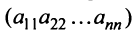 или
или 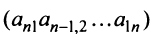 соответственно главной и побочной диагоналей матрицы.
соответственно главной и побочной диагоналей матрицы.
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.

Номера столбцов 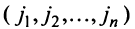 образуют при этом перестановку
образуют при этом перестановку 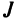 из
из 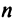 чисел:
чисел:  Всего существует
Всего существует 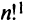 различных перестановок из
различных перестановок из 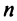 натуральных чисел.
натуральных чисел.
Введем понятие беспорядка, или инверсии, в перестановке 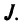 Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел
Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел 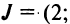
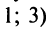 имеется одна инверсия (2; 1), а в перестановке
имеется одна инверсия (2; 1), а в перестановке 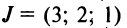 — три: (3; 2), (3; 1), (2; 1). Обозначим через
— три: (3; 2), (3; 1), (2; 1). Обозначим через 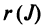 количество инверсий в перестановке
количество инверсий в перестановке 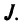
Возвращаясь к наборам (1.5) из элементов матрицы 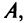 мы можем каждому такому набору поставить в соответствие произведение его элементов:
мы можем каждому такому набору поставить в соответствие произведение его элементов:

и число 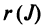 , равное количеству инверсий в перестановке
, равное количеству инверсий в перестановке 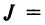
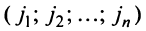 из номеров соответствующих столбцов.
из номеров соответствующих столбцов.
Определение. Определителем квадратной матрицы 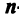 -го порядка, или определителем
-го порядка, или определителем 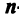 -го порядка, называется число, равное алгебраической сумме
-го порядка, называется число, равное алгебраической сумме 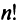 членов, каждый из которых является произведением
членов, каждый из которых является произведением 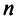 элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как
элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как 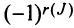 , где
, где 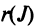 — число инверсий в перестановке
— число инверсий в перестановке 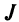 из номеров столбцов элементов матрицы, ест при этом номера строк записаны в порядке возрастания:
из номеров столбцов элементов матрицы, ест при этом номера строк записаны в порядке возрастания:
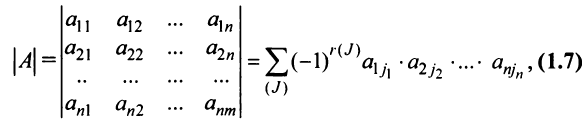 где сумма берется по всем перестановкам
где сумма берется по всем перестановкам 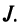 Проверим, например, что при
Проверим, например, что при 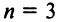 мы получаем введенный ранее определитель третьего порядка (1.4):
мы получаем введенный ранее определитель третьего порядка (1.4):
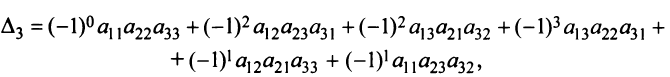
то же число, что и по формуле (1.4).
Заметим, что с ростом 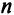 резко увеличивается число членов определителя
резко увеличивается число членов определителя 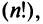 поэтому даже для
поэтому даже для 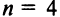 использование формулы (1.7) весьма трудоемко (получим 24 слагаемых!).
использование формулы (1.7) весьма трудоемко (получим 24 слагаемых!).
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 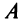
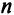 -го порядка.
-го порядка.
Минором 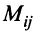 элемента
элемента 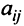 матрицы
матрицы 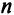 -го порядка называется
-го порядка называется
определитель матрицы  -го порядка, полученной из матрицы
-го порядка, полученной из матрицы 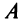 вычеркиванием
вычеркиванием 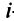 -й строки и
-й строки и 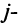 го столбца.
го столбца.
Например, минором элемента 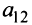 матрицы
матрицы  третьего порядка будет:
третьего порядка будет: 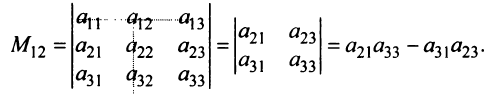 Каждая матрица
Каждая матрица 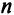 -го порядка имеет
-го порядка имеет 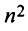 миноров
миноров 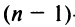 -го порядка.
-го порядка.
Алгебраическим дополнением 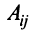 элемента
элемента 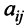 матрицы
матрицы 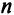 -го порядка называется его минор, взятый со знаком
-го порядка называется его минор, взятый со знаком 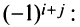

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца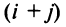 — четное число, и отличается от минора знаком, когда
— четное число, и отличается от минора знаком, когда 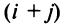 — нечетное число.
— нечетное число.
Например, 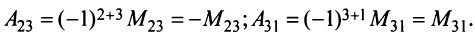
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
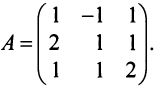
Решение:
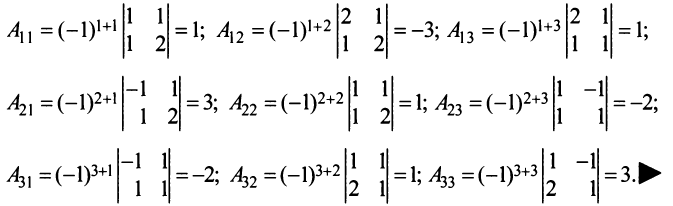 Важное значение для вычисления определителей имеет следующая теорема.
Важное значение для вычисления определителей имеет следующая теорема.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
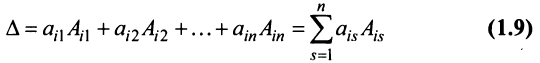
(разложение по элементам  -й строки;
-й строки; 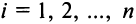 );
);
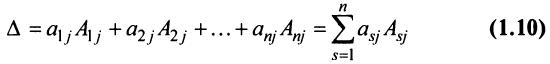
(разложение по элементам 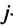 -го столбца;
-го столбца; 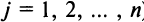 ).
).
 Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки:
Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки: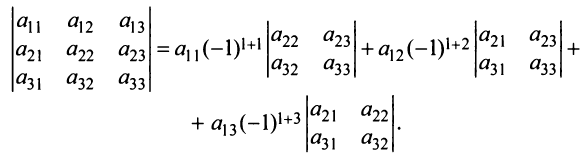
 Точнее данная теорема является частным случаем теоремы Лапласа.
Точнее данная теорема является частным случаем теоремы Лапласа.
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы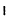 :
:

Решение:
Раскладывая по первому столбцу, получаем:
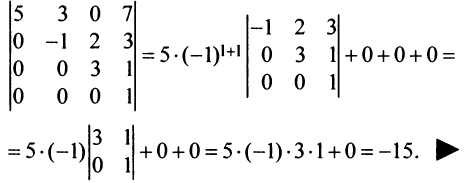
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 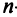 -го порядка к вычислению более простых определителей
-го порядка к вычислению более простых определителей 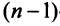 -го порядка.
-го порядка.
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 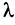 , то ее определитель умножится на это число
, то ее определитель умножится на это число 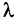 .
.
Пусть определитель исходной матрицы равен  . Для определенности первую строку матрицы умножим на
. Для определенности первую строку матрицы умножим на 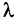 , получим новый определитель
, получим новый определитель 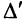 , который разложим по элементам первой строки:
, который разложим по элементам первой строки:
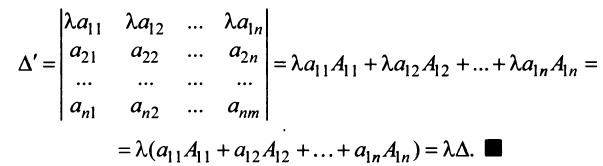
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 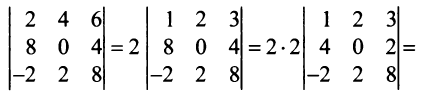
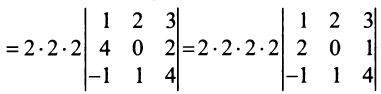 , но
, но 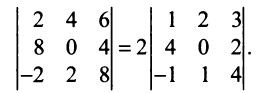
3. При транспонировании матрицы ее определитель не изменяется: 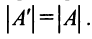
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: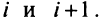 Разложим определитель исходной матрицы
Разложим определитель исходной матрицы  по элементам
по элементам  -й строки, а определитель новой матрицы (с переставленными строками)
-й строки, а определитель новой матрицы (с переставленными строками) 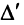 — по элементам
— по элементам 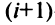 -й строки. Разложения будут отличаться только знаком, так как в формуле (1.9) для
-й строки. Разложения будут отличаться только знаком, так как в формуле (1.9) для 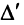 каждое алгебраическое дополнение будет иметь противоположный знак (множители
каждое алгебраическое дополнение будет иметь противоположный знак (множители 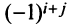 сменятся на множители
сменятся на множители 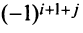 , поэтому
, поэтому 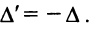
Если переставить не соседние строки, а, скажем,  -ю и
-ю и 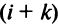 -ю, то такую перестановку можно представить как последовательное смещение
-ю, то такую перестановку можно представить как последовательное смещение  -й строки на
-й строки на 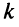 строк вниз (при этом каждый раз знак определителя меняется),
строк вниз (при этом каждый раз знак определителя меняется), 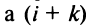 -й строки на
-й строки на 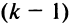 вверх, что тоже сопровождается
вверх, что тоже сопровождается 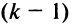 изменением знака, т.е. знак поменяется нечетное число
изменением знака, т.е. знак поменяется нечетное число 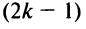 раз:
раз: 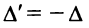 .
.
Доказательство для столбцов аналогично.
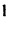 Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (или выше) главной диагонали, равны нулю.
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (или выше) главной диагонали, равны нулю.
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.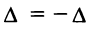 , откуда
, откуда 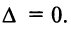
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 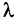 , получаем по свойству
, получаем по свойству 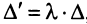 , где
, где  имеет две одинаковые строки и по свойству 5 равен 0.
имеет две одинаковые строки и по свойству 5 равен 0.
7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
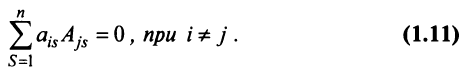
Рассмотрим квадратную матрицу 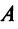 и вспомогательную матрицу
и вспомогательную матрицу 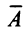 , полученную из матрицы
, полученную из матрицы 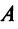 заменой
заменой 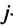 -й строки на
-й строки на  -ю:
-ю:
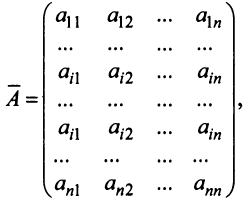
т.е. матрица 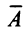 имеет две одинаковые строки, поэтому согласно свойству 5 ее определитель равен 0. Вычисляя его разложением по элементам
имеет две одинаковые строки, поэтому согласно свойству 5 ее определитель равен 0. Вычисляя его разложением по элементам 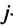 -й строки, получаем:
-й строки, получаем:
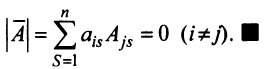
Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
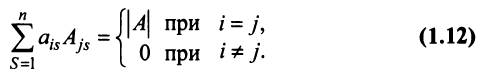 8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Пусть для определенности к элементам  -Й строки матрицы прибавим элементы
-Й строки матрицы прибавим элементы 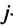 -й строки, умноженные на
-й строки, умноженные на 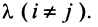 Тогда первая строка матрицы имеет вид:
Тогда первая строка матрицы имеет вид: 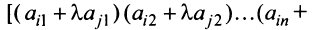
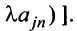 Определитель полученной матрицы вычислим разложением по элементам
Определитель полученной матрицы вычислим разложением по элементам  -й строки:
-й строки:
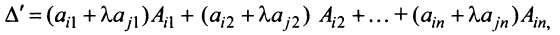
где 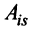 — алгебраические дополнения элементов
— алгебраические дополнения элементов  -й строки исходной матрицы
-й строки исходной матрицы 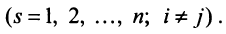 Раскроем скобки и получим после преобразования:
Раскроем скобки и получим после преобразования:
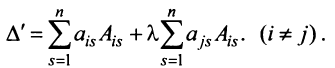
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.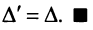
9. Сумма произведений произвольных чисел 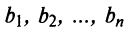 на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 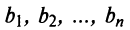 .
.
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 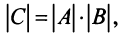 где
где 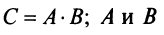 —матрицы
—матрицы 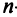 -го порядка.
-го порядка.
Замечание. Из свойства 10 следует, что даже если 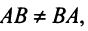 то
то 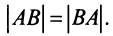
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
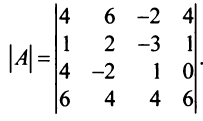
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем  Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы 2-й строки (кроме одного). Для этого элементы 3-го столбца матрицы, предварительно умножив на (—13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно:
Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы 2-й строки (кроме одного). Для этого элементы 3-го столбца матрицы, предварительно умножив на (—13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно: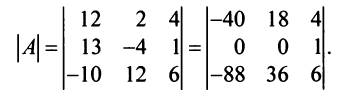
Раскладывая по элементам множители, получаем: 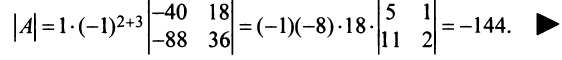
Обратная матрица
Для каждого числа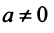 существует обратное число
существует обратное число 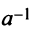 такое, что произведение
такое, что произведение 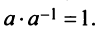 Для квадратных матриц тоже вводится аналогичное понятие.
Для квадратных матриц тоже вводится аналогичное понятие.
Определение. Матрица 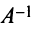 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 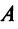 , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 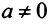 является необходимым и достаточным условием существования числа
является необходимым и достаточным условием существования числа 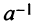 то для существования матрицы
то для существования матрицы  таким условием является требование
таким условием является требование 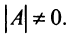
Если определитель матрицы отличен от нуля 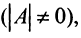 то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при
то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при 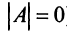 )— вырожденной, или особенной.
)— вырожденной, или особенной.
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица  существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Необходимость. Пусть матрица 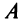 имеет обратную
имеет обратную  , т.е
, т.е 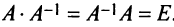 . По свойству 10 определителей имеем
. По свойству 10 определителей имеем
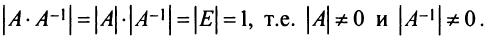
Достаточность. Пусть 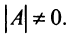 Рассмотрим квадратную матрицу
Рассмотрим квадратную матрицу 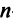 -го порядка,
-го порядка, 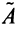 называемую присоединенной*, элементы которой являются алгебраическими дополнениями элементов матрицы
называемую присоединенной*, элементы которой являются алгебраическими дополнениями элементов матрицы 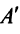 , транспонированной к
, транспонированной к 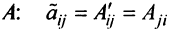
 Тогда элементы произведения матриц
Тогда элементы произведения матриц 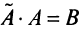 определяются по правилу умножения матриц:
определяются по правилу умножения матриц: 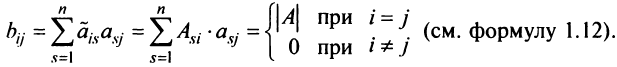 Поэтому матрица
Поэтому матрица 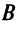 является диагональной, элементы ее главной диагонали равны определителю исходной матрицы:
является диагональной, элементы ее главной диагонали равны определителю исходной матрицы:
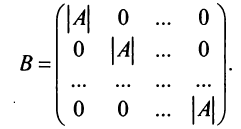
Аналогично доказывается, что произведение 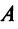 на
на 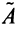 равно той же матрице
равно той же матрице 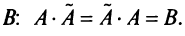 Отсюда следует, что если в качестве обратной матрицы взять матрицу.
Отсюда следует, что если в качестве обратной матрицы взять матрицу.
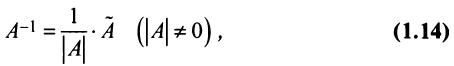
то произведения 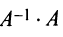 и
и 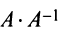 равны единичной матрице
равны единичной матрице 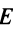
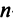 -го порядка:
-го порядка: 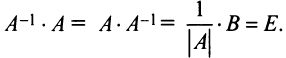
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 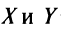 такие, что
такие, что 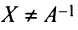 и
и 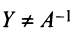 , где матрица
, где матрица  получена по формуле (1.14), и выполняются равенства:
получена по формуле (1.14), и выполняются равенства: 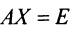 и
и 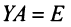 . Тогда, умножая на
. Тогда, умножая на слева первое из них, получаем:
слева первое из них, получаем: 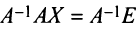 , откуда
, откуда 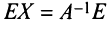 , т.е.
, т.е. 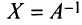 . Аналогично, умножая второе равенство на
. Аналогично, умножая второе равенство на  справа, получаем
справа, получаем 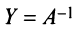 . Единственность доказана.
. Единственность доказана. 
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
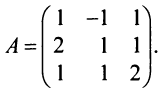
Решение:
1°. Определитель матрицы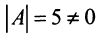 (см. пример 1.6), т.е. матрица
(см. пример 1.6), т.е. матрица  — невырожденная и обратная матрица
— невырожденная и обратная матрица  существует.
существует.
2°. Находим матрицу 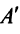 , транспонированную к
, транспонированную к  :
:
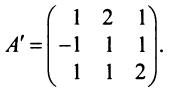
3°. Находим алгебраические дополнения элементов матрицы 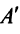 и составляем из них присоединенную матрицу
и составляем из них присоединенную матрицу 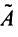 , учитывая, что
, учитывая, что 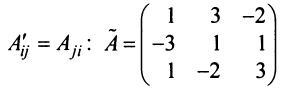
4° . Вычисляем обратную матрицу 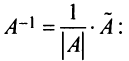
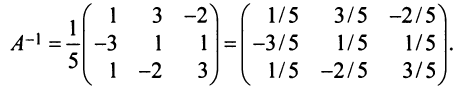 5°. Проверяем правильность вычисления обратной матрицы по формулам:
5°. Проверяем правильность вычисления обратной матрицы по формулам:
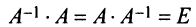 (рекомендуем в этом убедиться самому читателю). ►
(рекомендуем в этом убедиться самому читателю). ►
Для невырожденных матриц выполняются следующие свойства:
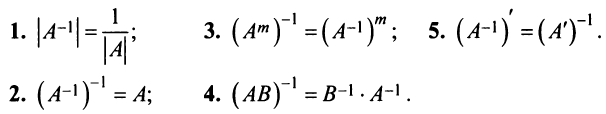
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице  размера
размера  вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы
вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы 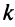 -то порядка, где
-то порядка, где 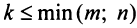 . Определители таких подматриц называются минорами
. Определители таких подматриц называются минорами 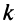 -го порядка матрицы
-го порядка матрицы  .
.
Например, из матрицы 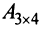 можно получить подматрицы первого, второго и третьего порядков.
можно получить подматрицы первого, второго и третьего порядков.
Определение. Рангом матрицы  называется наивысший порядок отличных от нуля миноров этой матрицы.
называется наивысший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы  обозначается
обозначается 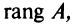 или
или 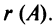
Из определения следует: а) ранг матрицы 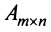 не превосходит меньшего из ее размеров, т.е.
не превосходит меньшего из ее размеров, т.е. 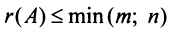 ;
;
б) 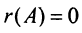 тогда и только тогда, когда все элементы матрицы равны нулю, т.е.
тогда и только тогда, когда все элементы матрицы равны нулю, т.е. 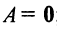 ;
;
в) для квадратной матрицы 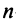 -го порядка
-го порядка 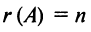 тогда и только тогда, когда матрица
тогда и только тогда, когда матрица  — невырожденная.
— невырожденная.
Пример №11
Вычислить ранг матрицы
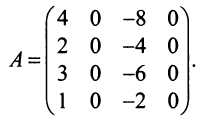
Решение:
Матрица  имеет четвертый порядок, поэтому
имеет четвертый порядок, поэтому 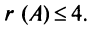 Однако
Однако 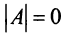 так как матрица
так как матрица  содержит нулевой столбец, поэтому
содержит нулевой столбец, поэтому 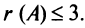 Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители, значит
Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители, значит 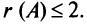 Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом
Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом 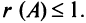 Поскольку матрица
Поскольку матрица  содержит ненулевые элементы, т.е. невырожденные подматрицы первого порядка, то
содержит ненулевые элементы, т.е. невырожденные подматрицы первого порядка, то 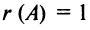 . ►
. ►
Пример №12
Вычислить ранг матрицы

Решение:
Для матрицы 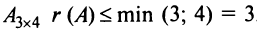 .
.
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):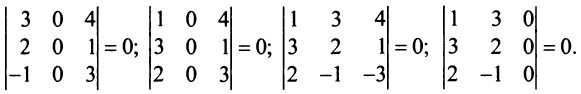
Поскольку все миноры третьего порядка нулевые,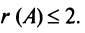 Так как существует ненулевой минор второго порядка, например,
Так как существует ненулевой минор второго порядка, например,
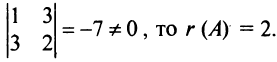 ►
►
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
 При изучении свойств определителей было показано, что при преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. В результате сохраняется наивысший порядок отличных от нуля миноров исходной матрицы, т.е. ее ранг не изменяется.
При изучении свойств определителей было показано, что при преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. В результате сохраняется наивысший порядок отличных от нуля миноров исходной матрицы, т.е. ее ранг не изменяется. 
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица  называется ступенчатой, если она имеет вид:
называется ступенчатой, если она имеет вид: 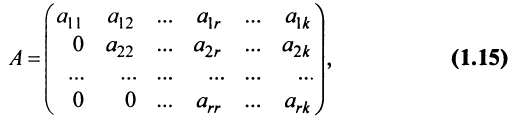 где
где 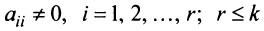 .
.
Замечание. Условие 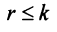 всегда может быть достигнуто транспонированием матрицы.
всегда может быть достигнуто транспонированием матрицы.
Очевидно, что ранг ступенчатой матрицы равен 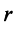 , так как имеется минор
, так как имеется минор 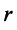 -го порядка, не равный нулю:
-го порядка, не равный нулю:
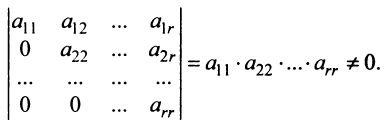
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
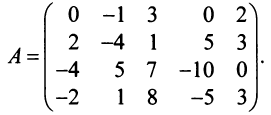
Решение:
1°. Если 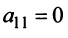 , то при перестановке строк или столбцов добиваемся того, что
, то при перестановке строк или столбцов добиваемся того, что 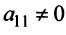 . В данном примере поменяем местами, например, 1-ю и 2-ю строки матрицы (см. ниже).
. В данном примере поменяем местами, например, 1-ю и 2-ю строки матрицы (см. ниже).
2°. Если 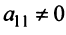 , то умножая элементы 2-й, 3-й и 4-й строк на подходящие числа (именно на
, то умножая элементы 2-й, 3-й и 4-й строк на подходящие числа (именно на 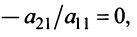
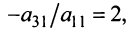
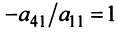 ) и прибавляя полученные числа соответственно к элементам 2-й1, 3-й и 4-й строк, добьемся того, чтобы все элементы 1-го столбца (кроме
) и прибавляя полученные числа соответственно к элементам 2-й1, 3-й и 4-й строк, добьемся того, чтобы все элементы 1-го столбца (кроме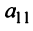 ) равнялись нулю:
) равнялись нулю:
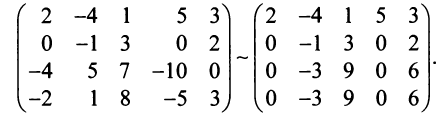 3°. Если в полученной матрице
3°. Если в полученной матрице  (у нас
(у нас 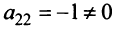 ), то умножая элементы 3-й и 4-й строк на подходящие числа (а именно, на
), то умножая элементы 3-й и 4-й строк на подходящие числа (а именно, на 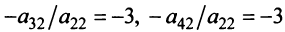 ), добьемся того, чтобы все элементы 2-го столбца (кроме
), добьемся того, чтобы все элементы 2-го столбца (кроме 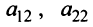 ) равнялись нулю. Если в процессе преобразований получаются строки (или столбцы), целиком состоящие из нулей (как в данном примере), то отбрасываем эти строки (или столбцы):
) равнялись нулю. Если в процессе преобразований получаются строки (или столбцы), целиком состоящие из нулей (как в данном примере), то отбрасываем эти строки (или столбцы):
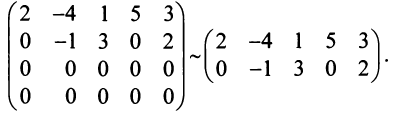
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
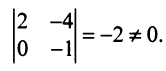 Поэтому ранг полученной ступенчатой, а следовательно, и данной матрицы равен 2. ►
Поэтому ранг полученной ступенчатой, а следовательно, и данной матрицы равен 2. ►
Для рангов матриц справедливы следующие соотношения:

5)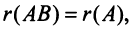 если
если 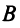 — квадратная матрица и
— квадратная матрица и 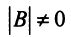
6) 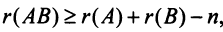 где
где 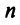 – число столбцов матрицы
– число столбцов матрицы  или строк матрицы
или строк матрицы  .
.
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.
 матрице
матрице  обозначим ее строки следующим образом:
обозначим ее строки следующим образом:
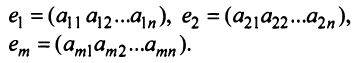
Две строки матрицы называются равными, если равны их соответствующие элементы: 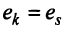 , если
, если 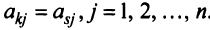
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
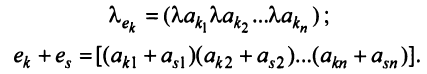
Строка е называется линейной комбинацией строк 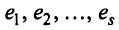 матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: 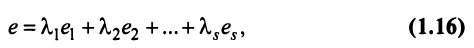
где 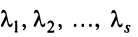 — любые числа.
— любые числа.
Строки матрицы 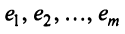 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 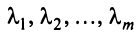 .т, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
.т, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
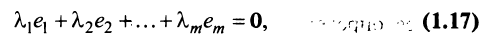
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.
 Действительно, пусть для определенности в формуле (1.17)
Действительно, пусть для определенности в формуле (1.17) 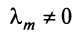 , тогда
, тогда 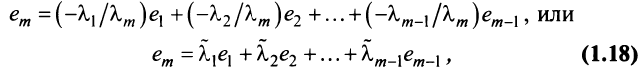
где 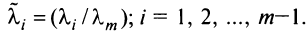
Таким образом, строка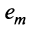 является линейной комбинацией остальных строк.
является линейной комбинацией остальных строк. 
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 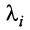 равны нулю, т.е.
равны нулю, т.е. 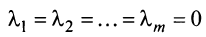 , то строки
, то строки 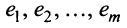 называются линейно независимыми.
называются линейно независимыми.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).
 Пусть матрица
Пусть матрица  размера
размера 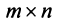 имеет
имеет 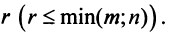
Это означает, что существует отличный от нуля минор 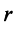 -го порядка. Всякий ненулевой минор
-го порядка. Всякий ненулевой минор 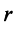 -го порядка будем называть базисным минором. Пусть для определенности это минор
-го порядка будем называть базисным минором. Пусть для определенности это минор

Тогда строки матрицы 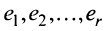 линейно независимы. Действительно, предположим противное, т.е. одна из этих строк, например
линейно независимы. Действительно, предположим противное, т.е. одна из этих строк, например 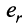 , является линейной комбинацией остальных:
, является линейной комбинацией остальных:
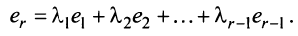
Вычтем из элементов 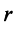 -й строки элементы 1-й строки, умноженные на
-й строки элементы 1-й строки, умноженные на 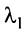 , элементы 2-й строки, умноженные на
, элементы 2-й строки, умноженные на 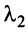 , и т.д., наконец, элементы
, и т.д., наконец, элементы 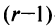 -й строки, умноженные на
-й строки, умноженные на 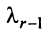 . На основании свойства 8 (см. § 1.4) при таких преобразованиях матрицы ее определитель
. На основании свойства 8 (см. § 1.4) при таких преобразованиях матрицы ее определитель  не изменится, но так как теперь г-я строка будет состоять из одних нулей, то
не изменится, но так как теперь г-я строка будет состоять из одних нулей, то 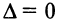 — противоречие, и наше предположение о том, что строки
— противоречие, и наше предположение о том, что строки 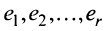 матрицы линейно зависимы, неверно.
матрицы линейно зависимы, неверно.
Строки 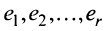 назовем базисными.
назовем базисными.
Покажем, что любые 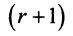 строк матрицы линейно зависимы, т.е. любая строка выражается через базисные.
строк матрицы линейно зависимы, т.е. любая строка выражается через базисные.
Рассмотрим минор 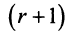 -го порядка, который получается
-го порядка, который получается
при дополнении рассматриваемого минора элементами еще одной строки 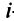 и столбца
и столбца 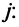

Этот минор равен нулю, так как ранг матрицы равен 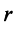 , поэтому любой минор более высокого порядка равен нулю.
, поэтому любой минор более высокого порядка равен нулю.
Раскладывая его по элементам последнего (добавленного) столбца, получаем 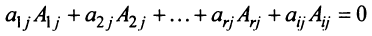 , где последнее алгебраическое дополнение
, где последнее алгебраическое дополнение 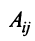 совпадает с базисным минором
совпадает с базисным минором  и поэтому отлично от нуля, т.е.
и поэтому отлично от нуля, т.е. 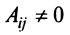 .
.
Разделив последнее равенство на 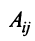 , можем выразить элемент
, можем выразить элемент 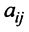 как линейную комбинацию:
как линейную комбинацию:

где 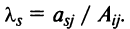
Фиксируем значение 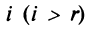 и получаем, что для любого
и получаем, что для любого 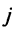
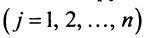 элементы
элементы 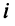 -й строки
-й строки 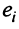 линейно выражаются через элементы строк
линейно выражаются через элементы строк 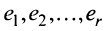 т.е.
т.е.  -я строка есть линейная комбинация базисных:
-я строка есть линейная комбинация базисных:
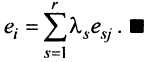
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
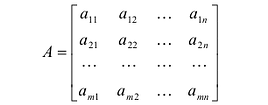 (9.1)
(9.1)
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 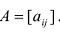 . Числа
. Числа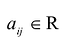 называются элементами матрицы, индекс i обозначает номер строки, а индекс j – номер столбца, на пересечении которых расположен элемент.
называются элементами матрицы, индекс i обозначает номер строки, а индекс j – номер столбца, на пересечении которых расположен элемент.
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 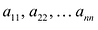 называется главной диагональю, состоящая из элементов а,п,
называется главной диагональю, состоящая из элементов а,п, 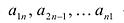 – побочной диагональю.
– побочной диагональю.
Квадратная матрица: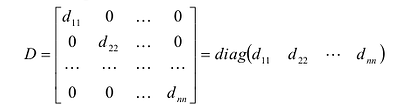
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 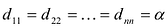 , то такая матрица называется скалярной. Скалярная матрица, у которой
, то такая матрица называется скалярной. Скалярная матрица, у которой 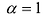 называется единичной и обозначается буквой Е. Например, единичная матрица третьего порядка:
называется единичной и обозначается буквой Е. Например, единичная матрица третьего порядка:
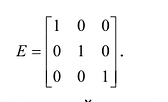
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 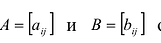 одинакового размера называется матрица
одинакового размера называется матрица 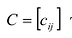 того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. 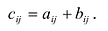
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается – А.
Произведением матрицы 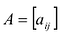 на число
на число 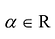 называется матрица, все элементы которой равны соответствующим элементам матрицы А, умноженным на число
называется матрица, все элементы которой равны соответствующим элементам матрицы А, умноженным на число 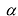 .
.
Умножение матрицы на действительное число обладает следующими свойствами:
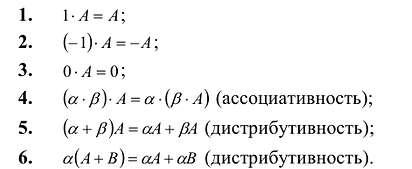
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 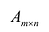 на матрицу
на матрицу 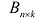 называется матрица
называется матрица
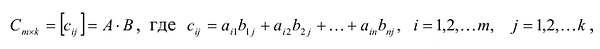
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
 В)- С = А
В)- С = А  (В
(В  С) – ассоциативность умножения;
С) – ассоциативность умножения; - (А + ВС = АС + ВС, А-(В + С)= АВ + АС – свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
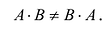
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 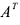 .
.
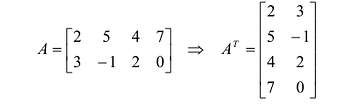
Свойства транспонирования: 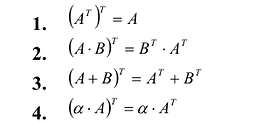
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 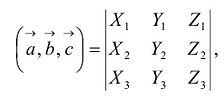 , или в свернутой форме
, или в свернутой форме 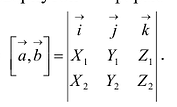
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
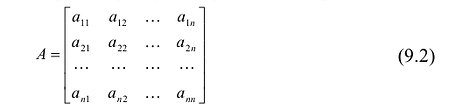
Для записи определителя n-го порядка матрицы А будем применять обозначения  . При n = 1 матрица A состоит из одного элемента и ее определитель равен этому элементу. При n = 2 получаем определитель
. При n = 1 матрица A состоит из одного элемента и ее определитель равен этому элементу. При n = 2 получаем определитель 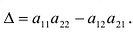
Минором 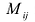 элемента
элемента 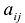 матрицы A называют определитель матрицы (n-1)-го порядка, получаемого из матрицы Л вычеркиванием i-той строки и j-го столбца.
матрицы A называют определитель матрицы (n-1)-го порядка, получаемого из матрицы Л вычеркиванием i-той строки и j-го столбца.
Пример №14
Найти минор 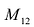 матрицы:
матрицы:
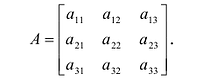
По определению, минор 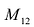 элемента
элемента 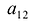 есть определитель матрицы, получаемой из матрицы А вычеркиванием первой строки и второго столбца. Следовательно,
есть определитель матрицы, получаемой из матрицы А вычеркиванием первой строки и второго столбца. Следовательно, 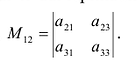
Алгебраическим дополнением элемента 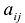 матрицы А называется минор
матрицы А называется минор 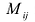 взятый со знаком
взятый со знаком 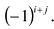 Алгебраическое дополнение элемента
Алгебраическое дополнение элемента 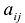 обозначается
обозначается 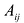 следовательно,
следовательно, 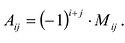
Пример №15
Найти алгебраическое дополнение элемента 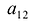 , матрицы А из примера 7.
, матрицы А из примера 7.
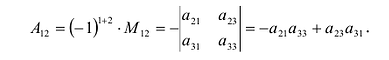
Определителем квадратной матрицы А n-го порядка 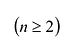 называется число:
называется число:
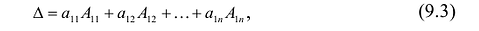
где аи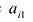 – элементы первой строки матрицы (9.2), а
– элементы первой строки матрицы (9.2), а 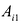 их алгебраические дополнения
их алгебраические дополнения 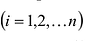 .
.
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 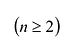 называется число:
называется число:
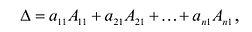 (9.4)
(9.4)
где 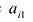 – элементы первого столбца матрицы (9.2), а
– элементы первого столбца матрицы (9.2), а 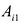 их алгебраические дополнения
их алгебраические дополнения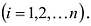 .
.
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
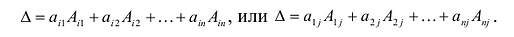
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе  две одинаковые сроки местами. Тогда, по свойству 2 получим определитель
две одинаковые сроки местами. Тогда, по свойству 2 получим определитель 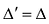 , но с другой стороны, определитель не изменится, т.е.
, но с другой стороны, определитель не изменится, т.е.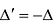 . Отсюда
. Отсюда .
.
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя  умножить на число
умножить на число 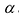 , то определитель умножится на
, то определитель умножится на 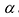 .
.
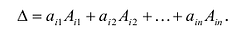
Умножим элементы i-той строки на 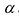 . Тогда получим определитель:
. Тогда получим определитель:
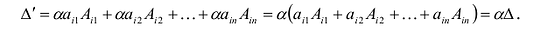
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя  есть сумма двух слагаемых, то определитель
есть сумма двух слагаемых, то определитель  равен сумме двух определителей: у одного из них i-той строкой (столбцом) служат первые слагаемые, а у другого – вторые.
равен сумме двух определителей: у одного из них i-той строкой (столбцом) служат первые слагаемые, а у другого – вторые.
Разложив определитель  по i -той строке получим:
по i -той строке получим:
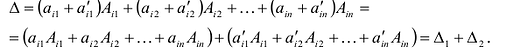
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя  соответствующие элементы j-ой строки, умноженные на число
соответствующие элементы j-ой строки, умноженные на число 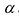 , получим определитель
, получим определитель 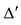 Определитель
Определитель 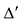 равен сумме двух определителей: первый есть
равен сумме двух определителей: первый есть , а второй равен нулю, так как у него i-тая и j-тая строки пропорциональны.
, а второй равен нулю, так как у него i-тая и j-тая строки пропорциональны.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:

Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 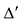 , который получается из данного определителя
, который получается из данного определителя  заменой j-той строки i-той строкой. Определитель
заменой j-той строки i-той строкой. Определитель 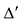 равен нулю, так как у него две одинаковые строки. Разложив его по j-той строке получим:
равен нулю, так как у него две одинаковые строки. Разложив его по j-той строке получим:
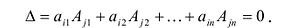
Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 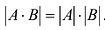 .
.
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы 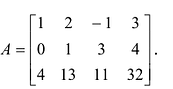
Минор первого порядка (элемент 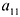 ) отличен от нуля. Окаймляющий его минор
) отличен от нуля. Окаймляющий его минор 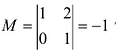 тоже не равен нулю.
тоже не равен нулю.
Далее рассмотрим миноры, окаймляющие минор М :
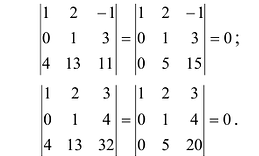
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:

с разрешающим элементом 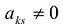 называется следующая совокупность преобразований со строками матрицы:
называется следующая совокупность преобразований со строками матрицы:
- > k первой строке прибавить k-ю, умноженную на число
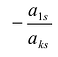 и т.д.;
и т.д.;
> k последней строке прибавить k — го, умноженную на число 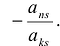 После выполнения этих преобразований получается матрица:
После выполнения этих преобразований получается матрица:
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 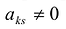 называется следующая совокупность преобразований со столбцами матрицы:
называется следующая совокупность преобразований со столбцами матрицы:
- > к первому столбцу прибавить k-й, умноженный на число
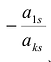 и т.д.;
и т.д.; - > к последнему столбцу прибавить k -й, умноженный на число
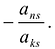
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы 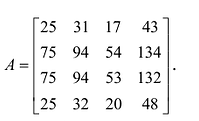
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.

Вычитая далее вторую строку из третьей и последней, имеем:

Последняя матрица содержит отличный от нуля минор 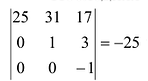 третьего порядка, определитель же самой матрицы А равен нулю. Следовательно,
третьего порядка, определитель же самой матрицы А равен нулю. Следовательно, 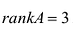
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А – квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е – единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 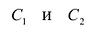 – матрицы, обратные к матрице А. Тогда
– матрицы, обратные к матрице А. Тогда 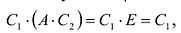 с другой стороны,
с другой стороны, 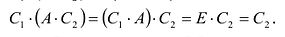
Откуда 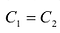 . Обратную матрицу к матрице А обозначают
. Обратную матрицу к матрице А обозначают 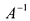 .
.
Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 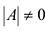 .
.
Пусть А имеет обратную матрицу. Тогда 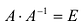 и, применяя теорему об умножении определителей, получаем
и, применяя теорему об умножении определителей, получаем 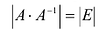 или
или 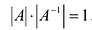
Следовательно, 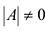 .
.
Пусть 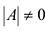 . Укажем явное выражение матрицы
. Укажем явное выражение матрицы 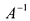 через элементы матрицы А, а именно: если
через элементы матрицы А, а именно: если 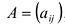 , то:
, то:
здесь 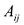 – алгебраическое дополнение к элементу
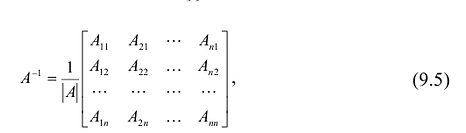
– алгебраическое дополнение к элементу 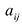 . Матрица (9.5) получается из матрицы А следующим образом. Сначала вместо каждого элемента
. Матрица (9.5) получается из матрицы А следующим образом. Сначала вместо каждого элемента 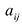 пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную
пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную 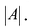
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице

Так как 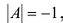 , то
, то 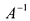 существует. Вычислим алгебраические дополнения элементов матрицы А:
существует. Вычислим алгебраические дополнения элементов матрицы А: 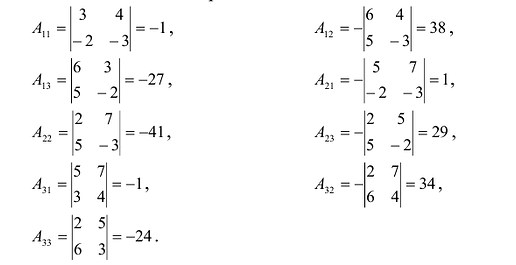
Матрицу 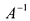 находим в два приема, согласно формуле (9.5). Сначала запишем матрицу В, состоящую из алгебраических дополнений элементов
находим в два приема, согласно формуле (9.5). Сначала запишем матрицу В, состоящую из алгебраических дополнений элементов 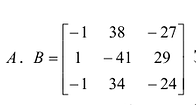 Затем матрица В транспонируется и умножается на число обратное
Затем матрица В транспонируется и умножается на число обратное 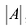 , в данном случае – на (-1). Окончательно получаем:
, в данном случае – на (-1). Окончательно получаем:
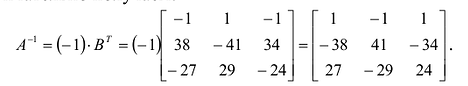
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В – невырожденные матрицы одинакового порядка, то: 
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 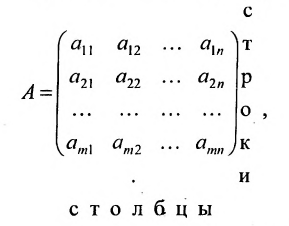 (3.1.1) состоящая из m строк и n столбцов, называется матрицей размером
(3.1.1) состоящая из m строк и n столбцов, называется матрицей размером  .
.
Числа 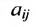 называются элементами матрицы. Каждый элемент матрицы имеет два индекса, первый индекс i обозначает номер строки, второй индекс j – номер столбца.
называются элементами матрицы. Каждый элемент матрицы имеет два индекса, первый индекс i обозначает номер строки, второй индекс j – номер столбца.
Матрицы удобно обозначать в виде 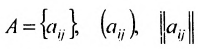 , при
, при 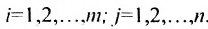 . Фигурные (круглые) скобки, двойные прямые вертикальные линии показывают, что
. Фигурные (круглые) скобки, двойные прямые вертикальные линии показывают, что 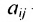 – типовой элемент матрицы А, в котором индексы i и j последовательно принимают все значения от 1 до указанных конечных величин.
– типовой элемент матрицы А, в котором индексы i и j последовательно принимают все значения от 1 до указанных конечных величин.
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу  которая называется транспонированной по отношению к А. Если размер А
которая называется транспонированной по отношению к А. Если размер А 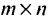 , то
, то 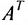 размерности
размерности 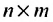 . Повторное транспонирование приводит к исходной матрице:
. Повторное транспонирование приводит к исходной матрице: 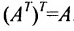 .
.
Пример №19
Рассмотрим матрицу

элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы – годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце – цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:

Хотя элементы матрицы 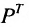 те же, что и матрицы Р, обе матрицы не одинаковые. Взаимосвязь этих матриц проявляется в том, что строки матрицы Р являются столбцами матрицы
те же, что и матрицы Р, обе матрицы не одинаковые. Взаимосвязь этих матриц проявляется в том, что строки матрицы Р являются столбцами матрицы 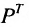 .
.
Если, элементы 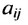 матрицы А неотрицательные (положительные) действительные числа
матрицы А неотрицательные (положительные) действительные числа 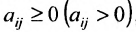 , то матрица А называется неотрицательной (положительной) и записывается
, то матрица А называется неотрицательной (положительной) и записывается 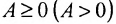 .
.
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 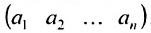 , называется матрицей-строкой. Матрица, состоящая из одного столбца
, называется матрицей-строкой. Матрица, состоящая из одного столбца
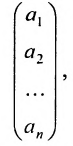
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом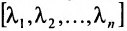 :
: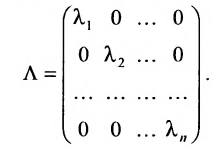
Если в диагональной матрице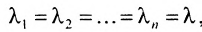 то она называется скалярной. Скалярная матрица, у которой диагональные элементы равны 1, называется единичной:
то она называется скалярной. Скалярная матрица, у которой диагональные элементы равны 1, называется единичной:
 Квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю, называется верхнетреугольной (“матрица А). Аналогично, если в квадратной матрице нулю равны все элементы, стоящие выше главной диагонали, то она называется нижнетреугольной (матрица В).
Квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю, называется верхнетреугольной (“матрица А). Аналогично, если в квадратной матрице нулю равны все элементы, стоящие выше главной диагонали, то она называется нижнетреугольной (матрица В).
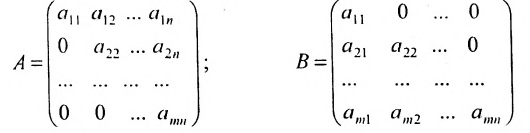
Например, 
Матрица A – верхнеугольная, а В – нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,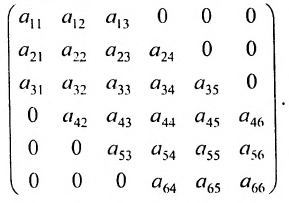
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы: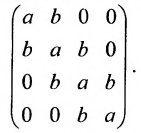
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 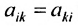 ; если же
; если же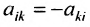 , то матрица А называется кососимметрической. Симметрическая матрица совпадает с транспонированной матрицей, т.е.
, то матрица А называется кососимметрической. Симметрическая матрица совпадает с транспонированной матрицей, т.е. 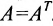 .
.
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:

Элемент 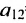 =0,29, характеризующий зависимость использования мощностей и изменения объёмов запасов, совпадает с элементом
=0,29, характеризующий зависимость использования мощностей и изменения объёмов запасов, совпадает с элементом 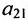 =0,29, характеризующим зависимость между изменением объёмов запасов и использованием мощностей; элемент
=0,29, характеризующим зависимость между изменением объёмов запасов и использованием мощностей; элемент 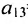 =0,15, характеризующий зависимость между изменением общей величины хозяйственных запасов и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом
=0,15, характеризующий зависимость между изменением общей величины хозяйственных запасов и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом 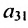 =0,15, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и изменением общей величины хозяйственных запасов; элемент
=0,15, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и изменением общей величины хозяйственных запасов; элемент 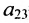 =0,71, характеризующий зависимость между степенью использования производственных мощностей и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом
=0,71, характеризующий зависимость между степенью использования производственных мощностей и суммой совокупного оборота с поправкой на сезонность, совпадает с элементом 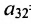 =0,71, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и степенью использования производственных мощностей.
=0,71, характеризующим зависимость между суммой совокупного оборота с поправкой на сезонность и степенью использования производственных мощностей.
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 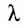 и все элементы одного ряда выше диагонали равны единице, а все другие элементы равны нулю, называется клеткой Жордана:
и все элементы одного ряда выше диагонали равны единице, а все другие элементы равны нулю, называется клеткой Жордана:

Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.

Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 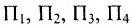 и для их производства используются материалы
и для их производства используются материалы 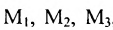 , то система норм материальных затрат, которая представляет собой основу плана снабжения, может быть представлена в виде таблицы (матрицы):
, то система норм материальных затрат, которая представляет собой основу плана снабжения, может быть представлена в виде таблицы (матрицы):

где 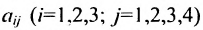 есть норма расхода
есть норма расхода 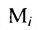 i-го материала на производство единицы
i-го материала на производство единицы 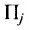 j-го продукта. Так норма расхода материала
j-го продукта. Так норма расхода материала 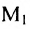 на производство единицы продукта
на производство единицы продукта 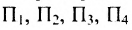 соответственно равна
соответственно равна 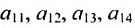 и т.д.
и т.д.
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица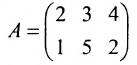
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам – возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы  матрицы А совпадают с соответствующими элементами
матрицы А совпадают с соответствующими элементами матрицы В, т.е. выполняются
матрицы В, т.е. выполняются  скалярные равенства
скалярные равенства 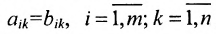 , которые равносильны равенству А=В.
, которые равносильны равенству А=В.
Определение 3.2.1. Суммой матриц А а В размерности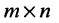 называется матрица S=A+B той же размерности, элементы которой Sik равны суммам соответствующих элементов матриц А и В:
называется матрица S=A+B той же размерности, элементы которой Sik равны суммам соответствующих элементов матриц А и В: 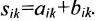
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
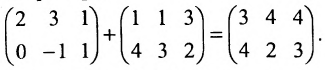
Определение 3.2.2. Произведением матрицы А на скаляр 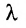 называется матрица
называется матрица 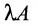 той же размерности, что и А, элементы которой получены из элементов матрицы А умножением на
той же размерности, что и А, элементы которой получены из элементов матрицы А умножением на 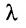 . Например,
. Например,
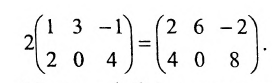
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 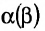 обладают свойствами:
обладают свойствами:
- А + В = В + А – (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
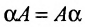 .
.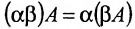 .
.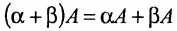 .
.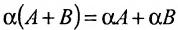 .
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 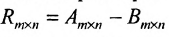 , её элементы равны разностям соответствующих элементов матриц А и В:
, её элементы равны разностям соответствующих элементов матриц А и В: 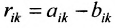 .
.
Например,
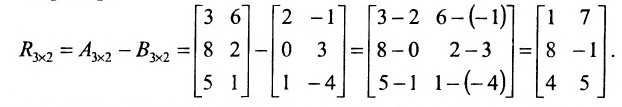
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
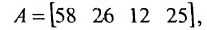
а соответствующие цены с помощью матрицы-столбца:
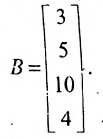
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар): 
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:

Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
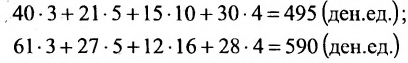
Представим итоговые данные по выручке в виде матрицы-столбца:
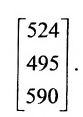
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
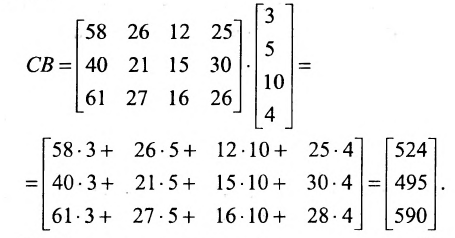
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение  существует только в том случае, когда число элементов в строках матрицы С (т.е. число столбцов) равно числу элементов, составляющих вектор-столбец В (т.е. числу строк). При соблюдении этого равенства, произведение
существует только в том случае, когда число элементов в строках матрицы С (т.е. число столбцов) равно числу элементов, составляющих вектор-столбец В (т.е. числу строк). При соблюдении этого равенства, произведение  образует вектор-столбец, содержащий столько элементов, сколько строк насчитывается в матрице С. Следовательно, если в матрице С содержится т строк и q столбцов и порядок матрицы-столбца В равен q, тогда произведение
образует вектор-столбец, содержащий столько элементов, сколько строк насчитывается в матрице С. Следовательно, если в матрице С содержится т строк и q столбцов и порядок матрицы-столбца В равен q, тогда произведение 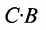 представляет собой матрицу-столбец порядка т, причем i-й элемент этого вектора равен
представляет собой матрицу-столбец порядка т, причем i-й элемент этого вектора равен
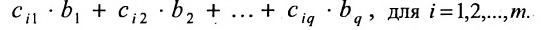
Аналогичным образом определяется произведение матрицы-строки 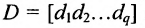 на матрицу Р. Оно существует в том случае,
на матрицу Р. Оно существует в том случае,
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 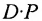 образует матрицу-строку, содержащую столько же элементов, сколько столбцов насчитывается в матрице Р. При этом произведение
образует матрицу-строку, содержащую столько же элементов, сколько столбцов насчитывается в матрице Р. При этом произведение 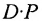 равно
равно 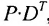 , произведение
, произведение 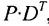 может к не существовать, несмотря на то что, существует произведение
может к не существовать, несмотря на то что, существует произведение 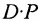 , и наоборот.
, и наоборот.
Пример №21
Пусть матрица

характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки – с продолжительностью подписки от одного года до двух лет; третья строка – с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца – возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца – возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 – имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =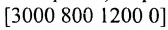 .
.
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:

Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 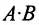 определено, когда число столбцов в А равно числу строк в В. Тогда произведение
определено, когда число столбцов в А равно числу строк в В. Тогда произведение 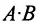 содержит то же количество строк, что и матрица А, и то же количество столбцов, что и матрица В.
содержит то же количество строк, что и матрица А, и то же количество столбцов, что и матрица В.
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 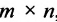 , то произведение
, то произведение 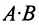 является матрицей размерности
является матрицей размерности 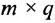 , т. е.:
, т. е.:
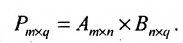
Определение 3.2.4. Произведением матрицы А размерности 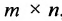 на матрицу В размерности
на матрицу В размерности 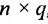 называется матрица Р размерности
называется матрица Р размерности 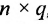 , элементы которой
, элементы которой 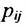 определяется формулами:
определяется формулами:
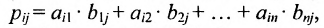
, при  , т.е.
, т.е.  элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ого столбца матрицы В.
элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ого столбца матрицы В.
- Заказать решение задач по высшей математике
Пример №22
Пусть 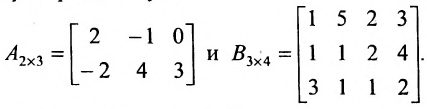 Матрица А содержит три столбца, а В содержит три строки. Следовательно, матрицы А и В согласованные для умножения. Тогда
Матрица А содержит три столбца, а В содержит три строки. Следовательно, матрицы А и В согласованные для умножения. Тогда 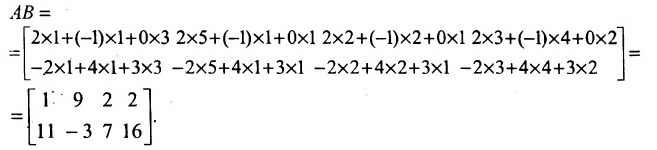
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 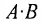 . Например,
. Например, 
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 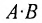 к
к 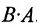 . Если размеры матрицы A равны
. Если размеры матрицы A равны 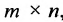 , то оба произведения существуют только в том случае, когда размеры матрицы В равны
, то оба произведения существуют только в том случае, когда размеры матрицы В равны 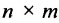 . Тогда произведение
. Тогда произведение 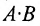 образует квадратную матрицу порядка m, а произведение
образует квадратную матрицу порядка m, а произведение 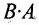 – квадратную матрицу n. Поэтому размеры АВ могут быть равны ВА в том случае, когда m = n, т.е. когда обе матрицы квадратные и имеют один и тот же порядок равный m. При этом указанные произведения матриц могут не иметь ни одного одинакового элемента, полученного в результате суммирования произведений соотвстствующих элементов исходных матриц. Поэтому, если даже существуют оба произведения АВ и ВА и оба они имеют одинаковый порядок, вообще говоря, они не обязательно должны быть равны между собой, что и показывает приведенный выше пример.
– квадратную матрицу n. Поэтому размеры АВ могут быть равны ВА в том случае, когда m = n, т.е. когда обе матрицы квадратные и имеют один и тот же порядок равный m. При этом указанные произведения матриц могут не иметь ни одного одинакового элемента, полученного в результате суммирования произведений соотвстствующих элементов исходных матриц. Поэтому, если даже существуют оба произведения АВ и ВА и оба они имеют одинаковый порядок, вообще говоря, они не обязательно должны быть равны между собой, что и показывает приведенный выше пример.
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например, 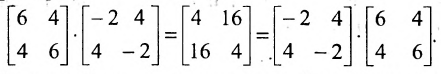
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 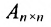 представляет собой квадратную матрицу п-ого порядка, а
представляет собой квадратную матрицу п-ого порядка, а 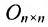 – аналогичную матрицу, все элементы которой составляют нули, тогда
– аналогичную матрицу, все элементы которой составляют нули, тогда
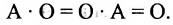
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 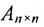 представляет собой квадратную матрицу n-ого порядка, а
представляет собой квадратную матрицу n-ого порядка, а 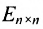 – аналогичную единичную матрицу, то
– аналогичную единичную матрицу, то
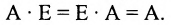
Единичная матрица того же порядка служит единицей в матричной алгебре. Например, 
Отметим, что произведение матрицы на скалярную величину так же коммутативно: 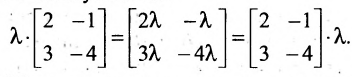
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n – натуральное число, больше единицы, то 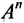 есть произведение n матриц равных А. Для действий со степенями матриц справедливы следующие правила:
есть произведение n матриц равных А. Для действий со степенями матриц справедливы следующие правила: 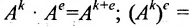
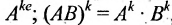 ,если АВ = ВА.
,если АВ = ВА.
Значением многочлена
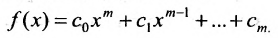
с числовыми коэффициентами 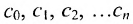 от матрицы А или значением многочлена
от матрицы А или значением многочлена  при х = А называется матрица
при х = А называется матрица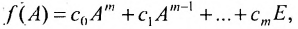
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
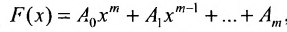
где х- переменное и 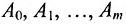 – квадратные матрицы с числовыми элементами одного и того же порядка n. Число n называется порядком многочлена F(x). Если
– квадратные матрицы с числовыми элементами одного и того же порядка n. Число n называется порядком многочлена F(x). Если 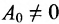 , то число m называется степенью матричного многочлена F{x). Если матрица
, то число m называется степенью матричного многочлена F{x). Если матрица 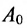 не вырождена, т.е.
не вырождена, т.е. 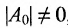 , то матричный многочлен F(x) называется регулярным.
, то матричный многочлен F(x) называется регулярным.
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 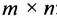 :
: 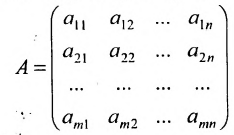
Обозначим столбцы матрицы А следующим образом: 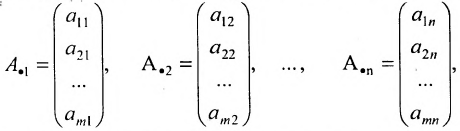
их называют векторами-столбцами; а строки:
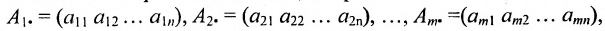
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам – число деталей трех видов, необходимых для производства одной игрушки трёх типов:
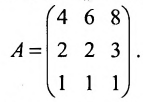
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:

Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.

Эти потребности в сырье определяются умножением матриц
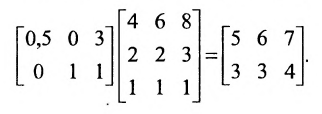
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
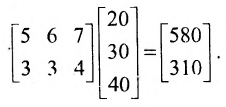
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
Пример №24
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ. 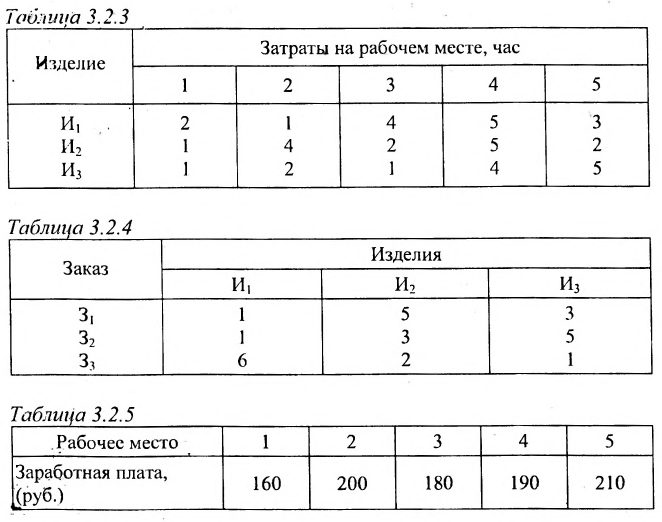
Решение. Введем в рассмотрение следующие матрицы:
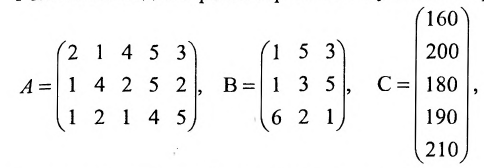 где А – матрица затрат, В – матрица спроса, С – матрица почасовой зарплаты.
где А – матрица затрат, В – матрица спроса, С – матрица почасовой зарплаты.
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А – между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):
 находим заработную плату, приходящуюся на заказ
находим заработную плату, приходящуюся на заказ  равную 23920 руб., на заказ
равную 23920 руб., на заказ  – 23640 руб. и на заказ
– 23640 руб. и на заказ  – 24850 руб.
– 24850 руб.
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые: 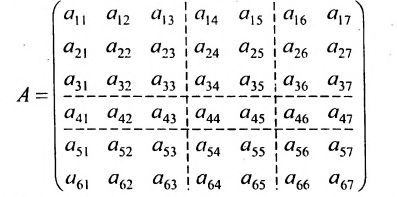
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
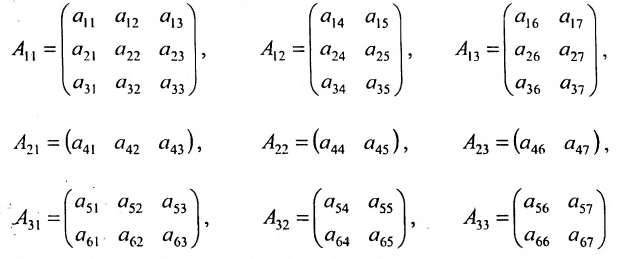
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например, 
В матрице В клетки 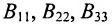 – квадратные матрицы третьего, второго и первого порядка соответственно.
– квадратные матрицы третьего, второго и первого порядка соответственно.
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 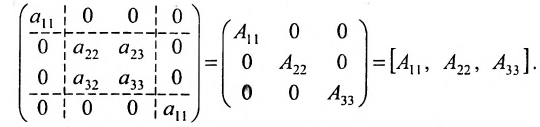 Квазидиагональная матрица обозначается
Квазидиагональная матрица обозначается 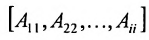 , где
, где
 – её диагональные квадратные клетки.
– её диагональные квадратные клетки.
Если к квадратной матрице а добавить снизу матрицу-строку, справа – матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 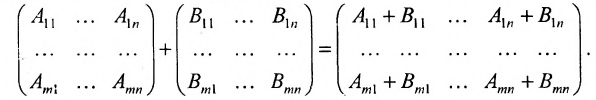 Подчеркнем, что можно складывать только конформные матрицы. В противном случае равенство не имеет смысла.
Подчеркнем, что можно складывать только конформные матрицы. В противном случае равенство не имеет смысла.
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр: 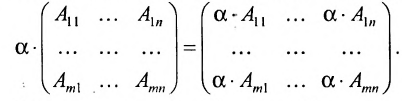
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
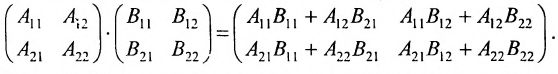
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
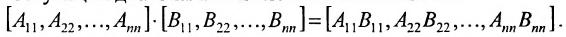
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
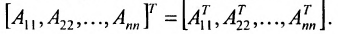
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
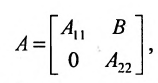
где  – квадратные блоки, включающие ненулевые элементы; О – блок, состоящий только из нулей; В – блок, элементы которого могут принимать любые значения, называется разложимой матрицей.
– квадратные блоки, включающие ненулевые элементы; О – блок, состоящий только из нулей; В – блок, элементы которого могут принимать любые значения, называется разложимой матрицей.
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах 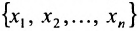
или и рассматриваются их суммы. Символом операции
и рассматриваются их суммы. Символом операции
суммирования служит заглавная греческая буква  (сигма). Тогда,
(сигма). Тогда,
например, сумму 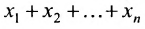 можно записать в видех
можно записать в видех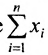 . Числа сточщие под знаком
. Числа сточщие под знаком  и над ним, называются пределами суммирования и указывают наибольшие и наименьшие значения индекса суммирования, между которыми расположены его промежуточные значения.
и над ним, называются пределами суммирования и указывают наибольшие и наименьшие значения индекса суммирования, между которыми расположены его промежуточные значения.
Для оператора суммирования справедливы следующие тождества:
- 1.
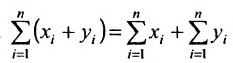
- 2.
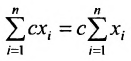
- 3.
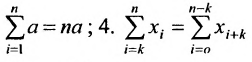 ;
; - 5.
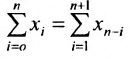
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» – П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
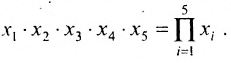
Перестановки
Рассмотрим n целых чисел (элементов)  . Их можно располагать в различном порядке. Всевозможные расположения этих чисел называются перестановками. Перестановка
. Их можно располагать в различном порядке. Всевозможные расположения этих чисел называются перестановками. Перестановка 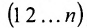 , в которой числа идут в порядке возрастания, называется натуральной. Например, из трех чисел можно составить 6 перестановок: (123), (132), (213), (231), (312), (321). Справедливо следующее утверждение: «Из n чисел можно составить n! перестановок». Символ n! читается юн факториал» и обозначает произведение последовательных натуральных чисел: 0!=1; 1!=1;
, в которой числа идут в порядке возрастания, называется натуральной. Например, из трех чисел можно составить 6 перестановок: (123), (132), (213), (231), (312), (321). Справедливо следующее утверждение: «Из n чисел можно составить n! перестановок». Символ n! читается юн факториал» и обозначает произведение последовательных натуральных чисел: 0!=1; 1!=1; 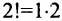 ;
; 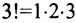 ; …
; … 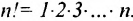 .
.
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае – нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
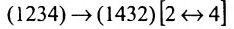
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида

или более компактно: 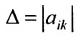 . Каждый элемент
. Каждый элемент  имеет два индекса, первый из которых указывает, какой строке принадлежит элемент, а второй – какому столбцу.
имеет два индекса, первый из которых указывает, какой строке принадлежит элемент, а второй – какому столбцу.
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов  , взятых по одному из каждой
, взятых по одному из каждой
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали – строки, а вертикали – столбцы.
Введем величину:
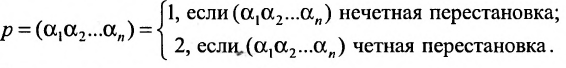
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
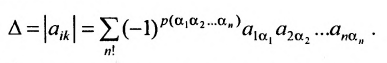
Суммирование распространяется на все перестановки  из n чисел 1,2,…,n, что условно обозначили символом n!
из n чисел 1,2,…,n, что условно обозначили символом n!
В частности, определителем второго порядка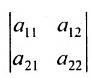 называется алгебраическая сумма двух слагаемых
называется алгебраическая сумма двух слагаемых 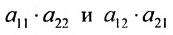 , каждое из которых равно произведению двух элементов. Согласно определению 3.6.1, первое слагаемое имеет знак «+», а второе – знак «-». Следовательно, для нахождения определителя второго порядка, нужно из произведения элементов, стоящих на главной диагонали вычесть произведение элементов стоящих на побочной диагонали:
, каждое из которых равно произведению двух элементов. Согласно определению 3.6.1, первое слагаемое имеет знак «+», а второе – знак «-». Следовательно, для нахождения определителя второго порядка, нужно из произведения элементов, стоящих на главной диагонали вычесть произведение элементов стоящих на побочной диагонали:
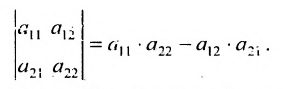
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 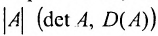 .
.
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
 . Величина определителя при его транспонировании (т. е. при замене его строк соответствующими столбцами) не меняется.
. Величина определителя при его транспонировании (т. е. при замене его строк соответствующими столбцами) не меняется.
Доказательство. Рассмотрим определитель  . Протранспонируем его; получим определитель
. Протранспонируем его; получим определитель 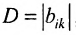 , т. е. элементы строки и i-го столбца определителя
, т. е. элементы строки и i-го столбца определителя 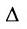 совпадают с элементами из i-й строки и k-го столбца определителя D. Тогда по определению
совпадают с элементами из i-й строки и k-го столбца определителя D. Тогда по определению
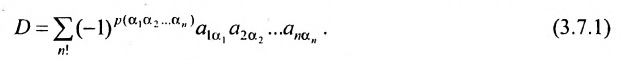
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
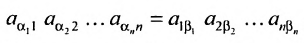
Перестановки 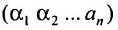 и
и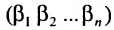 разные, но обладают одинаковой четностью, так как одним и тем же числом транспозиций перестановка
разные, но обладают одинаковой четностью, так как одним и тем же числом транспозиций перестановка 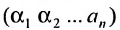 переводится в натуральную, а перестановку
переводится в натуральную, а перестановку 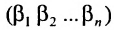 получаем из натуральной. Поэтому
получаем из натуральной. Поэтому 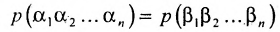 , и равенство (3.7.1) принимает вид:
, и равенство (3.7.1) принимает вид:
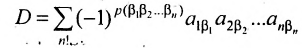
Так как 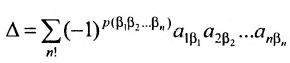 то
то  чтo и требовалось доказать.
чтo и требовалось доказать.
Из свойства 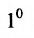 вытекает, что строки и столбцы определителя равноправны. Поэтому любое свойство доказанное для строк, справедливо и для столбцов.
вытекает, что строки и столбцы определителя равноправны. Поэтому любое свойство доказанное для строк, справедливо и для столбцов.
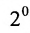 . Если в определителе поменять местами две строки (столбца), то у него изменится только знак, а абсолютная величина останется прежней.
. Если в определителе поменять местами две строки (столбца), то у него изменится только знак, а абсолютная величина останется прежней.
Доказательство. Рассмотрим определитель  , в котором переставим l-ую и m-ую строки. При этом считаем, что
, в котором переставим l-ую и m-ую строки. При этом считаем, что  . Получим определитель
. Получим определитель 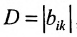 , элементы которого связаны с элементами определителя
, элементы которого связаны с элементами определителя  соотношениями
соотношениями
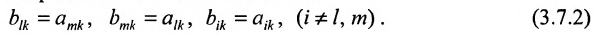
В силу равенств (3.7.2) преобразуем определитель
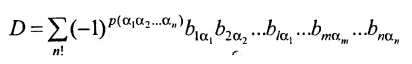
к виду
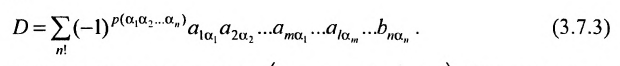
Выполним в перестановке 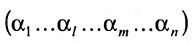 одну транспозицию
одну транспозицию 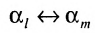 , в результате четность перестановки изменится на противоположную:
, в результате четность перестановки изменится на противоположную:
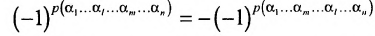
Затем поменяем местами сомножители 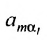 и
и 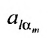 в произведении
в произведении 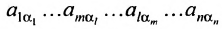 . Произведение при этом не изменится, а равенство (3.7.3) примет вид
. Произведение при этом не изменится, а равенство (3.7.3) примет вид
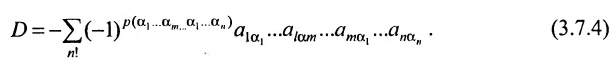
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку  , т. к.
, т. к. 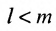 , а перестановка из
, а перестановка из
вторых индексов такая же, как и в выражении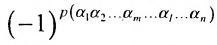 . Поэтому сумма правой части формулы (3.7.4) равна определителю
. Поэтому сумма правой части формулы (3.7.4) равна определителю  , т. е.
, т. е. 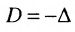 . что и требовалось доказать.
. что и требовалось доказать.
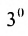 . Определитель с двумя одинаковыми строками (столбцами) равен нулю.
. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 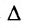 определителя. С другой стороны, по свойству
определителя. С другой стороны, по свойству 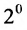 в результате перестановки знак определителя изменится, т. с.
в результате перестановки знак определителя изменится, т. с. 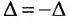 . Следовательно,
. Следовательно, 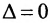 .
.
 . Если все элементы строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
. Если все элементы строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
Доказательство. Пусть в определителе 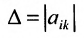 l-тая строка содержит общий множитель, тогда по определению его можно записать в виде:
l-тая строка содержит общий множитель, тогда по определению его можно записать в виде:
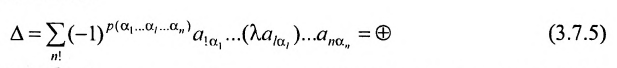
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 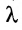 , его можно вынести за знак суммы, т. с. преобразовать
, его можно вынести за знак суммы, т. с. преобразовать
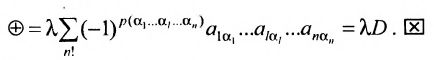
Из свойства  вытекает:
вытекает:
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству  общий множитель у одной из строк, пропорциональной другой, можно вынести за знак определителя. Получим определитель с двумя одинаковыми строками, а в силу свойства
общий множитель у одной из строк, пропорциональной другой, можно вынести за знак определителя. Получим определитель с двумя одинаковыми строками, а в силу свойства 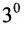 он равен нулю.
он равен нулю.
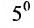 . Если все элементы строки (столбца) являются суммами из одинакового числа слагаемых, то определитель равен сумме определителей, у которых элементами этой строки (столбца) служат отдельные слагаемые.
. Если все элементы строки (столбца) являются суммами из одинакового числа слагаемых, то определитель равен сумме определителей, у которых элементами этой строки (столбца) служат отдельные слагаемые.
Доказательство. Пусть все элементы 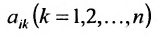 i-той строки определителя
i-той строки определителя  являются суммами из одинакового числа слагаемых:
являются суммами из одинакового числа слагаемых: 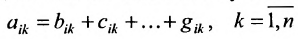 . Тогда определитель имеет вид:
. Тогда определитель имеет вид:
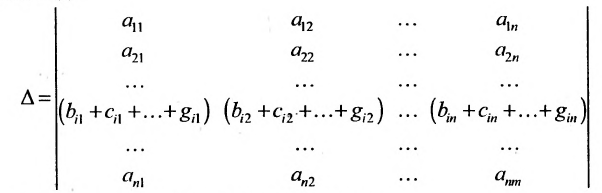
В силу определения его можно записать:
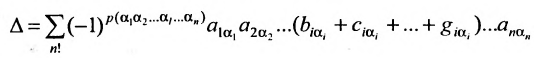
но так как 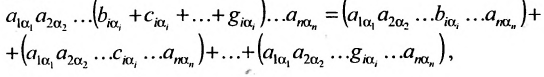
то
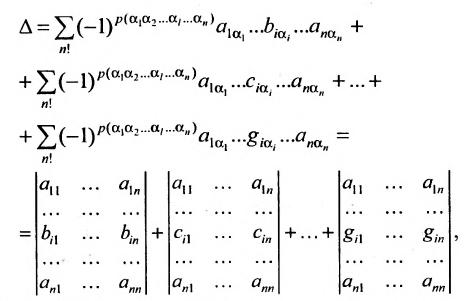
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
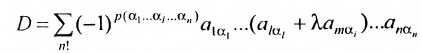 полученный из
полученный из 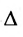 прибавляем к элементам l строки соответствующие элементы m строки, то в силу свойства
прибавляем к элементам l строки соответствующие элементы m строки, то в силу свойства  его можно представить в виде суммы двух определителей, т. е.
его можно представить в виде суммы двух определителей, т. е.

так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 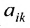 , то полученный определитель (n-1)-го порядка называется минором исходного определителя
, то полученный определитель (n-1)-го порядка называется минором исходного определителя  , соответствующего элементу
, соответствующего элементу 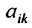 , и обозначается
, и обозначается 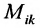 . Например, если
. Например, если
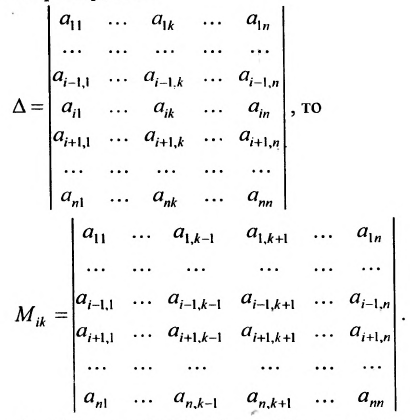
Определение 3.8.1. Минор 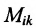 с определенным знаком, зависящим от четности суммы i+k номеров строки и столбца, на пересечении которых находится элемент
с определенным знаком, зависящим от четности суммы i+k номеров строки и столбца, на пересечении которых находится элемент 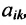 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 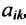 в определителе
в определителе  и обозначается
и обозначается
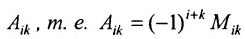 .
.
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 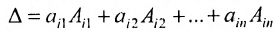 .
.
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства: 
Представим каждый элемент i-й строки определителя в виде суммы n слагаемых, из которых n-1 слагаемое равно нулю
в виде суммы n слагаемых, из которых n-1 слагаемое равно нулю
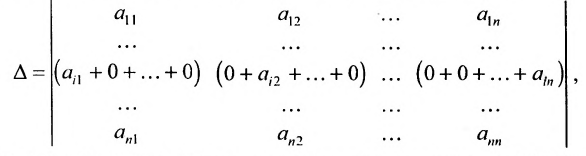
тогда его можно представить в виде суммы определителей (по свойству  ):
):

Определитель 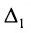 по лемме 2 равен произведению элемента
по лемме 2 равен произведению элемента 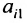 на его алгебраическое дополнение в этом определителе. Но так как определитель
на его алгебраическое дополнение в этом определителе. Но так как определитель 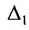 отличается от
отличается от  лишь элементами i-й строки, го это алгебраическое дополнение совпадает с алгебраическим дополнением
лишь элементами i-й строки, го это алгебраическое дополнение совпадает с алгебраическим дополнением 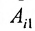 элемента
элемента 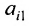 , определителя
, определителя 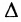 , так как эта строка и столбец будут вычеркнуты, а все остальные элементы определителя
, так как эта строка и столбец будут вычеркнуты, а все остальные элементы определителя 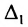 , и
, и 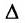 совпадают.
совпадают.
Следовательно,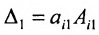 .
.
Аналогично 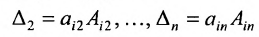 и поэтому (т. к.
и поэтому (т. к. 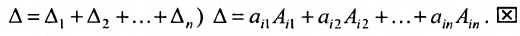
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
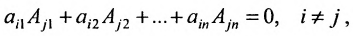 , где i, j – строки определителя
, где i, j – строки определителя  .
.
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е. 
Если удобнее получить нули по одну сторону от побочной диагонали, то  где
где 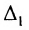 приведен уже к треугольному виду.
приведен уже к треугольному виду.
3) Если определитель 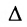 порядка n после разложения по строке или столбцу и после преобразования, выражается через определители того же вида, но более низких порядков, то полученное равенство называется рекуррентным. Вычисляют столько определителей данного вида начальных порядков, сколько их входит в правую часть рекуррентного соотношения. Далее вычисляют определители высших порядков, используя рекуррентные соотношения, до тех пор, пока не удастся заметить общую закономерность для получаемых выражений. Для общего случая доказывают индукцией по п эту закономерность.
порядка n после разложения по строке или столбцу и после преобразования, выражается через определители того же вида, но более низких порядков, то полученное равенство называется рекуррентным. Вычисляют столько определителей данного вида начальных порядков, сколько их входит в правую часть рекуррентного соотношения. Далее вычисляют определители высших порядков, используя рекуррентные соотношения, до тех пор, пока не удастся заметить общую закономерность для получаемых выражений. Для общего случая доказывают индукцией по п эту закономерность.
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
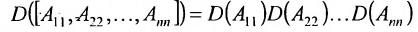 .
.
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
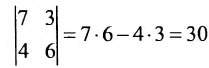 .
.
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком “+” и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
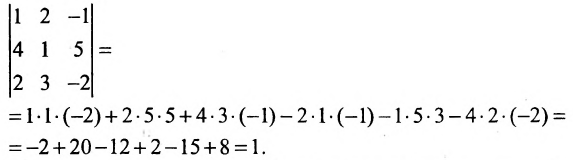
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,

(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
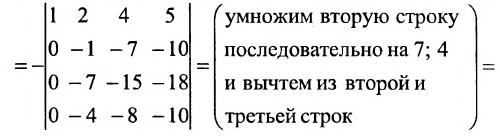

(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
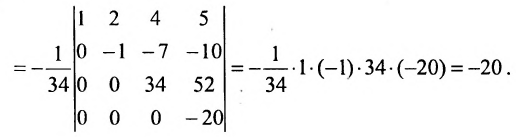
Матрицы и операции над матрицами
Матрицей размера 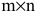 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел 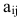
 вида
вида 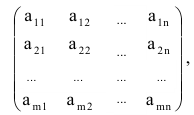 состоящая из m строк и n столбцов. Числа
состоящая из m строк и n столбцов. Числа 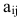 называются элементами матрицы, где i – индекс строки, j – индекс столбца. Обозначение:
называются элементами матрицы, где i – индекс строки, j – индекс столбца. Обозначение: 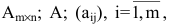
Например, элемент 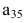 (читается «а три пять») в таблице будет расположен в третьей строке и пятом столбце.
(читается «а три пять») в таблице будет расположен в третьей строке и пятом столбце.
Суммой двух матриц одинакового размера 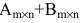 называется матрица
называется матрица 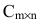 того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц
того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц 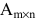 и
и 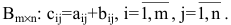
Например,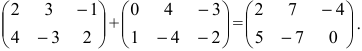
Произведением матрицы 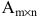 на действительное число
на действительное число 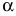 . называется такая матрица
. называется такая матрица 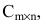 что
что 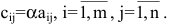
Например,
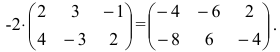 Если количество столбцов первой матрицы (множимой) равно количеству строк второй матрица (множителя), то матрицы называются согласованными.
Если количество столбцов первой матрицы (множимой) равно количеству строк второй матрица (множителя), то матрицы называются согласованными.
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера  (n столбцов) на матрицу В размера
(n столбцов) на матрицу В размера  (n строк) называется матрица С размера
(n строк) называется матрица С размера 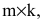 каждый элемент которой
каждый элемент которой 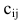 равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ro столбца матрицы В, т.е.
равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-ro столбца матрицы В, т.е. 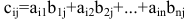 («i-ю строку первой матрицы умножаем на j-й столбец второй матрицы»). Число строк матрицы произведения С равно числу строк матрицы А, а число столбцов матрицы С равно числу столбцов матрицы В.
(«i-ю строку первой матрицы умножаем на j-й столбец второй матрицы»). Число строк матрицы произведения С равно числу строк матрицы А, а число столбцов матрицы С равно числу столбцов матрицы В.
Пример:
Даны матрицы
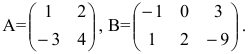
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
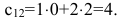
Тогда 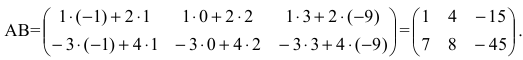
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 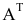 или
или 
Например, 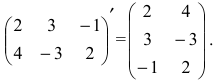
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Определитель матрицы и его свойства
8 февраля 2018
В этом уроке мы детально рассмотрим несколько ключевые вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.
Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)
И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.
Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $left[ mtimes n right]$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:
[A=left[ mtimes n right]]
Или вот так:
[A=left( {{a}_{ij}} right),quad 1le ile m;quad 1le jle n.]
Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $left[ mtimes n right]$ и ${{a}_{ij}}$ возникает одна и та же проблема:
Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
Помните её? У неё есть начало координат (точка $O=left( 0;0 right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=left( 1;2 right)$, $B=left( 3;1 right)$ и т.д.
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Геометрическое определение
Прежде всего хотел бы отметить, что определитель существует только для квадратных матриц вида $left[ ntimes n right]$. Определитель — это число, которое cчитается по определённым правилам и является одной из характеристик этой матрицы (есть другие характеристики: ранг, собственные вектора, но об этом в других уроках).
Ну и что это за характеристика? Что он означает? Всё просто:
Определитель квадратной матрицы $A=left[ ntimes n right]$ — это объём $n$-мерного параллелепипеда, который образуется, если рассмотреть строки матрицы в качестве векторов, образующих рёбра этого параллелепипеда.
Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:
Задача. Найдите определители матриц:
[left| begin{matrix} 1 & 0 \ 0 & 3 \end{matrix} right|quad left| begin{matrix} 1 & -1 \ 2 & 2 \end{matrix} right|quad left| begin{matrix}2 & 0 & 0 \ 1 & 3 & 0 \ 1 & 1 & 4 \end{matrix} right|]
Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.
Первый параллелограмм построен на векторах ${{v}_{1}}=left( 1;0 right)$ и ${{v}_{2}}=left( 0;3 right)$:
Определитель 2×2 — это площадь параллелограмма Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна
[S=1cdot 3=3]
Второй параллелограмм построен на векторах ${{v}_{1}}=left( 1;-1 right)$ и ${{v}_{2}}=left( 2;2 right)$. Ну и что с того? Это тоже прямоугольник:
Ещё один определитель 2×2 Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:
[begin{align} & left| {{v}_{1}} right|=sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}}=sqrt{2}; \ & left| {{v}_{2}} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2}; \ & S=left| {{v}_{1}} right|cdot left| {{v}_{2}} right|=sqrt{2}cdot 2sqrt{2}=4. \end{align}]
Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:
Определитель 3×3 — это объём параллелепипеда Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:
[V=Scdot h]
где $S$ — площадь основания (в нашем случае это площадь параллелограмма на плоскости $OXY$), $h$ — высота, проведённая к этому основанию (по сути, $z$-координата вектора ${{v}_{3}}$).
Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:
[begin{align} & S=2cdot 3=6; \ & V=Scdot h=6cdot 4=24. \end{align}]
Вот и всё! Записываем ответы.
Ответ: 3; 4; 24.
Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.
Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.
И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:
В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.
И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)
Алгебраическое определение
При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.
Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.
Правда, там появится новая проблема… но обо всём по порядку.
Перестановки и инверсии
Давайте выпишем в строчку числа от 1 до $n$. Получится что-то типа этого:
[1;2;3;4;5;…;n-1;n]
Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:
[1;3;2;4;5;…;n-1;n]
А можно — не особо соседние:
[n;2;3;4;5;…;n-1;1]
И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.
Определение. Перестановка длины $n$ — строка из $n$ различных чисел, записанных в любой последовательности. Обычно рассматриваются первые $n$ натуральных чисел (т.е. как раз числа 1, 2, …, $n$), а затем их перемешивают для получения нужной перестановки.
Обозначаются перестановки так же, как и векторы — просто буквой и последовательным перечислением своих элементов в скобках. Например: $p=left( 1;3;2 right)$ или $p=left( 2;5;1;4;3 right)$. Буква может быть любой, но пусть будет $p$.:)
Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:
[begin{align} & {{p}_{1}}=left( 1;2;3;4;5 right) \ & {{p}_{2}}=left( 1;3;2;5;4 right) \ & {{p}_{3}}=left( 5;4;3;2;1 right) \end{align}]
Естественно, перестановку длины $n$ можно рассматривать как функцию, которая определена на множестве $left{ 1;2;…;n right}$ и биективно отображает это множество на себя же. Возвращаясь к только что записанным перестановкам ${{p}_{1}}$, ${{p}_{2}}$ и ${{p}_{3}}$, мы вполне законно можем написать:
[{{p}_{1}}left( 1 right)=1;{{p}_{2}}left( 3 right)=2;{{p}_{3}}left( 2 right)=4;]
Количество различных перестановок длины $n$ всегда ограничено и равно $n!$ — это легко доказуемый факт из комбинаторики. Например, если мы захотим выписать все перестановки длины 5, то мы весьма заколебёмся, поскольку таких перестановок будет
[n!=5!=1cdot 2cdot 3cdot 4cdot 5=120]
Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.
Определение. Инверсия в перестановке $p=left( {{a}_{1}};{{a}_{2}};…;{{a}_{n}} right)$ — всякая пара $left( {{a}_{i}};{{a}_{j}} right)$ такая, что $i lt j$, но ${{a}_{i}} gt {{a}_{j}}$. Проще говоря, инверсия — это когда большее число стоит левее меньшего (не обязательно соседнего).
Мы будем обозначать через $Nleft( p right)$ количество инверсий в перестановке $p$, но будьте готовы встретиться и с другими обозначениями в разных учебниках и у разных авторов — единых стандартов тут нет. Тема инверсий весьма обширна, и ей будет посвящён отдельный урок. Сейчас же наша задача — просто научиться считать их в реальных задачах.
Например, посчитаем количество инверсий в перестановке $p=left( 1;4;5;3;2 right)$:
[left( 4;3 right);left( 4;2 right);left( 5;3 right);left( 5;2 right);left( 3;2 right).]
Таким образом, $Nleft( p right)=5$. Как видите, ничего страшного в этом нет. Сразу скажу: дальше нас будет интересовать не столько само число $Nleft( p right)$, сколько его чётность/ нечётность. И тут мы плавно переходим к ключевому термину сегодняшнего урока.
Что такое определитель
Пусть дана квадратная матрица $A=left[ ntimes n right]$. Тогда:
Определение. Определитель матрицы $A=left[ ntimes n right]$ — это алгебраическая сумма $n!$ слагаемых, составленных следующим образом. Каждое слагаемое — это произведение $n$ элементов матрицы, взятых по одному из каждой строки и каждого столбца, умноженное на (−1) в степени количество инверсий:
[left| A right|=sumlimits_{n!}{{{left( -1 right)}^{Nleft( p right)}}cdot {{a}_{1;pleft( 1 right)}}cdot {{a}_{2;pleft( 2 right)}}cdot …cdot {{a}_{n;pleft( n right)}}}]
Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.
Благодаря этому можно без ограничения общности считать, что индексы $i$ множителей ${{a}_{i;j}}$ «пробегают» значения 1, …, $n$, а индексы $j$ являются некоторой перестановкой от первых:
[j=pleft( i right),quad i=1,2,…,n]
А когда есть перестановка $p$, мы легко посчитаем инверсии $Nleft( p right)$ — и очередное слагаемое определителя готово.
Естественно, никто не запрещает поменять местами множители в каком-либо слагаемом (или во всех сразу — чего мелочиться-то?), и тогда первые индексы тоже будут представлять собой некоторую перестановку. Но в итоге ничего не поменяется: суммарное количество инверсий в индексах $i$ и $j$ сохраняет чётность при подобных извращениях, что вполне соответствует старому-доброму правилу:
От перестановки множителей произведение чисел не меняется.
Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)
Матрица 2×2
Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.
Поэтому давайте рассмотрим квадратную матрицу размером 2×2:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right]]
Поскольку количество строк в ней $n=2$, то определитель будет содержать $n!=2!=1cdot 2=2$ слагаемых. Выпишем их:
[begin{align} & {{left( -1 right)}^{Nleft( 1;2 right)}}cdot {{a}_{11}}cdot {{a}_{22}}={{left( -1 right)}^{0}}cdot {{a}_{11}}cdot {{a}_{22}}={{a}_{11}}{{a}_{22}}; \ & {{left( -1 right)}^{Nleft( 2;1 right)}}cdot {{a}_{12}}cdot {{a}_{21}}={{left( -1 right)}^{1}}cdot {{a}_{12}}cdot {{a}_{21}}={{a}_{12}}{{a}_{21}}. \end{align}]
Очевидно, что в перестановке $left( 1;2 right)$, состоящей из двух элементов, нет инверсий, поэтому $Nleft( 1;2 right)=0$. А вот в перестановке $left( 2;1 right)$ одна инверсия имеется (собственно, 2 < 1), поэтому $Nleft( 2;1 right)=1.$
Итого универсальная формула вычисления определителя для матрицы 2×2 выглядит так:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right|={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}]
Графически это можно представить как произведение элементов, стоящих на главной диагонали, минус произведение элементов на побочной:
Рассмотрим пару примеров:
Задача. Вычислите определитель:
[left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|;quad left| begin{matrix} 7 & 12 \ 14 & 1 \end{matrix} right|.]
Решение. Всё считается в одну строчку. Первая матрица:
[5cdot 9-8cdot 6=45-48=-3]
И вторая:
[7cdot 1-14cdot 12=7-168=-161]
Ответ: −3; −161.
Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.
Матрица 3×3
Теперь рассмотрим квадратную матрицу размера 3×3:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right]]
При вычислении её определителя мы получим $3!=1cdot 2cdot 3=6$ слагаемых — ещё не слишком много для паники, но уже достаточно, чтобы начать искать какие-то закономерности. Для начала выпишем все перестановки из трёх элементов и посчитаем инверсии в каждой из них:
[begin{align} & {{p}_{1}}=left( 1;2;3 right)Rightarrow Nleft( {{p}_{1}} right)=Nleft( 1;2;3 right)=0; \ & {{p}_{2}}=left( 1;3;2 right)Rightarrow Nleft( {{p}_{2}} right)=Nleft( 1;3;2 right)=1; \ & {{p}_{3}}=left( 2;1;3 right)Rightarrow Nleft( {{p}_{3}} right)=Nleft( 2;1;3 right)=1; \ & {{p}_{4}}=left( 2;3;1 right)Rightarrow Nleft( {{p}_{4}} right)=Nleft( 2;3;1 right)=2; \ & {{p}_{5}}=left( 3;1;2 right)Rightarrow Nleft( {{p}_{5}} right)=Nleft( 3;1;2 right)=2; \ & {{p}_{6}}=left( 3;2;1 right)Rightarrow Nleft( {{p}_{6}} right)=Nleft( 3;2;1 right)=3. \end{align}]
Как и предполагалось, всего выписано 6 перестановок ${{p}_{1}}$, … ${{p}_{6}}$ (естественно, можно было бы выписать их в другой последовательности — суть от этого не изменится), а количество инверсий в них меняется от 0 до 3.
В общем, у нас будет три слагаемых с «плюсом» (там, где $Nleft( p right)$ — чётное) и ещё три с «минусом». А в целом определитель будет считаться по формуле:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right|=begin{matrix} {{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}- \ -{{a}_{13}}{{a}_{22}}{{a}_{31}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{11}}{{a}_{23}}{{a}_{32}} \end{matrix}]
Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило:
Правило треугольника. Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так:
Определитель матрицы 3×3: правило треугольников
Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:)
Задача. Вычислите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 1 \end{matrix} right|]
Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей:
[begin{align} & 1cdot 5cdot 1+2cdot 6cdot 7+3cdot 4cdot 8= \ & =5+84+96=185 \end{align}]
Теперь разбираемся с побочной диагональю:
[begin{align} & 3cdot 5cdot 7+2cdot 4cdot 1+1cdot 6cdot 8= \ & =105+8+48=161 \end{align}]
Осталось лишь вычесть из первого числа второе — и мы получим ответ:
[185-161=24]
Вот и всё!
Ответ: 24.
Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:)
Общая схема вычисления определителей
Как мы знаем, с ростом размерности матрицы $n$ количество слагаемых в определителе составляет $n!$ и быстро растёт. Всё-таки факториал — это вам не хрен собачий довольно быстро растущая функция.
Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.
Готовы? Поехали!
Что такое минор матрицы
Пусть дана произвольная матрица $A=left[ mtimes n right]$. Заметьте: не обязательно квадратная. В отличие от определителей, миноры — это такие няшки, которые существуют не только в суровых квадратных матрицах. Выберем в этой матрице несколько (например, $k$) строк и столбцов, причём $1le kle m$ и $1le kle n$. Тогда:
Определение. Минор порядка $k$ — определитель квадратной матрицы, возникающей на пересечении выбранных $k$ столбцов и строк. Также минором мы будем называть и саму эту новую матрицу.
Обозначается такой минор ${{M}_{k}}$. Естественно, у одной матрицы может быть целая куча миноров порядка $k$. Вот пример минора порядка 2 для матрицы $left[ 5times 6 right]$:
Выбор $k = 2$ столбцов и строк для формирования минора
Совершенно необязательно, чтобы выбранные строки и столбцы стояли рядом, как в рассмотренном примере. Главное, чтобы количество выбранных строк и столбцов было одинаковым (это и есть число $k$).
Есть и другое определение. Возможно, кому-то оно больше придётся по душе:
Определение. Пусть дана прямоугольная матрица $A=left[ mtimes n right]$. Если после вычеркивания в ней одного или нескольких столбцов и одной или нескольких строк образуется квадратная матрица размера $left[ ktimes k right]$, то её определитель — это и есть минор ${{M}_{k}}$. Саму матрицу мы тоже иногда будем называть минором — это будет ясно из контекста.
Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.
Пример. Пусть дана матрица
[A=left[ begin{matrix} begin{matrix} 1 \ 2 \ 3 \end{matrix} & begin{matrix} 7 \ 4 \ 0 \end{matrix} & begin{matrix} 9 \ 5 \ 6 \end{matrix} & begin{matrix} 0 \ 3 \ 1 \end{matrix} \end{matrix} right]]
Выбирая строку 1 и столбец 2, получаем минор первого порядка:
[{{M}_{1}}=left| 7 right|=7]
Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка:
[{{M}_{2}}=left| begin{matrix} 5 & 3 \ 6 & 1 \end{matrix} right|=5-18=-13]
А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка:
[{{M}_{3}}=left| begin{matrix} 1 & 7 & 0 \ 2 & 4 & 3 \ 3 & 0 & 1 \end{matrix} right|]
Считать этот определитель мне уже в лом. Но он равен 53.:)
Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.
Алгебраические дополнения
«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.
Определение. Пусть дана квадратная матрица $A=left[ ntimes n right]$, в которой выбран минор ${{M}_{k}}$. Тогда дополнительный минор для минора ${{M}_{k}}$ — это кусок исходной матрицы $A$, который останется при вычёркивании всех строк и столбцов, задействованных при составлении минора ${{M}_{k}}$:
Дополнительный минор к минору ${{M}_{2}}$ Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска.
Обозначаются дополнительные миноры с помощью «звёздочки»: $M_{k}^{*}$:
[M_{k}^{*}=left| Anabla {{M}_{k}} right|]
где операция $Anabla {{M}_{k}}$ буквально означает «вычеркнуть из $A$ строки и столбцы, входящие в ${{M}_{k}}$». Эта операция не является общепринятой в математике — я её сам только что придумал для красоты повествования.:)
Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.
Определение. Алгебраическое дополнение минора ${{M}_{k}}$ — это дополнительный минор $M_{k}^{*}$, умноженный на величину ${{left( -1 right)}^{S}}$, где $S$ — сумма номеров всех строк и столбцов, задействованных в исходном миноре ${{M}_{k}}$.
Как правило, алгебраическое дополнение минора ${{M}_{k}}$ обозначается через ${{A}_{k}}$. Поэтому:
[{{A}_{k}}={{left( -1 right)}^{S}}cdot M_{k}^{*}]
Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:
Пример. Дана матрица 4×4:
[A=left[ begin{matrix} 1 & 2 & 3 & 4 \ 5 & 6 & 7 & 8 \ 9 & 10 & 11 & 12 \ 13 & 14 & 15 & 16 \end{matrix} right]]
Выберем минор второго порядка
[{{M}_{2}}=left| begin{matrix} 3 & 4 \ 15 & 16 \end{matrix} right|]
Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор:
[M_{2}^{*}=left| begin{matrix} 5 & 6 \ 9 & 10 \end{matrix} right|=50-54=-4]
Осталось найти число $S$ и получить алгебраическое дополнение. Поскольку мы знаем номера задействованных строк (1 и 4) и столбцов (3 и 4), всё просто:
[begin{align} & S=1+4+3+4=12; \ & {{A}_{2}}={{left( -1 right)}^{S}}cdot M_{2}^{*}={{left( -1 right)}^{12}}cdot left( -4 right)=-4end{align}]
Ответ: ${{A}_{2}}=-4$
Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.
Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:
Теорема Лапласа
И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.
Теорема Лапласа о разложении определителя. Пусть в матрице размера $left[ ntimes n right]$ выбрано $k$ строк (столбцов), причём $1le kle n-1$. Тогда определитель этой матрицы равен сумме всех произведений миноров порядка $k$, содержащихся в выбранных строках (столбцах), на их алгебраические дополнения:
[left| A right|=sum{{{M}_{k}}cdot {{A}_{k}}}]
Причём таких слагаемых будет ровно $C_{n}^{k}$.
Ладно, ладно: про $C_{n}^{k}$ — это я уже понтуюсь, в оригинальной теореме Лапласа ничего такого не было. Но комбинаторику никто не отменял, и буквально беглый взгляд на условие позволит вам самостоятельно убедиться, что слагаемых будет именно столько.:)
Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.
Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.
Разложение определителя по строке и столбцу
То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.
Читайте и наслаждайтесь:
Следствие из Теоремы Лапласа (разложение определителя по строке/столбцу). Пусть в матрице размера $left[ ntimes n right]$ выбрана одна строка. Минорами в этой строке будут $n$ отдельных клеток:
[{{M}_{1}}={{a}_{ij}},quad j=1,…,n]
Дополнительные миноры тоже легко считаются: просто берём исходную матрицу и вычёркиваем строку и столбец, содержащие ${{a}_{ij}}$. Назовём такие миноры $M_{ij}^{*}$.
Для алгебраического дополнения ещё нужно число $S$, но в случае с минором порядка 1 это просто сумма «координат» клетки ${{a}_{ij}}$:
[S=i+j]
И тогда исходный определитель можно расписать через ${{a}_{ij}}$ и $M_{ij}^{*}$ согласно теореме Лапласа:
[left| A right|=sumlimits_{j=1}^{n}{{{a}_{ij}}cdot {{left( -1 right)}^{i+j}}cdot {{M}_{ij}}}]
Это и есть формула разложения определителя по строке. Но то же верно и для столбцов.
Из этого следствия можно сразу сформулировать несколько выводов:
- Эта схема одинаково хорошо работает как для строк, так и для столбцов. На самом деле чаще всего разложение будет идти именно по столбцам, нежели по строкам.
- Количество слагаемых в разложении всегда ровно $n$. Это существенно меньше $C_{n}^{k}$ и уж тем более $n!$.
- Вместо одного определителя $left[ ntimes n right]$ придётся считать несколько определителей размера на единицу меньше: $left[ left( n-1 right)times left( n-1 right) right]$.
Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)
Что ж, попробуем посчитать одну такую задачку?
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{matrix} right|]
Решение. Разложим этот определитель по первой строке:
[begin{align} left| A right|=1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|+ & \ 2cdot {{left( -1 right)}^{1+2}}cdot left| begin{matrix} 4 & 6 \ 7 & 9 \end{matrix} right|+ & \ 3cdot {{left( -1 right)}^{1+3}}cdot left| begin{matrix} 4 & 5 \ 7 & 8 \end{matrix} right|= & \end{align}]
[begin{align} & =1cdot left( 45-48 right)-2cdot left( 36-42 right)+3cdot left( 32-35 right)= \ & =1cdot left( -3 right)-2cdot left( -6 right)+3cdot left( -3 right)=0. \end{align}]
Ответ: 0.
Задача. Найдите определитель:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|]
Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему.
Итак, раскладываем определитель по четвёртому столбцу:
[begin{align} left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=0cdot {{left( -1 right)}^{1+4}}cdot left| begin{matrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{2+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{3+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|+ & \ +0cdot {{left( -1 right)}^{4+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right| & \end{align}]
И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся:
[begin{align} & left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|=0+0+1-1-1-0=-1; \ & left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|=0+1+1-0-0-1=1. \end{align}]
Возвращаемся к исходнику и находим ответ:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=1cdot left( -1 right)+left( -1 right)cdot 1=-2]
Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:)
Ответ: −2
Основные свойства определителя
В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?
Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:
- Если поменять две строчки (столбца) местами, определитель поменяет знак;
- Если одну строку (столбец) умножить на число $k$, то весь определитель тоже умножится на число $k$;
- Если взять одну строку и прибавить (вычесть) её сколько угодно раз из другой, определитель не изменится;
- Если две строки определителя одинаковы, либо пропорциональны, либо одна из строк заполнена нулями, то весь определитель равен нулю;
- Все указанные выше свойства верны и для столбцов.
- При транспонировании матрицы определитель не меняется;
- Определитель произведения матриц равен произведению определителей.
Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.
Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.
Давайте посмотрим, как это работает на практике:
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|]
Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней.
В результате мы получим новую матрицу, но её определитель будет тем же:
[begin{matrix} left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|begin{matrix} downarrow \ -4 \ -3 \ -2 \end{matrix}= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 4-4cdot 1 & 1-4cdot 2 & 2-4cdot 3 & 3-4cdot 4 \ 3-3cdot 1 & 4-3cdot 2 & 1-3cdot 3 & 2-3cdot 4 \ 2-2cdot 1 & 3-2cdot 2 & 4-2cdot 3 & 1-2cdot 4 \end{matrix} right|= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 0 & -7 & -10 & -13 \ 0 & -2 & -8 & -10 \ 0 & -1 & -2 & -7 \end{matrix} right| \end{matrix}]
Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу:
[begin{matrix} 1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|+0cdot {{left( -1 right)}^{2+1}}cdot left| … right|+ \ +0cdot {{left( -1 right)}^{3+1}}cdot left| … right|+0cdot {{left( -1 right)}^{4+1}}cdot left| … right| \end{matrix}]
Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать.
Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1):
[left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|=cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|]
Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица:
[begin{align} & left( -1 right)cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|begin{matrix} -7 \ -2 \ uparrow \end{matrix}=left( -1 right)cdot left| begin{matrix} 0 & -4 & -36 \ 0 & 4 & -4 \ 1 & 2 & 7 \end{matrix} right|= \ & =cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right| \end{align}]
Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ:
[left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left( 16+144 right)=-160]
Вот так и разбиваются мечты. Всего-то −160 в ответе.:)
Ответ: −160.
Парочка замечаний перед тем, как мы перейдём к последней задаче:
- Исходная матрица была симметрична относительно побочной диагонали. Все миноры в разложении тоже симметричны относительно той же побочной диагонали.
- Строго говоря, мы могли вообще ничего не раскладывать, а просто привести матрицу к верхнетреугольному виду, когда под главной диагональю стоят сплошные нули. Тогда (в точном соответствии с геометрической интерпретацией, кстати) определитель равен произведению ${{a}_{ii}}$ — чисел на главной диагонали.
Идём дальше. Последняя задача в сегодняшнем уроке.
Задача. Найдите определитель:
[left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|]
Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных:
[begin{align} & left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|= \ & =left| begin{matrix} 1 & 1-1 & 1-1 & 1-1 \ 2 & 4-2 & 8-2 & 16-2 \ 3 & 9-3 & 27-3 & 81-3 \ 5 & 25-5 & 125-5 & 625-5 \end{matrix} right|= \ & =left| begin{matrix} 1 & 0 & 0 & 0 \ 2 & 2 & 6 & 14 \ 3 & 6 & 24 & 78 \ 5 & 20 & 120 & 620 \end{matrix} right| \end{align}]
Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк:
[cdot left| begin{matrix} 2 & 6 & 14 \ 6 & 24 & 78 \ 20 & 120 & 620 \end{matrix} right|=cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|]
Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему:
[begin{align} & 240cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|begin{matrix} downarrow \ -1 \ -1 \end{matrix}=240cdot left| begin{matrix} 1 & 3 & 7 \ 0 & 1 & 6 \ 0 & 3 & 24 \end{matrix} right|= \ & =240cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 1 & 6 \ 3 & 24 \end{matrix} right|= \ & =240cdot 1cdot left( 24-18 right)=1440 \end{align}]
Порядок. Задача решена.
Ответ: 1440
Всё. Хорош читать этот бред.:)
Смотрите также:
- Обратная матрица

- Умножение матриц

- Геометрическая вероятность

- Решение задач B12: №448—455

- Задачи на проценты: формула, упрощающая вычисления

- Задача B4 про три дороги — стандартная задача на движение

Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы  второго порядка, надо от произведения
второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:
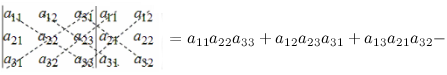
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение. 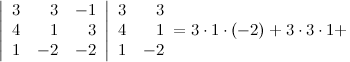
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Содержание:
- Матрицы – основные определения
- Действия над матрицами
- Транспонирование матриц
- Матрица и её определение
- Обратная матрица
- Ранг матрицы
- Матрицы и общие сведения о матрицах
- Перемножение матриц и его свойства
- Матрицы, действия над матрицами
- Определители
- Ранг матрицы и способы его вычисления
- Обратная матрица
- Линейная алгебра
- Числовые матрицы и действия над ними
- Определение матриц и некоторые их разновидности
- Действия над матрицами
- Системы линейных алгебраических уравнений. Основные определения
Матрицы – основные определения
Понятие матрицы впервые появилось в середине прошлого столетия в работах английских математиков У. Гамильтона (1805-1865) и А. Келли (1821-1895). В современной прикладной математике матрицы и связанные с ними понятия используются очень широко при решении самых разнообразных задач. В частности, использование матриц значительно упрощает решение сложных систем уравнений.
Матрицей называют прямоугольную таблицу с m строчек и n столбцов, составленную из чисел или любых объектов.
Ограничимся рассмотрением только действительных матриц, то есть матриц составленных из действительных чисел:

Числа  называют элементами матрицы. Первый индекс i означает номер строчки, второй j – номер столбца. Количество строчек и столбцов важно для матрицы, поэтому часто говорят, что матрица имеет тип
называют элементами матрицы. Первый индекс i означает номер строчки, второй j – номер столбца. Количество строчек и столбцов важно для матрицы, поэтому часто говорят, что матрица имеет тип  или что матрица имеет размер
или что матрица имеет размер  . Строчки и столбцы ещё называют рядами матрицы.
. Строчки и столбцы ещё называют рядами матрицы.
Матрицы обозначают:
– круглыми скобками или двойными вертикальными черточками:

– большими буквами А, В, С:

– через сокращённую запись:

В зависимости от чисел  вида и расположения элементов выделяют следующие типы матриц:
вида и расположения элементов выделяют следующие типы матриц:
– если  то матрицу называют квадратной;
то матрицу называют квадратной;
– если  то матрицу называют прямоугольной;
то матрицу называют прямоугольной;
– если  (матрица типа
(матрица типа  ), то её называют строчечной или вектором-строчки;
), то её называют строчечной или вектором-строчки;
– если n=1 (матрица типа  ), то её называют столбцовой, или вектором-столбца;
), то её называют столбцовой, или вектором-столбца;
– матрица типа  скаляр (число);
скаляр (число);
(если рассмотреть следующие матрицы

то видим, что матрица А – квадратная, матрицы В, С – прямоугольные, матрица D – вектор-строчки, матрица М – вектор-столбец, матрица К – скаляр);
– если все элементы квадратной матрицы, кроме  при
при  равны 0, то матрицу называют диагональной
равны 0, то матрицу называют диагональной

– если все ненулевые элементы диагональной матрицы равны 1, то её называют единичной матрицей и обозначают Е:

(если ввести символ Кронекера

тогда единичную матрицу можно записать в сокращённом виде  );
);
– если все элементы матрицы – нули, то её называют нулевой матрицей

– матрицы вида:

называют треугольными (нижняя треугольная и верхняя треугольная).
Действия над матрицами
Над матрицами можно выполнять определённые действия, которые, по аналогии с числами, называют сложением, вычитанием, умножением. Также существуют действия, которые определены только для матриц. Введём правила действий над матрицами.
1. Матрицы считают равными, если они одного и того же типа, то есть имеют одинаковое количество строчек и столбцов, и соответствующие элементы равны, то есть матрицы  равны
равны  , если
, если  .
.
2. Суммой двух матриц  и
и  одинакового типа называют матрицей
одинакового типа называют матрицей  того же типа, элементы которой равны сумме соответствующих элементов матриц А и В, то есть
того же типа, элементы которой равны сумме соответствующих элементов матриц А и В, то есть 
Свойства действий сложения матриц:

Пример.
а) Найти сумму матриц А и В.
Пусть

Тогда

б) Записать матрицу А как сумму матриц:

3. Аналогично вычисляют разность матриц:

4. Произведением матрицы  (или произведением числа на матрицу) называют матрицу, элементы которой получены умножением элементов матрицы А на число k:
(или произведением числа на матрицу) называют матрицу, элементы которой получены умножением элементов матрицы А на число k:

Свойства действий умножения матрицы на число:

4. Матрица (-1)А=-А называется противоположной для А.
(Если матрицы отрицаются только знаками своих элементов, то их называют противоположными).
Пример.

5. Умножение матриц.
Если количество столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  , то для них определена матрица
, то для них определена матрица  , которую называют их произведением.
, которую называют их произведением.
Элементы матрицы С находят по следующим правилам:
элемент  равный сумме попарных произведений элементов i-ой строчке матрицы А и j-ого столбца матрицы B.
равный сумме попарных произведений элементов i-ой строчке матрицы А и j-ого столбца матрицы B.
Пример. Найти произведение матриц А и В, если

Решения. Согласно приведённого правила, что бы найти  элементы первого ряда матрицы А почленно умножаем на элементы первого столбца матрицы В; с12 — элементы первого ряда матрицы А на элементы второго столбца матрицы В; с21 — элементы второго ряда матрицы А на элементы первого столбца матрицы В; с22— элементы второго ряда матрицы А на элементы второго столбца матрицы В. Получим:
элементы первого ряда матрицы А почленно умножаем на элементы первого столбца матрицы В; с12 — элементы первого ряда матрицы А на элементы второго столбца матрицы В; с21 — элементы второго ряда матрицы А на элементы первого столбца матрицы В; с22— элементы второго ряда матрицы А на элементы второго столбца матрицы В. Получим:

Свойства действий умножения матриц:

Внимание! 
Если АВ=ВА, то матрицы называют коммутативными. Единичная матрица Е коммутативная с любой другой, то есть АЕ=ЕА=А и играет роль единицы при умножении.
Пример.
а) Найти произведение матриц АВ и ВА если:


Как видим, 
б) Проверить существуют ли произведения АВ и ВА, если

Решение. Количество столбцов матрицы А совпадает с количеством строчек матрицы В, следовательно можно найти произведение матриц АВ:

Найти произведение матриц ВА невозможно, поскольку количество столбцов матрицы В не совпадает с количеством строчек матрицы А.
Транспонирование матриц
Если в матрице  типа
типа  заменить строчки столбцами, то получим так называемую транспонированную матрицу
заменить строчки столбцами, то получим так называемую транспонированную матрицу  типа
типа  .
.
Пример.

Свойства действий транспонирования матриц:
– дважды транспонированная матрица равна начальной

– транспонированная матрица суммы равна сумме транспонированных матриц слагаемых

– транспонированная матрица произведения равна произведению транспонированных матриц сомножителей, взятому в обратном порядке

7. Матрица называется симметричной, если она совпадает со своей транспонированной матрицей, то есть если 
Очевидно, что
– симметричная матрица обязательно квадратная;
– элементы, симметричные относительно основной диагонали равны;
– произведение  является симметричной матрицей.
является симметричной матрицей.
Пример.

8. Две матрицы называют эквивалентными, если одна получена из другой с помощью элементарных преобразований.
Элементарными преобразованиями матриц называют следующие операции:
а) перестановка двух строк или столбцов матрицы;
б) умножение всех элементов любой строки (столбца) на одно и тоже число, отличное от нуля;
в) прибавление к элементам любой строки (столбца) соответствующих элементов другой строки (столбца), умножение на одно и тоже число.
Пример. Рассмотрим матрицы:

Матрицы А, В, С, D эквивалентны, поскольку: матрица В получена из матрицы А перестановкой первой и второй строки; матрица С получена из матрицы А через умножение всех элементов второй строки на число 5; матрица D получена из матрицы А с помощью замены третьей строки суммой удвоенных элементов первой строки с элементами третьей.
Матрица и её определение
Матрицей называется прямоугольная таблица из m × n чисел, содержащая m строк и n столбцов, взятая в квадратные или круглые скобки. (1.2)
(1.2)
Или коротко [ аij ] (i = 1, 2, …, m; j = 1, 2, …, n).
В этом случае считают, что матрица имеет размерность m × n. Матрицы обозначают большими латинскими буквами А, В, С, Е, …
Числа aij называются элементами матрицы, где первый индекс i означает номер строки, а второй j — номер столбца. Если количество строк не равно количеству столбцов, то есть m ≠ n, то матрица называется прямоугольной, размерности m × n, а если m = n — квадратной. В этом случае число m = n называется порядком матрицы. Элементы квадратной матрицы, в которых i = j , образуют главную диагональ.
Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю, то есть
А = 
Здесь отдельные элементы главной диагонали могут быть нулевыми.
Если в диагональной матрицы все элементы главной диагонали равны единице, то ее называют единичной матрицей. Она обозначается буквой Е и имеет вид:
Е = 
Две матрицы А и В называются равными, если они имеют равное количество строк и столбцов и соответствующие элементы которых совпадают.
Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Ее обозначают буквой О.
Если матрица состоит только из одной строки, то она называется матрицей-строкой.
Матрица, состоящая из одного столбца, называется матрицей-столбцом.
Если в матрице А поменять строки на столбцы, а столбцы — на соответствующие строки, то полученную матрицу называют транспонированной и обозначают АT.
Если определитель квадратной матрицы равен нулю  , то матрица А называется вырожденной (или особенной) и при
, то матрица А называется вырожденной (или особенной) и при  — невырожденной (или неособенной).
— невырожденной (или неособенной).
матрица вида
А = 
а матрица
А = 
Матрицу
A = 
называют матрицей трапецеидального вида, если одновременно a11, a22, …, ajj отличные от нуля.
Пример 1. Заданs матрицы:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
Здесь:
1) A — прямоугольная матрица размерности 2 × 3,
2) AT — транспонированная матрица к матрице A;
3) B — матрица-столбец;
4) C — матрица-строка;
5) D — диагональная матрица четвертого порядка;
6) О — нулевая матрица второго порядка.
Пример 2. Для изготовления пяти видов елочных украшений на фабрике тратится определенное количество материала. Конкретные цифровые данные указаны в таблице:
 Охарактеризовать содержание строк и столбцов этой таблицы.
Охарактеризовать содержание строк и столбцов этой таблицы.
Решение. Указанные 15 чисел можно записать в виде прямоугольной матрицы размерности 3 × 5.

Каждые строка и столбец этой матрицы имеют определенный экономический смысл. Так, элементы первой строки указывают количество израсходованного стекла (в кг) на изготовление каждого из пяти видов елочных украшений. Числа второй строки указывают на потребности в количестве железных прищепок, необходимых для изготовления этих изделий. Элементы третьей строки характеризуют потребности в краске (в кг), которая используется при изготовлении соответствующего вида продукции.
Столбцы матрицы указывают на конкретное количество стекла, железных прищепок и краски, которые нужны на изготовление каждого из пяти видов елочных украшений. Так, например, элементы третьего столбца означают, что на изготовления украшений третьего вида нужно 2,8 кг стекла, 185 шт. железных прищепок и 1,4 кг краски.
Пример 3. Цены на некоторые виды товара характеризуются в гривнах, долларах США (USD), евро (EUR), английских фунтах (GBR) и рублях России (RUR).

Охарактеризовать содержание отдельных элементов таблицы.
Решение. Числовые данные этой таблицы можно записать в виде прямоугольной матрицы:

Каждый элемент имеет определенный экономический смысл. Например, элемент a21 значит, что женская кофта стоит 120 гр., элемент a32 означает, что спортивный костюм стоит 60,4 долларов США, а элемент a44 указывает на цену сапог в 52,4 английских фунтов. Элементы, например, первой строки определяют цены мужской куртки в различных денежных единицах: 1230 грн.; 232,1 долларов США; 238,8 евро; 155,3 английских фунтов; 7318,5 российских рублей.
Действия над матрицами
Пусть заданы две матрицы одной размерности m × n:

Определение. Суммой (разностью) двух матриц А и В называется такая матрица С размерности m × n, элементы которой сij равны алгебраической сумме (разности) соответствующих элементов aij и bij матриц А и В, то есть:

Из этого определения вытекают свойства:
1. A + B = B + A (коммутативность)
2. A + (B + C) = (A + B) + C (ассоциативность)
3. A ± 0 = 0 ± A = A (нейтральность)
4. (A ± B) T = AT ± BT (транспонированность).
Пример 1. Найти сумму и разность матриц.

Решение.

Пример 2. Три магазина “Продтовары” продают продукты в течение рабочего дня. Данные о торговле двух смен характеризуются таблицами:
I смена:

II смена

Найти данные о совокупной однодневной продаже товара каждым магазином.
Решение. Содержание этих таблиц можно записать в виде двух прямоугольных таблиц:

Сумма этих двух матриц характеризует данные о совокупную однодневную продажу каждого из видов продукции:

Определение. Произведением матрицы A на число k (или числa k на матрицу A) называется матрица, элементами которой являются произведения элементов матрицы A на число k:
A ⋅ k = k ⋅ A = k ⋅
Из определения произведения матрицы на число (или числа на матрицу) вытекает, что
1. k (mA) = (km) A;
2. (k + m) A = A (k + m) = kA + mA = Ak + Am;
3. λ (A + B) = λA + λB;
4. λA = 0, если λ = 0;
5. λA = 0, если A = 0.
Пример 3. Найти матрицу 4A, если матрица
A = 
Решение. Согласно определению, получим:
4A = 
Пример 4. Вычислить матрицу C = 2A – 4B, если

Решение. Использовав формулу умножения матрицы на число и формулу вычитания матриц, получим:


Пример 5. Предприятие производит три вида продукции А, В, С. Нормы затрат ресурсов на единицу продукции заданы в таблице:

Найти затраты ресурсов на изготовление 6 комплектов продукции.
Решение. Затраты ресурсов на производство единицы продукции можно представить в виде матрицы:
A = 
Каждый элемент матрицы имеет определенный экономический смысл. Например, a21 = 2 означает, что на изготовление единицы вида продукции A расходуется 2 кг сырья Y; элемент a12 = 4 означает, что для изготовления единицы вида продукции B нужно потратить 4 шт. единиц сырья X.
Очевидно, что для нахождения затрат на изготовление 6 комплектов продукции, нужно вычислить матрицу 6 A, то есть
6A = 6 
Замечание. Умножение матрицы на число отличается от умножения определителя на число. Матрицу умножают на число k, умножив все ее элементы на это число. Если определитель умножается на число k, то умножают на него все элементы одной какой-нибудь строки (или столбца).
Пусть матрица A содержит m строк и p столбцов, а матрица B имеет p строк и n столбцов.
Определение. Произведением матриц А и В называется матрица С, элементы сij которой равны сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B, то есть cij = ai1 b1j + ai2 b2j + … + aip bpj (i = 1, 2, …, m; j = 1, 2, …, n).
Произведение матрицы A на матрицу B обозначают АВ (A × B). Умножение матрицы A на матрицу B выполняется по следующей схеме:

Здесь элемент cij находят как скалярное произведение элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B.
Произведение матриц характеризуется свойствами:
1. AE = EA = A;
2. A⋅ 0 = 0 ⋅ A = 0;
3. AB ≠ BA (некоммутативность)
4. (AB) C = A (BC) (ассоциативность)
5. C (A+B) = CA + CB , (A+B) C= AC + BC (дистрибутивность)
6. (A ⋅ B)T = BT ⋅ AT.
Это свойство имеет место для произвольного числа множителей

7. Определитель произведения двух квадратных матриц равен произведению их определителей.
Пример 6. Найти произведения AB и BA, если

и убедиться, что AB ≠ BA.
Решение.
AB = 
аналогично
BA = 
Отсюда следует, что AB ≠ BA.
Пример 7. Найти произведение AB, если

Решение.
AB = 

(Здесь произведение BA неопределенный, так как количество столбцов первой матрицы не равно количеству строк второй матрицы).
Пример 8. Найти произведение AE, если
A = 
Решение.
AE = 


(Легко убедиться, что имеет место и равенство EA = A).
Пример 9. Найти произведение AB, если

Решение. Произведение этих матриц возможен, поскольку количество столбцов матрицы A равно числу строк матрицы B.
Получим
AB = 
Пример 10. Дана матрица:
A =  Найти А2.
Найти А2.
Решение.
А2 = A ⋅ A = 
= 
Замечание 1. Произведение двух матриц может быть нулевой матрицей и тогда, когда каждая из матриц сомножителей не является нулевой.
Пример 11. Найти произведение матриц:
A ⋅ B = 
= 

Замечание 2. Произведением двух диагональных матриц одного и того же порядка является диагональная матрица того же порядка.
Пример 12. Найти произведение диагональных матриц:

Тогда
A⋅ B = 
Для таких двух матриц произведение коммутативно:
A⋅ B = B⋅ A.
Пример 13. Торгово-строительная компания заключила договор на строительство 6 жилых домов, 3 офисных зданий и 4 домов отдыха. Цены на отдельные виды материалов следующие: кирпич — 32 у.е./тыс. шт., цемент — 300 у.е./т., лес круглый — 44 у.е./м3, оцинкованное железо — 6 у.е./м2, стекло — 5 у.е./м2.
Информация о количестве материалов на каждый вид строительства представлена в таблице:

Необходимо найти:
1) общее количество материалов;
2) цену материалов для каждого вида строения;
3) общую стоимость материалов.
Решение. 1) Запишем в виде матрицы А данные, которые характеризуют количество материалов на каждый вид строения, а данные об их ценах — в виде матрицы-столбца С.

Обозначим данные о договоре, заключенном на строительство сооружений через 
Чтобы найти общее количество материалов для строительства, нужно перемножить матрицы В и А и найти произведение BA, то есть
BА = 
Таким образом, для выполнения договора на строительство 6 жилых, 3 офисных и 4 домов отдыха компания должна приобрести 960 тыс. шт. кирпича; 116 т цемента; 506 м3 круглого леса; 2580 м2 оцинкованного железа и 1780 м2 стекла.
2) Чтобы найти общую стоимость материалов для каждого вида строительства, нужно перемножить матрицу А на матрицу-столбец С, составленную из чисел, характеризующих цены на соответствующие материалы:


Стоимость материалов для строительства жилого дома составляет 8860 у.е., для строительства офиса — 9348 у.е. и для строительства дома отдыха — 7740 у.е.
3) Для того, чтобы найти общую стоимость строительства согласно договора 6 жилых, 3 офисных и 4 домов отдыха нужно найти произведение матриц

Это же число можно получить еще так:

Таким образом, общая стоимость всего здания составляет 112 164 у.е.
Обратная матрица
Определение 1. Квадратная матрица А n-го порядка называется невырожденной (или неособенной), если ее определитель  не равен нулю.
не равен нулю.
Определение 2. Квадратная матрица А n-го порядка называется вырожденной (или особенной), если ее определитель  равен нулю.
равен нулю.
Определение 3. Матрица А-1 называется обратной матрицей для квадратной невырожденной матрицы А, если выполняются равенства AA-1 = A-1A = E.
ТЕОРЕМА. Если матрица А n-го порядка невырожденная, то для нее существует обратная матрица А-1.
Доказательство. Пусть задана квадратная невырожденная матрица А, то есть ее определитель  ≠ 0.
≠ 0.
A = 
Рассмотрим другую матрицу
В = 
где Aij — алгебраические дополнения элементов aij матрицы A.
Найдем произведение АВ:
АВ =  = C .
= C .
Каждый элемент cij матрицы С равен
cij = ai1 Aj1 + ai2 Aj2 + … + ain Ajn.
Если i ≠ j, то есть выражение, которое является суммой произведений элементов i-й строки на алгебраические дополнения элементов другой строки определителя матрицы А. По теореме аннулирования эта сумма равна нулю.
Если i = j, то выражение cii = ai1Ai1 + ai2Ai2 + … + ainAin представляет собой сумму произведений элементов произвольной строки на соответствующие алгебраические дополнения этой строки определителя матрицы А. По теореме Лапласа такая величина равна определителю матрицы  .
.
То есть матрица С имеет вид
С = 
Если каждый элемент этой матрицы С разделить на  (т.е. умножить ее на
(т.е. умножить ее на  ), то получим единичную матрицу Е, то есть
), то получим единичную матрицу Е, то есть

Это доказывает теорему.
Итак, обратная матрица имеет вид:

Дадим схему нахождения обратной матрицы для заданной квадратной невырожденной матрицы.
1. Вычислим определитель матрицы  .
.
2. Транспонирует матрицу A, то есть получаем матрицу:

3. Находим алгебраические дополнения каждого элемента транспонированной матрицы АТ и запишем их в виде матрицы АП:

4. Делим каждый элемент матрицы АП на определитель матрицы A, то есть умножим число
 на матрицу АП. Полученная матрица будет обратной:
на матрицу АП. Полученная матрица будет обратной:

Матрица АП, которая составлена из алгебраических дополнений элементов транспонированной матрицы, называется присоединенной (или союзной) к матрице A.
Замечание 1. Присоединенная матрица будет иметь такой же вид AП, если транспонировать матрицу, составленную из алгебраических дополнений элементов матрицы A.
Пример 1. Найти обратную матрицу для матрицы
A = 
и показать, что AA-1 = A-1A = E.
Решение. Определитель этой матрицы

Транспонированная матрица AТ имеет вид

Найдем алгебраические дополнения каждого элемента этой матрицы


Присоединена матрица будет такой:

Обратная матрица А-1 для заданной матрицы А имеет вид

Легко проверить, что

Пример 2. Найти обратную матрицу для матрицы
A = 
Решение. Вычислим определитель этой матрицы:

Поскольку  , то есть матрица A вырождена, то обратной для нее не существует.
, то есть матрица A вырождена, то обратной для нее не существует.
Замечание 2. Квадратная невырожденная матрица второго порядка  имеет обратную A-1 , и она находится по формуле:
имеет обратную A-1 , и она находится по формуле: 
Пример 3. Найти обратную матрицу к матрице
A = 
Решение. Заданная квадратная матрица второго порядка невырожденная, поскольку ее определитель

поэтому обратная к матрице A существует, и ее можно найти по предыдущей формуле:

Ранг матрицы
Рассмотрим прямоугольную матрицу размерности m × n (1.2).
Определение. Рангом матрицы называется самый высокий порядок отличных от нуля миноров. Его обозначают через r (или rang (A)).
Из определения вытекают следующие свойства ранга матрицы.
1. Ранг матрицы равен нулю только тогда, когда матрица нулевая. В других случаях ранг матрицы равен некоторому положительному числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел m и n, то есть 0 ≤ r ≤ min (m, n).
3. Для квадратной матрицы n-го порядка r = n только тогда, когда матрица невырожденная.
4. Если r <n то определитель матрицы равен нулю.
Рассмотрим два метода нахождения ранга матрицы.
Первый метод — метод окантовки — заключается в следующем. Если все миноры 1-го порядка, то есть элементы матрицы, равны нулю, то r = 0.
Если хотя бы один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю, то r = 1. Аналогично, если минор 2-го порядка отличен от нуля, то исследуем миноры 3-го порядка. Таким способом находят минор k-го порядка и проверяют, не равны ли нулю миноры (k + 1)-го порядка. Если все миноры (k + 1)-го порядка равны нулю, то ранг матрицы A равен числу k. Такие миноры (k + 1)-го порядка, как правило, находят путем “окантовки” минора k-го порядка.
Пример 1. Найти ранг матрицы:
A =  .
.
Решение. Все миноры 2-го порядка

равны нулю. Значит, ранг матрицы A равен единице: r (A) = 1.
Пример 2. Найти ранг матрицы:
A =  .
.
Решение. Поскольку в матрице A есть миноры 1-го порядка, отличные от нуля, то ее ранг может быть равен единице. Минор 2-го порядка

но, например, минор

отличен от нуля. Окантовывая минор М2 , получим минор 3-го порядка (в матрице A показано пунктиром)

Рассмотрим миноры 4-го порядка, которые окантовывают данный минор М3

Все они равны нулю, потому, что первая и четвертая строки пропорциональны. Значит ранг матрицы A равен 3 (r = 3).
Рассмотрен способ нахождения ранга матрицы не всегда удобный, поскольку нужно вычислять большое количество миноров.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при сведении ее в диагональному виду.
Элементарными преобразованиями матрицы называются такие операции:
1) перестановка местами любых двух строк (или столбцов);
2) умножение каждого элемента произвольной строки (или столбца) на отличное от нуля число;
3) вычеркивания строки (или столбца), которая содержит все нулевые элементы;
4) прибавление к элементам произвольной строки (или столбца) соответствующих элементов другой строки (или столбца), умноженных на одно и тоже отличное от нуля число.
При таких элементарных преобразованиях ранг матрица не изменяется.
Две матрицы называются эквивалентными, если одна из них получается из второй с помощью конечного числа элементарных преобразований. Эквивалентные матрицы не равны между собой, зато они имеют одинаковые ранги.
Если матрицы A и B эквивалентны, то это записывают так: ⇔.
С помощью элементарных преобразований матрицу можно свести к диагональному виду. Ранг такой матрицы равен числу отличных от нуля диагональных элементов.
Пример 3. Найти ранг матрицы
A = 
Решение.
1-й шаг. В заданной матрице переставим первую и вторую строки. На месте элемента а11 имеем элемент, равный 1.
2-й шаг. Добавим к элементам второй и третьей строк соответствующие элементы первой строки, умноженные на “–3”, а к элементам четвертой строки — соответствующие элементы первой, помноженные на “–5”.
3-й шаг. В первой строке можно автоматически записать все нули, кроме первого элемента “1”. Этого можно добиться, если к элементам 2-го, 3-го, 4-го и 5-го столбцов прибавить соответствующие элементы первого столбца, умноженные соответственно на числа: “–3”, “–3”, “–2”, “–5”.
4-й шаг. Добавим к элементам третьей и четвертой строк соответствующие элементы второй строки, умноженные на число “–2”.
5-й шаг. Во второй строке на месте элементов “–7”, “–3”, “–11” запишем нули (аналогично как на третьем шаге).
Рассмотренные шаги приведения матрицы A к диагональному виду покажем схематически так:

В последний матрице вычеркнем третью строчку и третий и четвертый столбцы, которые содержат все нулевые элементы:
A ⇔ 
Ранг этой матрицы равен трем, а значит и ранг матрицы A тоже равен 3, то есть r = 3.
Пример 4. Найти ранг матрицы:
A = 
Решение.
1-й шаг. Из элементов второй строки вычтем соответствующие элементы первой и поменяем их местами.
2-й шаг. К элементам второй и третьей строк добавим соответствующие элементы первой, умноженные соответственно на “–3” и “–5”.
3-й шаг. Запишем в первой строке все нули, кроме первого элемента “1”.
4-й шаг. Вычтем соответствующие элементы второй и третьей строк.
5-й шаг. Подобно тому, как на 3-м шаге, получим во второй строке нули на месте элементов “9” и “–7”. Покажем рассмотрены шаги схематично.

Ранг последней матрицы равен двум, а значит и ранг матрицы A равен 2, то есть r = 2.
Матрицы и общие сведения о матрицах
Многие экономические задачи связаны с обработкой информации, которая представлена таблицами данных. Поэтому исключительно важную роль играет понятие матрицы.
Определение 1. Матрицей называется прямоугольная таблица, составленная из чисел. Размерностью (или размером) матрицы называется пара чисел  , где
, где  – число строк,
– число строк,  – число столбцов в таблице.
– число столбцов в таблице.
Матрицы обозначают обычно большими латинскими буквами и записывают следующим образом:

Здесь  – произвольный элемент матрицы, стоящий в i-й строке и j -м столбце. Кроме круглых скобок для обозначения матриц используют и квадратные.
– произвольный элемент матрицы, стоящий в i-й строке и j -м столбце. Кроме круглых скобок для обозначения матриц используют и квадратные.
Пример №22
Три завода выпускают пять различных видов продукции. Отчет о производстве за год в тыс. ед. представлен матрицей:

Где, например,  = 4 (тыс. ед.) – количество продукции 3-го вида, выпущенное 2-м заводом в течение этого года. Размерность этой матрицы 3×5.
= 4 (тыс. ед.) – количество продукции 3-го вида, выпущенное 2-м заводом в течение этого года. Размерность этой матрицы 3×5.
Если число строк в матрице равно числу столбцов, т.е. размерность матрицы  , то матрица называется квадратной порядка
, то матрица называется квадратной порядка  . Элементы
. Элементы  образуют главную диагональ квадратной матрицы. Матрица, состоящая из одной строки (одного столбца) называется вектор-строкой (
образуют главную диагональ квадратной матрицы. Матрица, состоящая из одной строки (одного столбца) называется вектор-строкой ( ). Действительно, вектор-строка размерности
). Действительно, вектор-строка размерности  – это фактически вектор из
– это фактически вектор из  , а вектор-столбец размерности
, а вектор-столбец размерности  – вектор из
– вектор из  . Например,
. Например,
 .
.
Если все элементы матрицы равны нулю, то матрица называется нулевой. Две матрицы одинаковой размерности равны, если равны их соответствующие элементы. Транспонированной матрицей к матрице А называют матрицу  , которая получается, если в матрице А меняют местами соответствующие строки и столбцы. Для матрицы (1) получим
, которая получается, если в матрице А меняют местами соответствующие строки и столбцы. Для матрицы (1) получим

Размерность этой матрицы 5 x 3.
Над матрицами можно производить ряд операций. Матрицы одинаковой размерности можно складывать. Сложить две матрицы означает сложить их элементы, стоящие на одинаковых местах.
Матрицы можно умножать на число. Это означает, что все элементы матрицы надо умножить на данное число.
Пример №23
Если ассортимент продукции заводов из примера 1 не изменился в течение следующего года, то отчет о производстве за второй год тоже имеет вид матрицы:

Если же в течение третьего года производство каждого вида продукции на каждом заводе увеличилось на 20% по сравнению со вторым годом, то отчет за третий год будет таким:

Отчет же за три года будет выглядеть следующим образом:

Перемножение матриц и его свойства
Важнейшей операцией линейной алгебры является операция умножения матриц.
Пусть даны две матрицы: А – размерности  и В – размерности
и В – размерности  . Т.к. количество столбцов первой матрицы равно количеству строк второй матрицы, то можно умножить матрицу А на матрицу В. Результатом умножения будет матрица С – размерности
. Т.к. количество столбцов первой матрицы равно количеству строк второй матрицы, то можно умножить матрицу А на матрицу В. Результатом умножения будет матрица С – размерности  (правило для запоминания:
(правило для запоминания:  ). Элемент полученной матрицы
). Элемент полученной матрицы  равен скалярному произведение двух векторов: i-й строки матрицы А и j-го столбца матрицы В, т.е.
равен скалярному произведение двух векторов: i-й строки матрицы А и j-го столбца матрицы В, т.е.

Пример №24
Даны матрицы:
 Произведение матрицы А на матрицу В равно
Произведение матрицы А на матрицу В равно

Произведение АВ оказалось возможным, т.к. число столбцов первой матрицы совпадает с числом строк второй и равно 3. В то же время, произведение ВА невозможно, т.к. теперь число столбцов первой матрицы равно 3, а число строк второй – 2 .
Приведем основные свойства умножения матриц.
1. Как известно, для любых чисел а и b выполняется свойство: ab = ba. Для матриц, в общем случае, АВ  ВА. Например,
ВА. Например,
 2. Единичной матрицей Е называется квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные нули. Особенности умножения на эту матрицу такие: АЕ = ЕА = А.
2. Единичной матрицей Е называется квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные нули. Особенности умножения на эту матрицу такие: АЕ = ЕА = А.
3. Произведение матриц подчиняется сочетательному закону: (АВ)С = А(ВС).
4. При перемножении матриц и транспонировании имеет место свойство:  .
.
Пример №25
Предприятие выпускает три вида продукции  , используя два вида сырья
, используя два вида сырья  . Нормы расхода сырья характеризуются матрицей
. Нормы расхода сырья характеризуются матрицей 
Например,  = 3 означает, что на выпуск единицы продукции
= 3 означает, что на выпуск единицы продукции  расходуется 3 единицы сырья
расходуется 3 единицы сырья  .
.
1) Требуется определить затраты сырья, необходимые для выполнения плана выпуска продукции:  – 100 ед.,
– 100 ед.,  – 50 ед.,
– 50 ед.,  – 80 ед. 2) Стоимость единицы сырья составляет:
– 80 ед. 2) Стоимость единицы сырья составляет:  – 15 грн.,
– 15 грн.,  – 22 грн. Рассчитать общие расходы на приобретение сырья, необходимые для выполнения плана 1).
– 22 грн. Рассчитать общие расходы на приобретение сырья, необходимые для выполнения плана 1).
Решение:
1) Введем вектор-столбец плана выпуска продукции:

Рассчитаем затраты сырья, необходимые для выполнения этого плана:
 2) Введем вектор-строку стоимостей единиц сырья:
2) Введем вектор-строку стоимостей единиц сырья:  = (15 22).
= (15 22).
Общие расходы на приобретения сырья, необходимые для выполнения плана:

Решая подобные задачи в дальнейшем, можно без рассуждений использовать формулу:  .
.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Матрицы, действия над матрицами
Матрицей  размера
размера  называется таблица, что складывается из
называется таблица, что складывается из  рядов и
рядов и  столбцов.
столбцов.

Иногда матрица  обозначается не круглыми скобками, а двойными вертикальными отрезками:
обозначается не круглыми скобками, а двойными вертикальными отрезками:  или квадратными скобками:
или квадратными скобками:
Матрица размерности  называется квадратной матрицей
называется квадратной матрицей  – ого порядка. Элементы
– ого порядка. Элементы  в этом случае образуют главную диагональ матрицы.
в этом случае образуют главную диагональ матрицы.
Определитель, сложенный из элементов квадратной матрицы, называется определителем (детерминантом) матрицы и обозначают так:

Квадратная матрица, в которой на главной диагонали стоят единицы, а другие элементы равны нулю, называется единичной и обозначается 

Если все элементы матрицы равны нулю, то такую матрицу называют нулевой и обозначают 
Две матрицы  и
и  называют равными , если они одинакового размера и равны их элементы, что стоят на одинаковых местах.
называют равными , если они одинакового размера и равны их элементы, что стоят на одинаковых местах.
Произведением числа  на матрицу
на матрицу  по определениям является матрица
по определениям является матрица

Таким образом, чтобы умножить матрицу  на число
на число  , нужно каждый элемент матрицы умножить на это число.
, нужно каждый элемент матрицы умножить на это число.
Суммой матриц  и
и  одинакового размера
одинакового размера  называется матрица
называется матрица  размера
размера  , элементы которой находят так:
, элементы которой находят так:
 для всех
для всех  и
и 
Следует, складывание матриц приводится к складыванию соответственных элементов этих матриц.
Отнимание матриц обозначаются через действия, которые уже рассматривали:

то есть отнимание двух матриц приводится к отниманию их соответственных элементов. Очевидно, что отнимать можно только матрицы одинакового размера.
Произведением матрицы  и
и  называется матрица
называется матрица  элемент
элемент  которой равен сумме произведений
которой равен сумме произведений  – го ряда матрицы
– го ряда матрицы  на соответственные элементы
на соответственные элементы  – ного столбца матрицы
– ного столбца матрицы  то есть
то есть

Для произведения матриц в общем случае справедливы соотношения:

(если же, обычно, существует каждый из слагаемых).
Операции складывания матриц имеют свойства:

4. Если  тогда
тогда  – противоположная к
– противоположная к  матрица.
матрица.
Операции умножения матриц имеют такие свойства:

Квадратная матрица  результат умножения этой матрицы на саму себя. Аналогично вводится понятие
результат умножения этой матрицы на саму себя. Аналогично вводится понятие  – нной степени матрицы
– нной степени матрицы  , то есть
, то есть

Если в матрице  поменять местами ряды и столбцы, то получим матрицу
поменять местами ряды и столбцы, то получим матрицу  которую называют транспонированной к матрице
которую называют транспонированной к матрице 
Решение примеров и задач:
Пример 1.1.
Для матриц:

найти матрицы 
Решение.



Отметим, что 
Матрицы дают возможность укоротить записи и использовать одинаковые соображения для разных объектов.
Задача 1.2
Предприятие выпускает продукцию двух видов, используя при этом сырье трех типов. Затраты сырья на производстве продукции задаются матрицей  где
где  – количество единиц сырья
– количество единиц сырья  – ого типа, что используется для производства единицы продукции
– ого типа, что используется для производства единицы продукции  – ого вида. План ежедневного выпуска продукции превышает 90 единиц продукции первого вида и 120 единиц продукции второго вида. Стоимость единицы каждого типа сырья соответственно равны 8, 5 и 10 рублей. Обозначить общие затраты сырья
– ого вида. План ежедневного выпуска продукции превышает 90 единиц продукции первого вида и 120 единиц продукции второго вида. Стоимость единицы каждого типа сырья соответственно равны 8, 5 и 10 рублей. Обозначить общие затраты сырья  необходимой для ежедневного выпуска продукции, а также общую стоимость
необходимой для ежедневного выпуска продукции, а также общую стоимость  этого сырья.
этого сырья.
Решение . Запишем план выпуска продукции в виде матрицы  Тогда общие затраты сырья планового выпуска продукции можно найти как произведение матрицы
Тогда общие затраты сырья планового выпуска продукции можно найти как произведение матрицы  и
и  то есть
то есть

Следует, для ежедневного выпуска продукции используется 930, 390 и 540 единиц сырья первого, второго и третьего типов соответственно.
Зададим стоимость единицы каждого типа сырья матрицы  Тогда общая стоимость сырья:
Тогда общая стоимость сырья:

Заметим, что использование матриц а этой задаче привело к наглядности, упрощения и компактности вычислений.
Определители
Число  называется определителем (детерминантом) второго порядка и обозначается так:
называется определителем (детерминантом) второго порядка и обозначается так:

Числа  – элементы определителя, причем первая цифра индекса в записи числа указывает на номер порядка, в котором стоит этот элемент, а вторая цифра интекса – на номер столбца. Диагональ, на которой размещены элементы
– элементы определителя, причем первая цифра индекса в записи числа указывает на номер порядка, в котором стоит этот элемент, а вторая цифра интекса – на номер столбца. Диагональ, на которой размещены элементы  и
и  называется главной диагональю, а диагональ, на которой находится
называется главной диагональю, а диагональ, на которой находится  и
и  называется побочной. Следует, определитель второго порядка равен разнице произведений элементов главной и побочной диагоналей.
называется побочной. Следует, определитель второго порядка равен разнице произведений элементов главной и побочной диагоналей.
Аналогично, определителем третьего порядка называется число, что образуется из девяти чисел по такому правилу:

Эта сумма складывается из шести произведений. В каждое произведение входит по одному числу из каждого порядка и в то же время до одного элемента из каждого столбца. Знаки произведений легко запомнить воспользовавшись схемами:

Напомним основные свойства определителей третьего порядка
- Величина определителя не изменяется, если его ряды заменить столбцами, причем каждый ряд заменяют столбиком с тем же самым номером.
- Если в определителе поменять местами только два ряда (или два столбика), то определитель изменяет знак на противоположный, сохраняя абсолютное значение.
- Если определитель имеет два одинаковых столбца или два одинаковых ряда. то он равен нулю.
- Если определитель содержит два пропорциональных ряда (столбца), то значение его равно нулю. Если элементы некоторого ряда (столбца) равны нулю, то и сам определитель равен нулю.
- Если все элементы некоторого ряда (столбца) умножить на одно и то же число, то значение определителя так же умножиться на то же число. Это подразумевает, что общий множитель всех элементов ряда (столбца) можно вынести за знак определителя.
- Если каждый элемент некоторого ряда (столбца) является сумма двух слагаемых, то определитель можно предоставить в виде суммы двух определителей: в первом из них на месте каждой суммы остается только первое слагаемое, а во втором – только второе слагаемое (другие элементы определителя сохраняются).
- Значение определителя не изменяется, если к элементами некоторого ряда (столбца) прибавить соответственные элементы другого параллельного ряда (столбца), умножив их поочередно на одно и то же число.
Если в определителе  вычеркнуть
вычеркнуть  – нный порядок и
– нный порядок и  – нный столбец, на пересечении которых размещен элемент
– нный столбец, на пересечении которых размещен элемент  то получим определитель второго порядка, который называется минором
то получим определитель второго порядка, который называется минором  элемента
элемента  Алгебраическими дополнениями
Алгебраическими дополнениями  элемента
элемента  определителя
определителя  называется соответственный ему минор со знаком, который вычисляется по такому правилу:
называется соответственный ему минор со знаком, который вычисляется по такому правилу:

Еще одно свойство определителя.
8. Определитель равен сумме произведений элементов некоторого ряда (столбца) на соответственные их алгебраические дополнения.
Если по этому правилу раскрыть определитель  по первому порядку, то получим:
по первому порядку, то получим:

Решение примеров:
Пример 1.11.
Вычислить определитель

Решение. Сделаем этого двумя способами:
а) Вычислим определитель раскладывая его по элементам третьего порядка (используем свойство 8).

б) В этом случае, образуем нули во втором порядке (или в нем есть единица или же выбирается тот ряд ( или столбец), в котором пропорциональные элементы). Для этого к элементам второго столбца прибавим элементы первого, предварительно умножив их в уме на 2, потом к элементам третьего столбца прибавим элементы первого столбца, умноженные перед этим на – 3. Значение определителя при этом, согласно со свойствами 7, не измениться.

Пример 1.12
Вычислить определитель третьего порядка

Решение. Преобразуем определитель таким образом, чтобы ниже главной диагонали все элементы его стали нулями. Тогда из определитель равен произведению диагональных элементов.
Найдем разницу первого и второго рядов, а потом умножим первый порядок на 2 и отнимем от третьего порядка. Получим определитель

Отняв второй порядок от третьего, получим:


Пример 1.13
Вычислить определитель четвертого порядка

Решение. Сложим первый ряд к второму и четвертому, получим определитель

Переставим первый и третий столбцы:

Сложим второй порядок к третьему и четвертому ряду и вынесем общий множитель элементов третьего и четвертого ряда:

Отняв третий ряд от четвертого, получим:

Ранг матрицы и способы его вычисления
Матрица имеет ранг  если среди ее миноров существует хотя бы один минор порядка
если среди ее миноров существует хотя бы один минор порядка  отличный от нуля, а все миноры порядка
отличный от нуля, а все миноры порядка  и высшего равен нулю, или не существуют.
и высшего равен нулю, или не существуют.
Пример 1.29
Найти ранг матрицы 
Решение. Эта матрица третьего порядка, следует, ее ранг не может быть больше трех. Определитель третьего порядка равен нулю:

но существует минор второго порядка  Ранг матрицы
Ранг матрицы  равен двум,
равен двум, 
Пример 1.30
Найти ранг матрицы 
Решение. Эта матрица имеет размер  потому ее ранг не больше 3. Существует определитель третьего порядка
потому ее ранг не больше 3. Существует определитель третьего порядка  Следует,
Следует, 
Элементарными преобразованиями матрицы называют такие ее преобразования:
- Транспортировка, то есть замена каждого ряда столбцом с тем же номером и наоборот.
- Перестановка двух рядов или двух столбиков.
- Умножение всех элементов ряда или столбца на любое число не равное нулю.
- Складывание всех элементов ряда или столбца соответственных элементов параллельного ряда, умножено на одно и то же число.
Матрицы полученные одна из другой элементарными преобразованиями, называются эквивалентными. Эквиваленты матрицы не равны одна другой, но при элементарных преобразований матриц ее ранг не изменяется.
Пример 1.31.
Найти ранг матрицы 
Решение. Разделим элементы первого ряда на 2, получим эквивалентную матрицу ( ранг этой матрицы равен рангу исходной):

Отнимем от третьего ряда второй, умноженный на 3.

При нахождении ранга матрицы, как правило, нужно вычислить большое количество определителей. Чтобы облегчить этот процесс, используют специальные способы. Ранг можно вычислить, например, так: над матрицей последовательно выполняют элементарные преобразования до тех пор, пока в каждом ряде и каждом столбце стоит не более одного ненулевого элемента. Тогда ранг матрицы будет равен числу этих ненулевых элементов.
Пример 1.32
Найти ранг матрицы 
Решение. Преобразуем в нули все элементы первого ряда, кроме первого элемента, для чего первый и второй столбец оставим без изменения, вместо третьего столбца запишем разницу между первым и третьим столбцом, а вместо четвертого – сумму четвертого и первого, умноженного на (-2).

Далее без изменения оставим первый и третий столбцы, вместо второго запишем разницу между третьим и вторым столбцами, а вместо четвертого – сумму четвертого столбца и третьего, умноженного на -4.

И наконец, остаточный столбик преобразуем на нули. Вместо него запишем разницу между вторым и четвертым столбцами.

Полученная матрица содержит три ненулевых элемента, то есть 
Обратная матрица
Матрица  называется обратной к матрице
называется обратной к матрице  если
если

Отсюда вытекает. что обратную матрицу могут иметь только квадратные матрицы.

То есть обратная матрица складывается из алгебраических дополнений к элементам рядов, которые записываются в столбцы с соответственными номерами, а потом каждое алгебраическое дополнение делится на детерминант матрицы.
Обратную матрицу можно использовать при решение системы линейных алгебраических уравнений матричным способом: матрицу – столбец  находят как произведение матрицы
находят как произведение матрицы  обратной к матрице системы, и матрице – столбца свободных членов
обратной к матрице системы, и матрице – столбца свободных членов  то есть
то есть

Решение примеров:
Пример 1.45
Найти матрицу  обратную к матрице
обратную к матрице

Решение. Вычислим определитель матрицы  и алгебраические дополнения всех элементов
и алгебраические дополнения всех элементов

Обратная матрица имеет вид:

Матрица  найдена правильно, потому что:
найдена правильно, потому что:


Пример 1.46
Найти матрицу  обратную к матрице
обратную к матрице

Решение. Поскольку определитель матрицы

то для матрицы  существует обратная матрица
существует обратная матрица  Найдем алгебраические дополнения элементов матрицы
Найдем алгебраические дополнения элементов матрицы  .
.

тогда

Легко можно определить, что  то есть
то есть

Задача 1.47
В цеху предприятия изготовляют две модели женской одежды. На изготовление первой модели тратят 2 м ткани, для изготовления второй – 3 м. При этом на изготовление этих моделей тратится 4 и 5 часов соответственно. Известно, что месячный запас ткани 100 м, а рабочее время ограниченно – 190 часов. Сложить такой план месячного изготовления этих моделей одежды, при котором полностью используются ресурсы (ткань и время).
Решение. Обозначим через  и
и  количество единиц месячного выпуска первой и второй моделей соответственно. По условию задачи сложим систему линейных уравнений:
количество единиц месячного выпуска первой и второй моделей соответственно. По условию задачи сложим систему линейных уравнений:

Решим эту систему матричным способом. Запишем ее в матричном виде: 
где 
Для матрицы  найдем обратную матрицу
найдем обратную матрицу  Поскольку:
Поскольку:

Тогда

Решением системы является

Следует, для использования ресурсов еженедельно нужно изготовить 25 единиц первой и 10 единиц второй модели одежды.
Заметим, что при решении экономических задач удобно использовать матричный способ. Вычислив один раз обратную матрицу и изменив ограничения на ресурсы (ежедневные, ежемесячные, ежегодные и так далее), получим план для выпуска продукции.
Линейная алгебра
Линейная алгебра как самостоятельная математическая дисциплина начала формироваться в XVIII веке, когда в работах немецкого математика Г.Ф.Лейбница и швейцарского математика Г. Крамера впервые было введено понятие определителя (детерминанта) и приведены общие формулы для определения решений систем линейных уравнений. Позже английскими математиками А. Келли и Дж. Сильвестром было введено понятие матрицы и заложены основы матричного исчисления, что является аппаратом для компактной записи и анализа систем уравнений. Именно эти понятия линейной алгебры широко используются в прикладных задачах экономики. Так, для характеристики параметров производственных или бизнес-процессов выходные данные предоставляются в виде матрицы размером 
Методы линейной алгебры также применяются для обоснования управленческих решений, при обработке результатов наблюдений и тому подобное. Например, решение задач оптимизации планов работы предприятия, изучение спроса, планирование транспортных артерий можно свести к решению систем  линейных уравнений с
линейных уравнений с  неизвестными.
неизвестными.
После изучения данной темы вы сможете:
• использовать числовые матрицы для формирования и анализа таблиц исходных данных в экономике;
• использование систем линейных уравнений при разработке линейных экономико-математических моделей;
• применять понятие линейных векторных пространств с целью геометрической интерпретации экономических задач;
• иметь представление о собственных числа и собственные векторы квадратных матриц в аналитических задачах экономики;
• использовать собственные числа и собственные векторы квадратных матриц при разработке экономико-математических моделей;
• применять модель межотраслевого баланса (многоотраслевой экономики) для решения реальных задач экономики;
• строить линейную модель обмена (модель международной торговли) при решении конкретных задач.
Числовые матрицы и действия над ними
Для чего нужны матрицы? Например для решения задачи об использовании сырья:
Рассмотрим реальную задачу планирования выпуска промышленной продукции на примере отдельного предприятия, производящего электродвигатели как общего, так и специального назначения. Кроме электродвигателей, завод производит сложные изделия бытового и сельскохозяйственного назначения. Сформулируем задачу о распределении материальных ресурсов при изготовлении четырех основных видов продукции электродвигателей AИP 80, AИP 90, АИР 100 и электрических насосов БЦ 1,1-20.
Основными факторами производства являются сырье, полуфабрикаты, которые доставляются на предприятие, топливо и транспорт. Однако их объемы имеют определенные ограничения. Удельные затраты (затраты на изготовление единицы изделия каждого вида) и общие объемы имеющихся ресурсов (в соответствующих единицах) приведены в таблице 1.1.
Удельные затраты материальных ресурсов и объемы их имеющихся запасов Таблица 1.1

Задача состоит в построении такого плана производства основных видов продукции, который бы обеспечил полное использование материальных ресурсов, которые имеет в наличии предприятие. Составим математическую модель задачи, то есть опишем поставленную задачу с помощью математической символики. Введем обозначения величин, которые являются числовыми характеристиками плана производства. Пусть,  – количество двигателей AИP 80, которое соответствует полному использованию имеющихся ресурсов;
– количество двигателей AИP 80, которое соответствует полному использованию имеющихся ресурсов;  – количество двигателей AИP 90;
– количество двигателей AИP 90;  – количество двигателей AИP 100;
– количество двигателей AИP 100;  – количество электрических насосов БЦ 1,1-20. Согласно условию задачи и с данными табл. 1.1 должны выполняться следующие равенства:
– количество электрических насосов БЦ 1,1-20. Согласно условию задачи и с данными табл. 1.1 должны выполняться следующие равенства:

Мы получили систему линейных уравнений – уравнений первой степени относительно неизвестных, – которая и является математической моделью задачи о полном использовании материальных ресурсов. Такие системы известны со школьного курса математики, но методы иx решения и, тем более, исследования для произвольного конечного числа уравнений и неизвестных в школьном курсе не изучаются (методы решения этой системы будут приведены позднее).
В общем случае задача о полном использовании ресурсов формулируется так: пусть предприятие выпускает продукцию  наименований, для производства которой используются
наименований, для производства которой используются  видов ресурсов. Потребности в ресурсах определенного вида для изготовления единицы продукции каждого типа, общее количество ресурсов каждого вида представлены в виде таблицы 1.2.
видов ресурсов. Потребности в ресурсах определенного вида для изготовления единицы продукции каждого типа, общее количество ресурсов каждого вида представлены в виде таблицы 1.2.
Задача о полном использовании ресурсов Таблица 1.2

Необходимо определить количество продукции каждого из наименований, которое надо выработать предприятию, чтобы имеющиеся ресурсы были полностью использованы.
Составим математическую модель задачи. Пусть  – количества продукции соответствующего наименования, которую производит предприятие. Тогда по данным таблицы 1.2 должны выполняться равенства:
– количества продукции соответствующего наименования, которую производит предприятие. Тогда по данным таблицы 1.2 должны выполняться равенства:

Таким образом, нахождение решения задачи о полном использовании сырья сведено к решению системы  линейных уравнений с
линейных уравнений с  неизвестными. Для исследования и решения таких систем применяются понятия матриц и определителей, которые являются основным математическим аппаратом для изучения систем линейных уравнений.
неизвестными. Для исследования и решения таких систем применяются понятия матриц и определителей, которые являются основным математическим аппаратом для изучения систем линейных уравнений.
Определение матриц и некоторые их разновидности
Числовой матрицей размером  на
на  называется прямоугольная таблица чисел, которая имеет
называется прямоугольная таблица чисел, которая имеет  строк и
строк и  столбцов. Числа, которые составляют матрицу, называют ее элементами.
столбцов. Числа, которые составляют матрицу, называют ее элементами.
Матрицы обозначают большими буквами латинского алфавита  и другими, а иx элементы – соответствующими строчными буквами с двойными индексами
и другими, а иx элементы – соответствующими строчными буквами с двойными индексами  где индекс и соответствует номеру строки матрицы
где индекс и соответствует номеру строки матрицы  а
а  – номеру ее столбца
– номеру ее столбца  . К примеру,
. К примеру,

Каждый элемент  матрицы
матрицы  находится на пересечении
находится на пересечении  -й строки и
-й строки и  -гo столбца. При изображении матриц множество элементов берут в круглые (или в квадратные) скобки.
-гo столбца. При изображении матриц множество элементов берут в круглые (или в квадратные) скобки.
В общем случае элементами матрицы могут быть другие объекты: векторы, функции, иx производные и т. д.
В теоретических исследованиях при ссылке на матрицу определенного размера обычно применяют обозначения 
Матрица  в которой количество строк равно числу столбцов
в которой количество строк равно числу столбцов  и равно
и равно  , называется квадратной матрицей порядка
, называется квадратной матрицей порядка  (или
(или  -го порядка) в противном случае
-го порядка) в противном случае  матрицу называют прямоугольной.
матрицу называют прямоугольной.
Матрицей-строкой называется матрица размера  , то есть состоящая из одной строки.
, то есть состоящая из одной строки.
Матрицей-столбцом называется матрица размера  , которая имеет один столбец.
, которая имеет один столбец.
Если рассматривается матрица-строка (или матрица-столбец), то для ее элементов номер строки (или, соответственно, номер столбца) указывать не надо.
Матрица может состоять даже из одного элемента.
Нулевой матрицей называют матрицу, все элементы которой равны нулю. Она обозначается буквой  .
.
Главной диагональю квадратной матрицы  называется совокупность ее элементов, имеющих одинаковые индексы
называется совокупность ее элементов, имеющих одинаковые индексы  , то есть это элементы
, то есть это элементы  а совокупность элементов
а совокупность элементов  называют побочной диагональю квадратной матрицы.
называют побочной диагональю квадратной матрицы.
Симметричной называется квадратная матрица, в которой все элементы, расположенные симметрично относительно главной диагонали, есть попарно равными между собой. То есть для произвольных ее элементов при  выполняется соотношение:
выполняется соотношение: 
Если элементы каждой строки матрицы  записать в столбец, не нарушая порядка их расположения, то получим матрицу
записать в столбец, не нарушая порядка их расположения, то получим матрицу  , которая называется транспонированной к матрице
, которая называется транспонированной к матрице  :
:

а сама операция перехода от матрицы  к матрице
к матрице  называется транспонирование матрицы. Понятно, что дважды транспонированная матрица дает исходную матрицу:
называется транспонирование матрицы. Понятно, что дважды транспонированная матрица дает исходную матрицу:  , а симметричная матрица совпадает со своей транспонированной.
, а симметричная матрица совпадает со своей транспонированной.
Верхней (нижней) треугольной матрицей называется ненулевая квадратная матрица, все элементы которой, расположенные ниже (выше) главной диагонали, равны нулю.
Диагональной матрицей называется квадратная матрица, в которой все элементы, кроме, возможно, элементов главной диагонали, равны нулю. Такую матрицу целесообразно задавать перечнем ее диагональных элементов, указывая только один индекс: 
Единичной матрицей называется диагональная матрица, все элементы главной диагонали которой равны единице:

Обозначения единичной матрицы удобно сопровождать индексом, который указывает на ее порядок, следовательно, единичная матрица размера  обозначается
обозначается  .
.
Символические определения основных типов матриц и их примеры приведены в таблице 1.3.
Основные разновидности матриц Таблица 1.3

Действия над матрицами
Элементы двух матриц одинакового размера, которые стоят на пересечении одних и тех же (по номеру) строк и столбцов называются соответствующими.
Матрицы  и
и  одинакового размера называются равными, если их соответствующие элементы равны между собой:
одинакового размера называются равными, если их соответствующие элементы равны между собой:

Над матрицами определены следующие действия (операции): умножение матрицы на скаляр, добавление матриц, умножение матриц. Рассмотрим определение и свойства этих операций.
1. Произведением матрицы  со скаляром
со скаляром  называется матрица
называется матрица  соответствующие элементы которой являются произведением элементов матрицы
соответствующие элементы которой являются произведением элементов матрицы  с постоянным множителем
с постоянным множителем  :
:

Если  , то получаем матрицу, которая называется противоположною (к) матрице
, то получаем матрицу, которая называется противоположною (к) матрице  :
: 
2. Суммой матриц  и
и  одинакового размера называют матрицу
одинакового размера называют матрицу  того же размера, каждый элемент
того же размера, каждый элемент  которой является суммой соответствующих элементов исходных матриц:
которой является суммой соответствующих элементов исходных матриц:

Согласно с определением нулевой матрицы имеем: 
Последствие: разницу двух матриц  можно рассматривать как сумму матриц, если к матрице
можно рассматривать как сумму матриц, если к матрице  добавить матрицу, которая противоположна матрице
добавить матрицу, которая противоположна матрице  :
:

Найдем матрицу  , если
, если

Поскольку заданные матрицы имеют одинаковый размер, то указанные действия можно выполнить. Следовательно,


Операции сложения матриц и умножения матрицы на скаляр называются линейными операциями над матрицами. Эти операции сводятся к соответствующим арифметических действий над числами и имеют те же свойства, что и операции над числами. Приведем эти свойства:
 коммутативность (переставной закон);
коммутативность (переставной закон);
 – ассоциативность (соединительный закон);
– ассоциативность (соединительный закон);
 – дистрибутивность (распределительный закон).
– дистрибутивность (распределительный закон).
Произведением матрицы  размера
размера  на матрицу
на матрицу  размера
размера  называется матрица
называется матрица  размера
размера  , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:  · Соответственно:
· Соответственно:

С (1.5) следует правило, называют правилом  строка на столбец
строка на столбец :
:
чтобы вычислить элемент  произведения матриц
произведения матриц  , надо элементы
, надо элементы  й строки матрицы
й строки матрицы  умножить на соответствующие по номеру элементы
умножить на соответствующие по номеру элементы  столбца матрицы
столбца матрицы  и найти сумму полученных произведений.
и найти сумму полученных произведений.
Найдем за этим правилом произведение  , где
, где

Количество столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  (
( ), следовательно, матрицу
), следовательно, матрицу  можно умножить на матрицу
можно умножить на матрицу  . Поскольку матрица
. Поскольку матрица  имеет две строки, а матрица
имеет две строки, а матрица  – один столбец, то их произведением будет матрица-столбец с двумя строками:
– один столбец, то их произведением будет матрица-столбец с двумя строками:

Понятно, что для приведенных матриц не существует произведение матрицы  на матрицу
на матрицу  , поскольку матрица
, поскольку матрица  имеет один столбец, а матрица
имеет один столбец, а матрица  – две строки.
– две строки.
Из определения произведения матриц вытекают следующие свойства операций умножения матриц.
1. Для того, чтобы две матрицы  и
и  можно было умножить, необходимо и достаточно, чтобы количество столбцов
можно было умножить, необходимо и достаточно, чтобы количество столбцов  первой матрицы (множимого
первой матрицы (множимого  ) равно количеству строк
) равно количеству строк  второй матрицы (множителя
второй матрицы (множителя  ); соответственно, произведением матрицы размера
); соответственно, произведением матрицы размера  на матрицу размера
на матрицу размера  будет матрица размера
будет матрица размера  .
.
2. Если матрицы  и
и  являются квадратными матрицами одинакового размера, то существуют и произведение
являются квадратными матрицами одинакового размера, то существуют и произведение  , и произведение
, и произведение  , но может быть, что
, но может быть, что  , то есть для произведения матриц в общем случае не выполняется переставной закон. Однако произведения единичной матрицы
, то есть для произведения матриц в общем случае не выполняется переставной закон. Однако произведения единичной матрицы  с матрицей
с матрицей  (того же размера) слева и справа равны между собой и равны матрицы
(того же размера) слева и справа равны между собой и равны матрицы 
3. Для произведения матриц выполняется ассоциативный закон, а именно:

Приведем свойства, присущие действиям над матрицами, в виде таблицы:
Свойства операций над матрицами Таблица 1.4

Системы линейных алгебраических уравнений. Основные определения
Построение математических моделей процессов и явлений во всех сферах деятельности человека требует разработок соответствующего математичноrо аппарата, и системы линейных алгебраических уравнений является его важной составляющей. Эти уравнения играют важную роль и при построении математических моделей экономических процессов.
Системой линейных алгебраических уравнений (СЛАУ) называется совокупность  уравнений первой степени, то есть линейных уравнений, относительно
уравнений первой степени, то есть линейных уравнений, относительно  неизвестных
неизвестных  , которые в каждом уравнении являются числовыми характеристиками одного и того же процесса. Ее можно предоставить в развернутом виде :
, которые в каждом уравнении являются числовыми характеристиками одного и того же процесса. Ее можно предоставить в развернутом виде :

где  – неизвестные характеристики, в отношении которых построена математическая модель задачи;
– неизвестные характеристики, в отношении которых построена математическая модель задачи;
 – коэффициенты при неизвестных (параметры модели), где индексы
– коэффициенты при неизвестных (параметры модели), где индексы  и
и  указывают, соответственно, на номера уравнения и неизвестного;
указывают, соответственно, на номера уравнения и неизвестного;
 – свободные члены (правые части уравнений), которые тоже являются параметрами математической модели.
– свободные члены (правые части уравнений), которые тоже являются параметрами математической модели.
Краткая запись системы уравнений (1.6) можно получить с помощью символа  , который означает почленное суммирование:
, который означает почленное суммирование:

Вернемся. к примеру, в котором рассматривалась математическая модель задачи об использовании. ресурсов. Если записать удельные затраты ресурсов как матрицу  , запасы ресурсов – как матрицу-столбец
, запасы ресурсов – как матрицу-столбец  , и неизвестные компоненты плана производства представить также как матрицу-столбец
, и неизвестные компоненты плана производства представить также как матрицу-столбец  то по определению произведения матриц систему линейных алгебраических уравнений (1.6) можно представить в виде матричного уравнения (матричная форма системы)
то по определению произведения матриц систему линейных алгебраических уравнений (1.6) можно представить в виде матричного уравнения (матричная форма системы)

Приведем еще один способ представления системы уравнений с помощью матриц. Пусть матрица-столбец  описывает расходы производства на изготовление. единицы
описывает расходы производства на изготовление. единицы  й продукции по всем
й продукции по всем  видам ресурсов. Каждая из этих матриц состоит из элементов соответствующего столбца. матрицы
видам ресурсов. Каждая из этих матриц состоит из элементов соответствующего столбца. матрицы  . Итак, все матрицы
. Итак, все матрицы  имеют одинаковый размер
имеют одинаковый размер  .
.
Расходы ресурсов на изготовление  й продукции в объеме
й продукции в объеме  определяются как произведение матрицы
определяются как произведение матрицы  со скаляром
со скаляром  . Тогда общие затраты ресурсов на изготовление всех видов продукции равны их общим запасам, которые описываются матрицей-столбцом
. Тогда общие затраты ресурсов на изготовление всех видов продукции равны их общим запасам, которые описываются матрицей-столбцом  , если производство является сбалансированным, то есть запасы ресурсов в полном объеме расходуются на изготовление продукции. Следовательно, имеем еще одну форму представления СЛАУ:
, если производство является сбалансированным, то есть запасы ресурсов в полном объеме расходуются на изготовление продукции. Следовательно, имеем еще одну форму представления СЛАУ:

Матрицу  , которая составлена из коэффициентов при неизвестных системы уравнений (1.6), называют основной матрицей системы. Присоединяя справа (через вертикальную черту) к матрице
, которая составлена из коэффициентов при неизвестных системы уравнений (1.6), называют основной матрицей системы. Присоединяя справа (через вертикальную черту) к матрице  матрицу-столбец свободных членов
матрицу-столбец свободных членов  получаем матрицу
получаем матрицу  , которую называют расширенной матрицей системы:
, которую называют расширенной матрицей системы:

Понятно, что операции над строками расширенно и матрицы являются операциями над соответствующими уравнениями системы.
Решением системы уравнений называется такой набор чисел 
 , который при его подстановке вместо неизвестных
, который при его подстановке вместо неизвестных 
 в каждое уравнение системы превращает эти уравнения в числовые тождества.
в каждое уравнение системы превращает эти уравнения в числовые тождества.
Система линейных алгебраических уравнений называется совместной, если она имеет по крайней мере одно решение, и несовместимой, если она не имеет никакого решения. Совместимую систему уравнений называют определенной, если она имеет единственное решение, и неопределенной, если количество решений более одного.
Система линейных уравнений называется неоднородной, если хотя бы один элемент матрицы-столбца свободных членов отличается от нуля. Если все элементы  равны нулю, то такая система линейных уравнений называется однородной. Однородная система уравнений имеет вид:
равны нулю, то такая система линейных уравнений называется однородной. Однородная система уравнений имеет вид:

где  основная матрица системы;
основная матрица системы;
 матрица-столбец неизвестных;
матрица-столбец неизвестных;
 матрица-столбец свободных членов, которая содержит только нули.
матрица-столбец свободных членов, которая содержит только нули.
Лекции:
- Расстояние между скрещивающимися прямыми
- Нахождение промежутков возрастания и убывания функции
- Изменить порядок интегрирования
- Производная функции заданной неявно
- Методы определенного интегрирования
- Обыкновенные дифференциальные уравнения
- Частные производные. Частные дифференциалы
- Теорема об остатке
- Найти частные производные
- Уравнения с двумя переменными