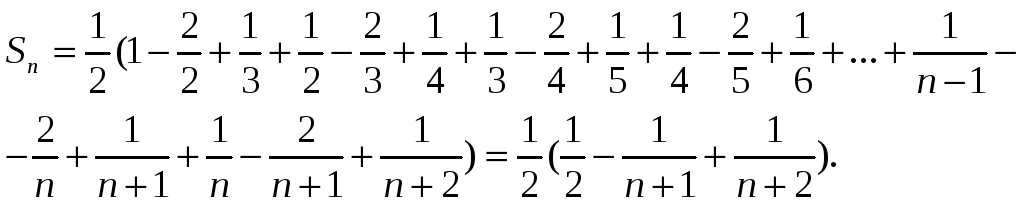Как найти общие члены двух прогрессий

Нахождение общего члена ряда по заданным первым членам. Первая часть.

Числовой ряд можно задать по-разному. Чаще всего просто используют запись вида $sumlimits_{n=1}^{infty}u_n$. Однако изредка указывают несколько первых членов ряда, по которым нужно восстановить общий член ряда. Честно говоря, подобные задачи не имеют единственного решения, и это будет продемонстрировано в примере №1. Впрочем, есть некие общие приёмы, которые применяют в стандартных случаях.

Для начала стоит запомнить несколько последовательностей. Например, квадраты натуральных чисел, т.е. последовательность $u_n=n^2$. Вот несколько первых членов этой последовательности:

$$
begin{equation}
1;; 4;; 9;; 16;; 25;; 36;; 49;; 64; ;81; ldots
end{equation}
$$

Как мы получили эти числа? показатьскрыть

Также стоит иметь в виду члены последовательности $u_n=n^3$. Вот несколько первых её членов:

$$
begin{equation}
1;; 8;; 27;; 64;; 125;; 216;; 343;; 512;;729; ldots
end{equation}
$$

Кроме того, для формирования общего члена ряда частенько используется последовательность $u_n=n!$, несколько первых членов которой таковы:

$$
begin{equation}
1;; 2;; 6;; 24;; 120;; 720;; 5040; ldots
end{equation}
$$

Что обозначает “n!”? показатьскрыть

Часто используются также арифметическая и геометрическая прогрессии. Если первый член арифметической прогрессии равен $a_1$, а разность равна $d$, то общий член арифметической прогрессии записывается с помощью такой формулы:

$$
begin{equation}
a_n=a_1+dcdot (n-1)
end{equation}
$$

Что такое арифметическая прогрессия? показатьскрыть

Стоит также отметить геометрическую прогрессию. Если первый член прогрессии равен $b_1$, а знаменатель равен $q$, то общий член геометрической прогрессии задаётся такой формулой:

$$
begin{equation}
b_n=b_1cdot q^{n-1}
end{equation}
$$

Что такое геометрическая прогрессия? показатьскрыть

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Пример №1

Найти общий член ряда $frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+ldots$.

Решение

Суть таких задач состоит в том, чтобы заметить закономерность, которая присуща первым членам ряда. И на основании этой закономерности сделать вывод о виде общего члена. Что означает фраза “найти общий член”? Она означает, что необходимо найти такое выражение, подставляя в которое $n=1$ получим первый член ряда, т.е. $frac{1}{7}$; подставляя $n=2$ получим второй член ряда, т.е. $frac{2}{9}$; подставляя $n=3$ получим третий член ряда, т.е. $frac{3}{11}$ и так далее. Нам известны первые четыре члена ряда:

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}.
$$

Давайте двигаться постепенно. Все известные нам члены ряда – дроби, поэтому резонно предположить, что и общий член ряда тоже представлен дробью:

$$
u_n=frac{?}{?}
$$

Наша задача – выяснить, что же скрывается под знаками вопроса в числителе и знаменателе. Сначала обратимся к числителю. В числителях известных нам членов ряда стоят числа 1, 2, 3 и 4. Заметьте, что номер каждого члена ряда равен числителю. У первого члена в числителе стоит единица, у второго – двойка, у третьего – тройка, у четвёртого – четвёрка.

Логично предположить, что у n-го члена в числителе будет стоять $n$:

$$
u_n=frac{n}{?}
$$

Кстати сказать, к этому выводу мы можем прийти и иным путём, более формальным. Что представляет собой последовательность 1, 2, 3, 4? Отметим, что каждый последующий член этой последовательности на 1 больше, чем предыдущий. Мы имеем дело с четырьмя членами арифметической прогрессии, первый член которой $a_1=1$, а разность $d=1$. Используя формулу (4), получим выражение общего члена прогрессии:

$$
a_n=1+1cdot (n-1)=1+n-1=n.
$$

Итак, угадывание или формальный расчёт – дело вкуса. Главное – мы записали числитель общего члена ряда. Перейдём к знаменателю.

В знаменателях мы имеем последовательность 7, 9, 11, 13. Это четыре члена арифметической прогрессии, первый член которой равен $b_1=7$, а разность $d=2$. Общий член прогрессии найдем, используя формулу (4):

$$
b_n=7+2cdot (n-1)=7+2n-2=2n+5.
$$

Полученное выражение, т.е. $2n+5$, и будет знаменателем общего члена ряда. Итак:

$$
u_n=frac{n}{2n+5}.
$$

Общий член ряда получен. Давайте проверим, подходит ли найденная нами формула $u_n=frac{n}{2n+5}$ для вычисления уже известных членов ряда. Найдём члены $u_1$, $u_2$, $u_3$ и $u_4$ по формуле $u_n=frac{n}{2n+5}$. Результаты, естественно, должны совпасть с заданными нам по условию первыми четырьмя членами ряда.

$$
u_1=frac{1}{2cdot 1+5}=frac{1}{7};; u_2=frac{2}{2cdot 2+5}=frac{2}{9};; u_3=frac{3}{2cdot 3+5}=frac{3}{11};; u_4=frac{4}{2cdot 4+5}=frac{4}{13}.
$$

Всё верно, результаты совпадают. Заданный в условии ряд можно записать теперь в такой форме: $sumlimits_{n=1}^{infty}frac{n}{2n+5}$. Общий член ряда имеет вид $u_n=frac{n}{2n+5}$.

В принципе, если речь идёт о стандартном примере, то можно считать, что ответ получен. Однако если вам интересно поисследовать вопрос более детально, то прошу читать далее. Вопрос вот в чём: является ли найденное выше представление общего члена единственным? Ответ на этот вопрос далеко не столь очевидный, как кажется на первый взгляд. Например, давайте продолжим заданный в условии ряд таким образом:

$$
frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+0+0+0+0+0+0+0+ldots
$$

Разве такой ряд не имеет право на существование? Ещё как имеет. И для этого ряда можно записать, что

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}; ; u_n=0; (n≥ 5).
$$

Можно записать и иное продолжение. Например, такое:

$$
frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+frac{1}{5}+frac{1}{6}+frac{1}{7}+frac{1}{8}+frac{1}{9}+frac{1}{10}+ldots
$$

И такое продолжение ничему не противоречит. При этом можно записать, что

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}; ; u_n=frac{1}{n}; (n≥ 5).
$$

Если первые два варианта показались вам чересчур формальными, то предложу третий. Давайте запишем общий член в таком виде:

$$
u_n=frac{n}{n^4-10n^3+35n^2-48n+29}.
$$

Вычислим первые четыре члена ряда, используя предложенную формулу общего члена:

begin{aligned}
& u_1=frac{1}{1^4-10cdot 1^3+35cdot 1^2-48cdot 1+29}=frac{1}{7};\
& u_2=frac{2}{2^4-10cdot 2^3+35cdot 2^2-48cdot 2+29}=frac{2}{9};\
& u_3=frac{3}{3^4-10cdot 3^3+35cdot 3^2-48cdot 3+29}=frac{3}{11};\
& u_4=frac{4}{4^4-10cdot 4^3+35cdot 4^2-48cdot 4+29}=frac{4}{13}.
end{aligned}

Как видите, предложенная формула общего члена вполне корректна. И таких вариаций можно придумать бесконечно много, их количество ничем не ограничено. В стандартных примерах, конечно, используется стандартный набор неких известных последовательностей (прогрессии, степени, факториалы и т.д.). Однако в таких задачах всегда присутствует неопределённость, и об этом желательно помнить.

Во всех последующих примерах эта неоднозначность оговариваться не будет. Решать станем стандартными способами, которые приняты в большинстве задачников.

Ответ: общий член ряда: $u_n=frac{n}{2n+5}$.

Пример №2

Записать общий член ряда $frac{1}{1cdot 5}+frac{1}{3cdot 8}+frac{1}{5cdot 11}+frac{1}{7cdot 14}+frac{1}{9cdot 17}+ldots$.

Решение

Нам известны первые пять членов ряда:

$$
u_1=frac{1}{1cdot 5};; u_2=frac{1}{3cdot 8}; ; u_3=frac{1}{5cdot 11}; ; u_4=frac{1}{7cdot 14}; ; u_5=frac{1}{9cdot 17}.
$$

Все известные нам члены ряда – дроби, значит и общий член ряда будем искать в виде дроби:

$$
u_n=frac{?}{?}.
$$

Сразу обратим внимание на числитель. Во всех числителях стоят единицы, поэтому и в числителе общего члена ряда будет единица, т.е.

$$
u_n=frac{1}{?}.
$$

Теперь обратимся к знаменателю. В знаменателях известных нам первых членов ряда расположены произведения чисел: $1cdot 5$, $3cdot 8$, $5cdot 11$, $7cdot 14$, $9cdot 17$. Первые из этих чисел таковы: 1, 3, 5, 7, 9. Данная последовательность имеет первый член $a_1=1$, а каждый последующий получается из предыдущего прибавлением числа $d=2$. Иными словами, это первые пять членов арифметической прогрессии, общий член которой можно записать с помощью формулы (4):

$$
a_n=1+2cdot (n-1)=1+2n-2=2n-1.
$$

В произведениях $1cdot 5$, $3cdot 8$, $5cdot 11$, $7cdot 14$, $9cdot 17$ вторые числа таковы: 5, 8, 11, 14, 17. Это элементы арифметической прогрессии, первый член которой $b_1=5$, а знаменатель $d=3$. Общий член этой прогрессии запишем с помощью всё той же формулы (4):

$$
b_n=5+3cdot (n-1)=5+3n-3=3n+2.
$$

Сведём результаты воедино. Произведение в знаменателе общего члена ряда таково: $(2n-1)(3n+2)$. А сам общий член ряда имеет следующий вид:

$$
u_n=frac{1}{(2n-1)(3n+2)}.
$$

Для проверки полученного результата найдём по формуле $u_n=frac{1}{(2n-1)(3n+2)}$ те четыре первых члена ряда, которые нам известны:

begin{aligned}
& u_1=frac{1}{(2cdot 1-1)(3cdot 1+2)}=frac{1}{1cdot 5};\
& u_2=frac{1}{(2cdot 2-1)(3cdot 2+2)}=frac{1}{3cdot 8};\
& u_3=frac{1}{(2cdot 3-1)(3cdot 3+2)}=frac{1}{5cdot 11};\
& u_4=frac{1}{(2cdot 4-1)(3cdot 4+2)}=frac{1}{7cdot 14};\
& u_5=frac{1}{(2cdot 5-1)(3cdot 5+2)}=frac{1}{9cdot 17}.
end{aligned}

Итак, формула $u_n=frac{1}{(2n-1)(3n+2)}$ позволяет точно вычислить члены ряда, известные из условия. При желании заданный ряд можно записать так:

$$
sumlimits_{n=1}^{infty}frac{1}{(2n-1)(3n+2)}=frac{1}{1cdot 5}+frac{1}{3cdot 8}+frac{1}{5cdot 11}+frac{1}{7cdot 14}+frac{1}{9cdot 17}+ldots
$$

Ответ: общий член ряда: $u_n=frac{1}{(2n-1)(3n+2)}$.

Продолжение этой темы рассмотрим в второй и третьей частях.

Условие

Решение

Написать комментарий

Содержание

• Определение арифметической прогрессии
  • Формула общего члена арифметической прогрессии
• Сумма первых n членов арифметической прогрессии
  • Формула суммы первых n членов арифметической прогрессии

Определение арифметической прогрессии

Определение. Числовая последовательность, каждый член которой получается из предыдущего прибавлением одного и того же числа называется арифметической прогрессией. Число называется разностью арифметической прогрессии.

То есть арифметическая прогрессия определяется рекуррентным соотношением

   

Например, последовательность нечётных натуральных чисел

   

является арифметической прогрессией, так как любой её член отличается от предыдущего на 2.

Общий член арифметической прогрессии задаётся формулой

   

Например, последовательность образует арифметическую прогрессию с разностью и первым членом Поэтому её общий член может быть задан соотношением

   

Пример 1. Найти одиннадцатый член арифметической прогрессии, если её первый член а разность

Решение. По формуле для общего члена арифметической прогрессии имеем

   

Теорема. Последовательность тогда и только тогда является арифметической прогрессией, когда каждый её член, начиная со второго, равен полусумме предыдущего и последующего членов:

   

Доказательство. По определению арифметической прогрессии для всех имеем

   

Отсюда

   

то есть

   

Сумма первых n членов арифметической прогрессии

В качестве примера найдём сумму всех натуральных чисел от 1 до 100, то есть вычислим сумму

   

Решение. Можно сидеть и долго складывать все числа по порядку. Но есть более простой способ. Запишем сумму этих чисел, а под ней — ту же сумму, но в обратной последовательности:

   

Теперь почленно сложим эти суммы:

   

   

Отсюда

По легенде, школьный учитель математики, надеясь надолго занять детей, предложил им сосчитать эту сумму. Среди тех детей был будущий великий математик Карл Гаусс. Юный Гаусс быстро заметил, что попарные суммы членов с противоположных концов равны: и т.д, и уже через несколько минут подошёл к учителю с ответом:

Этим же приёмом удобно воспользоваться и при вычислении суммы первых членов арифметической прогрессии, если заметить, что

   

Действительно,

   

   

Сумма первых n членов арифметической прогресиии

   

равна полусумме первого и n-ного её членов, умноженной на число членов, то есть

   

Доказательство. Запишем сумму сначала в прямом порядке, а затем — в обратном:

   

   

Сложим почленно эти два равенства и воспользуемся тем, что :

   

   

Отсюда находим

   

1.21. Основные понятия сходимости числовых рядов.

Числовым
рядом называется
выражение вида
,
где

являются членами
числового ряда
и представляют собой действительные
или комплексные числа.

Числовой
ряд задается с помощью формулы
общего члена ряда
,
описывающей зависимость члена ряда от
его номера.

Пример 1.Найти
общий член ряда
.

Решение.
Последовательные числители образуют
арифметическую прогрессии. 1,3,5,7,…;
й
член прогрессии находим по формуле
Здесь
,
поэтому
.
Последовательные знаменатели образуют
геометрическую прогрессии.

-й
член этой прогрессии
.
Следовательно, общий член ряда

Пример 2.
Найти общий член ряда

Решение.
Показатель степени каждого члена
совпадает с номером этого члена, поэтому
показатель степени
го
члена равен
.
Числители дробей 2/3,3/7,4/11,5/15,… образуют
арифметическую прогрессию с первым
членом 2 и разностью 1. Поэтому
-й
числитель равен
.
Знаменатели образуют арифметическую
прогрессию с первым членом 4 и разностью
4. Следовательно,
-й
знаменатель равен
.
Итак, общим членом ряда является

Сумма

первых

членов ряда называется
-й
частичной суммой
ряда.
Рассмотрим последовательность частичных
сумм числового ряда:

,

,

,
…

Определение.
Если существует конечный предел

последовательности частичных сумм
ряда, то говорят, что числовой ряд
сходится.
Этот предел называют суммой
ряда
.

Числовой
ряд называют расходящимся,
если

не существует или
.

Пример
1.
Рассмотрим ряд 1/2+1/4+1/8+1/16+…+

Сторона
квадрата равна единице, следовательно
площадь 1/2+1/4+1/16+1/32+…. . . = 1

Пример
2.
Числовой ряд

является сходящимся. Это легко доказать,
рассмотрев последовательность частичных
сумм. Действительно,

,
,

,
…,

.

Следовательно,
,
т.е. ряд сходится.

Пример 3.
Найти сумму ряда
.

Решение.
Разлагаем общий член ряда на простейшие
дроби:

Выписываем несколько
членов ряда так, чтобы было видно, какие
слагаемые сокращаются при вычислении
частичной суммы ряда:
.

Составляем
ю
частичную сумму ряда:

Вычисляем сумму ряда по формуле
, получаем
.
Ряд сходится и его сумма равна 1/2.

Пример 4.
Найти сумму ряда
.

Решение. Разложим
общий член ряда

на простейшие дроби с помощью метода
неопределенных коэффициентов:

.
Умножая на знаменатель левой части,
придем к тождеству

Полагая последовательно

находим: при
:
1=2A; A=1/2; при
:

при


Таким образом,
,
т.е.
.
Выписываем несколько членов ряда, чтобы
было видно, какие слагаемые сокращаются
при вычислении частичной суммы ряда:

.

Составляем
ю
частичную сумму ряда и сокращаем все
слагаемые, какие возможно:

Вычисляем сумму
ряда по формуле
,
получаем.

Числовой
ряд
расходится,
так как последовательность частичных
сумм


не имеет предела.

Известным числовым
рядом является геометрическая прогрессия:

Сумма
первых

членов прогрессии находится по формуле
,
.
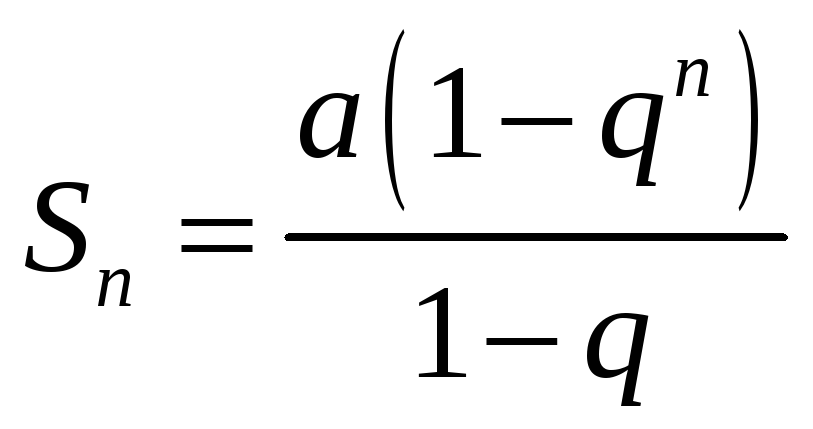
Предел этой суммы равен:

,

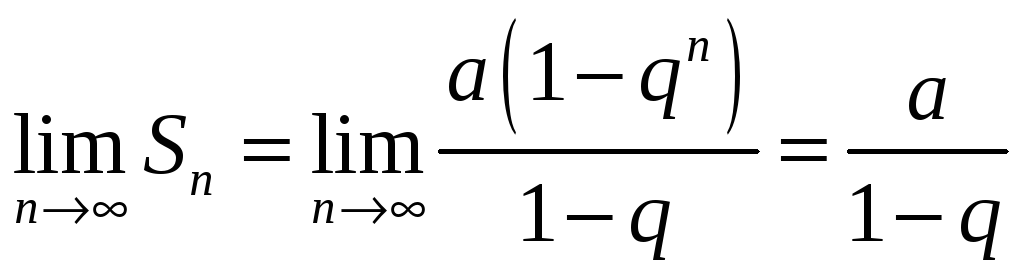
если
,
так как
.
Если
,
то
,
поэтому
,
ряд расходится. Если
,
то ряд принимает вид
.
Последовательность частичных сумм

расходится,
,
следовательно, расходится и ряд. При

ряд принимает вид

– в этом случае

при четном

и

при нечетном
.
Следовательно,

не существует, а ряд расходится.

Пример 5.
Исследовать сходимость ряда
.

Решение.
Ряд составлен из членов бесконечно
убывающей геометрической прогрессии
и поэтому сходится. Найдем сумму ряда.
Здесь(знаменатель
прогрессии) Следовательно,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #