Как найти общие делители двух чисел паскаль

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var
  a, b, d: integer;

begin
  write('Введите два числа: ');
  readln(a, b);
  if a < b then d := a + 1 else d := b + 1; 
  {так как мы используем цикл с постусловием, 
  необходимо минимальное значение увеличить на один,
  иначе цикл repeat, в силу своих конструктивных особенностей,
  не учтет это минимальное число  
  и не сделает его кандидатом в НОД. Например, 5 и 25.}
  repeat d := d - 1
  until (a mod d = 0) and (b mod d = 0);
  write('NOD = ', d)
end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A,  B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

Доказательство:

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

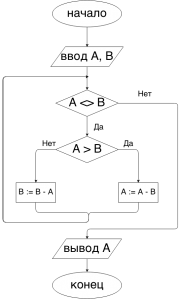
Блок — схема алгоритма Евклида «с вычитанием»

Программа

var
  a, b: integer;

begin
  write('a = '); 
  readln(a);
  write('b = ');
  readln(b);
  while a <> b do 
    if a > b then 
      a := a - b 
    else 
      b := b - a;
  writeln('NOD = ', a);
end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var
  a, b: integer;

begin
  write('a = ');
  readln(a);
  write('b = ');
  readln(b);
  while (a <> 0) and (b <> 0) do
    if a >= b 
    then 
      a := a mod b 
    else 
      b := b mod a;
  write(a + b)
end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Приведем 3 программы поиска наибольшего общего делителя двух натуральных чисел, основанных на:

• алгоритме Евклида
• перебора возможных делителей числа
• разложения чисел на простые множители

Что такое наибольший общий делитель двух натуральных чисел m и n, или НОД(m, n)

НОД двух натуральных чисел – это такое наибольшее натуральное число, которое одновременно делит без остатка оба этих числа.

Алгоритм Евклида

Евклид – древнегреческий математик, геометр, автор первого из дошедших до нас теоретических трактатов по математике.

Алгоритм Евклида – один из наиболее ранних численных алгоритмов в истории. Евклид впервые дал описание этого алгоритма в книгах «Начала». Изначально этот алгоритм назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль.

Сформулируем алгоритм

Пусть даны два натуральных числа m и n. Пока числа m и n не равны (или их разница не равна 0), большее число заменить их разницей. В качестве ответа взять любое из чисел.

Пример:

Пусть m = 12, n = 18

12<>18, n = 18 – 12 = 6

12<>6, m = 12 – 6 = 6

6<>6, НОД(12, 18) = 6

Программа на языке программирования Паскаль (алгоритм Евклида)

var m, n:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);  

  readln(m,n);

  while m<>n do

  begin

    if m>n then m:=m-n

           else n:=n-m;

  end;

  writeln(‘НОД(m,n): ‘,m);

end.

Результат запуска программы

Перебор возможных делителей числа

Будем использовать алгоритм, разобранный ранее в этом блоге.

Запустим цикл for с счетчиком k от 1 до n, будем проверять условие: если число n делится на значение счетчика k без остатка (n mod k = 0), то значение счетчика k – это делитель числа n, значение k можно вывести на экран или сохранить в отдельной переменной.

Поскольку нам нужен наибольший общий делитель чисел m и n, поэтому запустим цикл до минимального из чисел m и n (другое будет лишним), и будем проверять условие: если число m делится на значение счетчика цикла k без остатка и число n делится на значение счетчика цикла k без остатка одновременно (воспользуемся операцией and), это и будет их общий делитель.

Программа на языке программирования Паскаль (перебор возможных делителей числа)

var m, n, k, p:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);

  readln(m,n);

  for k:=1 to min(m,n) do 

  begin

    if (m mod k = 0) and (n mod k=0) then p:=k;

  end;

  writeln(‘НОД(m,n): ‘,p);

end.

Функция min будет работать в PascalABC.NET, в случае использования другой среды, нужно до цикла определить наибольшее число из m и n.

Разложение чисел на простые множители

Ранее мы разбирали алгоритм разложения натурального числа на простые множители. 

Как связаны простые множители числа и НОД. Приведем пример.

Пусть m = 18,  n = 12

Выполним разложение на простые множители.

Множители числа m: 2 3 3

Множители числа n: 2 2 3

Выделим их общие простые множители – это числа 2 и 3. В качестве наибольшего общего делителя нужно взять из произведение: 2 * 3 = 6. НОД(12, 18) = 6.

Пусть m = 36,  n = 48

Множители числа m: 2 2 3 3

Множители числа n: 2 2 2 2 3

Общие простые множители – это числа 2 2 3. Произведение этих множителей равно 12. НОД(36, 48) = 12.

Для нахождения НОД двух чисел нужно выполнить их разложение на простые множители и в качестве ответа взять произведение их общих множителей.

Как будем решать задачу

Для хранения множителей числа воспользуемся списком (PascalABC.NET), в него легко добавлять значение командой add.

Описание списка с именем nod в блоке var

var nod:List<integer>;

Создание нового пустого списка в теле программы

nod:=new List<integer>;

Добавление значения в конец списка

nod.add(значение);

Создадим два списка (s1 и s2) для хранения множителей числа m и n соответственно. С помощью конструкции вложенных циклов переберем все элементы списков и сравним на равенство, если множители равны, сохраним их в списке nod, а значения элементов списков сделаем равными -1 и -2 соответственно (чтобы далее их повторное сравнение на равенство было ложным) . В качестве ответа возьмем произведение элементов списка nod командой nod.Product.

Программа на языке программирования Паскаль (разложение чисел на простые множители)

var

  m, n, k1, k2: integer;      

  s1, s2, nod: List<integer>;

begin

  writeln(‘Введите два натуральных числа m и n:’);   

  readln(m, n);  

  s1 := new List<integer>; 

  s2 := new List<integer>; 

  nod := new List<integer>;

  k1 := 2; k2 := 2;  

  while (m > 1) or (n > 1) do   

  begin

    while m mod k1 = 0 do     

    begin

      m := m div k1;      

      s1.Add(k1); //добавить значение в список можно и так: s1+=k1;

    end;     

    k1 += 1;     

    while n mod k2 = 0 do    

    begin

      n := n div k2;       

      s2.Add(k2);     

    end;     

    k2 += 1;   

  end;   

  //writeln(s1, s2); 

  for k1:=0 to s1.Count-1 do //элементы списка нумеруются с 0, длина списка s1.count

    for k2:=0 to s2.Count-1 do

      if s1[k1]=s2[k2] then //s1[k1] – обращение к элементу списка по его номеру

        begin 

        nod.Add(s1[k1]);

        s1[k1]:=-1;

        s2[k2]:=-2;

        end;

  //println(s1,s2,nod);

  println(‘НОД(m,n): ‘,nod.Product);

end.

Это программа состоит из самого большого количества строк. Насколько она эффективна?

Задача на применение НОД

Даны числа: a = 2³ • 3¹⁰ • 5 • 7² , b = 2⁵ • 3 • 11. Чему равен  НОД (a,b)?

Вычисление наибольших общих делителей

Просмотров 1.1к. Обновлено 15 октября 2021

Найти наибольшие общие делители (НОД) для множества пар чисел.

Пусть пользователь будет вводить пары чисел, а на экран будут выводиться наибольшие общие делители этих чисел. В таком случае программу можно организовать следующим образом.

В основной ветке программы будет цикл, в теле которого будут

1. запрашиваться два числа,
2. вызываться функция для вычисления наибольшего общего делителя,
3. возвращаемый функцией результат выводиться на экран.

Условие прекращения работы цикла основной программы — ввод пользователем двух нулей.

НОД будет вычисляться в функции, которая будет получать два числа, а возвращать их НОД. Алгоритм нахождения НОД может быть следующим. Пока оба числа не равны нулю, находить остаток от деления большего числа на меньшее и присваивать его переменной, где хранилось большее число. После цикла сложить значения обоих переменных, — это и есть НОД.

На самом деле НОД содержится только в одной переменной, а вторая имеет нулевое значение (это условие окончания цикла). Однако нам неизвестно какая из двух содержит 0, поэтому проще их сложить, чем это выяснять.

Почему НОД можно определить таким способом (следует знать, что он не единственный)? Представим, что у нас два числа: 18 и 12. Остаток от деления 18 на 12 будет 6. Далее имеется два числа 12 и 6. Остаток от деления первого на второе равен 0. Он записывается на место числа 12. Получаем 0 и 6. Таким образом 12 делится нацело на 6, а вот как пояснить логически, что и 18 на него должно делиться?

Pascal

var a, b: word;

 
function gcd(c, d: word): word;

    begin

        while (c <> 0) and (d <> 0) do

            if c > d then

                c := c mod d

            else

                d := d mod c;

        gcd := c + d;

    end;

 
begin

    repeat

        write('Two numbers: ');

        readln(a,b);

        writeln('GCD: ', gcd(a,b));

    until (a = 0) and (b = 0);

end.

Two numbers: 56 18

GCD: 2

Two numbers: 196 144

GCD: 4

Two numbers: 305 809

GCD: 1

Two numbers: 810 3220

GCD: 10

Two numbers: 15000 10500

GCD: 1500

Two numbers: 0 200

GCD: 200

Two numbers: 0 0

GCD: 0

Язык Си

#include < stdio.h>

int gcd (int, int);

 
main() {

    int a, b;

    do {

        printf("Two numbers: ");

        scanf("%d%d", &a, &b);

        printf("GCD: %dn", gcd(a,b));

    } while (a != 0 || b != 0);

}

 
int gcd(int c, int d) {

    while (c != 0 && d != 0) {

        if (c > d) c = c % d;

        else d = d % c;

    }

    return c + d;

}

Python

def gcd(c,d):

    while c != 0 and d != 0:

        if c > d:

            c %= d

        else:

            d %= c

    return c + d

 
a = b = 1

while a != 0 or b != 0:

    a = input("Two numbers: ")

    a = a.split()

    b = int(a[1])

    a = int(a[0])

    print("GCD:", gcd(a,b))

КуМир

алг 

нач

  цел а, б

  нц

    вывод "Введите два целых числа: "

    ввод а, б

    вывод "НОД = ", НОД(а,б), нс

  кц_при а = 0 и б = 0

кон

 
алг цел НОД (цел а, цел б)

нач

  цел в, г

  в := а

  г := б

  нц пока в <> 0 и г <> 0

    если в > г то в := mod(в,г)

     иначе г := mod(г,в)

    все

  кц

  знач := в + г

кон

Basic-256

do

	print "Введите два числа:"

	input a

	input b

	gosub gcd

until a = 0 and b = 0

end

 
gcd:

	c = a

	d = b

	while c<>0 and d<>0

		if c>d then

			c = c % d

		else 

			d = d % c

		endif

	endwhile

	print "НОД = " + (c+d)

return

Формулировка. Даны два натуральных числа. Найти их наибольший общий делитель.

Примечание: наибольшим общим делителем (сокращенно пишут НОД) двух натуральных чисел m и n называется наибольший из их общих делителей. Обозначение: НОД(m, n).

Примечание 2: общим делителем двух натуральных чисел называется натуральное число, на которое натуральное число, которое является делителем обоих этих чисел.

Например, найдем НОД(12, 8):

Выпишем все делители числа 12: 1, 2, 3, 4, 6, 12;

Выпишем все делители числа 8: 1, 2, 4, 8;

Выпишем все общие делители чисел 12 и 8: 1, 2, 4. Из них наибольшее число – 4. Это и есть НОД чисел 12 и 8.

Решение. Конечно, при решении мы не будем выписывать делители и выбирать нужный. В принципе, ее можно было бы решить как задачу 15, начав цикл с наименьшего из двух заданных чисел (так как оно тоже может быть НОД, например, НОД(12, 4) = 4). Но мы воспользуемся так называемым алгоритмом Евклида нахождения НОД, который выведен с помощью математических методов. В самом простейшем случае для заданных чисел m и n он выглядит так:

1)          Если m неравно n, перейти к шагу 2, в противном случае вывести m и закончить алгоритм;

2)          Если m > n, заменить m на m – n, в противном случае заменить n на n – m;

3)          Перейти на шаг 1

Как видим, в шаге 2 большее из двух текущих чисел заменяется разностью большего и меньшего.

Приведем пример для чисел 12 и 8:

1. Так как 12 > 8, заменим 12 на 12 – 8 = 4;
2. Так как 8 > 4, заменим 8 на 8 – 4 = 4;
3. 4 = 4, конец.

Не проводя каких-либо рассуждений над алгоритмом и не доказывая его корректности, переведем его описание в более близкую для языка Pascal форму:

Алгоритм на естественном языке:

1)      Ввод m и n;

2)      Запуск цикла с предусловием m < > n. В цикле:

1. Если m > n, то переменной m присвоить m – n, иначе переменной n присвоить n – m;

3)      Вывод m:

Код:

1. program GreatestCommonDiv;
2. var
3. m, n: word;
4. begin
5. readln(m, n);
6. while m <> n do begin
7. if m > n then begin
8. m := m — n
9. end
10. else begin
11. n := n — m
12. end
13. end;
14. writeln(m)
15. end.