Заказать задачи по любым предметам можно здесь от 10 минут
Метод Гаусса
- Метод Гаусса
- Пример 1
- Пример 2
- Несовместность системы (нет решений)
- Пример 3
- Общее и частное решение системы (бесконечное множество решений)
- Пример 4
Пусть задана система линейных алгебраических уравнений: $$begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = b_1 \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = b_2 \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = b_3 end{cases}. $$
- Запишем систему уравнений в виде расширенной матрицы, состоящей из коэффициентов и столбца свободных членов. Вертикальная черта используется для удобства оформления. $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ a_{21} & a_{22} & a_{23} & | & b_2 \ a_{31} & a_{32} & a_{33} & | & b_3 end{pmatrix} $$
- С помощью элементарных преобразований матрицы (вычитание одной строки из другой, умноженной на коэффициент, удаление одинаковых и нулевых строк, деление строки на число отличное от нуля) получаем нули под главной диагональю $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ 0 & a_{22} & a_{23} & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
- Используя элементарные преобразования, изложенные в пункте 2, приводим матрицу к виду содержащему нули везде, кроме главной диагонали $$ begin{pmatrix} a_{11} & 0 & 0 & | & b_1 \ 0 & a_{22} & 0 & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
| Пример 1 |
| Решить систему уравнений методом Гаусса $$begin{cases} x_1 + 2 x_2 + x_3 = 5 \ -x_1 + 3 x_2 -2 x_3 = 3 \ – x_1 -7 x_2 + 4 x_3 = -5 end{cases}. $$ |
| Решение |
|
Запишем расширенную матрицу, состоящую из коэффициентов при неизвестных $x_1, x_2, x_3$ и отдельно столбец свободных членов $b_1, b_2, b_3$. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ -1 & 3 & -2 & | & 3 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$ Приведем матрицу к нижнетреугольному виду (под главной диагональю должны быть нули) с помощью элементарных преобразований. Прибавим ко второй строке первую. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$ Далее прибавляем к третьей строке первую. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & -5 & 5 & | & 0 end{pmatrix}$$ Теперь осталось к третьей строке прибавить вторую строку, чтобы под главной диагональю были только нули. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 4 & | & 8 end{pmatrix}$$ Замечаем, что в третьей строке стоят числа, которые можно сократить на четыре. Для этого выполняем деление всей третьей строки на 4. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Теперь выполняем обратный ход Гаусса снизу вверх. Прибавляем ко второй строке третью строку. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & 0 & | & 10 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Сразу замечаем, что вторую строку можно сократить на 5. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Продолжаем обратный ход, вычитаем третью строку из первой. $$begin{pmatrix} 1 & 2 & 0 & | & 3 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Осталось из первой строки вычесть вторую строку, умноженную на 2, для того, чтобы в первой строке появился ноль. $$begin{pmatrix} 1 & 0 & 0 & | & -1 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$ Теперь перепишем получившуюся матрицу в виде системы уравнений, чтобы в дальнейшем получить чему равны неизвестные $x_1, x_2, x_3$. $$begin{cases} x_1 = -1 \ x_2 = 2 \ x_3 = 2 end{cases}$$ |
| Ответ |
| $$x_1 = -1, x_2 = 2, x_3 = 2$$ |
| Пример 2 |
| Решить систему линейных алгебраических уравнений методом Гаусса $$begin{cases} 2x_1 + 5 x_2 + 4x_3 + x_4 = 20 \ x_1 + 3 x_2 + 2x_3 +x_4 = 11 \ 2x_1 +10 x_2 + 9 x_3 + 7x_4 = 40 \ 3x_1 + 8x_2 + 9x_3 + 2x_4 = 37 end{cases}. $$ |
| Решение |
|
Записываем расширенную матрицу $$ begin{pmatrix} 2&5&4&1&|&20 \ 1&3&2&1&|&11 \ 2&10&9&7&|&40 \ 3&8&9&2&|&37 end{pmatrix}.$$ Умножаем вторую строку на 2 и вычитаем из неё первую строчку. Из третьей строки просто вычитаем первую. Умножаем четвертую строку на 2 и вычитаем из неё первую строку, умноженную на 3. Получаем матрицу $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&5&5&6&|&20 \ 0&1&6&1&|&14 end{pmatrix}.$$ Берем вторую строку, умноженную на 5 и вычитаем из третьей. Затем вторую строку вычитаем из четвертой. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&6&0&|&12 end{pmatrix}$$ Теперь умножаем третью строку на 6 и вычитаем её из четвертой строки, умноженной на 5. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&-6&|&0 end{pmatrix}$$ Получили нижнетреугольную матрицу, то есть ниже главной диагонали расположены нули. Теперь проделываем элементарные преобразования снизу вверх, так называемый обратный ход Гаусса. Но прежде замечаем, что появилась строка, в которой можно выполнить сокращение. А именно в четвертой строке можно разделить все числа на (-6). И получаем $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Вот теперь вычитаем четвертую строчку из третьей, второй и первой. $$begin{pmatrix} 2&5&4&0&|&20 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Из второй строки мы не будем вычить третью, потому что там итак стоит ноль, ради которого мы проводим элементарные преобразования, поэтому пропускаем этот шаг. Умножаем на 4 третью строку и вычитаем её из первой, умноженной на 5. $$begin{pmatrix} 10&25&0&0&|&60 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Замечаем, что в первой строке можно все числа сократить на 5. $$begin{pmatrix} 2&5&0&0&|&12 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Теперь остался последний шаг это умножить вторую строку на 5 и вычесть из первой. $$begin{pmatrix} 2&0&0&0&|&2 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$ Замечаем, что первую строку можно сократить на 2, а третью строку на 5. $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix}$$ Переписываем матрицу в виде привычной системы уравнений и получаем ответ $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix} sim begin{cases} x_1 = 1 \ x_2 = 2 \ x_3 = 2 \ x_4 = 0 end{cases}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x_1 = 1, x_2 = 2, x_3 = 2, x_4 = 0$$ |
Несовместность системы (нет решений)
Если в результате элементарных преобразований появилась нулевая строка вида $$begin{pmatrix} 0&0&0&|&b end{pmatrix} text{ где } b neq 0,$$то система уравнений не имеет решений. На этом алгоритм Гаусса заканчивает свою работу и можно записывать ответ, что система несовместна, то есть нет решений.
| Пример 3 |
| Найти решение системы линейных уравнений методом Гаусса $$begin{cases} 7x_1 – 2x_2 – x_3 = 2 \ 6x_1 – 4x_2 – 5x_3 = 3 \ x_1 + 2x_2 + 4x_3 = 5 end{cases}.$$ |
| Решение |
|
Как обычно пишем расширенную матрицу по коэффициентам при неизвестных переменных и столбцу свободных членов $$begin{pmatrix} 7&-2&-1&|&2 \ 6&-4&-5&|&3 \ 1&2&4&|&5 end{pmatrix}.$$ Запускаем алгоритм Гаусса. Идём сверху вниз. Умножаем вторую строку на 7 и вычитаем из неё первую строчку умноженную на 6. Затем первую строку вичитаем из третьей, умноженной на 7. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&16&29&|&33 end{pmatrix}$$ Далее по алгоритму прибавляем вторую строку к третьей. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&0&0&|&42 end{pmatrix}$$ Видим, что в результате элементарных преобразований появилась строка в которой все нули, кроме свободного члена. Это означает, что система несовместа, то есть у системы уравнений нет решения. |
| Ответ |
| Нет решений, так как система несовместна. |
Общее и частное решение системы (бесконечное множество решений)
Часто после элементарных преобразований в расширенной матрице появляются нулевые строки вида $$begin{pmatrix} 0&0&0&|&0 end{pmatrix}.$$ Такую строку нужно вычеркивать из матрицы и система уравнений будет иметь бесконечное множество решений. Разберем это на практике.
| Пример 4 |
| Найти общее и два частных решения системы линейных алгебраических уравнений методом Гаусса $$begin{cases} x_1+x_2-x_3=4 \ 3x_1+2x_2-5x_3=7 \ 3x_1+x_2-7x_3=2 end{cases}.$$ |
| Решение |
|
Составляем расширенную матрицу $$begin{pmatrix} 1&1&-1&|&4 \ 3&2&-5&|&7 \ 3&1&-7&|&2 end{pmatrix}.$$ Из второй и третьей строки вычетаем первую, умноженную на 3. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&-2&-4&|&-10 end{pmatrix}$$ Из третьей строки вычитаем вторую, домноженную на 2. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$ Теперь согласно обратному ходу Гаусса вторую строку прибавляем к первой. $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$ По окочанию элементарных преобразований получилась строка, в которой все элементы равны нулю. Значит, система имеет бесконечное множество решений. Для его записи понадобится отличать базисные и свободные переменные. Обычно за базисные берут переменные, которые стоят на главной диагонали, а остальные свободные. В нашем случае базисными будут $x_1, x_2$, а свободной $x_3$. Переписываем матрицу в виде системы $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix} sim begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases}.$$ Так как $x_1, x_2$ являются базисными переменными, то их переносим в левую часть равенства, а всё остальное в правую часть. Получившееся называют общим решением решением системы уравнений $$begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases} sim begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$ Чтобы получить частное решение системы уравнений нужно вместо свободного $x_3$ подставить любое число, например $x_3 = 0$. Тогда получаем, что $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}.$$ Возьмем ещё например $x_3 = 1$ и получаем $$begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$ Можно брать различные числа вместо $x_3$ и получать бесконечное множество решений. |
| Ответ |
|
Общее решение системы уравнений $$begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$ Частные решения системы уравнений $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}, begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$ |

Сегодня разбираемся с методом Гаусса для решения систем линейных алгебраических уравнений. О том, что это за системы, можно почитать в предыдущей статье, посвященной решению тех же СЛАУ методом Крамера. Метод Гаусса не требует каких-то специфических знаний, нужна лишь внимательность и последовательность. Несмотря на то что с точки зрения математики для его применения хватит и школьной подготовки, у студентов освоение этого метода часто вызывает сложности. В этой статье попробуем свести их на нет!
Метод Гаусса
Метод Гаусса – наиболее универсальный метод решения СЛАУ (за исключением ну уж очень больших систем). В отличие от рассмотренного ранее метода Крамера, он подходит не только для систем, имеющих единственное решение, но и для систем, у которых решений бесконечное множество. Здесь возможны три варианта.
- Система имеет единственное решение (определитель главной матрицы системы не равен нулю);
- Система имеет бесконечное множество решений;
- Решений нет, система несовместна.
Итак, у нас есть система (пусть у нее будет одно решение), и мы собираемся решать ее методом Гаусса. Как это работает?
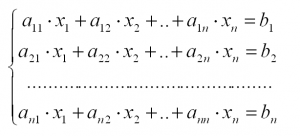
Метод Гаусса состоит из двух этапов – прямого и обратного.
Прямой ход метода Гаусса
Сначала запишем расширенную матрицу системы. Для этого в главную матрицу добавляем столбец свободных членов.
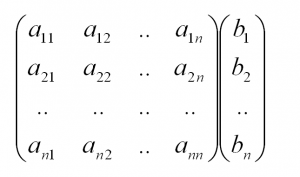
Вся суть метода Гаусса заключается в том, чтобы путем элементарных преобразований привести данную матрицу к ступенчатому (или как еще говорят треугольному) виду. В таком виде под (или над) главной диагональю матрицы должны быть одни нули.
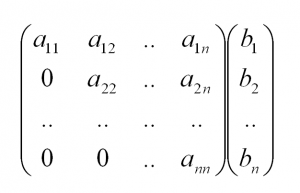
Что можно делать:
- Можно переставлять строки матрицы местами;
- Если в матрице есть одинаковые (или пропорциональные) строки, можно удалить их все, кроме одной;
- Можно умножать или делить строку на любое число (кроме нуля);
- Нулевые строки удаляются;
- Можно прибавлять к строке строку, умноженную на число, отличное от нуля.
Обратный ход метода Гаусса
После того как мы преобразуем систему таким образом, одна неизвестная Xn становится известна, и можно в обратном порядке найти все оставшиеся неизвестные, подставляя уже известные иксы в уравнения системы, вплоть до первого.
Когда интернет всегда под рукой, можно решить систему уравнений методом Гаусса онлайн. Достаточно лишь вбить в онлайн-калькулятор коэффициенты. Но согласитесь, гораздо приятнее осознавать, что пример решен не компьютерной программой, а Вашим собственным мозгом.
Пример решения системы уравнений методом Гаусс
А теперь – пример, чтобы все стало наглядно и понятно. Пусть дана система линейных уравнений, и нужно решить ее методом Гаусса:
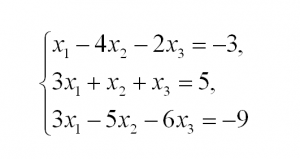
Сначала запишем расширенную матрицу:
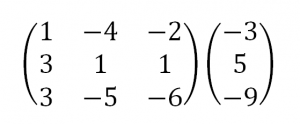
Теперь займемся преобразованиями. Помним, что нам нужно добиться треугольного вида матрицы. Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой и получим:
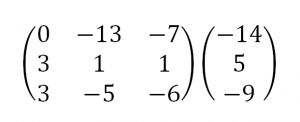
Затем умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
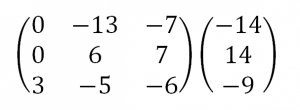
Умножим 1-ую строку на (6). Умножим 2-ую строку на (13). Добавим 2-ую строку к 1-ой:
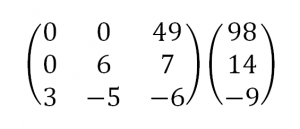
Вуаля – система приведена к соответствующему виду. Осталось найти неизвестные:
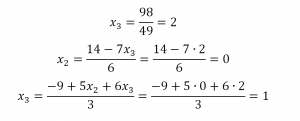
Система в данном примере имеет единственное решение. Решение систем с бесконечным множеством решений мы рассмотрим в отдельной статье. Возможно, сначала Вы не будете знать, с чего начать преобразования матрицы, но после соответствующей практики набьете руку и будете щелкать СЛАУ методом Гаусса как орешки. А если Вы вдруг столкнетесь со СЛАУ, которая окажется слишком крепким орешком, обращайтесь к нашим авторам! Заказать недорого реферат вы можете, оставив заявку в Заочнике. Вместе мы решим любую задачу!
![]()
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Содержание:
Базисные и свободные переменные:
Пусть задана система
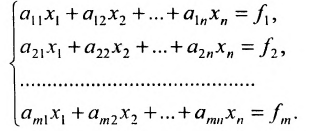
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
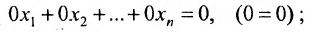
- умножение обеих частей одного из уравнений системы на любое действительное число
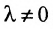 ;
; - перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)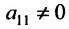 . Если это не так, то переставим уравнения системы так, чтобы
. Если это не так, то переставим уравнения системы так, чтобы 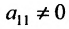 .
.
На первом шаге метода Гаусса исключим неизвестное 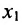 из всех уравнений системы (6.1.1), начиная со второго. Для этого последовательно умножим первое уравнение системы на множители
из всех уравнений системы (6.1.1), начиная со второго. Для этого последовательно умножим первое уравнение системы на множители
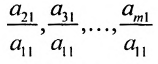 и вычтем последовательно преобразованные уравнения из второго, третьего, …, последнего уравнения системы (6.1.1). В результате получим эквивалентную систему:
и вычтем последовательно преобразованные уравнения из второго, третьего, …, последнего уравнения системы (6.1.1). В результате получим эквивалентную систему:
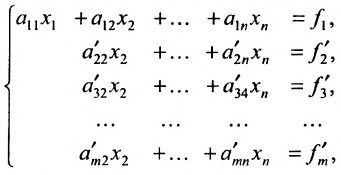 (6.1.2)
(6.1.2)
в которой коэффициенты 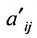 вычислены по формулам:
вычислены по формулам:
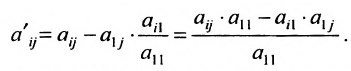 На втором шаге метода Гаусса исключим неизвестное
На втором шаге метода Гаусса исключим неизвестное 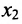 из всех уравнений системы (6.1.2) начиная с третьего, предполагая, что
из всех уравнений системы (6.1.2) начиная с третьего, предполагая, что 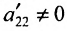 (в противном случае, переставим уравнения системы (6.1.2)
(в противном случае, переставим уравнения системы (6.1.2)
чтобы это условие было выполнено). Для исключения неизвестного 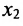 последовательно умножим второе уравнение системы (6.1.2) на множетели
последовательно умножим второе уравнение системы (6.1.2) на множетели 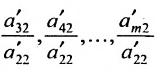 и вычтем последовательно преобразованные уравнения из третьего, четвёртого, последнего,…,уравнения системы (6.1.2). В результате получим эквивалентную систему:
и вычтем последовательно преобразованные уравнения из третьего, четвёртого, последнего,…,уравнения системы (6.1.2). В результате получим эквивалентную систему:
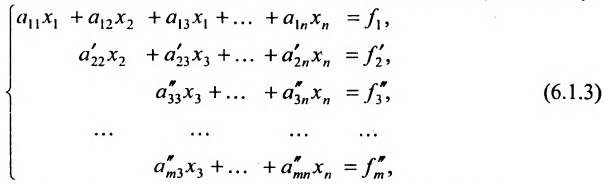
в которой коэффициенты 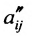 вычислены по формулам:
вычислены по формулам:
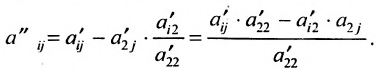
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
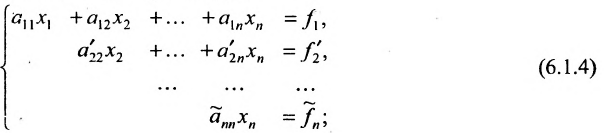
или
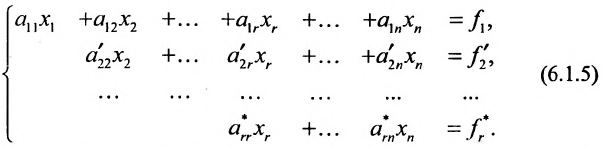
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
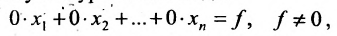 , то это означает, что система (6.1.1) несовместна.
, то это означает, что система (6.1.1) несовместна.
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 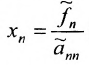 подставляем найденное значение
подставляем найденное значение 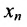 в предпоследнее уравнение системы (6.1.4) и находим значение
в предпоследнее уравнение системы (6.1.4) и находим значение 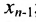 ; и т.д. двигаясь снизу вверх в системе (6.1.4) находим единственные значения неизвестных
; и т.д. двигаясь снизу вверх в системе (6.1.4) находим единственные значения неизвестных 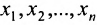 которые и определяют единственное решение системы (6.1.1). Построение решения системы (6.1.4) называют обратным ходом метода Гаусса.
которые и определяют единственное решение системы (6.1.1). Построение решения системы (6.1.4) называют обратным ходом метода Гаусса.
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного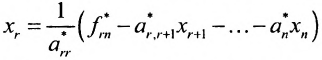 которое выражается через неизвестные
которое выражается через неизвестные 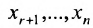 . Найденное выражение подставляем в предпоследнее уравнение системы (6.1.5) и выражаем неизвестное
. Найденное выражение подставляем в предпоследнее уравнение системы (6.1.5) и выражаем неизвестное 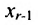 через неизвестные
через неизвестные 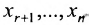 и т.д. Двигаясь снизу вверх в системе (6.1.5) находим выражения неизвестных
и т.д. Двигаясь снизу вверх в системе (6.1.5) находим выражения неизвестных 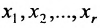 через неизвестные
через неизвестные 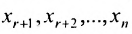 При этом неизвестные
При этом неизвестные 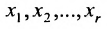 называются базисными неизвестными, а неизвестные
называются базисными неизвестными, а неизвестные 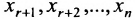 – свободными. Так как свободным неизвестным можно придавать любые значения и получать соответствующие значения базисных неизвестных, то система (6.1.5), а, следовательно, и система (6.1.1) в этом случае имеет бесконечное множество решений. Полученные выражения базисных неизвестных через свободные неизвестные называются общим решением системы уравнений (6.1.1).
– свободными. Так как свободным неизвестным можно придавать любые значения и получать соответствующие значения базисных неизвестных, то система (6.1.5), а, следовательно, и система (6.1.1) в этом случае имеет бесконечное множество решений. Полученные выражения базисных неизвестных через свободные неизвестные называются общим решением системы уравнений (6.1.1).
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 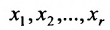 , начинающие уравнения ступенчатой системы, называются базисными, а остальные неизвестные – свободными.
, начинающие уравнения ступенчатой системы, называются базисными, а остальные неизвестные – свободными.
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности .
.
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 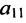 было не равно нулю:
было не равно нулю:

2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
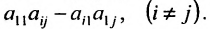
Матрица после первого шага примет вид
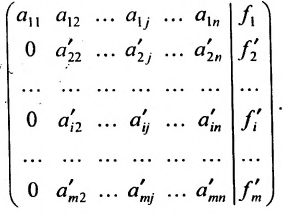
3. Выполните второй шаг метода Гаусса, предполагая, что 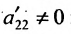 : во втором столбце начиная с третьей строки, запишите нули, а все другие элементы вычислите по формуле
: во втором столбце начиная с третьей строки, запишите нули, а все другие элементы вычислите по формуле
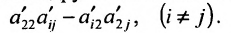
После второго шага матрица примет вид 
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида 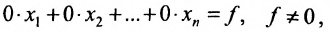
тогда данная система несовместна;
б) либо придём к матрице вида:
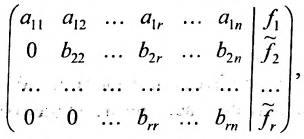
где 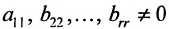 . Возможное уменьшение числа строк
. Возможное уменьшение числа строк 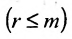
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
5.1. r=n:
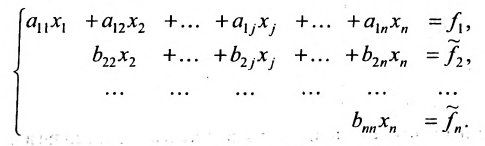
Система имеет единственное,решение 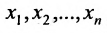 , которое находим из системы обратным ходом метода Гаусса. Из последнего уравнения находите
, которое находим из системы обратным ходом метода Гаусса. Из последнего уравнения находите 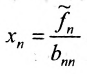 . Из предпоследнего уравнения находите
. Из предпоследнего уравнения находите 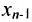 затем из третьего от конца –
затем из третьего от конца – 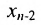 и т.д., двигаясь снизу вверх, найдём все неизвестные
и т.д., двигаясь снизу вверх, найдём все неизвестные 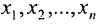 .
.
5.2.  :
:
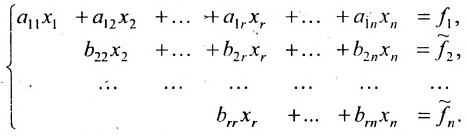
Тогда r неизвестных будут базисными, а остальные (n-r) – свободными. Из последнего уравнения выражаете неизвестное 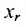 через
через 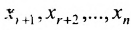 . Из предпоследнего уравнения находите
. Из предпоследнего уравнения находите 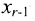 и т.д.
и т.д.
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
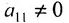 (если
(если 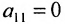 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 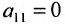 );
); - элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
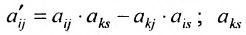 – разрешающий элемент (см. схему).
– разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 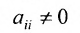 (диагональный элемент матрицы);
(диагональный элемент матрицы);
2) элементы разрешающей строки оставляем без изменения;
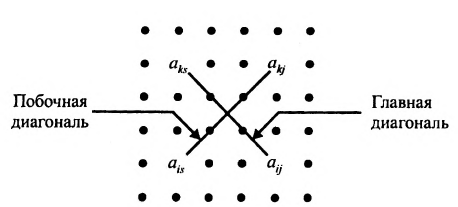
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
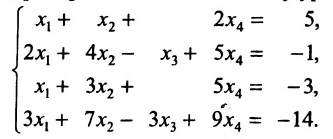
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 

Из последней матрицы находим следующее решение системы
уравнении: 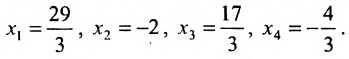
Ответ: 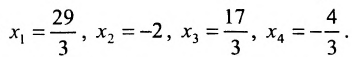
Пример:
Решить систему уравнений:
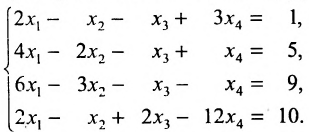
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
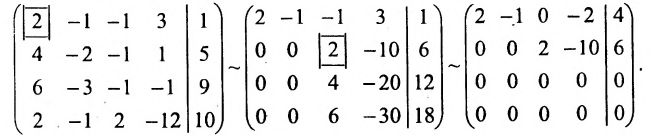
Система привелась к ступенчатому виду (трапециевидной форме):

в которой неизвестные 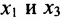 – базисные, а
– базисные, а 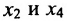 – свободные. Из второго уравнения системы (6.1.6) находим выражение
– свободные. Из второго уравнения системы (6.1.6) находим выражение 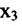 через
через 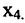 . Из первого уравнений найдём выражение
. Из первого уравнений найдём выражение 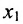 через
через 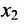 и
и 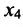 . Система имеет бесконечное множество решений. Общее решение системы имеет вид:
. Система имеет бесконечное множество решений. Общее решение системы имеет вид:
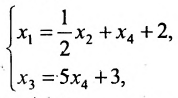
в котором 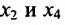 принимают любые значения из множества действительных чисел.
принимают любые значения из множества действительных чисел.
Если в общем решении положить 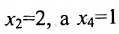 , то получим решение
, то получим решение 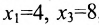 , которое называется частным решением заданной системы.
, которое называется частным решением заданной системы.
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде: 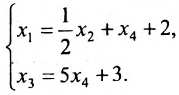
Пример:
Решить систему уравнений:
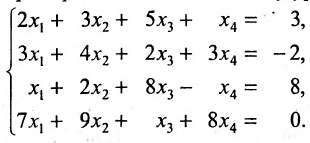
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
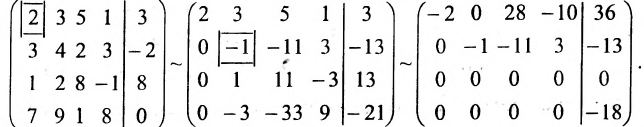 В последней матрице мы получили четвёртую строку, которая равносильна уравнению
В последней матрице мы получили четвёртую строку, которая равносильна уравнению 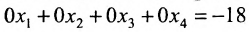 . Это означает, что заданная система не имеет решений.
. Это означает, что заданная система не имеет решений.
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 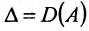 не равен нулю
не равен нулю 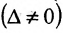 , то система имеет единственное решение, которое можно найти по формулам Крамера:
, то система имеет единственное решение, которое можно найти по формулам Крамера: 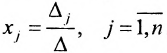 , где определитель
, где определитель 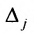 получен из определи-теля
получен из определи-теля 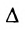 заменой j-ro столбца столбцом свободных членов.
заменой j-ro столбца столбцом свободных членов.
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 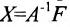 и оно является единственным.
и оно является единственным.
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа – единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева – единичную.
Пример:
Найти обратную матрицу для матрицы: 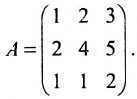
Решение:
Так как
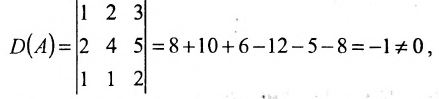
то обратная матрица существует. Составим расширенную мат-рицу и применим алгоритм полного исключения:
существует. Составим расширенную мат-рицу и применим алгоритм полного исключения:

тогда
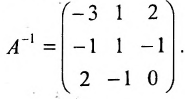
Покажем, что 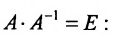
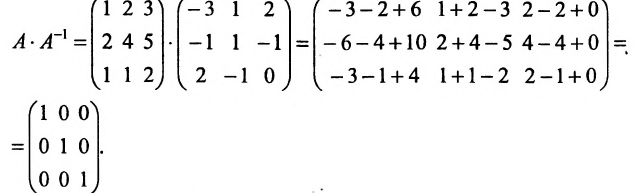
ответ 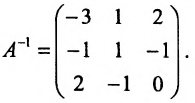
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 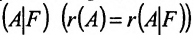 .
.
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 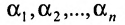 – какое-либо её решение (возможно единственное). По определению решения системы получаем:
– какое-либо её решение (возможно единственное). По определению решения системы получаем:
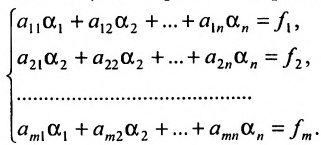
Из этих равенств следует, что последний столбец матрицы есть линейная комбинация остальных ее столбцов с коэффициентами
есть линейная комбинация остальных ее столбцов с коэффициентами 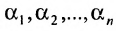 , то есть система вектор-столбцов матрицы
, то есть система вектор-столбцов матрицы 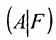 линейно зависима (свойство 3 п.2.5) и значит последний столбец матрицы
линейно зависима (свойство 3 п.2.5) и значит последний столбец матрицы 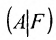 не изменяет ранга матрицы А, т.е.
не изменяет ранга матрицы А, т.е.
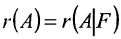 .
.
Достаточность. Пусть 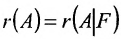 . Рассмотрим r базисных
. Рассмотрим r базисных
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 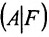 . В этом случае последний столбец матрицы
. В этом случае последний столбец матрицы 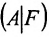 можно представить как линейную комбинацию базисных столбцов, а следовательно, и как линейную комбинацию всех столбцов матрицы А, то есть
можно представить как линейную комбинацию базисных столбцов, а следовательно, и как линейную комбинацию всех столбцов матрицы А, то есть
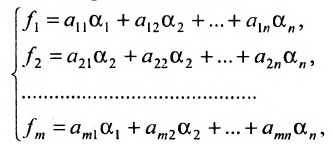
где  – коэффициенты линейных комбинаций. А это означает, что
– коэффициенты линейных комбинаций. А это означает, что  – решение системы (6.1.1), следовательно,
– решение системы (6.1.1), следовательно,
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 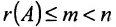 . Значит система неопределенная.
. Значит система неопределенная.
В случае 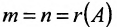 по теореме 6.2.2 получаем, что система имеет единственное решение. Так как
по теореме 6.2.2 получаем, что система имеет единственное решение. Так как 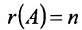 , то определитель
, то определитель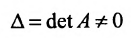 и квадратная матрица А имеет обратную x матрицу
и квадратная матрица А имеет обратную x матрицу 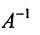 и её решение можно найти по формуле:
и её решение можно найти по формуле: 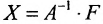 , где Х- столбец неизвестных, F— столбец свободных членов, или по формулам Крамера.
, где Х- столбец неизвестных, F— столбец свободных членов, или по формулам Крамера.
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
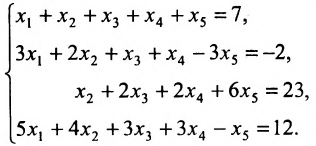
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса. 
Из последней матрицы следует, что ранг расширенной матрицы 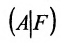 не может быть больше ранга матрицы А системы. Так как
не может быть больше ранга матрицы А системы. Так как
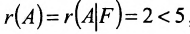 , то заданная система совместная и неопределённая.
, то заданная система совместная и неопределённая.
- Заказать решение задач по высшей математике
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 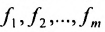 равны нулю, то есть система имеет следующий вид:
равны нулю, то есть система имеет следующий вид:
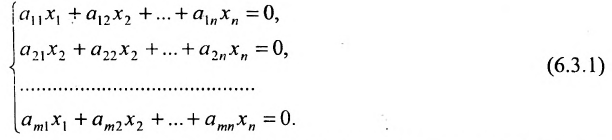
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
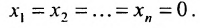
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r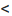 n).
n).
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 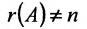 и так как он не может быль больше n то
и так как он не может быль больше n то 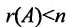 .
.
Достаточность. Если 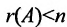 , то в силу теоремы 6.2.2 система (6.3.1) имеет бесчисленное множество решений. А так как только одно решение является нулевым, то все остальные решения ненулевые.
, то в силу теоремы 6.2.2 система (6.3.1) имеет бесчисленное множество решений. А так как только одно решение является нулевым, то все остальные решения ненулевые. 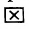
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию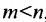 , то и
, то и 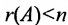 . Следовательно, в силу теоремы 6.3.1 система имеет ненулевые решения.
. Следовательно, в силу теоремы 6.3.1 система имеет ненулевые решения.
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 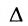 равнялся нулю.
равнялся нулю.
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
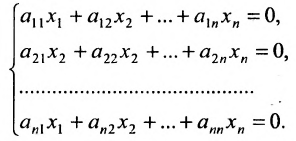 (6.3.2)
(6.3.2)
Если определитель матрицы системы 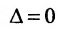 , то ранг матрицы
, то ранг матрицы 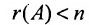 , тогда в силу теоремы 6.3.1 система (6.3.2) имеет ненулевое решение, так как условие
, тогда в силу теоремы 6.3.1 система (6.3.2) имеет ненулевое решение, так как условие 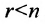 является необходимым и достаточным условием для существования ненулевого решения. Заметим, что если определитель матрицы системы (6.3.2) не равен нулю, то
является необходимым и достаточным условием для существования ненулевого решения. Заметим, что если определитель матрицы системы (6.3.2) не равен нулю, то 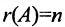 в силу теоремы 6.3.1 она имеет только нулевое решение.
в силу теоремы 6.3.1 она имеет только нулевое решение.
Пример:
Решить систему однородных линейных уравнений:
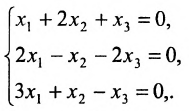
Решение:
Составим матицу системы и применим алгоритм полного исключения: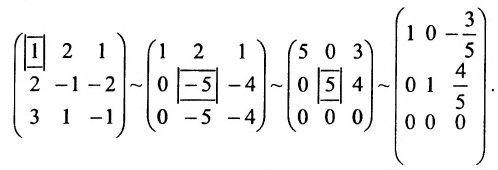
Из последней матрицы следует, что 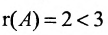 и система имеет бесчисленное множество решений.
и система имеет бесчисленное множество решений.
Используя последнюю матрицу, последовательно находим общее решение: 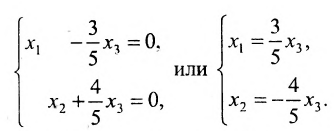
Неизвестные 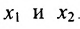 – базисные,
– базисные, 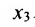 – свободная неизвестная,
– свободная неизвестная, 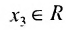 .
.
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
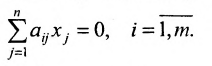 (6.4.1)
(6.4.1)
Любое решение
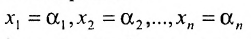
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку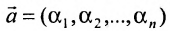 или как вектор-столбец
или как вектор-столбец 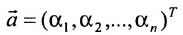 . Поэтому имеют смысл такие понятия, как сумма двух решений, произведение решения на число, линейная комбинация решений, линейная зависимость или независимость системы решений. Непосредственной подстановкой в систему (6.4.1) можно показать, что:
. Поэтому имеют смысл такие понятия, как сумма двух решений, произведение решения на число, линейная комбинация решений, линейная зависимость или независимость системы решений. Непосредственной подстановкой в систему (6.4.1) можно показать, что:
1) сумма двух решений также является решением системы, т.е.
если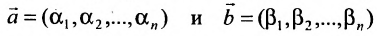 – решения системы
– решения системы
(6.4.1), то и 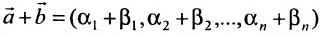 – решение системы (6.4.1);
– решение системы (6.4.1);
2) произведение решений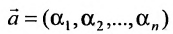 на любое число
на любое число 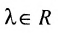 есть решение системы, т.е.
есть решение системы, т.е. 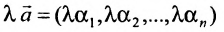 – решение системы.
– решение системы.
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)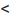 n), то система (6.4.1) имеет бесконечное множество фундаментальных систем решений, причём каждая из них состоит из n-r решений и любые n-r линейно независимые решения составляют фундаментальную систему.
n), то система (6.4.1) имеет бесконечное множество фундаментальных систем решений, причём каждая из них состоит из n-r решений и любые n-r линейно независимые решения составляют фундаментальную систему.
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
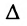 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули. - Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
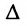 , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных. - Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель  , можно получать всевозможные фундаментальные системы решений.
, можно получать всевозможные фундаментальные системы решений.
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
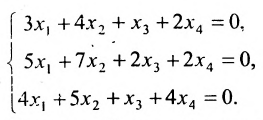
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
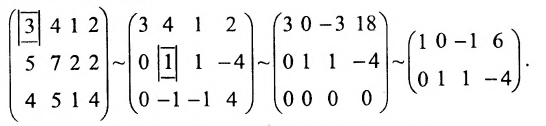
Для последней матрицы составляем систему:
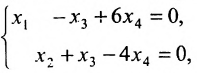 ,
,
, из которой находим общее решение:
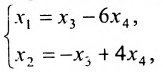
в котором 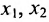 — базисные неизвестные, а
— базисные неизвестные, а 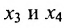 – свободные неизвестные.
– свободные неизвестные.
Построим фундаментальную систему решений. Для этого выбираем определитель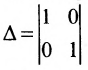 и свободным неизвестным придаём поочерёдно значения, равные элементам первой, а затем второй строк, т.е. положим вначале
и свободным неизвестным придаём поочерёдно значения, равные элементам первой, а затем второй строк, т.е. положим вначале 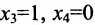 и получим из общего решения
и получим из общего решения 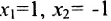 ; затем полагаем
; затем полагаем 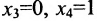 , из общего решения находим:
, из общего решения находим: 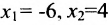 .
.
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 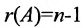 то
то 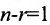 , и значит, фундаментальная система состоит из одного решения. Следовательно, любое ненулевое решение образует фундаментальную систему. В этом случае любые два решения различаются между собой лишь числовыми множителями.
, и значит, фундаментальная система состоит из одного решения. Следовательно, любое ненулевое решение образует фундаментальную систему. В этом случае любые два решения различаются между собой лишь числовыми множителями.
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 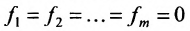 , то полученная однородная система называется приведенной для системы (6.1.1).
, то полученная однородная система называется приведенной для системы (6.1.1).
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
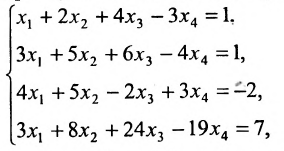
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
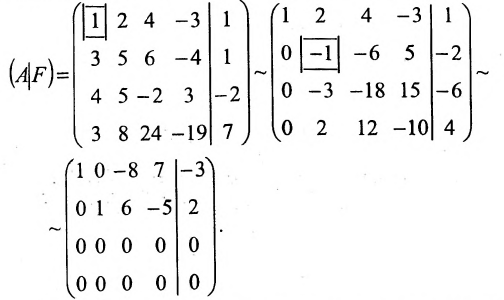 ,
,
Преобразованной матрице соответствует система уравнений:
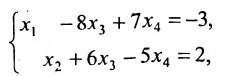
из которой находим общее решение системы:

, где 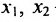 — базисные неизвестные, а
— базисные неизвестные, а 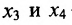 – свободные неизвестные.
– свободные неизвестные.
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 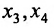 в общее решение системы нули, получаем частное решение исходной системы:
в общее решение системы нули, получаем частное решение исходной системы: 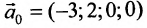 .
.
Очевидно, что общее решение приведенной системы имеет вид:

Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:

где 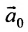 – • некоторое решение (вектор-строка) системы (6.1.1);
– • некоторое решение (вектор-строка) системы (6.1.1);
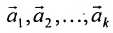 – фундаментальная система решений системы (6.4.1);
– фундаментальная система решений системы (6.4.1);
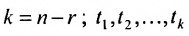 – любые действительные числа.
– любые действительные числа.
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 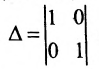 и придадим поочерёдно свободным неизвестным значения, равные элементам строк. Пусть
и придадим поочерёдно свободным неизвестным значения, равные элементам строк. Пусть 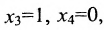 тогда из общего решения (6.4.3) приведенной системы находим
тогда из общего решения (6.4.3) приведенной системы находим 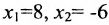 ; если же
; если же 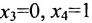 , то
, то 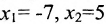 . Следовательно, фундаментальную систему решений образуют решения:
. Следовательно, фундаментальную систему решений образуют решения: 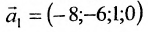 и
и 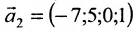 . Тогда общее решение заданной системы в векторной форме имеет вид:
. Тогда общее решение заданной системы в векторной форме имеет вид: 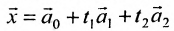 , где
, где 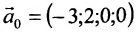 – частное решение заданной системы;
– частное решение заданной системы; 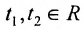 .
.
Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
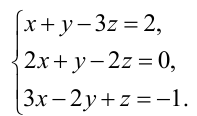
Решение:
Выпишем расширенную матрицу данной системы 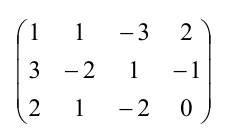 и произведем следующие элементарные преобразования над ее строками:
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: 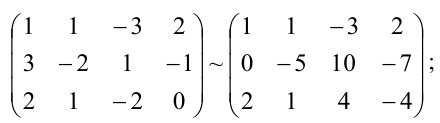
б) третью строку умножим на (-5) и прибавим к ней вторую: 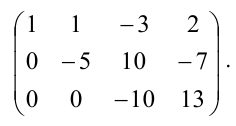
В результате всех этих преобразований данная система приводится к треугольному виду: 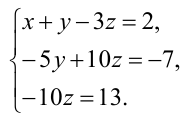
Из последнего уравнения находим 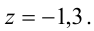 Подставляя это значение во второе уравнение, имеем
Подставляя это значение во второе уравнение, имеем 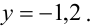 Далее из первого уравнения получим
Далее из первого уравнения получим 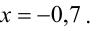
Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
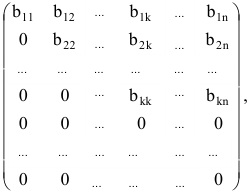
где все диагональные элементы 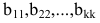 отличны от нуля. Тогда ранг полученной матрицы равен рангу исходной матрицы и равен k.
отличны от нуля. Тогда ранг полученной матрицы равен рангу исходной матрицы и равен k.
Пример:
Найти ранг матрицы
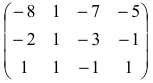
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
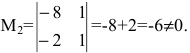 Существуют два минора третьего порядка, окаймляющих минор
Существуют два минора третьего порядка, окаймляющих минор 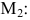
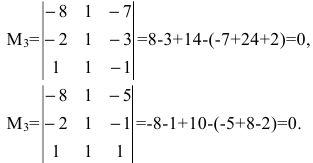 Т.к. миноры третьего порядка равны нулю, ранг матрицы равен двум. Базисным минором является, например, минор
Т.к. миноры третьего порядка равны нулю, ранг матрицы равен двум. Базисным минором является, например, минор 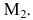
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим: 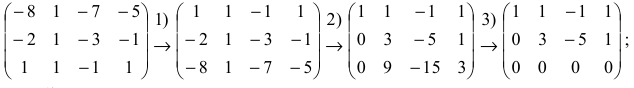
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ
Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.
Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.
У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.
Определения и обозначения
Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.
Для начала систематизируем знания о системах линейных уравнений.
СЛАУ в зависимости от её элементов может иметь:
- Одно решение;
- много решений;
- совсем не иметь решений.
В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.
Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:
- перемена мест уравнений системы;
- почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
- сложение к обеим частям одного из уравнений определённых частей другого уравнения.
Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.
Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:
где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.
Если =
=
=
, тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.
Множественные числа ,
,
называются решением СЛАУ, если при подстановке
,
,
в СЛАУ получим числовые тождества.
Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:
– это основная матрица СЛАУ.
– матрица столбец неизвестных переменных.
– матрица столбец свободных членов.
Если к основной матрице добавить в качестве
– ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой
, а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:
Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.
Если с системой уравнений:
Произвести такие действия:
тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.
Теперь можно перейти непосредственно к методу Гаусса.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Простейшие преобразования элементов матрицы
Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:
Из уравнения запишем расширенную матрицу:
Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.
Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.
На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:
1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:
.
2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).
3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.
4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.
5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:
Для удобства умножаем первую строку на (-3):
Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:
В итоге получилось такое преобразование:
Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:
В матрице верхняя строка преобразовалась:
Первую строку делим на и преобразовалась нижняя строка:
И верхнюю строку поделили на то же самое число :
Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.
Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:
.
Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.
Алгоритм решения методом Гаусса пошагово
После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:
Шаг 1. Переписываем систему в виде матрицы
Записываем матрицу:
Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю
Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на
.
Шаг 3. Приводим матрицу к ступенчатому виду
Теперь вторую строку можно поделить на 2 и получается:
Верхнюю строку делим на и приводим матрицу к ступенчатому виду:
Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.
Шаг 4. Записываем эквивалентную систему
После наших элементарных преобразований получилась эквивалентная система:
Шаг 5. Производим проверку (решение системы обратным путём)
Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:
находим :
,
,
.
После находим
:
,
.
Тогда:
.
Как видим, уравнение решено правильно, так как ответы в системе совпадают.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений
Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.
Дана система уравнений:
Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.
Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную
:
Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим
. И последнее, находим первое уравнение
.
Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.
Когда выражается через
и
в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:
- берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на
,
- берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на
.
И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:
Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:
В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно
, чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.
Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.
В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.
Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений
Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.
Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.
В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:
1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.
Например, вам попалась подобная система:
У нас получается такая ситуация
Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.
Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.
2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где
– число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло
вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:
Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:
В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных
,
и
, и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.
3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной
. Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной
. Если же
уже исключались, тогда переходим к
,
и т. д.
Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :
Такая система уравнений после преобразования выглядит так:
Вы наверное уже обратили внимание, что вместе с исключились
и
. Поэтому решение методом Гаусса продолжаем исключением переменной
из всех уравнений системы, а начнём мы с третьего уравнения:
Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:
Допусти, что система уравнений стала:
В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:
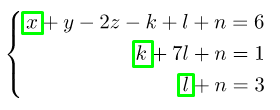
В нашем примере это ,
и
. В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:
Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: ,
,
, где
,
,
– произвольные числа.
Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.
В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении:
, а из первого уравнения получаем:
=
=
В итоге, получился результат, который можно и записать.
Ответ
,
,
,
,
,
.
Примеры решения методом Гаусса
Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.
Задача
Решить систему линейных алгебраических уравнений методом Гаусса:
Решение
Выписываем матрицу, куда добавляем столбец свободных членов:
Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:
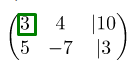
Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой
превратился в
. Для этого можно ко второй строке прибавить первую строку и умножить на
.Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на
(разрешающий элемент данного шага).
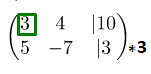
Соответственно, первая строка остаётся неизменной, а вторая поменяется:
Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на
и только после этого ко второй строке прибавить изменённую после умножения на
вторую строку. Вот что получилось:
. Теперь прибавляем со второй строки
первую строку
. У нас получился
, который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:
Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.
Итак, у нас получился ступенчатый вид матрицы:
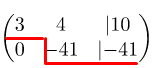
Записываем новую систему уравнений:
Для проверки решаем систему обратным ходом. Для этого находим сначала :
Так как найден, находим
:
.
Подставляем в изначальную нашу систему уравнений найденные и
:
и
.
Как видите из решения, система уравнений решена верно. Запишем ответ.
Ответ
Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.
Задача
Решить систему уравнений методом Гаусса:
Решение
Составляем матрицу, куда вписываем и свободные члены:
Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку:
. В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем
, и
. Аналогично,
и
. И умножаем свободный член
. Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:
Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:
Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:
В результате получилась ступенчатая система уравнений:
Сначала находим :
,
.
Обратный ход:
Итак, уравнение системы решено верно.
Ответ
,
,
.
Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.
Задача
Решите систему уравнений методом Гаусса:
Решение
В уравнении , то есть
– ведущий член и пусть
≠ 0
Из данного уравнения составим расширенную матрицу:
Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: ,
,
. Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную
из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в
теперь стоит 0.
Поменяем вторую и третью строку местами и получим:
Получилось так, что =
b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную
из третьей и четвёртой строк:
Получилась такая матрица:
Также, учитывая, что =
, умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную
и получаем новую систему уравнений:
Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,
из третьего: =
=
=
второе уравнение находим: =
=
= 2,
из первого уравнения: =
.
Значит, решение системы такое: (1, 2, -1, -2).
Ответ
,
,
,
.
Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.
Задача
Решить систему уравнений методом Гаусса:
Решение
Записываем расширенную матрицу системы:
Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:
Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:
Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:
Получился ступенчатый вид уравнения:
Проверяем:
,
,
,
,
.
.
Ответ
,
,
.
Заключение
Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.
Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.
Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.
Литература для общего развития:
![]() Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.
Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.
![]() Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.
Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 февраля 2022 года; проверки требуют 15 правок.
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы[1].
История[править | править код]
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах».
Описание метода[править | править код]
Пусть исходная система выглядит следующим образом:
Её можно записать в матричном виде:
где
Матрица 

Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
где 
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных 
Тогда переменные 
Если хотя бы одно число 

Пусть 

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 


,
где 
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
| Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. |
Критерий совместности[править | править код]
Упомянутое выше условие 

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
| Теорема Кронекера — Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия:
|
Алгоритм[править | править код]
Блок-схема представлена на рисунке. Данный рисунок — адаптированный для написания программы на языке C/C++, где a — расширенная матрица, последний столбец в которой — столбец свободных членов. Количество строк — n.
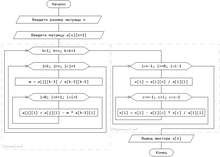
Алгоритм Гаусса для решения СЛАУ
Описание[править | править код]
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
- На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. Для этого среди элементов первого столбца матрицы выбирают ненулевой, перемещают содержащую его строку в крайнее верхнее положение, делая эту строку первой. Далее ненулевые элементы первого столбца всех нижележащих строк обнуляются путём вычитания из каждой строки первой строки, домноженной на отношение первого элемента этих строк к первому элементу первой строки. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают, пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
- На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует 
Этот метод опирается на:
| Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
Простейший случай[править | править код]
В простейшем случае алгоритм выглядит так:
- Прямой ход:
- Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Пример[править | править код]
Покажем, как методом Гаусса можно решить следующую систему:
Обнулим коэффициенты при 


Теперь обнулим коэффициент при 

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
из третьего;
из второго, подставив полученное
из первого, подставив полученные
и
.
Таким образом, исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
Реализация алгоритма на языке программирования C#[править | править код]
namespace Gauss_Method { class Maths { /// <summary> /// Метод Гаусса (Решение СЛАУ) /// </summary> /// <param name="Matrix">Начальная матрица</param> /// <returns></returns> public static double[] Gauss(double[,] Matrix) { int n = Matrix.GetLength(0); //Размерность начальной матрицы (строки) double[,] Matrix_Clone = new double[n, n + 1]; //Матрица-дублер for (int i = 0; i < n; i++) for (int j = 0; j < n + 1; j++) Matrix_Clone[i, j] = Matrix[i, j]; // Прямой ход (Зануление нижнего левого угла) for (int k = 0; k < n; k++) //k-номер строки { for (int i = 0; i < n + 1; i++) //i-номер столбца Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k]; //Деление k-строки на первый член !=0 для преобразования его в единицу for (int i = k + 1; i < n; i++) //i-номер следующей строки после k { double K = Matrix_Clone[i, k] / Matrix_Clone[k, k]; //Коэффициент for (int j = 0; j < n + 1; j++) //j-номер столбца следующей строки после k Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K; //Зануление элементов матрицы ниже первого члена, преобразованного в единицу } for (int i = 0; i < n; i++) //Обновление, внесение изменений в начальную матрицу for (int j = 0; j < n + 1; j++) Matrix[i, j] = Matrix_Clone[i, j]; } // Обратный ход (Зануление верхнего правого угла) for (int k = n - 1; k > -1; k--) //k-номер строки { for (int i = n; i > -1; i--) //i-номер столбца Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k]; for (int i = k - 1; i > -1; i--) //i-номер следующей строки после k { double K = Matrix_Clone[i, k] / Matrix_Clone[k, k]; for (int j = n; j > -1; j--) //j-номер столбца следующей строки после k Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K; } } // Отделяем от общей матрицы ответы double[] Answer = new double[n]; for (int i = 0; i < n; i++) Answer[i] = Matrix_Clone[i, n]; return Answer; } } }
Применение и модификации[править | править код]
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:
Достоинства метода[править | править код]
- Для матриц ограниченного размера — менее трудоёмкий по сравнению с другими методами.
- Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
- Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы[3].
Устойчивость метода Гаусса[править | править код]
Метод Гаусса для плохо обусловленных матриц коэффициентов является вычислительно неустойчивым. Например, для матриц Гильберта метод приводит к очень большим ошибкам даже при небольшой размерности этих матриц. Уменьшить вычислительную ошибку можно с помощью метода Гаусса с выделением главного элемента, который является условно устойчивым[4]. Широкое применение метода Гаусса связано с тем, что плохо обусловленные матрицы встречаются на практике относительно редко.
Неоптимальность метода Гаусса[править | править код]
В 1969 году Штрассен доказал, что большие матрицы можно перемножить за время 
См. также[править | править код]
- Метод Гаусса — Жордана
- Метод Крамера
- Система линейных алгебраических уравнений
- Теорема Кронекера — Капелли
- Фундаментальная система решений
- Элементарные преобразования матрицы
- Метод Гаусса (оптимизация)
- Метод покоординатного спуска (Гаусса — Зейделя)
- Метод Якоби
Примечания[править | править код]
- ↑ Н. Ш. Кремер, 2.3. «Метод Гаусса», стр. 44
- ↑ Такого расположения минора можно добиться перестановкой столбцов основной матрицы и соответствующей перенумерацией переменных.
- ↑ Н. Ш. Кремер, 2.4. «Система m линейных уравнений с n переменными», стр. 49
- ↑ УСТОЙЧИВОСТЬ И ТОЧНОСТЬ ПРЯМЫХ МЕТОДОВ (недоступная ссылка)
- ↑ Strassen V. Gaussian Elimination is not Optimal (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, Iss. 4. — P. 354—356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411
Литература[править | править код]
- И. М. Виноградов. Гаусса метод // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.|место = М. |издательство = Лаборатория Базовых Знаний |год = 2000 |страницы = |isbn =}}
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575—576.
- Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов / Под ред. Н. Ш. Кремера. — 3-е изд. — М.: ЮНИТИ-ДАНА, 2007. — 479 с. — ISBN 5-238-00991-7.
Ссылки[править | править код]
- Press, WH; Teukolsky, SA; Vetterling, WT & Flannery, BP (2007), Section 2.2, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8









