Пересечение двух плоскостей
Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей – так называемые общие точки.
Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ1
и γ2.
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.
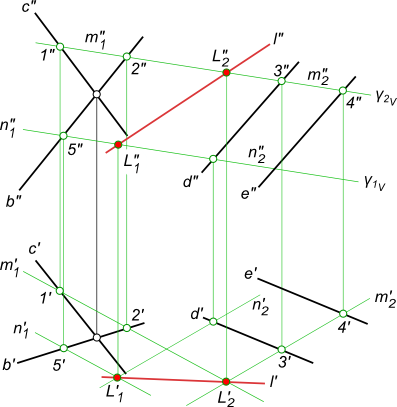
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей – линию l.
Определить линию пересечения l плоскостей заданных следами αH,
αV и βH, βV.
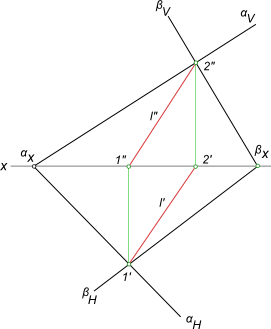
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV.
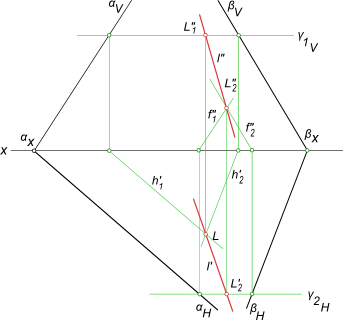
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV причем αV ║ βV.
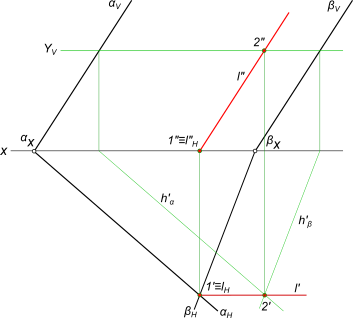
Пересечение двух плоскостей
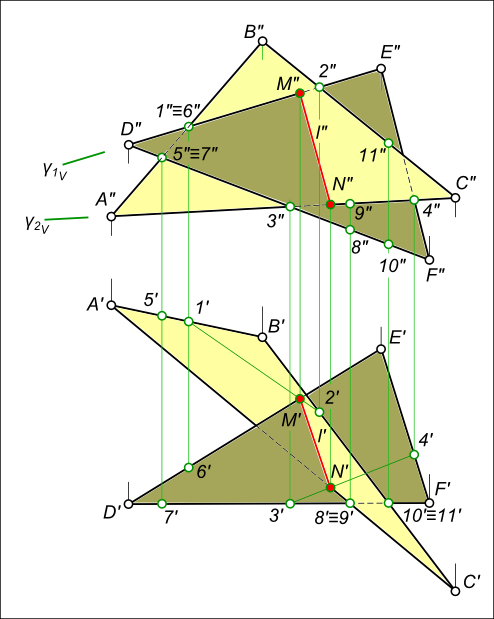
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии – точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии – точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.
Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций – 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` – будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций – 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ – будет видна вершина C с прилегающими сторонами до линии пересечения.
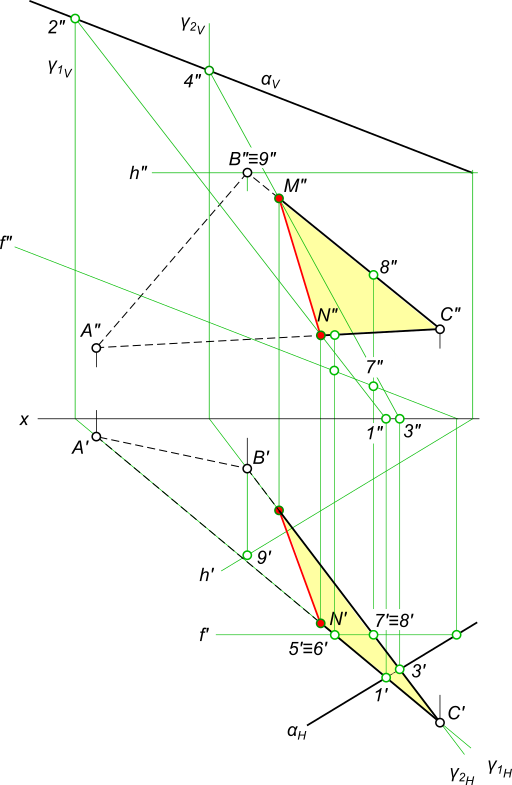
Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)
Пересечение двух плоскостей
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом
+
Параллельные плоскости.
Плоскости будут параллельными:
- если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 6);
- если плоскости параллельны, то параллельны их одноименные следы (рис. 7).


Плоскости пересекаются
Для построения линии пересечения двух плоскостей необходимо
- или найти две точки, каждая из которых принадлежит обеим плоскостям;
- или найти одну точку, принадлежащей двум плоскостям, и направление линии пересечения.
В обоих случаях задача заключается в нахождении точек, общих для двух плоскостей.
Плоскости в пространстве могут занимать различное положение. рассмотрим три случая построения линии их пересечения.
- Линия пересечения двух проецирующих плоскостей
Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронтальная проекция линии пересечения перпендикулярна оси проекций.

- Линия пересечения плоскости общего положения и проецирующей плоскости
В этом случае одна проекция линии пересечения совпадает с проекцией проецирующей плоскости на той плоскости проекций, которой она перпендикулярна.
На рис. 9 показано построение проекций линии пересечения горизонтально-проецирующей плоскости, заданной следами, c плоскостью общего положения (треугольник ABC).
На горизонтальной проекции (рис. 9) в пересечении следа плоскости PН и сторон АС и ВС треугольника АВС находим горизонтальные проекции n и m линии пересечения. По линиям связи находим фронтальные проекции точек M и N линии пересечения.
При взгляде по стрелке на плоскость V по горизонтальной проекции видно, что часть треугольника правее линии пересечения МN (mn) находится перед плоскостью Р, то есть будет видимой на фронтальной плоскости проекций. Остальная часть — за плоскостью Р, то есть невидима.

Линия пересечения двух плоскостей общего положения
Построение линии пересечения двух плоскостей общего положения осуществляется с помощью дополнительных плоскостей- посредников.
Общий прием построения линии пересечения таких плоскостей заключается в следующем. Вводим вспомогательную плоскость (посредник) и строим линии пересечения вспомогательной плоскости с двумя заданными. В пересечении построенных линий находим общую точку двух плоскостей. Чтобы найти вторую общую точку, повторяем построение с помощью еще одной вспомогательной плоскости.

Соединяем полученные точки М и N и определяем взаимную видимость фигур.

Задача. Построить линию пересечения двух плоских фигур, заданных треугольниками с координатами вершин:
ΔABC — A(16,2,0), B(10,9,7), C(1,4,3)
ΔDEF — D (5,9,0), E (16,1,5), F (9,1,9)
На рис. 11 дано построение линии пересечения двух треугольников. Решение выполняем в следующей последовательности. Проводим две вспомогательные горизонтально-проецирующие плоскости — плоскость P через сторону ED и плоскость Q через сторону DF треугольника DEF. Плоскость P пересекает треугольник ABC по прямой 1-2.
В пересечении фронтальных проекций 1′-2′ и d’e‘ находим фронтальную проекцию точки M(m’) линии пересечения. Плоскость Q пересекает треугольник ABC по прямой 3-4. В пересечении фронтальных проекций 3′-4′ и b‘c‘ находим фронтальную проекцию точки N(п’) линии пересечения. Горизонтальные проекции этих точек, а следовательно, и линии пересечения, находим, проводя линии связи.
Соединяем точки M и N. Взаимную видимость треугольников на плоскостях проекций определяем с помощью конкурирующих точек.


3. Так как прямые AB и MN лежат в одной плоскости P, то определяют точку их пересечения (точку K), которая является точкой пересечения прямой AB с плоскостью Q.
3.(•)K = (AB) ∩(MN)
4. Определяют взаимную видимость прямой AB и плоскости Q.
Задача: Определить точку пересечения прямой АВ с плоскостью треугольника СDE (рис. 5). Точки задаются координатами:
A(9,1,2), B(2,7,6), C(11,7,4), D(2,4,2), E(5,0,7)
Задачу решаем по выше рассмотренному плану.
• Через прямую AB проводим вспомогательную фронтальнопроецирующую плоскость P.
(AB) P V
• Строим линию пересечения (12) заданной плоскости Q (∆ CDE) и вспомогательной плоскости P.
(12) = P ∩Q( CDE)
• Так как прямые (AB) и (12) лежат


 в одной плоскости P, то определяем точку
в одной плоскости P, то определяем точку
их пересечения (точку K), которая являет-
ся точкой пересечения прямой AB с плос-
костью Q.
(•)K = (12)∩(AB)
|
• |
Определяем взаимную видимость |
|
|
прямой AB и плоскости Q. |
||
|
Для определения видимых участков |
||
|
прямой AB анализируем положение точек |
||
|
на скрещивающихся прямых (конкури- |
||
|
рующих точек). |
||
|
(•)1 CD |
(•)4 АВ |
|
|
(•)3 AB |
(•)5 СD |
|
|
Рис. 5 |
Y1 >Y3 |
Z4 > Z5 |
Взаимное положение двух плоскостей
Параллельные плоскости. Плоскости будут параллельными:
•если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 6);
•если плоскости параллельны, то параллельны их одноименные следы
(рис. 7).
33

Плоскости пересекаются
Для построения линии пересечения двух плоскостей необходимо
•или найти две точки, каждая из которых принадлежит обеим плоскостям;
•или найти одну точку, принадлежащей двум плоскостям, и направление линии пересечения.
Вобоих случаях задача заключается в нахождении точек, общих для двух плоскостей.
Плоскости в пространстве могут занимать различное положение. рассмотрим три случая построения линии их пересечения.
1.Линия пересечения двух проецирующих плоскостей




 Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронталь-
Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронталь- 



 ная проекция линии пересечения перпендикулярна оси проекций.
ная проекция линии пересечения перпендикулярна оси проекций.
Рис. 8
2. Линия пересечения плоскости общего положения и проецирующей плоскости
В этом случае одна проекция линии пересечения совпадает с проекцией проецирующей плоскости на той плоскости проекций, которой
34

|
она перпендикулярна. На рис. 9 по- |
|||
|
казано построение проекций линии |
|||
|
пересечения |
горизонтально- |
||
|
проецирующей плоскости, заданной |
|||
|
следами, c плоскостью общего по- |
|||
|
ложения (треугольник ABC). |
|||
|
На горизонтальной проекции |
|||
|
(рис. 9) в пересечении следа плоско- |
|||
|
сти PН и сторон АС и ВС треуголь- |
|||
|
ника АВС находим горизонтальные |
|||
|
проекции n и m линии пересечения. |
|||
|
По линиям связи находим фрон- |
|||
|
тальные проекции точек M и N ли- |
|||
|
нии пересечения. |
|||
|
Рис. 9 |
При взгляде по стрелке на |
||
|
плоскость V по горизонтальной про- |
|||
|
екции видно, что часть треугольника правее линии пересечения MN (mn) |
|||
|
находится перед плоскостью P, то есть будет видимой на фронтальной |
|||
|
плоскости проекций. Остальная часть − за плоскостью P, то есть неви- |
|||
|
дима. |
Линия пересечения двух плоскостей общего положения
Построение линии пересечения двух плоскостей общего положения осуществляется с помощью дополнительных плоскостейпосредников.
Общий прием построения линии пересечения таких плоскостей заключается в следующем. Вводим вспомогательную плоскость (посредник) и строим линии пересечения вспомогательной плоскости с двумя заданными. В пересечении построенных линий находим общую точку двух плоскостей. Чтобы найти вторую общую точку, повторяем построение с помощью еще одной вспомогательной плоскости.
(12) = Q ∩∆ABC
(34) = Q ∩∆EFK
(•)M = (12) ∩(34)
(56) = P ∩∆ABC
(78) = P ∩∆EFK
(•)N = (56) ∩(78)
Соединяем полученные точки М и N и определяем взаимную
видимость фигур.
Рис. 10
35

При решении подобных задач удобнее в качестве посредников применять проецирующие плоскости.
Задача. Построить линию пересечения двух плоских фигур, заданных треугольниками с координатами вершин:
∆ABC – A(16,2,0), B(10,9,7), C(1,4,3)
∆DEF – D(5,9,0), E(16,1,5), F(9,1,9)
На рис. 11 дано построение линии пересечения двух треугольников. Решение выполняем в следующей последовательности. Проводим
две вспомогательные горизонтально-проецирующие плоскости − плоскость P через сторону ED и плоскость Q через сторону DF треугольника DEF. Плоскость P пересекает треугольник ABC по прямой 1-2. В пересечении фронтальных проекций 1′-2′ и d′e′ находим фронтальную проекцию точки M(m′) линии пересечения. Плоскость Q пересекает треугольник ABC по прямой 3-4. В пересечении фронтальных проекций 3′-4′ и b′c′ находим фронтальную проекцию точки N(n′) линии пересечения. Горизонтальные проекции этих точек, а следовательно, и линии пересечения, находим, проводя линии связи.
Соединяем точки M и N. Взаимную видимость треугольников на плоскостях проекций определяем с помощью конкурирующих точек.
1.(ED) P H
2.(12) = P ∩ ∆ABC 3.(•)M = (12) ∩(ED)
4.(FD) Q H
5.(34) = Q ∩∆ABC 6.(•)N = (34) ∩(FD)
36

Лекция5.Поверхности
Способы задания поверхности
Существуют различные способы задания поверхности.
1. Аналитический способ
Поверхность в этом случае описана математическим выражением и представляется как геометрическое место точек или линий, удовлетворяющих уравнению F(x, y, z) = 0.
Например, поверхность шара задана уравнением: x2+y2+z2=r2. 2. Задание поверхности каркасом.
Этот способ используется при задании сложных поверхностей. Поверхность задается семейством линий, принадлежащих поверхности (каркасом). Каркасы могут быть сетчатые, линейчатые, точечные.
При задании поверхности каркасом необходимо иметь ряд ее параллельных сечений, которые можно рассматривать как положения образующей переменного вида. Такой способ применяется при изготовлении кузовов автомобилей, в самолетостроении и судостроении.
Способ задания поверхности каркасом с помощью линий пересечения поверхности плоскостями уровня применяется в топографии, горном и дорожном деле. Проекции линии уровня на плоскость проекций с соответствующими отметками представляют собой карту рельефа местности. Поверхность, отнесенная к земной поверхности, называется топо-
графической (рис. 1).
Рис. 1
3. Кинематический способ
В начертательной геометрии поверхности рассматриваются как
|
множество последовательных по- |
|
|
Образующая |
ложений движущейся линии. Та- |
|
кой способ образования поверх- |
|
|
ности называется кинематиче- |
|
|
ским. |
|
|
Линия (кривая или прямая) |
|
|
Направляющая |
движется в пространстве и созда- |
|
ет поверхность. Она называется |
|
|
Рис. 2 |
37
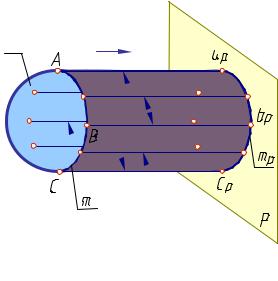
образующей. Как правило, образующая движется по второй линии. Эта линия называется направляющей (рис. 2).
Классификация поверхностей
Поверхности можно разделить на несколько классов в зависимости от формы образующей, а также от формы, числа и расположения направляющих:
1.Поверхности закономерные и незакономерные.
2.Линейчатые (образованные перемещением прямой линии) и нелинейчатые (криволинейные) поверхности.
3.Поверхности развертывающиеся (или торсы) и неразвертываю-
щиеся.
Развертывающиеся поверхности – поверхности, которые после разреза их по образующей могут быть односторонне совмещены с плоскостью без наличия разрывов и складок.
Неразвертывающиеся поверхности – поверхности, которые не мо-
гут быть совмещены с плоскостью без наличия разрывов и складок.
4.Поверхности с образующей постоянной формы и поверхности с образующей переменной формы.
5.Поверхности с поступательным, вращательным или винтовым движением образующей.
Задание поверхности на чертеже
Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов называется определи-
телем поверхности.
Определитель поверхности состоит из двух частей:
•геометрической части,
включающей постоянные геометри-
Ωl 
 ческие элементы (точки, линии), ко-
ческие элементы (точки, линии), ко-
|
торые участвуют в образовании по- |
||
|
верхности; |
||
|
• алгоритмической |
части, |
|
|
задающей закон движения обра- |
||
|
зующей, характер изменения ее |
||
|
формы. |
||
|
Когда какая-нибудь поверх- |
||
|
ность Ω проецируется с помощью |
||
|
Рис. 3 |
параллельных лучей на |
плоскость |
|
проекций P, то проецирующие пря- |
мые, касающиеся поверхности Ω, образуют цилиндрическую поверхность (рис. 3). Эти проецирующиеся
38

прямые касаются поверхности Ω в точках, образующих некоторую линию m, которая называется контурной линией.
Проекция контурной линии m на плоскость P, mp, называется очер-
ком поверхности.
Чтобы сделать чертеж более наглядным строят очерк поверхности, а также ее наиболее важные линии и точки.
Линейчатые поверхности
Гранные поверхности Гранной поверхностью называется поверхность, образованная пе-
ремещением прямолинейной образующей по ломаной направляющей. Гранные поверхности можно разделить на два вида: пирамидальные (рис. 4, а) и призматические (рис. 4, б).
Пирамидальная поверхность Призматическая поверхность
Рис. 4
Пирамидальной называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят через некоторую неподвижную точку S. Определитель поверхности – ломаная направляющая m и точка S.
Призматической называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят параллельно некоторому заданному направлению l. Определитель поверхности – ломаная направляющая m и направление l.
Точка на поверхности
Точка принадлежит поверхности, если она принадлежит какой-
нибудь линии, принадлежащей поверхности.
Линия принадлежит поверхности, если она проходит через точки,
принадлежащие поверхности.
Следовательно, если точка принадлежит поверхности, то ее проекции принадлежат одноименным проекциям линии этой поверхности.
39

Точки M и N принадлежат соответственно пирамидальной и призматической поверхностям, так как принадлежат прямым, расположенным на этих поверхностях.
Часть пространства, ограниченная со всех сторон поверхностью, называется телом.
Многогранники
Многогранником называется тело, ограниченное плоскими многоугольниками. Рассмотрим два многогранника – пирамиду и призму.
Пирамида представляет собой многогранник, у которого одна грань − основание (произвольный многоугольник). Остальные грани (боковые) − треугольники с общей вершиной S, называемой вершиной пирамиды.
Для задания на чертеже пирамиды достаточно задать ее основание и вершину. Чтобы построить проекции точки на поверхности пирамиды, нужно через эту точку провести вспомогательную прямую, принадлежащую поверхности пирамиды (рис. 5).
|
Ω – пирамида SABC. (•) М (m′) Ω. |
m – ? |
||||||
|
(•) М S1 |
(•) М 2–3 |
(•) М B4 |
|||||
Рис. 5
Призмой называется многогранник, у которого основания – равные многоугольники с соответственно параллельными сторонами. Боковые грани призмы − параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой (рис. 6), если нет – наклонной (рис. 7). Для задания призмы достаточно задать одно ее основание и боковое ребро. Чтобы построить недостающую проекцию точки, лежащей на грани призмы, нужно через эту точку провести прямую.
40

Σ – призма ABC. (•) М (m′) Σ. m – ?
Σ – призма ABC. (•) М (m′) Σ. m – ?
Пересечение многогранников плоскостями
В пересечении гранных поверхностей плоскостями получаются многоугольники. Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.
Многоугольник сечения может быть построен двумя способами:
1.Вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;
2.Стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.
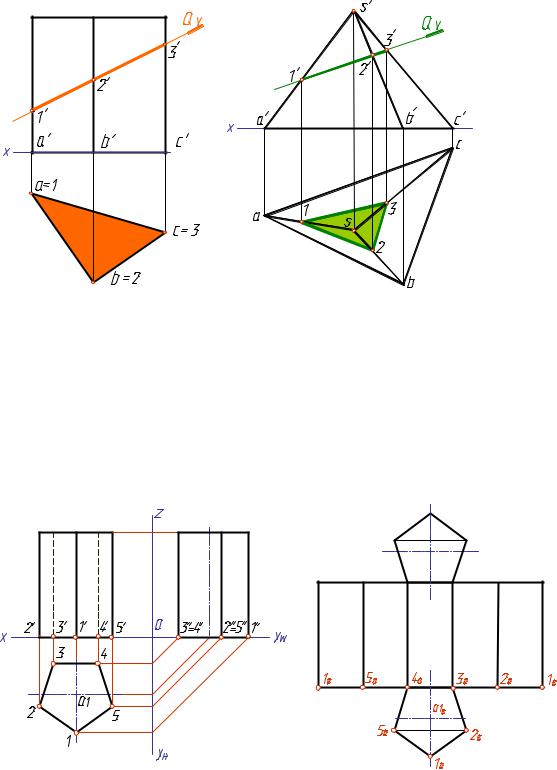
В качестве примера построим сечение призмы (рис. 8) и пирамиды (рис. 9) фронтально-проецирующими плоскостями.
Секущая плоскость является фронтально – проецирующей, следовательно, все линии, лежащие в этой плоскости (в том числе и фигура
сечения на фронтальной проекции), совпадут с фронтальным следом QV плоскости Q. Таким образом, фронтальные проекции фигур сечения
1′2′3′ определятся при пересечении фронтальных проекций ребер призмы и пирамиды со следом QV. Горизонтальные проекции точек 1, 2 и 3 находим при помощи линий связи на горизонтальных проекциях соответствующих ребер.
Грани прямой призмы на плоскость, которой они перпендикулярны, проецируются в линии, ребра – в точки. Поэтому все точки и линии, находящиеся на гранях и ребрах призмы проецируется соответственно на эти линии и точки. Проекция фигуры сечения призмы совпадает с горизонтальной проекцией самой призмы (рис. 8).
41
|
Ω – призма ABC. |
Q V |
|
|
Ω∩Q = |
123 |
|
|
Рис. 8 |
Ω – пирамида SABC. Q V
Ω∩Q = 123
Развертки многогранников Развертка поверхности призмы
При построении развертки поверхности любого многогранника все его грани располагают в одной плоскости. В результате построения развертки получают плоскую фигуру, в которой все грани многогранника сохраняют свою форму, натуральные размеры и последовательность расположения.
Рассмотрим построение развертки поверхности пятиугольной призмы (рис. 5.9).
Для построения развертки боковой поверхности проводим горизонтальную прямую линию, на которой откладываем пять отрезков, каждый из которых равен ширине грани или стороне пятиугольного основа-
42

ния. Можно взять величину этого отрезка с ортогонального чертежа, где сторона основания проецируется без искажения. Получаем точки 10…50. Затем из этих точек вверх проводим перпендикуляры (ребра боковой поверхности призмы), на которых откладываем высоту призмы, взятую на фронтальной или профильной проекции.
Далее строим два основания. Для этого через середину стороны грани 3040 (или любой другой) проводим центровую линию, на которую с горизонтальной проекции переносим расстояние от стороны 34 до центра О1 и вершины основания. Строим точку О10 и проводим вторую центровую линию основания. Для нахождения точек 20 и 50 на горизонтальной проекции точки 2 и 5 соединяем прямой линией. Измеряем расстояние от точки пересечения этой линии с центровой до стороны 34 и переносим это расстояние на соответствующую центровую линию на развертке. Проводим параллельно стороне 3040 прямую, на которую с горизонтальной проекции переносим расстояние от осевой линии до точек 2 и 5. Полученные точки 10 … 50 соединяем отрезками, получаем основание. Таким же образом строим второе основание.
Развертка поверхности правильной пирамиды
Так как боковые ребра правильной пирамиды равны между собой и все грани равнобедренные треугольники, то развертку боковой поверхности пирамиды начинаем строить с проведения дуги радиусом, равным размеру ребра боковой поверхности пирамиды (рис. 11).
На фронтальную и горизонтальную плоскости проекций ребра пирамиды проецируются с искажением, так как расположены наклонно относительно плоскостей H и V. На профильной плоскости проекций ребра S2 и S3 тоже проецируются с искажением, так как расположены наклонно к плоскости W, а ребро S1 проецируется в натуральную величину, потому что располагается параллельно плоскости W. Радиусом, равным
43
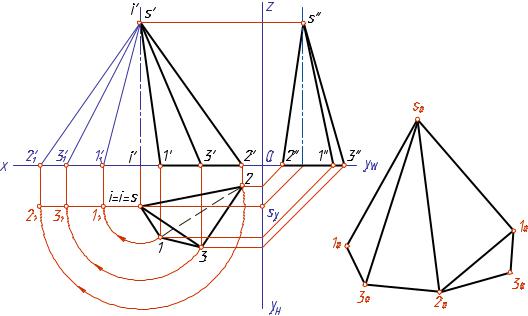
длине ребра S1 (s′′1′′), описываем дугу. На ней от произвольно выбранной точки откладываем три хорды, равные стороне основания. Размер стороны основания берем с горизонтальной проекции пирамиды. Затем для построения основания на развертке из точек 10 и 30 радиусом, равным стороне основания, проводим дуги до взаимного пересечения в точ-
ке 20. Развертка поверхности неправильной пирамиды
Развертка поверхности неправильной пирамиды будет состоять из неправильных треугольников боковой поверхности и неправильного треугольника, лежащего в основании, совмещенных в одну плоскость, причем их взаимное расположение на развертке должно соответствовать взаимному расположению на ортогональных проекциях. Так как у неправильной пирамиды стороны основания разные и ребра боковой поверхности не равны между собой, сначала находим натуральную величину всех боковых ребер (рис. 12).
Для этого используем один из способов определения натуральной величины отрезка прямой общего положения. В данном случае использован способ вращения. Боковые ребра вращаем вокруг оси, проведенной через вершину пирамиды S перпендикулярно плоскости Н. На чертеже
фронтальная проекция оси i′i′ проведена через фронтальную проекцию
вершины s′ перпендикулярно оси Ox. Горизонтальные проекции ребер s1, s2, и s3 поворачиваем до положения, параллельного оси Ox. При этом горизонтальные проекции точек 1, 2 и 3 займут положение 11, 21 и 31. От этих точек проводим линии проекционной связи на фронтальную плоскость проекций для получения их фронтальных проекций 1′1, 2′1 и 3′1. Затем фронтальные проекции точек соединяем с фронтальной проекцией
44

s′ вершины S прямыми линиями, которые и будут натуральными величи-
нами ребер (1′1s′, 2′1s′и 3′1s′).
Стороны основания 12, 23 и 13 спроецировались в натуральную величину на горизонтальную плоскость проекций. Зная натуральные величины всех элементов пирамиды, приступаем к построению развертки ее поверхности. При построении развертки боковой поверхности используем способ построения треугольников по трем заданным сторонам. Построение можно начать с любой грани боковой поверхности, например с грани 1S3 (рис. 5.12). Сначала на свободном месте чертежа проводим произвольную прямую и на ней откладываем натуральную величину стороны основания 1030, взятую с горизонтальной проекции. Затем из точки 10 радиусом, равным натуральной величине ребра S1 (s′1′1), а из точки 30 радиусом, равным натуральной величине ребра S3 (s′3′1), делаем засечки до пересечения в точке S0, которая будет вершиной развертки боковой поверхности пирамиды. Далее строим боковую грань 3S2. Для этого на фронтальной проекции циркулем измеряем натуральную величину ребра S2 (s′2′1) и на развертке этим радиусом из вершины S0, а из точки 30 радиусом 32, взятым с горизонтальной проекции, делаем засечки до пересечения в точке 20. Соединив точку 20 прямой линией с вершиной S0, получим вторую грань 30S020 боковой поверхности пирамиды. Третья грань и основание сроятся тем же способом.
Криволинейные поверхности
Коническая поверхность образуется движением прямолинейной образующей по криволинейной направляющей. При этом образующая проходит через некоторую неподвижную точку S, которая называется вершиной (рис. 13).
( m, s)
Рис. 13
Коническая поверхность определена на чертеже, если заданы направляющая и вершина. Тело, ограниченное конической поверхностью и плоскостью, называется конусом. Конус будет круговым, если в его основании лежит круг.
Точка N принадлежит конической поверхности, так как она принадлежит образующей f этой поверхности; nочка K принадлежит кониче-
45

|
ской |
поверхности, так как она принадлежит образующей S1 (k s1, |
|
|
k′s′1′) данной поверхности (рис. 13). |
||
|
Цилиндрическая поверхность образуется движением прямолиней- |
||
|
ной образующей параллельно заданной прямой линии l по криволиней- |
||
|
ной направляющей (рис. 14). |
||
|
( m, l) |
||
|
Рис. 14 |
||
|
Цилиндрическая поверхность определена, если задана направляю- |
||
|
щая и образующая. Для построения чертежа цилиндрической поверхно- |
||
|
сти удобно выбирать в качестве направляющей линию пересечения ци- |
||
|
линдрической поверхности с плоскостью проекций или другой плоско- |
||
|
стью, ей параллельной. |
||
|
Цилиндрическая поверхность также может быть незамкнутой или |
||
|
замкнутой. Тело, ограниченное цилиндрической замкнутой поверхно- |
||
|
стью и двумя параллельными плоскостями, называется цилиндром. Ци- |
||
|
линдрические поверхности различают по виду нормального сечения, на- |
||
|
пример, круговой цилиндр, эллиптический цилиндр и т.д. |
||
|
Точка N принадлежит цилиндрической поверхности, так как она |
||
|
принадлежит образующей f этой поверхности; |
||
|
точка K принадлежит цилиндрической поверхно- |
||
|
сти, так как она принадлежит образующей, про- |
||
|
ходящей через точку 1 параллельно направлению |
||
|
S данной поверхности (рис. 14). |
||
|
Торс (поверхность с ребром возврата) обра- |
||
|
зуется движением прямолинейной образующей, |
||
|
касающейся во всех своих положениях некоторой |
||
|
Рис. 15 |
пространственной кривой, называемой ребром |
|
|
возврата (от франц. tors − витой, крученный). |
||
|
Ребро возврата m является направляющей торса. Торс состоит из |
||
|
двух полостей, разделенных ребром возврата (рис. 15). |
||
|
Если ребро возврата вырождается в точку, поверхность торса пре- |
||
|
вращается в коническую. В случае, когда ребро возврата вырождается в |
||
|
бесконечно удаленную точку, торсовая поверхность превращается в ци- |
||
|
линдрическую. |
||
|
46 |

Лекция6.Поверхности вращения
Поверхностью вращения называется поверхность, образованная вращением образующей вокруг неподвижной оси (рис. 1). Эта поверхность определяется на чертеже заданием образующей и оси вращения.
Рис. 1
Каждая точка образующей l описывает при своем вращении окружность, лежащую в плоскости, перпендикулярной оси вращения, с центром на оси. Эти окружности называются параллелями. Наибольшая из этих параллелей называется экватором, наименьшая − горлом.
Плоскость, проходящую через ось поверхности вращения, называют меридианальной. Линию ее пересечения с поверхностью – меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.
На чертеже ось вращения II располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.
Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности.
Цилиндр вращения
Цилиндром вращения называется поверхность, образованная вращением прямой вокруг параллельной ей оси.
Если ось цилиндра перпендикулярна горизонтальной плоскости проекций, то горизонтальные проекции точек, лежащих на его поверхно-
47

|
сти, будут расположены на окружности, в которую спроецируется ци- |
|||
|
линдр на горизонтальную плоскость Н (рис. 2). |
|||
|
Задача. Найти недостающие проекции точек M и K (рис. 2). |
|||
|
ϕ(l, II) |
|||
|
M (m′) |
|||
|
K(k) |
|||
|
m (m1 |
, m2 |
) – ? |
|
|
k′ (k′1 |
, k′2 |
) – ? |
|
|
Для того, чтобы найти горизонтальную проек- |
|||
|
цию точки М, проведем линию связи от фронталь- |
|||
|
ной проекции М(m′) до пересечения с горизонталь- |
|||
|
ной проекцией цилиндра (окружностью). Задача |
|||
|
имеет два ответа: точки m1 и m2. |
|||
|
Однозначно определить положение фронталь- |
|||
|
ной проекции точки К по одной только горизон- |
|||
|
тальной проекции k невозможно. По линии связи, |
|||
|
Рис. 2 |
проведенной от горизонтальной проекции этой точ- |
||
|
ки, на |
поверхности цилиндра может находиться |
||
|
бесчисленное множество точек. В этом случае необходима дополнитель- |
|||
|
ная информация о положении точки К. |
|||
|
При пересечении цилиндра вращения плоскостью, параллельной |
|||
|
оси вращения, в сечении получаются две прямые – образующие (рис. 3). |
|||
|
Если секущая плоскость перпендикулярна оси вращения, в резуль- |
|||
|
тате сечения получится окружность (рис. 4). |
|||
|
В общем случае, когда секущая плоскость наклонена к оси враще- |
|||
|
ния цилиндра, в сечении получается эллипс (рис. 5). |
|
Рис. 3 |
Рис. 4 |
Рис. 5 |
|||||||||||
48

|
Рис. 6 |
|||
|
Сечение цилиндра плоскостью |
|||
|
В общем случае построение |
|||
|
линии пересечения |
поверхности |
||
|
плоскостью заключается в нахож- |
|||
|
дении общих точек, то есть точек, |
|||
|
принадлежащих одновременно се- |
|||
|
кущей плоскости и поверхности. |
|||
|
Для нахождения этих точек |
|||
|
применяют способ |
дополнитель- |
||
|
Рис. 7 |
ных секущих плоскостей: |
||
|
1.Проводят дополнительную |
|||
|
плоскость. |
2.Строят линии пересечения дополнительной плоскости с поверхностью и дополнительной плоскости с заданной плоскостью.
3.Определяют точки пересечения полученных линий. Дополнительные плоскости проводят таким образом, чтобы они
пересекали поверхность по наиболее простым линиям.
Нахождение точек линии пересечения начинают с определения характерных (опорных) точек. К ним относятся
•верхние и нижние, левая и правая и точки границы видимости;
•точки, характеризующие данную линию пересечения (для эл-
липса − точки большой и малой осей).
Для более точного построения линии пересечения необходимо построить еще и дополнительные (промежуточные) точки.
Прямой круговой конус Сечение конуса плоскостью
В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии.
49

•Если секущая плоскость проходит через вершину конуса, в его сечении получается две прямые − образующие (треугольник) (рис. 8, а).
•В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (рис. 8, б).
Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 8, в, г, д) – в зависимости от величины угла наклона секущей плоскости.
•Эллипс получается в том случае, когда угол β наклона секущей плоскости меньше угла наклона α образующих конуса к его основанию
(0<β < α), т.е. когда плоскость пересекает все образующие данного конуса (рис. 8, в).
•Если углы α и β равны (то есть секущая плоскость параллельна
одной из образующих конуса), в сечении получается парабола
(рис. 8, г).
• Если секущая плоскость направлена под углом, который изменяется в пределах 90° β > α, то в сечении получается гипербола. В этом случае секущая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная
(рис. 8, д).
|
β |
α |
β |
β |
|
|
α |
α |
|||
|
б |
в |
г |
д |
|||||||||||||||||||||||||||||||
|
а |
Рис. 8
50

|
Точка на конусе |
||||
|
Для конуса наиболее простыми линиями |
||||
|
являются прямые (образующие) и окружности. |
||||
|
Горизонтальную проекцию точки A найдем |
||||
|
с помощью образующей. Проведем через точку A |
||||
|
и вершину конуса S вспомогательную фронталь- |
||||
|
но-проецирующую плоскость P(PV). Она пересе- |
||||
|
кает конус по двум образующимSM и SN. Их фрон- |
||||
|
тальные проекции совпадают. Строим горизон- |
||||
|
тальные проекции образующих. Затем проводим |
||||
|
через точку a′ линию связи. На пересечении ли- |
||||
|
нии связи и горизонтальных проекций образую- |
||||
|
щих определим горизонтальную проекцию точки. |
||||
|
Задача имеет два ответа: точки a1 |
и a2 (рис. 9). |
|||
|
(•)A SN |
или |
(•)A SM |
||
|
Горизонтальную проекцию точки B найдем, |
||||
|
построив окружность, на которой она лежит. Для |
||||
|
этого через точку |
проведем |
горизонтальную |
Рис. 9 |
|
|
плоскость T(TV), которая пересекает конус по ок- |
||||
|
ружности радиуса r. |
(•)B Окр r
Строим горизонтальную проекцию этой окружности. Через точку b′ проведем линию связи до ее пересечения с окружностью. Задача также
|
имеет два ответа − точки b1 и b2. |
||||
|
Рассмотрим пример построения проекций линии пересечения ко- |
||||
|
нуса фронтально – проецирующей плоскостью P(PV). В этом случае в се- |
||||
|
чении получается |
эллипс |
|||
|
(рис. 10). |
||||
|
Сначала |
определим |
|||
|
характерные |
(опорные) |
|||
|
точки. |
||||
|
Фронтальная |
проек- |
|||
|
ция линии сечения совпа- |
||||
|
дает с фронтальным следом |
||||
|
P(PV ) конус= |
плоскости PV. Нижняя точ- |
|||
|
ка 1 лежит на образующей |
||||
|
AS, верхняя − 2 на обра- |
||||
|
Рис. 10 |
зующей ΒS. Эти точки оп- |
|||
|
ределяют положение боль- |
||||
|
шой оси эллипса. Малая |
||||
|
ось эллипса |
перпендику- |
51

Сечение шаровой поверхности плоскостью
Пересечем поверхность шара фронтально-проецирующей плоскостью Q(QV) (рис. 12). Построение начинаем с определения характерных точек.
(•)1,2 гл. меридиану
Точки 1 и 2 находятся на главном меридиане. Эти точки − концы малой оси эллипса, а также это самая высокая и самая низкая точки. Их
52
(•)A Окр. r
Рис. 11
Шаровой поверхностью (или сфе-
рой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.
Если шаровая поверхность пересе-
кается плоскостью, то в сечении всегда
получается окружность, которая может спроецироваться:
– в прямую, если секущая плоскость
перпендикулярна плоскости проекций;
– в окружность, если секущая плос-
кость параллельна плоскости проекций.
Например, окружность с радиусом r, равным расстоянию от оси вращения шара до очерка (рис. 11);
– в эллипс, если секущая плоскость не параллельна плоскости проекций.
Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находится эта точка.
лярна большой оси. Чтобы найти малую ось, разделим отрезок 1-2 на две равные части. Точки 3 и 4 определяют малую ось эллипса. Точки 5 и 6, расположенные на образующих CS и DS, являются точками границы видимости для профильной плоскости проекций. Проекции точек 1, 2, 5 и 6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек 3 и 4, проводим дополнительную секущую плоскость T(TV). Она рассекает конус по окружности радиуса r. На этой окружности находятся проекции данных точек. Для точного построения необходимо определить дополнительные (случайные точки). Проекции этих точек находим аналогично точкам 3 и 4 или проводя через эти точки образующие. Соединяем полученные проекции точек. Определяем видимость. На горизонтальной плоскости все точки, лежащие на поверхности конуса, видимы. На профильной − точки 5, 3, 1, 4, 6 видимы, остальные − нет.
Шаровая поверхность

горизонтальные и профильные проекции строим по фронтальным проекциям.
|
Рис. 12 |
(•)3,4 профильному очерку |
|
Точки 3 и 4 находятся на |
|
|
профильном меридиане и оп- |
|
|
ределяют видимость на про- |
фильной плоскости проекций. Горизонтальные проекции точек находим по профильным проекциям.
(•)5,6 экватору
Точки 5 и 6 принадлежат экватору и являются точками границы видимости на горизонтальной проекции. Профильные проекции точек находим по горизонтальным проекциям.
Чтобы найти положение большой оси эллипса (точки 7 и 8) разделим отрезок 1′2′ пополам. Фронтальные проекции точек (точки 7′ и 8′) совпадают с серединой этого отрезка. В этой же точке находится фронтальная проекция центра окружности сечения. На горизонтальную плоскость диаметр окружности проецируется без искажения. Поэтому точки 7 и 8 будут находиться на расстоянии R от центра окружности сечения
(рис. 12).
Для большей точности строим несколько дополнительных точек. Полученные точки соединяем плавной кривой линией с учетом ее
видимости.
Тор Тор − поверхность, полученная вращением окружности вокруг оси,
лежащей в плоскости этой окружности, но не проходящей через ее центр.
Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор − кольцо» (рис. 13); если ось касается окружности, поверхность называется «закрытый тор» (рис. 14 – 16). Тор, изображенный на рис. 15, называется также «тор-яблоко», а на рис. 16 – «тор-лимон». Сфера – частный случай торовой поверхности.
53

|
Рис. 13 |
Рис. 14 |
Рис. 15 |
Рис. 16 |
(•)А окр.r
Поверхности, образованные вращением кривых второго порядка:
а) эллипсоид вращения − поверхность, полученная вращением эллипса вокруг оси (рис. 17). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вра-
щения (рис. 17, б), при вращении вокруг малой оси − сжатым эллипсоидом вращения (рис. 17, а, в);
б) параболоид вращения − поверхность, образованная вращением параболы вокруг ее оси (рис. 18);
в) двухполостный гиперболоид вращения − поверхность, обра-
зованная вращением гиперболы вокруг ее действительной оси (рис. 19).
а
бв
54

Развертка поверхности цилиндра
Развертка поверхности цилиндра представляет собой развернутую боковую поверхность цилиндра и его оснований, совмещенных в одной плоскости (рис. 20).
Для ее построения проводим прямую линию, на которой откладываем отрезок, равный длине окружности основания (2πR). Из концов отрезка проводим перпендикулярные отрезки, равные высоте цилиндра, и полученные точки соединяем. К боковой поверхности цилиндра пристраиваем два основания, как показано на рис. 20, б.
Развертку боковой поверхности цилиндра можно выполнить приближенно, разделив окружность основания на 12 равных частей и отложив на прямой 12 хорд. Далее построение ведется, как описано выше.
|
а |
б |
|
Рис. 20 |
|
|
Развертка поверхности конуса |
Развертка боковой поверхности конуса представляет собой круговой сектор, у которого радиус равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. Если радиус окружности основания обозначить буквой R, длину образующей боковой поверхности – L, то угол сектора α можно определить по формуле α=360°×R/L. На рис. 21 показано построение развертки поверхности конуса. Сначала проводим дугу радиусом, равным длине образующей (L), которую берем с фронтальной или профильной проекции крайних образующих, потому что на эти плоскости проекций крайние образующие проецируются без искажения, так как они располагаются параллельно плоскостям проекций. Затем строим угол α, который определяем по приведенной выше формуле. Получаем сектор, являющийся развернутой боковой поверхностью конуса. К любой точке дуги сектора пристраиваем основание конуса.
55

Развертку боковой поверхности конуса можно выполнить приближенно, разделив окружность основания на 12 равных частей и отложив по дуге радиуса 12 хорд. Далее построение ведется, как описано выше.
Развертка поверхности шара
Сферическая поверхность относится к неразвертываемым поверхностям, и поэтому развертка поверхности шара может быть выполнена только приближенными способами. Рассмотрим один из способов выполнения развертки шара.
Для выполнения развертки поверхности шара поверхность делят меридианами на равные части. На рис. 22, а шар разделен на 12 равных частей. Представим себе, что все 12 частей поверхности шара отогнуты от полюсов и поставлены в вертикальное положение. Сферическая поверхность условно развернется как цилиндрическая поверхность, состоящая из 12 вертикально расположенных секций. Если эти секции разместить в одной плоскости, то получится приближенная развертка поверхности шара, рис. 22, б.
Для построения 12 меридианов очерковые окружности шара на горизонтальной и фронтальной проекциях делят на 12 равных частей. На горизонтальной проекции меридианы спроецируются в отрезки, проходящие через центр проекции шара. Фронтальные проекции этих меридианов будут кривыми, и их строят с помощью параллелей, проведенных через точки деления фронтального меридиана.
Для построения развертки достаточно знать размеры одной секции. На рис. 22, а выделена одна такая секция, на проекциях которой отмечены точки пересечения двух меридианов, являющихся ее сторонами, с па-
56

раллелями. Так как экватор делит секцию на две одинаковые части (верхнюю и нижнюю). То точки взяты только на той части секции, которая расположена выше экватора.
Самый широкий участок секции расположен по экватору. Его ширина равна 2πR/12, то есть 1/12 части экватора. Длина выпрямленной секции равна πR, то есть длине половины развернутого меридиана.
При развертке поверхности шара экватор развернется в отрезок, длина которого будет равна 2πR. Построение начинают с проведения прямой, на которой откладывают 12 отрезков, равных 2πR/12. На рис. 22, б показано построение только части развертки поверхности шара, так как все секции одинаковы.
Через середину построенных отрезков проводят оси симметрии перпендикулярно экватору. Затем вверх и вниз от экватора откладывают длину развернутых участков меридианов, заключенных между параллелями. Их длина равна 2πR/12. Через полученные точки параллельно экватору проводят прямые линии, на которых откладывают отрезки развернутых параллелей (3040, 5060). Эти отрезки равны 1/12 длины окружности, в которую проецируется соответствующая параллель на горизонтальной проекции. Построенные точки соединяют плавной кривой линией и обводят по лекалу.
Эту же развертку можно выполнить, заменяя развернутые дуги хордами, измеренными на ортогональных проекциях.
57

Лекция7.Винтовыеповерхности.Пересечениеповерхностей
Винтовая линия
Винтовая линия (гелиса) – это про- 


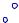
 странственная кривая, образованная движе-
странственная кривая, образованная движе- 
 нием точки, совершающей одновременно
нием точки, совершающей одновременно 
 поступательное и вращательное движение.
поступательное и вращательное движение. 

 Рассмотрим цилиндрическую винто-
Рассмотрим цилиндрическую винто- 



 вую линию (рис. 1) и построим две ее про-
вую линию (рис. 1) и построим две ее про- 
 екции.
екции.
Для этого используем две проекции
цилиндра, каждую из которых делим на
двенадцать равных частей. При перемеще-
нии точки из первого положения во второе
ее горизонтальная проекция перемещается
по окружности на одну двенадцатую часть,
а фронтальная – вверх на одну двенадцатую.
|
Совершая полный оборот, точка в |
|
|
пространстве опишет винтовую линию. Вы- |
|
|
Рис. 1 |
сота, на которую поднимается точка по |
|
прямой за полный оборот, называется ша- |
|
|
гом винтовой линии. Если ось винтовой ли- |
|
|
нии перпендикулярна горизонтальной плоскости проекций, то горизон- |
|
|
тальная проекция винтовой линии есть окружность, а фронтальная – си- |
|
|
нусоида. |
|
|
На одной поверхности цилиндра может быть несколько винтовых |
|
|
линий. |
Винтовые поверхности
Винтовой поверхностью называется поверхность, образованная при перемещении какой-либо линии (образующей) по винтовой линии (направляющей).
Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или гели-
коидом (от франц. helic − спираль, винтовая линия). Геликоид называется прямым или наклонным в зависимости от того, перпендикулярна образующая оси геликоида или наклонна.
Рассмотрим некоторые виды линейчатых винтовых поверхностей. 1.Прямой геликоид образуется движением прямолинейной образующей l по двум направляющим. Одна из направляющих является цилинд-
рической винтовой линией m, а другая − ее осью II. Причем во всех своих положениях образующая l параллельна плоскости, которая называется
58

плоскостью параллелизма, перпендикулярной оси II (рис. 2). У прямого геликоида образующая l пересекает ось II под прямым углом.
2. Наклонный геликоид отличается от прямого геликоида тем, что его образующая l пересекает ось геликоида под постоянным углом α, не равным прямому углу. Во всех своих положениях образующая l параллельна образующим некоторого конуса вращения. У этого конуса угол
между образующей и осью, параллельной оси геликоида, равен ϕ. Он на-
зывается направляющим конусом наклонного геликоида (рис. 3).
Его направляющими являются цилиндрическая винтовая линия m и ее ось II. Образующие геликоида параллельны соответствующим образующим направляющего конуса.
Если образующие геликоида пересекают его ось, то геликоид на-
зывается закрытым, если нет – открытым.
3. Открытый геликоид образуется при винтовом движении прямолинейной образующей l, касающейся во всех свих положениях поверхности малого цилиндра и параллельно плоскости параллелизма, проведенной перпендикулярно оси геликоида (рис. 4).
59
Соседние файлы в папке Винокурова ИГ и НГ
- #
- #
- #
- #
- #
- #
- #
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
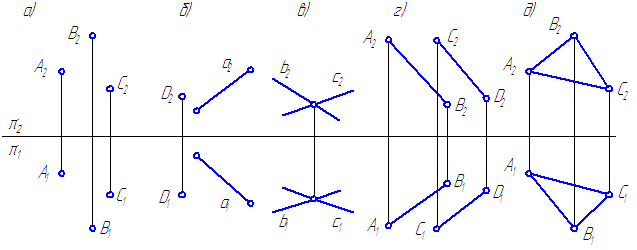
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.

Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
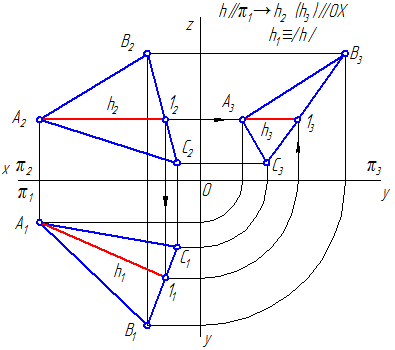
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
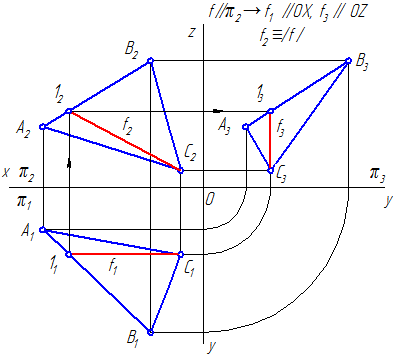
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
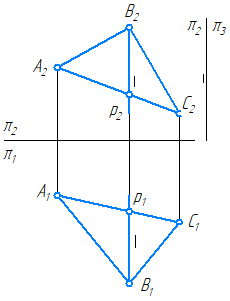
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
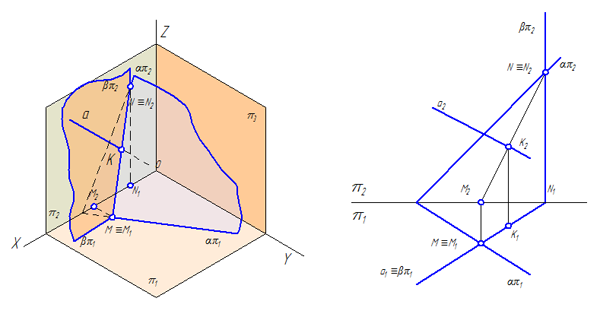
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
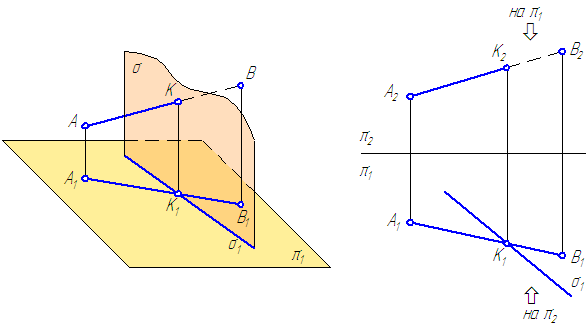
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей. 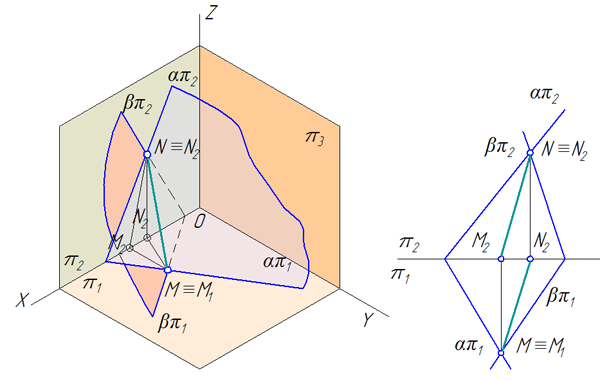
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
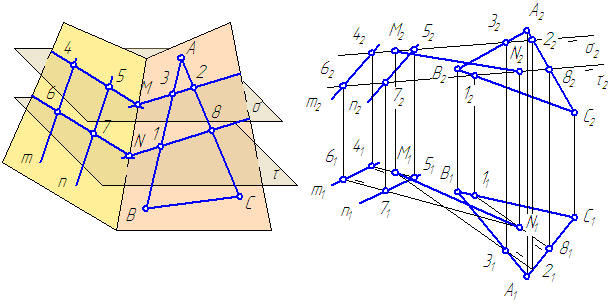
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
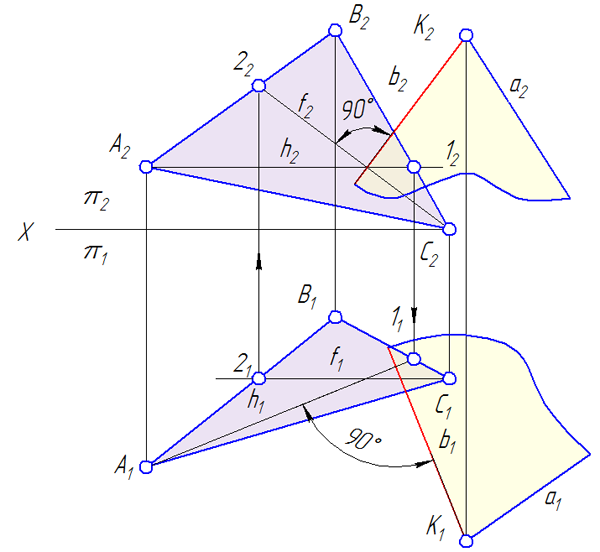
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.

Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).

Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
Содержание:
Взаимное положение плоскостей:
Две плоскости могут быть: 1) параллельными; 2 ) пересекающимися.
Основным признаком параллельности плоскостей является параллельность двух пересекающихся прямых одной плоскости двум пересекающимся прямым другой плоскости. Например, плоскость, заданная пересекающимися прямыми 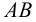
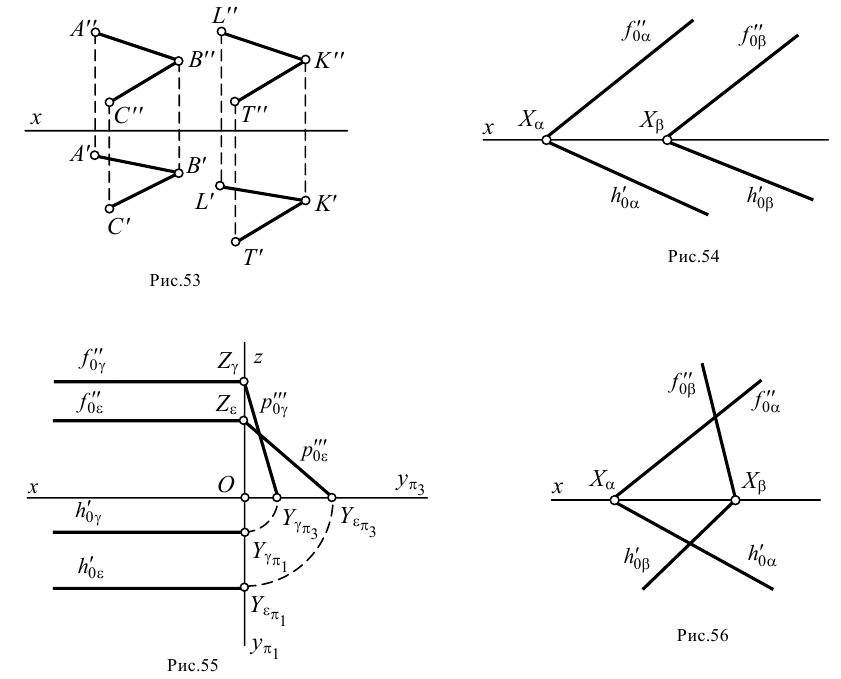
Такими прямыми могут служить и следы плоскостей: если два следа одной плоскости параллельны одноименным следам другой плоскости, то такие плоскости взаимно параллельны (рис.54). Исключением из этого правила являются проецирующие плоскости, т.е. плоскости, перпендикулярные одной из плоскостей проекций. На рис.55 изображены профильно-проецирующие плоскости 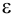 и
и 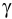 , горизонтальные и фронтальные следы которых параллельны между собой, а профильные – пересекаются. Следовательно, плоскости
, горизонтальные и фронтальные следы которых параллельны между собой, а профильные – пересекаются. Следовательно, плоскости  и
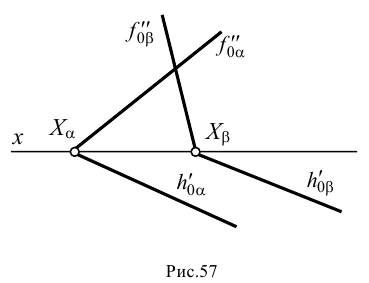
и  также пересекаются. Таким образом, если хотя бы одна пара одноименных следов двух плоскостей пересекается, то эти плоскости пересекаются (рис.56 и 57).
также пересекаются. Таким образом, если хотя бы одна пара одноименных следов двух плоскостей пересекается, то эти плоскости пересекаются (рис.56 и 57).
Пример 10. Построить следы плоскости р, проходящей через данную точку К и параллельной плоскости а (рис.58).
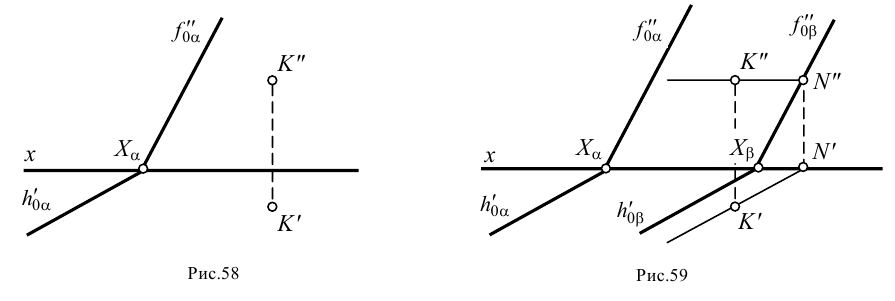
1. Через заданную точку 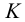 проводим любую прямую частного положения, например горизонталь (рис.59) искомой плоскости: фронтальная проекция горизонтали проходит через проекцию
проводим любую прямую частного положения, например горизонталь (рис.59) искомой плоскости: фронтальная проекция горизонтали проходит через проекцию 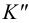 и параллельна оси
и параллельна оси 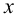 ; горизонтальная проекция горизонтали проходит через
; горизонтальная проекция горизонтали проходит через 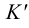 и параллельна горизонтальному следу
и параллельна горизонтальному следу 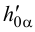 заданной плоскости.
заданной плоскости.
2. Строим проекции фронтального следа этой горизонтали: горизонтальная проекция фронтального следа (точка 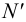 ) лежит в пересечении горизонтальной проекции горизонтали с осью
) лежит в пересечении горизонтальной проекции горизонтали с осью 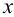 ; фронтальная проекция фронтального следа (точка
; фронтальная проекция фронтального следа (точка 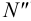 ) лежит в пересечении линии проекционной связи, проведенной из точки
) лежит в пересечении линии проекционной связи, проведенной из точки 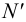 , и фронтальной проекции горизонтали.
, и фронтальной проекции горизонтали.
3. Через точку 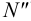 проводим фронтальный след
проводим фронтальный след 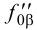 плоскости
плоскости 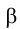 параллельно
параллельно 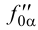 . В пересечении
. В пересечении 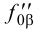 с осью
с осью 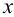 отмечаем точку схода следов
отмечаем точку схода следов 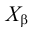 , через которую параллельно
, через которую параллельно 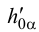 проводим след
проводим след 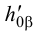 .
.
Линией пересечения двух плоскостей является прямая, все точки которой являются общими для обеих плоскостей. Таким образом, в общем случае для нахождения линии пересечения необходимо найти хотя бы две точки, общие для обеих плоскостей. Такими точками могут быть, например, точки пересечения одноименных следов плоскостей 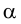 и
и 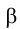 – точки
– точки 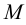 и
и 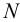 (рис.60). Через них и пройдет линия пересечения.
(рис.60). Через них и пройдет линия пересечения.
На эпюре проекции линии пересечения пройдут через точки пересечения одноименных следов плоскостей 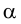 и
и 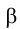 . В пересечении горизонтальных следов находим проекцию общей точки
. В пересечении горизонтальных следов находим проекцию общей точки 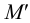 (фронтальная проекция этой точки
(фронтальная проекция этой точки 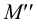 лежит на оси
лежит на оси 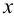 ), а в пересечении фронтальных следов -точки
), а в пересечении фронтальных следов -точки 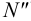 (горизонтальная проекция
(горизонтальная проекция 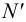 также лежит на оси
также лежит на оси 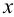 ). Соединив одноименные проекции
). Соединив одноименные проекции 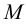 и
и 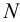 , получаем две проекции линии пересечения.
, получаем две проекции линии пересечения.
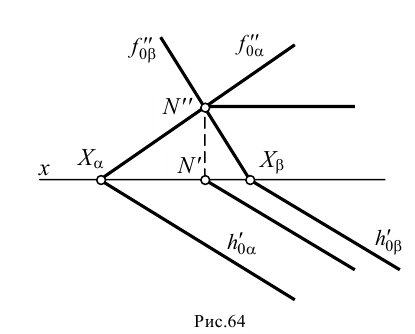
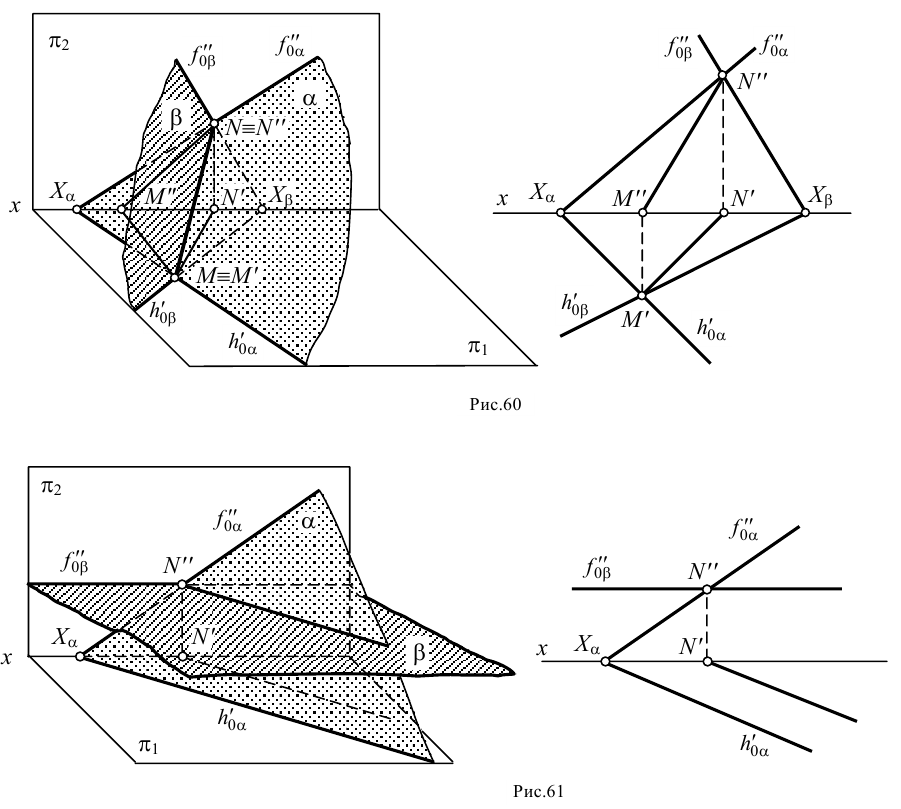
Но далеко не всегда на эпюре мы можем найти эти точки. Рассмотрим несколько примеров.
1. Пусть дана пара плоскостей, из которых одна – плоскость общего положения 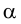 , а другая -горизонтальная плоскость
, а другая -горизонтальная плоскость 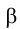 (рис.61). Одну общую точку – точку
(рис.61). Одну общую точку – точку 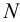 – найти легко в пересечении фронтальных следов.
– найти легко в пересечении фронтальных следов.
Поскольку плоскость 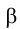 – горизонтальная, она параллельна плоскости проекция
– горизонтальная, она параллельна плоскости проекция 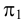 и, следовательно, не имеет горизонтального следа. Из школьного курса геометрии известно, что две параллельные плоскости пересекаются третьей плоскостью по параллельным прямым. Следовательно, линией пересечения плоскостей
и, следовательно, не имеет горизонтального следа. Из школьного курса геометрии известно, что две параллельные плоскости пересекаются третьей плоскостью по параллельным прямым. Следовательно, линией пересечения плоскостей 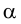 и
и 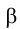 будет горизонталь.
будет горизонталь.
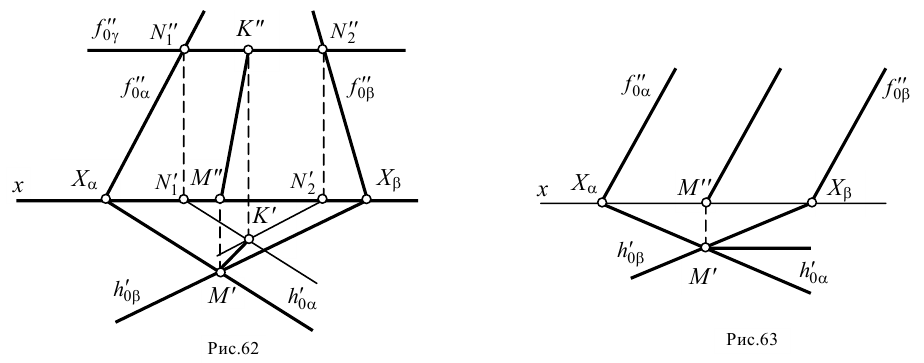
2. Теперь возьмем две плоскости общего положения 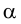 и
и 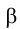 , у которых одноименные следы, например фронтальные, в пределах чертежа не пересекаются (рис.62).
, у которых одноименные следы, например фронтальные, в пределах чертежа не пересекаются (рис.62).
Первая общая точка – точка 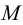 – находится в пересечении горизонтальных следов плоскостей
– находится в пересечении горизонтальных следов плоскостей 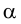 и
и 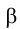 . Для нахождения второй общей точки выбираем произвольную вспомогательную плоскость, например горизонтальную плоскость
. Для нахождения второй общей точки выбираем произвольную вспомогательную плоскость, например горизонтальную плоскость 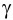 , и строим линии пересечения двух пар плоскостей:
, и строим линии пересечения двух пар плоскостей: 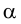 и
и 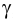 ;
; 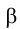 и
и 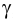 (см. п.1). Эти линии пересеклись в точке
(см. п.1). Эти линии пересеклись в точке 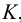 , которая является общей для всех трех плоскостей. Теперь у нас есть точки
, которая является общей для всех трех плоскостей. Теперь у нас есть точки 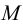 и
и 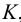 , общие для плоскостей
, общие для плоскостей 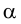 и
и 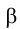 . Через эти точки можно провести линию пересечения двух этих плоскостей.
. Через эти точки можно провести линию пересечения двух этих плоскостей.
3. Если фронтальные следы двух плоскостей параллельны, то линией их пересечения будет фронталь (рис.63). В этом легко убедиться, если воспользоваться вспомогательной горизонтальной плоскостью, как в п.2.
По аналогии можно доказать, что если у пересекающихся плоскостей параллельны горизонтальные следы, то линией их пересечения будет горизонталь (рис.64).
Прямая, пересекающая плоскость
Прямая, пересекающая плоскость, имеет с ней одну общую точку, называемую точкой встречи прямой с плоскостью.
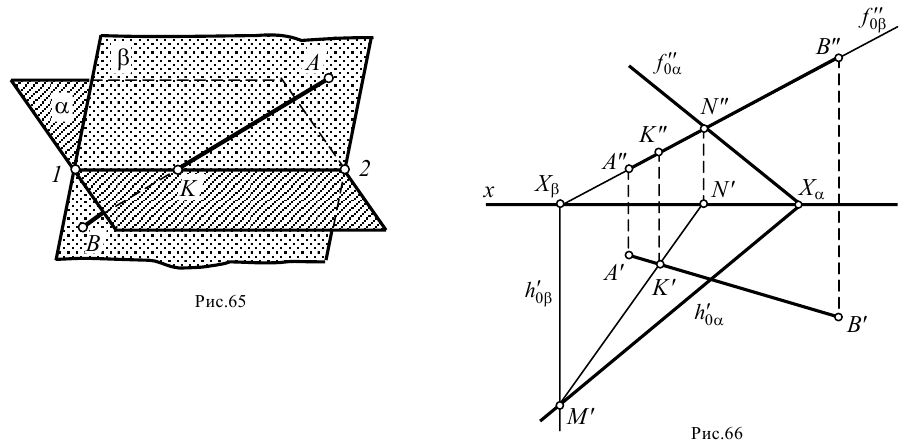
Рассмотрим задачу о нахождении точки встречи прямой линии с плоскостью в общем виде. Пусть нам дана плоскость 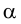 и прямая
и прямая 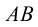 , ее пересекающая (рис.65). Проводим через прямую
, ее пересекающая (рис.65). Проводим через прямую 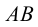 любую плоскость, например плоскость
любую плоскость, например плоскость 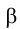 . Далее строим линию пересечения плоскостей
. Далее строим линию пересечения плоскостей 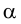 и
и 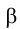 -прямую
-прямую  . Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка
. Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка 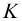 , лежащая на прямой
, лежащая на прямой 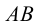 , принадлежит обеим плоскостям. Точка
, принадлежит обеим плоскостям. Точка 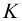 будет искомой точкой встречи прямой
будет искомой точкой встречи прямой 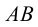 с плоскостью
с плоскостью  .
.
Рассмотрим порядок нахождения точки встречи прямой  с плоскостью
с плоскостью  на эпюре (рис.66):
на эпюре (рис.66):
- через заданную прямую
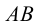 проводим любую вспомогательную плоскость (удобнее, если это будет плоскость частного положения – например, фронтально-проецирующая плоскость
проводим любую вспомогательную плоскость (удобнее, если это будет плоскость частного положения – например, фронтально-проецирующая плоскость 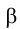 );
); - находим линию пересечения плоскостей
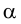 и
и 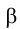 – прямую
– прямую 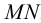 ;
; - горизонтальная проекция
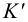 искомой точки встречи лежит в пересечении горизонтальных проекций прямой
искомой точки встречи лежит в пересечении горизонтальных проекций прямой 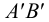 и линии пересечения
и линии пересечения 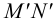 ;
; - в пересечении линии проекционной связи, проведенной из
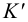 , и фронтальной проекции прямой получаем точку
, и фронтальной проекции прямой получаем точку 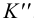 .
.
Определение взаимной видимости геометрических элементов
Взаимная видимость геометрических элементов определяет позиционное отношение одной геометрической фигуры (прямой, плоскости и т.д.) по отношению к другой в определенном направлении. Обычно это направление перпендикулярно плоскости проекций.
Взаимная видимость на эпюре определяется с помощью конкурирующих точек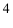 , которые выбирают на той плоскости проекций, в направлении на которую определяют взаимную видимость. Взаимная видимость в направлении на каждую из плоскостей проекций определяется отдельно.
, которые выбирают на той плоскости проекций, в направлении на которую определяют взаимную видимость. Взаимная видимость в направлении на каждую из плоскостей проекций определяется отдельно.
 См. раздел 2.5 «Взаимное положение двух прямых».
См. раздел 2.5 «Взаимное положение двух прямых».
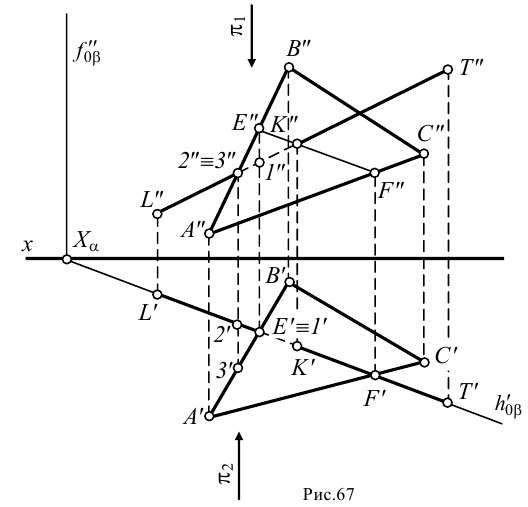
Рассмотрим определение взаимной видимости прямой 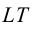 и плоскости, заданной треугольником
и плоскости, заданной треугольником 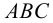 (рис.67). Будем считать треугольник непрозрачным. Прежде всего находим точку встречи прямой
(рис.67). Будем считать треугольник непрозрачным. Прежде всего находим точку встречи прямой 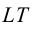 с плоскостью треугольника. Через прямую
с плоскостью треугольника. Через прямую 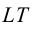 проводим вспомогательную плоскость
проводим вспомогательную плоскость 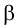 и строим линию пересечения плоскости
и строим линию пересечения плоскости 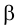 и плоскости треугольника
и плоскости треугольника 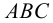 -прямую
-прямую 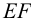 . Находим искомую точку
. Находим искомую точку 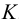 . Затем последовательно определяем взаимную видимость в направлении на плоскости проекций
. Затем последовательно определяем взаимную видимость в направлении на плоскости проекций 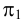 и
и 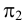 .
.
Для определения видимости в направлении на плоскость 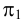 , выбираем конкурирующие точки, например
, выбираем конкурирующие точки, например 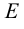 и
и 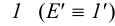 . Эти точки принадлежат разным геометрическим фигурам
. Эти точки принадлежат разным геометрическим фигурам 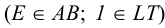 , но они расположены на одной проецирующей прямой, перпендикулярной плоскости
, но они расположены на одной проецирующей прямой, перпендикулярной плоскости 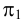 поэтому на эту плоскость они проецируются в одну точку. Находим фронтальную проекцию
поэтому на эту плоскость они проецируются в одну точку. Находим фронтальную проекцию 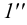 точки
точки 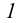 (проекция
(проекция 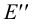 уже была найдена при предыдущих построениях).
уже была найдена при предыдущих построениях).
Из двух точек видимой будет та, фронтальная проекция которой расположена дальше от оси проекций. В нашем примере – это точка 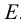 . Следовательно, на горизонтальной проекции видимой будет прямая
. Следовательно, на горизонтальной проекции видимой будет прямая 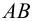 , принадлежащая плоскости треугольника, а отрезок прямой
, принадлежащая плоскости треугольника, а отрезок прямой 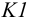 -«невидимым». В точке
-«невидимым». В точке 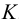 прямая
прямая 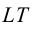 пересекает плоскость и отрезок
пересекает плоскость и отрезок 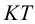 становится видимым.
становится видимым.
Для определения взаимной видимости в направлении на 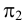 выбираем на ней проекции конкурирующих точек. Пусть это будут точки
выбираем на ней проекции конкурирующих точек. Пусть это будут точки 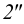 и
и 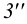
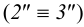 . Находим их горизонтальные проекции и определяем по ним взаимную видимость точек. Дальше от оси
. Находим их горизонтальные проекции и определяем по ним взаимную видимость точек. Дальше от оси 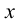 будет точка
будет точка 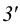 , принадлежащая
, принадлежащая 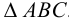 . Следовательно отрезок
. Следовательно отрезок 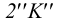 – «невидим».
– «невидим».
- Заказать чертежи
Проецирование плоских фигур. Пересечение плоских фигур
Плоской называют такую фигуру, все точки которой лежат в одной плоскости и ограничены линиями, составляющими контур этой фигуры. Простейшей плоской фигурой является многоугольник.
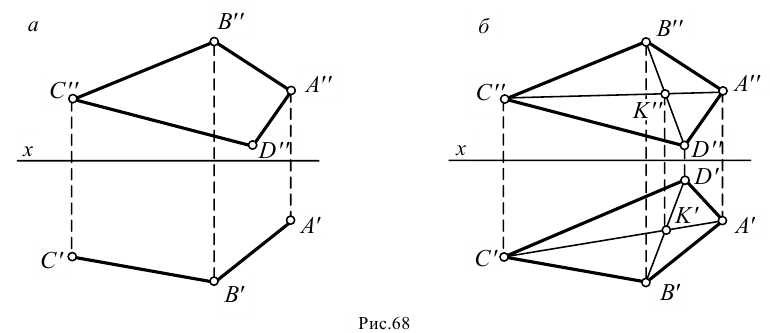
Для однозначного определения положения многоугольника в пространстве необходимо убедиться, чтобы все его точки находятся в одной плоскости.
Например, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис.68, а). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей (рис.68, б).
Линия пересечения двух плоских фигур, как и линия пересечения двух плоскостей, определяется двумя точками, общими для этих фигур. Такие точки могут быть найдены как точки пересечения сторон одной фигуры с плоскостью другой.
На рис.69 найдена линия пересечения треугольников 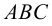 и
и 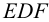 . Для этого выполнены следующие построения.
. Для этого выполнены следующие построения.
Сначала найдена точка 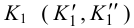 пересечения стороны
пересечения стороны 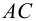 треугольника
треугольника 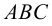 с плоскостью треугольника
с плоскостью треугольника 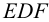 . Затем аналогично построена точка
. Затем аналогично построена точка 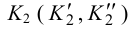 пересечения другой стороны, например стороны
пересечения другой стороны, например стороны 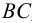 , с плоскостью треугольника
, с плоскостью треугольника 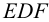 .
.
Для построения точки 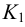 через сторону
через сторону 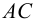 проведена вспомогательная фронтально-проецирующая плоскость
проведена вспомогательная фронтально-проецирующая плоскость 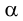 и построена прямая
и построена прямая 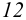 пересечения вспомогательной плоскости
пересечения вспомогательной плоскости 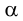 и треугольника
и треугольника 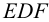 . На пересечении горизонтальных проекций
. На пересечении горизонтальных проекций 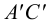 и
и 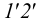 определена горизонтальная проекция
определена горизонтальная проекция 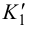 точки встречи. Ее фронтальная проекция
точки встречи. Ее фронтальная проекция 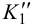 построена на фронтальной проекции
построена на фронтальной проекции 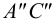 .
.
Для построения точки 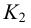 через сторону
через сторону 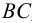 проведена горизонтально-проецирующая плоскость
проведена горизонтально-проецирующая плоскость 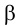 . Затем построена прямая
. Затем построена прямая  пересечения плоскости
пересечения плоскости 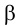 и треугольника
и треугольника 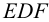 и на пересечении
и на пересечении 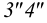 с
с 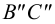 найдена фронтальная проекция
найдена фронтальная проекция 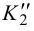 . Точка
. Точка 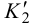 построена на горизонтальной проекции
построена на горизонтальной проекции 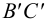 .
.
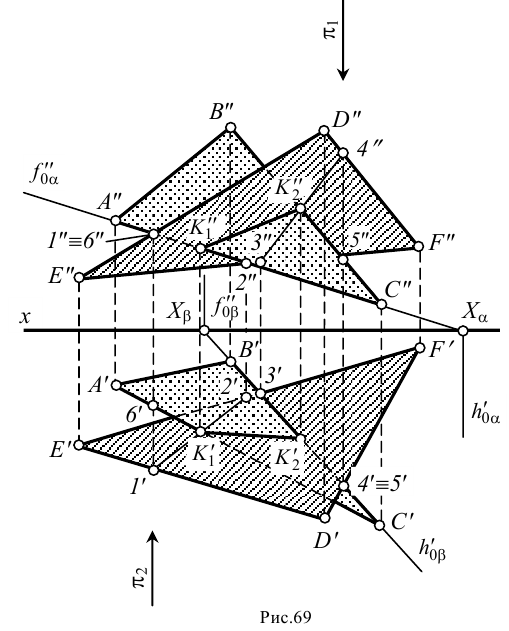
Зная две точки, общие для заданных плоскостей, проводим через них линию пересечения 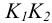 с проекциями
с проекциями 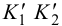 и
и 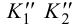 .
.
Определяем видимость плоскостей друг относительно друга с помощью конкурирующих точек, например, точек  и
и  – на горизонтальной плоскости проекций
– на горизонтальной плоскости проекций 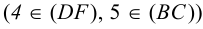 и точек
и точек 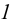 и
и 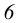 – на фронтальной плоскости проекций
– на фронтальной плоскости проекций 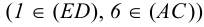 .
.
Прямая, перпендикулярная плоскости
Предположим, что дана некоторая плоскость 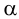 и прямая
и прямая 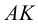 – перпендикуляр к этой плоскости, причем точка
– перпендикуляр к этой плоскости, причем точка 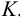 , лежащая в плоскости
, лежащая в плоскости 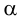 , является основанием перпендикуляра (рис.70). Если прямая
, является основанием перпендикуляра (рис.70). Если прямая 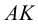 – перпендикуляр, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
– перпендикуляр, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
Через точку 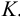 проводим горизонталь
проводим горизонталь 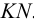 . Угол
. Угол 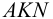 – прямой. По теореме о том, что прямой угол проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций, угол
– прямой. По теореме о том, что прямой угол проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций, угол 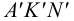 – тоже прямой.
– тоже прямой.
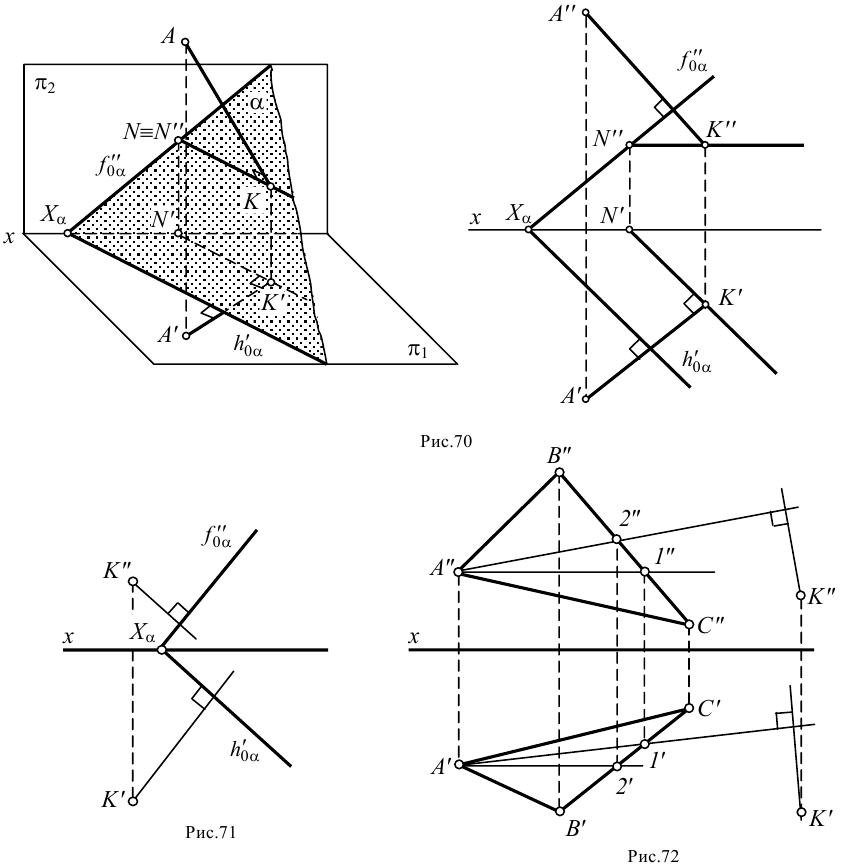
Таким образом, горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали и горизонтальному следу плоскости. Аналогично можно доказать, что фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали и фронтальному следу плоскости.
Пример:
Из точки 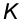 опустить перпендикуляр к плоскости, заданной следами (рис.71), и к плоскости, заданной треугольником (рис.72).
опустить перпендикуляр к плоскости, заданной следами (рис.71), и к плоскости, заданной треугольником (рис.72).
- Из точки
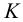 проводим перпендикуляр к плоскости
проводим перпендикуляр к плоскости 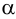 , заданной следами: горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости
, заданной следами: горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости 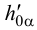 ; фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости
; фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости 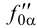 .
. - Из точки
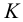 проводим перпендикуляр к плоскости, заданной треугольником
проводим перпендикуляр к плоскости, заданной треугольником 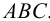 . Строим горизонталь
. Строим горизонталь 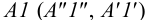 и фронталь
и фронталь 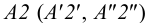 заданной плоскости. Из точки
заданной плоскости. Из точки 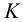 проводим перпендикуляр к заданной плоскости: горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали
проводим перпендикуляр к заданной плоскости: горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали 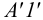 ; фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали
; фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали 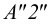 .
.
Взаимно перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.
Рассмотрим построение плоскости 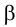 , перпендикулярной плоскости
, перпендикулярной плоскости 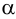 и проходящей через прямую
и проходящей через прямую 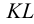 (рис.73). Из любой точки прямой
(рис.73). Из любой точки прямой 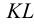 , например из точки
, например из точки 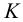 , проводим перпендикуляр к заданной плоскости
, проводим перпендикуляр к заданной плоскости 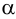 . Строим проекции следов прямой
. Строим проекции следов прямой 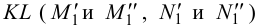 и перпендикуляра
и перпендикуляра 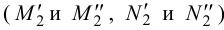 .
.
Через горизонтальные проекции горизонтальных следов 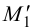 и
и 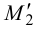 проводим горизонтальный след плоскости
проводим горизонтальный след плоскости 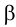 ; через фронтальные проекции фронтальных следов
; через фронтальные проекции фронтальных следов 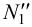 и
и 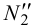 – ее фронтальный след. Проверяем правильность построений: следы
– ее фронтальный след. Проверяем правильность построений: следы 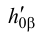 и
и 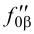 пересекаются в точке схода следов
пересекаются в точке схода следов  , на оси
, на оси  .
.
Таким образом, плоскость 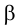 перпендикулярна плоскости
перпендикулярна плоскости 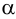 , так как проходит через прямую
, так как проходит через прямую 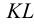 , перпендикулярную плоскости
, перпендикулярную плоскости 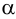 . Следует обратить внимание на то, что одноименные следы плоскостей
. Следует обратить внимание на то, что одноименные следы плоскостей 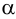 и
и 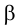 не перпендикулярны друг другу.
не перпендикулярны друг другу.
Действительно, одноименные следы двух взаимно перпендикулярных плоскостей общего положения не перпендикулярны друг другу. Наоборот, если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то сами плоскости не перпендикулярны между собой.
Если одна из рассматриваемых плоскостей является плоскостью частного положения, то существует несколько очевидных случаев, когда перпендикулярность следов может служить признаком перпендикулярности самих плоскостей. Например, перпендикулярность горизонтальных следов плоскости общего положения а и горизонтально-проецирующей плоскости 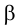 соответствует взаимной перпендикулярности этих плоскостей (рис.74). Это нетрудно доказать, выбрав в плоскости
соответствует взаимной перпендикулярности этих плоскостей (рис.74). Это нетрудно доказать, выбрав в плоскости 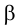 прямую
прямую 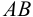 , перпендикулярную плоскости
, перпендикулярную плоскости 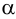 .
.
По аналогии с рассмотренным примером перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.
- Взаимное расположение точки, прямых и плоскостей
- Перпендикулярность геометрических объектов
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Поверхности вращения
- Пересечение прямой линии с поверхностью
- Построение линии пересечения поверхностей
- Проецирование прямой
