Уравнения прямых в пространстве
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями
в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости
и
пересекаются (см. условие (4.25)), поскольку их нормали
и
неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений
(4.31)
Система (4.31) называется общим уравнением прямой в пространстве.
Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту
треугольника.
Решение. Прямая является линией пересечения двух плоскостей: плоскости
, треугольника
и плоскости
, проходящей через точку
перпендикулярно вектору
(рис.4.26). По формуле (4.21) составим уравнение плоскости
проходящей через три точки
По формуле (4.14) составим уравнение плоскости , проходящей через точку
перпендикулярно вектору
Следовательно, общее уравнение (4.31) прямой имеет вид
Параметрическое уравнение прямой в пространстве
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном пространстве заданы точка
и ненулевой вектор
(рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору
и проходящей через точку
.
Выберем на прямой произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.28).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы
и
коллинеарны. Запишем условие коллинеарности:
, где
— некоторое действительное число (параметр). Учитывая, что
, получим векторное параметрическое уравнение прямой в пространстве:
(4.32)
где — направляющий вектор прямой, а
— радиус-вектор заданной точки
принадлежащей прямой.
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где — координаты направляющего вектора
прямой. Параметр
в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина
пропорциональна расстоянию от заданной точки
до точки
. Физический смысл параметра
в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки
по прямой. При
точка
совпадает с заданной точкой
. При возрастании параметра
движение происходит в направлении направляющего вектора.
Каноническое уравнение прямой в пространстве
Выразим параметр из каждого уравнения системы (4.33):
, а затем исключим этот параметр:
(4.34)
Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.
Замечания 4.6.
1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:
а) каноническое уравнение — это уравнение
прямой, параллельной оси аппликат (рис.4.29,а);
б) каноническое уравнение — это уравнение
прямой, параллельной координатной плоскости
(рис.4.29,б).
2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор
, где
, также является направляющим вектором для той же прямой.
Переход от общего уравнение к каноническому
3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1) найти любое решение системы
определяя тем самым координаты точки
, принадлежащей прямой;
2) найти направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей:
3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):
6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки
, а коэффициентам
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
, т.е. совокупность всех прямых, проходящих через точку
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис. 4.30). Требуется:
а) составить каноническое уравнение прямой, содержащей высоту треугольника;
б) составить общее уравнение прямой, содержащей биссектрису треугольника.
Решение. а) Общее уравнение прямой получено в примере 4.13:
Перейдем от общего уравнения к каноническому.
1) Найдем любое решение системы, например,
(это координаты точки
).
2) Найдем направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей
3) Запишем каноническое уравнение (4.34): .
б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор
этой прямой. Учитывая, что диагональ ромба является биссектрисой,
, где
и
— единичные векторы, одинаково направленные с векторами
и
соответственно. Находим
Составляем каноническое уравнение прямой .
Записывая двойное равенство в виде системы, получаем общее уравнение прямой
Расстояние от точки до прямой в пространстве
Найдем расстояние от точки
до прямой
, заданной каноническим уравнением (рис.4.31)):
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, то есть.
(4.35)
Уравнение прямой, проходящей через две заданные точки
Пусть в координатном пространстве заданы две точки
и
. Требуется составить уравнение прямой, проходящей через заданные точки.
Как показано в разд., точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию (рис.4.32):
, где
— некоторое действительное число (параметр). Это уравнение, а также его координатную форму
(4.36)
будем называть аффинным уравнением прямой, проходящей через две точки и
.
Выражая параметр из каждого уравнения системы (4.36), получаем:
. Исключая параметр
, приходим к уравнению прямой, проходящей через две точки
и
:
(4.37)
Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор
т.е. подставляя
Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.33). Требуется:
а) составить уравнение прямой ;
б) составить уравнение прямой, содержащей медиану треугольника;
в) найти высоту треугольника, опущенную на сторону
.
Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки
б) Находим координаты середины стороны
. Составляем уравнение (4.37) прямой
в) Искомую высоту находим по формуле (4.35), полагая
и
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.
Уравнение прямой в пространстве: общие сведения
Уравнение прямой на плоскости в прямоугольной системе координат Oxy – это линейное уравнение с переменными x и y, которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.
Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x, y, z, которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение Ax+By+Cz+D=0, где x, y, z – переменные, а А, В, С и D – некоторые действительные числа (А, В, С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат Oxyz? Найдем ответ на этот вопрос в следующих пунктах темы.
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей
Вспомним аксиому:
Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.
Рассмотрим это утверждение в алгебраическом толковании.
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и задано, что прямая a – это линия пересечения двух плоскостей α и β, которые соответственно описываются уравнениями плоскости A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Поскольку прямая a – это множество общих точек плоскостей α и β, то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.
Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
Общее же решение системы уравнений _A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 определит координаты каждой точки прямой a, т.е. по сути задает саму прямую a.
Резюмируем: прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой уравнений двух плоскостей, которые пересекаются:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
Приведем пример описания прямой линии в пространстве при помощи системы уравнений:
x+3y-21z+113y+14z-2=0
Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.
Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.
Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.
Параметрические уравнения прямой в пространстве
x=x1+ax·λy=y1+ay·λz=z1+az·λ, где x1, y1, z1 – координаты некой точки прямой; аx, аy и az (одновременно не равны нулю) – координаты направляющего вектора прямой. а·λ – некий параметр, принимающий любые действительные значения.
Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел (x, y, z), соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ=0, тогда из параметрических уравнений прямой в пространстве получим координаты:
x=x1+ax·0y=y1+ay·0z=z1+az·0⇔x=x1y=y1z=z1
Рассмотрим конкретный пример:
Пусть прямая задана параметрическими уравнениями вида x=3+2·axy=-2·ayz=2+2·az.
Заданная прямая проходит через точку М1(3, 0, 2); направляющий вектор этой прямой имеет координаты2, -2, 2.
Ответ: 2, -2, 2,
Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.
Канонические уравнения прямой в пространстве
Если разрешить каждое из параметрических уравнений прямой
x=x1+ax·λy=y1+ay·λz=z1+az·λ относительно параметра λ, возможно просто перейти к каноническим уравнениям прямой в пространстве x-x1ax=y-y1ay=z-z1az.
Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М1(x1, y1, z1), и у которой направляющий вектор равен a→=(ax, ay, az). Например, задана прямая, описываемая каноническим уравнением x-11=y2=z+57. Эта прямая проходит через точку с координатами (1, 0, -5), ее направляющий вектор имеет координаты (1, 2, -7).
Отметим, что одно или два числа из чисел аx, аy и аz в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x-x1ax=y-y1ay=z-z1az является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:
x=x1+ax·λy=y1+ay·λz=z1+az·λ, где λ∈R.
Если одно из чисел аx, аy и az канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел аx, аy и az равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x+43=y-52=z+20, лежит в плоскости z=-2, параллельной координатной плоскости Oxy, а координатная ось Oy описывается каноническими уравнениями x0=y1=z0.
Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.
1. Общее уравнение прямой.
Прямая в пространстве
может быть задана как пересечение двух
плоскостей:
 .
.
(1)
О1.
Геометрическое место точек пространства,
удовлетворяющих системе уравнений (1),
называется
прямой
в пространстве,
а
система уравнений (1) называется общим
уравнением прямой.
З1. Для того чтобы
система уравнений (1) определяла прямую
в пространстве необходимо и достаточно,
чтобы нормальные вектора плоскостей,
определяющих
прямую,
![]() и
и![]() были неколлинеарными, т.е. выполняется
были неколлинеарными, т.е. выполняется
одно из неравенств:![]() или
или![]() .
.
Пусть прямая
проходит через точку
![]()
параллельно вектору
![]() ,
,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:
![]() .
.
(2)
З2. Если в уравнении
(2) одна из проекций направляющего вектора
равна 0, то это означает, что прямая
перпендикулярна соответствующей
координатной оси.
Пример 1.
Как расположена прямая
![]() относительно координатных осей.
относительно координатных осей.
Согласно замечанию
2 эта прямая будет перпендикулярна осям
абсцисс и ординат (параллельна оси
аппликат) и будет проходить через точку
![]() .
.
Приравняв каждую
дробь уравнения (2) параметру
![]() ,
,
получимпараметрическое
уравнение прямой:

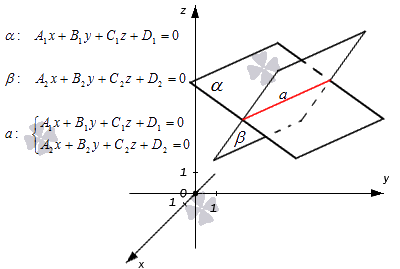
Пример 2.
Записать уравнение прямой
![]() в параметрическом виде.
в параметрическом виде.
Приравняем каждую
дробь к параметру
![]() :
: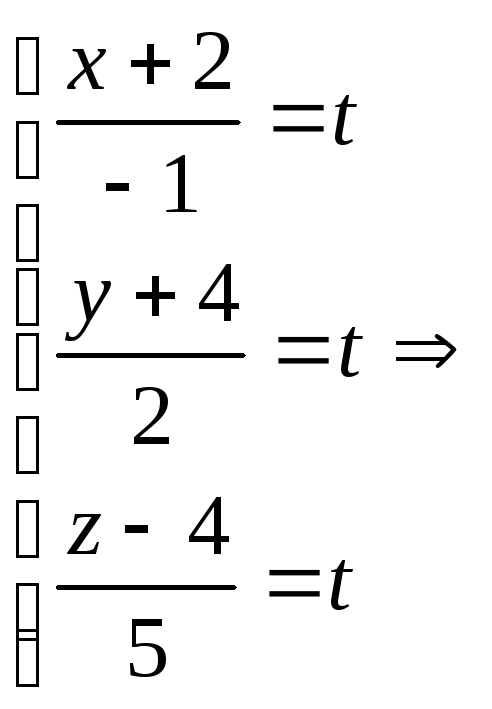
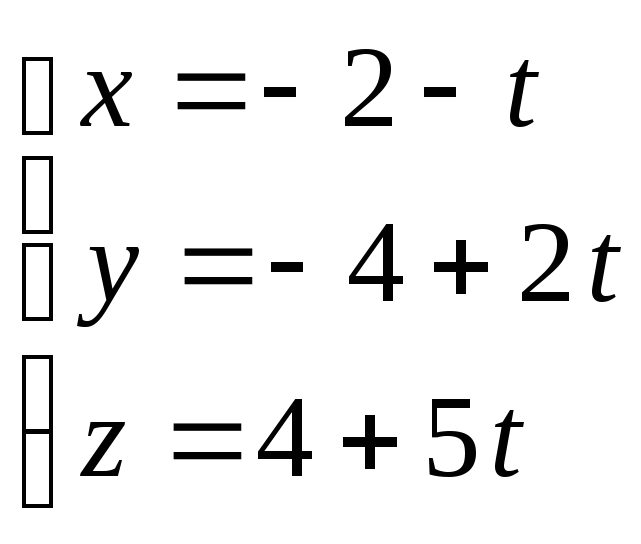 .
.
Если пря-
мая проходит через
две известные точки
![]() и
и![]() ,
,
то ее уравнение имеет вид (см.Лекцию
№ 7):
![]()
![]() и назы-ваетсяуравнением
и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.
2. Основные задачи.
а) Переход
от общего уравнения прямой к каноническому.
Пусть прямая задана общим уравнением
 .
.
Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:
– находят
координаты любой точки, удовлетворяющие
приведенной системе, для чего одну из
переменных величин, например
![]() ,
,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;
– направляющий
вектор
![]() прямой находят как векторное произведение
прямой находят как векторное произведение
нормальных векторов
![]() и
и
![]() :
:
![]() ;
;
– зная
точку, через которую проходит прямая,
и направляющий вектор прямой записывают
каноническое уравнение прямой.
Пример 3.
Записать уравнение прямой
 в каноническом и параметрическом виде.
в каноническом и параметрическом виде.
Положив
![]() ,
,
получим СЛАУ Складывая уравнения, найдем
Складывая уравнения, найдем![]() .
.
Подставив это значение переменной![]() во второе уравнение системы, по-лучим
во второе уравнение системы, по-лучим![]() .
.
Таким образом, прямая проходит через
точку
![]() .
.
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:
б)
Угол
между пересекающимися прямыми.
Угол
между двумя пересека-ющимися прямыми
определяется как угол между их
направляющими векторами.
Если прямые
![]() и
и![]() имеют направляющие вектора
имеют направляющие вектора
![]() и
и
![]() ,
,
соответственно,
то угол между прямыми определяется по
формуле:
![]() .
.
Сл1.
Если
прямые перпендикулярны (![]()
![]() ),
),
тоусловием
перпен-дикулярности
прямых является
равенство:
![]() .
.
Сл2.
Если прямые параллельны, то направляющие
вектора коллинеарны, следовательно,
условие
параллельности прямых:
![]() .
.
в)
Координаты
точки пересечения прямой и плоскости.
Пусть прямая
![]() задана общим уравнением
задана общим уравнением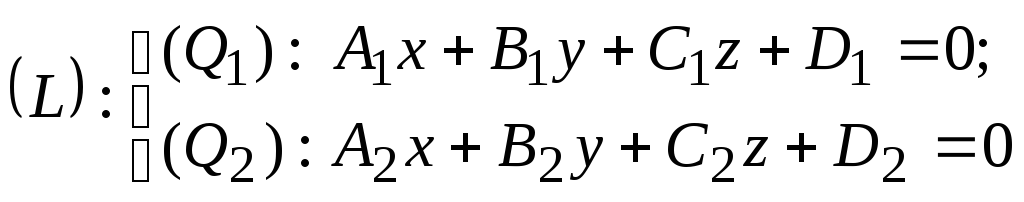 ,
,
а плоскость![]() уравнением
уравнением![]() .Так
.Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:
 .
.
Если прямая
![]() задана
задана
каноническим уравнением![]()
![]() ,
,
а плоскость
![]() уравнением
уравнением![]() ,
,
то поступают по следующей
схеме:
– переходят
от канонического уравнения прямой к
параметрическому, т.е. записывают
уравнение прямой в виде
 ;
;
– полученные
выражения подставляют в уравнение
заданной плоскости
и
находят параметр
![]() :
:![]() .
.
Рассмотрим возможные
случаи:
1) если
выполняются условия
 ,
,
то прямая не пересекает плоскость
(прямая параллельна плоскости);
2) при
условиях
 прямая лежит на плоскости;
прямая лежит на плоскости;
3) если
![]() ,
,
прямая пересекает плоскость в одной
точке.
– вычисляют
координаты точки пересечения, подставив
найденное значение
![]() в параметрическое уравнение прямой
в параметрическое уравнение прямой
 .
.
г)
Угол
между прямой и плоскостью.
Пусть дана плоскость
![]() с нормальным вектором
с нормальным вектором![]() и пересекающая ее прямая
и пересекающая ее прямая![]() с направляющим вектором
с направляющим вектором
![]()
(Рис.
53).

![]()
![]()
![]()
![]()
![]()
![]() Рис.
Рис.
53.
Угол между
прямой
и
плоскостью.
![]()
Угол
![]() является углом между прямой
является углом между прямой![]() и плоскостью
и плоскостью![]() .
.
Угол между нормальным вектором плоскости
и прямой обозначим через![]() .
.
Из рисунка видно, что![]() .
.
Следовательно,
![]()
![]() .
.
Сл1.
Если прямая
перпендикулярна плоскости (![]()
![]() ),
),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:
![]() .
.
Сл2.
Если прямая
параллельна плоскости (![]() ),
),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (![]() ),
),
следовательно,условие
параллельности прямой и плоскости:
![]() .
.
21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Общие уравнения прямой в пространстве. Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Если плоскости π1: A1x + B1y + C1z + D1 = 0, π2: A2x + B2y + C2z + D2 = 0 не параллельны, то пересекаются по прямой. Точка M(x; y; z) принадлежит этой прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению каждой из плоскостей, т.е. являются решениями системы уравнений

которую называют общими уравнениями прямой.
Векторное уравнение прямой. Описание прямой в пространстве при помощи общих уравнений — не единственный способ. Прямую L в пространстве можно также однозначно задать любой ее точкой M0 и параллельным ей ненулевым вектором s.
Любой ненулевой вектор, параллельный прямой, называют направляющим вектором прямой.
Если точка M принадлежит прямой L, то это эквивалентно тому, что вектор M0M коллинеарен вектору s (рис. 6.1). Так как s ≠ 0, то вектор s является базисом в пространстве V1 коллинеарных ему векторов. Поэтому для некоторого числа t выполняется равенство M0M = ts. Так как M0M = OM — OM0 = r — r0, где r и r0 — радиус-векторы точек M и M0 соответственно, то условие M ∈ L можно записать в виде уравнения
r = r0 + ts, (6.2)
которое называют векторным уравнением прямой в пространстве.

Параметрические уравнения прямой в пространстве. Предположим, что известны координаты {l; m; n} направляющего вектора s прямой L и точки M0(x0; y0; z0) ∈ L в прямоугольной системе координат. Обозначим через (x; y; z) координаты произвольной точки M.
Критерием принадлежности точки M прямой L является условие коллинеарности векторов M0M = {x — x0; y — y0; z — z0} и s (см. рис. 6.1), что равносильно пропорциональности их координат (см. теорему 2.6). Обозначив через t коэффициент пропорциональности, получим равенства x — x0 = tl, y — y0 = tm, z — z0 = tn. Но тогда
 M0M и s, состоящую в пропорциональности их координат (см. следствие 2.1).
M0M и s, состоящую в пропорциональности их координат (см. следствие 2.1).
В знаменателе канонических уравнений допускается нулевое значение. Чтобы понять смысл нулевых значений параметров l, m, n, обратим внимание на параметрические уравнения прямой (6.3), в которых нет проблемы нулевых знаменателей. Например, при l = 0 из (6.3) следует, что x = x0. Мы видим, что если в канонических уравнениях один из знаменателей (или два, но не все три) равен нулю, то соответствующий числитель тоже равен нулю.
Уравнения прямой, проходящей через две точки. Каждая прямая в пространстве однозначно задается любыми двумя своими различными точками. Если известны координаты этих точек M1(x1; y1; z1) и M2(x2; y2; z2), то в качестве направляющего вектора прямой подходит ненулевой вектор M1M2 = {x2 — x1; y2 — y1; z2 — z1}. Зная его координаты и координаты точки M1 на прямой, можно записать канонические уравнения прямой (6.4). В результате получим
(x – x1)/(x2 – x1) = (y – y1)/(y2 – y1) = (z – z1)/(z2 – z1) –
уравнения прямой, проходящей через две точки.
Пример 6.1. Точки M1(1;2;3) и M2(3; 2; 1) определяют проходящую через них прямую
(x – 1)/ (3 – 1) = (y – 2)/ (2 – 2) = (z – 3)/ (1 – 3). Нуль в знаменателе второй дроби означает, что для координат всех точек прямой выполнено равенство y = 2. Поэтому прямая расположена в плоскости y – 2 = 0, параллельной координатной плоскости xOz и пересекающей ось ординат в точке с ординатой 2.
Изменение формы уравнений прямой. Переход от канонических уравнений прямой к параметрическим и обратно достаточно очевиден и сводится к введению или исключению параметра t. Одна форма уравнений непосредственно записывается по другой, так как в них используются одни и те же параметры, задающие координаты точки на прямой и координаты направляющего вектора.
Пример 6.2. Найдем координаты точки B, симметричной точке A(2; 3; — 1) относительно
прямой L: (x – 1)/1 = (y + 2)/-1 = (z – 1)/2.
В вычислениях будем опираться на следующее геометрическое построение точки B: а) через точку A проводим плоскость π, перпендикулярную прямой L; б) находим точку M пересечения прямой L и плоскости π; в) отрезок AM удлиняем до отрезка AB так, чтобы точка M оказалась в середине отрезка AB (рис. 6.2).

Так как плоскость π перпендикулярна прямой L, то в качестве нормального вектора n плоскости можно выбрать направляющий вектор прямой L: n = {1; — 1; 2}. По известным координатам нормального вектора плоскости п и принадлежащей ей точки A записываем уравнение плоскости π в виде (5.2): 1(х — 2) + (—1)(у — 3) + 2(z + 1) = 0.
Чтобы найти координаты точки M пересечения прямой и плоскости по их уравнениям, запишем параметрические уравнения прямой L: х = 1 + t, у = —2 — t, z = 1 + 2t. Подставив эти выражения для координат точки на прямой в уравнение плоскости, для параметра t получим уравнение (1 + t — 2) — (—2 — t — 3) + 2(1 + 2t + 1) = 0, решение которого дает значение параметра для точки M. Найдя это значение t = —4/3 и подставив его в параметрические уравнения прямой, получим координаты точки пересечения x = 1 — 4/3 = —1/3, у = —2 + 4/3 = —2/3, z =1 — 8/3 = —5/3. Поскольку эта точка должна делить отрезок AB пополам, ее координаты, согласно (4.13), равны полусумме соответствующих координат точек A и B. Следовательно, обозначив через (хB; уB; zB) координаты точки B, получим равенства (2 + xB)/2 = -1/3(3 + yB)/2 = – 2/3(-1 + zB)/2 = -5/3. Отсюда xB = -8/3, yB = -13/3, zB = -7/3#
Достаточно просто выполняется переход от канонических уравнений к общим. Нетрудно увидеть, что на самом деле канонические уравнения представляют собой особую форму записи общих уравнений. Действительно, двойное равенство (6.4) равносильно системе двух линейных уравнений
(x – x0)/l – (y – y0)/m = 0, (x – x0)/l – (z – z0)/n = 0, (6.5)
которые представляют собой частный вид общих уравнений прямой в пространстве.
Самым сложным является переход от общих уравнений к каноническим или параметрическим.
Так как плоскости π1 и π2, соответствующие отдельным уравнениям из общих у (6.1) прямой, не параллельны, то хотя бы один из определителей второго порядка 
 , представляющих собой координаты векторного произведения нормальныхвекторов этих плоскостей, не равен нулю. Предполагая, что первый из этих определителей является ненулевым:
, представляющих собой координаты векторного произведения нормальныхвекторов этих плоскостей, не равен нулю. Предполагая, что первый из этих определителей является ненулевым:  изложим три способа перехода от общих уравнений к каноническим или параметрическим.
изложим три способа перехода от общих уравнений к каноническим или параметрическим.
Первый способ состоит в том, что в системе (6.1) для z назначают два различных значения и по формулам Крамера находят два различных решения системы двух уравнений с двумя неизвестными х и у. Эти два решения системы (6.1) дают координаты двух разных точек M1 и M2 на прямой. А две известные точки прямой позволяют найти уравнение прямой, проходящей через две точки, которое фактически совпадает с каноническими уравнениями прямой.

Отметим, что в качестве направляющего вектора s прямой, заданной общими уравнениями (6.1), можно выбрать n1×n2 — векторное произведение двух нормальных векторов плоскостей (рис. 6.3). Действительно, это векторное произведение является вектором, который ортогонален каждому нормальному вектору, а потому он параллелен как одной, так и другой плоскости, т.е. параллелен их линии пересечения. Нахождение одной точки на прямой и ее направляющего вектора можно рассматривать как второй способ перехода от общих уравнений прямой к ее каноническим уравнениям.
Пример 6.3. Найдем канонические уравнения прямой, совпадающей с линией пересечения плоскостей π1: х — у + z — 2 = 0, π2: х + у — z = 0.
Чтобы найти координаты некоторой точки на прямой, подставляем в уравнения плоскостей z = 0 и решаем соответствующую систему двух линейных уравнений относительно х и у

Значения х =1 и у = —1 единственного решения системы получаются сложением и вычитанием уравнений системы. Итак, точка с координатами (1; —1; 0) расположена на прямой.
В качестве направляющего вектора прямой берем векторное произведение n1 × n2 нормальных векторов n1 = {1; — 1; 1} и n2 = {1; 1; —1} плоскостей π1 и π2. По формуле (3.2) для вычисления векторного произведения в координатах находим

т.е. направляющим вектором прямой будет s = {0;2; 2}. Найденный вектор s для простоты
заменим коллинеарным ему вектором {0; 1; 1}.
Проведенные вычисления позволяют написать канонические уравнения искомой прямой
(x – 1)/0 = (y + 1)/1 = z/1. #
Третий способ перехода от общих уравнений прямой к ее каноническим или параметрическим уравнениям состоит в следующем. Решаем систему (6.1) по правилу Крамера относительно неизвестных х и у, рассматривая неизвестное z как параметр:

Обозначив z через t и добавив уравнение z = t, получим параметрические уравнения прямой:

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.
Параметрическое и каноническое уравнение прямой в пространстве
Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку
параллельно направляющему вектору
.
Пусть, – произвольная точка прямой, тогда векторы
и
коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:
(1)
это и есть канонические уравнения прямой.
Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:
(2)
Уравнение прямой в пространстве, которая проходит через две заданные точки
Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.
Итак, через две точки и
можно не только геометрично провести линию, но и сложить её уравнения.
За направляющий вектор возьмём , тогда по формуле (1) у нас получается:
(3)
уравнение прямой в пространстве, которые проходят через две заданные точки.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Общее уравнение прямой – переход к каноническому уравнению
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.
Пусть известны их уравнения:
(4)
Тогда система (4) называется общим уравнением прямой.
Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку
этой прямой.
Точку находим, как один из решений системы (4). Например, положив в (4)
находим
, тогда и точку
. Направляющий вектор
, который параллелен к каждой из плоскостей
и
и перпендикулярен к их нормальным векторам
и
, то есть
,
. (см. рис. 1). Поэтому вектор
можно найти при помощи векторного произведения
и
=
x
=
Найдены координаты и
подставим в каноническое уравнение (1).
Например, от общих уравнений прямой:
Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём
. Нормальные векторы
и
. Тогда направляющий вектор
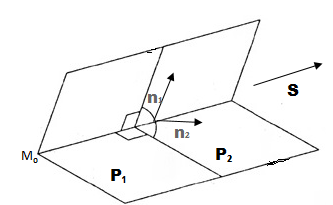
Рис. 1
x
=
,
и канонические уравнения станут:
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Угол между двумя прямыми :
и
равен углу между их направляющими векторами и
, поэтому
=
(5)
Условия параллельности и перпендикулярности прямых соответственно запишутся:
и
.
(6)
Примеры решения задач
Давайте рассмотрим первый пример, где можно двумя способами построить прямую:
Задача
При точке и направляющем векторе
необходимо:
- составить каноническое уравнение прямой;
- построить эту прямую.
Решение
1) По формуле (1) запишем каноническое уравнение прямой :
=
.
2) Рассмотрим два способа построения прямой .
Первый способ
В системе координат строим вектор
и точку
и проводим через точку
прямую параллельную вектору
.
Второй способ
По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:
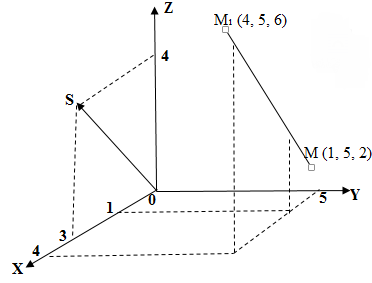
На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой
. Так при
находим координаты
. Через две точки
и
проводим прямую
.
Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:
Задача
Найти острый угол между прямыми:
,
(7)
Решение
По формуле (7) получаем:
=
=
=
Так как , тогда угол
тупой,
, а острый угол
.
Ответ
.
Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.
Задача
Составить уравнение прямой , которая проходит через точку
и параллельна прямой
.
Решение
От параметрического уравнения переходим к каноническому При условии параллельности прямых
то есть направляющим вектором новой прямой может служить известный вектор
и по формуле (1) у нас получается:
.
Ответ
.
