Общий числитель дробей находят так же, как общий знаменатель.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Находят НОК числителей, затем
знаменатель и числитель
дроби умножают на частное
от деления НОК на исходный числитель каждой дроби.
Пример.
2/7 и 7/9
Задача –
преобразовать дроби так, чтобы их числители были одинаковыми.
НОК чисел 2 и 7 – 14.
14:2=7
Дробь 2/7 будет выглядеть как 14/49 ( сократив на 7 получим исходную 2/7)
14:7=2
Дробь 7/9 станет дробью 14/18 ( сократив на 2 получим 7/9)
————————————
Замечу, что приведение дроби к общему знаменателю – гораздо привычнее. т.к. прибегать к нему приходится постоянно.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Сложение дробей
Поддержать сайт![]()
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
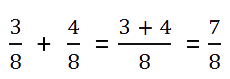
C помощью букв это правило сложения можно записать так:
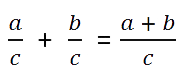
Запомните!
![]()
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
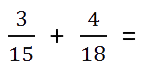
Как найти общий знаменатель
Находим НОК (15, 18).
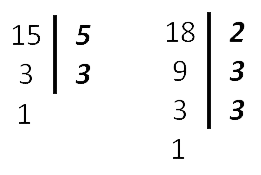
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
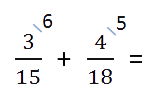
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
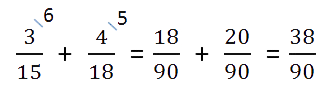
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
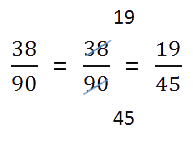
- Eсли в результате получилась
- Ещё раз весь пример целиком.
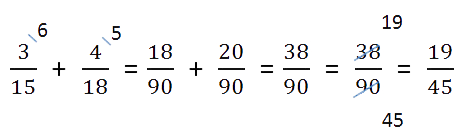
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
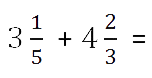
Складываем целые части.
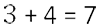
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем.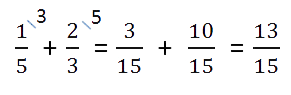
- Сложить полученные результаты из пунктов 1 и 2.
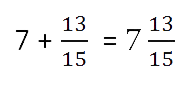
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
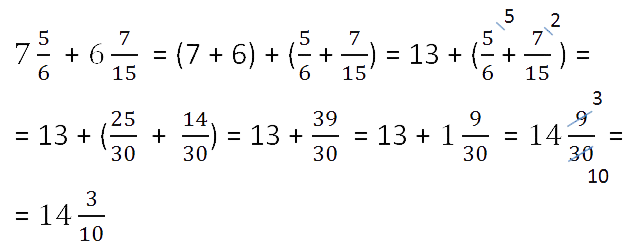
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov

Профиль
Благодарили: 0
Сообщений: 1

Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева

Профиль
Благодарили: 0
Сообщений: 2

Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( – ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов

Профиль
Благодарили: 0
Сообщений: 1

Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova

Профиль
Благодарили: 0
Сообщений: 1

Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов

Профиль
Благодарили: 0
Сообщений: 1

Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + + ![]()
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
![]()
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин

Профиль
Благодарили: 0
Сообщений: 1

Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков

Профиль
Благодарили: 0
Сообщений: 2

Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк

Профиль
Благодарили: 0
Сообщений: 1

Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей![]()
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан

Профиль
Благодарили: 0
Сообщений: 1

Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина

Профиль
Благодарили: 0
Сообщений: 2

Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева

Профиль
Благодарили: 0
Сообщений: 2

Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко

Профиль
Благодарили: 0
Сообщений: 1

Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
![]() как решить?4
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова

Профиль
Благодарили: 0
Сообщений: 1

Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров

Профиль
Благодарили: 0
Сообщений: 1

Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
Содержание материала
- Сложение дробей с одинаковыми знаменателями
- Видео
- НОЗ и НОК
- Как устроена десятичная дробь
- Как привести десятичную дробь к новому знаменателю
- Чтобы найти общий знаменатель, перемножим знаменатели:
- Вычитание дробей с разными знаменателями
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
Пример.

C помощью букв это правило сложения можно записать так:
 Запомните!
Запомните! 
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Видео
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
16=8*2; 6= 3*2
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.
Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
- Найти НОК.
- Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
- Умножить обе части каждой дроби на их дополнительные множители.
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
- Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
- Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
- Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Как привести десятичную дробь к новому знаменателю
Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель — для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4
2.5
=
2.5 × 101 × 10
=
2510
=
5 × 5 2 × 5
=
52
=
5 × 22 × 2
=
104
Чтобы найти общий знаменатель, перемножим знаменатели:
Дополнительный множитель к первой дроби:
Дробь примет вид:
Дополнительный множитель ко второй дроби:
Дробь примет вид:
Дополнительный множитель к третьей дроби:
Дробь примет вид:
Итак, были дроби:
Запишем полученные дроби с общим знаменателем:
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби  можно вычесть дробь
можно вычесть дробь  , поскольку у этих дробей одинаковые знаменатели. А вот от дроби
, поскольку у этих дробей одинаковые знаменатели. А вот от дроби  нельзя вычесть дробь
нельзя вычесть дробь  , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения: 
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям  и
и 
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:

Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Получили ответ 
Попробуем изобразить наше решение с помощью рисунка. Если от  пиццы отрезать
пиццы отрезать  пиццы, то получится
пиццы, то получится  пиццы
пиццы

Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:

Приведение дробей  и
и  к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби
к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби  и
и  . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
. Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):

Первый рисунок изображает дробь  (восемь кусочков из двенадцати), а второй рисунок — дробь
(восемь кусочков из двенадцати), а второй рисунок — дробь  (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь
(три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь  и описывает эти пять кусочков.
и описывает эти пять кусочков.
Пример 2. Найти значение выражения 
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:

Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:

Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:

Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:

В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь  , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
, нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:


Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби  на найденный НОД, то есть на 10
на найденный НОД, то есть на 10

Получили ответ 
Теги
Как сравнить дроби, у которых и числители, и знаменатели разные?
В таких случаях применяют основное свойство дроби.
1 способ. Приведение дробей к общему знаменателю.
Наименьший общий знаменатель данных дробей — (30).
Приведём дроби к общему знаменателю (30).
.
Сравним полученные дроби:
, поэтому и
415<56
.
2 способ. Приведение дробей к общему числителю.
Умножим и числитель, и знаменатель первой дроби на (5), а второй — на (4):
.
Сравним полученные дроби:
((75>24)), поэтому
415<56
.
Приведение к одинаковому числителю полезно в случае, когда знаменатели дробей большие.
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Основное свойство рациональных чисел гласит:
(frac{p}{q}=frac{p times n}{q times n})
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Рассмотрим пример:
(frac{1}{2}=frac{1 times 4}{2 times 4}=frac{4}{8})
Получаем,
(frac{1}{2}=frac{4}{8})
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Приведите дроби с разными знаменателями к наименьшему общему знаменателю .
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
НОК(14,20)= 2⋅5⋅2⋅7=140
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь (frac{1}{20}) домножить на 7, чтобы получить знаменатель 140.
(frac{1}{20}=frac{1 times 7}{20 times 7}=frac{7}{140})
А вторую дробь умножить на 10.
(frac{3}{14}=frac{3 times 10}{14 times 10}=frac{30}{140})
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
- Нужно разложить на простые множители знаменатели дробей.
- Нужно найти наименьшее общее кратное (НОК) для знаменателей данных дробей.
- Привести дроби к общему знаменателю, то есть умножить и числитель и знаменатель дроби на множитель.
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей (frac{2}{11}, frac{1}{15}, frac{3}{22})
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби (frac{2}{11}, frac{1}{15}, frac{3}{22}) к общему знаменатели равному 330.
(begin{align}
frac{2}{11}=frac{2 times 30}{11 times 30}=frac{60}{330} \\
frac{1}{15}=frac{1 times 22}{15 times 22}=frac{22}{330} \\
frac{3}{22}=frac{3 times 15}{22 times 15}=frac{60}{330} \\
end{align})
Вопросы по теме:
Какой общий знаменатель у дробей (bf frac{2}{25}) и (bf frac{1}{14})?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
( begin{align}
frac{2}{25}=frac{2 times 14}{25 times 14}=frac{28}{350} \\
frac{1}{14}=frac{1 times 25}{14 times 25}=frac{25}{350} \\
end{align})
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей (frac{2}{25}) и (frac{1}{14}) знаменателем может быть число 700, 1400 и т.д.
