Алгоритм Евклида
Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).
Python
#!/usr/bin/env python
a = 18
b = 30
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
print (a+b)
Perl:
sub nod
{
return $_[0] != 0 ? nod ( ( $_[1] % $_[0] ), $_[0] ) : $_[1];
}
C:
int gcd(int a, int b) {
int c;
while (b) {
c = a % b;
a = b;
b = c;
}
return abs(a);
}
Pascal:
function nod( a, b: longint): longint;
begin
while (a <> 0) and (b <> 0) do
if a >= b then
a:= a mod b
else
b:= b mod a;
nod:= a + b;
end;
Java:
public class GCD {
public static int gcd(int a,int b) {
while (b !=0) {
int tmp = a%b;
a = b;
b = tmp;
}
return a;
}
}
C#:
int gcd(int a, int b)
{
while (b != 0)
b = a % (a = b);
return a;
}
Given two integer numbers, the task is to find count of all common divisors of given numbers?
Examples :
Input : a = 12, b = 24 Output: 6 // all common divisors are 1, 2, 3, // 4, 6 and 12 Input : a = 3, b = 17 Output: 1 // all common divisors are 1 Input : a = 20, b = 36 Output: 3 // all common divisors are 1, 2, 4
It is recommended to refer all divisors of a given number as a prerequisite of this article.
Naive Solution
A simple solution is to first find all divisors of first number and store them in an array or hash. Then find common divisors of second number and store them. Finally print common elements of two stored arrays or hash. The key is that the magnitude of powers of prime factors of a divisor should be equal to the minimum power of two prime factors of a and b.
- Find the prime factors of a using prime factorization.
- Find the count of each prime factor of a and store it in a Hashmap.
- Prime factorize b using distinct prime factors of a.
- Then the total number of divisors would be equal to the product of (count + 1)
of each factor. - count is the minimum of counts of each prime factors of a and b.
- This gives the count of all divisors of a and b.
C++
#include <bits/stdc++.h>
using namespace std;
map<int, int> ma;
void primeFactorize(int a)
{
for(int i = 2; i * i <= a; i += 2)
{
int cnt = 0;
while (a % i == 0)
{
cnt++;
a /= i;
}
ma[i] = cnt;
}
if (a > 1)
{
ma[a] = 1;
}
}
int commDiv(int a, int b)
{
primeFactorize(a);
int res = 1;
for(auto m = ma.begin();
m != ma.end(); m++)
{
int cnt = 0;
int key = m->first;
int value = m->second;
while (b % key == 0)
{
b /= key;
cnt++;
}
res *= (min(cnt, value) + 1);
}
return res;
}
int main()
{
int a = 12, b = 24;
cout << commDiv(a, b) << endl;
return 0;
}
Java
import java.util.*;
import java.io.*;
class GFG {
static HashMap<Integer, Integer> ma = new HashMap<>();
static void primeFactorize(int a)
{
for (int i = 2; i * i <= a; i += 2) {
int cnt = 0;
while (a % i == 0) {
cnt++;
a /= i;
}
ma.put(i, cnt);
}
if (a > 1)
ma.put(a, 1);
}
static int commDiv(int a, int b)
{
primeFactorize(a);
int res = 1;
for (Map.Entry<Integer, Integer> m : ma.entrySet()) {
int cnt = 0;
int key = m.getKey();
int value = m.getValue();
while (b % key == 0) {
b /= key;
cnt++;
}
res *= (Math.min(cnt, value) + 1);
}
return res;
}
public static void main(String args[])
{
int a = 12, b = 24;
System.out.println(commDiv(a, b));
}
}
Python3
import math
ma = {}
def primeFactorize(a):
sqt = int(math.sqrt(a))
for i in range(2, sqt, 2):
cnt = 0
while (a % i == 0):
cnt += 1
a /= i
ma[i] = cnt
if (a > 1):
ma[a] = 1
def commDiv(a, b):
primeFactorize(a)
res = 1
for key, value in ma.items():
cnt = 0
while (b % key == 0):
b /= key
cnt += 1
res *= (min(cnt, value) + 1)
return res
a = 12
b = 24
print(commDiv(a, b))
C#
using System;
using System.Collections.Generic;
class GFG{
static Dictionary<int,
int> ma = new Dictionary<int,
int>();
static void primeFactorize(int a)
{
for(int i = 2; i * i <= a; i += 2)
{
int cnt = 0;
while (a % i == 0)
{
cnt++;
a /= i;
}
ma.Add(i, cnt);
}
if (a > 1)
ma.Add(a, 1);
}
static int commDiv(int a, int b)
{
primeFactorize(a);
int res = 1;
foreach(KeyValuePair<int, int> m in ma)
{
int cnt = 0;
int key = m.Key;
int value = m.Value;
while (b % key == 0)
{
b /= key;
cnt++;
}
res *= (Math.Min(cnt, value) + 1);
}
return res;
}
static void Main()
{
int a = 12, b = 24;
Console.WriteLine(commDiv(a, b));
}
}
Javascript
<script>
let ma = new Map();
function primeFactorize(a)
{
for(let i = 2; i * i <= a; i += 2)
{
let cnt = 0;
while (a % i == 0)
{
cnt++;
a = parseInt(a / i, 10);
}
ma.set(i, cnt);
}
if (a > 1)
{
ma.set(a, 1);
}
}
function commDiv(a,b)
{
primeFactorize(a);
let res = 1;
ma.forEach((values,keys)=>{
let cnt = 0;
let key = keys;
let value = values;
while (b % key == 0)
{
b = parseInt(b / key, 10);
cnt++;
}
res *= (Math.min(cnt, value) + 1);
})
return res;
}
let a = 12, b = 24;
document.write(commDiv(a, b));
</script>
Output:
6
Time Complexity: O(√n log n)
Auxiliary Space: O(n)
Efficient Solution –
A better solution is to calculate the greatest common divisor (gcd) of given two numbers, and then count divisors of that gcd.
C++
#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
int commDiv(int a, int b)
{
int n = gcd(a, b);
int result = 0;
for (int i = 1; i <= sqrt(n); i++) {
if (n % i == 0) {
if (n / i == i)
result += 1;
else
result += 2;
}
}
return result;
}
int main()
{
int a = 12, b = 24;
cout << commDiv(a, b);
return 0;
}
Java
class Test {
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static int commDiv(int a, int b)
{
int n = gcd(a, b);
int result = 0;
for (int i = 1; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
if (n / i == i)
result += 1;
else
result += 2;
}
}
return result;
}
public static void main(String args[])
{
int a = 12, b = 24;
System.out.println(commDiv(a, b));
}
}
Python3
from math import sqrt
def gcd(a, b):
if a == 0:
return b
return gcd(b % a, a)
def commDiv(a, b):
n = gcd(a, b)
result = 0
for i in range(1,int(sqrt(n))+1):
if n % i == 0:
if n/i == i:
result += 1
else:
result += 2
return result
if __name__ == "__main__":
a = 12
b = 24;
print(commDiv(a, b))
C#
using System;
class GFG {
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static int commDiv(int a, int b)
{
int n = gcd(a, b);
int result = 0;
for (int i = 1; i <= Math.Sqrt(n); i++) {
if (n % i == 0) {
if (n / i == i)
result += 1;
else
result += 2;
}
}
return result;
}
public static void Main(String[] args)
{
int a = 12, b = 24;
Console.Write(commDiv(a, b));
}
}
PHP
<?php
function gcd($a, $b)
{
if ($a == 0)
return $b;
return gcd($b % $a, $a);
}
function commDiv($a, $b)
{
$n = gcd($a, $b);
$result = 0;
for ($i = 1; $i <= sqrt($n);
$i++)
{
if ($n % $i == 0)
{
if ($n / $i == $i)
$result += 1;
else
$result += 2;
}
}
return $result;
}
$a = 12; $b = 24;
echo(commDiv($a, $b));
?>
Javascript
<script>
function gcd(a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
function commDiv(a, b)
{
let n = gcd(a, b);
let result = 0;
for (let i = 1; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
if (n / i == i)
result += 1;
else
result += 2;
}
}
return result;
}
let a = 12, b = 24;
document.write(commDiv(a, b));
</script>
Output :
6
Time complexity: O(n1/2) where n is the gcd of two numbers.
Auxiliary Space: O(1)
This article is contributed by Aarti_Rathi and Shashank Mishra ( Gullu ). If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Another Approach:
1. Define a function “gcd” that takes two integers “a” and “b” and returns their greatest common divisor (GCD) using the Euclidean algorithm.
2. Define a function “count_common_divisors” that takes two integers “a” and “b” and counts the number of common divisors of “a” and “b” using their GCD.
3. Calculate the GCD of “a” and “b” using the “gcd” function.
4. Initialize a counter “count” to 0.
5. Loop through all possible divisors of the GCD of “a” and “b” from 1 to the square root of the GCD.
6. If the current divisor divides the GCD evenly, increment the counter by 2 (because both “a” and “b” are divisible by the divisor).
7. If the square of the current divisor equals the GCD, decrement the counter by 1 (because we’ve already counted this divisor once).
8. Return the final count of common divisors.
9. In the main function, define two integers “a” and “b” and call the “count_common_divisors” function with these integers.
10. Print the number of common divisors of “a” and “b” using the printf function.
C
#include <stdio.h>
int gcd(int a, int b) {
if(b == 0) {
return a;
}
return gcd(b, a % b);
}
int count_common_divisors(int a, int b) {
int gcd_ab = gcd(a, b);
int count = 0;
for(int i = 1; i * i <= gcd_ab; i++) {
if(gcd_ab % i == 0) {
count += 2;
if(i * i == gcd_ab) {
count--;
}
}
}
return count;
}
int main() {
int a = 12;
int b = 18;
int common_divisors = count_common_divisors(a, b);
printf("The number of common divisors of %d and %d is %d.n", a, b, common_divisors);
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b) {
if(b == 0) {
return a;
}
return gcd(b, a % b);
}
int count_common_divisors(int a, int b) {
int gcd_ab = gcd(a, b);
int count = 0;
for(int i = 1; i * i <= gcd_ab; i++) {
if(gcd_ab % i == 0) {
count += 2;
if(i * i == gcd_ab) {
count--;
}
}
}
return count;
}
int main() {
int a = 12;
int b = 18;
int common_divisors = count_common_divisors(a, b);
cout<<"The number of common divisors of "<<a<<" and "<<b<<" is "<<common_divisors<<"."<<endl;
return 0;
}
Java
import java.util.*;
public class Main {
public static int gcd(int a, int b) {
if(b == 0) {
return a;
}
return gcd(b, a % b);
}
public static int countCommonDivisors(int a, int b) {
int gcd_ab = gcd(a, b);
int count = 0;
for(int i = 1; i * i <= gcd_ab; i++) {
if(gcd_ab % i == 0) {
count += 2;
if(i * i == gcd_ab) {
count--;
}
}
}
return count;
}
public static void main(String[] args) {
int a = 12;
int b = 18;
int commonDivisors = countCommonDivisors(a, b);
System.out.println("The number of common divisors of " + a + " and " + b + " is " + commonDivisors + ".");
}
}
Python3
import math
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
def count_common_divisors(a, b):
gcd_ab = gcd(a, b)
count = 0
for i in range(1, int(math.sqrt(gcd_ab)) + 1):
if gcd_ab % i == 0:
count += 2
if i * i == gcd_ab:
count -= 1
return count
a = 12
b = 18
common_divisors = count_common_divisors(a, b)
print("The number of common divisors of", a, "and", b, "is", common_divisors, ".")
C#
using System;
public class MainClass
{
public static int GCD(int a, int b)
{
if (b == 0)
{
return a;
}
return GCD(b, a % b);
}
public static int CountCommonDivisors(int a, int b)
{
int gcd_ab = GCD(a, b);
int count = 0;
for (int i = 1; i * i <= gcd_ab; i++)
{
if (gcd_ab % i == 0)
{
count += 2;
if (i * i == gcd_ab)
{
count--;
}
}
}
return count;
}
public static void Main()
{
int a = 12;
int b = 18;
int commonDivisors = CountCommonDivisors(a, b);
Console.WriteLine("The number of common divisors of {0} and {1} is {2}.", a, b, commonDivisors);
}
}
Javascript
function gcd(a, b) {
if(b === 0) {
return a;
}
return gcd(b, a % b);
}
function count_common_divisors(a, b) {
let gcd_ab = gcd(a, b);
let count = 0;
for(let i = 1; i * i <= gcd_ab; i++) {
if(gcd_ab % i === 0) {
count += 2;
if(i * i === gcd_ab) {
count--;
}
}
}
return count;
}
let a = 12;
let b = 18;
let common_divisors = count_common_divisors(a, b);
console.log(`The number of common divisors of ${a} and ${b} is ${common_divisors}.`);
Output
The number of common divisors of 12 and 18 is 4.
The time complexity of the gcd() function is O(log(min(a, b))), as it uses Euclid’s algorithm which takes logarithmic time with respect to the smaller of the two numbers.
The time complexity of the count_common_divisors() function is O(sqrt(gcd(a, b))), as it iterates up to the square root of the gcd of the two numbers.
The space complexity of both functions is O(1), as they only use a constant amount of memory regardless of the input size.
Last Updated :
13 Apr, 2023
Like Article
Save Article
Вариант 1
var a,b:longint;
function NOD(x,y:longint):longint; { функция поиска наиб. общ. делителя }
begin
if x<>0 then NOD:=NOD(y mod x,x) else NOD:=y;
end;
function NOK(x,y:longint):longint; { функция поиска наим. общ. кратного }
begin
NOK:=( x div NOD(x,y) ) * y;
end;
begin { основная программа }
readln(a,b);
writeln( 'НОД этих чисел = ', NOD(a,b) );
writeln( 'НОК этих чисел = ', NOK(a,b) );
end.
Вариант 2 Переборный алгоритм
var a, b, d: integer;
begin
write('Введите два числа: ');
readln(a, b);
if a < b then d := a + 1 else d := b + 1;
{так как мы используем цикл с постусловием, необходимо минимальное значение увеличить на один,
иначе цикл repeat, в силу своих конструктивных
особенностей, не учтет это минимальное число и
не сделает его кандидатом в НОД. Например, 5 и 25.}
repeat d := d - 1
until (a mod d = 0) and (b mod d = 0);
write('NOD = ', d)
end.
Вариант 3
var
m,n,r:integer;
label lb;
begin
write('Введите первое число:');readln(m);
write('Введите второе число:');readln(n);
lb:r:=m mod n;
if r=0 then writeln('НОД = ',n)
else
begin
m:=n;
n:=r;
goto lb;
end;
end.
Вариант 4 Алгоритм Евклида с вычитанием
Пусть a и b — целые числа, тогда верны следующие утверждения:
Все общие делители пары a и b являются также общими делителями пары a — b, b;
И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b; НОД(A, B) = НОД(A — B, B), если A > B; НОД(A, 0) = A.
Доказательство:
Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналогично предыдущему. Поэтому t — также общий делитель a и b. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а. Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.
var a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while a <> b
do if a > b then a := a - b else b := b - a;
writeln('NOD = ', a);
end.
Вариант 5 Алгоритм Евклида с делением
Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r). Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.
var a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while (a <> 0) and (b <> 0)
do if a >= b then a := a mod b else b := b mod a;
write(a + b)
end.
Вариант № 6
Program test2(input,output);
Const N = 5;
Var
С: array[1..5] of integer;
A,B:integer;
function HOК (A, В:integer):integer;
begin
HOK:=A*B/ HOD(A,B);
end;
function НОD(А, В:integer):integer;
var
X,Y:integer;
begin
X:= A; Y: = В;
1:IF X = Y THEN HOD:=X;
IF X > Y THEN begin
X:= X – Y;goto 1;
end;
IF Y > X THEN begin
Y:= Y – X;goto 1;
end;
end;
Begin
FOR i= 1 ТО N READ (C[i]);
A:= С ([l])
FOR i = 1 TO N–1 begin B:=С[i + 1];
A:= HOK(A,B);
end;
writeln ("HOK="; A);
end.
Вариант 7
Program N_O_D (Input, Output);
Var
A, B: LongInt;
NOD : LongInt;
Begin
WriteLn ('PASCAL: Нахождение Н.О.Д. двух заданных чисел.');
Writeln ('Введите числа, для которых ищется НОД:');
Write('Первое число: ');ReadLn (A);
Write('Второе число: ');ReadLn (B);
If (A < B)ThenNOD := A Else NOD := B;
While Not( (A mod NOD = 0) and (B mod NOD = 0) ) do
NOD := NOD - 1;
WriteLn ('НОД = ',NOD);
ReadLn;
End.
Program N_O_D (Input, Output);
Var
A, B: LongInt;
NOK, NOD : LongInt;
Begin
WriteLn ('PASCAL: Нахождение Н.О.К. двух заданных чисел.');
WriteLn ('Введите числа, для которых ищется НОК:');
Write ('Первое число: ');ReadLn (A);
Write ('Второе число: ');ReadLn (B);
If (A < B)ThenNOD := A Else NOD := B;
While Not ( (A Mod NOD = 0) And (B Mod NOD = 0) ) Do
NOD := NOD - 1;
A := A Div NOD;
B := B Div NOD;
NOK := A * B * NOD;
WriteLn ('НОК = ', NOK);
ReadLn;
End.
Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.
Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.
Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.
Переборный алгоритм
Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.
var
a, b, d: integer;
begin
write('Введите два числа: ');
readln(a, b);
if a < b then d := a + 1 else d := b + 1;
{так как мы используем цикл с постусловием,
необходимо минимальное значение увеличить на один,
иначе цикл repeat, в силу своих конструктивных особенностей,
не учтет это минимальное число
и не сделает его кандидатом в НОД. Например, 5 и 25.}
repeat d := d - 1
until (a mod d = 0) and (b mod d = 0);
write('NOD = ', d)
end.
Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.
Алгоритм Евклида «с вычитанием»
Пусть a и b — целые числа, тогда верны следующие утверждения:
- Все общие делители пары a и b являются также общими делителями пары a — b, b;
- И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
- НОД(A, B) = НОД(A — B, B), если A > B;
- НОД(A, 0) = A.
Доказательство:
- Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
- Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
- Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
- Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.
Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.
Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.
Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.
На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.
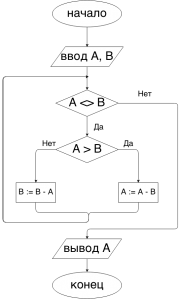
Блок — схема алгоритма Евклида «с вычитанием»
Программа
var
a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while a <> b do
if a > b then
a := a - b
else
b := b - a;
writeln('NOD = ', a);
end.
Алгоритм Евклида с «делением»
Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).
Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.
Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.
var
a, b: integer;
begin
write('a = ');
readln(a);
write('b = ');
readln(b);
while (a <> 0) and (b <> 0) do
if a >= b
then
a := a mod b
else
b := b mod a;
write(a + b)
end.
На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.
Исходник программы, задача которой – нахождение наибольшего общего делителя (НОД или Алгоритм Евклида) для двух, введённых с клавиатуры чисел. Используется цикл WHILE, есть пояснительные комментарии ко всем важным строкам программы. Скачать исходник просмотреть исходный код программы можно ниже.
Исходный код программы:
var a,b,c: integer; //Описание переменных
begin //Начало программы
writeln('Введите a,b: '); //Диалог с пользователем
read(a,b); //Чистывание чисел
while b<>0 do //Вход в цикл while, пока b не равно 0
begin
c := a mod b; //Присваивание с остатка деления a/b
a := b;
b := c;
end;
writeln('Наибольший Общий Делитель = ',a); //Вывод делителя
end.//конец программыСкачать:
nod.pas
Дата: 2012-04-07 18:52:48 Просмотров: 46713
Теги: Паскаль исходник Pascal WHILE циклы