НОД, НОД
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Определения:
- Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
- Наименьшее общее кратное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка
Способы нахождения НОД двух чисел:
1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Выписываем все делители числа а;
- Выписываем все делители числа b;
- Выбираем среди них общие делители;
- Среди общих делителей выбираем самое большое число – это и есть НОД(a, b).
2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Найти делители меньшего из данных чисел.
- Найти, начиная с большего, тот из выписанных делителей, который является также делителем другого числа.
- Записать найденное число – НОД.
3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.
- Находим разложение чисел на простые множители.
- Подчеркиваем общие числа.
- Находим произведение подчеркнутых чисел у одного числа.
- Записываем ответ.
4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел вычитанием.
- Из большего числа вычитается меньшее.
- Если получается 0, то числа равны друг другу и являются наибольшим общим делителем.
- Если результат вычитания не равен 0, то большее число заменяется на результат вычитания.
- Переход к пункту 1.
Способы нахождения НОК двух чисел:
1 способ: Метод перебора
1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
2 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители
- Разложить данные числа на простые множители.
- Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним – разложение остальных чисел.
- Подчеркнуть в разложении меньшего числа множители, которые не вошли в разложение бóльшего числа и добавить эти множители в разложение большего числа.
- Полученное произведение записать в ответ.
Свойства наибольшего общего делителя:
- НОД(a, b) = НОД(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОД(a, 0) = |a|
- НОД(a, к • a) = |a|, при любом к ∈ Z
- НОД(a, НОД(b, с)) = НОД(НОД(a, b), c)
Свойства наименьшего общего кратного:
- НОК(a, b) = НОК(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)
Содержание
- Наибольший общий делитель (НОД), свойства и формулы
- Понятие наибольшего общего делителя
- Свойства наибольшего общего делителя
- Способы нахождения наибольшего общего делителя
- 1. Разложение на множители
- 2. Алгоритм Евклида
НОД, НОД
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Определения:
- Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
- Наименьшее общее кратное (НОК) двух целых чиселm и n есть наименьшее натуральное число , которое делится на m и n без остатка
Способы нахождения НОД двух чисел:
1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Выписываем все делители числа а;
- Выписываем все делители числа b;
- Выбираем среди них общие делители;
- Среди общих делителей выбираем самое большое число – это и есть НОД(a, b).
2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Найти делители меньшего из данных чисел.
- Найти, начиная с большего, тот из выписанных делителей, который является также делителем другого числа.
- Записать найденное число – НОД.
3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.
- Находим разложение чисел на простые множители.
- Подчеркиваем общие числа.
- Находим произведение подчеркнутых чисел у одного числа.
- Записываем ответ.
4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел вычитанием.
- Из большего числа вычитается меньшее.
- Если получается 0, то числа равны друг другу и являются наибольшим общим делителем.
- Если результат вычитания не равен 0, то большее число заменяется на результат вычитания.
- Переход к пункту 1.
Способы нахождения НОК двух чисел:
1 способ: Метод перебора
1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
2 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители
- Разложить данные числа на простые множители.
- Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
- Подчеркнуть в разложении меньшего числа множители, которые не вошли в разложение бóльшего числа и добавить эти множители в разложение большего числа.
- Полученное произведение записать в ответ.
Свойства наибольшего общего делителя:
- НОД(a, b) = НОД(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОД(a, 0) = |a|
- НОД(a, к • a) = |a|, при любом к ∈ Z
- НОД(a, НОД(b, с)) = НОД(НОД(a, b), c)
Свойства наименьшего общего кратного:
- НОК(a, b) = НОК(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)
Источник
Наибольший общий делитель (НОД), свойства и формулы

О чем эта статья:
5 класс, 6 класс
Понятие наибольшего общего делителя
Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.
Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4. Но у этой пары чисел есть и другие общие делители: 1, -1 и -4.
Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.
Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).
Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:
Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.
- Зафиксируем все делители четырех: ±4, ±2, ±1.
- А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
- Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.
Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.
Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.
Еще один пример. Рассчитаем НОД для 28 и 64.
- Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Свойства наибольшего общего делителя
У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.
Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.
Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.
Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.
Доказательство
Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.
Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.
В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.
- Например, НОД (25, 25) = 25.
Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.
- Например, НОД (4, 40) = 4, так как 40 кратно 4.
Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.
Доказательство
Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.
Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.
Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).
Доказательство
Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.
Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.
Способы нахождения наибольшего общего делителя
Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.
1. Разложение на множители
Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.
Пример 1. Найти НОД (84, 90).
- Разложим числа 84 и 90 на простые множители:
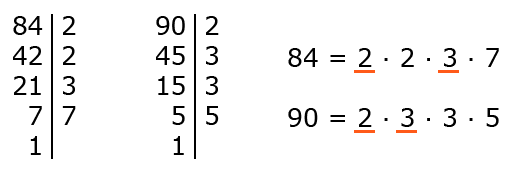
Подчеркнем все общие множители и перемножим их между собой:
Ответ: НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
- Разложим 15 и 28 на простые множители:
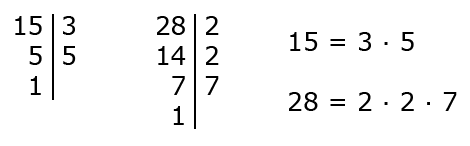
Ответ: НОД (15, 28) = 1.
Пример 3. Найти НОД для 24 и 18.
- Разложим оба числа на простые множители:

Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.

Перемножим общие множители:
НОД (24, 18) =2 * 3 = 6
Ответ: НОД (24, 18) = 6
2. Алгоритм Евклида
Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.
Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.
Пример 1. Найти НОД для 24 и 8.
Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.
В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:
- Большее число поделить на меньшее.
- Меньшее число поделить на остаток, который получается после деления.
- Первый остаток поделить на второй остаток.
- Второй остаток поделить на третий и т. д.
- Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.
Пример 2. Найти наибольший общий делитель чисел 140 и 96:
- 140 : 96 = 1 (остаток 44)
- 96 : 44 = 2 (остаток 8)
- 44 : 8 = 5 (остаток 4)
- 8 : 4 = 2
Последний делитель равен 4 — это значит: НОД (140, 96) = 4.
Ответ: НОД (140, 96) = 4
Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:
- Найти наибольший общий делитель любых двух чисел из данных.
- Найти НОД найденного делителя и третьего числа.
- Найти НОД последнего найденного делителя и четвёртого числа и т. д.
Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.
Источник
Библиографическое описание:
Нахождение наибольшего общего делителя различными методами / П. Р. Красикова, А. В. Лиджиева, А. Н. Алиева [и др.]. — Текст : непосредственный // Юный ученый. — 2017. — № 1 (10). — С. 46-47. — URL: https://moluch.ru/young/archive/10/742/ (дата обращения: 18.05.2023).
Наибольший общий делитель (НОД) нам известен из школьного курса математики. Тема вызывает особое к себе отношение, в связи с активным применением за пределами школьного кабинета. Мы знаем два способа вычисления наибольшего общего делителя, и на основе этих материалов можем попробовать определиться с более удобными методами.
Метод перебора общих делителей.
- Определяем все возможные делители числа а;
- Определяем все возможные делители числа b;
- Среди них находим делители, которые являются общими;
- Среди количества общих делителей определяем самое наибольшее число, оно и будет являться наибольшим общим делителем чисел а и b — НОД (a, b).
Пример: найдите НОД (24; 60).
Введём обозначения: делители числа обозначим буквой Д.
Д (24) = {1; 2;3; 4;6;8; 12; 24};
Д (60) = {1; 2; 3; 4;5; 6;10; 12; 15; 20; 30;60}.
Д (24; 60) = {1; 2; 4;12}.
НОД (24; 60) = 12.
Такой способ может быть удобен в тех случаях, когда количество делителей хотя бы у одного из чисел невелико.
Метод нахождения НОД натуральных чисел с помощью разложения на простые множители.
- Разложим числа на простые множители.
- Подчеркиваем общие простые множители.
- Находим произведение подчеркнутых простых множителей у одного числа — это будет являться наибольшим общим делителем чисел а и b — НОД (a, b).
Пример: найдите НОД (24; 60).
Произведём разложение на простые множители числа
24 = 2·2·2·3, 60 = 2·2·5·3.
НОД (36, 48) = 2·2·3 = 12 [1, c. 24]
Данный способ будет удобен только для разложения небольших чисел на простые множители.
Рассмотрим другой способ нахождения общего делителя двух чисел. Он называется алгоритмом Евклида.
Алгоритм Евклида нахождения НОД двух натуральных чисел вычитанием.
- Из большего числа вычтем меньшее число.
- Если получается нуль, то числа равны друг другу и будут являться НОД.
- Если результат вычитания не равен нулю, то большее число заменяется на результат вычитания.
- Переход к пункту 1.
Пример: найти НОД (24; 60).
Решение: найдем разность чисел 60 и 24: 60–24 = 36. Затем большее число заменим на результат вычитания. Теперь найдем НОД (24; 36).
36–24 = 12. Далее заменим 36 на 12. Затем находим НОД (24; 12).
24–12 = 12. Заменив 24 на 12, находим НОД (12; 12).
12–12 = 0, так как разность равна 0, то НОД — это уменьшаемое или вычитаемое.
НОД (24; 60) = НОД (24; 36) = НОД (24; 12) = НОД (12; 12) = 12.
Рассмотренный метод нахождения наибольшего общего делителя имеет свои особенности. Например, в случае нахождения НОД (300; 5) придётся исполнить 60 операций вычитания. Поэтому рассмотрим другой алгоритм Евклида, который может способствовать ускорению вычислительных действий.
Алгоритм Евклида нахождения НОД двух натуральных чисел делением.
- Большее число делится на меньшее.
- Если делится без остатка, то меньшее число и есть наибольший общий делитель.
- Если есть остаток, то большее число заменяем на остаток от деления.
4. Переход к пункту 1.
Пример: найти НОД (432; 111).
Решение: разделив 432 на 111, получаем равенство 432 = 111*3+99.
Выполнив деление 111 на 99, получаем равенство 111 = 99*1+12.
Деление 99 на 12 дает равенство 99 = 12*8+3.
12 делится на 3 без остатка, то есть 12 = 3*4, следовательно НОД (432; 111) = 3 [2, c 88].
Бинарный алгоритм Евклида нахождения НОД двух натуральных чисел.
Бинарный алгоритм Евклида вычисления НОД несёт в себе более быстрый характер. Рассмотрим структуру данного алгоритма:
- Если оба числа a и b чётные, то НОД (a; b) = 2*НОД (a/2; b/2);
- Если a нечётное, b чётное, то НОД (a; b) = НОД (a; b/2);
- Если оба числа a и b нечётные a > b, то НОД (a; b) = НОД ((a-b); b);
- Если a = b, то НОД (a; b) =a.
Пример: найти НОД (1118; 2064).
Решение: НОД (1118; 2064) = 2*НОД (559; 1032) = 2*НОД (559; 516) = 2*НОД (559;258) = 2*НОД (559; 129) = 2*НОД (430; 129) = 2*НОД (215; 139) = 2*НОД (86; 129) =
= 2*НОД (43; 129) = 2*НОД (43; 86) = 2*НОД (43; 43) = 2*43 = 86.
НОД (1118; 2064) = 86 [3].
Анализируя различные методы нахождения наибольшего общего делителя, можно прийти к мнению, что идеальных методов не бывает. Каждый метод характеризуется своими положительными и отрицательными сторонами. В каждом конкретном случае, мы должны определиться с выбором наиболее эффективного метода для того, чтобы максимально бережно отнестись к затраченному времени, которого на экзаменах как всегда будет не хватать.
Литература:
1. Виленкин Н. Я. и др. Математика, 6 класс: учебник для общеобразовательных учреждений. — М.: Мнемозина, 2013. — 288 с.
2. Макарычев Ю. Н., Миндюк Н. Г. Алгебра: Дополнительные главы к школьному учебнику 8 кл.: учебное пособие для школ и классов с углубленным изучением математики.- М.: Просвещение, 1996.- 207 с.
3. Щетников А. И. Алгоритм Евклида и непрерывные дроби. — Новосибирск: АНТ, 2003 г.-103 с.
Основные термины (генерируются автоматически): общий делитель, большее число, число, результат вычитания, бинарный алгоритм, меньшее число, возможный делитель числа, общий делитель чисел, алгоритм, множитель.

Вычисление НОД двух чисел m и n методом последовательного перебора.
Шаг 1. Присвоить значение функции min[m,n] переменной t;
Шаг 2. Разделить m на t. Если остаток равен 0, перейти к шагу 3; иначе перейти к шагу 4;
Шаг 3. Разделить n на t. Если остаток равен 0, вернуть t в качестве ответа и закончить работу, иначе перейти к шагу 4;
Шаг 4. Вычесть 1 из t. Перейти к шагу 2.
Программа отказывается работать из-за следующих ошибок:
C:Program Files (x86)Dev-CppMinGW64x86_64-w64-mingw32liblibmingw32.a(lib64_libmingw32_a-crt0_c.o) In function `main’:
C:crossdevsrcmingw-w64-v3-gitmingw-w64-crtcrtcrt0_c.c undefined reference to `WinMain’
C:UsersUserDesktopРаботы по C++collect2.exe [Error] ld returned 1 exit status
| C++ | ||
|
На этой странице вы узнаете
- Как быстро работает программа?
- Есть ли смысл перебирать делители после корня?
- Что количество делителей может сказать о самом числе?
Гадание на кофейной гуще или на картах Таро? Может, на ромашке? Хотя лучше не доверять свои отношения цветку. Наша судьба — только в наших руках. А судьба чисел предопределена заранее. Сегодня мы будем предсказывать их жизнь и судьбу по делителям. Но главная проблема — найти эти делители.

Постановка проблемы. Переборное решение
Встречали ли вы странных персонажей в задачах, которым резко понадобилось купить 50 арбузов? А что подумаете, если ваш учитель математики задаст найти число, у которого 50 делителей?
Поиск делителей в математике не самый сложный процесс. Есть разные способы: разложение на простые множители, обычный перебор и так далее. Сложность задания будет зависеть от самого числа. Довольно быстро получится найти делители числа 24 — число небольшое, красивое, удобное. Нахождение делителей числа 1234567 займет гораздо больше времени.
Я предлагаю включить компьютер, открыть среду разработки и заставить код сделать за нас всю работу.
Идея в следующем:
- Создадим список, в который мы сохраним все делители числа.
- С помощью цикла for переберем все числа из диапазона от 1 до самого числа.
- Если в переборе мы нашли такое число, которое является делителем исходного — остаток от деления будет равен 0 — сохраним это число в список.
В итоге мы получим список всех делителей исходного числа.
number = 1234567
dels = []
for i in range(1, number + 1):
if number % i == 0:
dels.append(i)
print(dels)
_____________________________________________________________________
Вывод: [1, 127, 9721, 1234567]У этого метода есть очень большая проблема — время его работы.
Программа выполняет команды очень быстро, но не бесконечно быстро.
Время работы программы можно измерить. Например, Sublime Text 3 занимается этим автоматически. И он помог посчитать, что программа выше выполнилась за 0.2 секунды. Давайте постепенно повышать ставки и смотреть, сколько времени понадобится этой же программе для поиска делителей других чисел:
— число 1234567 — 0.2 секунды;
— число 12345670 — 0.9 секунды;
— число 123456700 — 8.0 секунд;
— число 1234567000 — 115.7 секунд.
С числом 1234567 программа сделала 1234567 шагов цикла for, и справилась неимоверно быстро. Но чем больше ей придется выполнять команд, тем дольше придется работать.
Замеры времени зависят от многих факторов, например, мощности компьютера. Но мы можем повысить эффективность работы программы.
Ускоренный перебор делителей
Идея ускоренного перебора делителей заключается в том, что, найдя один делитель, мы сразу можем подобрать второй — его пару.
Возьмем число 24. Найдя его делитель 2, мы сразу можем сказать, что у 24 есть еще один делитель — 12, потому что 12 = 24 / 2. Интересная мысль? Давайте ее развивать.
Найдем по такой логике все делители числа 16.
- Самый простой делитель числа — 1. И по этой логике сразу найдем второй делитель — само число 16, так как 16 / 1 = 16.

- Проверим число 2. Это делитель, так что сразу найдем его пару: 16 / 2 = 8.

- Проверяем число 3 — это не делитель, его просто пропускаем.

- При проверке числа 4 мы столкнемся с интересной ситуацией. Его парой будет 16 / 4 = 4 — то же самое число, а мы ищем различные пары. Значит, у корня числа пары не будет: найдя корень, мы найдем только один делитель.

Если мы продолжим перебор, числа 5, 6 и 7 — не будут делителями. А за ними — 8, делитель, который мы уже нашли.
Нет. Найдя “маленький” делитель, при ускоренном переборе мы можем найти его пару, которая будет “большим” делителем. Перебирая делители, рано или поздно мы дойдем до корня числа, у которого нет пары. Перебирая числа после корня, мы будем находить только “большие” делители, которые уже нашли в паре с “маленькими”.
Если у числа целого корня нет, перебираем до его округленного вниз значения.
Нам нет смысла перебирать числа после корня, так что будем перебирать до предельно близкого к нему значения, но не больше.
Логика программы будет такой:
- Перебираем числа от 1 до корня исходного числа.
- Если мы нашли корень числа, добавляем в список делителей только его.
- Если мы нашли не корень, а обычный делитель — добавляем в список сразу пару делителей.
Пример реализации ускоренного перебора делителей для числа 1234567000:
number = 1234567000
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
print(len(dels))
_____________________________________________________________________
Вывод: 64Эта программа нашла все делители числа и выдала их количество — 64. А на ее работу ушло меньше секунды.
Но и это не панацея. Что, если нам придется проверить делители сразу нескольких чисел? Например, мы хотим найти все числа, у которых ровно 7 делителей, в диапазоне от 1 до 10000.
Программу надо немного модифицировать:
- заведем переменную-счетчик, которая будет считать подходящие числа;
- number сделаем перебираемой переменной по нужному диапазону с помощью цикла for;
- ускоренный перебор будет внутри перебора number;
- в конце каждого шага цикла проверяем — если делителей у числа ровно 7, то увеличиваем наш счетчик на 1.
Теперь программа будет выглядеть следующим образом:
count = 0
for number in range(1, 10000):
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) == 7:
count += 1
print(count)
_____________________________________________________________________
Вывод: 2Эта программа работала всего 0.2 секунды. Звучит неплохо, но давайте снова поднимать ставки:
- диапазон 1 — 10000 — 0.2 секунды;
- диапазон 1 — 100000 — 2.6 секунды;
- диапазон 1 — 1000000 — 80.2 секунды.
Время снова увеличивается очень быстро. Что можно с этим сделать?
Еще более ускоренный перебор делителей
Не считаем, что не нужно
Обратите внимание — программа выше нашла среди чисел 1–10000 всего 2 числа, имеющих ровно 7 делителей. А сколько же у остальных? Может быть и больше, может быть и меньше. Например, у числа 9864 делителей аж 24 штуки. Стоило ли тратить время на поиск их всех, если количество делителей больше 7?
Конечно, нет. Как только мы нашли 8 штук, мы уже можем понять, что анализировать число далее нам неинтересно. Значит, нужно остановить работу цикла.
Команда break полностью останавливает работу цикла.
Мы можем модернизировать нашу последнюю программу: если в переборе делителей мы увидим, что их больше семи, завершаем цикл командой break.
count = 0
for number in range(1, 10000):
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) > 7:
break
if len(dels) == 7:
count += 1
print(count)При этом завершится именно цикл перебора делителей i, так как break находится именно в нем, а цикл перебора number продолжит свою работу.
Давайте произведем замеры еще раз:
- диапазон 1-10000 — 0.2 секунды;
- диапазон 1-100000 — 2.1 секунды;
- диапазон 1-1000000 — 53.5 секунды.
В последнем случае мы сэкономили около трети от времени работы программы. Но и это не предел.
Не считаем, что не нужно 2.0
Вернемся на несколько абзацев выше, когда мы искали делители числа 16. Мы нашли 5 делителей — 2 пары и 1 корень, который не даст пару. Это справедливо для любого числа: целый корень не будет давать пару ни с каким другим числом, а все остальные делители — будут.
Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем.
Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.
Нам нужны числа, у которых ровно 7 делителей. Следовательно, нам нужны числа, у которых есть целый корень. Это можно проверить, вычислив точный корень числа и его округленное значение. Если они совпадут, значит, округлять корень было некуда и он целый.
Но как пропускать числа, которые нам не нужны?
Команда continue останавливает работу текущего шага цикла и сразу переходит к следующему.
Если мы найдем число number, у которого нет целого корня, мы можем применить команду continue: данный шаг цикла перебора number завершается, и мы сразу перейдем к следующему.
Включить эту проверку в программу можно следующим образом:
count = 0
for number in range(1, 10000):
if number ** 0.5 != int(number ** 0.5):
continue
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) > 7:
break
if len(dels) == 7:
count += 1
print(count)
Снова посмотрим на время работы программы при разных диапазонах:
- диапазон 1-100000 — 0.1 секунды;
- диапазон 1-1000000 — 0.5 секунды;
- диапазон 1-10000000 — 4.5 секунды;
- диапазон 1-100000000 — 44.4 секунды.
А делители — это вообще для чего? А таблицы со временем — это точно важно? Может, подождать проще, чем учить все это?
Нахождению делителей чисел посвящена задача 25 ЕГЭ, и без этих теоретических знаний решить ее крайне сложно. Что же касается времени работы, то за ним приходится следить внимательнейшим образом, ведь в задачах могут встречаться ситуации, когда надо найти делители для сотен миллионов чисел за раз!
Зная все особенности ускорения перебора делителей и поиска чисел с конкретными делителями, за считанные секунды можно решать задачи огромных диапазонов.
Фактчек
- Ускоренный перебор делителей подразумевает нахождение делителей попарно, при этом перебирать делители достаточно только до корня числа.
- Команда break полностью останавливает работу цикла, а команда continue завершает работу лишь текущего шага цикла, перенося нас сразу на следующий.
- Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем. Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.
Проверь себя
Задание 1.
Для чего нужен ускоренный перебор делителей?
- Обычный перебор слишком скучный
- Для большей точности вычислений
- Для ускорения работы программы
Задание 2.
Найдите количество делителей числа 2568568668.
- 5
- 6
- 7
- 8
Задание 3.
Найдите, сколько чисел из диапазона от 2000 до 1002000 имеют ровно 5 делителей.
- Ни одного
- 1
- 10
- 8
Ответы: 1. — 3; 2. — 3; 3. — 4.
