Как найти общий делитель в pascal

Приведем 3 программы поиска наибольшего общего делителя двух натуральных чисел, основанных на:

• алгоритме Евклида
• перебора возможных делителей числа
• разложения чисел на простые множители

Что такое наибольший общий делитель двух натуральных чисел m и n, или НОД(m, n)

НОД двух натуральных чисел – это такое наибольшее натуральное число, которое одновременно делит без остатка оба этих числа.

Алгоритм Евклида

Евклид – древнегреческий математик, геометр, автор первого из дошедших до нас теоретических трактатов по математике.

Алгоритм Евклида – один из наиболее ранних численных алгоритмов в истории. Евклид впервые дал описание этого алгоритма в книгах «Начала». Изначально этот алгоритм назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль.

Сформулируем алгоритм

Пусть даны два натуральных числа m и n. Пока числа m и n не равны (или их разница не равна 0), большее число заменить их разницей. В качестве ответа взять любое из чисел.

Пример:

Пусть m = 12, n = 18

12<>18, n = 18 – 12 = 6

12<>6, m = 12 – 6 = 6

6<>6, НОД(12, 18) = 6

Программа на языке программирования Паскаль (алгоритм Евклида)

var m, n:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);  

  readln(m,n);

  while m<>n do

  begin

    if m>n then m:=m-n

           else n:=n-m;

  end;

  writeln(‘НОД(m,n): ‘,m);

end.

Результат запуска программы

Перебор возможных делителей числа

Будем использовать алгоритм, разобранный ранее в этом блоге.

Запустим цикл for с счетчиком k от 1 до n, будем проверять условие: если число n делится на значение счетчика k без остатка (n mod k = 0), то значение счетчика k – это делитель числа n, значение k можно вывести на экран или сохранить в отдельной переменной.

Поскольку нам нужен наибольший общий делитель чисел m и n, поэтому запустим цикл до минимального из чисел m и n (другое будет лишним), и будем проверять условие: если число m делится на значение счетчика цикла k без остатка и число n делится на значение счетчика цикла k без остатка одновременно (воспользуемся операцией and), это и будет их общий делитель.

Программа на языке программирования Паскаль (перебор возможных делителей числа)

var m, n, k, p:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);

  readln(m,n);

  for k:=1 to min(m,n) do 

  begin

    if (m mod k = 0) and (n mod k=0) then p:=k;

  end;

  writeln(‘НОД(m,n): ‘,p);

end.

Функция min будет работать в PascalABC.NET, в случае использования другой среды, нужно до цикла определить наибольшее число из m и n.

Разложение чисел на простые множители

Ранее мы разбирали алгоритм разложения натурального числа на простые множители. 

Как связаны простые множители числа и НОД. Приведем пример.

Пусть m = 18,  n = 12

Выполним разложение на простые множители.

Множители числа m: 2 3 3

Множители числа n: 2 2 3

Выделим их общие простые множители – это числа 2 и 3. В качестве наибольшего общего делителя нужно взять из произведение: 2 * 3 = 6. НОД(12, 18) = 6.

Пусть m = 36,  n = 48

Множители числа m: 2 2 3 3

Множители числа n: 2 2 2 2 3

Общие простые множители – это числа 2 2 3. Произведение этих множителей равно 12. НОД(36, 48) = 12.

Для нахождения НОД двух чисел нужно выполнить их разложение на простые множители и в качестве ответа взять произведение их общих множителей.

Как будем решать задачу

Для хранения множителей числа воспользуемся списком (PascalABC.NET), в него легко добавлять значение командой add.

Описание списка с именем nod в блоке var

var nod:List<integer>;

Создание нового пустого списка в теле программы

nod:=new List<integer>;

Добавление значения в конец списка

nod.add(значение);

Создадим два списка (s1 и s2) для хранения множителей числа m и n соответственно. С помощью конструкции вложенных циклов переберем все элементы списков и сравним на равенство, если множители равны, сохраним их в списке nod, а значения элементов списков сделаем равными -1 и -2 соответственно (чтобы далее их повторное сравнение на равенство было ложным) . В качестве ответа возьмем произведение элементов списка nod командой nod.Product.

Программа на языке программирования Паскаль (разложение чисел на простые множители)

var

  m, n, k1, k2: integer;      

  s1, s2, nod: List<integer>;

begin

  writeln(‘Введите два натуральных числа m и n:’);   

  readln(m, n);  

  s1 := new List<integer>; 

  s2 := new List<integer>; 

  nod := new List<integer>;

  k1 := 2; k2 := 2;  

  while (m > 1) or (n > 1) do   

  begin

    while m mod k1 = 0 do     

    begin

      m := m div k1;      

      s1.Add(k1); //добавить значение в список можно и так: s1+=k1;

    end;     

    k1 += 1;     

    while n mod k2 = 0 do    

    begin

      n := n div k2;       

      s2.Add(k2);     

    end;     

    k2 += 1;   

  end;   

  //writeln(s1, s2); 

  for k1:=0 to s1.Count-1 do //элементы списка нумеруются с 0, длина списка s1.count

    for k2:=0 to s2.Count-1 do

      if s1[k1]=s2[k2] then //s1[k1] – обращение к элементу списка по его номеру

        begin 

        nod.Add(s1[k1]);

        s1[k1]:=-1;

        s2[k2]:=-2;

        end;

  //println(s1,s2,nod);

  println(‘НОД(m,n): ‘,nod.Product);

end.

Это программа состоит из самого большого количества строк. Насколько она эффективна?

Задача на применение НОД

Даны числа: a = 2³ • 3¹⁰ • 5 • 7² , b = 2⁵ • 3 • 11. Чему равен  НОД (a,b)?

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var
  a, b, d: integer;

begin
  write('Введите два числа: ');
  readln(a, b);
  if a < b then d := a + 1 else d := b + 1; 
  {так как мы используем цикл с постусловием, 
  необходимо минимальное значение увеличить на один,
  иначе цикл repeat, в силу своих конструктивных особенностей,
  не учтет это минимальное число  
  и не сделает его кандидатом в НОД. Например, 5 и 25.}
  repeat d := d - 1
  until (a mod d = 0) and (b mod d = 0);
  write('NOD = ', d)
end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A,  B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

Доказательство:

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

Блок — схема алгоритма Евклида «с вычитанием»

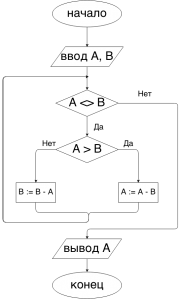
Программа

var
  a, b: integer;

begin
  write('a = '); 
  readln(a);
  write('b = ');
  readln(b);
  while a <> b do 
    if a > b then 
      a := a - b 
    else 
      b := b - a;
  writeln('NOD = ', a);
end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var
  a, b: integer;

begin
  write('a = ');
  readln(a);
  write('b = ');
  readln(b);
  while (a <> 0) and (b <> 0) do
    if a >= b 
    then 
      a := a mod b 
    else 
      b := b mod a;
  write(a + b)
end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Напишите программу для вычисления наибольшего общего делителя двух целых чисел. Задачу решим двумя способами: используя оператор repeat, используя оператор while.

Примечание: наибольшим общим делителем (сокращенно пишут НОД) двух натуральных чисел m и n называется наибольший из их общих делителей. Обозначение: НОД(m, n).

Например, найдем НОД(12, 8):
Выпишем все делители числа 12: 1, 2, 3, 4, 6, 12;
Выпишем все делители числа 8: 1, 2, 4, 8;
Выпишем все общие делители чисел 12 и 8: 1, 2, 4. Из них наибольшее число – 4. Это и есть НОД чисел 12 и 8.

Решение

Воспользуемся так называемым алгоритмом Евклида нахождения НОД, который выведен с помощью математических методов. В самом простейшем случае для заданных чисел m и n он выглядит так:

1) Если m неравно n, перейти к шагу 2, в противном случае вывести m и закончить алгоритм;
2) Если m > n, заменить m на m − n, в противном случае заменить n на n − m;
3) Перейти на шаг 1

Как видим, в шаге 2 большее из двух текущих чисел заменяется разностью большего и меньшего.

Приведем пример для чисел 12 и 8:

1) Так как 12 > 8, заменим 12 на 12 − 8 = 4;
2) Так как 8 > 4, заменим 8 на 8 − 4 = 4;
3) 4 = 4, конец.

1 способ

С использованием оператора while.

Алгоритм на естественном языке:

1) Ввод m и n;
2) Запуск цикла с предусловием m < > n. В цикле:
   Если m > n, то переменной m присвоить m − n, иначе переменной n присвоить n − m;
3) Вывод m:

Код:

program nod1;
var
   x, y: integer;
   nod: integer;
begin
   writeln (‘m=’);
   readln (m);
   writeln (‘n=’);
   readln (n);
   while m<>n do
     if m>n then m:=m-n
      else n:=n-m;
     nod:=m;
     writeln(‘НОД = ‘, nod)
end.

2 способ

С использованием оператора repeat.
Код:

program nod2;
var
   x, y: integer;
   nod: integer;
begin
   writeln (‘m=’);
   readln (m);
   writeln (‘n=’);
   readln (n);
   repeat
     if m>n then m:=m-n;
     if m<n then n:=n-m
   until m=n;
   nod:=m;
   writeln(‘НОД = ‘, nod)
end.

Опубликовано: 25.03.2018
Обновлено: 12.03.2020

Зачастую начинающие программисты знакомятся со средой Turbo Pascal посредством простейших задач. Первые задания, которые реализует пользователь в коде: вывести на экран какой-либо текст, найти НОД и НОК натуральных чисел, посчитать, сколько четвергов в месяце, и т.д. Зачастую встречаются и задачи с математическим уклоном. Прежде чем реализовать свои знания в программном коде, необходимо изучить дополнительный материал. Например, как найти НОД и НОК двух чисел в “Турбо Паскале”.

Нахождение НОД в математике

Наибольший общий делитель – число, которое считается максимальным при разложении на составляющие. Записывается краткая форма определения как НОД. Например, рассмотрим рисунок. Здесь даны числа 140 и 175. Их наибольшим делителем является 35, то есть НОД (140,175)=35.

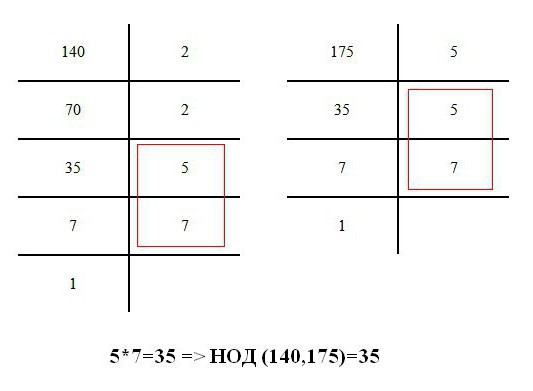
Чтобы не возникало дополнительных вопросов о том, как найти НОД двух чисел, следует придерживаться такого алгоритма:

• Найти простейшие делители первого числа.
• Эту же операцию проделать со вторым числом.
• Отыскать в наборе делителей первого и второго чисел общие показатели.
• Обвести их ручкой другого цвета.
• Перемножить общие делители (если их несколько) или выписать единственный (если числа простые, то их НОД будет равен 1).

Рассмотрим следующий рисунок. На нем показано, что даже такие большие числа, как 816 и 455, не имеют НОД, кроме 1.

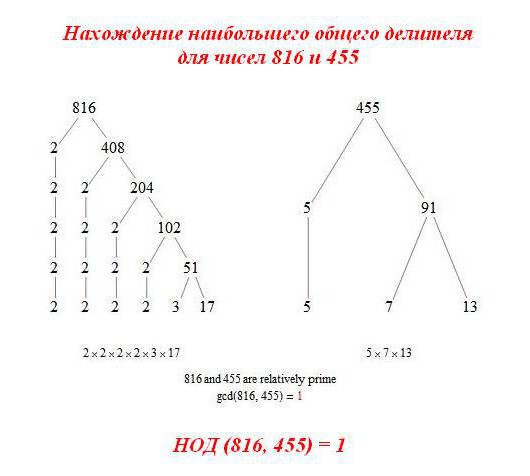
Существует второй способ нахождения поставленной задачи. Алгоритм Евклида в математике выглядит следующим образом:

• Даны числа.
• Выбрать следует максимальное.
• Его делят на минимальное.

• 

  Теперь второе заданное число нужно разделить на получившийся остаток.

• Первый остаток делится на второй, получившийся от предыдущей операции.
• Вторую остаточную часть делим на третью и т.д.
• Операция деления проводится до тех пор, пока остаток не будет равен 0.
• Последний делитель и отвечают критерию НОД.

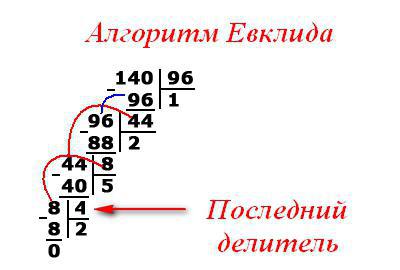
Для нахождения НОД более трех натуральных чисел рекомендуется придерживаться схемы работы (возьмем числа 140, 96, 64):

• В первом действии нужно повторить вышеописанный алгоритм для первых двух чисел.
• Найти НОД найденного делителя и заданного третьего числа.
• Отыскать НОД получившегося делителя и четвертого числа и т.д.

Нахождение НОК в математике

Если в программировании возникает вопрос о том, как найти НОД двух чисел, то он обязательно сопряжен со вторым: нахождение НОК. Наименьшим общим кратным двух чисел называют такое минимальное натуральное число, которое может поделиться и на первое, и на второе.

Первый способ:

• Даны два или более чисел.
• Выписать все кратные для каждой позиции.
• Выбрать наименьшее общее кратное.

Второй способ:

• Разложить все числа на простейшие множители.
• Записать в строчку все делители первого числа и добавить сюда же те сомножители, которые есть в других разложениях, но отсутствуют в первом.
• Вычислить произведение.

НОД в “Паскале”: алгоритм работы

Как найти НОД двух чисел? “Паскаль” – язык программирования, на котором будет написан код. Сначала необходимо придерживаться алгоритма, указанного выше. И здесь математика приходит на помощь. Алгоритм работы задачи поможет найти НОД двух натуральных чисел. В Turbo Pascal это будет выглядеть следующим образом:

• Вывод на экран приглашения ввести с клавиатуры 2 неотрицательных числа.
• Запуск цикла while, где условием будет число 1 <> число 2 (условно a и b).
• Тело цикла включает такие действия: если a > b, тогда a:= a – b, иначе b:= b – a.
• Вывод на экран результата.

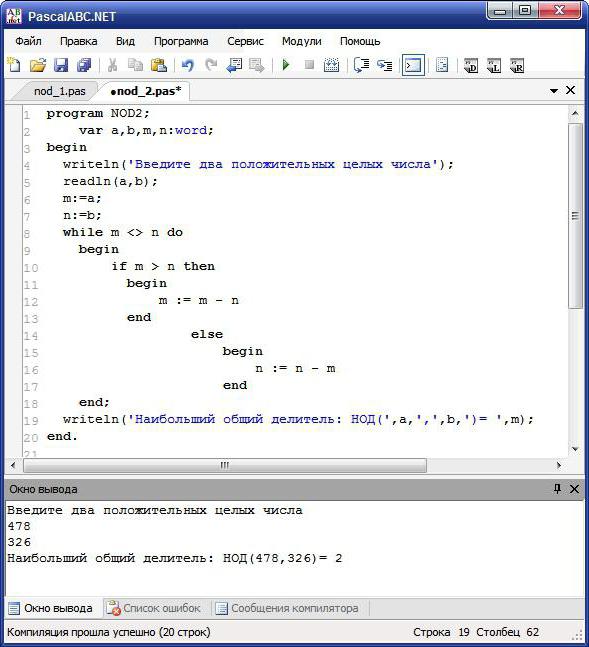
НОД в “Паскале”: решение методом Евклида

Как найти НОД двух чисел посредством простого, но действенного метода?

• Ввод положительных чисел.
• Вызов написанной функции, вычисляющей НОД. В самой функции выполняются следующие действия: проверка условия, какое число больше; присвоение другим переменным изначальных данных; в цикле с предусловием (r2 <> 0, т.е. пока переменная не будет равняться 0) находится остаток от деления и переменным присваиваются результаты; присвоение имени функции готового результата.
• Вывод результата на экран.

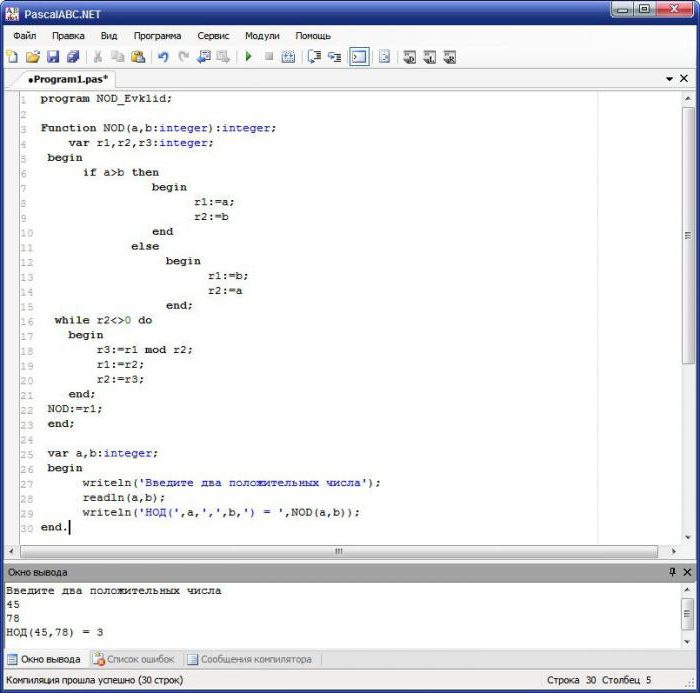
Многие программисты считают, что оба варианта нахождения НОД очень схожи, поэтому в Интернете первый метод могут выдавать за алгоритм Евклида.

НОК в “Паскале”: как устроена программа?

Здесь уже были рассмотрены 2 алгоритма, поясняющие, как найти НОД двух чисел. Теперь осталось усвоить, как выглядит программа поиска НОК в Turbo Pascal. Алгоритм работы при программировании таков:

• Ввод двух чисел.
• Присвоение двум другим переменным заданных значений.
• Нахождение произведения изначальных элементов.
• В цикле с предусловием (while) оформить условие: если первое число больше второго (n > m), тогда можно найти посредством вычитания результат (n:= n – m); иначе выполнить эту операцию, но в обратную сторону (m:= m – n).
• Вывести на экран результат, при котором найденное произведение будет делиться посредством функции div на число m.

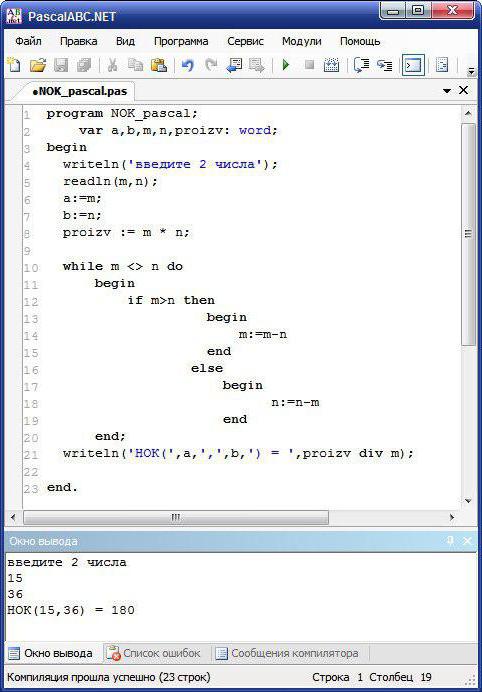
Для чего вводятся две переменные a и b? С той целью, чтобы грамотно вывести на экран результат. В цикле с предусловием первоначальные значения переменных потеряются, поэтому вывести в скобках заданные пользователем m, n не представится возможным. Конечно, строку 21 можно значительно упростить, написав только writeln (proizv div m). Но пользователь, который впервые будет знакомиться с программой, не поймет, что выведено на экран.

Ручная трассировка:

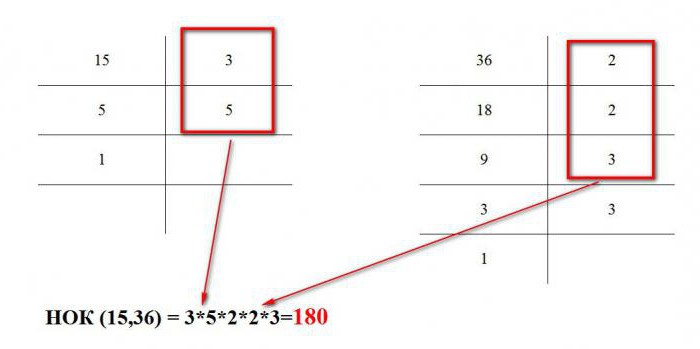
Как видно, ничего сложного в поиске решения НОД и НОК нет: ни в “Паскале”, ни, собственно, в математике.

Алгоритм Евклида

Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).

Python

#!/usr/bin/env python
a = 18
b = 30
 
while a!=0 and b!=0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print (a+b)

Perl:

 sub nod
 {
 return  $_[0] != 0  ?  nod ( ( $_[1] % $_[0] ), $_[0] )  :  $_[1];
 }

C:

 int gcd(int a, int b) {
   int c;
   while (b) {
      c = a % b;
      a = b;
      b = c;        
   }
   return abs(a);
 }

Pascal:

  function nod( a, b: longint): longint; 
  begin
   while (a <> 0) and (b <> 0) do
     if a >= b then 
       a:= a mod b 
     else 
       b:= b mod a;
   nod:= a + b;
  end;

Java:

public class GCD {
    public static int gcd(int a,int b) {
        while (b !=0) {
            int tmp = a%b;
            a = b;
            b = tmp;
        }
        return a;
    }
}

C#:

int gcd(int a, int b)
{
    while (b != 0)
        b = a % (a = b);
    return a;
}