Как найти общий интеграл однородного уравнения - Сайт, где вы сможете решить свои вопросы

Как найти общее решение однородного дифференциального уравнения

СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ

Однородные ДУ первого порядка
1. Пример 1
2. Пример 2
3. Пример 3
Однородные линейные ДУ второго порядка
1. Пример 4
2. Пример 5

Данный тип задачи часто ставит студентов в тупик. Поэтому они присылают их на решение к нам. Мы написали данную статью, чтобы помочь разобраться в этой теме. Итак, прежде, чем приступать решать дифференциальное уравнение, необходимо понять к какому виду оно принадлежит. Сначала определить порядок, затем уже линейность и однородность. В данном материале рассмотрим однородные уравнения первого и второго порядка и как их решать. В зависимости от этого будет разный алгоритм действий. Так как в первом случае однородность уравнения по переменным, а во втором по правой части. Далее разберемся подробнее об этом.

Однородные ДУ первого порядка

Если после подстановки в уравнение вместо $x$ и $y$ соответствующих $lambda x$ и $lambda y$ можно добиться уничтожения всех $lambda$, то уравнение является однородным первого порядка.

Такие уравнения имеют общий вид $$P(x,y)dx+Q(x,y)dy=0,$$ где $P(x,y)$ и $Q(x,y)$ однородные функции одинакового порядка, то есть выполняются условия $P(lambda x,lambda y) = lambda^n P(x,y)$ и $Q(lambda x,lambda y) = lambda^n Q(x,y)$.

Алгоритм решения:

Проверить уравнение на однородность с помощью $lambda$
Привести уравнение к виду $y’ = f(frac{y}{x})$
Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
Решить уравнение методом разделяющихся переменных.

Пример 1

Решить однородное дифференциальное уравнение первого порядка $$y’=e^frac{y}{x}+frac{y}{x}.$$

Решение

Подставляя $lambda$ перед $x$ и $y$ в исходное уравнение получаем $$y’ = e^frac{lambda y}{lambda x} + frac{lambda y}{lambda x},$$ в котором все $lambda$ сокращаются, и это означает, что перед нами однородное дифференциальное уравнение первого порядка.

Выполняем замену $frac{y}{x} = t Rightarrow y’ = t’x + t$ в исходном уравнении и получаем: $$t’x+t=e^t+t$$ $$t’x=e^t.$$ Данное уравнение с разделяющимися переменными. Записываем его соответствующим образом и переносим всё, что содержит $t$ в левую часть, а то что с $x$ в правую: $$frac{dt}{dx} x=e^t$$ $$frac{dt}{e^t}=frac{dx}{x}.$$ Интегрируем обе части уравнения: $$int frac{dt}{e^t}=int frac{dx}{x}$$ $$-e^{-t} = ln|x|+C.$$

Теперь необходимо выполнить обратную замену $t = frac{y}{x}$, чтобы вернуться к $y$ $$-e^{-frac{y}{x}} = ln|x| + C.$$ Записываем ответ в виде общего интеграла $$e^{-frac{y}{x}}+ln|x|=C.$$

Ответ

$$e^{-frac{y}{x}}+ln|x|=C$$

Пример 2

Найти решение однородного дифференциального уравнения первого порядка $$(x^2+2xy)dx+xydy=0.$$

Решение

Подставляем перед всеми иксами и игриками дополнительную константу $lambda$, чтобы убедиться в однородности уравнения: $$( (lambda x)^2 + 2lambda x lambda y)d(lambda x) + lambda x lambda y d(lambda y) = 0$$ $$lambda^3 (x^2+2xy)dx+lambda^3 xydy = 0$$ $$(x^2+2xy)dx+xydy=0.$$ Как видно, все $lambda$ уничтожились, поэтому действительно дано однородное ДУ первого порядка.

Приведем уравнение к виду $y’ = f(frac{y}{x})$. Разделим уравнение на $x^2$ и $dx$. Получим $$(1+2frac{y}{x})+frac{y}{x}frac{dy}{dx} = 0.$$ Теперь выполняем замену $$frac{y}{x}=t, qquad frac{dy}{dx} = t’x+t.$$ Подставляем это в уравнение и получаем $$(1+2t)+t(t’x+t) = 0, $$ и раскрываем скобки и упрощаем: $$1+2t+t’tx+t^2=0$$ $$t’tx + (t+1)^2=0.$$

Получившееся уравнение является ДУ с разделяющимися переменными. Поэтому начинаем резделять переменные $t$ и $x$ по разные стороны от знака равенства. Записываем уравнение в виде $$frac{dt}{dx}tx = -(t+1)^2.$$ Делим обе части на $(t+1)^2$ и $x$, затем умножаем на $dx$ $$frac{tdt}{(t+1)^2} = -frac{dx}{x}.$$

Последнее равенство нужно проинтегрировать, чтобы вытащить $t(x)$ $$int frac{tdt}{(t+1)^2} = – int frac{dx}{x}.$$ Решаем первый интеграл методом разложения: $$int frac{tdt}{(t+1)^2} = int frac{(t+1)-1}{(t+1)^2}dt = int frac{t+1}{(t+1)^2}dt – int frac{dt}{(t+1)^2} = $$ $$ = int frac{dt}{t+1} – int frac{dt}{(t+1)^2} = $$ $$ = ln|t+1| + frac{1}{t+1} + C.$$ Решаем второй интеграл $$int frac{dx}{x} = ln|x| + C.$$ Возвращаемся к равенству двух интегралов и подставляем полученные решения $$ln|t+1| + frac{1}{t+1} = -ln|x|+C.$$

Вспоминаем, что в начале решения задачи была сделана подстановка $frac{y}{x}=t$, и значит, назад нужно вернуться к $y$ $$ln|frac{y}{x}+1|+frac{1}{frac{y}{x}+1} = -ln|x| + C.$$ Выполняем преобразования последнего уравнения: $$ln|frac{x+y}{x}|+frac{x}{y+x}=-ln|x|+C$$ $$ln|x+y|-ln|x|+frac{x}{y+x}=-ln|x|+C$$ $$ln|x+y|+frac{x}{x+y}=C.$$ Выразить $y$ просто так не получится. Поэтому оставим ответ в таком виде, который называется общий интеграл дифференциального уравнения.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ln|x+y|+frac{x}{x+y}=C$$

Пример 3

Решить однородное дифференциальное уравнение $$xy’ sinfrac{y}{x}+x=ysin frac{y}{x}.$$

Решение

Как всегда начинает с проверки на однородность с помощью подстановки $lambda$ в исходное ДУ $$lambda xy’ sinfrac{lambda y}{lambda x}+lambda x=lambda ysin frac{lambda y}{lambda x}.$$ Видим, что все $lambda$ сокращаются и уравнение приобретает вид из условия задачи. Значит, это однородное ДУ первого порядка.

Придадим ему вид $y’=f(frac{y}{x})$ для удобства замены. Для этого разделим обе части уравнения на $x$ $$y’ sinfrac{y}{x}+1=frac{y}{x} sin frac{y}{x}.$$ Теперь делаем подстановку $frac{y}{x}=t$ и $y’=t’x+t$: $$(t’x+t) sin t + 1 = t sin t$$ $$t’x sin t + tsin t+1=tsin t$$ $$t’x sin t=-1.$$ Получили уравнение с разделяющимися переменными. Всё, что с $t$ налево, всё что с $x$ направо: $$frac{dt}{dx} x sin t = -1$$ $$sin t dt = -frac{dx}{x}.$$

Интегрируем обе части равенства: $$int sin t dt = -int frac{dx}{x}$$ $$-cos t = -ln|x|+C.$$ Выполняем обратную замену в последнем уравнении $$cos frac{y}{x} = ln|x|+C.$$ Так как выразить $y$ достаточно тяжело, то запишем ответ в виде общего интеграла $$cos frac{y}{x}-ln|x|=C.$$

Ответ

$$cos frac{y}{x}-ln|x|=C$$

Однородные линейные ДУ второго порядка с постоянными коэффициентами

Такие уравнения имеют следующий общий вид $$y”+py’+qy=0, $$ где $p$ и $q$ постоянные коэффициенты. Чтобы решить такие уравнения первым делом нужно составить характеристический многочлен $$lambda^2+plambda + q = 0, $$ который получается путем замены всех $y$ на $lambda$ в степенях, соответствующих порядку производной $y$ $$y” Rightarrow lambda^2, quad y’ Rightarrow lambda, quad y Rightarrow 1.$$ Затем в зависимости от найденных корней $lambda_1$ и $lambda_2$ составляется общее решение:

Если $lambda_1 neq lambda_2$, тогда $y=C_1e^x + C_2e^x$
Если $lambda_1 = lambda_2$, тогда $y=C_1e^x + C_2xe^x$
Если $lambda_{1,2} = alpha pm beta i$, тогда $y=C_1e^{alpha x} cos beta x + C_2 e^{alpha x} sin beta x$.

Пример 4

найти общее решение однородного дифференциального уравнения второго порядка $$y”-9y=0.$$

Решение

Составляем характеристический многочлен путем замены $y$ на $lambda$ в степени, соответствующей порядку производной и находим его корни: $$lambda^2 – 9 = 0$$ $$(lambda – 3)(lambda+3)=0$$ $$lambda_1=3, quad lambda_2=-3.$$

Так как получили действительные корни, отличающиеся друг от друга, то общее решение однородного уравнения будет выглядеть следующим образом $$y=C_1e^{-3x}+C_2e^{3x}.$$

Ответ

$$y=C_1e^{-3x}+C_2e^{3x}$$

Пример 5

Решить однородное дифференциальное уравнение второго порядка $$y”-6y’+25y=0.$$

Решение

Составим характеристическое уравнение путем замены $y$ на $lambda$ $$lambda^2 – 6lambda + 25 = 0.$$ Решим квадратное уравнение. Вычислим его дискриминант $$D = b^2-4ac = (-6)^2 – 4cdot 1 cdot 25 = 36 – 100 = -64.$$ Теперь найдем значения корней $$lambda_{1,2} = frac{-b pm sqrt{D}}{2} = frac{6pm 8i}{2} = 3pm 4i.$$ В итоге получили комплексно-сопряженные корни, значит, общее решение будет выглядеть $$y = C_1 e^{3x}cos 4x + C_2 e^{3x}sin 4x.$$

Ответ

$$y = C_1 e^{3x}cos 4x + C_2 e^{3x}sin 4x$$

Источник

Однородные дифференциальные уравнения первого порядка

Определение

Как определить однородное дифференциальное уравнение

Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx : y → ty , x → tx . Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.

Пример

Определить, является ли данное уравнение однородным

Делаем замену y → ty , x → tx .

Делим на t 2 .

.
Уравнение не содержит t . Следовательно, это однородное уравнение.

Метод решения однородного дифференциального уравнения

Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux . Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux ,
где u – функция от x . Дифференцируем по x :
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f ( u ) – u ) .

При f ( u ) – u ≠ 0 и x ≠ 0 получаем:

Интегрируем:

Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:

Заменим постоянную интегрирования C на ln C , тогда

Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C . Тогда общий интеграл примет вид:

Далее следует рассмотреть случай f ( u ) – u = 0 .
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).

Всякий раз, когда мы, в процессе преобразований, делим какое-либо уравнение на некоторую функцию, которую обозначим как g ( x, y ) , то дальнейшие преобразования справедливы при g ( x, y ) ≠ 0 . Поэтому следует отдельно рассматривать случай g ( x, y ) = 0 .

Пример решения однородного дифференциального уравнения первого порядка

Проверим, является ли данное уравнение однородным. Делаем замену y → ty , x → tx . При этом y′ → y′ .
,
,
.
Сокращаем на t .

Постоянная t сократилась. Поэтому уравнение является однородным.

Делаем подстановку y = ux , где u – функция от x .
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0 , |x| = x . При x ≤ 0 , |x| = – x . Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0 , а нижний – к значениям x ≤ 0 .
,
Умножаем на ± dx и делим на .

При u 2 – 1 ≠ 0 имеем:

Интегрируем:

Интегралы табличные,
.

Применим формулу:
( a + b )( a – b ) = a 2 – b 2 .
Положим a = u , .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.

Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C .

Умножаем на x и подставляем ux = y .
,
.
Возводим в квадрат.
,
,
.

Теперь рассмотрим случай, u 2 – 1 = 0 .
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 19-07-2012 Изменено: 24-02-2015

Как решить однородное дифференциальное уравнение

Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения: y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.

Примеры решения однородных дифференциальных уравнений 1-го порядка.

1) Решить уравнение

Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда

u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки

u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,

Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0

В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u

ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда

ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:

По свойству логарифмов:

Это — общий интеграл уравнения.

Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.

2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.

Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:

u’x=1/u. Так как u — функция от икса, u’=du/dx:

Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).

и поскольку в обеих частях стоят табличные интегралы, сразу же получаем

Выполняем обратную замену:

Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:

3) Найти общий интеграл однородного уравнения:

(x²-y²)dy-2xydx=0.

Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):

(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:

xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:

(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:

x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:

x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):

В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:

(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем:

По свойствам логарифмов:

Вспоминаем условие u≠0. Отсюда y≠0. При С=0 y=0, значит, потери решений не происходит, и y=0 входит в общий интеграл.

Можно получить запись решения в другом виде, если слева оставить слагаемое с x:

Геометрический смысл интегральной кривой в этом случае — семейство окружностей с центрами на оси Oy и проходящих через начало координат.

Задания для самопроверки:

Так как u=y/x, u²=y²/x², то есть y²=u²x²,

2) Проверив, что данное уравнение является однородным, делаем замену y=ux, отсюда y’=u’x+u. Подставляем в условие:

Делим обе части уравнения на x:

Интегрируем обе части:

и, умножив на x обе части уравнения, получаем:

Однородные дифференциальные уравнения
и приводящиеся к ним

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.

[spoiler title=”источники:”]

Как решить однородное дифференциальное уравнение

http://mathhelpplanet.com/static.php?p=odnorodnye-differentsialnye-uravneniya

[/spoiler]

Источник

Дифференциальное
уравнение первого порядка

(9)

называется
однородным
относительно
переменных x
и y,
если
– однородная функция нулевой степени
относительно своих аргументов.

Дифференциальное
уравнение первого порядка

(10)

называется
однородным
относительно
переменных x
и y,
если
и– однородные функции одной и той же
степениk
относительно своих аргументов.

Функция
называетсяоднородной
степени k
относительно переменных x
и y,
если для произвольного действительного
числа a
выполняется равенство

Однородное
дифференциальное уравнение первого
порядка (как уравнение (9), так и уравнение
(10)) может быть представлено в виде

. (11)

Метод
интегрирования однородных дифференциальных
уравнений состоит в следующем. Однородное
дифференциальное уравнение приводится
к виду (11). Вводится новая переменная
или,
где(),
и после подстановки в уравнение (11)
приходим к уравнению с разделяющимися
переменными относительно переменнойxи новой функцииt(x).

В
задании 2 необходимо решить однородное
обыкновенное дифференциальное уравнение
первого порядка.

Задание
2. Найти
общий интеграл (общее решение)
дифференциального уравнения. Сделать
проверку.

a)
, b),

c)
, d).

Решение:
Во всех случаях имеем однородные
относительно переменных x
и y
обыкновенные дифференциальные уравнения
первого порядка. Все они могут быть
сведены к уравнению вида (11). В случаях
a),
c),
d)
предварительно необходимо показать,
что эти уравнения являются однородными,
а затем привести их к виду (11).

Задание
2a.
.

Данное
уравнением является уравнением первого
порядка. Рассмотрим функцию
.
Эта функция является однородной функцией
нулевой степени, так как для произвольного
действительного числаa
выполняется равенство

Таким
образом, данное уравнением является
однородным и его можно свести к уравнению
(11). Для этого разделим числитель и
знаменатель правой части на x:

;

Сделаем
замену переменной
или,
где.
Найдеми подставим в преобразованное уравнение

;

;;

;

Пришли
к уравнению первого порядка с разделяющимися
переменными относительно переменной
x
и новой искомой функции t(x).
Заменяя
и разделяя переменные, получим

;

Проинтегрируем
обе части полученного уравнения

Возвращаясь к
исходному уравнению, получим

Умножив
обе части равенства на два и уединяя
произвольную постоянную, получим общий
интеграл уравнения с разделяющимися
переменными

Для
нахождения общего интеграла исходного
уравнения вернемся к старой переменной
через замену
:

Таким
образом, общий интеграл исходного
уравнения примет вид:

Сделаем
проверку.
Вычислим производную искомой функции
как функции, заданной неявно.

,
,

;

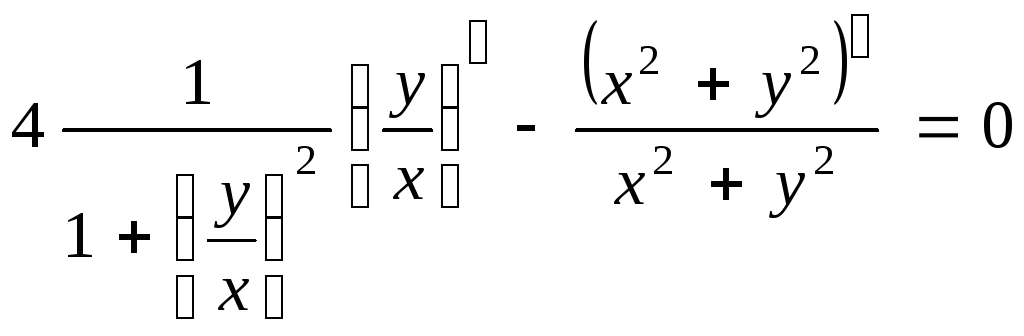
Подставим найденное
значение в искомое уравнение

и получим
тождество (верное равенство).

Ответ:
общий интеграл

Задание
2b.

.

Имеем
обыкновенное дифференциальное уравнение
первого порядка, однородное относительно
переменных x
и y.
Сделаем замену переменной
или,
где.
Найдеми подставим в исходное уравнение

;

Проинтегрируем
обе части полученного уравнения

Интеграл,
стоящий в правой части является табличным
.

Найдем
интеграл от дробно рациональной функции,
стоящей слева. Для этого можно, например,
разложить подынтегральную функцию на
сумму простейших или, выделив в знаменателе
полный квадрат и сделав замену переменной,
прийти к табличному интегралу.

Тогда, возвращаясь
к исходному уравнению, получим

Возвращаясь к
старой переменной, получим

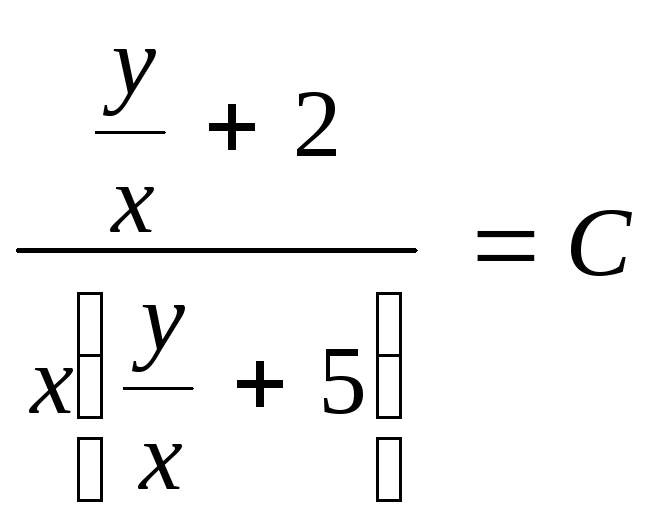
Откуда после
преобразований записываем общий интеграл

Проверка
выполняется аналогично тому, как это
делалось в предыдущих заданиях.

Ответ:
общий интеграл
.

Задание
2c.
.

Данное
уравнением является уравнением первого
порядка. Рассмотрим функцию
.
Эта функция является однородной функцией
нулевой степени, так как для произвольного
действительно числаa
выполняется равенство

Таким
образом, данное уравнение является
однородным и его можно решить аналогично
тому, как это показано в пункте a),
предварительно разделив числитель и
знаменатель правой части на
.

Сделаем
замену переменной

или
,;

;

Пришли
к уравнению первого порядка с разделяющимися
переменными относительно переменной
x
и новой искомой функции t(x).

;

Тогда

Таким
образом, общий интеграл исходного
уравнения примет вид:

Проверку
выполняется аналогично предыдущим
примерам.

Ответ:
общий интеграл
.

Задание
2d.
.

Рассмотрим
функции
,.
Эти функции являются однородными первой
степени относительно переменныхx
и y.
Действительно:

Тогда исходное
уравнение может быть сведено к уравнению
вида (9), а затем к виду (11).

Заметим,
что полученное уравнение совпадает с
уравнением из задания 2(a),
то есть пришли к случаю, который уже
рассмотрен.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения:y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.

Примеры решения однородных дифференциальных уравнений 1-го порядка.

1) Решить уравнение

$[y' = frac{y}{x}(1 + ln y - ln x).]$

Решение:

u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки

u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,

$[xfrac{{du}}{{dx}} = u cdot ln u.]$

$[frac{{du}}{{u cdot ln u}} = frac{{dx}}{x}]$

Интегрируем:

$[int {frac{{du}}{{u cdot ln u}} = int {frac{{dx}}{x}} } ]$

В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u

$[int {frac{{dt}}{t} = int {frac{{dx}}{x}} } ]$

ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда

$[ln frac{y}{x} = Cx]$

По свойству логарифмов:

$[ln y - ln x = Cx, Rightarrow frac{{ln y - ln x}}{x} = C]$

Это — общий интеграл уравнения.

Ответ:

$[frac{{ln y - ln x}}{x} = C.]$

2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.

Решение:

u’x+u=1/u+u. Упрощаем:

u’x=1/u. Так как u — функция от икса, u’=du/dx:

$[xfrac{{du}}{{dx}} = frac{1}{u}.]$

$[udu = frac{{dx}}{x}.]$

Интегрируем:

$[int {udu = int {frac{{dx}}{x},} } ]$

и поскольку в обеих частях стоят табличные интегралы, сразу же получаем

$[frac{{{u^2}}}{2} = ln left| x right| + C]$

Выполняем обратную замену:

$[frac{{{{(frac{y}{x})}^2}}}{2} = ln left| x right| + C, Rightarrow frac{{{y^2}}}{{2{x^2}}} - ln left| x right| = C.]$

$[frac{{{2^2}}}{{2 cdot {1^2}}} - ln 1 = C, Rightarrow 2 - 0 = C, Rightarrow C = 2.]$

Ответ:

$[frac{{{y^2}}}{{2{x^2}}} - ln left| x right| = 2.]$

3) Найти общий интеграл однородного уравнения:

(x²-y²)dy-2xydx=0.

Решение:

Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):

x²(1-u²)(xdu+udx)-2ux²dx=0

(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:

xdu-u²xdu+udx-u³dx-2udx=0,

xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:

(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:

x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:

$[frac{{1 - {u^2}}}{{u(1 + {u^2})}}du = frac{{dx}}{x}.]$

Интегрируем:

$[int {frac{{1 - {u^2}}}{{u(1 + {u^2})}}du = int {frac{{dx}}{x}.} } ]$

$[frac{{1 - {u^2}}}{{u(1 + {u^2})}} = frac{1}{u} - frac{{2u}}{{1 + {u^2}}},]$

$[int {frac{{du}}{u}} - int {frac{{2udu}}{{1 + {u^2}}}} = int {frac{{dx}}{x}.} ]$

$[int {frac{{du}}{u}} - int {frac{{d(1 + {u^2})}}{{1 + {u^2}}}} = int {frac{{dx}}{x}.} ]$

$[ln left| u right| - ln left| {1 + {u^{^2}}} right| = ln left| x right| + ln left| C right|]$

$[ln left| u right| - ln left| {1 + {u^{^2}}} right| - ln left| x right| = ln C]$

По свойствам логарифмов:

$[ln left| {frac{u}{{x(1 + {u^{^2}})}}} right| = ln C, Rightarrow frac{u}{{x(1 + {u^{^2}})}} = C]$

Обратная замена

$[frac{{frac{y}{x}}}{{x(1 + {{(frac{y}{x})}^2})}} = C, Rightarrow frac{y}{{{x^2} cdot frac{{{x^2} + {y^2}}}{{{x^2}}}}} = C, Rightarrow frac{y}{{{x^2} + {y^2}}} = C.]$

Вспоминаем условие u≠0. Отсюда y≠0. При С=0 y=0, значит, потери решений не происходит, и y=0 входит в общий интеграл.

Ответ:

$[frac{y}{{{x^2} + {y^2}}} = C.]$

Замечание

Можно получить запись решения в другом виде, если слева оставить слагаемое с x:

$[int {frac{{du}}{u}} - int {frac{{d(1 + {u^2})}}{{1 + {u^2}}}} = int {frac{{dx}}{x}.} ]$

$[ln left| x right| = ln left| u right| - ln left| {1 + {u^{^2}}} right| + ln left| C right|]$

$[ln left| x right| = ln left| {frac{{Cu}}{{1 + {u^{^2}}}}} right|, Rightarrow x = frac{{Cu}}{{1 + {u^{^2}}}}, Rightarrow {x^2} + {y^2} = Cy.]$

Задания для самопроверки:

1) (x²+y²)dx-xydy=0

$[xy' = 3sqrt {{x^2} + {y^2}} + y.]$

Показать решение

Источник

1. Уравнения с разделяющимися переменными

Общий вид уравнений

. (8.10)

С учетом равенства

(8.11)

уравнение (8.10) может быть записано в виде .

Разделим обе части на произведение функций M(x)∙Q(y) (при условии ) и после сокращения получим: . Так как переменные разделены, проинтегрируем уравнение
почленно:. После нахождения интегралов получаем общий интеграл
исходного ДУ. Предполагая, что, мы могли потерять решения. Следовательно, необходимо
подстановкой M(x)=0, Q(y)=0 в исходное уравнение сделать проверку. В том
случае, когда данные функции удовлетворяют уравнению, они также являются его решениями.

Пример 8.2. Проинтегрировать уравнение .

Решение. Представим уравнение в виде. Разделим переменные: . Проинтегрируем уравнение:

После
применения теоремы о сумме логарифмов и потенцирования получаем

– общий интеграл исходного уравнения

2.
Однородные дифференциальные уравнения первого порядка

Общий вид уравнений

, (8.12)

где M(x;y) и N(x;y)– однородные функции аргументов x и y одного и
того же измерения m, то есть
имеют место равенства

. (8.13)

Метод решения уравнения (8.12) – деление на переменную
x в
степени измерения m: . Далее уравнение преобразуются с помощью следующей замены:

. (8.14)

Однородное уравнение (8.12) принимает вид: – уравнение с
разделяющимися переменными. Следовательно, дальнейшее решение – по пункту 1.

Пример 8.3. Проинтегрировать уравнение .

Решение. Поделим уравнение на x², получим. После замены (8.14) заданное по условию уравнение принимает
вид ,. В результате интегрирования получим . После обратной замены – искомый общий
интеграл

Пример 8.4. Найти общее решение
(общий интеграл) дифференциального уравнения .

Решение. Правая часть уравнения обладает свойством . Поэтому заданное
уравнение является однородным дифференциальным уравнением первого порядка.
Совершим замену , где u – некоторая
функция от аргумента x. Отсюда . Исходное уравнение приобретает вид

или . Разделим переменные: .

После
интегрирования обеих частей уравнения получаем

. Таким образом,

Потенцируя,
находим .

Итак,
общий интеграл исходного уравнения приобретает вид cy=x²+y², где c – произвольная
постоянная

3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными

Общий вид уравнений

, (8.15)

где – числа.

При c₁=c₂=0 уравнение
является однородным. Рассмотрим два случая при c₁ и c₂ не равных нулю одновременно.

1) Определитель. Вводят новые переменные u и v, положив x=u+x₀, y=v+y₀, где (x₀;y₀) – решение системы уравнений.

В результате данной подстановки уравнение (8.15)
становится однородным.

Пример 8.5. Найти общее решение
(общий интеграл) дифференциального уравнения .

Решение. Определитель , следовательно,
решаем систему уравнений . Получаем значения x₀= –1; y₀=2, с
использованием которых осуществляем
замену x=u–1;y=v+2, при этом . Заданное по условию
ДУ принимает вид:

, (*) – однородное ДУ относительно функции v и переменной u.

Обозначим . Уравнение (*) принимает вид: . Продолжим преобразования:. Проинтегрируем уравнение:

С помощью формул
интегрирования (4.8) и (4.17) получаем:

Осуществим обратную
подстановку:

– общий интеграл исходного уравнения

2) Определитель. Это означает пропорциональность коэффициентов или

. Уравнение (8.15) принимает вид: . С помощью замены

, оно приводится к
уравнению с разделяющимися переменными вида .

Пример 8.6. Найти общее решение
(общий интеграл) дифференциального уравнения

Решение. Определитель , следовательно, осуществляем замену

Исходное
уравнение принимает вид:

или .

Далее . Разделим переменные: или . Проинтегрируем уравнение:

После обратной замены получим: – общий интеграл
исходного уравнения

4.
Линейные дифференциальные уравнения первого порядка

Общий вид уравнений

, (8.16)

где
P(x) и Q(x) –
заданные функции (могут быть постоянными).

Уравнение (8.16) может быть решено двумя способами.

1) Метод Бернулли-Фурье состоит в том,
что решение ищется в виде произведения двух неизвестных функций y(x)=u(x)∙v(x) или коротко y=u∙v, при этом . Одна из функций будет представлять общую часть решения и
содержать константу интегрирования c, другая функция может быть взята в частном виде при
конкретном значении константы (общее решение ДУ первого порядка должно содержать
одну константу интегрирования). Подставим выражения y и в (8.16), после чего
оно принимает вид:

. (8.17)

Функцию v(x) подберем в частном виде так, чтобы выражение в
скобках обратилось в ноль. Для этого решим уравнение с разделяющимися
переменными или . Отсюда в результате интегрирования получим: . Так функция v(x) выбиралась произвольно, то можно положить c = 1, тогда . Подставив найденную v(x) в (8.17), приходим к еще одному уравнению с
разделяющимися переменными . Интегрируя его, получим функцию . Общее решение исходного ДУ (8.16) принимает вид

. (8.18)

Пример 8.7. Проинтегрировать уравнение с помощью метода
Бернулли.

Решение. Данное уравнение является линейным ДУ первого порядка с
функциями . Применим подстановку
y=u∙v, где u и v – некоторые функции аргумента x. Так
как y=u∙v, то , и заданное уравнение принимает вид:

.
(**)

Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть или

Полагая c=1, получим
u=cos x.
При таком выборе функции u уравнение
(**) примет вид:

. Отсюда v=tg x+c. Тогда – общее решение
заданного уравнения.

Общее решение заданного ДУ можно также получить,
пользуясь непосредственно формулой (8.18):

По условию задачи имеем: P(x)=tg x, . Следовательно, . Так как, то с использованием основного логарифмического тождества
получаем:

Таким образом, – общее решение исходного дифференциального
уравнения

2) Метод Лагранжа иначе называют методом вариации произвольной постоянной.
Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть
исходное уравнение без правой части . Разделив переменные и проинтегрировав, в найденном решении
полагают постоянную c функцией c(x). После этого функцию y дифференцируют и вместе с подставляют в исходное
уравнение. При этом получают уравнение относительно неизвестной функции c(x), отыскав
которую, подставляют ее в y – общее решение заданного линейного неоднородного
уравнения (с правой частью).

Пример 8.8. Проинтегрировать уравнение с помощью метода
Лагранжа (сравни с примером 8.7).

Решение. Решим сначала соответствующее линейное однородное ДУ
первого порядка или . Разделим переменные: . В результате интегрирования получаем: – общее решение
соответствующего однородного уравнения. Применим метод варьирования константы,
то есть предположим c=c(x). Тогда общее решение исходного линейного
неоднородного уравнения будет иметь вид: . Подставим y и в исходное уравнение:

. После сокращений получим:
. Разделим переменные и проинтегрируем: .

Подставляя найденное c(x) в y, имеем общее решение линейного неоднородного
уравнения:

5.
Уравнения Бернулли

Общий вид уравнений

. (8.19)

При n=1 (8.19)– уравнение с разделяющимися переменными. При n=0 (8.19)– линейное ДУ.

Рассмотрим . Метод решения – деление уравнения на , после чего (8.19) принимает вид .
С помощью замены z=y^–ⁿ⁺¹
исходное уравнение становится линейным относительно функции z(x):

, (8.20)

то есть его решение находится аналогично пункту 4. На
практике искать решение уравнения (8.17) удобнее методом Бернулли в виде
произведения неизвестных функций y=u∙v. Заметим, что y=0 – всегда является решением исходного уравнения
(8.17).

Пример 8.9. Проинтегрировать уравнение .

Решение. Заданное
уравнение является уравнением Бернулли. Положим y=u∙v, тогда и уравнение примет
вид:

Выберем функцию u так, чтобы выполнялось равенство:. Разделим переменные и
проинтегрируем:

. При c=1 получим функцию.

Тогда заданное уравнение после сокращения на u примет
вид: или – уравнение
с разделяющимися переменными. Находим его общее решение:. Интегрируя последнее уравнение,
получим: . Следовательно, общее решение заданного уравнения имеет вид:

6. Уравнения
в полных дифференциалах

6.1. Общий вид уравнений

, (8.21)

где
левая часть есть полный дифференциал некоторой функции F(x;y), то есть . В этом случае ДУ (8.21) можно записать в виде, а его общий интеграл будет F(x;y)=c.

Условие, по которому можно судить, что выражение является полным
дифференциалом, можно сформулировать в виде следующей теоремы.

Теорема 8.2.
Для того чтобы выражение , где функции M(x;y) и N(x;y), их частные
производные и непрерывны в некоторой
области D плоскости x0y, было
полным дифференциалом, необходимо и
достаточно выполнение условия

(8.22)

Таким образом, согласно определению полного
дифференциала (6.6) должны выполняться равенства:

. (8.23)

Формула (8.22) представляет собой теорему Шварца,
согласно которой смешанные производные второго порядка функции F(x;y) равны.

Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x, получим:

. (8.24)

Здесь
мы применили метод вариации произвольной постоянной, так как предположили, что
константа c зависит от y (либо
является числом). Продифференцировав (8.24) по переменной y
и приравняв производную к функции N(x;y), мы получим уравнение для нахождения неизвестной c(y).
Подставив c(y) в (8.24), находим функцию F(x;y) такую, что.

Пример 8.10. Решить
уравнение .

Решение. Здесь функция .

Проверим условие (8.22): . Следовательно, левая часть заданного уравнения представляет собой полный дифференциал
некоторой функции F(x;y). Для ее
отыскания проинтегрируем функцию M(x;y) по
переменной x, считая y=const:

Пусть c=c(y),
тогда . Продифференцируем данную функцию по y,
получим . Отсюда .

Найденное c(y) подставляем в функцию F(x;y), получаем
решение заданного ДУ:

Если условие (8.22) не выполняется, то ДУ (8.21) не
является уравнением в полных дифференциалах.

Однако это уравнение иногда можно привести к уравнению
в полных дифференциалах умножением его на некоторую функцию μ(x;y), называемую интегрирующим множителем.

Чтобы уравнение было уравнение в полных
дифференциалах, должно выполняться условие

. (8.25)

Выполнив дифференцирование и приведя подобные
слагаемые, получим: . Для нахождения μ(x;y) надо
проинтегрировать полученное ДУ в частных производных. Решение этой задачи не
простое. Нахождение интегрирующего множителя может быть упрощено, если
допустить существование μ как функции только одного аргумента x либо
только y.

6.2. Пусть μ = μ(x). Тогда уравнение (8.25) принимает вид:

(8.26)

При этом подынтегральное выражение должно зависеть только от x.

6.3. Пусть
μ = μ(y). Тогда
аналогично можно получить

, (8.27)

где подынтегральное выражение должно зависеть только
от y.

Пример 8.11. Решить
уравнение .

Решение. Здесь , то есть . Проверим существование интегрирующего множителя. По
формуле (8.26) составляем подынтегральное выражение:

, оно зависит только от
переменной x. Следовательно, уравнение имеет интегрирующий
множитель μ(x). В нашем
случае он имеет вид . Умножая исходное уравнение на
μ=x, получаем: , то есть уравнение в полных дифференциалах. Действительно, для него. Решив его аналогично пункту 6.1, найдем, что общий
интеграл исходного уравнения имеет вид

7. Дифференциальные уравнения, неразрешенные относительно производной

К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра .

7.1.
Уравнение Лагранжа

Общий вид уравнений

, (8.28)

где
φ
и ψ– известные функции от . После введения параметра уравнение (8.28)
принимает вид

. (8.29)

Продифференцируем его по x:

. (8.30)

Полученное уравнение (8.30) является линейным уравнением относительно
неизвестной функции x = x(p). Решив
его, найдем:

x = λ(p;c). (8.31)

Исключая параметр p из уравнений
(8.29) и (8.31), получаем общий
интеграл уравнения (8.28) в
виде y = γ(x;c).

Примечание. При переходе к уравнению (8.30) мы делили на . При этом могли быть потеряны решения, для которых или p = p₀=const. Это
означает, что p₀ является
корнем уравнения p = φ(p)=0 (смотри уравнение (8.30)). Тогда
решение для уравнения (8.28)
является особым