В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
Калькулятор объема куба
Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧊 Что считает калькулятор
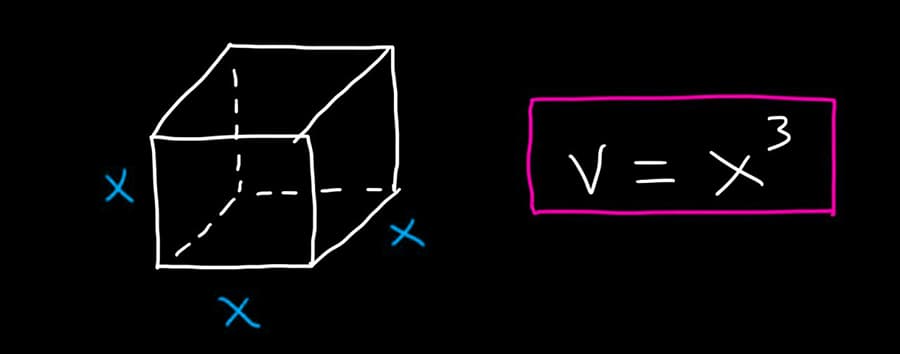
Калькулятор объема куба — это инструмент, который позволяет вычислять объем любого куба и выводить результат в разных единицах измерения.
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы.
Как использовать калькулятор
Укажите значение стороны куба, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения. Кроме того, можно указать диагональ куба или диагональ любой его стороны.
Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема куба зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты куба некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема куба требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. В некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
Где можно применить калькулятор
Калькулятор объема куба может быть использован во многих областях, где требуется расчет объема кубической формы. Некоторые из таких областей включают:
- 🧱 Строительство. Калькулятор объема куба может использоваться строителями при расчете объема кубических блоков, бетонных кубов, кирпичей и других материалов, используемых в строительстве.
- 🏭 Производство. Калькулятор объема куба может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемые в производстве кубических изделий.
- 📦 Логистика. Калькулятор объема куба может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- 🎓 Образование. Калькулятор объема куба может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема кубических форм.
- 🎨 Интерьер и дизайн. Калькулятор объема куба может использоваться в дизайне интерьера для расчета объема кубических элементов, таких как шкафы, полки, столы и другие.
- 🛠️ Ремонт и обслуживание. Калькулятор объема куба может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены кубических элементов, таких как плитка, обои и другие.
📐 Как посчитать объем куба
Объем куба можно вычислить самостоятельно, используя формулу
V = a³
где V – объем куба, a – длина ребра.
Для того, чтобы вычислить объем куба, нужно измерить длину одного из его ребер с помощью линейки или другого инструмента измерения длины. После этого возведите полученное значение в куб, используя калькулятор или ручной расчет.
Например, если длина ребра куба равна 5 см, то объем куба будет равен V = 5³ = 125 кубических сантиметров.
Важно помнить, что все единицы измерения должны быть одинаковыми – если длина ребра измеряется в сантиметрах, то и объем будет выражен в кубических сантиметрах.
🤔 Полезные советы
Несколько советов, которые могут помочь при вычислении объема куба:
- Определите длину одной из сторон куба. Обычно все стороны куба одинаковые, поэтому вы можете выбрать любую.
- Возведите длину стороны куба в квадрат. Это даст вам площадь одной грани куба.
- Умножьте площадь одной грани куба на 6. Это даст вам общую площадь поверхности куба.
- Определите длину любой из диагоналей куба. Вы можете использовать формулу теоремы Пифагора для нахождения длины диагонали, если известна длина стороны.
- Возвести длину диагонали куба в куб. Это даст вам объем куба.
- Если известна масса куба, можно использовать плотность материала для расчета его объема. Для этого нужно разделить массу на плотность.
- Убедитесь, что вы используете одни и те же единицы измерения при расчете. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть выражен в кубических сантиметрах.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое объем куба и как его рассчитать?
Объем куба — это мера его вместимости, то есть объем пространства, которое он занимает. Он рассчитывается по формуле V = a³, где a – длина ребра куба.
Как найти длину ребра куба, если известен его объем?
Для этого нужно извлечь кубический корень из объема: a = V^(1/3). Это позволит определить длину ребра куба, зная его объем.
Что произойдет с объемом куба, если увеличить длину его ребра вдвое?
Объем куба увеличится в 8 раз. Это происходит потому, что объем куба пропорционален кубу его длины: V ~ a³. Если длина ребра увеличивается вдвое, то объем увеличивается в 222=8 раз.
Какие единицы измерения используются для объема куба?
Объем куба измеряется в кубических единицах длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Загрузить PDF
Загрузить PDF
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
-

1
Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
- Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
-

2
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза. Если s — длина ребра куба, то s * s *s = s3 и, таким образом, вы вычислите объем куба.
- Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть, другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень.
- В нашем примере объем куба равен 5 * 5 *5 = 53 = 125.
-

3
К ответу припишите единицы измерения объема (если вы этого не сделаете, ваша оценка может быть снижена). Так как объем — это количественная характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические единицы (кубические сантиметры, кубические метры и так далее).
- В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах (или в см3). Итак, объем куба равен 125 см3.
- Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих кубических единицах. Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м3.
Реклама
-

1
В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых можно найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.
- Площадь поверхности куба равна 6s2, где s — длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так как у куба 6 равных граней).
- Рассмотрим пример. Площадь поверхности куба равна 50 см2. Найдите объем куба.
-

2
Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь одной грани куба). В свою очередь площадь одной грани куба равна s2, где s — длина ребра куба.
- В нашем примере: 50/6 = 8,33 см2 (не забывайте, что площадь измеряется в квадратных единицах — см2, м2 и так далее).
-

3
Так как площадь одной грани куба равна s2, то извлеките квадратный корень из значения площади одной грани и получите длину ребра куба.
- В нашем примере, √8,33 = 2,89 см.
-

4
Возведите в куб полученное значение, чтобы найти объем куба (как описано в предыдущем разделе).
- В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см3. К ответу не забудьте приписать кубические единицы.
Реклама
-

1
Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив диагональ на √2.
- Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см3.
- Запомните: d2 = 2s2, где d — диагональ грани куба, s — ребро куба. Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае ребер), то есть d2 = s2 + s2 = 2s2.
-

2
Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3. Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный D2 = 3s2 (где D — диагональ куба, s — ребро куба).
- Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет — это ребро, а второй катет — это диагональ грани куба, равная 2s2), то есть D2 = s2 + 2s2 = 3s2.
- Рассмотрим пример. Диагональ куба равна 10 м. Найдем объем куба:
- D2 = 3s2
- 102 = 3s2
- 100 = 3s2
- 33,33 = s2
- 5,77 м = s
- Объем куба равен 5,773 = 192,45 м3
Реклама
Об этой статье
Эту страницу просматривали 604 184 раза.
Была ли эта статья полезной?
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим
Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример – объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a – длина, b – ширина, c – высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще – достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³.
Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед – фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула.
Galina7v7 7 лет назад Если ваш вопрос трактовать так: “как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах.
Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона – 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3
Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно – длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических.
moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать.
vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы – это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3.
EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
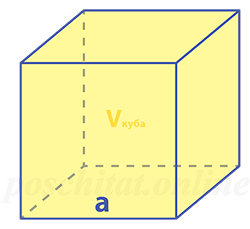
Объём куба через ребро
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
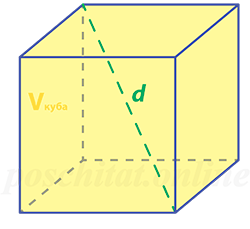
Объём куба через диагональ
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
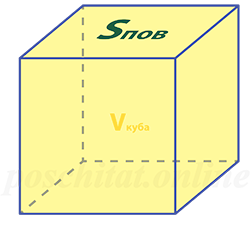
Объём куба через площадь поверхности
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
