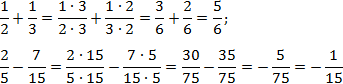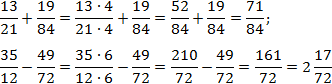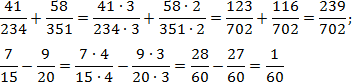Как найти общий множитель для больших чисел

Finding the greatest common factor, or GCF, of two numbers is useful in many situations in math, but particularly when it comes to simplifying fractions. If you’re struggling with this or finding common denominators, learning two methods for finding common factors will help you achieve what you’re setting out to do. First, though, it’s a good idea to learn about the basics of factors; then, you can look at two approaches for finding common factors. Finally, you can look at how to apply your knowledge to simplify a fraction.

What Is a Factor?

Factors are the numbers you multiply together to produce another number. For example, 2 and 3 are factors of 6, because 2 × 3 = 6. Similarly, 3 and 3 are factors of 9, because 3 × 3 = 9. As you may know, prime numbers are numbers that have no factors other than themselves and 1. So 3 is a prime number, because the only two whole numbers (integers) that can multiply together to give 3 as an answer are 3 and 1. In the same way, 7 is a prime number, and so is 13.

Because of this, it’s often helpful to break down a number into “prime factors.” This means finding all of the prime number factors of another number. It basically breaks the number down into its fundamental “building blocks,” which is a useful step towards finding the greatest common factor of two numbers and is also invaluable when it comes to simplifying square roots.

Finding the Greatest Common Factor: Method One

The simplest method for finding the greatest common factor of two numbers is to simply list all of the factors of each number and look for the highest number that both of them share. Imagine that you want to find the highest common factor of 45 and 60. First, look at the different numbers you can multiply together to produce 45.

The easiest way to start is with the two you know will work, even for a prime number. In this case, we know 1 × 45 = 45, so we know 1 and 45 are factors of 45. These are the first and last factors of 45, so you can just fill in from there. Next, work out whether 2 is a factor. This is easy, because any even number will be divisible by 2, and any odd number won’t. So we know that 2 isn’t a factor of 45. What about 3? You should be able to spot that 3 is a factor of 45, because 3 × 15 = 45 (you can always build on what you know to work this out, for example, you’ll know that 3 × 12 = 36, and adding threes to this leads you to 45).

Next, is 4 a factor of 45? No – you know 11 × 4 = 44, so it can’t be! Next, what about 5? This is another easy one, because any number ending in 0 or 5 is divisible by 5. And with this, you can easily spot that 5 × 9 = 45. But 6 is no good because 7 × 6 = 42 and 8 × 6 = 48. From this you can also see that 7 and 8 aren’t factors of 45. We already know 9 is, and it’s easy to see that 10 and 11 aren’t factors. Continue this process, and you’ll spot that 15 is a factor, but nothing else is.

So the factors of 45 are: 1, 3, 5, 9, 15 and 45.

For 60, you run through the exact same process. This time the number is even (so you know 2 is a factor) and divisible by 10 (so 5 and 10 are both factors), which makes things a bit easier. After going through the process again, you should see that the factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

Comparing the two lists shows that 15 is the greatest common factor of 45 and 60. This method can be time consuming, but it’s simple and it will always work. You can also start at any high common factor you can spot straight away, and then simply look for higher factors of each number.

Finding the Greatest Common Factor: Method Two  

The second method of finding the GCF for two numbers is to use prime factors. The process of prime factorization is a little easier and more structured than finding every factor. Let’s go through the process for 42 and 63.

The process of prime factorization basically involves breaking the number down until you’re only left with prime numbers. It’s best to start with the smallest prime (two) and work from there. So for 42, it’s easy to see that 2 × 21 = 42. Then work from 21: Is 2 a factor? No. Is 3? Yes! 3 × 7 = 21, and 3 and 7 are both prime numbers. This means the prime factors of 42 are 2, 3 and 7. The first “break” used 2 to get to 21, and the second broke this down into 3 and 7. You can check this by multiplying all of your factors together and checking you get the original number: 2 × 3 × 7 = 42.

For 63, 2 isn’t a factor, but 3 is, because 3 × 21 = 63. Again, 21 breaks down into 3 and 7 – both prime – so you know the prime factors! Checking shows that 3 × 3 × 7 = 63, as required.

You find the highest common factor by looking at which prime factors the two numbers have in common. In this case, 42 has 2, 3 and 7, and 63 has 3, 3 and 7. They have 3 and 7 in common. To find the highest common factor, multiply all of the common prime factors together. In this case, 3 × 7 = 21, so 21 is the greatest common factor of 42 and 63.

The previous example can be solved more quickly this way too. Because 45 is divisible by three (3 × 15 = 45), and 15 is also divisible by three (3 × 5 = 15), the prime factors of 45 are 3, 3 and 5. For 60, it’s divisible by two (2 × 30 = 60), 30 is divisible by two as well (2 × 15 = 30), and then you’re left with 15, which we know has three and five as prime factors, leaving 2, 2, 3 and 5. Comparing the two lists, three and five are the common prime factors, so the greatest common factor is 3 × 5 = 15.

In the event that there are three or more common prime factors, you multiply them all together in the same way to find the greatest common factor.

Simplifying Fractions With Common Factors

If you’re presented with a fraction like 32/96, it can make any calculations that come after it very complicated unless you can spot a way to simplify the fraction. Finding the lowest common factor of 32 and 96 will tell you the number to divide both by, to get a simpler fraction. In this case:

32 = 2 × 16 \ 16 = 2 × 2 × 2 × 2 \ text{So } 32 = 2^5 = 2 × 2 × 2 × 2 × 2

For 96, the process gives:

96 = 48 × 2 \ 48 = 24 × 2 \ 24 = 12 × 2 \ 12 = 6 × 2 \ 6 = 3 × 2 \ text{So } 96 = 2^5 × 3 = 2 × 2 × 2 × 2 × 2 × 3

It should be clear that 2⁵ = 32 is the highest common factor. Dividing both parts of the fraction by 32 gives:

frac{32}{96} = frac{1}{3}

Finding common denominators is a similar process. Imagine that you had to add the fractions 15/45 and 40/60. We know from the first example that 15 is the highest common factor of 45 and 60, so we can immediately express them as 5/15 and 10/15. Since 3 × 5 = 15, and both numerators are also divisible by five, we can divide both parts of both fractions by five to get 1 /3 and 2/3. Now they are much easier to add and see that

frac{15}{45} + frac{40}{60} = 1

Как найти наименьший общий знаменатель

4 методика:Перечисление кратных Использование наибольшего общего делителяРазложение каждого знаменателя на простые множителиРабота со смешанными числами

Для сложения или вычитания дробей с разными знаменателями сначала необходимо найти их наименьший общий знаменатель (НОЗ). Таким числом будет наименьшее общее кратное (НОК) двух или более знаменателей. Вот несколько различных методов для вычисления НОЗ и информация о том, как подставить НОЗ обратно в уравнение для решения задачи.

Шаги

Метод 1 из 4: Перечисление кратных [1]

1. 
   1
   Перечислите кратные каждого знаменателя. Составьте список из нескольких кратных для каждого знаменателя в уравнении. Каждый список должен состоять из произведения знаменателя на 1, 2, 3, 4 и так далее.
2. Пример: 1/2 + 1/3 + 1/5
3. Кратные 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; т.д.
4. Кратные 3: 3 * 1 = 3; 3 * 2 = 6; 3 *3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; т.д.
5. Кратные 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; т.д.
6. 
   2
   Определите наименьшее общее кратное. Просмотрите каждый список и отметьте любые кратные числа, которые являются общими для каждого оригинального знаменателя. После выявления общих кратных определите наименьший знаменатель.
7. Обратите внимание, что если не найден общий знаменатель, возможно, потребуется продолжить выписывать кратные до тех пор, пока не появится общее кратное число.
8. Пример: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
9. НОЗ = 30
10. 
    3
    Перепишите исходное уравнение. Числители будут равны произведению на число, равное частному от деления НОЗ на соответствующий знаменатель.
11. Пример: 15 * (1/2); 10 * (1/3); 6 * (1/5)
12. Новое уравнение: 15/30 + 10/30 + 6/30
13. 
    4
    Решите. После нахождения НОЗ и изменения соответствующих дробей, просто вычислите значение этого сложения.
14. Пример: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30

Метод 2 из 4: Использование наибольшего общего делителя[2]

1. 
   1
   Вычислите наибольший общий делитель (НОД) для каждого знаменателя. Найдите НОД через перечисление возможных делителей каждого знаменателя.
2. Пример: 3/8 + 5/12
3. Делители 8: 1, 2, 4, 8
4. Делители 12: 1, 2, 3, 4, 6, 12
5. НОД: 4
6. 
   2
   Перемножьте знаменатели между собой.
7. Пример: 8 * 12 = 96
8. 
   3
   Разделите полученное значение на НОД. Полученное число будет наименьшим общим знаменателем (НОЗ).
9. Пример: 96 / 4 = 24
10. 
    4
    Перепишите исходное уравнение. Числители будут равны произведению на число, равное частному от деления НОЗ на соответствующий знаменатель.
11. Пример: 24 / 8 = 3; 24 / 12 = 2
12. 3 * (3/8) = 9/24; 2 * (5/12) = 10/24
13. 9/24 + 10/24
14. 
    5
    Решите уравнение. НОЗ найден; просто найдите значение этой суммы.
15. Пример: 9/24 + 10/24 = 19/24

Метод 3 из 4: Разложение каждого знаменателя на простые множители[3]

1. 
   1
   Разложите каждый знаменатель на простые множители. Напомним, что простые множители – числа, которые делятся только на 1 или самих себя.
2. Пример: 1/4 + 1/5 + 1/12
3. Простые множители 4: 2 * 2
4. Простые множители 5: 5
5. Простые множители 12: 2 * 2 * 3
6. 
   2
   Подсчитайте число раз каждый простой множитель есть у каждого знаменателя.
7. Пример: Есть две 2 для знаменателя 4; нуль 2 для 5; две 2 для 12
8. Есть нуль 3 для 4 и 5; одна 3 для 12
9. Есть нуль 5 для 4 и 12; одна 5 для 5
10. 
    3
    Возьмите только наибольшее число раз (эти множители есть в любом знаменателе) для каждого простого множителя.
11. Например: наибольшее число раз для множителя 2 – 2 раза; для 3 – 1 раз; для 5 – 1 раз.
12. 
    4
    Запишите по порядку найденные в предыдущем шаге простые множители (с учетом наибольшего числа раз).
13. Пример: 2, 2, 3, 5
14. 
    5
    Перемножьте эти числа. Результат произведения этих чисел равно НОЗ.
15. Пример: 2 * 2 * 3 * 5 = 60
16. НОЗ = 60
17. 
    6
    Перепишите исходное уравнение. Числители будут равны произведению на число, равное частному от деления НОЗ на соответствующий знаменатель.
18. Пример: 60/4 = 15; 60/5 = 12; 60/12 = 5
19. 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
20. 15/60 + 12/60 + 5/60
21. 
    7
    Решите.
22. Пример: 15/60 + 12/60 + 5/60 = 32/60 = 8/15

Метод 4 из 4: Работа со смешанными числами[4]

1. 
   1
   Преобразуйте каждое смешанное число в неправильную дробь. Для этого умножьте целую часть смешанного числа на знаменатель и сложите с числителем – это будет числитель неправильной дроби. Целое число тоже превратите в дробь (просто поставьте 1 в знаменателе).
2. Пример: 8 + 2 1/4 + 2/3
3. 8 = 8/1
4. 2 1/4, 2 * 4 + 1 = 8 + 1 = 9; 9/4
5. Переписанное уравнение: 8/1 + 9/4 + 2/3
6. 
   2
   Найти наименьший общий знаменатель. Вычислите НОЗ любым способом, описанным выше. Для этого примера мы будем использовать метод «перечисление кратных».
7. Обратите внимание, что вам не нужно перечислять кратные для 1, так как любое число, умноженное на 1, равно самому себе; иными словами, каждое число является кратным 1.
8. Пример: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; т.д.
9. 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; т.д.
10. НОЗ = 12
11. 
    3
    Перепишите исходное уравнение. Числители будут равны произведению на число, равное частному от деления НОЗ на соответствующий знаменатель.
12. Например: 12 * (8/1) = 96/12; 3 * (9/4) = 27/12; 4 * (2/3) = 8/12
13. 96/12 + 27/12 + 8/12
14. 
    4
    Решите уравнение.
15. Пример: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12

Что вам понадобится

• Карандаш
• Бумага
• Калькулятор (по желанию)

Общий знаменатель, понятие и определение.

Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.

Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.

Формула основного свойства рациональных чисел.

Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.

Наименьший общий знаменатель.

Что такое наименьший общий знаменатель?

Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.

Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:

Приведите дроби с разными знаменателями к наименьшему общему знаменателю .

Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.

У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2

Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2

Ответ: наименьший общий знаменатель будет равен 140.

Как привести дробь к общему знаменателю?

Нужно первую дробь (frac) домножить на 7, чтобы получить знаменатель 140.

Правила или алгоритм приведения дробей к общему знаменателю.

Алгоритм приведения дробей к наименьшему общему знаменателю:

1. Нужно разложить на простые множители знаменатели дробей.
2. Нужно найти наименьшее общее кратное (НОК) для знаменателей данных дробей.
3. Привести дроби к общему знаменателю, то есть умножить и числитель и знаменатель дроби на множитель.

Общий знаменатель для нескольких дробей.

Как найти общий знаменатель для нескольких дробей?

Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей (frac, frac, frac)

Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.

Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2

Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330

Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби (frac, frac, frac) к общему знаменатели равному 330.

Вопросы по теме:
Какой общий знаменатель у дробей (bf frac) и (bf frac)?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.

Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.

Это мы нашли наименьший общий знаменатель:

Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей (frac) и (frac) знаменателем может быть число 700, 1400 и т.д.

You may also like:

Что такое уравнение и корни уравнения? Как решить уравнение?

Деление рациональных чисел примеры и правила.

Нужен репетитор по математике (алгебре) или геометрии?

Умножения рациональных чисел, математика, примеры.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Свежие записи

• Решение линейных уравнений с одной переменной.
• Определение числовой функции. Область определения функции. Область значения функции.
• Определение функции. Способы задания функции.
• Десятичные дроби. Разряды и классы десятичных дробей.
• Что такое уравнение и корни уравнения? Как решить уравнение?

Пожалуйста отключите блокировку рекламы или добавьте сайт в исключения блокировщика, если желаете чтобы проект развивался.

Приведение дробей к общему знаменателю

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется . А искомые числа, «выравнивающие» знаменатели, называются .

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку . Это число намного меньше произведения .

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел обозначается . Например, ; .

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий.

Аналогично, . Множители 3 и 4 взаимно просты, а множитель 5 — общий.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, , следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!

Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Калькулятор наименьшего общего знаменателя (НОЗ)

В реальной жизни нам необходимо оперировать обыкновенными дробями. Однако чтобы сложить или вычесть дроби с разными знаменателями, например, 2/3 и 5/7, нам потребуется найти общий знаменатель. Приведя дроби к общему знаменателю, мы сможем легко осуществить операции сложения или вычитания.

Определение

Дроби — одна из самых сложных тем в начальной арифметике, и рациональные числа пугают школьников, которые встречаются с ними впервые. Мы привыкли оперировать с числами, записанными в десятичном формате. Куда проще сходу сложить 0,71 и 0,44, чем суммировать 5/7 и 4/9. Ведь для суммирования дробей их необходимо привести к общему знаменателю. Однако дроби куда точнее представляют значение величин, чем их десятичные эквиваленты, а в математике представление рядов или иррациональных чисел в виде дроби становится приоритетной задачей. Такая задача носит название «приведение выражения к замкнутому виду».

Если и числитель, и знаменатель дроби умножить или разделить на один и тот же коэффициент, то значение дроби не изменится. Это одно из самых важных свойств дробных чисел. К примеру, дробь 3/4 в десятичной форме записывается как 0,75. Если умножить числитель и знаменатель на 3, то получим дробь 9/12, что точно также равняется 0,75. Благодаря этому свойству мы можем умножать разные дроби таким образом, чтобы они все имели одинаковые знаменатели. Как это сделать?

Поиск общего знаменателя

Наименьший общий знаменатель (НОЗ) — это наименьшее общее кратное для всех знаменателей выражения. Найти такое число мы можем тремя способами.

Использование максимального знаменателя

Это один из самых простых, но трудоемких методов поиска НОЗ. Вначале из знаменателей всех дробей выписываем самое большое число и проверяем его делимость на меньшие числа. Если делится, то наибольший знаменатель и есть НОЗ.

Если в предыдущей операции числа делятся с остатком, то необходимо самое большое из них умножить на 2 и повторить проверку на делимость. Если оно делится без остатка, то новый коэффициент становится НОЗ.

Если нет, то самый большой знаменатель умножается на 3, 4 , 5 и так далее, пока не будет найдено наименьшее общее кратное для нижних частей всех дробей. На практике это выглядит так.

Пусть у нас есть дроби 1/5, 1/8 и 1/20. Проверяем 20 на делимость 5 и 8. 20 не делится на 8. Умножаем 20 на 2. Проверяем 40 на делимость 5 и 8. Числа делятся без остатка, следовательно, НОЗ (1/5, 1/8 и 1/20) = 40, а дроби превращаются в 8/40, 5/40 и 2/40.

Последовательный перебор кратных

Второй способ — это простой перебор кратных и выбор из них наименьшего. Для поиска кратных мы умножаем число на 2, 3, 4 и так далее, поэтому количество кратных устремляется в бесконечность. Ограничить эту последовательность можно пределом, которое представляет собой произведение заданных чисел. К примеру, для чисел 12 и 20 НОК находится следующим образом:

• выписываем числа, кратные 12 — 24, 48, 60, 72, 84, 96, 108, 120;
• выписываем числа, кратные 20 — 40, 60, 80, 100, 120;
• определяем общие кратные — 60, 120;
• выбираем наименьшее из них — 60.

Таким образом, для 1/12 и 1/20 общим знаменателем будет 60, а дроби преобразуются в 5/60 и 3/60.

Разложение на простые множители

Этот способ нахождения НОК наиболее актуален. Данный метод подразумевает разложение всех чисел из нижних частей дробей на неделимые множители. После этого составляется число, которое содержит множители всех знаменателей. На практике это работает так. Найдем НОК для той же пары 12 и 20:

• раскладываем на множители 12 — 2 × 2 × 3;
• раскладываем 20 — 2 × 2 × 5;
• объединяем множители таким образом, чтобы они содержали в себе числа и 12, и 20 — 2 × 2 × 3 × 5;
• перемножаем неделимые и получаем результат — 60.

В третьем пункте мы объединяем множители без повторов, то есть двух двоек достаточно для формирования 12 в комбинации с тройкой и 20 — с пятеркой.

Наш калькулятор позволяет определить НОЗ для произвольного количества дробей, записанных как в обыкновенной, так и в десятичной форме. Для поиска НОЗ вам достаточно ввести значения через табуляцию или запятую, после чего программа вычислит общий знаменатель и выведет на экран преобразованные дроби.

Пример из реальной жизни

Сложение дробей

Пусть в задаче по арифметике нам необходимо сложить пять дробей:

0,75 + 1/5 + 0,875 + 1/4 + 1/20

Решение вручную производилось бы следующим способом. Для начала нам необходимо представить числа в одной форме записи:

• 0,75 = 75/100 = 3/4;
• 0,875 = 875/1000 = 35/40 = 7/8.

Теперь у нас есть ряд обыкновенных дробей, которые необходимо привести к одинаковому знаменателю:

3/4 + 1/5 + 7/8 + 1/4 + 1/20

Так как у нас 5 слагаемых, проще всего использовать способ поиска НОЗ по наибольшему числу. Проверяем 20 на делимость остальными числами. 20 не делится на 8 без остатка. Умножаем 20 на 2, проверим 40 на делимость — все числа делят 40 нацело. Это и есть наш общий знаменатель. Теперь для суммирования рациональных чисел нам необходимо определить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Дополнительные множители буду выглядеть так:

• 40/4 = 10;
• 40/5 = 8;
• 40/8 = 5;
• 40/4 = 10;
• 40/20 = 2.

Теперь умножим числитель и знаменатель дробей на соответствующие дополнительные множители:

30/40 + 8/40 + 35/40 + 10/40 + 2/40

Для такого выражения мы можем легко определить сумму, равную 85/40 или 2 целых и 1/8. Это громоздкие вычисления, поэтому вы можете просто ввести данные задачи в форму калькулятора и сразу получить ответ.

Заключение

Арифметические операции с дробями — не слишком удобная вещь, ведь для поиска ответа приходится осуществлять множество промежуточных вычислений. Используйте наш онлайн-калькулятор для приведения дробей к общему знаменателю и быстрого решения школьных задач.

Рассмотрим три способа нахождения наименьшего общего кратного.

Нахождение путём разложения на множители

Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.

Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:

Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:

2 2 · 3 2 · 5 · 7 · 11 = 13 860

Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.

Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.

Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 – взаимно простые. Поэтому

НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.

Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.

Нахождение путём подбора

Второй способ заключается в нахождении наименьшего общего кратного путём подбора.

Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:

НОК (60, 30, 10, 6) = 60

В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:

1. Определяем наибольшее число из данных чисел.
2. Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.

Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них – это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:

24 · 1 = 24 – делится на 3, но не делится на 18.

24 · 2 = 48 – делится на 3, но не делится на 18.

24 · 3 = 72 – делится на 3 и на 18.

Таким образом, НОК (24, 3, 18) = 72.

Нахождение путём последовательного нахождения НОК

Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.

НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.

Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:

Делим произведение на их НОД:

Таким образом, НОК (12, 8) = 24.

Чтобы найти НОК трёх и более чисел используется следующий порядок действий:

1. Сначала находят НОК каких-нибудь двух из данных чисел.
2. Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
3. Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
4. Таким образом поиск НОК продолжается до тех пор, пока есть числа.

Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа – 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:

Делим произведение на их НОД:

Таким образом, НОК (12, 8, 9) = 72.

При сложении и вычитании алгебраический дробей с разными знаменателями сначала дроби приводят к общему знаменателю
. Это значит, находят такой один знаменатель, который делится на исходный знаменатель каждой алгебраической дроби, входящей в состав данного выражения.

Как известно, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, отличное от нуля, то значение дроби не изменится. Это является основным свойством дроби. Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).

Например, дана такая сумма алгебраических дробей:

Требуется упростить выражение, т. е. сложить две алгебраические дроби. Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.

Для числовых коэффициентов и переменных НОК ищется отдельно. НОК(3, 2) = 6, а НОК(x, y) = xy. Далее найденные значения перемножаются: 6xy.

Теперь надо определить, на какой множитель надо умножить 3x, чтобы получить 6xy:
6xy ÷ 3x = 2y

Значит, при приведении первой алгебраической дроби к общему знаменателю ее числитель надо умножить на 2y (знаменатель уже был умножен при приведении к общему знаменателю). Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.

Таким образом, получаем:

Далее уже можно действовать как с дробями с одинаковыми знаменателями: складываются числители, а в знаменателе пишется один общий:

После преобразований получается упрощенное выражение, представляющее собой одну алгебраическую дробь, являющуюся суммой двух исходных:

Алгебраические дроби в исходном выражении могут содержать знаменатели, представляющие собой многочлены, а не одночлены (как в приведенном выше примере). В таком случае, перед поиском общего знаменателя следует разложить знаменатели на множители (если это возможно). Далее общий знаменатель собирается из разных множителей. Если множитель есть в нескольких исходных знаменателях, то его берут единожды. Если множитель имеет разные степени в исходных знаменателях, то его берут с большей. Например:

Здесь многочлен a 2 – b 2 можно представить как произведение (a – b)(a + b). Множитель 2a – 2b раскладывается как 2(a – b). Таким образом, общий знаменатель будет равен 2(a – b)(a + b).

Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.

Как найти наименьший общий знаменатель – понятие

Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.

Как найти наименьший общий знаменатель – примеры

Рассмотрим примеры нахождения НОЗ.

Вычислить: 3/5 + 2/15.

Решение (Последовательность действий):

• Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
• Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
• Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
• Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.

Ответ: 3/5 + 2/15 = 11/15.

Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.

Вычислить: 1/2 – 5/12 + 3/6

Решение (последовательность действий):

• Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
• Получим: 1/2 – 5/12 + 3/6 = ?/12.
• Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
• Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.

Ответ: 1/2 – 5/12 + 3/6 = 7/12.

Умножение «крест-накрест»

Метод общих делителей

Задача. Найдите значения выражений:

Задача. Найдите значения выражений:

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест».

Общий знаменатель дробей

Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Смотрите также:

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются – этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них – в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую – на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом – так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода – приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать – в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Как найти наименьший общий знаменатель

Найдите значения выражений:

Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 – общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 – общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи – не предел!

Единственная проблема – как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Смотрите также:

Приведение дробей к общему знаменателю

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются – этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.

Для чего вообще надо приводить дроби к общему знаменателю?

Общий знаменатель, понятие и определение.

Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них – в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую – на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом – так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода – приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать – в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 – общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 – общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи – не предел!

Единственная проблема – как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Смотрите также:

Приведение дробей к общему знаменателю

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются – этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них – в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую – на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей.

Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом – так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода – приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать – в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 – общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 – общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи – не предел!

Единственная проблема – как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Смотрите также:

Приведение дробей к общему знаменателю

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются – этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них – в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую – на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом – так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода – приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа.

Приведение дробей к общему знаменателю

Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать – в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 – общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 – общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи – не предел!

Единственная проблема – как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Примеры. Привести следующие дроби к наименьшему общему знаменателю.

Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20:
5=4). Для 2-й дроби дополнительный множитель равен 5 (20:
4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20
).

Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8:
4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8
).

Данные дроби не являются несократимыми.

Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей:
Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16;
20)=2 4 ·
5=16·
5=80. Дополнительный множитель для 1-й дроби равен 5 (80:
16=5). Дополнительный множитель для 2-й дроби равен 4 (80:
20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80
).

Находим наименьший общий знаменатель НОЗ(5;
6 и 15)=НОК(5;
6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30:
5=6), дополнительный множитель ко 2-й дроби равен 5 (30:
6=5), дополнительный множитель к 3-ей дроби равен 2 (30:
15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30
).

Страница 1 из 1
1