Сегодня буду хулиганить, как хочу 😜 (в пределах разумного, конечно 😊). С чего бы это? Объясняю: первая причина – мои ученики, вторая причина – их школьные учителя. Теперь, более подробно.
Ученики 😘 должны иметь интерес к изучаемому предмету. Я не о химии вообще. Это яркая, замечательная наука, если рассматривать ее экспериментальную часть. Я о задачах по химии. Многие ребята не решают задачи, поскольку считают их сложными, скучными, непонятными. Перед родителями встает вопрос: “Как любимую зайку, лапушку, солнышко заставить готовиться к ЕГЭ по химии?!” А никак. Вы никогда не заставите учить предмет, как бы не старались. Насильно мил не будешь. Даже если вы найдете самого дорогого репетитора, заплатите ему бешеные деньги, привяжете ребенка к креслу и поставите рядом вооруженную охрану, ребенок будет только делать вид, что он слушает учителя и усердно учится. А сам будет прокручивать в голове совсем другие мысли, типа: “Чтобы ты, зараза, сдохла! Как я тебя ненавижу!” Как быть? Давайте вспомним себя в детстве. Что у нас было в голове до 18 лет? Правильно. Ветер майский пел нам песни и менял свое направление каждый день. Чем развлекается майский ветер? Блестящим фантиком, который беззаботно машет своими бумажными крылышками. В этот момент делай с ветром, что хочешь. Так и с ребенком. Если поманить его интересной формой и дать понятное, разложенное по полочкам, содержание, сердце “ветра” растает и задачи по химии превратятся в любимейшее занятие. Это много раз проверено на моем 30-ти летнем опыте работы. Поэтому я постоянно ищу новые фантики, а содержание у меня уже давным-давно отработано и разложено по полочкам.
Школьные учителя моих учеников 😡 – еще та категория читателей, особенно, старые бабушки-химички и дедушки-химичи. Лично у меня уже закончился словарный запас приличных слов, а неприличные слова писать запрещается (произносить их тоже нельзя, можно только в мыслях). Уважаемые коллеги (🤬 пи-пи-пи), я именно к вам (🤬 пи-пи-пи) обращаюсь, прежде чем писать (🤬 пи-пи-пи) комментарии, прочитайте хотя бы школьные учебники, чтобы не получилось вот так:
Однако, вернемся к основной теме. В статье “Секретная шпаргалка по химии. 4.3. Горение смеси газов” я рассказала о гипотетических (предполагаемых) алгоритмических приемах для 28 задания ЕГЭ и подробно описала первую фишку:
1) Расчеты по уравнениям реакции горения смеси газов, состав которой нужно определить предварительно
2) Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)
3) Определение состава смеси газообразных продуктов, если в условии избыток-недостаток, степень превращения или выход реакции
4) Задачи на изменение объема газовой смеси в процессе реакции
Сегодня речь пойдет о второй предполагаемой фишке “Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)”. Мое мнение – это абсолютно простые задачи. Самое сложное в них – решить систему уравнений с двумя неизвестными. Итак, поехали!
Задание 28*(1)
Для сжигания 20 л смеси пропана и бутана израсходовано 124 л кислорода. Определить объемный состав смеси.
Решаем задачу с применением Четырех Заповедей (шагов). Каждое выполненное действие обводится зеленым овалом.
1. Первая Заповедь. Выписать данные задачи в разделе “Дано”.
2. Вторая заповедь. Написать уравнение реакции.
В задаче протекает две реакции. При написании реакций, не забываем делать отступ над каждой – для дальнейших расчетов.
3. Третья заповедь. Сделать предварительные расчеты
Выписываем два досье – на пропан и бутан. В каждом досье прописываем объем газа. Пугаться не нужно, если мы не знаем значение объема. Что нам математика говорит? “Если не знаешь число – пиши неизвестное (Х или Y). Советую в каждое досье записать также объем кислорода, который был израсходован на сжигание газа. Для это выполняются стандартные расчеты по уравнению реакций. Как это сделать? Очень просто! Читайте мою статью: “Команда “Газы!” дана для всех! 4.1 Закон Гей-Люссака. Закон Авогадро. Горение” и
Составляем два алгебраических уравнения. Одно – по сумме объемов газов (20 л), второе – по общему объему кислорода, затраченного на сжигание (124 л). Решение системы уравнений лучше проводить методом сложения-вычитания (меньше действий, значит, меньше вероятность технической ошибки). В ответе мы получим объемы каждого газа.
4. Четвертая заповедь. Составить алгоритм решения задачи.
Алгоритм решения составляем по вопросу задачи: “Определить объемный состав смеси” Объемный состав смеси газов – это значения объемных долей каждого газа, которые определяют по формуле, описанной в статье “Вангую новую фишку в заданиях ЕГЭ по химии”
Решим еще парочку задач на закрепление алгоритма.
Задание 28*(2)
Для сжигания 10 л метан-пропановой смеси израсходовано 205 л воздуха. Определить объемный состав исходной смеси.
Задача решается аналогично предыдущей, только вначале следует “извлечь” кислород из 205 л воздуха. Кстати, мы должны помнить объемную долю кислорода в воздухе – 20% (более точно 21%).
Задание 28*(3)
2,8 л смеси СО и СО2 прореагировали с 0,56 г кислорода. Определить объемный состав исходной смеси.
Из двух газов в смеси, только один участвует в реакции горения – угарный газ. Его объем рассчитывают по уравнению реакции через объем кислорода. А вот объем кислорода рассчитывают по его массе, используя универсальную расчетную единицу – количество вещества (моль). Состав смеси хорошо виден в таблице. Кстати, делать расчеты по таблице очень удобно и я советую использовать такой технический прием для ускорения решения задач и визуализации алгоритма.
Задание 28*(4)
При сжигании 350 л смеси метана и ацетилена в кислороде получили 775 л смеси СО2 и кислорода с плотностью по воздуху 1,424. Вычислите объемный состав исходной смеси.
Достаточно своеобразная задача. Поэтому разберу ее подробно, по Четырем Заповедям.
1) Первая Заповедь. Выписать данные задачи в разделе “Дано”
2) Вторая Заповедь. Написать уравнения реакции
3. Третья Заповедь. Сделать предварительные расчеты по данным условия задачи и по уравнению реакции.
Небольшой стоп! Я предупредила, задача необычная – нужно найти состав смеси реагентов по составу смеси продуктов. Поэтому, первые предварительные расчеты – определить состав смеси продуктов по средней молярной массе. Этот прием я подробно описывала в статье статье “Вангую новую фишку в заданиях ЕГЭ по химии”.
После определения объемных долей газов-продуктов, определяем объем углекислого газа – это суммарный углекислый газ, который выделился и при сжигании метана, и при сжигании ацетилена.
Применяем уже известный нам алгоритм – “Определение объемного состав смеси по участникам процесса горения (задачи на уравнения с двумя неизвестными)”. На этапе предварительных расчетов определяем объемы газов-реагентов
4. Четвертая заповедь. Составить алгоритм решения задачи. Алгоритм решения составляется по вопросу задачи: “Вычислите объемный состав исходной смеси”. Объемный состав исходной смеси рассчитывается по формуле объемной доли (объем каждого газа делится на общий объем смеси). Эту и другие формулы я подробно разобрала в вышеуказанной статье “Вангую новую фишку в заданиях ЕГЭ по химии”
Вот и все. Задача решена. Усидчивым читателям – респект и уважуха 👍! Если еще остались силы, можете попробовать решить задачи самостоятельно, не подсматривая в мое объяснение. Если сил уже нет, идите пить чай с имбирем, шоколадом и горячими плюшками ☕️ 🍫 🥧 (рецепт отличных плюшек прочитаете в следующих статьях). И до скорого свидания на полях Яндекс Дзен!
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии http://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Звоните мне +7(903) 186-74-55. Приходите ко мне на курс, на Мастер-классы “Решение задач по химии” – и вы сдадите ЕГЭ с высочайшими баллами, и станете студентом престижного ВУЗа!
PS! Если вы не можете со мной связаться из-за большого количества звонков от моих читателей, пишите мне в личку ВКонтакте, или на Facebook. Я обязательно отвечу вам.
Репетитор по химии и биологии кбн В.Богунова
Для сравнения
количества газов в смеси по объему,
необходимо их объемы при температуре
смеси привести к
одинаковому
давлению.
Если этим
одинаковым давлением
является давление смеси
![]() ,
,
то приведенные
к этому
давлению объемы
компонентов называются парциальными.
Парциальный
(приведенный) объем
![]()
– это объем, который занимал бы i-тый
компонент, если бы он один находился
при температуре ![]()
и давлении смеси ![]() .
.
Для понимания
физического смысла парциального объема
рассмотрим смесь двух идеальных газов.
Как отмечалось ранее, молекулы обоих
газов равномерно распределены по всему
объему ![]() ,
,
занимаемому смесью при давлении ![]()
и температуре ![]() .
.
Представим себе,
что каким-то
образом удалось разделить
молекулы этих двух газов так, что в общем
объеме ![]()
первый газ занимает объем ![]() ,
,
а второй – ![]()
при одинаковой температуре ![]() .
.
Для того, чтобы эта гипотетическая
система находилась в
равновесии
и газы не
смешивались
за счет разности давлений, давление в
объемах ![]()
и ![]()
должно быть одинаковым
и равным общему давлению смеси ![]() ,
,
т. е.
![]()
Или в общем случае
![]()
Типичной
студенческой ошибкой
является подстановка в это уравнение
вместо
давления смеси
![]()
величины парциального давления ![]() .
.
1.4.4. Задание состава смеси идеальных газов объемными долями.
Во многих практических
задачах состав смеси газов задается
объемными долями:
![]() ,
,
![]()
где: ![]()
– парциальный объем i-го
газа в составе смеси газов, занимающей
объем ![]() .
.
Установим связь
между объемными и мольными долями газов
смеси.
Т. к. универсальная
газовая постоянная
![]() Дж / (кмоль · К)
Дж / (кмоль · К)
связана с удельными
газовыми постоянными ![]() ,
,
Дж / (кг · К), соотношением
![]() ,
,
то из определения
парциального объема идеального газа в
составе смеси получим:
![]() или
или ![]()
,
где: ![]() -число
-число
киломолей i-го
газа.
Просуммировав
значения ![]()
для всех газов, входящих в смесь, получим
![]() ,
,
где: ![]()
и ![]()
Разделив выражения
для ![]()
на выражение для ![]()
получим
![]()
Т. о. для смеси
идеальных
газов мольная
и объемная доли i-го
газа
равны между
собой по величине
![]() .
.
и
![]() .
.
1.4.5. Формулы пересчета для различных способов задания состава газовых смесей
Получим формулу
пересчета мольных долей на массовые и
наоборот.
Т. к. ![]() и
и ![]() ,
,
то 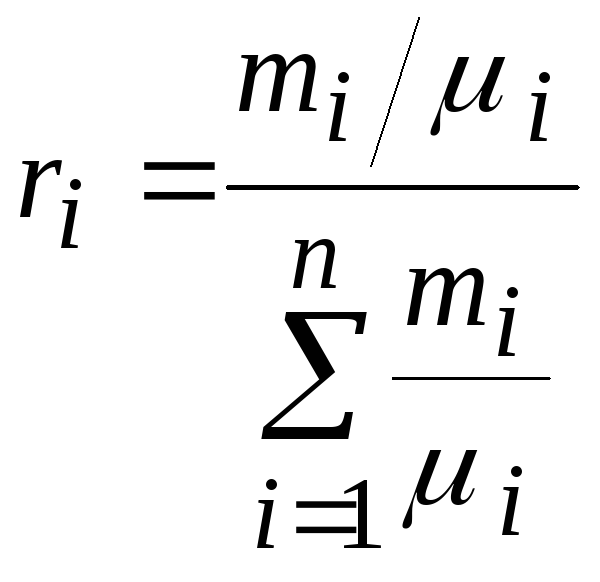
.
Разделив числитель
и знаменатель полученного выражения
на массу смеси ![]()
получим
 ,
,
или окончательно:
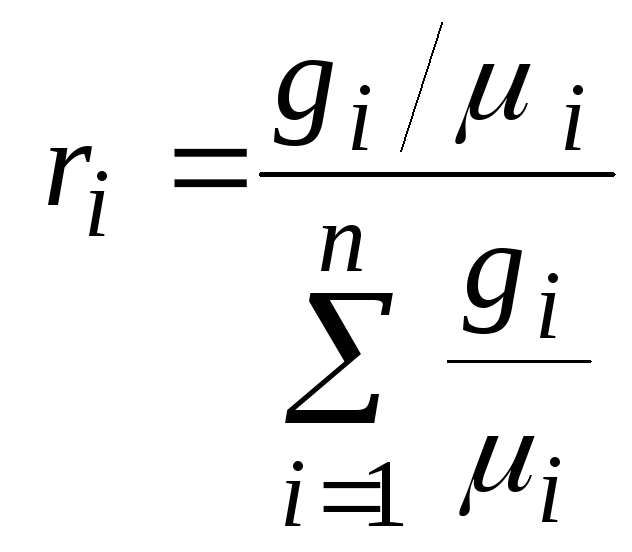
Т. к. ![]() и
и ![]() ,
,
то  .
.
Разделив числитель
и знаменатель этого выражения на ![]()
получим  ,
,
или окончательно

1.4.6. Кажущаяся молекулярная масса смеси газов
Для упрощения
расчетов смесь идеальных газов условно
полагают однородным
газом с той
же суммарной массой ![]()
и с тем же
суммарным числом молекул,
равным
![]() ,
,
где ![]()
– число молекул в единице объема смеси
газов;
![]() – число Авогадро
– число Авогадро
(число молекул в одном киломоле вещества):
![]() , 1 / кмоль
, 1 / кмоль
Молекулярная масса
такого однородного газа обозначается
![]()
и называется кажущейся молекулярной
массой смеси:
 .
.
Разделив числитель
и знаменатель этого выражения на ![]() ,
,
получим 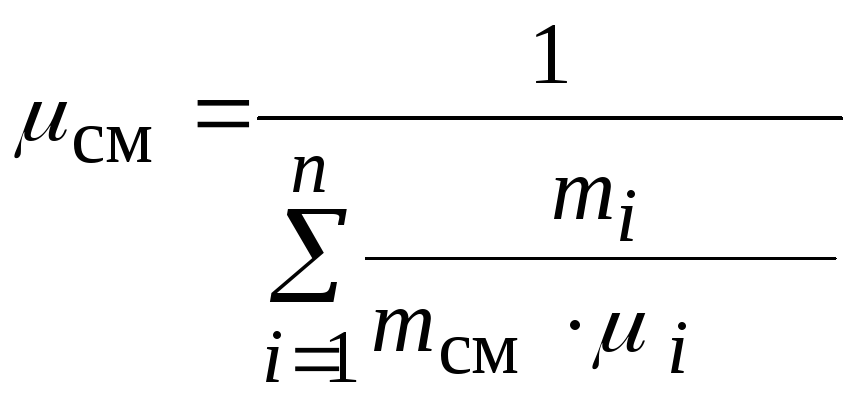 ,
,
или окончательно

Через мольные доли
величина ![]()
выражается проще:
 ,
,
или окончательно
![]()
Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.
Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.
При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация gi i-ного газа-компонента.
Здесь:
- N – количество газов, из которых состоит смесь;
- xi i-го газа – молярная концентрация указанного газа в составе смеси;
- νi – количество молей i-го газа, присутствующего в смеси.
Понятие парциального давления
Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:
Парциальным называется давление pi, которое могло бы создаваться i-ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.
Формула парциального давления будет выглядеть так:
pi=miμiRTV=μiRTV
Объем смеси здесь обозначен буквой V, ее температура – T.
Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.
Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:
p=∑i=1Npi=RTV∑i=1Nνi
Исходя из него, мы можем выразить парциальное давление так:
pi=xip.
Понятие парциального объема
У газовой смеси также есть такая характеристика, как парциальный объем.
Парциальный объем Vi i-газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.
Если речь идет о смеси идеальных газов, то к ней применим закон Амага:
V=∑i=1NVi
В самом деле, при выражении νi из формулы выше у нас получится следующее:
νi=pViRT; p=RTVpRT∑i=1NVi→V=∑i=1NVi
Для расчета парциального объема газа используется следующая формула:
Vi=xiV.
Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:
pV=mμsmRT.
Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:
pV=mRsmT.
Здесь параметры Rsm=Rμsm=R∑i=1Nqiμi означают удельную газовую постоянную смеси.
Условие: имеется сосуд объемом 1 м3, в котором находится 0,10·10-3 кг гелия и 0,5·10-3 кг водорода. Постоянная температура равна 290 К. Вычислите давление смеси и парциальное давление гелия в нем.
Решение
Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:
νi=miμi
Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μH2=2·10-3 кгмоль, мы можем найти количество его молей в смеси по формуле:
νH2=mH2μH2
Считаем, что получится:
νH2=0,5·10-32·10-3=0,25 (моль).
Точно такие же расчеты проводим и для гелия, зная, что μHe=4·10-3 кгмоль:
Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:
piV=νiRT.
Сначала рассчитаем давление водорода:
pH2V=νH2RT→pH2=νH2RTV
Парциальное давление будет равно:
pH2=0,25·8,31·2901=602,5 (Па).
Теперь то же самое подсчитываем для гелия:
pHe=0,025·8,31·2901=60,25 (Па).
Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:
p=pH2+pHe
Подставляем полученные ранее значения и находим нужный результат:
p=602,5+60,25=662,75 (Па).
Ответ: общее давление смеси составляет 662,75 Па, а парциальное давление гелия в смеси равно 60,25 Па.
Условие: дана смесь газов, состоящая из 1 кг углекислого газа и 0,5 кг O2. Если считать их идеальными, какой объем они будут занимать при давлении в 1 атм? Температура смеси равна 300К.
Решение
Начнем с вычисления общей массы газовой смеси.
m=mO2+mCO2
Значит, m=1+0,5=1,5.
Переходим к вычислению массовых компонентов смеси:
gO2=0,51,5=0,33;gCO2=11,5=0,67.
Тогда газовая постоянная смеси будет равна:
Rsm=R∑i=1Ngiμi
Rsm=8,310,3332·10-3+0,6746·10-3=200 ДжкгК.
Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:
Vsm=msmRsmTsmpsm
Вспомнив, что по условию давление равно 1 атм, что равно105 Па, вычислим объем:
Vsm=1,5·200·300105=0,9 м3.
Ответ: при указанных условиях смесь займет объем, равный 0,9 м3.
Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.
Определения
Давление – действующая на единицу поверхности сила, прямопропорциональная числу и скоростью сталкивающихся с этой поверхностью молекул, зависящей от температуры.
Парциальное давление – давление, оказываемое компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя этот объём и текущую температуру.
Объём – ограниченное чертой трёхмерное пространство, вмещающее вещество и отображающее его форму.
Парциальный объём – объём, занимаемый компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя первоначальное давление и температуру.
Идеальный газ – научная модель для познания газов, не учитывающая силу молекулярного взаимодействия.
Смесь идеальных газов – это совокупность газов, каждый из которого, находясь в смеси, при сохранении заданных условий, не вступает в химическую реакцию с остальными компонентами.
Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м3 и показывает количество конкретного компонента в единице объёма газовой смеси.
Парциальное давление
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем pi.
Формула
Формула парционального давления:
[p i=frac{m_{i}}{mu_{i}} frac{R T}{V}=mu_{i} frac{R T}{V}]
Где V– объём смеси, R = 8,31
Дж/моль*K– универсальная газовая постоянная, а T –
температура.
Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].
Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, vi– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где xi – молярная концентрация i-го газа.
Понятие парциального объёма
Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем Vi. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].
Формула
Пользуясь данным законом, можно вывести формулу нахождения парциального объёма через следующую формулировку:
[v_{i}=frac{p^{V_{i}}}{R T}]; [p=frac{R T}{V} frac{p}{R T} sum_{i}^{N}=mathbf{1}^{V}_{i}] , отсюда
следует, что — [boldsymbol{V=sum_{i}^{N}=1^{V_{i}}}, text{ а } boldsymbol{V_{i}=x_{i} V}].
Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:
[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.
[pV=mR_{s m} T] такой вариант уравнения содержит показатель Rsm, обозначающий удельную газовую составляющую смеси.
Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления парциального давления и объёма
Задача №1
Условие: в сосуде объёмом 2 м3, при постоянной температуре 290 К находится 0,20*10-3 кг гелия и 1*10-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.
Решение.
Сначала вычислим количество молей каждого компонента, используя следующую формулу:
[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]
Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:
[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]
Теперь можно найти количество молей водорода в смеси:
[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]
Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:
[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]
Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:
[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]
Сначала нужно рассчитать давление водорода:
[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]
Рассчитаем парциальное давление гелия:
[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]
Теперь найдём полное давление газовой смеси, сложив значения компонентов:
[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]
Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.
Задача №2
Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?
Решение.
Найдём суммарную массу газовой смеси:
[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]
Вычислим массовые компоненты смеси:
[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]
Тогда газовая постоянная смеси равняется:
[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]
Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 105 Па,вычислим объём смеси:
[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]
Ответ: при заданных условиях смесь займёт 0,45 м3.
Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.

