Как найти общий пройденный путь

Содержание материала

Кинематика
Видео
Как выглядит формула пути без времени, когда скорость тела уменьшается
Импульс
График скорости равномерного движения
Виды движения и формулы длины пути
Основные формулы электричества
Примеры решения задач

Кинематика

К оглавлению…

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

Видео

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]

Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:

[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]

Импульс

К оглавлению…

Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

График скорости равномерного движения

Т.к. скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.

На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.

Рисунок 1. Положительная и отрицательная скорости.

Если динозавр начнет двигаться к дому, то его скорость будет положительной, т.к. направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, т.к. направление движения противоположно направлению оси $x$.

Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.

Рисунок 2. График скорости равномерного движения.

Из графика видно, что скорость с течением времени не изменяется – она постоянна в любой выбранный момент времени. Из графика положительной скорости мы видим, что $upsilon = 6 frac{м}{с}$; из графика отрицательной — $upsilon = -4 frac{м}{с}$.

Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 с$.

$$S = upsilon t = 6 frac{м}{с} cdot 4 c = 24 м$.$

Виды движения и формулы длины пути

Длина пути при равномерном движении (v=const) точки равна:

где t₁ – начало отсчета движения, t₂ – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.

Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:

где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .

Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:

где a – постоянное ускорение, v – начальная скорость движения.

Основные формулы электричества

Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

Переходим к постоянному электрическому току:

Далее добавляем формулы по теме: “Магнитное поле электрического тока”

Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:

Ну и, конечно, куда же без электромагнитных колебаний:

Примеры решения задач

1. Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.

Переведем единицы измерения скорость в СИ и решим задачу.

$120 frac{км}{ч} = 120 cdot frac{1000 м}{3600 с} approx 33 frac{м}{с}$.

Дано:$upsilon=120 frac{км}{ч}$$t = 3 c$СИ:$upsilon=33 frac{м}{с}$

Найти:$S — ?$

Показать решение и ответ

Скрыть

Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t = 33 frac{м}{с} cdot 3 с approx 100 м$

Ответ: $100 м$

2. Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?

Переведем единицы измерения скорость в СИ и решим задачу.

$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$;

$900 км = 900 000 м$.

Дано:$upsilon_{ср} = 40 frac{км}{ч}$$S = 900 км$CИ:$upsilon_{ср} = 11 frac{м}{с}$$S = 900 000 м$

Найти:$t-?$

Показать решение и ответ

Скрыть

Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}} = frac{900 000 м}{11 frac{м}{с}} approx 82 000 с$.

Переведем время в часы:
$1 ч = 60 мин = 60 cdot 60 c = 3600 c$.

Тогда,
$t = frac{82 000 c}{3600 c} approx 23 ч$.

Ответ: $t = 82 000 c = 23 ч$.

Вычисление перемещения по графику проекции скорости

Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»

Теория

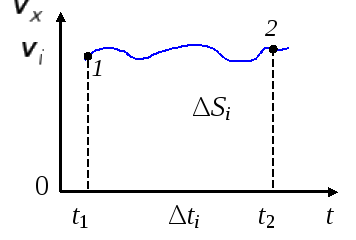
Пусть задан график зависимости проекции скорости ${ v }_{ x }$ от времени t (рис. 1).

Проекция перемещении тела ${ s }_{ x }$ за промежуток времени от ${ t }_{ 1 }$ до ${ t }_{ 2 }$ численно равна по величине площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ (см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:

— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);

— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).

Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:

— прямоугольника –

— треугольника – $S=frac { acdot h }{ 2 }$

— трапеции – $S=frac { a+b }{ 2 } cdot h$

Задачи

Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.

Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt= ${ t }_{ 2 }$ – ${ t }_{ 1 }$ =5с–1с=4c численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=1$ с и ${ t }_{ 2 }=5$ с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна

$S=frac { a+b }{ 2 } cdot h=frac { AD+BC }{ 2 } cdot DC$

где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения ${ s }_{ x }>0$ , т.к. проекция скорости ${ v }_{ x }>0$ .
${ s }_{ x }=S=16$ м.

Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.

Интервал времени	Путь
от 0 до 10 с	Ответ: м.
от 30 до 40 с	Ответ: м.

В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = ${ t }_{ 2 }$ – ${ t }_{ 1 }$ численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t),$ осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ .

На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).

${ S }_{ 1 }=frac { acdot h }{ 2 }$ ,

где a = 20 м/c, $h=triangle { t }_{ 1 }=10c-0c=10c$ . Тогда ${ S }_{ 1 }=100$ м.

Путь равен значению площади (путь всегда положительный, т.е. s > 0).

${ s }_{ 1 }={ S }_{ 1 }=100$ м.

На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).

${ S }_{ 2 }=frac { a+b }{ 2 } cdot h$ ,

где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда ${ s }_{ 2 }={ S }_{ 2 }=125$ м.

Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):

а) проекцию перемещения тела;

б) пройденный путь.

Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=4c-0=4c$ (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0$ с и ${ t }_{ 2 }=4$ с (рис. 8, площадь выделена штриховкой).

Так как при ${ t }_{ 0 }=3$ с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 }$ ,

где

${ a }_{ 1 }=30quad$ м/с, $quad { h }_{ 1 }=triangle { t }_{ 1 }=3c-0c=3c$

${ a }_{ 2 }$ =|-10 м/c|=10 м/c, $quad { h }_{ 2 }=triangle { t }_{ 2 }=4c-3c=1c$ .

Тогда ${ S }_{ 1 }=45$ м, $quad { S }_{ 2 }=5$ м.

а) Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ ; проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . В итоге получаем: ${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }={ S }_{ 1 }-{ S }_{ 2 },quad { s }_{ 1x }=$ 45м – 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).

$s={ S }_{ 1 }+{ S }_{ 2 }$ , s = 45 м + 5 м = 50 м.

Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.

Ответ: ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=6c-0=6c$ (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0 c$ и ${ t }_{ 2 }=6 c$ (рис. 10, площадь выделена штриховкой).

Так как при ${ t }_{ 01 }=2c$ и ${ t }_{ 02 }=4c$ проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 } ,quad { S }_{ 3 }=frac { { a }_{ 3 }cdot { h }_{ 3 } }{ 2 } ,$

где

${ a }_{ 1 }=3$ м/с, $h_{ 1 }=triangle { t }_{ 1 }=2c-0c=2c$

${ a }_{ 2 }=$ |-2 м/c| = 2 м/с, $h_{ 2 }=triangle { t }_{ 2 }=4c-2c=2c$

${ a }_{ 2 }=$ 3м/c, $h_{ 3 }=triangle { t }_{ 3 }=6c-4c=2c$ .

Тогда ${ S }_{ 1 }=3$ м, ${ S }_{ 2 }=2$ м, ${ S }_{ 3 }=3$ м.

Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ .

Проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . Проекция перемещения ${ s }_{ 3x }>0$ , т.к. проекция скорости ${ v }_{ 3x }>0$ . В итоге получаем:

${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }+{ s }_{ 3x }={ S }_{ 1 }-{ S }_{ 2 }+{ S }_{ 3 },quad { s }_{ x }=$ 3 м – 2 м + 3 м = 4 м.

Ответ: 4.

Задача 5. На рисунке приведен график зависимости v_x скорости тела от времени .

Определите путь, пройденный телом в интервале времени от 0 до 5 с.

Ответ: ____ м.

Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.

Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.

Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1

$S_1=frac{15cdot 3}{2}=22,5$ (м).

$S_2=frac{10cdot 2}{2}=10$ (м).

Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей S_1 и S_2 .

(м).
Ответ: 32,5 м

По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.

В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.

$S_{1x}=S_1=22,5$ (м).

В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.

$S_{2x}=-10$ (м).

Проекция перемещения за весь интервал времени будет равна $S_{o.x}=S_{1x}+S_{2x}$
$S_{o.x}=22,5+(-10)=12,5$ (м).

Ответ: 12,5 м

Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.

Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.

Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).

$S=frac{4+2}{2}cdot 10=30$ (м).

Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.

Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.

Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».

144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.

$v=frac{144000}{3600}=40$ м/с

Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как

(м/с)

Ответ: 25 м/с.

Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.

Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.

Рис.1

$S_1=frac{3+1}{2}cdot 10=20$ (м).
S_2=0
(м).

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Вычисление пройденного пути

Если
известен график зависимости проекции
скорости от времени, то можно найти
путь, пройденный точкой за время движения.
Выделим на графике (рис. 1.6) бесконечно
малый интервал времени
,
такой, чтобы проекцию скоростина этом интервале можно было считать
постоянной.

Рис.
1.6

–мгновенная
скорость.

Тогда
путь, пройденный точкой за время
,
равен

Путь,
пройденный точкой за время движения
,
равен сумме

или путь
равен интегралу от скорости по времени

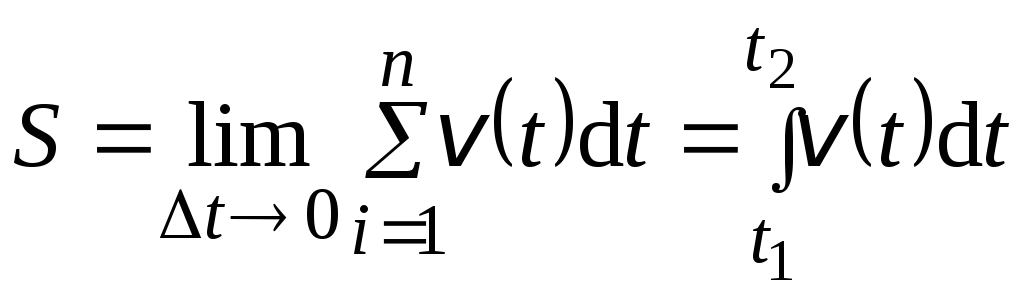
Физический
смысл интеграла– бесконечно большая
сумма бесконечно малых слагаемых.

Геометрический
смысл интеграла– площадь под кривой,
ограниченная двумя перпендикулярами
и осью абсцисс.

1.5. Ускорение

В
случае неравномерного движения для
описания изменения скорости с течением
времени вводят физическую величину –
ускорение.

Ускорение
характеризует быстроту изменения
скорости по величине и направлению.

Рассмотрим
общий случай, когда скорость меняется
по величине и направлению.

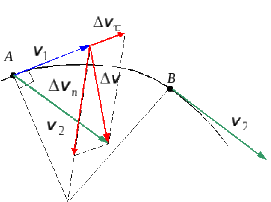
Пусть
материальная точка в положении Аимела скорость(рис. 1.7). Через промежуток
времениточка перешла в положениеВ, где ее
скорость оказалась равной:

или
.

Рис. 1.7

Средним
ускорением в интервале от
доназывается векторная величина, равная
отношению вектора изменения скоростик интервалу времени:

. (1.15)

Мгновенным
ускорением называется величина

. (1.16)

Таким
образом, ускорение
есть векторная величина, равная первой
производной скорости по времени.

Ускорениематериальной точки – это первая
производная от вектора скорости по
времени или вторая производная от
радиус-вектора по времени.

(1.17)

где
– проекции вектора ускорения на
координатные оси.

(1.18)

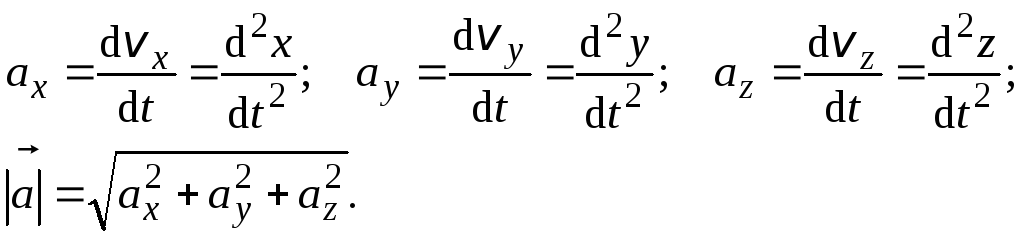
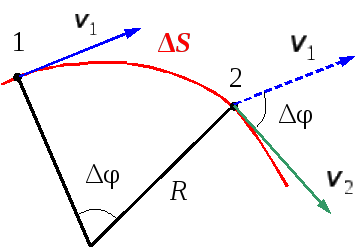
1.6. Понятие о кривизне траектории

Если
материальная точка движется по
криволинейной траектории, то отличие
этой траектории от прямолинейной
траектории характеризуется радиусом
кривизны или кривизной траектории.

Рис. 1.8

Δφ– угол между касательными в точках,
отстоящих друг от друга на расстоянии
ΔS.

Кривизна
траектории

(1.19)

Кривизна
траектории характеризует скорость
поворота касательной при движении или
степень искривленности кривой.

Радиус
кривизны траектории в данной точке есть
величина обратная кривизне:

(1.20)

Радиус
кривизны траектории в данной точке –
это радиус окружности, которая сливается
на бесконечно малом участке в данном
месте с кривой (рис. 1.8).

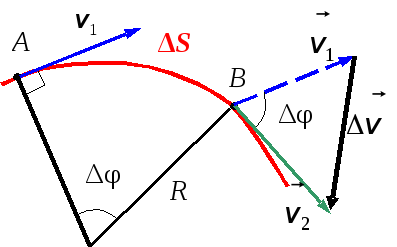
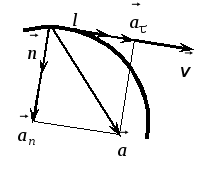
1.7. Нормальное и тангенциальное ускорение при криволинейном движении

Пусть
материальная точка движется по
криволинейной траектории. Рассмотрим
общий случай, когда скорость движения
меняется по величине и направлению.

Пусть
материальная точка в положении А
имела скорость
(рис. 1.9).Через промежуток времениточка перешла в положениеВ, где ее
скорость оказалась равной.

Рис. 1.9

еренесем векторпараллельно самому себе в точкуА(вектор)
и найдемравный.

Так
как в общем случае скорость может
меняться по величине и направлению,
то удобно разложить ускорение на две
составляющие. Для этого разложим на две
составляющие вектор
.

Из
точки Апо направлению скорости
отложим вектор,
по модулю равный вектору.
Очевидно, что вектор,
равный,
характеризует изменение скорости по
величине. Векторхарактеризует изменение скорости по
направлению

. (1.19)

Полное
ускорение

(1.21)

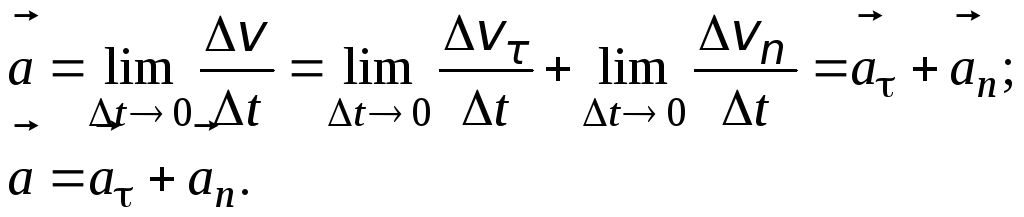
Составляющая
ускорение
называетсятангенциальным ускорением.Оно характеризует быстроту изменения
скорости по величине.Его численное
значение равно первой производной по
времени от модуля скорости:

. (1.22)

Определим
направление вектора
.
Принаправление векторастремится к направлению векторав точкеА траектории. Значит, векторнаправлен по касательной к траектории
(рис. 1.10).

Рис.
1.10

;

;
(1.23)

↑↑;

↑↑.

Составляющая
ускорения
называетсянормальным ускорением.Оно характеризует быстроту изменения
скорости по направлению. Нормальное
ускорение направлено по радиусу к центру
кривизны траектории.

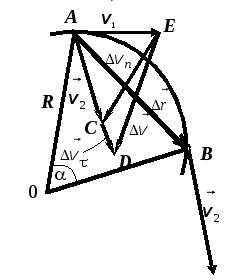
Найдем
выражение для
.
Восстановим в точкахАиВперпендикуляры к касательным. Они
пересекутся в точкеО. ПридугуАВ можно рассматривать как
дугу окружности радиусаR.
Из подобия треугольниковCAEиAOB

; (1.24)

. (1.25)

Итак,
нормальное ускорение

, (1.26)

где
R
– радиус кривизны траектории.

Радиус
кривизныпредставляет собой радиус
окружности, которая сливается в данном
месте с кривой на бесконечно малом ее
участке. Если траектория – окружность,
тоR– радиус этой
окружности.

Определим
направление вектора
.
При,
уголив пределе перпендикулярен,
следовательно,.
Полное ускорение равно по модулю:

Рис.
1.11

. (1.27)

Пусть
и– векторы единичной длины, один направлен
вдоль скорости, а другой – перпендикулярно
ему (рис. 1.11), при этом

Тогда
в векторном виде

;
;. (1.28)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Определение и формула пути
Виды движения и формулы длины пути
Единицы измерения пути
Примеры решения задач

Определение и формула пути

Линия, которую описывает материальная точка при своем движении, называется траекторией.

Определение

Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t₁ до t₂.

В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:

$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$

В цилиндрических координатах длина пути может быть выражена как:

$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$

В сферических координатах формулу длины пути запишем:

$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$

Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t₁ называют начальным положением.
Очень часто полагают t₁=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).

Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:

$$d s=|d bar{r}|=v d t$$

где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.

Виды движения и формулы длины пути

Длина пути при равномерном движении (v=const) точки равна:

$$s=vleft(t_{2}-t_{1}right)(5)$$

Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:

$$Delta s=langle vrangle Delta t(6)$$

где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .

Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:

$$s=v_{0} t+frac{a t^{2}}{2}(7)$$

где a – постоянное ускорение, v₀ – начальная скорость движения.

Единицы измерения пути

Основной единицей измерения пути в системе СИ является: [s]=м

В СГС: [s]=см

Примеры решения задач

Пример

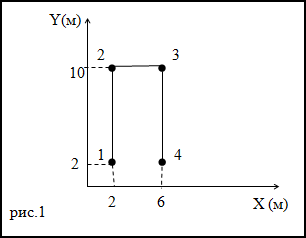
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.

Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:

$$6 – 2 = 4 (m)$$

Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:

$$8 + 4 + 8 = 20 (m)$$

Ответ. Путь равен 20 м, перемещение равно 4 м.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t² (м) . Какой путь пройдет материальная точка за 5 с?

Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:

$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$

Подставим в (2.1) функцию x=-0,2t², учтем, что $0 c leq t leq 5 c$ имеем:

$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$

Ответ. s=5м.

Читать дальше: Формула равноускоренного движения.

Источник

Расчёт
пути и времени движения

«Движение
– это жизнь»

Аристотель

В
данной теме будем применять приобретённые знания о механическом движении на
практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь
– это физическая величина, равная длине траектории, по которой двигалось тело,
в течение данного промежутка времени. Путь является скалярной величиной,
то есть, не имеет направления. Скорость при равномерном движении – это
величина, равная отношению пройденного пути к промежутку времени, за который
этот путь пройден.

Скорость
является векторной величиной, то есть, характеризуется как числовым значением,
так и направлением.

Средняя
скорость при неравномерном движении – это величина, равная отношению всего
пройденного пути к общему времени в пути.

Задача
1.
Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?

В
первую очередь, необходимо научиться правильно оформлять задачи по физике.
При решении любой задачи нужно писать «дано». То есть, в левой части
листа необходимо записать слово «дано», после которого ставится двоеточие, а
дальше в столбик перечисляете все исходные данные, которые указаны в условии
задачи. В нашем случае – это скорость и время в пути. После этого, нужно
очеркнуть данные и ниже (уже под линией) записать, что необходимо найти.
В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем
непосредственно к решению задачи.

А
теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть,
сколько километров автомобиль проходит за час. А время в условии дано в
минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в
часы.

В
общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами
измерения, можно (и даже нужно) переводить данные в систему СИ сразу после
того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в
км/ч необходимо

1 м/с = 3,6 км/ч

1 км/ч = 1/3,6 м/с

Время
в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому,
чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как
перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее
пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется
переводить данные в систему СИ.

Задача
2.
Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.

Получившееся
выражение, в котором остались, только те величины, которые были даны
изначально, называется расчетной формулой. Только в расчетную формулу необходимо
подставлять числовые значения, а до этого, все делается в буквенном виде.

Задача
3.
Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального
пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя
скорость?

Сразу
хочется обратить ваше внимание на распространенную ошибку. Среднюю
скорость нельзя находить как среднее арифметическое разных скоростей на разных
участках движения. В этом можно убедиться с помощью простых расчетов:
если подсчитать среднюю скорость, как среднее арифметическое скоростей, то
получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю
скорость как отношение всего пройденного пути к общему времени в пути. В
результате получим 214,3 м/с. Получается вроде небольшая разница. В
результате неверных расчётов за каждую секунду, пройденное расстояние
увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное
расстоянии будет больше на 8,6 км, а это существенно.

Задача
4.
Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть
своего пути велосипедист проехал за 3 минуты. За какое время велосипедист
проехал вторую часть, если общий путь составил 2 км?

Задача
5.
Определите по графику скорость равномерного движения тела.

Здесь,
конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не
нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика:
какие величины они обозначают и в каких единицах измеряются. Вертикальная ось –
обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах.
Значит, это график зависимости пройденного пути от времени. При равномерном
движении скорость постоянна, значит, можно путь, пройденный за определенный
промежуток времени, разделить на это время и, таким образом, найти скорость.
Для наибольшей точности желательно найти точку, на графике, наиболее близкую к
пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие
координаты, то есть, на значения пути и времени. Для этого из точки опускаем
перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.

Основные
выводы:

В
качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.

Источник

Кинематика

Видео

Как выглядит формула пути без времени, когда скорость тела уменьшается

Импульс

График скорости равномерного движения

Виды движения и формулы длины пути

Основные формулы электричества

Примеры решения задач

Теги

Вычисление перемещения по графику проекции скорости

Теория

Задачи

Вычисление пройденного пути

1.5. Ускорение

1.6. Понятие о кривизне траектории

1.7. Нормальное и тангенциальное ускорение при криволинейном движении

Определение и формула пути

Виды движения и формулы длины пути

Единицы измерения пути

Примеры решения задач

Добавить комментарий Отменить ответ

Кинематика

Видео

Как выглядит формула пути без времени, когда скорость тела уменьшается

Импульс

График скорости равномерного движения

Виды движения и формулы длины пути

Основные формулы электричества

Примеры решения задач

Теги

Вычисление перемещения по графику проекции скорости

Теория

Задачи

Вычисление пройденного пути

1.5. Ускорение

1.6. Понятие о кривизне траектории

1.7. Нормальное и тангенциальное ускорение при криволинейном движении

Определение и формула пути

Виды движения и формулы длины пути

Единицы измерения пути

Примеры решения задач

Вам также может понравиться

Как найти номер журнала в списке вак

Как правильно исправить абзац

Как найти шаблон в консультанте

Добавить комментарий Отменить ответ