Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
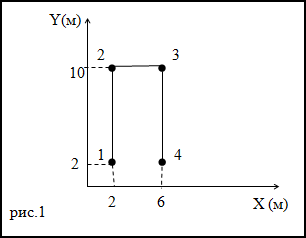
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Как найти время с помощью скорости и расстояния?
Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как найти расстояние за минуту?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи: Заяц убегал от Волка со скоростью 1 километр за 1 минуту.
Как найти км в час?
Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Как в математике обозначается скорость время и расстояние?
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой. Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут.
Как найти расстояние между двумя точками?
Вычисление расстояния между взятыми на плоскости двумя точками А(х А; у А) и В(х В; у В), выполняется по формуле d = √((х А – х В) 2 + (у А – у В) 2) , где d – длина отрезка, который соединяет эти точки на плоскости.
Сколько в среднем человек ходит км в час?
Средняя – 90 – 120 шагов в минуту, что составляет 4 – 5,5 км/ч; Быстрая – 120 – 140 шагов в минуту, что составляет 5,6 – 6,5 км/ч; Очень быстрая – более 140 шагов минуту, что составляет более 6,5 км/ч. Если человек старше 35 лет и никогда ранее не занимался спортом, то ему следует начинать с очень медленной ходьбы.
Сколько метр в одном км?
В 1 метре (м) содержится 100 сантиметров (см), 1 м = 100 см. В 1 километре(км) содержится 1000 метров, 1 км = 1000 м.
Что означает формула S V * t?
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t. Задачка 1.
Как записывается расстояние в математике?
Расстояние – это длина от одного пункта до другого. Большие расстояния, в основном, измеряются в метрах и километрах. Расстояние обозначается латинской буквой S.
Как найти расстояние между точками 7 класс?
Как найти расстояние между двумя заданными точками? Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.
Как узнать сколько километров?
Примечание.
- Откройте Google Карты на компьютере.
- Нажмите правой кнопкой мыши на пункт отправления.
- Нажмите Измерить расстояние.
- Чтобы создать путь для измерения, коснитесь любого места на карте. Точно так же можно добавить ещё несколько точек. …
- Когда закончите, на карточке внизу страницы нажмите «Закрыть» .
Сколько километров в 10000 шагов?
8 километров
В 10 000 шагов помещается от 7 до 8 километров в зависимости от длины шага. Они, конечно, не гарантируют полного здоровья, но могут повысить выносливость организма и его устойчивость перед инфекциями.
Какая скорость у человека в час?
30 км/ч — средняя скорость бега тренированного человека на короткой дистанции (100м — 400м). 20 км/ч — средняя скорость бега тренированного человека на средней дистанции (800м — 3км). 16 км/ч — средняя скорость бега тренированного человека на длинной дистанции (10км — 42км).
Как выглядит 1 километр?
Киломе́тр (сокращённо км, km) — широко распространённая кратная метру единица измерения расстояния. 1 км = 1000 м = 0,621 миль = 0,9374 версты = 1094 ярдов = 3281 футов = 1,057⋅10−13 световых лет = 6,67⋅10−9 а.
Сколько см в метре таблица?
Таблица мер измерения
| 1 т | тонна | 1 т = 10 ц = 1 000 кг = 106 г |
|---|---|---|
| 1 м | метр | 1 м = 10 дм |
| 1 дм | дециметр | 1 дм = 10 см = 0,1 м |
| 1 см | сантиметр | 1 см = 10 мм = 0,01 м |
| 1 мм | миллиметр | 1 мм = 1 000мк = 10-3 м |
•3 авг. 2020 г.
Что значит формула S VT?
S=v*t, где v — понятно что такое, S — расстояние, которое требуется найти, t — время, за которое объект прошел это расстояние. Таким образом вычисляется значение расстояния.
Как отмечается расстояние в геометрии?
Расстояние между двумя точками на координатной оси и замечание о его обозначении. Замечание . В геометрии и в школьной геометрии, в частности, принято обозначать одинаково и сам отрезок и его длину. Если имеется отрезок прямой, ограниченный точками А и В, то этот отрезок как геометрический объект обозначается АВ.
Содержание материала
- Кинематика
- Видео
- Как выглядит формула пути без времени, когда скорость тела уменьшается
- Импульс
- График скорости равномерного движения
- Виды движения и формулы длины пути
- Основные формулы электричества
- Примеры решения задач
Кинематика
К оглавлению…
Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:



Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):



Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:


Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):


Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

Видео
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

График скорости равномерного движения
Т.к. скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.

Если динозавр начнет двигаться к дому, то его скорость будет положительной, т.к. направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, т.к. направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.

Из графика видно, что скорость с течением времени не изменяется – она постоянна в любой выбранный момент времени. Из графика положительной скорости мы видим, что $upsilon = 6 frac{м}{с}$; из графика отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 с$.
$$S = upsilon t = 6 frac{м}{с} cdot 4 c = 24 м$.$
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:
где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v – начальная скорость движения.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

Переходим к постоянному электрическому току:

Далее добавляем формулы по теме: “Магнитное поле электрического тока”

Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:

Ну и, конечно, куда же без электромагнитных колебаний:

Примеры решения задач
1. Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 м}{3600 с} approx 33 frac{м}{с}$.
Дано:$upsilon=120 frac{км}{ч}$$t = 3 c$СИ:$upsilon=33 frac{м}{с}$
Найти:$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t = 33 frac{м}{с} cdot 3 с approx 100 м$
Ответ: $100 м$
2. Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$;
$900 км = 900 000 м$.
Дано:$upsilon_{ср} = 40 frac{км}{ч}$$S = 900 км$CИ:$upsilon_{ср} = 11 frac{м}{с}$$S = 900 000 м$
Найти:$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}} = frac{900 000 м}{11 frac{м}{с}} approx 82 000 с$.
Переведем время в часы:
$1 ч = 60 мин = 60 cdot 60 c = 3600 c$.
Тогда,
$t = frac{82 000 c}{3600 c} approx 23 ч$.
Ответ: $t = 82 000 c = 23 ч$.
Теги
Часть 1. Общий алгоритм поиска
Введение
Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.
Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.
Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.
В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.
Простая схема
Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.
Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».
Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.
Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.
Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.
Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.
Пример
Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.
Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.
Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?
Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.
Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».
Общий алгоритм
Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.
К тому же этот раздел невероятно прост.
Давайте попробуем формализовать наш пример, превратив его в псевдокод.
Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:
reachable = [start_node]
Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:
explored = []Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.
Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.
Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).
while reachable is not empty:Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:
node = choose_node(reachable)
Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:
if node == goal_node:
path = []
while node != None:
path.add(node)
node = node.previous
return pathНет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:
reachable.remove(node)
explored.add(node)Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:
new_reachable = get_adjacent_nodes(node) - exploredМы берём каждый из них:
for adjacent in new_reachable:
Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:
return NoneИ… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
if adjacent not in reachable
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
# If we get here, no path was found :(
return None
Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return pathВот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.
Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:
Интерактивное демо
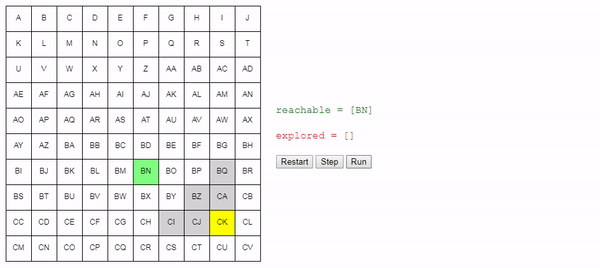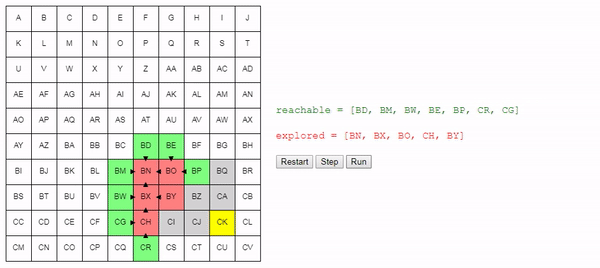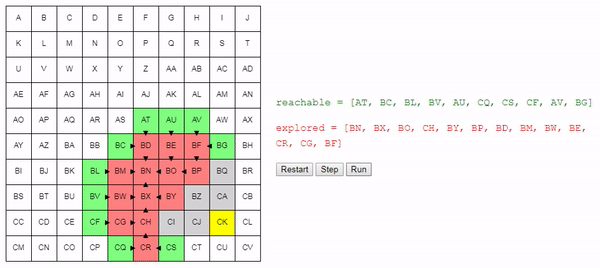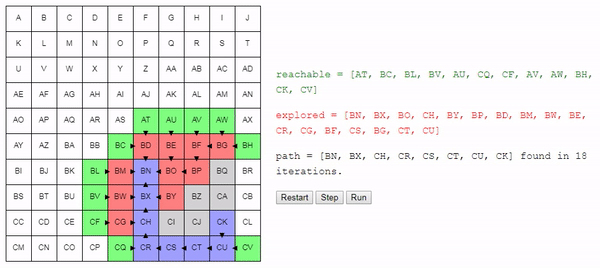
Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.
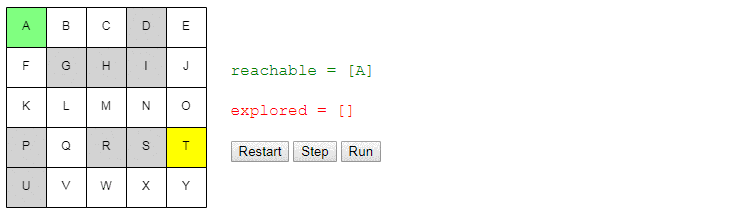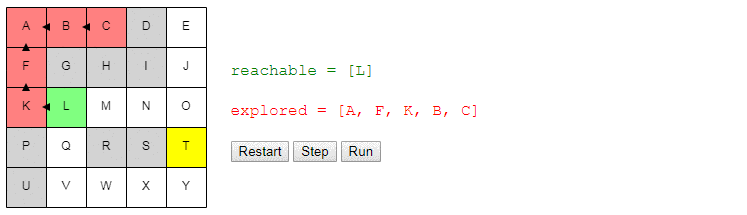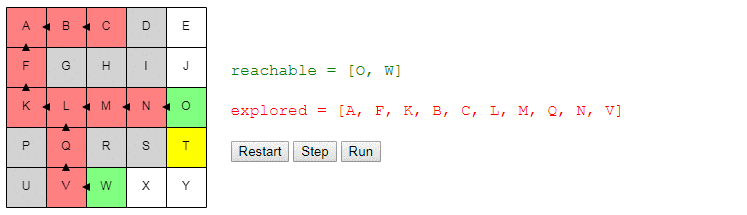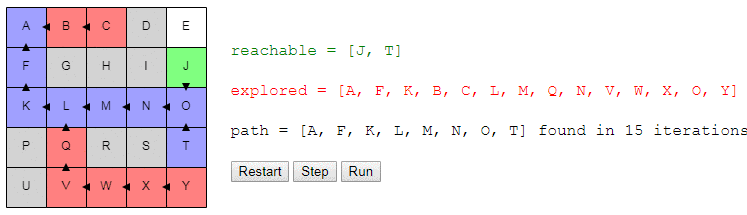
Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.
Заключение
Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.
Но что же отличает каждый алгоритм от другого, почему A* — это A*?
Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?
Часть 2. Стратегии поиска
Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.
Секретный ингредиент
В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?
Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:
node = choose_node(reachable)
Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.
Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.
Длина имеет значение
Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.
Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.
Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.
Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.
Тогда вот как будет выглядеть код:
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1Одинаковая стоимость поиска
Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.
Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.
Вот возможный пример функции choose_node:
function choose_node (reachable):
best_node = None
for node in reachable:
if best_node == None or best_node.cost > node.cost:
best_node = node
return best_nodeИнтуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:
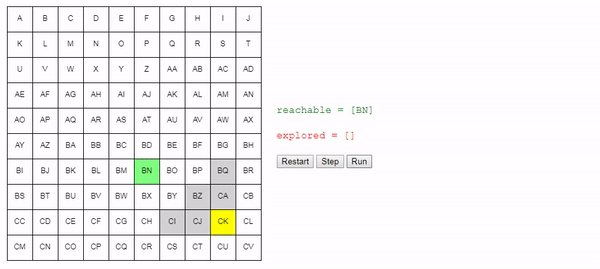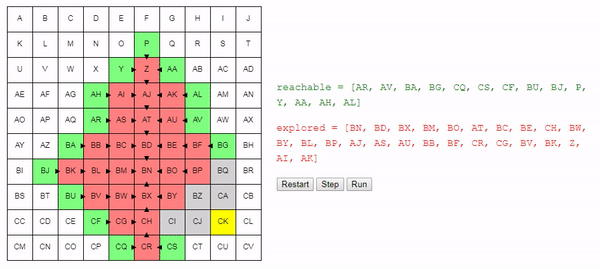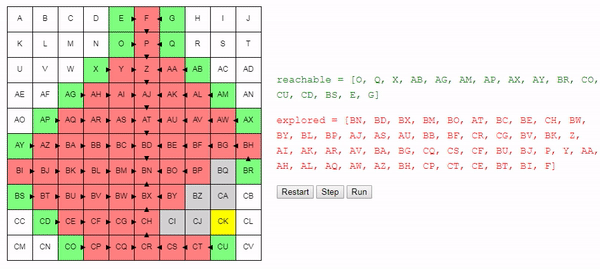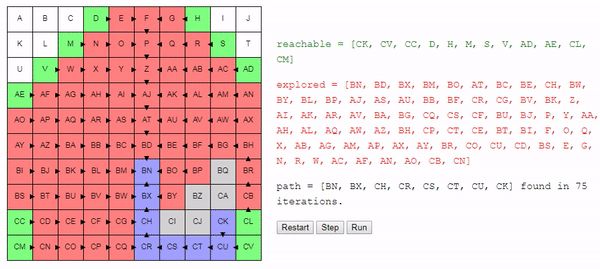
Заключение
Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.
Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?
Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?
Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.
Часть 3. Снимаем завесу тайны с A*
Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?
Волшебный алгоритм
Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:
function choose_node (reachable):
return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = magic(node, "кратчайший путь к цели")
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeЭто отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.
Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.
Не магический, но довольно потрясающий A*
К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:
# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:
cost_node_to_goal = distance(node, goal_node)Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.
Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.
Итак, вот немагическая версия choose_node:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeФункция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.
Интерактивное демо
Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение
Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.
Вот вам для справки полный псевдокод основного метода:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here that we haven't explored before?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
# First time we see this node?
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1
# If we get here, no path was found :(
return None
Метод build_path:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return path
А вот метод choose_node, который превращает его в A*:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeВот и всё.
А зачем же нужна часть 4?
Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.
Часть 4. A* на практике
Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.
Например, что будет, если наш мир не является сеткой?
Что если персонаж не может мгновенно поворачиваться на 90 градусов?
Как построить граф, если мир бесконечен?
Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?
Как найти кратчайший путь к любому из двух конечных узлов?
Функция стоимости
В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?
Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.
В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.
Функция критерия
Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.
Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.
Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.
В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».
Полная определённость не обязательна
Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.
Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.
Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!
Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.
Так почему бы нам просто не строить граф в процессе исследования?
Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.
За пределами трёх измерений
Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?
Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.
Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].
Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].
Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.
Заключение
Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.
Дальнейшее чтение
У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере: begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км. 
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} 
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$ 
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б) 
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | – | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | – | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | – | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
