К рычагу можно прикладывать две, или даже, несколько сил. В некоторых случаях рычаг остается неподвижным, то есть, находится в равновесии. Сформулируем условия, при которых рычаг, находящийся под действием нескольких сил, находится в равновесии.
Формула для условия равновесия рычага
Сумма вращательных моментов всех сил, приложенных к рычагу, должна равняться нулю.
На языке математики, это условие записывают так:
[large boxed { M_{1} + M_{2} + M_{3} + ldots + M_{n}= 0 } ]
Пояснение к формуле:
Для сил, вращающих рычаг в различные стороны, моменты будут иметь различные знаки. Поэтому, каждый вращательный момент в уравнение нужно подставлять со своим знаком!
Кратко условие знаков для моментов можно сформулировать так:
различные направления – разные знаки.
Например, если сила вращает рычаг по часовой стрелке, ее момент имеет знак «плюс», а если против часовой стрелки – то знак «минус».
Можно условиться наоборот: для сил, вращающих по часовой стрелке – знак «минус», а против часовой – знак «плюс». Главное, чтобы выполнялось условие: разные направления – разные знаки.
Советую освежить в памяти основные понятия о моменте силы. Для этого прочитайте такую статью (откроется в новой вкладке).
Для чего применяют рычаг
Рычаг позволяет поднимать или сдвигать тяжелые предметы с помощью малых сил.
То есть, рычаг помогает получить выигрыш в силе. Благодаря этому свойству мы часто пользуемся рычагами.
Однако, нужно помнить, что выигрыш в работе мы не получим, так как работу за нас рычаг не выполнит.
Поэтому, во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии.
Примечание:
Если совсем упростить, то работа – это сила, умноженная на расстояние.
Рычаги широко используют в технике. Нередко, в различных механических устройствах используются изогнутые рычаги, например, Г-образные.
Каким бы ни был рассматриваемый рычаг – прямым, или изогнутым, общий алгоритм для расчета его равновесия будет неизменным.
Алгоритм расчета для рычага, находящегося в равновесии
Решаем задачу, связанную с моментами двух сил, приложенных к рычагу.
1). Обращаем внимание на три точки:
- точку приложения первой силы,
- точку, к которой приложена вторая сила
- и, точку, через которую проходит ось вращения.
2). Ищем прямые углы между силами и расстояниями. Если какой-либо угол отличается от прямого, раскладываем либо силу, либо расстояние от точки приложения силы до оси вращения.
3). Составляем по одному уравнению для каждого вращательного момента.
Как рассчитать вращательный момент, написано здесь (откроется в новой вкладке)
4). Все моменты сил суммируем между собой. Напоминаю, что каждый момент силы записываем со своим знаком в левую часть уравнения для суммы моментов. Когда рычаг находится в равновесии, правая часть этого уравнения равна нулю.
Примечание:
Если к рычагу прикладывают больше двух сил, алгоритм расчетов аналогичен. С той лишь разницей, что нужно будет рассчитать большее количество вращательных моментов и записать их со своими знаками в общее уравнение для условия равновесия.
Примеры расчетов для рычага, находящегося в равновесии
Рассмотрим несколько случаев равновесия рычага, на который действуют две силы.
Во всех случаях условимся, что:
- силы прикладываются к различным точкам рычага;
- точки приложения сил не совпадают с точкой рычага, через которую проходит ось вращения.
Рычаг горизонтальный, силы перпендикулярны, ось вращения находится между точками приложения двух сил
Такое приложение сил применяют в рычажных весах, или башенном подъемном кране
Вокруг красной точки (рис. 1) рычаг может вращаться, так как через нее, в направлении «от нас», проходит ось вращения.
Пояснение к словам «через красную точку, в направлении «от нас», проходит ось вращения»: Если деревянный рычаг приложить к стене, то ось вращения – это гвоздь, забитый в красную точку.
Рис. 1. К горизонтальному рычагу перпендикулярно приложены две силы, ось вращения находится между точками приложения сил
Нас интересует два отрезка рычага:
- расстояние от силы (F_{1}) до оси вращения (красной точки). Это расстояние на рисунке обозначено (d_{1});
- и расстояние от силы (F_{2}) до красной точки. На рисунке оно обозначено (d_{2});
Каждая сила приложена перпендикулярно рычагу, расположенному горизонтально. Поэтому, расстояние (d_{1}) – это плечо силы (F_{1}) , а расстояние (d_{2}) являются плечом силы (F_{2}).
Запишем вращательные моменты этих сил.
(M_{1} = F_{1} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Запишем условие равновесия рычага:
(M_{1} + M_{2} = 0)
Сила (F_{2}) относительно красной точки вращает рычаг по часовой стрелке. Условимся моменты этой силы считать положительным.
А сила (F_{1}) будет вращать рычаг относительно красной точки против часовой стрелки, поэтому, ее момент будем считать отрицательным.
Теперь подставим знаки моментов в условие равновесия:
[-M_{1} + M_{2} = 0]
Это уравнение можно записать в развернутом виде
( — F_{1} cdot d_{1} + F_{2} cdot d_{2} = 0) – условие равновесия для рычага из рис. 1.
Рычаг горизонтальный, раскладываем силу, приложенную под непрямым углом
Не всегда силу прикладывают под прямым углом к рычагу. На рисунке 2 изображен горизонтальный рычаг, одна из сил приложена к нему под углом, не равным 90 градусам.
Рис. 2. К горизонтальному рычагу приложены две силы, ось вращения находится между точками приложения сил, одна из сил приложена перпендикулярно, другая – под тупым углом
Чтобы записать условие равновесия рычага, разложим (рис. 3) на проекции силу (F_{1}) и возьмем ту ее часть, которая будет располагаться перпендикулярно расстоянию (d_{1}).
Рис. 3. Одна из сил приложена под тупым углом к горизонтальному рычагу, разложив ее, возьмем часть, перпендикулярную рычагу
Для разложения силы (F_{1}) удобно заменить угол, обозначенный одной дугой, на угол, обозначенный на рисунке 3 двумя дугами. Будем обозначать угол, обозначенный двумя дугами символом (gamma).
Тогда
[ begin{cases} F_{1} cdot cos(gamma) = F_{1s} \ F_{1} cdot sin(gamma) = F_{1t} end{cases} ]
Примечание:
Просто и доступно о разложении вектора на проекции написано тут (откроется в новой вкладке).
Для записи момента ( M_{1} ) выберем перпендикулярную рычагу силу ( F_{1t}).
(M_{1} = F_{1t} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Вспомним о том, что противоположные направления вращения обозначают противоположными знаками
[-M_{1} + M_{2} = 0]
В развернутом виде условие равновесия для рисунка 3 выглядит так:
( — F_{1t} cdot d_{1} + F_{2} cdot d_{2} = 0)
Или так:
( F_{2} cdot d_{2} = F_{1t} cdot d_{1} )
Рычаг наклонный, раскладываем силу, приложенную под непрямым углом
В некоторых задачах рассматривают равновесие рычага, находящегося под наклоном к горизонтали (рис. 4).
Рис. 4. Одна из сил приложена под тупым углом к наклонному рычагу, разложим ее, и используем для вычисления вращательного момента часть, перпендикулярную рычагу
Здесь сила (F_{2}) приложена к рычагу под прямым углом, а угол между силой (F_{1}) и рычагом, отличается от прямого.
Разложим силу (F_{1}) на части и выберем для вычисления вращательного момента часть силы, расположенную перпендикулярно рычагу. Для разложения используем угол, обозначенный на рисунке 4 одной дугой и символом (alpha).
[ begin{cases} F_{1} cdot cos(alpha) = F_{1s} \ F_{1} cdot sin(alpha) = F_{1t} end{cases} ]
Вращательные моменты сил (F_{1t}) и (F_{2}):
(M_{1} = F_{1t} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Условие равновесия для рисунка 4 в развернутом виде:
( — F_{1} cdot sin(alpha) cdot d_{1} + F_{2} cdot d_{2} = 0)
Рычаг наклонный, раскладываем расстояние
В некоторых задачах (рис. 5) удобнее раскладывать не силу, а расстояние ( d ). На рисунке 5 для вычисления момента силы (M_{1}) разложим расстояние (d_{1}) между силой (F_{1}) и осью вращения (красной точкой).
Подробно о том, как раскладывать расстояние между точкой приложения силы и осью вращения, читайте тут (откроется в новой вкладке).
Рис. 5. Одна из сил приложена под тупым углом к наклонному рычагу, разложим расстояние d и, используем часть, перпендикулярную силе, для вычисления вращательного момента
Пользуясь рисунком 5, запишем моменты:
(M_{1} = F_{1} cdot d_{1t})
(M_{2} = F_{2} cdot d_{2})
Нам указали тупой угол (alpha) между силой и расстоянием от точки приложения силы до оси вращения. Но чтобы разложить (d_{1}) на части, удобнее использовать другой угол, смежный с углом (alpha).
Рассмотрим подробнее часть рисунка, на которой отмечены углы (рис. 6)
Рис. 6. Углы альфа и гамма образуют развернутый угол, угол гамма, обозначенный двумя дугами, используем для разложения расстояния d на перпендикулярную и, параллельную силе части
Из рисунка 6 видно, что углы (alpha) и (gamma) образуют развернутый угол. То есть, сумма углов (alpha) и (gamma) равна 180 градусам.
[ alpha + gamma = 180^{o} ]
Синусы таких углов равны.
[ sinleft(alpha right) = sinleft(gamma right)]
Разложим расстояние (d_{1}) на перпендикулярную и параллельную силе части, используя вместо угла (alpha ) угол (gamma).
[ begin{cases} d_{1} cdot cos(gamma) = d_{1s} \ d_{1} cdot sin(gamma) = d_{1t} end{cases} ]
Теперь можно записать условие равновесия для рычага, находящегося на рисунке 5.
(- M_{1} + M_{2} = 0)
( — F_{1} cdot d_{1t} + F_{2} cdot d_{2} = 0)
( — F_{1} cdot d_{1} cdot sin(gamma) + F_{2} cdot d_{2} = 0)
Или, используя угол (alpha ):
[ F_{2} cdot d_{2} = F_{1} cdot d_{1} cdot sin(alpha) ]
Точки приложения сил находятся по одну сторону от оси вращения
Так прикладывают силы, например, при устройстве шлагбаума.
Рис. 7. К горизонтальному рычагу приложены две силы, они направлены перпендикулярно рычагу и лежат по одну сторону от оси вращения
Из рисунка 7 видно, что силы перпендикулярны рычагу, значит моменты сил выражаются простыми соотношениями:
(M_{1} = F_{1} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Сила (F_{2}) вращает рычаг по часовой стрелке относительно красной точки, поэтому, ее момент считаем положительным. Момент силы (F_{1}) отрицателен, так как она вращает рычаг относительно красной точки против часовой стрелки.
Равновесие рычага на рисунке 7 сохраняется, когда выполняется условие:
(- M_{1} + M_{2} = 0 )
(- F_{1} cdot d_{1} + F_{2} cdot d_{2} = 0)
Содержание:
Рычаг:
Взаимодействие может происходить через промежуточные тела.
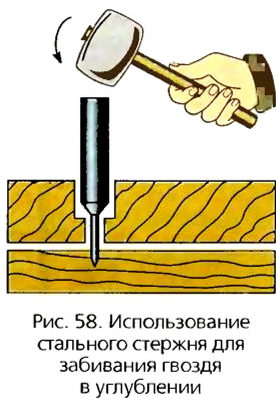
Взаимодействие может происходить не только при непосредственном контакте, но и при наличии промежуточных тел. Таких примеров можно привести большое количество. Так, если мастер забивает гвоздь в углублении, он ставит на головку гвоздя металлический стержень и по нему ударяет молотком (рис. 58). Молоток действует на стержень, который, в свою очередь, уже действует на гвоздь.
Можно ли изменять значения силы
Если взаимодействие между телами происходит через промежуточные тела, то можно изменять силы взаимодействия между ними. Оно может изменить как направление силы, так и ее значение. Одним из примеров такого использования промежуточных тел для взаимодействия между телами является рычаг. В быту и на производстве можно наблюдать много таких примеров.
Часто можно видеть, как тяжелый предмет поднимают или перемещают с помощью металлического стержня (рис. 59). В этом случае стержень называют рычагом.
Что такое рычаг
Рычагом называют жесткий стержень, имеющий ось вращения.
Ось вращения рычага может проходить через один из его концов или посередине рычага – между точками приложения сил.
Под действием нескольких сил рычаг может вращаться или быть неподвижным. В последнем случае говорят, что рычаг уравновешен.
Как уравновесить рычаг
Выясним, при каких условиях рычаг, на который действует несколько сил, будет уравновешен.
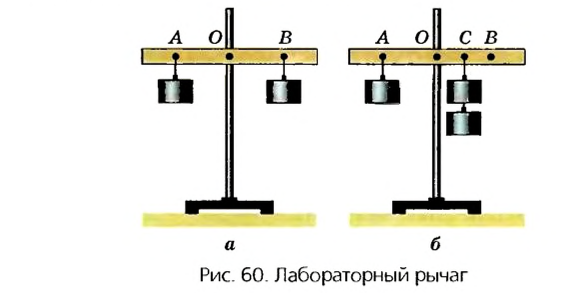
Для этого возьмем деревянную планку с отверстием посередине и поместим ее на оси, закрепленной в штативе (рис. 60). Это и будет рычаг. Слева от оси вращения повесим в точке А на расстоянии 10 см гирьку массой 102 г. В этом случае говорят, что точка А является точкой действия силы 1 Н. Под действием этой силы рычаг начнет вращаться против часовой стрелки. Для того чтобы он не вращался и оставался в горизонтальном положении, на другом конце рычага найдем такую точку В, при закреплении в которой гирьки массой 102 г рычаг перестанет вращаться. Измерив расстояние ОВ, увидим, что оно также равно 10 см. Таким образом, OA = ОВ, если Fl = F2. Если направление действия силы перпендикулярно к направлению оси вращения рычага, то расстояние от его оси вращения к направлению действия силы называют плечом силы.
Если силы, действующие на рычаг, находящийся в равновесии, равны, то равны и плечи этих сил.
Если левую гирьку оставить прикрепленной в точке А, а в точке В подвесить две такие гирьки массой по 102 г каждая, то равновесие рычага нарушится и он начнет вращаться. Достигнуть равновесия в этом случае можно, изменяя положение точки подвеса двух гирек. Так можно установить новое положение точки подвеса С. Измерив оба плеча, увидим, что правое плечо ОС в два раза меньше левого плеча OA.
В случае равновесия рычага плечо большей силы меньше, и наоборот, плечо меньшей силы больше.
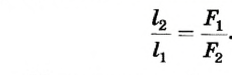
Используя свойства пропорции, получаем
В уравновешенном рычаге плечи сил обратно пропорциональны силам.
Что такое момент силы
Физическую величину, равную произведению силы на плечо, называют моментом силы. Единицей измерения момента силы является ньютон-метр (Н-м).
Сформулируем условие равновесия рычага в общем виде.
Рычаг пребывает в равновесии, если момент силы, вращающий рычаг по часовой стрелке, равен моменту силы, вращающему рычаг против часовой стрелки.
Конструктивно рычаг может быть таким, что силы будут действовать по одну сторону от оси вращения. Условие равновесия для него будет такое же, как и для рычага, рассмотренного выше.
Используя условие равновесия рычага, можно рассчитывать силы, действующие на него, или плечи этих сил.
Пример:
На одно из плеч рычага длиной 30 см действует сила 2 Н. Какая сила должна подействовать на другое плечо этого рычага длиной 15 см, чтобы он оставался неподвижным.
Дано:
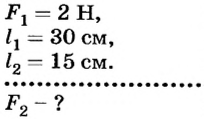
Решение
При условии равновесия рычага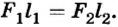 
Отсюда
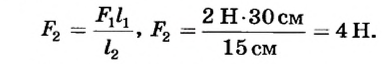
Ответ. На второе плечо рычага должна подействовать сила 4 Н.
Где используют рычаги
Рычаг известен человеку с того времени, когда человек взял палку, чтобы сбить плод с дерева. И вся следующая история человечества связана с использованием рычагов. Так, исследования историков показывают, что при строительстве пирамид древние египтяне использовали рычаги для поднятия тяжелых блоков на значительную высоту (рис. 61). Историкам науки известно, что древние римляне использовали рычаги для создания различных строительных и военных машин (рис. 62). Значительный вклад в теорию рычагов внес древнегреческий ученый и изобретатель Архимед. Сконструированные им машины помогали оборонять греческие города от захватчиков, подавать воду для орошения полей (рис. 63), перемещать значительные грузы на стройках, выполнять большое количество других подобных работ.
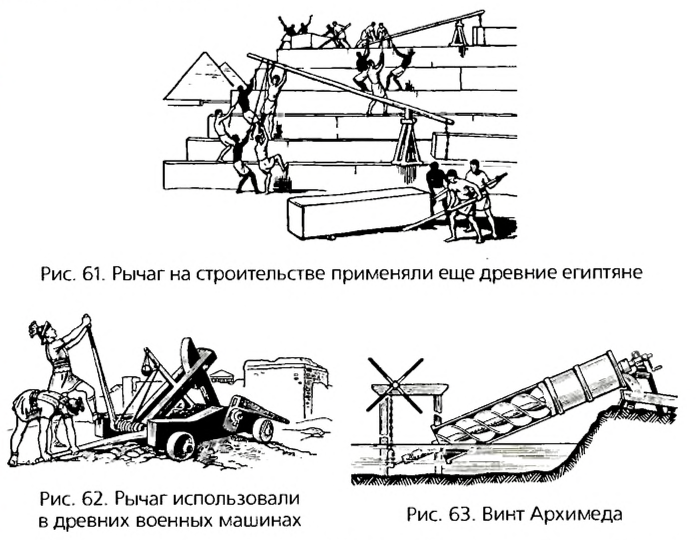
Рычаги широко используются и в современной технике, в самых разнообразных машинах.
Рычагом является стрела подъемного крана, используемого в строительстве. Она дает возможность получить выигрыш в силе или расстоянии. Момент силы, действующей на конце стрелы при подъеме груза, уравновешивается моментом противовеса, находящегося на противоположном конце стрелы.
Принцип рычага используется во многих устройствах и инструментах, которыми мы пользуемся ежедневно. На рисунке 64 изображены некоторые из них. На них легко найти части, исполняющие роль рычагов.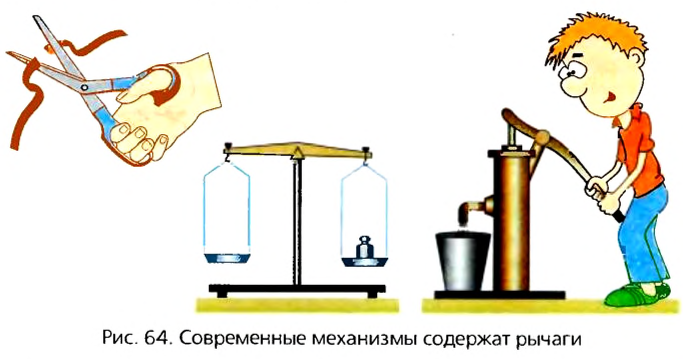
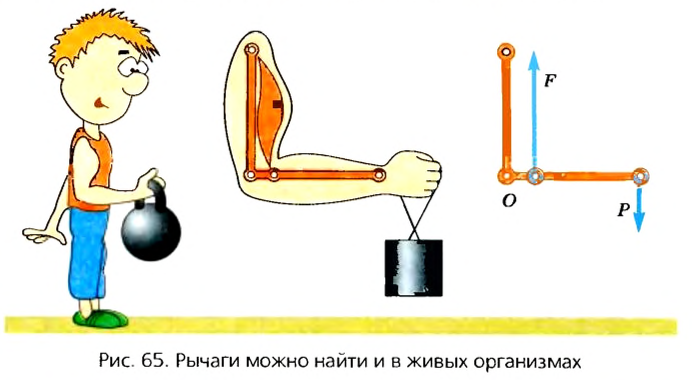
Рычаги можно найти и в живых организмах. По принципу рычага работают руки человека (рис. 65), ноги, голова.
Архимед (около 287-212 гг. до н. э.) – известный древнегреческий ученый. Научные труды касаются математики, механики, физики и астрономии. Автор многих изобретений и открытий, в том числе машины для орошения полей, винта, рычагов, блоков, военных метательных машин и пр. В его труде «О плавающих телах» изложены основы гидростатики.
Условие равновесия рычага и момент силы
Как уже отмечалось, рычаг — твёрдое тело, которое может вращаться около неподвижной опоры. Его применяют для изменения направления и значения силы, например для уравновешивания большой силы малой. Рычаг имеет следующие характеристики
(рис. 202).
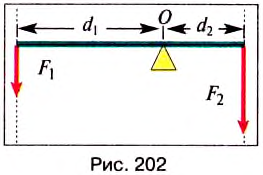
Точка приложения силы — это точка, в которой на рычаг действует другое тело.
Ось вращения — прямая, проходящая через неподвижную точку опоры рычага О, и вокруг которой он может свободно вращаться. Рассмотрим случай, когда ось вращения расположена между точками приложения сил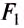 
и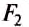 
.
Линия действия силы — это прямая, вдоль которой направлена сила.
Плечо силы — кратчайшее расстояние от оси вращения тела О до линии действия силы. Плечо силы обозначается буквой d. Единицей плеча силы в СИ является один метр (1 м).
Опыт. Возьмём рычаг, подобный изображённому на рис. 203. На расстоянии 10 см от оси вращения подвесим к нему 6 грузиков, каждый массой по 100 г. Чтобы уравновесить рычаг двумя такими же грузиками, нам придётся их подвесить с другой стороны рычага, но на расстоянии 30 см.
Следовательно, для того чтобы рычаг находился в равновесии, нужно к длинному плечу приложить силу, во столько раз меньшую, во сколько раз его длина больше длины короткого плеча. Такое правило рычага описывают формулой обратно пропорциональной зависимости: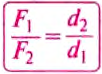 
,
где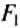 
и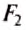 
— силы, действующие на рычаг; 
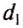и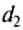 
— плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.
Рычаг находится в равновесии тогда, когда значения сил, действующих на него, обратно пропорциональны плечам этих сил.
С тех пор, когда Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский учёный П. Вариньон придал ему более общую форму, используя понятие момента силы.
Момент силы М– это физическая величина, значение которой опре-Г деляется произведением модуля силы F, вращающей тело, и ее плеча d :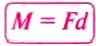 
.
Единицей момента силы в СИ является один ньютон-метр (1 Н • м), равный моменту силы 1 Н, приложенной к плечу 1 м.
Докажем, что рычаг находится в равновесии под действием двух сил, если значение момента М1 силы, вращающей рычаг против часовой стрелки, равно значению момента М2 силы, вращающей его по часовой стрелке, т.е.: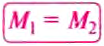 
Из правша рычага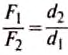 
на основе свойства пропорции вытекает
равенств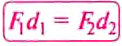о:
. Но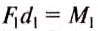 
— момент силы, вращающей рычаг против часовой стрелки (рис. 202),
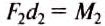— момент силы, вращающей рычаг по часовой стрелке. Таким образом: 
,
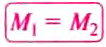что и требовалось доказать. Итак, правило (условие) равновесия рычага можно ещё сформулировать так.
Рычаг находится в равновесии под действием двух сил, если значение момента силы, вращающей рычаг против часовой стрелки, равно значению момента силы, вращающей его по часовой стрелке.
Момент силы — важная физическая величина, она характеризует действие силы, показывает, что оно зависит и от модуля силы, и от её плеча. Например, мы знаем, что действие силы на дверь зависит и от модуля силы, и оттого, где приложена сила: дверь тем легче повернуть, чем дальше от оси вращения приложена сила, действующая на неё; гайку легче открутить длинным гаечным ключом, чем коротким; ведро тем легче вытянуть из колодца, чем длиннее ручка ворота.
Основы статики и равновесие рычага
Еще в давние времена люди использовали обычную палку в качестве рычага, выигрывая этим в силе. На рисунке 2.35 показано, как с помощью рычага можно поднять по ступенькам большие каменные глыбы, например для строительства пирамид.
В древних книгах по механике, написанных учеными Греции и Египта, главным образом рассматривались вопросы статики. Важнейшие открытия в этой области принадлежали великому греческому философу Аристотелю, который и дал название «механика» науке, изучающей простейшие движения материальных тел, находящихся в природе или создающихся людьми в процессе их деятельности.
Ученые уже тогда понимали значение статики как одной из основных составляющих фундамента механики. Дальнейшее развитие науки и, особенно, техники подтвердило правильность их вывода: действие огромного количества £ механизмов и машин базируется на законах о равновесии сил.
Аристотель (384-322 до н. э.) – один из известнейших ученых Древней Греции. Изучал вопросы ста-тики, разработал классификацию механических движений, сформулировал закон прямолинейного распространения света, объяснил природу атмосферных явлений и др.
Основы науки о равновесии были заложены еще Архимедом. Именно он ввел в физику такое понятие, как центр тяжести и момент силы относительно точки и оси, определил положение центра тяжести для многих тел и фигур, математически обосновал законы рычага, сформулировал правила приложения параллельных сил.
- Заказать решение задач по физике
В своей работе «О равновесии плоских фигур» Архимед опирался на положения, которые считал само собой разумеющимися:
Архимед (287-212 до н. э.) – древнегреческий физик, математик, исследователь, инженер. Изучал условия равновесия тел, простые механизмы, плавание тел и др. Установил, что соотношение длины любой окружности к ее диаметру (число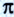 
) колеблется между 
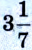и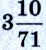 
(3,142 – 3,140); на то время это были точные данные.
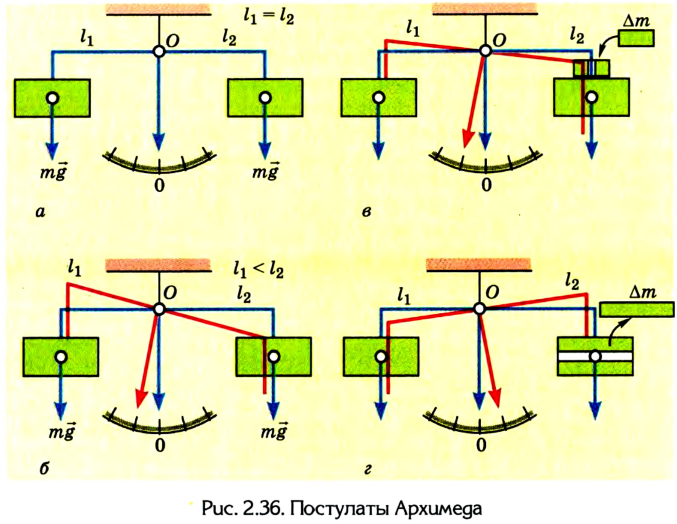
- одинаковые грузы, приложенные к одинаковым плечам рычага, уравновешиваются (рис. 2.36, а);
- одинаковые грузы, приложенные к неодинаковым плечам рычага, не находятся в равновесии; груз, приложенный к более длинному рычагу, падает (рис. 2.36, б);
- если грузы, подвешенные к неодинаковым плечам рычага, уравновешиваются и к одному из них что-либо прибавить, то равновесие нарушится и этот груз будет падать (рис. 2.36, в);
- если при тех же условиях, что в предыдущем случае, один груз уменьшить, то равновесие нарушится, и тогда другой груз будет падать (рис. 2.36, г).
Рычаг находится в равновесии, если плечи сил обратно пропорциональны значениям сил, действующих на него
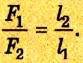
Из этих положений Архимед сделал вывод: грузы пребывают в равновесии, когда плечи рычага обратно пропорциональны грузам:
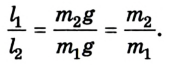
Условия равновесия тел. Устойчивое и неустойчивое равновесие
Равновесие – состояние тела, при котором в рассматриваемой системе отсчета отсутствуют перемещения каких-либо его точек под действием приложенных к нему сил.
Вспомним, что момент силы относительно какой-либо оси равен произведению модуля силы на ее плечо: М = Fl. Плечом силы l называется кратчайшее расстояние от оси вращения до линии действия данной силы. Момент силы считается положительным, если сила стремится повернуть тело по часовой стрелке, и отрицательным, если такое действие противоположно. Для равновесия тел необходимы два условия: 1) геометрическая сумма приложенных к телу сил равна нулю: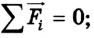 
2) алгебраическая сумма моментов сил относительно любой неподвижной оси равна нулю: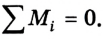
Момент силы: М = Fl.
Условия равновесия тел:
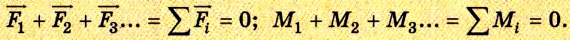
Равновесие устойчивое, если при незначительном смещении тело вновь возвращается в положение равновесия (рис. 2.37).
При неустойчивом равновесии незначительное смещение тела вызывает в дальнейшем значительное удаление его от исходного положения (рис. 2.38).
Равновесие тела может быть устойчивым, неустойчивым и безразличным.
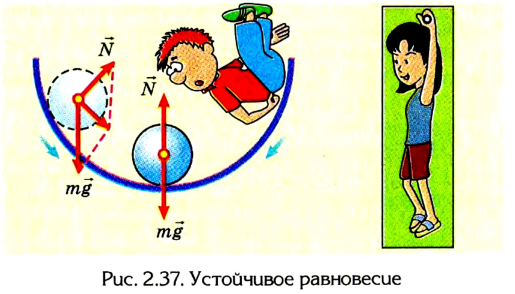
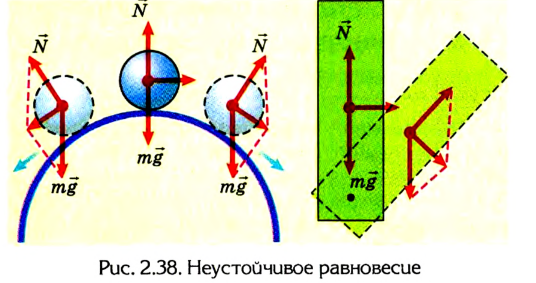
Если любые смещения тела не нарушают его состояния равновесия, то можно говорить о безразличном равновесии (рис. 2.39).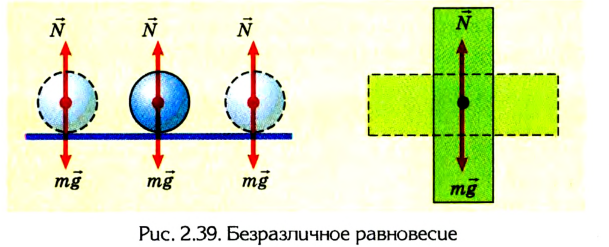
Примеры решения задач на равновесие рычага
Рассмотрим примеры решения задач статики.
Пример №1
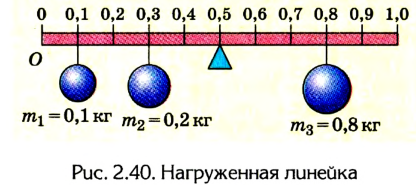
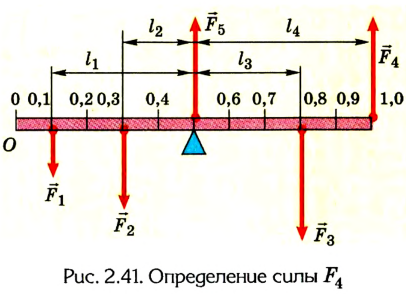
Метровая линейка, весом которой можно пренебречь, положена средним делением на подставку и нагружена гирями (рис. 2.40). Какого направления и значения сила должна быть приложена на делении 1 м для того, чтобы линейка находилась в равновесии? Какой будет сила реакции опоры, если приложить эту силу?
Решение:
Выполняем рисунок в соответствии с условием задачи (рис. 2.41), указав силы и их плечи. Линейка под действием моментов сил может вращаться вокруг неподвижной оси О, которая проходит через точку О. Будем считать положительными все моменты, вращающие систему по часовой стрелке. В задаче это момент силы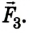 
Отрицательные моменты создают силы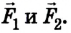 
Для упрощения вычислений значение ускорения свободного падения будем считать равным 10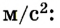 
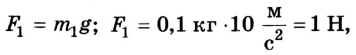
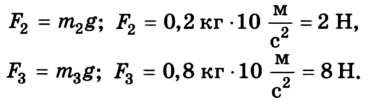
Предположим, что для равновесия системы на конце линейки 1 м должна быть приложена сила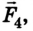 
направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответе значение силы получится со знаком “-“. Для решения задачи воспользуемся вторым условием равновесия тела:
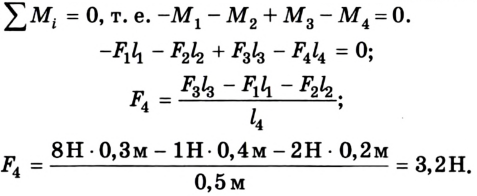
Ответ: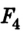
= 3,2H, направление силы выбрано правильно.
Пример №2
Метровая линейка, весом которой можно пренебречь, положена крайними точками на две опоры и нагружена гирями, как в предыдущей задаче. Нужно определить силы реакции опор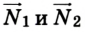 
(рис. 2.42).
Решение:
Чтобы определить силу реакции опоры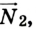 
можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:
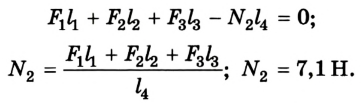
Чтобы определить силу реакции опоры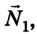 
действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м: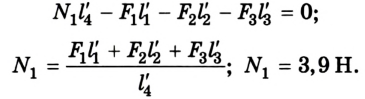
Чтобы найти силы реакции опор, можно воспользоваться правилом сложения параллельных сил. Им же можно пользоваться и для контроля найденных значений.
Ответ: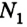 
= 3,9 H; 
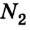=7,1 Н.
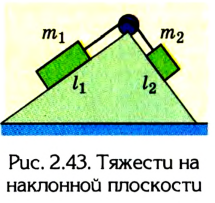
Оригинальный метод решения задач статики был предложен Симоном Сте-вином (1548-1620). Для случаев равновесия тел на наклонной плоскости он доказал, что массы тел соотносятся как длины плоскостей, которые их образуют (рис. 2.43):
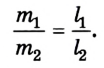
Он же установил принцип сложения статических сил (треугольник сил): три силы, действующие на одну точку, находятся в равновесии тогда, когда они бывают параллельны и пропорциональны трем сторонам плоского треугольника (рис. 2.44). Приведем пример решения одной из задач статики с применением треугольника сил.
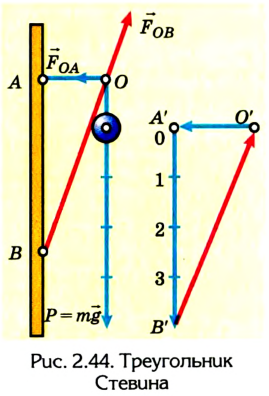
Пример №3
На кронштейне висит лампа весом 4 Н. Найти значение сил упругости в деталях ОА и ОВ.
Дано:
Р = 4 Н
– ?
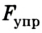Решение:
Выбираем масштаб построения треугольника. Пусть 1 см на рисунке соответствует значению силы 1 Н. Теперь строим сторону треугольника
А’В’, длина которой известна: 4 см = 4 Н. Эта сторона параллельна направлению силы тяжести, действующей на лампу. Из точки А’ проводим линию, параллельную направлению действия силы в подвесе ОА, а потом из точки В’ – параллельную направлению действия силы в упоре ОВ. На пересечении линий находится точка О’. Таким образом мы получили замкнутый треугольник сил. Зная масштаб, при помощи линейки измеряем значения силы упругости в подвесе ОА (О’А’) и силы реакции в упоре ОВ (О’В’).
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
Целевая стоимость капитала характеризует желаемое соотношение заемных и собственных средств. Предприятие может в расчете на эффект финансового рычага стремиться к дополнительному заемному финансированию. В таком случае интерес будет представлять новая структура капитала и соответствующая ей общая стоимость всего финансирования в будущем. [c.171]
Нагромождая холдинговые компании, можно в значительной степени использовать эффект финансового рычага применительно к контролируемым активам и прибыли. Предположим, что холдинговая компания А владеет 20% акций холдинговых компаний В, С и D, которые в свою очередь владеют 20-процентными контрольными пакетами акций девяти действующих компаний. Таким образом, каждый доллар капитала каждой из действующих компаний — в совокупности 9 дол. — компания А способна контролировать, инвестируя 0,36 дол., (0,20 х 0,20 х 9 дол.), или 4% общей стоимости капитала действующих компаний. До тех пор, пока действующие компании получают прибыль и способны выплачивать дивиденды своим акционерам (а именно, холдинговым компаниям), все идет хорошо. В 1920-е годы наблюдалась тенденция излишнего использования холдинговыми компаниями пирамидального принципа, особенно в коммунальной сфере. В 1930-х годах тот же эффект финансового рычага привел к увеличению убытков, и большая часть пирамид развалилась. Из-за многочисленных злоупотреблений холдинговых компаний в 1935 г. был принят закон о холдинговых коммунальных компаниях, который ограничил их деятельность. [c.701]
Как мы видим, при одинаковой общей рентабельности производства 20% рентабельность собственного капитала предприятия А составляет 20%, а предприятия Б — КэБ = 25%, т.е. она на 5% больше. Это объясняется тем, что на предприятии Б одна часть активов — 1000 млн руб. (основного и оборотного капитала) — финансируется ресурсами, которые обходятся предприятию в среднем в 15%. Разница в 5%, получаемая благодаря использованию заемных средств, называется эффектом финансового рычага . [c.309]
Выводы комплексного план-факт анализа исполнения сводного бюджета являются важнейшей предпосылкой планирования на следующий бюджетный период. Величина количественного эффекта, оказываемого на интегральный показатель того или иного бюджетного параметра, фактически является мерой рычага, то есть четкого, количественно обоснованного понимания того, в каком сегменте бизнеса меры по корректировке управленческой политики дадут наибольший эффект. Это напрямую определяет приоритеты предприятия на следующий бюджетный период. Так, очевидно, что финансовое планирование в следующем периоде должно иметь своей целью общее сокращение величины текущих обязательств за счет уменьшения ча- [c.480]
Эффект финансового левереджа (рычага) рассчитывается как изменение ставки доходности собственного капитала фирмы вследствие изменения доли заемных средств в общей стоимости имущества фирмы. Положительный эффект финансового левереджа будет достигаться, если ставка доходности собственного капитала фирмы (р) будет выше средней ставки процента по займам фирмы (г), то есть р>г. Разница между рил, скорректированная на величину налоговых отчислений, называется дифференциалом финансового рычага, d = (l-T j(p-r), где Тс— налоговая ставка, выраженная в процентах. При этом положительный или отрицательный знак дифференциала финансового рычага будет определять соответственно положительный или отрицательный характер эффекта финансового рычага. Сила воздействия или плечо финансового рычага будет равно коэффициенту соотношения заемных и собственных средств фирмы п = Кз/с = Кз/Кс- В итоге эффект финансового рычага будет представлять собой произведение своего дифференциала на свое плечо. Отметим, что попытки усилить воздействие финансового рычага за счет увеличения его плеча ведут к повышению финансового риска вложений в корпорацию и могут изменить знак дифференциала с плюса на минус. Поэтому использование финансового рычага в финансовой политике фирмы требует точных и обоснованных расчетов. [c.161]
Назовите три основных типа общих стратегий фирмы. В чем заключается эффект синергизма или стратегического рычага [c.75]
Обобщающим показателем является производственно-финансовый леверидж, который представляет произведение. уровней производственного и финансового левериджа. Он отражает общий риск, связанный с возможным недостатком средств для возмещения производственных расходов и финансовых издержек по обслуживанию внешнего долга. Следует отметить, что сочетание мощного операционного рычага с мощным финансовым рычагом может оказаться губительным для предприятия, так как предпринимательский и финансовый риски взаимно умножаются, мультиплицируя неблагоприятные эффекты. [c.359]
Таким образом, кредиторская задолженность увеличивает эффект финансового рычага. При наличии кредиторской задолженности необходимо проводить перерасчет суммы заемных средств, экономической рентабельности активов, средней процентной ставки за кредит г. При корректировке г (средней расчетной ставки процента) необходимо учитывать фактические финансовые издержки по всем кредитам и общую сумму заемных средств с учетом кредиторской задолженности. [c.331]
Однако на практике эффект финансового рычага следует применять с большой осторожностью, постоянно проводя сравнение ставки за кредит и рентабельность общего капитала предприятия. Если ставка за кредит будет выше рентабельности общего капитала предприятия, то это будет приводить к снижению рентабельности собственного капитала при увеличении суммы заемных средств. В этом случае увеличение суммы кредитов лишено смысла и может вызвать неплатежеспособность корпорации (фирмы, предприятия), привести к невозможности обеспечить возврат кредитов или к большой задолженности в оплате полученного сырья, материалов, в выдаче заработной платы персоналу. [c.332]
Эффект производственного рычага показывает, во сколько раз изменение прибыли больше темпов прироста объема реализации. Увеличение прибыли происходит за счет эффекта масштаба производства. При этом чем больше доля постоянных расходов в общей сумме издержек, тем больше эффект производственного рычага. [c.67]
Следующим значимым показателем для измерения совокупных экономических результатов, достигаемых при различном соотношении собственного и заемного капитала предприятия, является показатель “финансовый рычаг”, который измеряет эффект, заключающийся в повышении рентабельности собственного капитала с помощью увеличения доли заемного капитала в общей его сумме. [c.131]
В формировании рациональной структуры источников средств исходят обычно из самой общей целевой установки найти такое соотношение между заемными и собственными средствами, при котором стоимость акции предприятия будет наивысшей. Это, в свою очередь, становится возможным при достаточно высоком, но не чрезмерном эффекте финансового рычага. Уровень задолженности служит для инвестора чутким рыночным индикатором благополучия предприятия. Чрезвычайно высокий удельный вес заемных средств в пассивах свидетельствует о повышенном риске банкротства. Если же предприятие предпочитает обходиться собственными средствами, то риск банкротства ограничивается, но инвесторы, получая относительно скромные дивиденды, считают, что предприятие не преследует цели максимизации прибыли, и начинают сбрасывать акции, снижая рыночную стоимость предприятия. [c.170]
Структура активов. Если предприятие располагает значительными активами общего назначения, которые по самой своей природе способны служить обеспечением кредитов, то увеличение доли заемных средств в структуре пассива вполне логично. В этой связи становится понятно, почему компании по операциям с недвижимостью могут себе позволить иметь повышенный уровень эффекта финансового рычага, а узкоспециализированные в технико-экономическом отношении предприятия вынуждены довольствоваться в основном собственными средствами [c.178]
Подведем некоторые итоги, вспомнив, кстати, и об эффекте финансового рычага. Если у предприятия а) солидный (для большинства предприятий — более 10%) запас финансовой прочности б) благоприятное значение силы воздействия операционного рычага при разумном удельном весе постоянных затрат в общей их сумме в) высокий уровень экономической рентабельности активов, нормальное значение дифференциала и спокойное значение финансового рычага — это предприятие весьма привлекательно для инвесторов, кредиторов, страховых обществ и других субъектов экономической жизни. [c.203]
Так и доложим Общему собранию акционеров, а заодно покажем и вариантные расчеты суммы чистой прибыли на акцию при тех или иных соотношениях заемных и собственных средств. Не исключено, что, оценив при этом суммарную степень риска, выраженную в уровне сопряженного эффекта операционного и финансового рычагов, акционеры согласятся на снижение нормы распределения прибыли на дивиденды и наращивание собственных средств за счет нераспределенной прибыли. [c.212]
На изменение размера чистого рабочего капитала соотношение источников финансирования оборотных активов оказывает решающее влияние. Если при неизменном объеме краткосрочных финансовых обязательств будет расти доля оборотных активов, финансируемых за счет собственных источников и долгосрочного заемного капитала, то размер чистого рабочего капитала будет увеличиваться. Естественно, в этом случае будет повышаться финансовая устойчивость предприятия, но снижаться эффект финансового рычага и расти средневзвешенная стоимость капитала в целом (так как процентная ставка по долгосрочным займам в силу большего их риска выше, чем по краткосрочным займам). Соответственно, если при неизменном участии собственного капитала и долгосрочных займов в формировании оборотных активов будет расти сумма краткосрочных финансовых обязательств, то размер чистого рабочего капитала будет сокращаться. В этом случае может быть снижена общая средневзвешенная стоимость капитала, достигнуто более [c.327]
Формирование рациональной структуры источников средств сводится во многом к определению оптимального соотношения между заемными и собственными средствами. В работе [3] при этом исходят из самой общей целевой установки найти такое соотношение между заемными и собственными средствами, при котором стоимость акции предприятия будет наивысшей. Это, в свою очередь, становится возможным при достаточно высоком эффекте финансового рычага. [c.32]
Произведенные расчеты позволяют определить силу эффекта производственного рычага . Для этого следует из общей суммы выручки от реализации продукции исключить переменные затраты, а результат разделить на сумму прибыли. [c.152]
В целях повышения роли экономических рычагов и стимулов в расширении выпуска изделий высокого качества и в обеспечении систематического обновления ассортимента продукции устанавливаются поощрительные надбавки к оптовой цене на новую высокоэффективную продукцию и скидки с оптовой цены на морально устаревшую продукцию, качество которой не отвечает современным требованиям. Надбавка к оптовой цене за эффективность и качество устанавливается на срок до одного года, а на продукцию особой сложности — до двух лет. Если изделию в течение этого срока присваивается государственный Знак качества, то срок действия надбавки продлевается. В этом случае общий срок действия надбавки не может превышать четырех лет, а для продукции особой сложности — пяти лет. Размер надбавки зависит от годового экономического эффекта, от выпуска и использования продукции. Надбавка может быть увеличена в 1,5 раза на новую высокоэффективную продукцию и на продукцию, которой присвоен государственный Знак качества, когда производство этой продукции основано на разработках, призванных открытиями или изобретениями. [c.351]
Эффект рычага”, или действие рычага, позволяет изучить воздействие определенных постоянных затрат (затраты на оборудование или денежные затраты) на определенные виды прибыли (общую валовую прибыль или прибыль акционеров). Это название связано с тем, что постоянные затраты оказывают на прибыль воздействие, подобное эффекту рычага. [c.110]
Концепция достижения экономического роста на основе выбора небольшого количества четких приоритетов в инвестиционной деятельности разработана английским экономистом У. Ростоу и названа концепцией самоподдерживающегося роста . При этом в общем смысле под региональным экономическим ростом принято понимать такое увеличение масштабов регионального производства, которое обеспечивается за счет роста количества применяемых факторов производства и на основе повышения их качества, которое характеризует интенсивный тип этого роста. Существуют два подхода и два механизма стимулирования экономического роста в регионе. Первый приемлем в условиях неполного использования своих экономических ресурсов. Экономический механизм решения этой проблемы объясняется теорией занятости. Суть ее состоит в том, чтобы через бюджетные инвестиции и эффект рычага вовлечь свободные ресурсы, увеличить валовой региональный продукт. Второй используется тогда, когда имеющиеся производственные мощности задействованы полностью, и дальнейшее развитие регионального хозяйства связано с повышением его конкурентоспособности, структурной перестройкой, повышением производительности труда и общей эффективности производства за счет применения организационных инноваций и новых технологий. Механизм такого развития объясняется теорией экономического роста, источником которого являются не бюджетные инвестиции, а капиталовложения, осуществляемые предприятиями. [c.52]
Операционно-финансовый рычаг наряду с эффектом роста рентабельности собственного капитала в результате роста объема продаж и привлечения заемных средств, отражает общий риск снижения рентабельности и получения убытков. [c.202]
Задача снижения совокупного риска организации сводится к выбору одного из трех вариантов 1) сочетание высокого уровня эффекта финансового рычага со слабой силой воздействия операционного рычага 2) сочетание низкого уровня эффекта финансового рычага с сильным операционным рычагом 3) сочетание умеренных уровней эффектов финансового и операционного рычагов. В самом общем виде критерием выбора того или иного варианта служит максимально возможная курсовая стоимость акции организации при минимальном риске, что достигается за счет компромисса между риском и доходностью. [c.65]
Из расчетов следует чем выше удельный вес заемных средств в общей сумме используемого капитала, тем выше эффект финансового рычага и, соответственно, больше уровень прибыли на собственный капитал (в расчете намеренно игнорируется возможный рост цены заемного капитала по мере наращения плеча финансового рычага). По предприятию А эффект финансового рычага отсутствует, поскольку оно не использует в своей хозяйственной деятельности заемный капитал. [c.342]
Задание 6.12. Рассчитать эффект финансового рычага по предприятиям А—F (табл. 6.19). По результатам проведенных расчетов сделать выводы о взаимосвязи удельного веса заемных средств в общей сумме используемого предприятием капитала и эффекта финансового рычага. [c.351]
Общий эффект рычага будет соответствовать в таком случае произведению двух эффектов [c.196]
Эффект общего рычага (degree of total leverage, DTL) объединяет коэффициенты операционного и финансового рычагов, представляя собой их произведение, или же результат деления изменения чистой прибыли в процентах на изменение объема продаж в процентах (см. формулу 9.7). [c.270]
Общий предпринимательский риск, оцениваемый как чувствительность чистой прибыли к изменениям объемов продаж Д5, выражается совмещенным эффектом финансового и производственного рычагов (англ. Joint Effe t — JE) [c.169]
Использование различных видов показателей рентабельности позволяет определить влияние структурных элементов капитала на финансовый результат. Одним из инструментов такого рода анализа в рамках концепции метода прямого счета (dire t osting) является понятие операционного (производственного) рычага. В общем смысле, операционный рычаг определяет возможность получения большего или меньшего изменения прибыли при одном и том же снижении выручки. Образное представление этого понятия дано на рис. 8.3. Эффект производственного рычага можно вычислить по формуле Эпр = 1 + РС/П5, где Пб — прибыль до налогообложения (балансовая) F — постоянные затраты. [c.392]
В теории финансового менеджмента существует понятие финансового рычага (левериджа9). Уровень эффекта финансового рычага количественно позволяет оценить возможность увеличения прибыли предприятия за счет использования заемных средств. В общем случае, к эффекту финансового рычага относят любое, в том числе и отрицательное влияние заемных средств на рентабельность предприятия. Существуют две модели финансового рычага — европейская и американская. [c.394]
Общая (портфельная) стратегия фирмы формирует определенный состав и структуру инвестиционного портфеля организации. Эффективно распределенные между стратегическими единицами бизнеса (СЕБ) инвестиции могут создать эффект синэргизма или стратегического рычага, когда определенные затраты на совокупность различных типов стратегий приводят к гораздо более существенным преимуществам в деятельности фирмы, обусловленным удачным дополнением или сотрудничеством между СЕБ. [c.59]
Для оценки уровня финансового риска и измерения экономических результатов, достигаемых при различном соотношении собственного и заемного капитала, на четвертом этапе определяется финансовый рычаг, который измеряет эффект, заключающийся в повышении рентабельности собственного капитала с помоп ью увеличения доли заемного капитала в общей сумме. Расчет уровня эффекта финансового рычага открывает широкие возможности но определению безопасного объема заемных средств и оценки риска кредитора. Если привлечение новых заемных средств приносит предприятию увеличение уровня эффекта финансового рычага, то такое заимствование выгодно. [c.129]
СДЕЛЬНАЯ ЗАРАБОТНАЯ ПЛАТА — форма оплаты труда, при которой работник получает вознаграждение в соответствии с количеством и качеством выработанной им продукции или выполненной работы. Применяется на работах, где результаты труда поддаются точному и полному учету наибольший эффект дает при использовании технически обоснованных норм выработки. С. з. п. соот. ветствует социалистическому принципу оплаты по труду, строится на научной основе и является важнейшим рычагом повышения производительности труда, способствует сочетанию общегосударственных интересов с личными интересами каждого работника. Правильная организация С. з. п. обеспечивает действенный контроль за количеством и качеством труда, способствует улучшению организации труда и производства. Применение С. 8. п. материально заинтересовывает рабочих в распространении передового опыта новаторов производства. С. з. п. применяется в форме прямой и косвенной, сдельно-прогрессивной, сдельно-премиальной и аккордной систем оплаты труда. Каждая из них может быть в зависимости от форм организации труда индивидуальной или коллективной (бригадной). При бригадной форме организации труда нормы выработки устанавливаются в целом для всей бригады. Сдельные расценки исчисляются на основании общих бригадных норм и тарифных ставок, соответствующих разрядам выпод- [c.286]
После анализа сводки доходов изучают баланс компании, т.е. ее общее финансовое положение. Помимо стандартных пропорций, характеризующих финансовое положение компании, необходимо рассмотреть ее капитальную структуру, чтобы оценить эффект рычага на В /А. Эффект рычага в данном случае — это влияние фиксированных платежей (по облигациям и преф-акциям) на В/А. Рост или снижение дохода по указанным платежам оборачивается соответственно сверхпропорциональным ростом или снижением В /А. Такой эффект возникает, если в капитальной структуре имеются облигации и префакции, и он тем ощутимее, чем больше доля старших ценных бумаг. Рыночное “поведение” акций компаний, имеющих в своей капитализации префакции (или облигации), отличаются большей нестабильностью. [c.82]
Каждому типу управления оборотными активами должна соответствовать определенная политика их финансирования, т. е. управления краткосрочными обязательствами. Признаком агрессивной политики управления краткосрочными пассивами служит значительный удельный вес (более 50 %) краткосрочных кредитов и займов в общей сумме источников средств. При такой политике у предприятия может вырасти эффект финансового леверид-жа (рычага) до 30-50 % рентабельности активов. Однако увеличиваются и постоянные издержки за счет процентных платежей по заемным средствам. В результате повысится и сила воздей- [c.122]
Эффект финансового рычага можно объединить с эффектом операционного рычага для получения общего эффекта рычага. За счет этого будет еще больше усилено влияние колеба- [c.195]
Сак уже было отмечено ранее, само понятие рычага ( левериджа ) казывает на наличие в общей структуре затрат компании постоян-юй составляющей, которая тем не менее может возникнуть в ре-ультате самых разных действий и явлений. Как правило, леверидж — лагоприятный фактор для бизнеса, возникновение которого, однако южет породить и определенные проблемы. Понятие операционного ычага означает, что некоторая часть текущих затрат предприятия ос-ается постоянной в довольно широком диапазоне и не зависит от избиений объема производства. Таким образом, прибыль будет меняться е прямо пропорционально объему выпуска продукции и выручке быстрее. Положительный эффект это го явления сохраняется, как мы видим, если эти объемы достаточно высоки. Если же он сокращают-я ввиду неблагоприятной ситуации на рынке, то операционная при- [c.212]
Ученик
(52),
на голосовании
12 лет назад
Голосование за лучший ответ
Leonid
Высший разум
(388685)
12 лет назад
Если рычаг в равновесии, то отношения плеч обратно пропорциональны отношениям сил. А сумма плеч равна, понятное дело, 2 м. Так что имеем сумму двух чисел и их отношение. Это два уравнения с двумя неизвестными. Выразите в одном уравнении одно неизвестное через другоей и подставьте во второе уравнение.
Валентина Вавилова(Серкова)
Гений
(62183)
12 лет назад
Пусть длина 1 плеча d1, тогда d2= 2 – d1. Так как силы отратно пропорциональны плечам, запишем:
F1 / F2= (2 -d1) / d1. Решим уравнение относительно d1.
F1*d1=2*F2 – F1*d1.
F1*d1 + F2*d1=2*F2.
d1( F1+F2)=2*F2.
d1= 2F2 / ( F1+F2).
d1=2*140 / ( 20+140)=1,75м.
d2=2 – 1,75=0,25м.
d1=1,75м . d2=0,25м.
В “данной задаче” плечи рычага найти невозможно. Но если к “данной задаче” добавить фразу “рычаг находится в равновесии” или “находящегося в равновесии”, то задача моментально решается, просто в уме. Я не знаю, кто поленился дописать эту фразу, автор вопроса или автор задачи, но этот пример ясно показывает, что из условия задачи нельзя выкидывать ни одного слова.
Ну, а теперь, само решение. Пусть одно плечо рычага х см, тогда длина другого (17-х) см. Равновесие рычага устанавливается при равенстве моментов. Правда возникает неопределённость, к какому плечу какая сила приложена? Но она разрешается в процессе решения. Моменты сил равны 24*х и 27*(17-х) или 27*х и 24*(17-х) и уравнения равновесию либо 24*х=27*(17-х) – уравнение 1, либо 27*х=24*(17-х) – уравнение 2.
Решаем первое уравнение: 24*х=27*(17-х), х=9 см. Итак одно плечо (для меньшей силы) 9 см, тогда плечо для другой (для большей силы) 17-9=8 см.
Решаем второе уравнение: 27*х=24*(17-х), х=8 см. Итак плечо для большей силы – 9 см, а для меньшей силы – 17-8=9 см. Оба способа привели к одному и тому же решению.
