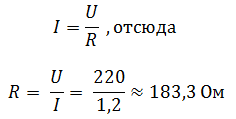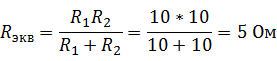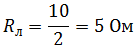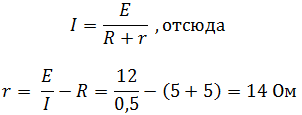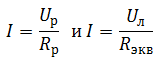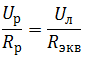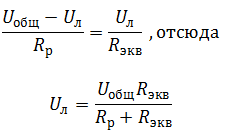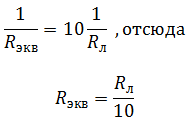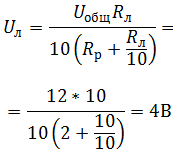Что бы ни происходило в мире, учиться надо всегда. Кстати, для тех, кто не знает, как организовать учебу на удаленке, мы подготовили отдельную статью. А сегодня займемся решением задач на последовательное и параллельное соеднинение проводников. Решение задач – отличный способ, чтобы успокоить нервы и не поддаваться панике.
Присоединяйтесь к нам в телеграме: там вас ждут актуальные новости и приятные скидки.
Последовательное и параллельное соединение проводников: решение задач
Как решать задачи с параллельным и последовательным соединением проводников? Для начала повторите теорию, вспомните общую памятку по решению физических задач и на всякий случай держите под рукой формулы.
Задача №1 на последовательное соединение проводников
Условие
Проводники сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника равно 12 В. Определите напряжение, сопротивление и силу тока в цепи на втором проводнике, а также полное напряжение.
Решение
По закону Ома:
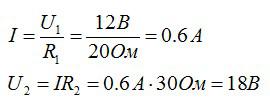
Для последовательного соединения проводников:
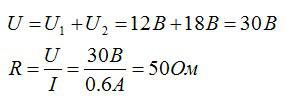
Ответ: 50 Ом; 18 В; 0,6 А; 30 В.
Задача №2 на параллельное соединение проводников
Условие
Два проводника соединены параллельно. Сила тока в первом проводнике равна 0,5 А, во втором — 1 А. Сопротивление первого проводника составляет 18 Ом. Определите сопротивление второго проводника и силу тока на всем участке цепи.
Решение
Для параллельного соединения:
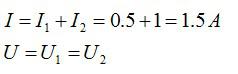
По закону Ома:
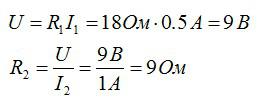
При решении задач не забывайте проверять размерности величин и при необходимости переводить их в систему СИ.
Ответ: 1,5 А; 9 Ом.
Задача №3 на последовательное и параллельное соединение проводников
Условие
Электрогрелка состоит из трех одинаковых секций. Во сколько раз быстрее грелка будет нагревать некоторое количество воды от 10 до 100 градусов Цельсия при параллельном включении всех секций, нежели при последовательном их включении?
Решение
Пусть сопротивление каждой секции равно R. Тогда при параллельном включении их в сеть напряжение на каждой секции равно напряжению в сети (U), и на трех секциях будет выделяться тепло:
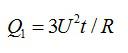
При последовательном соединении суммарное сопротивление цепи равно 3R, а выделяющееся количество теплоты:
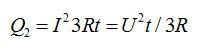
Как видим, выделяющееся тепло для первой схемы в 9 раз больше, так что и скорость нагрева воды будет в 9 раз выше.
Ответ: в 9 раз.
Задача №4 на смешанное соединение проводников
Условие
Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Определите силу тока во всей электрической цепи.
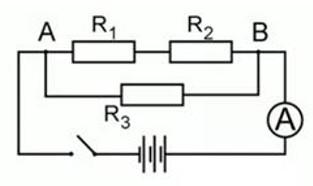
Решение
Согласно схеме, искомая сила тока – это сила тока, протекающая через амперметр.
Резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним.
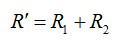
Резисторы 1 и 2 можно заменить эквивалентным сопротивлением R со штрихом и перерисовать схему в упрощенном виде:
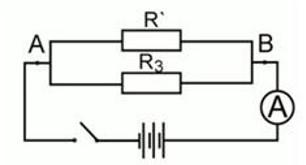
Сопротивления R3 и R со штрихом соединены параллельно, можно найти общее сопротивление электрической цепи по формуле для параллельного соединения:
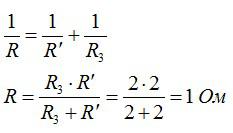
Теперь цепь можно перерисовать в еще более упрощенном виде и рассчитать силу тока по закону Ома:
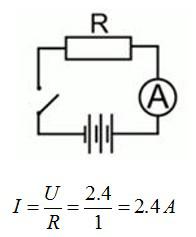
Ответ: 2.4 А.
Задача №5 на закон Кирхгофа
Правила Кирхгофа применяются для расчета сложных электрических цепей.
Условие
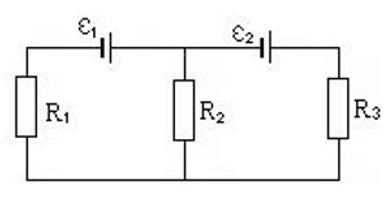
Три сопротивления R1 = 5 Ом, R2 = 1 Ом, R3 = 3 Ом и два источника тока соединены так, как показано на рисунке. Внутренними сопротивлениями источников тока можно пренебречь. ЭДС первого источника тока равна 1,4 В, и сила тока, текущего через сопротивление R3, равна I3= 1 А. Определите ЭДС второго источника тока.
Решение
Выберем направление обхода контуров по часовой стрелке и запишем закон Кирхгофа для точки A (расположим ее между двумя источниками и сопротивлением R2) и двух контуров:
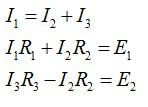
Подставим числа, получим
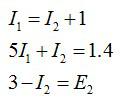
Решая систему уравнений, получаем ответ: Е2=3.6 В.
Ответ: 3.6 В.
Вопросы на параллельное и последовательное соединение проводников
Вопрос 1. Схематически изобразите последовательное соединение проводников
Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:
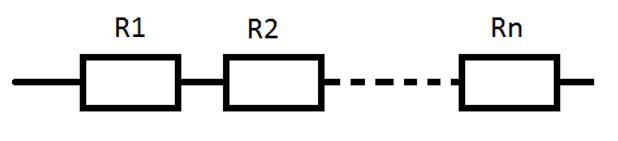
Вопрос 2. Схематически изобразите параллельное соединение проводников
Ответ. На рисунке ниже изображено параллельное соединение проводников:
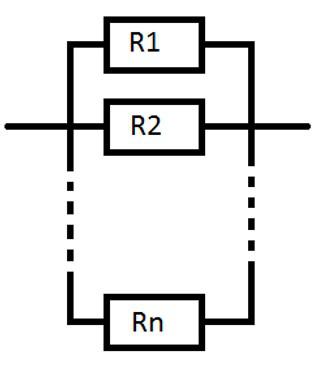
Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.
Ответ. При последовательном соединении:
- Сила тока во всех проводниках одинакова.
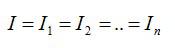
- Общее напряжение равно сумме напряжений на каждом проводнике.
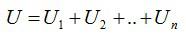
- Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
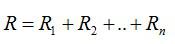
Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.
Ответ. Для параллельного соединения проводников:
- Напряжение на всех проводниках одинаково.
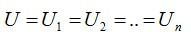
- Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.
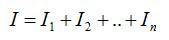
- Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
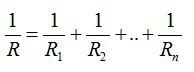
Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?
Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.
Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.
Соловьев Валерий Иванович
преподаватель – методист высшей категории
Таврический колледж ФГАОУ ВО «Крымский
федеральный университет имени В. И. Вернадского»
г. Симферополь, Республика Крым
Решение типовых задач по расчету электрических цепей
постоянного и переменного тока
Изучение электротехники предусматривает овладение теоретическими
знаниями и приобретение определенных практических навыков. Особая роль в этом
процессе, наряду с выполнением лабораторных и практических работ, отводится
решению задач, которые позволяют использовать полученные теоретические сведения
по конкретным разделам и темам электротехники.
Настоящее методическое пособие предназначено для закрепления
теоретического материала по разделам:
·
Электрическое и магнитное
поле;
·
Электрические цепи
постоянного тока;
·
Электрические цепи
переменного тока.
Пособие содержит
примеры решения типовых задач по электротехнике.
Раздел 1. Элетрическое и магнитное поле
Задача №1
В
электрическом поле при перемещении заряда q = 2•10‾4
к совершена работа A = 0,4 дж. Определить напряжение между
начальной и конечной точками пути.
Решение:
U = ![]() =
= ![]() = 2000
= 2000
в = 2 кв.
Ответ:
Напряжение между начальной и конечной точками пути при перемещении заряда q
= 2•10‾4 к равно 2 кв .
Задача №2
Определить напряженность магнитного поля и магнитную
индукцию в точках, расположенных на расстояниях 0,2; 0,4 и 1
см от оси прямолинейного провода. Радиус провода r = 0,4
см; электрический
ток в проводе I = 50А и магнитная проницаемость μ
= 1.
Решение:
Точка, лежащая на расстоянии 0,2
см от оси провода, находится внутри провода:
H![]() =
= ![]() =
= ![]() = 1000
= 1000 ![]() ;
;
B![]() = μ
= μ![]() • H
• H![]() = 4
= 4![]() • 10
• 10![]() •2000 = 25 гс.
•2000 = 25 гс.
Точка, лежащая на расстоянии 0,4
см от оси провода, находится на его поверхности:
H![]() =
= ![]() =
= ![]() = 2000
= 2000![]() ;
;
B![]() = μ
= μ![]() • H
• H![]() = 4
= 4![]() = 25 гс.
= 25 гс.
Точка, лежащая на расстоянии 1
см, лежит за пределами провода:
H![]() =
= ![]() =
= ![]() = 800
= 800 ![]() ;
;
B![]() = μ
= μ![]() • H
• H![]() = 4
= 4![]() = 10 гс.
= 10 гс.
Ответ: Напряженность
магнитного поля и магнитная индукция в точках, расположенных на расстояниях 0,2;
0,4 и 1 см от оси прямолинейного провода равна
H![]() = 1000
= 1000 ![]() ;
;
B![]() = 25 гс.
= 25 гс.
H![]() = 2000
= 2000![]() ;
;
B![]() = 25 гс.
= 25 гс.
H![]() = 800
= 800![]() ;
;
B![]() = 10 гс.
= 10 гс.
Раздел 2. Электрические цепи постоянного тока
Задача №3
Найти сопротивление между точками А и D,
приведенной на рисунке электрической схемы, если каждое из трех сопротивлений
равно 1 Ом. (Сопротивлением соединительных проводов пренебречь).

Решение:
Так как точки А и С, а также точки В и D
соединены проводниками, сопротивление которых мы не учитываем, то схему представленную
в условии задачи можно заменить эквивалентной схемой.

Из нее видно, что сопротивление между точками А и D можно
вычислить по формуле для параллельного соединения проводников.
![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
Откуда
R![]() =
= ![]() =
= ![]()
![]() 0,33 Ом.
0,33 Ом.
Ответ: Сопротивление между
точками А и D равно
R![]()
![]() 0,33 Ом.
0,33 Ом.
Задача №4
Мощность, потребляемая нагрузочным сопротивлением RH = 9,9 Ом, измеряется с помощью
вольтметра и амперметра. Вольтметр показывает 120В, амперметр 12А.
Считая, что показания приборов не содержат
погрешностей (ошибки исключены с помощью поправок), подсчитать мощность, выделяющуюся
в сопротивлении RH. Найти погрешность измерения
мощности.

Решение:
Мощность, выделяющаяся в сопротивлении Rн , подсчитанная по показаниям приборов,
Риз
= UI = 120 ∙ 12 = 1440 Вт,
Действительное значение этой мощности
Р = I![]() ∙ Rн = 122 ∙ 9,9 = 1425,6 Вт.
∙ Rн = 122 ∙ 9,9 = 1425,6 Вт.
Абсолютная погрешность измерения
ΔP = Риз – Р = 1440 —
1425,6 = 14,4 Вт.
Относительная
погрешность измерения
δ = ΔP/Р = 14,4/1425,6 = 0,0101 ≈ 1%.
Таким образом,
проведя измерение абсолютно точными приборами, получаем значение мощности, на 1
% отличающееся от действительного.
Такая погрешность, вызванная
самой схемой измерения, называется систематической или методической.
Эта погрешность
может быть найдена и непосредственно по известной формуле
δ = RA / Rн
Внутреннее
сопротивление амперметра
RA =
![]() – Rн =
– Rн =![]() – 9,9 = 0,1 Ом
– 9,9 = 0,1 Ом
Погрешность
δ = RA / Rн = 0,1/9,9 = 0,0101.
Ответ: Погрешность измерения мощности δ
= 0,0101 ≈ 1%.
Задача №5
Для изготовления обмотки нагревательного прибора при напряжении
220 В и токе 2 А применяется нихромовая лента. Определить длину
ленты, приняв допустимую плотность тока δ = 10 ![]() :
:
ρнихрома= 1,1 ![]() – удельное сопротивление нихрома.
– удельное сопротивление нихрома.
Решение:
S = ![]() =
= ![]() = 0,2 мм
= 0,2 мм![]() .
.
Сопротивление обмотки
r
= ![]() =
= ![]() = 110 ом.
= 110 ом.
Определяем
длину ленты
l = ![]() =
= ![]() = 20
= 20
м.
Ответ: Длина нихромовой
ленты равна 20 м.
Задача №6
Определить сопротивление медного провода линии передачи
сечением
S = 95мм![]() , длиной l = 120
, длиной l = 120
км при
температурах О и 20 °С.
ρмеди= 0,0175 ![]() – удельное сопротивление меди.
– удельное сопротивление меди.
αмеди = 0,004
![]() – температурный коэффициент меди.
– температурный коэффициент меди.
Решение:
r![]() = ρ•
= ρ•![]() ;
;
так
как ρ задано как раз для температуры 20° С, то, подставляя значения l и S, находим:
r ![]() = 0,0175 •
= 0,0175 • ![]() = 21,7 ом.
= 21,7 ом.
Сопротивление провода при 0° С
r![]() = r
= r![]() •
•![]() =21,7 + 21,7 • 0,004 (-20
=21,7 + 21,7 • 0,004 (-20 ![]() C) = 20 ом.
C) = 20 ом.
Ответ: Сопротивление медного провода линии
передачи сечением S = 95мм![]() , длиной l = 120
, длиной l = 120
км при
температурах О и 20°С равно 20 ом.
Задача №7
Определить напряжение на выходе делителя напряжения, который
подключен к источнику питания 10 В в следующих случаях:
а) напряжение снимается со всего делителя напряжения;
б) напряжения снимается с половины витков делителя
напряжения;
в) напряжение снимается с 1/4 витков делителя напряжения.

Решение:
Напряжение на выходе делителя определяется по формуле:
U![]() = I • R
= I • R
С другой стороны, ток переменного резистора находится из
соотношения
I
= ![]()
Следовательно, отношение напряжения на выходе делителя и напряжения
питания пропорционально отношению сопротивлений R и R![]() т.е.
т.е.
U![]() =
= ![]() • U
• U![]()
Отсюда находим искомые значения напряжений на выходе делителя
а) U![]() =
= ![]() = 10 В;
= 10 В;
б) U![]() =
= ![]() = 5 В;
= 5 В;
в) U![]() =
= ![]() = 2,5 В.
= 2,5 В.
Ответ:
а) напряжение снимается со всего делителя напряжения
U![]() = 10 В;
= 10 В;
б) напряжения
снимается с половины витков делителя напряжения
U![]() = 5 В;
= 5 В;
в) напряжение снимается с 1/4 витков делителя напряжения U![]() = 2,5 В.
= 2,5 В.
Задача №8
Определять токи и напряжения в электрической цепи,
изображенной на рисунке, при следующих ее данных: Е = 2 в; r![]() = 0,5 ом; r
= 0,5 ом; r![]() = 3,5 ом; r
= 3,5 ом; r![]() = 5 ом; r
= 5 ом; r![]() = 100 ом; r
= 100 ом; r![]() =25 ом.
=25 ом.

Решение:
Находим проводимость параллельно соединенных ветвей
gАБ
= g2![]() + g3 +
+ g3 +
g4 = ![]() +
+![]() +
+![]() = 0,25
= 0,25
![]() ,
,
откуда следует, что сопротивление этого участка
r![]() =
=![]() = 4 ом.
= 4 ом.
общее
сопротивление всей цепи
r = r![]() + r
+ r![]() + r
+ r![]() = 0,5 + 3,5 + 4 = 8 ом.
= 0,5 + 3,5 + 4 = 8 ом.
Ток в неразветвленной части цепи
I![]() =
= ![]() =
= ![]() = 0,25 А.
= 0,25 А.
Напряжение между точками АБ
U![]() = I
= I![]() • r
• r![]() = 0,25 • 4 = 1 В.
= 0,25 • 4 = 1 В.
Токи в отдельных ветвях
I![]() =
= ![]() =
= ![]() = 0,2 А;
= 0,2 А;
I![]() =
= ![]() =
= ![]() = 0,01 А;
= 0,01 А;
I![]() =
= ![]() =
= ![]() = 0,04 А.
= 0,04 А.
Ответ: токи и напряжения в электрической
цепи равны:
U![]() = 1 В.
= 1 В.
I![]() = 0,25 А.
= 0,25 А.
I![]() =
=
0,2 А;
I![]() =
=
0,01 А;
I![]() = 0,04 А.
= 0,04 А.
Задача №9
При разомкнутом ключе К показания вольтметра 2,1
В. Когда ключ замкнут, амперметр фиксирует ток 1А. Внешнее
сопротивление цепи R = 2 Ом. Определить ЭДС источника Е, внутреннее
сопротивление источника R![]() и напряжение на зажимах источника U.
и напряжение на зажимах источника U.

Решение:
Когда цепь тока разорвана, вольтметр, подключенный к
зажимам источника, практически фиксирует значение ЭДС.
Следовательно,
E = 2,1 В.
Для определения R![]() необходимо воспользоваться законом Ома
необходимо воспользоваться законом Ома
для всей цепи:
I = ![]() ,
,
Откуда
R![]() + R =
+ R = ![]() =
= ![]() = 2,1 Ом.
= 2,1 Ом.
Так как известно, что внешнее сопротивление цепи R=
2 Ом, то внутренне сопротивление источника
R![]() = 2,1 – 2 = 0,1 Ом.
= 2,1 – 2 = 0,1 Ом.
Напряжение на зажимах источника
U = E – R![]() I
I
или
U = RI
Подставляя значения в приведенные выражения, получим
U = 2,1 – 0,1 • 1 = 2 B;
U = 2 • 1 = 2В;
Применение формулы U = E – R![]() I предпочтительней, так как
I предпочтительней, так как
подчеркивается тот факт, что напряжение на зажимах источника меньше ЭДС, причем
с увеличением тока это напряжение уменьшается.
Ответ: E = 2,1 В.
R![]() = Ом.
= Ом.
U = 2 B;
Задача №10
Для электрической цепи представленной на рисунке, методом двух
узлов, определить токи во всех ее ветвях. Задачу решить в общем виде, учесть,
что известны следующие параметры электрической цепи: E1, E2, Ri1, Ri2, R1, R2, R3.

Решение:
Решение
данной задачи состоит в расчете сложной цепи переменного тока методом двух
узлов. Для этого надо применительно к представленной на рисунке
электрической схеме:
1)
выбрать направления всех токов одинаковыми
2)
найти проводимости всех ветвей, См,
G1 = ![]()
G2 =![]()
G3 =![]()
3)
определить узловое напряжение Uab
Uab = ![]()
(E2G2 – со знаком “минус”, так как E2 имеет противоположное I2 направление);
4) определить токи в ветвях;
I1 = (E1 –
UAB)G1
I2 =
(-E2 – UAB)G2
I3 =
(0 – UAB)G3
5)
если в
результате расчетов какой – либо ток будет получен со знаком «минус», значит,
его действительное направление противоположно выбранному на схеме.
Действительное направление необходимо показать пунктиром на схеме.
Задача №11
Генератор постоянного тока с параллельным
возбуждением работает на нагрузку, сопротивление которой Rн = 5 Ом,
сопротивление обмотки якоря Rя = 0,2 Ом, сопротивление обмотки возбуждения RB=230
Ом, напряжение на зажимах генератора U =230 В.
Определить: а) ЭДС генератора; б) электромагнитную
мощность; в) потери мощности в обмотках якоря и возбуждения?

Решение:
Токи
нагрузки
Iн = U/Rн = 230/5 = 46А
возбуждения
Iв = U/Rв = 230/230 = 1А
Якоря
Iя = Iн
+ Iв = 46 + 1 = 47A
ЭДС генератора
Е = U + Iя ∙ Rя = 230+47 ∙ 0,2 = 239,4 В
Электромагнитная
мощность
Pэ = Е ∙ Iя = 239,4 ∙ 47 = 11251,8 Вт.
Потери мощности
в меди обмотки якоря
Рмя
= Iя ![]() ∙ Rя = 472 ∙ 0,2 = 441,8 Вт
∙ Rя = 472 ∙ 0,2 = 441,8 Вт
Потери
мощности в меди обмотки возбуждения
Рмв
= Iв ![]() ∙ Rв = 12 ∙ 230 = 230 Вт
∙ Rв = 12 ∙ 230 = 230 Вт
Добавочные потери в соответствие ГОСТом составляют
1 % от
полезной мощности генератора
Рдоб = 0,01 UIн = 0,01 ∙ 230 ∙ 46 = 105,8 Вт
Потери в щеточных контактах
Рк = 2ΔUIя = 2 ∙ 0,5 ∙ 47 = 47 Вт
Ответ: ЭДС генератора Е =
239,4 В; электромагнитную мощность
Pэ = 11251,8 Вт; потери мощности в обмотках якоря Рмя
= 441,8 Вт и возбуждения Рмв = 230 Вт.
Задача №12
Чему равны одинаковые электрические токи,
протекающие в двух параллельных проводах, которые расположены на расстоянии, а
= 20 см друг от друга, если на каждый метр провода действует сила F![]() = 100 н/м?
= 100 н/м?
μ![]() = 4
= 4![]()
![]() – магнитная постоянная.
– магнитная постоянная.
Для воздуха μ![]() = 1
= 1
Решение:
I![]() =
= ![]() =
= ![]() =
=
10000А.
Ответ: Электрические
токи, протекающие в двух параллельных проводах, которые расположены на
расстоянии, а = 20 см равны 10000А.
Задача №13
Три конденсатора, емкости которых С![]() = 20 мкф, С
= 20 мкф, С![]() = 25 мкф и С
= 25 мкф и С![]() = 30 мкф, соединяются последовательно.
= 30 мкф, соединяются последовательно.
Определить общую емкость.
Решение:
Записываем формулу для определения общей емкости трех последовательно соединенных конденсаторов.
![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() = 0,05
= 0,05
+ 0,04 + 0,033 = 0,123.
C![]() =
= ![]() = 8,13 мкф.
= 8,13 мкф.
Ответ: Общая
емкость трех конденсаторов, соединенных последовательно равна 8,13 мкф.
Задача №14
Определите
емкость батареи конденсаторов, если емкость первого конденсатора С![]() = 1 мкФ, второго – С
= 1 мкФ, второго – С![]() = 2 мкФ, третьего – С
= 2 мкФ, третьего – С![]() = 4 мкФ.
= 4 мкФ.

Решение:
Конденсаторы С![]() и С
и С![]() соединены параллельно, поэтому их
соединены параллельно, поэтому их
общая емкость
C![]() = С
= С![]() + С
+ С![]() ;
;
Конденсатор C![]() соединен последовательно с C
соединен последовательно с C![]() . По
. По
формуле последовательного соединения конденсаторов имеем:
![]() =
= ![]() +
+ ![]() ;
;
C![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = 0,86 мкф.
= 0,86 мкф.
Ответ: C![]() = 0,86 мкф.
= 0,86 мкф.
Задача №15
Три одинаковых конденсатора соединены параллельно в батарею.
Определите емкость батареи, если известно, что при подключении аккумулятора (U
= 2 В) на обкладках каждого
конденсатора накапливается заряд, равный 10![]() Кл.
Кл.
Решение:
При параллельном соединении конденсаторов имеем:
C
= C![]() + C
+ C![]() + C
+ C![]() = 3 C
= 3 C![]()
U = U![]() =U
=U![]() =U
=U![]()
Следовательно,
С = 3
C![]() = 3
= 3![]() ,
,
т. к. C![]() =
= ![]() ; С = 3 •
; С = 3 • ![]() = 1,5 • 10
= 1,5 • 10![]() Ф.
Ф.
Ответ: Емкость батареи конденсаторов равна С = 1,5
• 10![]() Ф.
Ф.
Задача №16
Три конденсатора С![]() , С
, С![]() , С
, С![]() емкостью
емкостью
2 мкф каждый соединены параллельно. Определить их общую емкость.
Решение:
Записываем формулу для определения общей емкости трех
параллельно соединенных конденсаторов. Но, так как, емкость всех трех
конденсаторов одинакова то, можно воспользоваться, более простой формулой.
С![]() = 3 • С
= 3 • С![]() = 3 • 2 = 6 мкф.
= 3 • 2 = 6 мкф.
Ответ: Общая
емкость трех конденсаторов, соединенных параллельно равна 6 мкф.
Задача №17
Пространство между плоскопараллельными металлическими
пластинам заполнено парафинированной бумагой. Определить допустимое и пробивное
напряжения между пластинами при условии, что допустимое напряжение должно быть
меньше пробивного в 2,5 раза. Расстояние между пластинами d = 0,I мм.
εпр = 104
![]() – пробивная напряженность
– пробивная напряженность
парафинированной бумаги.
Решение:
Пробивное напряжение:
U пр =
ε пр • d =104 • 0,1 = 1000 в.
Допустимое напряжение
U =![]() =
= ![]() = 400 в.
= 400 в.
Ответ: Пробивное
напряжение между пластинами равно 1000 в.
Допустимое напряжение по условию задачи должно
быть меньше
пробивного в 2,5 раза и равно 400
в.
Раздел 3. Электрические цепи переменного тока
Задача №18
Электротехническое устройство с потребляемой мощностью
50 Вт и напряжением питания 110 В нужно включить в сеть переменного
напряжения 220 В частотой 50 Гц. Найти емкость конденсатора, который
необходимо подключить последовательно данному устройству, чтобы скомпенсировать
избыточное напряжение.
Решение:
Для решения задачи необходимо определить ток и
напряжение компенсирующего конденсатора, что позволит найти его реактивное
сопротивление, а следовательно, и емкость. Поэтому ток в цепи не должен
превышать
I = ![]() =
= ![]() = 0,455
= 0,455
A.
Напряжение на конденсаторе должно быть равно
векторной разности напряжений питания и нагрузки:
U![]() =
= ![]() =
= ![]() = 191
= 191
В.
Зная напряжение и ток конденсатора, находим его реактивное
сопротивление:
Х![]() =
= ![]() =
= ![]() = 420 Ом.
= 420 Ом.
По известной формуле для определения емкостного
сопротивления
X![]() =
= ![]() ;
;
находим искомую емкость конденсатора
С = ![]() =
= ![]() = 7,6 • 10
= 7,6 • 10![]() Ф
Ф
= 7,6 мкФ.
Ответ: Емкость конденсатора, который необходимо
подключить последовательно данному устройству, чтобы скомпенсировать избыточное
напряжение С = 7,6 мкФ.
Задача №19
В электрическую цепь переменного тока напряжением U = 220В, частотой
f = 50Гц включена катушка с индуктивностью L = 0,0127Гн и активным сопротивлением R![]() = 3Ом.
= 3Ом.
Определить:
1) реактивное сопротивление катушки;
2) ток в катушке;
3) активную мощность катушки;
4) реактивную мощность катушки;
5) энергию, запасаемую в магнитном поле
катушки.
Решение:
X![]() = ωL = 2
= ωL = 2![]() fL = 2 • 3,14 • 50 • 0,0127 = 4 Oм;
fL = 2 • 3,14 • 50 • 0,0127 = 4 Oм;
Z = ![]() =
= ![]() =5 Oм;
=5 Oм;
I = ![]() =
= ![]() = 44A;
= 44A;
P = U![]() • I = I
• I = I![]() • R
• R![]() = 44
= 44![]() • 3 = 1936 • 3 = 5808 Вт;
• 3 = 1936 • 3 = 5808 Вт;
Sin φ = ![]() =
= ![]() = 0,8;
= 0,8;
Q = UI sinφ = 220 • 44 • 0,8 = 7744 Вар;
W![]() = LI
= LI![]() = 0,0127 • 44
= 0,0127 • 44![]() = 24,59 дж.
= 24,59 дж.
Ответ:
X![]() = 4 Oм;
= 4 Oм;
Z = 5 Oм;
I
= 44A;
P
= 5808 Вт;
Sin φ = 0,8;
Q = 7744 Вар;
W![]() =
=
24,59 дж.
Задача №20
К генератору переменного электрического тока с напряжением
U = 240В и частотой f = 50Гц присоединен конденсатор с емкостью
C = 40 мкф.
Определить: 1) реактивное сопротивление емкости X![]() ;
;
2) ток в электрической цепи;
3) реактивную мощность цепи Q![]() ;
;
4) максимальную энергию, запасаемую
в
электрическом поле конденсатора W![]() .
.
Решение:
X![]() =
= ![]() =
= ![]()
![]()
![]() = 80 Ом.
= 80 Ом.
I = ![]() =
= ![]() = 3
= 3
A.
Q![]() = U • I = 240 • 3 = 720 Вар.
= U • I = 240 • 3 = 720 Вар.
W![]() = C•U
= C•U![]() = 40 • 10
= 40 • 10![]() •240
•240![]() = 2,7 дж.
= 2,7 дж.
Ответ: Реактивное сопротивление емкости X![]() = 80 Ом.
= 80 Ом.
Ток в электрической
цепи I = 3
A;
Реактивная мощность
цепи Q![]() = 720 Вар;
= 720 Вар;
Максимальная
энергия, запасаемая в электрическом поле
конденсатора W![]() = 2,7 дж.
= 2,7 дж.
Задача №21
В электрическую цепь переменного тока напряжением U = 220 В, частотой
f
= 50 Гц включена
катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R![]() = 6 Ом.
= 6 Ом.
Определить: X![]() ; Z ; U
; Z ; U![]() ; U
; U![]() ; cosφ.
; cosφ.
Решение:
X![]() = ωL = 2
= ωL = 2![]() =
=
2 • 3,14 • 50 • 0,0255 = 8 Oм;
Z = ![]() =
= ![]() = 10 Oм;
= 10 Oм;
I = ![]() =
= ![]() = 22
= 22
A;
U![]() = I R =
= I R =
22 • 6 = 132 B;
U![]() = U
= U![]() = I • X
= I • X![]() = 22 •
= 22 •
8 = 176 B;
Cos φ = ![]() =
= ![]() = 0,6.
= 0,6.
Ответ: X![]() = 8 Oм;
= 8 Oм;
Z = 10 Oм;
I
= 22 A;
U![]() = 132 B;
= 132 B;
U![]() = U
= U![]() = 176
= 176
B;
Cos
φ = 0,6.
Задача №22
В электрическую сеть напряжением 220В включено 16
одинаковых электрических ламп мощностью по 100Вт каждая. Определить
необходимое сечение медного провода, соединяющего эти электрические лампочки.
Площадь поперечного сечения Наиболее допустимый
медного провода, мм![]() электрический
электрический
ток, А
0,50
10
0,75 13
1,0 15
Решение:
Полная мощность
Р = P ламп • 16 = 100 • 16 = 1600 Вт.
Ток в проводе
I = ![]() =
= ![]() = 7,273 А.
= 7,273 А.
По таблице, приведенной в условии задачи, выбираем сечение
провода;
S = 0,50
мм![]() .
.
Ответ: Сечение медного провода, необходимое для
подключения 16 одинаковых электрических ламп мощностью по 100Вт каждая
в электрическую сеть напряжением 220В равно 0,50
мм![]() .
.
Задача №23
Генератор переменного тока, используемый для
получения переменной электродвижущей силы, имеет частоту вращения 2800 об/мин.
Определить частоту, период и угловую частоту электрического
тока, возникающего при подключении генератора к нагрузке, если число пар
полюсов генератора равно 6.
Решение:
Частота
электрического тока генератора
f = pn/60 = 6 ∙ 2800/60 = 280 Гц.
Период
Т= 1
/ f = 1/280 = 0,0036 с
и
угловая частота
ω = 2π/Т = 2 π f = 2 ∙ 3,14 ∙ 280 = 1750 1/с.
Ответ: Частота электрического
тока равна f = 280 Гц,
период
электрического тока равен Т= 0,0036 с,
угловая частота электрического тока равна ω = 1750 1/с.
Задача №24
В электрическую цепь переменного тока напряжением U = 220 В, частотой
f = 50 Гц включена катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R![]() = 6 Ом; I
= 6 Ом; I
= 22 A; U![]() = 132 B; Cos
= 132 B; Cos
φ = 0,6.
Определить:
1) максимальную мощность в активном сопротивлении
P![]() ;
;
2) активную мощность;
3) реактивную мощность;
4) полную мощность.
Решение:
P![]() = 2 U
= 2 U![]() I = 2 • 132 • 22 = 5808 Вт.
I = 2 • 132 • 22 = 5808 Вт.
P = UI
cos φ = 220 • 22 • 0,6 = 2904 Вт.
Q = UI
sin φ =220 • 22 • 0,8 = 3872 Вар.
S = UI = 220 • 22 = 4840 BA.
Ответ: P![]() = 5808 Вт.
= 5808 Вт.
P = 2904 Вт.
Q = 3872 Вар.
S = 4840 BA.
Задача №25
Лампа накаливания включена параллельно с линейным резистором
R2 = 30 Ом.

Построить зависимость эквивалентного
сопротивления Rэк цепи от напряжения U на его зажимах.
Методом последовательных приближений
определить напряжение U при токе в неразветвленной части цепи I = 5А.
Вольт-амперная характеристика лампы задана в таблице.
|
U, B |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
I, A |
0 |
0,6 |
1,1 |
1,5 |
1,85 |
2,15 |
2,4 |
Решение:
Построим вольт-амперные характеристики элементов цепи.

На рисунке: I(U) —
характеристика лампы и I2(U) — характеристика резистора R2.
Сложив ординаты
этих характеристик при различных значениях напряжения, получим вольт-амперную
характеристику всей цепи, т. е. зависимость тока в неразветвленной части цепи
от приложенного напряжения I(U). Эквивалентное сопротивление схемы найдем
как отношение Rэк = U/I для различных значений приложенного напряжения.
Результаты вычислений приведены на графике представленном
на рисунке.
Закон Ома для всей цепи.
ЗАДАЧИ на ЕГЭ
Формулы, используемые на уроках физики в 10-11 классах «Закон Ома для всей цепи. Расчет электрических цепей» для подготовки к ЕГЭ по физике.

Смотрите также другие конспекты по решению задач:
ЕГЭ: Закон Ома для участка цепи
ОГЭ: Закон Ома в 8 классе
Закон Ома для всей цепи.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Вольтметр, подключенный к лампочке, показывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?
Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать бесконечно большим, а силу тока, текущего через вольтметр, равной нулю. 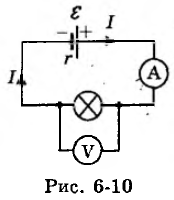
РЕШЕНИЕ.
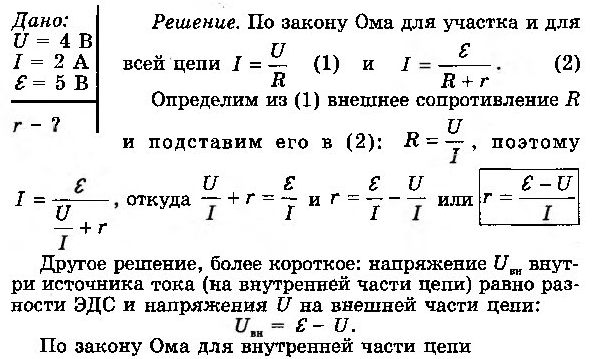
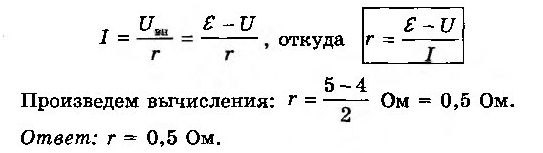
Задача № 2.
Дана схема (рис. 6-11, а). Во сколько раз изменится сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л2 вдвое больше сопротивления лампы Л1, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л1. 
Задача № 3.
В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Найти силу тока короткого замыкания Iк.з.
Смотреть решение и ответ

Задача № 4.
Вольтметр, подключенный к полюсам источника тока при разомкнутой внешней цепи, показал U1 = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U2 = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить еще один такой же (рис. 6-12, б) ? Что покажет этот вольтметр, если второй резистор присоединить к первому параллельно (рис. 6-12, в)? 
Задача № 5.
Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Построить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от внешнего сопротивления R.
Задача № 6.
Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I1 = 3 А . Какую силу тока I2 покажет этот амперметр, если его зашунтировать сопротивлением Rш = 0,1 Ом?
Задача № 7.
Дана схема (рис. 6-16). Емкости конденсаторов С1, С2 и ЭДС источника тока ε известны. Известно также, что ток короткого замыкания Iк.з. этого источника в три раза превосходит ток I, текущий в этой цепи. Найти напряженности Е1 и Е2 полей в конденсаторах, если расстояния между их обкладками равны d. 
Задача № 8.
Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Определить напряжения U1 и U2 на конденсаторах и заряды q1 и q2 этих конденсаторов. 
Смотреть решение и ответ

Задача № 9.
Имеется N одинаковых источников тока, которые соединяют сначала последовательно, затем параллельно, подключая каждый раз к одному и тому же внешнему сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при этом изменяется напряжение на внешней части цепи?
Задача № 10.
Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит посередине прибора (рис. 6-21, а). Найти показания вольтметров U1 и U2, подключенных к потенциометру, если их сопротивления R1 = 6 кОм и R2 = 4 кОм. Внутренним сопротивлением r источника тока пренебречь. 
Задача № 11.
Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Найти силу тока I2 в сопротивлении R2. 
Задача № 12.
Проволока из нихрома образует кольцо диаметром D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом такой же проволокой. Найти разность потенциалов φb – φа между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм2. 
Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Решение задач на закон Ома для участка и полной цепи
Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.
Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула закона Ома для участка цепи:
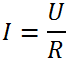
Формула закона Ома для полной цепи:
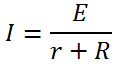 Задача 1
Задача 1
Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.
|
Дано U = 220 В I = 1,2 А |
Решение Согласно закону Ома для участка цепи:
|
|
Найти R – ? |
|
|
Ответ: R = 183,3 Ом. |
Задача 2
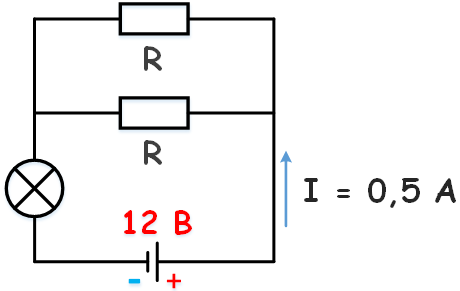
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
|
Дано E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом |
Решение Найдем экв. сопротивление двух параллельно соединённых резисторов:
Сопротивление лампочки:
Согласно закону Ома для полной цепи:
|
|
Найти r – ? |
|
|
Ответ: r = 14 Ом. |
Задача 3
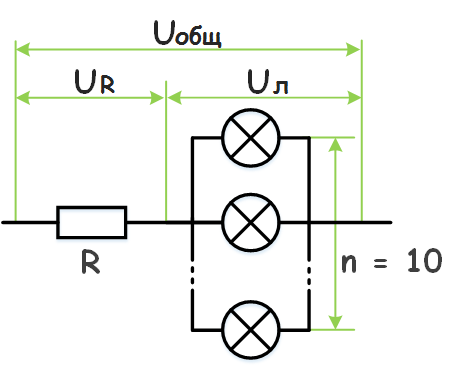
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.
|
Дано Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом |
Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи:
При последовательном соединении ток в цепи общий:
Выразим Uл через Uобщ:
Найдем Rэкв:
Окончательно получим:
|
|
Найти Uл – ? |
|
|
Ответ: Uл = 4 В. |
Задача 4
Как определить длину мотка медной проволоки, не разматывая его?
Решение:
Для решения данной задачи необходимо воспользоваться формулой:
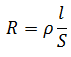
отсюда длина проволоки
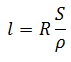
В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.
Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив диаметр проволоки и по формуле Πr2 вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.
Задача 5
Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?
Решение:
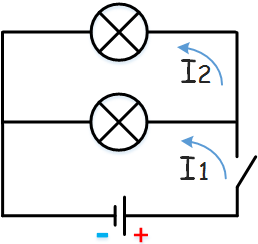
При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I1 и I2 проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.
Смешанное соединение проводников. Расчёт электрических цепей
Повторение. Факты про последовательное и параллельное соединение проводников.
1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:
![]()
2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:
![]()
3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:
![]()
4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
![]()
5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:
![]()
6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:
![]()
Задача 1
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. Рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.
Дано: ![]() ;
; ![]()
Найти: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Решение
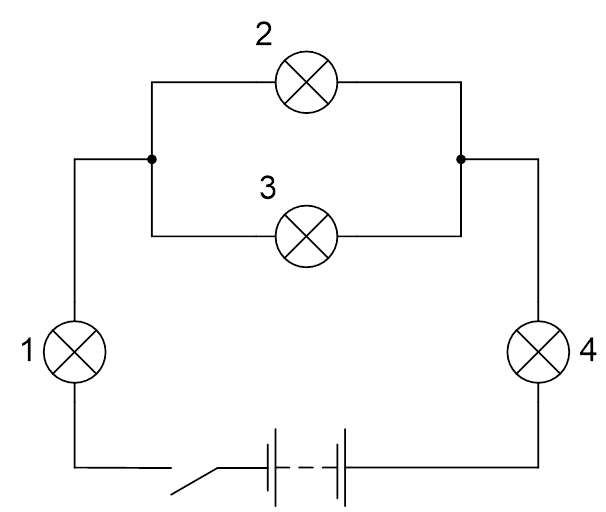
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.
Проводимость участка цепи, состоящего из ламп 2 и 3, равна:
![]()
Следовательно, сопротивление этого участка равно:
![]()
Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:
![]()
Согласно закону Ома, сила тока всей цепи равна:
![]()
Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:
![]()
Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
![]()
Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:
![]()
Отсюда сила тока в каждой лампе равна:
![]()
![]()
Ответ: ![]() ;
; ![]()
Задача 2
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. Рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.
Дано: ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Найти: ![]() ,
, ![]() ,
, ![]()
Решение
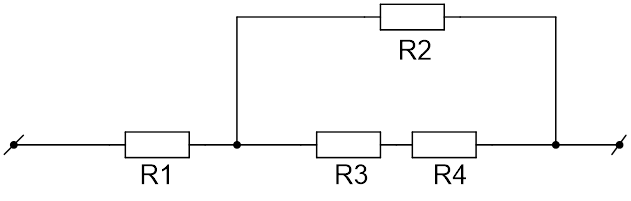
Рис. 2. Иллюстрация к задаче
Через резистор ![]() течёт такой же ток, как и через весь участок (
течёт такой же ток, как и через весь участок (![]() ), следовательно, согласно закону Ома:
), следовательно, согласно закону Ома:
![]()
То есть для нахождения ![]() нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором
нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором ![]() , другая часть с резисторами
, другая часть с резисторами ![]() :
:
![]()
Резистор ![]() соединён параллельно резисторам
соединён параллельно резисторам ![]() и
и ![]() , следовательно:
, следовательно:
![]()
Резисторы ![]() и
и ![]() соединены последовательно, поэтому:
соединены последовательно, поэтому:
![]()
![]()
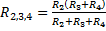
Следовательно, сопротивление всей цепи равно:
![]()
Подставим данное значение в формулу для нахождения тока в резисторе ![]() :
:
![]()
Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:
![]()
Отсюда:
![]()
![]()
![]()
При последовательном соединении силы тока одинаковы, поэтому:
![]()
Получили систему уравнений:
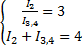
Решив эту систему получим, что:
![]()
![]()
Так как ![]() и
и ![]() соединены последовательно:
соединены последовательно:
![]()
Напряжение на резисторе ![]() равно:
равно:
![]()
Ответ: ![]() ;
; ![]() ;
; ![]()
Задача 3
Найдите полное сопротивление цепи (см. Рис. 3), если сопротивление резисторов ![]() ,
, ![]() ,
, ![]() . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
. Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
Дано: ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Найти: ![]() ,
, ![]() , ,
, , ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; 
Решение
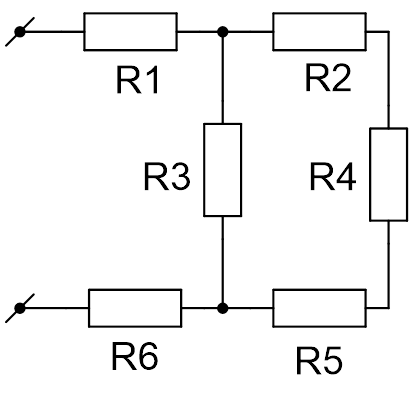
Рис. 3. Иллюстрация к задаче
Резисторы ![]() ,
, ![]() ,
, ![]() соединены последовательно, поэтому сопротивление на этом участке равно:
соединены последовательно, поэтому сопротивление на этом участке равно:
![]()
Резистор ![]() подключён параллельно участку с резисторами
подключён параллельно участку с резисторами ![]() ,
, ![]() ,
, ![]() , поэтому сопротивление на участке с резисторами
, поэтому сопротивление на участке с резисторами ![]() ,
,![]() ,
, ![]() ,
, ![]() равно:
равно:
![]()
Резисторы ![]() и
и ![]() соединены с участком цепи с резисторами
соединены с участком цепи с резисторами ![]() ,
,![]() ,
, ![]() ,
, ![]() последовательно, то есть общее сопротивление цепи равно:
последовательно, то есть общее сопротивление цепи равно:
![]()
Через резистор ![]() и
и ![]() (
(![]() ) неразветвлённой цепи течёт весь ток цепи, поэтому:
) неразветвлённой цепи течёт весь ток цепи, поэтому:
![]()
По закону Ома этот ток равен:
![]()
Общее напряжение цепи будет состоять из напряжений ![]() , так как
, так как ![]() ,
,![]() ,
, ![]() соединены последовательно (
соединены последовательно (![]() , потому что
, потому что ![]() и
и ![]() параллельны):
параллельны):
![]()
![]()
Согласно закону Ома:
![]()
Резисторы ![]() ,
, ![]() ,
, ![]() соединены последовательно, следовательно:
соединены последовательно, следовательно:
![]()
Ответ: ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Разветвление: Задача на бесконечную электрическую цепь
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.
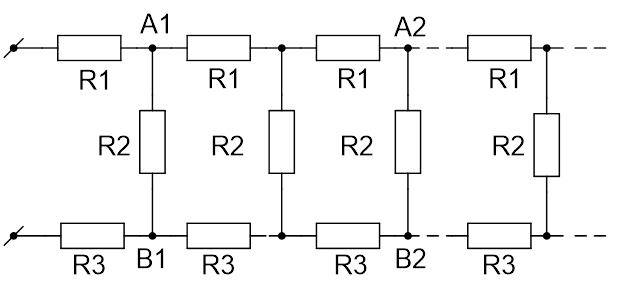
Рис. 4. Иллюстрация к задаче
Решение
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов ![]() и
и ![]() , не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена
, не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена ![]() , тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. Рис. 5) и записать для неё уравнение.
, тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. Рис. 5) и записать для неё уравнение.
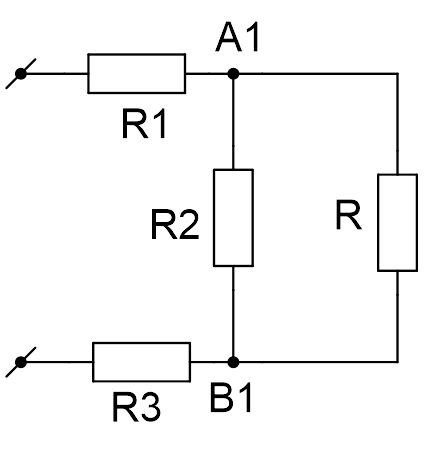
Рис. 5. Иллюстрация к задаче
![]()
![]()
Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:
![]()
Проанализировав данную формулу, можно заметить, что если ![]() , то общее сопротивление цепи
, то общее сопротивление цепи ![]() . То есть резистор с малым сопротивление
. То есть резистор с малым сопротивление ![]() практически закоротит всю последующую бесконечную цепь.
практически закоротит всю последующую бесконечную цепь.
Ответ: ![]()
Итоги
Мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.
Разветвление: Задача из ЕГЭ
Сопротивление каждого резистора в цепи (см. Рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами AиB. Напряжение на резисторе ![]() равно 12 В. Найти напряжение между выводами схемы на участке A–B(варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В.
равно 12 В. Найти напряжение между выводами схемы на участке A–B(варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В.
Дано: ![]() ;
; ![]()
Найти: 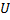
Решение
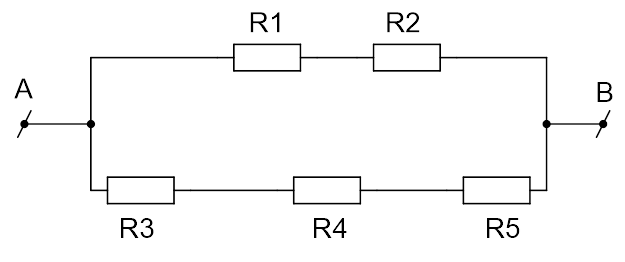
Рис. 6. Иллюстрация к задаче
Резисторы ![]() расположены последовательно, значит, силы тока на этих резисторах равны:
расположены последовательно, значит, силы тока на этих резисторах равны:
![]()
Так как, по условию, 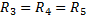 , то и напряжения на этих резисторах будут равны:
, то и напряжения на этих резисторах будут равны:
![]()
Следовательно, общее напряжения на участке, состоящем из резисторов ![]() , будет равно:
, будет равно:
![]()
Так как участок с резисторами ![]() соединён с участком с резисторами
соединён с участком с резисторами ![]() параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
![]()
Ответ: г) 36 В
Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений ![]() , даже если они не равны.
, даже если они не равны.
Вопросы к конспектам
Участок электрической цепи состоит из трех сопротивлений: ![]() ;
; ![]() ;
; ![]() (см. Рис. 7). Определите показания вольтметров
(см. Рис. 7). Определите показания вольтметров 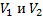 и амперметров
и амперметров ![]() , если амперметр
, если амперметр ![]() показывает силу тока 2 А.
показывает силу тока 2 А.
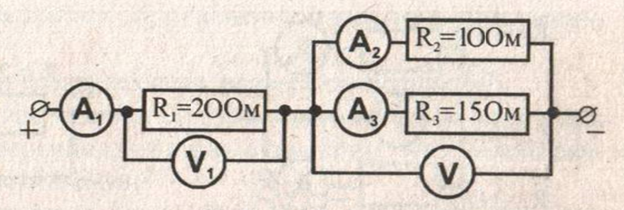
Рис. 7. Иллюстрация к задаче
Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?