Как найти общий заряд частицы

Общий заряд

общий электрический заряд, накопленный в потенциальной яме или дискретной области прибора с переносом заряда.

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
   карточек

Как найти заряд частицы по окружности

Заряженная частица движется в магнитном поле по окружности со скоростью v = 10 6 м/с. Индукция магнитного поля B = 0,3 Тл. Радиус окружности R = 4 см. Найти заряд q частицы, если известно, что ее энергия W = 12 кэВ

Дано:

W = 12 кэВ = 1,92·10 -15 Дж

Решение:

На частицу, движущуюся в магнитном поле действует сила Лоренца

которая является центростремительной

Ответ:

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

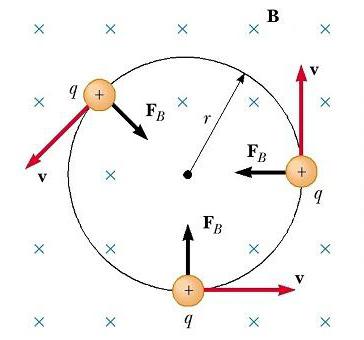
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

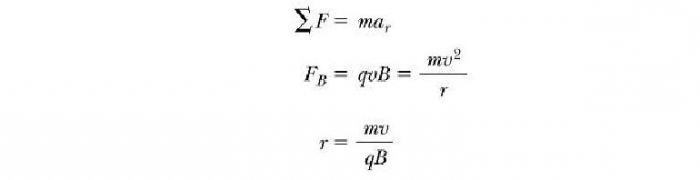
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

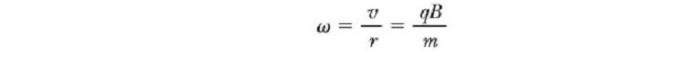
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

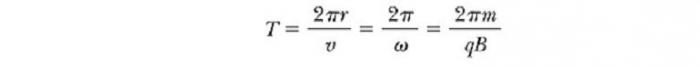
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

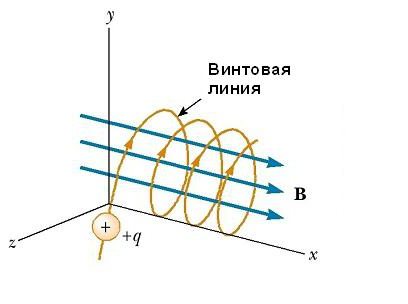
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

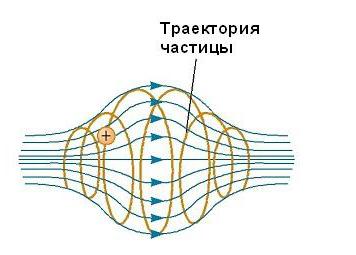
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

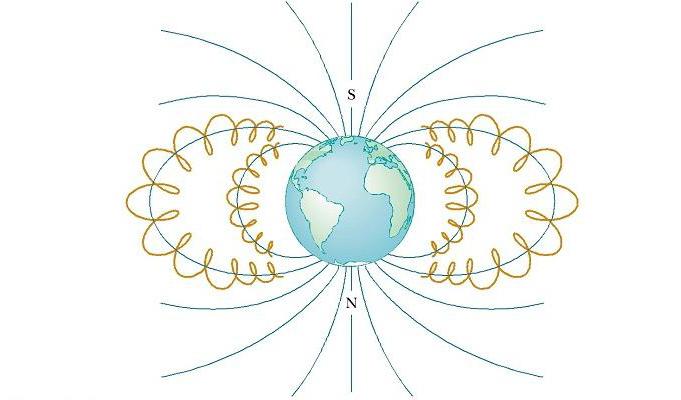
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

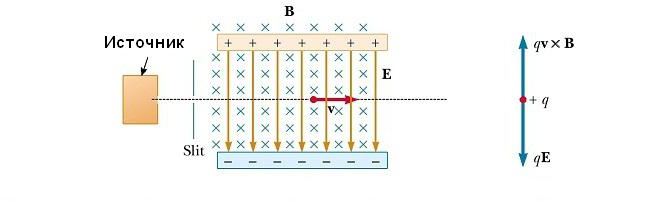
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

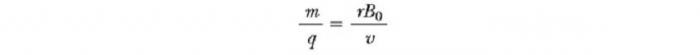
и затем, используя уравнение v=E/B, мы находим, что

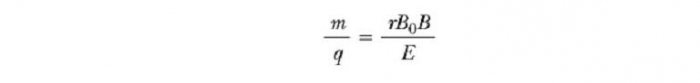
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

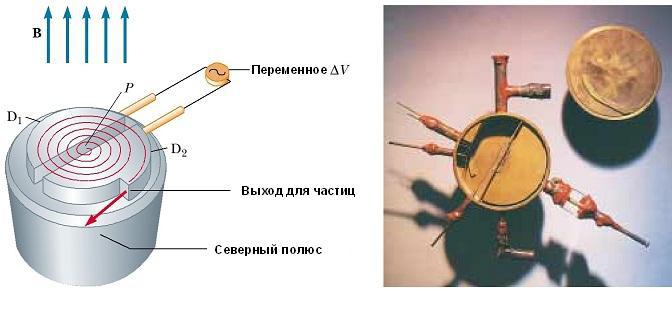
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

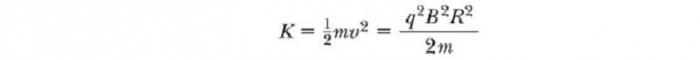
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Особенности формулы заряда q

Время на чтение:

Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.

Что такое электрический заряд q

Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.

Понятие из учебного пособия

Формула нахождения заряда

Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.

Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.

Как вычислять с помощью законов

Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.

Закон сохранения

Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.

Закон сохранения

Закон Кулона

Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.

Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.

Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.

Образец решения задач по теме «Электрический заряд»

Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.

Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?

Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.

Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. Задача состоит в определении первоначальных зарядов шаров.

Чтобы решить вторую задачу, нужно использовать ту же формулу Кулона, но немного видоизмененную: F=kq2/r2. Затем вывести из правила показатель q2. Он будет равен Fr2/k. Подставив известные значения и выполнив несложные расчеты, получится цифры в 10^-7 или 10 микрокулон.

Формула для решения

В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.

[spoiler title=”источники:”]

http://www.syl.ru/article/203046/new_dvijenie-zaryajennoy-chastitsyi-v-magnitnom-pole-formulyi-dvijenie-zaryajennyih-chastits-v-odnorodnom-magnitnom-pole

http://rusenergetics.ru/polezno-znat/formula-zaryada

[/spoiler]

Особенности формулы заряда q

Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.

Что такое электрический заряд q

Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.

Понятие из учебного пособия

Формула нахождения заряда

Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.

Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.

Как вычислять с помощью законов

Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.

Закон сохранения

Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.

Закон Кулона

Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.

Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.

Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.

Образец решения задач по теме «Электрический заряд»

Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.

Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?

Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.

Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. Задача состоит в определении первоначальных зарядов шаров.

Чтобы решить вторую задачу, нужно использовать ту же формулу Кулона, но немного видоизмененную: F=kq2/r2. Затем вывести из правила показатель q2. Он будет равен Fr2/k. Подставив известные значения и выполнив несложные расчеты, получится цифры в 10^-7 или 10 микрокулон.

В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.

Источник

Вычисления напряжения в сети электричества

В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.

Что такое напряжение в сети электричества.

Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.

Показатель напряжения на вольтметре

За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.

Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

Изображение вольтметра и электрической цепи

Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.

Формула закона Ома

Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.

Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.

Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.

Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.

Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.

Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.

Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].

Как найти сопротивление нагрузки

Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.

Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.

Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.

Последовательное/параллельное соединения

Как найти с помощью формулы напряжение

Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.

Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.

По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.

Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.

Как найти силу тока через сопротивление и напряжение

Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.

Мужчина считает силу тока

Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.

При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.

Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.

Источник

Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца

Теория к заданию 14 из ЕГЭ по физике

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).

Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:

Часто его записывают в виде $k=<1>/<4πε_0>$, где $ε_0=8.85×10^<-12>Кл^2$/$H·м^2$ — электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:

где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_<0>$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.

Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.

Энергия поля конденсатора

Энергия заряженного конденсатора выражается формулами

которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.

Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

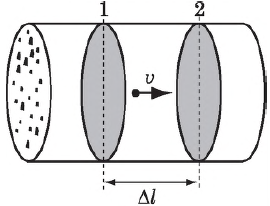
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_<0>nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t=<∆l>/<υ>$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:

В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).

Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.

Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

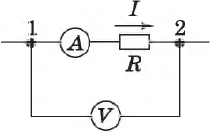
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:

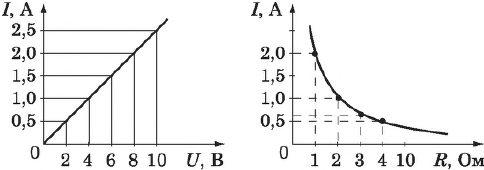
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I=/$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I=/$ следует:

1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.

Удельное сопротивление

Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:

где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы $R=ρ/$ следует, что

Величина, обратная $ρ$, называется удельной проводимостью $σ$:

Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^<-1>м^<-1>$.

На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^<-6>$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^<-2>$) Ом$·$м$м^2$/м, диэлектрики — в $10^<15>-10^<20>$ раз большим.

Зависимость сопротивления от температуры

С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.

Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:

Зависимость удельного сопротивления проводников от температуры выражается формулой:

В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=(<1>/<273>)K^<-1>$. Для растворов электролитов $α

Источник

Заряд иона определяется следующим образом:
Атом любого вещества состоит из электронной оболочки и ядра. Ядро состоит из двух типов частиц – нейтронов и протонов. Нейтроны не имеют электрического заряда, то есть электрический заряд нейтронов равен нулю. Протоны являются положительно заряженными частицами и имеют электрический заряд, равный +1. Количество протонов характеризует атомный номер данного атома.

2
Электронная оболочка атома состоит из электронных орбиталей, на которых расположено разное количество электронов. Электрон – отрицательно заряженная элементарная частица. Ее электрический заряд равен -1.
При помощи связей атомы могут также соединяться в молекулы.

3
В нейтральном атоме количество протонов равно количеству электронов. Поэтому его заряд равен нулю.
Чтобы определить заряд иона, необходимо знать его структуру, а именно количество протонов в ядре и количество электронов на электронных орбиталях.

4
Суммарный заряд иона получается в результате алгебраического суммирования зарядов входящих в него протонов и электронов. Число электронов в ионе может превышать число протонов, и тогда ион будет отрицательным. Если число электронов меньше числа протонов, то ион будет положительным.

5
Зная химический элемент, по таблице Менделеева мы можем определить его атомный номер, который равен количеству протонов в ядре атома этого элемента (например 11 у натрия) . Если один из электронов покинул атом натрия, то у атома натрия будет уже не 11, а 10 электронов. Атом натрия станет положительно заряженным ионом с зарядом зарядовое число равно = 11+(-10) = +1.
Обозначаться такой ион будет символом натрий с плюсом сверху, в случае заряда +2 – двумя плюсами и. т. д. Соответственно для отрицательного иона используется знак «минус» .

Нам известно, что телу можно сообщить заряд. Если не прикасаться после этого к телу, то полученный заряд будет оставаться на этом теле, то есть, перемещаться не будет.

Но если заставить заряд двигаться, можно наблюдать интересные явления. Потому, что именно движущиеся заряды создают:

1. выполнение работы электрическими двигателями;
2. выделение тепла в электрических нагревательных приборах;
3. свечение ламп накаливания.

Скорость теплового движения свободных электронов

Нам известно, что общий заряд тела состоит из большого количества элементарных зарядов.

К примеру, в твердых телах положительные заряды – это ядра атомов, или ионы. А отрицательные – это электроны.

А в жидкостях или газах – положительные и отрицательные заряды – это ионы.

Примечание: Ион – атом, у которого присутствует избыток электронов, либо наоборот, электронов меньше, чем в нейтральном атоме.

Рассмотрим твердый проводник, в нем присутствуют свободные заряды. Это такие электроны, которые оторвались от своего атома и свободно путешествуют по всему объему проводника.

Примечание: Проводник – это тело, в котором много свободных электронов.

Как известно из молекулярно-кинетической теории (МКТ), мельчайшие частицы вещества находятся в непрерывном движении. Это движение возникает под действием температуры, поэтому, его часто называют тепловым. Такое движение беспорядочное, то есть — хаотическое.

Рассчитаем, с какой скоростью электроны в проводнике беспорядочно перемещаются под действием температуры.

Для этого воспользуемся формулой среднеквадратичной скорости частиц из молекулярной физики:

[large v = sqrt{frac{3kT}{m}}]

Подставим в формулу такие числовые значения:

(large T = 300 left( Kright)) – комнатная температура +27 градусов Цельсия;

(large k = 1,38 cdot 10^{-23} left( frac{text{Дж}}{K}right) ) – постоянная Больцмана;

(large m = 9,1 cdot 10^{-31} left(text{кг}right) ) – масса электрона;

После расчетов получим скорость, примерно равную

[large v approx 117 left(frac{text{км}}{text{сек}}right) ]

Как видите, это очень большая скорость, более 100 километров в секунду.

Примечание: Физики свободные электроны в проводнике рассматривают, как частицы идеального газа. Его так и называют – электронный газ.

Однако, еще раз подчеркну, что тепловое движение – хаотическое. С помощью такого движения электрический ток не создать. Потому, что ток – это направленное движение зарядов.

Что такое электрический ток

Электрический ток – это направленное движение электрических зарядов.

В металлических проводниках движутся отрицательные заряды — электроны.

А в других проводниках, например, в жидких электролитах, направленно могут двигаться положительные и отрицательные ионы.

Внутри полупроводников заряд переносят электроны и дырки.

Примечание: Дырка – это псевдочастица, вакантное место для электрона. Она имеет положительный заряд, ее можно рассматривать, как пузырек, находящийся в электронном газе.

Мы видим, что электрический ток может создаваться движением, как положительных частиц, так и отрицательных.

При этом, положительные частицы будут притягиваться к отрицательному полюсу источника тока и двигаться по цепи к нему.

А отрицательные частицы будут притягиваться и двигаться к положительному полюсу источника тока.

Примечание: Чтобы определить направление движения заряженных частиц, можно воспользоваться аналогией с течением воды: Заряды, как вода, движутся оттуда, где их много, туда, где их мало. На заре изучения электричества считали, что во время протекания тока в телах протекает некая электрическая жидкость. Поэтому для электрического тока применяется аналогия с течением воды. Позже выяснилось, что никакой электрической жидкости в телах нет.

Если заряды движутся направленно, значит, и ток будет иметь направление.

Куда направлен ток

Как выбрать направление электрического тока? На движение каких частиц – положительных, или отрицательных, ориентироваться? Оказывается, направление тока — это условный выбор.

Физики договорились, что направление электрического тока совпадает с направлением движения положительных зарядов. Значит, ток направлен от «+» к «-» выводу источника тока.

Пусть, известно направление вектора напряженности (large vec{E} ) электрического поля. Чтобы определить направление тока, нужно считать, что в этом поле движутся положительно заряженные частицы.

Положительные заряды будут двигаться по направлению вектора (large vec{E} ), а отрицательные – навстречу вектору.

Примечание: В металлах электроны движутся от минуса к плюсу, а ток направлен от плюса к минусу

Примечание: Наличие направленного движения зарядов можно определить косвенно. Протекая по проводнику, ток воздействует на этот проводник. Известны тепловое, химическое, или магнитное действие тока.

Чем больше ток, то есть, чем он сильнее, тем более заметно его действие.

Что такое поперечное сечение проводника

Электрический ток – это направленно движущиеся по проводнику свободные заряды. Его можно определить, когда известно количество заряженных частиц, прошедших через проводник.

Проводник может быть достаточно длинным. Поэтому неудобно учитывать заряды, находящиеся во всей длине проводника.

Чтобы было проще посчитать количество зарядов, на проводнике выбирают точку в любом удобном месте.

Через эту точку мысленно проводят плоскость, располагая ее перпендикулярно по отношению к проводнику. Так как эта плоскость в проводнике ограничивает собой площадь S, ее часто называют площадью поперечного сечения проводника.

Для вычисления силы тока, ведут подсчет зарядов, прошедших через это сечение.

Как рассчитать площадь сечения

Проводник будем считать круглой трубкой, по аналогии с трубой, по которой течет жидкость. Пользуясь этой аналогией, так же, примем, что внутри такой трубки будут двигаться заряды, они обозначены кружками на рисунке.

Выделим на трубе какую-либо точку. Мысленно отрежем кусок трубы, проводя разрез перпендикулярно. Стенки трубки в месте отреза являются границей круга.

Площадь полученного круга можно вычислить по такой геометрической формуле:

[large boxed{ S_{0} = pi cdot frac{D^{2}}{4} = pi cdot R^{2} }]

(large S_{0} left( text{м}^{2} right)) – площадь круга;

(large pi approx 3,14) – число Пи;

(large D left(text{м}right)) – диаметр круга;

(large R left(text{м}right)) – радиус круга;

Проводник может иметь не только цилиндрическую форму. Промышленность изготавливает металлические проводники, имеющие квадратное, прямоугольное, треугольное или какое-либо другое сечение. Понятно, что площади таких сечений нужно рассчитывать, пользуясь другими геометрическими формулами.

Сила тока по определению

Силу тока (ток) обозначают большой латинской буквой (large I).

Постоянный ток можно рассматривать, как равномерное направленное движение заряженных частиц. Равномерное – значит, с одной и той же скоростью.

Если же ток изменяется, то будет изменяться и скорость движения зарядов.

Сила тока – это:

1. физическая величина;
2. отношение заряда, прошедшего через поперечное сечение проводника к длительности промежутка времени, в течение которого заряд проходил.

Ток равен заряду, прошедшему через поперечное сечение проводника за одну секунду.

Для постоянного тока используем формулу:

[large boxed{ I = frac{Delta q}{Delta t} }]

(large I left(Aright)) – ток (сила тока) в Амперах;

(large Delta q left( text{Кл}right) ) – заряд в Кулонах, прошедший через поперечное сечение проводника;

(large Delta t left( cright) ) – промежуток (кусочек) времени, в течение которого заряд прошел;

[large boxed{ 1 A = frac{1 text{Кл}}{1 c} }]

Если электрический ток не изменяется ни по величине, ни по направлению, то его называют постоянным.

Если хотя бы одна из характеристик изменяется, ток называют переменным. Он будет различным в разные моменты времени. Если задано уравнение, описывающее, как изменяется заряд, то для вычисления такого тока удобно пользоваться производной.

Исключаем путаницу с понятием силы

В физике исторически сложилось использование таких терминов, как

• сила тока,
• электродвижущая сила,
• лошадиная сила.

Эти единицы измерения имеют в своем названии слово «сила». Из механики известно, что сила – величина векторная, измеряется в Ньютонах. Однако, пусть это не вводит вас в заблуждение.

Ни одна из описанных величин не измеряется в Ньютонах. Перечисленные величины имеют другие единицы измерения:

• силу тока измеряют в Амперах,
• электродвижущую силу – в Вольтах,
• а лошадиная сила – это единица измерения мощности, ее можно перевести в Ватты в системе СИ.

Чтобы исключить путаницу, вместо термина «сила тока», можно употреблять слово «ток». Сравните выражения: «Силу тока измеряют в Амперах» и «ток измеряют в Амперах».

Как видно, вполне можно обойтись словом «ток», вместо «силы тока». Смысл от этого не изменится.

Что такое 1 Ампер в системе СИ

Сила тока в 1 Ампер была определена в системе СИ с помощью силы взаимного действия двух проводников с током.

Рассмотрим два тонких проводника (рис. 9). Каждый проводник имеет бесконечную длину. Расположим их в вакууме параллельно на расстоянии 1 метр один от другого.

Выделим на каждом проводнике кусочек длиной 1 метр.

Если проводники взаимодействуют с силой (large 2 cdot 10^{-7} ) Ньютона, приходящейся на каждый метр их длины, то по каждому из них течет постоянный ток 1 Ампер.

Ампер – это основная единица в системе СИ. А заряд Кулон – величина, определяемая с помощью Ампера.

1 Кулон – это заряд, проходящий за 1 секунду через поперечное сечение проводника с током 1 Ампер.

Один Ампер – много это, или мало

1 Ампер это 1 Кулон деленный на 1 секунду. Для большинства бытовых электроприборов это достаточно большая сила тока.

Например, через энергосберегающие лампы протекают токи 0,04 — 0,08 Ампера.

Большой плоский телевизор от электроосветительной сети потребляет ток 0,2 Ампера.

Лампа накаливания –примерно 0,5 Ампера.

Как видно, большинство электроприборов потребляют токи менее одного Ампера.

Поэтому, для тока часто применяют дольные единицы измерения:

миллиамперы, микроамперы, и наноамперы:

1мА (миллиампер)= 10⁻³ А

1мкА (микроампер) = 10⁻⁶ А

1нА (наноампер) = 10⁻⁹ А

Ток зарядки аккумулятора мобильного телефона может достигать 2 Ампер.

А через электрический обогреватель, или электрочайник, протекает ток силой до 10 Ампер.

Примечание: Ток силой всего 0,05 А может привести к летальному исходу. Будьте осторожны с электричеством!

В то же время, используют и токи, превышающие сотни Ампер. Например, на промышленных электростанциях.

Для таких токов применяют кратные единицы: килоампер, мегаампер.

1КА (килоампер)= 10³ А

1МА (мегаампер) = 10⁶ А

Связь между силой тока и скоростью движения зарядов

Рассмотрим металлический проводник. Мысленно выделим в нем два сечения площадью (large S ) на некотором расстоянии (large Delta x) одно от другого. Сечения располагаются поперечно проводнику.

В металлах электрический ток создается электронами. Обозначим (large e_{0}) заряд каждого электрона.

Заряды в проводнике, под действием электрического поля напряженностью (large vec{E} ) будут двигаться сонаправленно, от сечения к сечению.

При этом, они будут проходить путь (large Delta x) между двумя сечениями.

Если ток постоянный, то скорость движения зарядов изменяться не будет.

В таком случае, расстояние (large Delta x) и скорость (large v) движения электронов будут связаны формулой равномерного движения.

[large Delta x = v cdot Delta t]

(large Delta x left( text{м}right) ) – расстояние между двумя поперечными сечениями;

(large v left( frac{text{м}}{c}right) ) – скорость, с которой сонаправленно движутся заряды в проводнике; Эта скорость значительно меньше скорости теплового движения.

(large Delta t left( c right) ) – интервал времени, за который пройдено расстояние (large Delta x) между двумя поперечными сечениями;

Выразим из этой формулы время движения:

[large Delta t = frac {Delta x}{v} ]

Это выражение нам понадобится далее.

Сечения (large S )  и расстояние между ними (large Delta x) образуют в проводнике цилиндрический объем:

[large V = S cdot Delta x]

(large V left( text{м}^{3}right) ) – объем цилиндра;

В этом объеме содержится определенное количество электронов. Обозначим это количество: (large N ) штук.

Количество штук (large N ), расположенное в объеме (large V), называют концентрацией:

[large n = frac{N}{V} ]

(large n left( frac{text{штук}}{text{м}^{3}}right) ) – концентрация зарядов в объеме;

Найдем общий заряд всех заряженных частиц, расположенных в объеме (large V) между двумя поперечными сечениями:

[large Delta q = e_{0} cdot N]

Умножим правую часть уравнения на единицу, которую представим в виде дроби (displaystyle frac{V}{V}), в которой (large V) – это рассматриваемый объем. Тогда полный заряд можно записать в таком виде:

[large Delta q = e_{0} cdot N cdot 1 = e_{0} cdot N cdot frac{V}{V}]

Числитель V дроби и количество N частиц поменяем местами.

[large Delta q = e_{0} cdot V cdot frac{N}{V}]

Подставим в эту формулу выражение для объема:

[large Delta q = e_{0} cdot S cdot Delta x cdot frac{N}{V}]

Дробь в правой части заменим символом «n» концентрации:

[large Delta q = e_{0} cdot S cdot Delta x cdot n]

Средняя скорость совместного направленного движения зарядов (large v).

Применим определение силы тока:

[large I = frac {Delta q}{Delta t} ]

Подставим в это выражение формулу для общего заряда, прошедшего через сечение проводника:

[large I = frac {Delta q}{Delta t} =  frac {e_{0} cdot S cdot Delta x cdot n}{Delta t} ]

Выражение для удобства можно переписать так:

[large I = e_{0} cdot S cdot Delta x cdot ncdot frac {1}{Delta t} ]

Мы заранее выразили время (large Delta t ):

[large Delta t = frac {Delta x}{v} ]

Найдем для него обратную величину:

[large frac {1}{Delta t} = frac {v}{Delta x} ]

Подставим ее в формулу для тока:

[large I = e_{0} cdot S cdot Delta x cdot n cdot frac {v}{Delta x}]

Расстояние (Delta x) находится в числителе и в знаменателе, оно сократится. Окончательно получим выражение для связи между силой тока и скоростью движения зарядов:

[large boxed{I = e_{0} cdot S cdot n cdot {v}}]

Теперь можно утверждать, что

• чем больше зарядов помещаются в объеме,
• чем быстрее они сонаправленно двигаются
• и, чем толще проводник (чем больше площадь поперечного сечения),

тем больше ток.

Расчет скорости направленного движения электронов

Для этого можно использовать полученную формулу:

[large I = e_{0} cdot S cdot n cdot {v}]

Из нее можно выразить скорость:

[large boxed{frac{I}{e_{0} cdot S cdot n} = v}]

Чтобы найти скорость, с которой электроны движутся в проводнике, нужно: ток (I) разделить на заряд (е) электрона, концентрацию (n) электронов и площади сечения проводника (S).

Большинство соединительных проводников изготавливают из меди, или алюминия. Выберем медный проводник, имеющий цилиндрическую форму.

Площадь поперечного сечения выберем равной 1 миллиметру в квадрате:

[large S = 10^{-6} left( text{м}^{2}right) ]

Число атомов в объеме – концентрация, связано с плотностью вещества (ссылка). Для меди концентрацию атомов вычислить несложно. Она

[large n = 8,5 cdot 10^{28} left( frac{text{штук}}{text{м}^{3}}right) ]

равна концентрации электронов.

Примечание: Каждый атом меди отдает один из своих валентных электронов и, он превращается в свободный электрон. Поэтому, количество свободных электронов, находящихся в выбранном объеме меди будет равно количеству атомов в этом объеме.

Заряд электрона известен:

[large e_{0} = 1,6 cdot 10^{-19} left(text{Кл}right) ]

Предположим, в проводнике протекает ток силой 1 Ампер.

Тогда, скорость движения электронов:

[large v = frac{1}{1,6 cdot 10^{-19} cdot 10^{-6} cdot 8,5 cdot 10^{28}} ]

[large v = 7 cdot 10^{-5} left( frac{text{м}}{c}right) ]

Это меньше, чем 0,1 мм в секунду.

Скорость распространения электрического поля и скорость движения зарядов — в чем различия

Нужно различать скорость, с которой распространяется электрическое поле, при подключении к проводнику источника тока и скорость движения заряженных частиц в проводнике.

Скорость, с которой распространяется электрическое поле напряженностью (large vec{E}) – равна скорости света:

[large c = 3 cdot 10^{8} left( frac{text{м}}{c} right)]

А скорость направленного движения зарядов значительно меньше — менее 0,1 мм в секунду.

Примечание: В качестве скорости направленного движения свободных зарядов, выбирают среднее значение скорости, с которой перемещаются заряды во время протекания тока. Ее, так же, называют скоростью дрейфа.

В то же время, при комнатной температуре скорость беспорядочного теплового движения электронов немногим более 100 километров в секунду.

То есть, заряды быстро движутся хаотично, но при этом, они согласованно и достаточно медленно передвигаются в определенном направлении.

Такое движение можно сравнить с движением потока муравьев на лесной тропе. Каждый муравей в потоке движется хаотично. Но при этом, весь поток движется согласованно в выбранную сторону.

Пользуясь аналогией из окружающей природы, движение заряженных частиц во время протекания электрического тока можно сравнить с движением муравьев.

Каждая частица движется хаотически под действием температуры и одновременно с этим, все частицы смещаются в одном направлении в общем потоке под действием электрического поля.

Условия существования постоянного тока

Напомню, что ток называют постоянным, если его сила не изменяется со временем.

Для обозначения постоянного тока математики используют такую сокращенную запись:

[large boxed{ I = const }]

Чтобы ток мог существовать, нужно, чтобы выполнялись несколько условий.

Нужно, чтобы между телами, заряженными противоположно, непрерывно существовало электрическое поле. Так же, в цепи должны присутствовать свободные носители заряда. А сама электрическая цепь должна быть замкнутой.

Рассмотрим эти условия подробнее.

Создаем кратковременный ток и выясняем условия его существования

Можно создать электрический ток с помощью двух заряженных противоположно тел.

Ток – это движение зарядов. Поэтому, нужно обеспечить возможность зарядам двигаться. То есть, нужно создать между телами дорожку, по которой заряды начнут перемещаться из одного места пространства в другое.

Продемонстрировать возникновение тока на небольшой промежуток времени можно с помощью двух электрометров, заряженных противоположно.

Попробуем для начала соединить два заряженных тела куском диэлектрика (рис. 15).

Как видно, после соединения заряд каждого из электрометров не изменился.

Это значит, что ток не возник. Дело в том, что в диэлектрике все электроны связаны со своими атомами и свободных электронов нет.

Именно свободные заряды будут передвигаться и их согласованное направленное движение мы назовем электрическим током.

Поэтому, одним из условий существования тока будет наличие свободных зарядов. То есть, наличие проводника, содержащего такие заряды.

Условие 1. Чтобы ток существовал, требуется наличие свободных зарядов.

Однако, только лишь наличия проводника недостаточно. Действительно, в проводнике присутствуют свободные заряды. Но для того, чтобы эти заряды начали совместное движение в определенную сторону, нужно, чтобы на них подействовала сила, которая будет их передвигать в этом направлении.

Сила будет действовать на заряженную частицу, если ее поместить в электрическом поле.

Электрическое поле существует в пространстве вокруг заряженных тел.

Если соединить проводником два тела, имеющие противоположные заряды, то на свободные частицы в проводнике будет действовать электрическое поле. Это поле подхватит заставит двигаться электроны в определенном направлении.

Поэтому, еще одно условие для возникновения тока – это электрическое поле.

Условие 2. Чтобы ток существовал, требуется наличие электрического поля.

Ток течет в направлении движения положительных зарядов.

Соединив два заряженных металлических тела проводником, мы получим ток лишь на короткий промежуток времени. Это время будет составлять доли секунды.

Кроме того, в начальный момент времени сила тока будет самой большой. А далее будет убывать по мере того, как тела будут разряжаться и их потенциалы (ссылка) будут выравниваться.

Мы же хотим, чтобы ток протекал постоянно, или, по крайней мере, достаточно длительный промежуток времени, выбранный по нашему усмотрению. И чтобы во время протекания тока его сила не изменялась.

Как этого добиться? Мы вплотную приблизились к третьему условию существования постоянного электрического тока.

Как создать длительный ток и что для этого необходимо

Положительный заряд – это недостаток электронов, а отрицательный – это их избыток. В момент соединения тел проводником, отрицательные электроны устремились к положительно заряженному телу.

А в конце ток прекратился потому, что заряды тел скомпенсировались и тела превратились в электрически нейтральные. Нам известно, что нейтральные тела электрическое поле не создают.

Значит, ток существует до тех пор, пока существует электрическое поле. Поэтому, нужно каким-либо образом поддерживать электрическое поле. А для этого нужно, чтобы одно из тел обладало избыточным отрицательным зарядом. То есть, нужно поддерживать на одном из тел отрицательный, а на другом – положительный заряд. Пока заряды тел будут поддерживаться, ток будет существовать.

Чтобы на теле с положительным зарядом поддерживать этот заряд, нужно убирать с этого тела прибежавшие туда электроны и отправлять их обратно на отрицательно заряженное тело.

Такая схема по своему устройству напоминает фонтан, в котором насос поддерживает разность давлений. В нагнетающей воду трубе давление больше, чем в трубе, через которую вода поступает обратно в насос.

Именно благодаря этой разности, из одной трубы вода выплескивается вверх, а собранная в чашу вода попадает обратно в насос. При этом, по контуру циркулирует одно и то же количество воды, то есть, водяной контур замкнут. А ток воды в этом контуре поддерживается специальным устройством – насосом. Он совершает работу против силы тяжести.

Сторонние силы — что это такое

Подобно своеобразному насосу устроен источник тока. Внутри источника действуют сторонние силы. Они возвращают электроны на «-» контакт.

На заряды в электрическом поле будет действовать сила. Она называется силой Кулона и имеет электрическую природу. Электроны будут притягиваться к телу, имеющему положительный заряд.

Сила Кулона будет мешать возвращать электроны на отрицательное тело. Подобно силе тяжести, которая мешает воде в фонтане двигаться вверх.

Чтобы вернуть электроны на отрицательно («-») заряженное тело, нужно совершить работу против силы Кулона. Значит, должна присутствовать какая-то внешняя сила, возвращающая электроны на отрицательно («-») заряженное тело. Эта сила имеет неэлектрическую природу, она называется сторонней силой.

Теперь можно ответить на вопрос: Что такое источник тока?

Источник тока — это устройство, внутри которого сторонние силы перемещают заряды против сил Кулона. Сила Кулона – это сила, с которой электростатическое поле действует на заряд.

Во время существования электрического тока сами электроны не расходуются. Они, как вода в фонтане, циркулируют по замкнутой траектории.

Условие 3. Чтобы ток существовал длительно, электрическое поле нужно долговременно поддерживать.

Чтобы ток существовал постоянно, нужно, чтобы между заряженными противоположно телами электрическое поле существовало непрерывно.

Примечание: В качестве заряженных противоположно тел можно рассматривать контакты источника тока.

Для этого электроны нужно пропустить по замкнутому контуру, т. е. непрерывной электрической цепи. Поэтому, еще одно условие существования постоянного тока – это замкнутая электрическая цепь. Как только замыкается цепь, в направленное движение приходят все заряженные частицы, находящиеся в этой цепи.

Условие 4. Чтобы ток существовал, требуется, чтобы электрическая цепь была замкнутой.

В такой цепи заряды циркулируют по замкнутой траектории. То есть, заряд, вышедший из источника и совершивший полный оборот, попадет обратно в источник тока. Там он будет подхвачен сторонними силами и через противоположный вывод источника тока попадает обратно в цепь. Затем, будет двигаться далее и, совершит следующий круг. Поэтому, во время протекания электрического тока сами заряды не расходуются.

Во время протекания электрического тока заряды не расходуются. То есть, по замкнутой цепи двигаются одни и те же заряды. Совершив круг, они попадают в источник и, выходя из противоположного его вывода направляются обратно в цепь.

Нам известно, если на заряд действует сила и, под действием этой силы заряд перемещается, то эта сила совершает работу.

Это значит, что сторонние силы в источнике совершают работу. Подробнее о работе сторонних сил (ссылка).